Thermodynamics of binary liquid mixtures of cyclopentane with 2-propanol, 1-butanol and 2-butanol at different temperatures

Abstract

Densities and speeds of sound of the cyclopentane with 2-propanol, 1-butanol and 2-butanol are measured over the whole composition range at different temperatures in the range 288.15–308.15 K and atmospheric pressure using Anton Paar DSA 5000 densimeter. The experimental densities and speeds of sound have been used to calculate excess molar volumes, excess molar isentropic compressibilities and excess intermolecular free length. The partial molar volumes and apparent molar volumes at infinite dilution have also been calculated. The mixing quantities like (∂V ^E_m /∂T)_P and (∂H ^E_m /∂P)_T have been calculated at T = 298.15 K and these values are compared with the values calculated from Flory’s theory at equimolar composition.

Introduction

Non-ideal behaviour of binary liquid mixtures of cyclopentane with alkanols is of particular interest due to their simple structure and the self-association of alkanol through hydrogen bonding of the hydroxyl group, the extent and strength of which changes in the mixture. Excess thermodynamic properties are crucial for the chemical process design [1] as well as for progress in the thermodynamic theories and modelling of the liquid state. Excess compressibilities and excess molar volumes give important information about intermolecular forces determining the properties of the mixtures. Studies on the cyclopentane + n-alkanols mixtures due to their simple structure components are of particular interest. Moreover, n-alkanol molecules are self-associating; it is of interest to see how they behave in the presence of cyclopentane molecules, i.e. the extent to which hydrogen boding and self-association of n-alkanol molecules changes in mixture.

In continuation to our work on thermodynamic studies of binary liquid mixtures [2–4], in the present study, we report the experimental densities, ρ, and speeds of sound, u over the whole composition range at temperatures of 288.15, 298.15, and 308.15 K. From these experimental densities and speeds of sound, excess molar volume V ^E_m , isentropic compressibility, κ_S, excess molar isentropic compressibility, K ^E_S,m , and excess intermolecular free length, L ^E_f have been calculated for each of the binary liquid mixtures at all the temperatures. The results of V ^E_m , K ^E_S,m , and L ^E_f have been correlated with Redlich–Kister polynomial. Also, the partial molar volumes, $\bar{V}_{{{\text{m}},i}} ,$ apparent molar volumes, $\bar{V}_{\phi ,i}$ and their limiting values $\bar{V}_{{{\text{m}},i}}^{0} ,$ $\bar{V}_{\phi ,i}^{0} ,$ at infinite dilution have been calculated. An attempt has also been made to interpret the results by deriving the different mixing properties like (∂V ^E_m /∂T)_P, (∂H ^E_m /∂P)_T, and α ^E at T = 298.15 K. By using the Flory’s theory, the above thermodynamic mixing functions have been calculated and compared with experimental results.

Experimental

Materials

Cyclopentane, 2-propanol and 1-butanol were obtained from S.D. Fine Chemicals, India. 2-Butanol was obtained from Merck specialities Pvt Ltd, India. All the solvents, prior to experimental measurements were stored in dark bottles over 0.4 nm molecular sieves to reduce water content and were partially degassed with vacuum under nitrogen pressure. The estimated purities as per gas chromatographic analysis were better than 99.5 mol% for all liquid samples. Further, the purities of liquids were checked by comparing densities and speeds of sound of pure solvents at all studied temperatures, with their corresponding literature values [5–23]. The experimental and literature values are reported in Table 1.

Table 1 Experimental densities value ρ × 10³/kg m⁻³, speeds of sound values, u/m s⁻¹, and their literature values along with isobaric thermal expansivities α_p/kK⁻¹, molar isobaric heat capacities C _{p, m}/J K⁻¹ mol⁻¹, and the product K _{S, m}/mm³ mol⁻¹ MPa⁻¹ of the molar volume and isentropic compressibility of pure liquid components at several temperatures

Apparatus and procedure

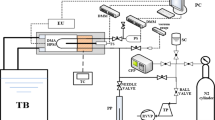
The densities and speeds of sound of the pure liquids and their mixtures were measured using an Anton Paar DSA 5000 densimeter. As the densities and speeds of sound are extremely sensitive to temperature, so it was controlled to ±0.01 K by built-in solid state thermostat. Before each series of measurements, the apparatus was calibrated with double distilled and degassed water, n-hexane, n-heptane, n-octane, cyclohexane and benzene. The sensitivity of the instrument corresponds to a precision in density and speeds of sound of 1 × 10⁻⁶ g cm⁻³ and 1 × 10⁻² m s⁻¹. The reproducibility of density and speeds of sound estimates was found to be within ±5 × 10⁻⁶ g cm⁻³ and ±5 × 10⁻² m s⁻¹, respectively.

The mole fraction of each mixture was obtained with an accuracy of 1 × 10⁻⁴ from the measured apparent masses of the components. All the mass measurements were performed on an electrical balance with a precision of ±0.01 mg. All masses were corrected for buoyancy. All molar quantities were based on the IUPAC table of atomic weights [24].

Results and discussion

Excess molar volumes and excess molar isentropic compressibilities

Experimental densities,ρ, and speeds of sound, u for binary mixtures of cyclopentane (1) + propan-2-ol (2), +butan-1-ol (2) and butan-2-ol (2) at T = 288.15, 298.15 and 308.15 K and atmospheric pressure are listed in Table 2. Excess molar volumes were calculated from our measured densities according to the following equation:

$$ V_{\text{m}}^{\text{E}} = \left( {x_{ 1} M_{ 1} + x_{ 2} M_{ 2} } \right)/\rho -x_{ 1} M_{ 1} /\rho_{ 1} -x_{ 2} M_{ 2} /\rho_{ 2} , $$

(1)

where x ₁ and x ₂ are mole fractions, M ₁ and M ₂ are molar masses and ρ ₁ and ρ ₂ are the densities of pure components 1 and 2, respectively. ρ is the density of the binary mixtures.

Table 2 Densities values, ρ × 10³/kg m⁻³, and speeds of sound values, u/m s⁻¹, for binary mixtures as a function of mole fraction, x ₁ of cyclopentane at several temperatures

Isentropic compressibilities κ_S were obtained from the relation

$$ \kappa_{\text{S}} = (\rho u^{2} )^{ - 1} = \, V_{\text{m}} \,(Mu^{2} )^{ - 1} , $$

(2)

where ρ is the density of the mixture.

Products K _S,m of the molar volume and the isentropic compressibility were calculated from:

$$ K_{{{\text{S}},{\text{m}}}} = - \, (\partial V/\partial P)_{\text{S}} = V\kappa_{\text{S}} = \Upsigma x_{\text{i}} M_{\text{i}} /(\rho u)^{ 2} $$

(3)

The corresponding excess molar quantities K ^E_S,m were calculated from the relation [25–27]

$$ K_{\text{S,m}}^{\text{E}} = K_{{{\text{S}},{\text{m}}}} -K_{\text{S,m}}^{{i{\text{d}}}} $$

(4)

where [25, 26]

$$ K_{\text{S,m}}^{{i{\text{d}}}} = \Upsigma x_{i} \left[ {K_{{{\text{S}},i}}^{*} - TA_{{{\text{P}},i}}^{*} \left\{ {\left( {\Upsigma x_{i} A_{{{\text{P}},i}}^{*} /\Upsigma x_{i} C_{{{\text{P}},i}}^{*} } \right) - \left( {A_{{{\text{P}},i}}^{*} /C_{{{\text{P}},i}}^{*} } \right)} \right\}} \right], $$

(5)

where x _i are the mole fraction of component i in the mixture, respectively. A ^*_P,i is the product of molar volume V ^* _i and the isobaric expansivity α ^*_P,i , C ^*_P,i is the isobaric molar heat capacity, and K ^*_S,i are the properties of the pure liquid component i, respectively.

The excess intermolecular length has also been calculated with the help of following relation:

$$ L_{\text{f}}^{\text{E}} = L_{\text{f}} - L_{\text{f}}^{{i{\text{d}}}} , $$

(6)

where L _f [= K/(u ρ ^1/2)] is intermolecular free length and K is a temperature-dependent constant (=93.875 + 0.375 × 10⁻⁸ T).

The values of V ^E_m , K ^E_S,m and L ^E_f graphically represented in Figs. 1, 2 and 3.

Fig. 1

Excess molar isentropic compressibility V ^E_m for cyclopentane (1) + 2-propanol (2) (circle) + 1-butanol (2) (triangle); + 2-butanol (2) (square) at a 298.15 K, b 308.15 K and c 318.15 K. Smooth lines have been drawn from polynomial fitting

Fig. 2

Excess molar isentropic compressibility K ^E_S,m for cyclopentane (1) + 2-propanol (2) (circle) + 1-butanol (2) (triangle); + 2-butanol (2) (square) at a 298.15 K, b 308.15 K and c 318.15 K. Smooth lines have been drawn from polynomial fitting

Fig. 3

Excess intermolecular free length L ^E_f for cyclopentane (1) + 2-propanol (2) (circle) + 1-butanol (2) (triangle); + 2-butanol (2) (square) at a 298.15 K, b 308.15 K and c 318.15 K. Smooth lines have been drawn from polynomial fitting

The measured speeds of sound u were fitted for each mixture with a polynomial expression given by

$$ u = \sum\limits_{i = 1}^k{A_{i} x_{1}^{i - 1}} $$

(7)

by the method of least squares with each point weighted equally. The coefficients A _i and standard deviations σ are summarized in Table 3.

Table 3 Coefficients A _i and standard deviations σ for least-squares representation by Eq. 7 for speeds of sound u/m s⁻¹ for binary mixtures at several temperatures and atmospheric pressure

The values of V ^E_m , K ^E_S,m and L ^E_f were fitted with a polynomial expression

$$ F(x) = x_{1} x_{2} \sum\limits_{i = 1} {A_{i} \left( {x_{1} -x_{2} } \right)^{i} } , $$

(8)

where A _i is the polynomial coefficients and k is the polynomial degree. Values of coefficients A _i and standard deviations σ are summarized in Table 4.

Table 4 Parameters A _i and standard deviations σ[F(x)] for least squares representation by Eq. 8 for binary mixtures at several temperatures and atmospheric pressure

Partial molar volumes and apparent molar volumes

The partial molar volumes $\bar{V}_{{{\text{m}},1}}$ and $\bar{V}_{{{\text{m}},2}}$ in these mixtures were evaluated [28, 29] over the complete composition range by using Eqs. 9 and 10:

$$ \bar{V}_{{{\text{m}},1}} = V_{\text{m}}^{\text{E}} + V_{{{\text{m}},1}}^{*} + x_{2} (\delta V_{\text{m}}^{\text{E}} /\delta x_{2} )_{{\rho ,{\text{T}}}} $$

(9)

and

$$ \bar{V}_{{{\text{m}},2}} = V_{\text{m}}^{\text{E}} + V_{{{\text{m}},2}}^{*} + (1 - x_{2} )(\delta V_{\text{m}}^{\text{E}} /\delta x_{2} )_{{\rho ,{\text{T}}}} $$

(10)

The derivatives of Eqs. 9 and 10 were obtained by differentiation of $V_{\text{m}}^{\text{E}}$ from Eq. 8. It leads to the following equations for the partial molar volumes of the solute cyclopentane (1) $\left( {\bar{V}_{{{\text{m}},1}} } \right)$ and the co-solvent alkanol (2) $\left( {\bar{V}_{{{\text{m}},2}} } \right):$

$$ \bar{V}_{{{\text{m}},1}} = V_{{{\text{m}},1}}^{*} + \left[ {\left( {1 - x_{1} } \right)^{2} \sum\limits_{i = 1} {A_{i} \left( {2x_{1} - 1} \right)^{i - 1} + x_{1} \left( {1 - x_{1} } \right)^{2} \sum\limits_{i = 1} {2\left( {i - 1} \right)A_{i} \left( {2x_{1} - 1} \right)^{i - 2} } } } \right] $$

(11)

and

$$ \bar{V}_{{{\text{m}},2}} = V_{{{\text{m}},2}}^{*} + \left[ {\left( {1 - x_{2} } \right)^{2} \sum\limits_{i = 1} {A_{i} \left( {1 - 2x_{2} } \right)^{i - 1} + x_{2} \left( {1 - x_{2} } \right)^{2} \sum\limits_{i = 1} {\left( { - 2} \right)\left( {i - 1} \right)A_{i} \left( {1 - 2x_{2} } \right)^{i - 2} } } } \right] $$

(12)

We are interested to focus on the partial molar volumes of cyclopentane at infinite dilution (x ₁ = 0) in alkanol and the partial molar volume of alkanol at infinite dilution (x ₂ = 0) in cyclopentane. Therefore, putting x ₂ = 1 (corresponding to x ₁ = 0) in Eq. 10 leads to

$$ \bar{V}_{{{\text{m}},1}}^{0} = V_{{{\text{m}},1}}^{*} + \sum\limits_{i = 1} {A_{i} \left( { - 1} \right)}^{i - 1} $$

(13)

Similarly, putting x ₂ = 0 in Eq. 11 leads to

$$ \bar{V}_{{{\text{m}},2}}^{0} = V_{{{\text{m}},2}}^{*} + \sum\limits_{i = 1} {A_{i} } $$

(14)

In Eqs 13 and 14, the $\bar{V}_{{{\text{m}},1}}^{0}$ and $\bar{V}_{{{\text{m}},2}}^{0}$ represent the partial molar volume of cyclopentane at infinite dilution in alkanol and the partial molar volume of the alkanol at infinite dilution in cyclopentane, respectively. All of these partial molar volumes at infinite dilution are evaluated by using the Redlich–Kister coefficients of Eq. 8. Instead of using the Redlich–Kister coefficients, we have also used another approach, which may be more convenient and accurate, by calculating apparent molar volumes in order to evaluate the partial molar volumes at infinite dilution. The apparent molar volumes $V_{\phi ,1}$ and V _ϕ,2 of the solute component cyclopentane in co-solvent and of the co-solvent alkanol in the solute can be expressed as

$$ V_{\phi ,1} = (V_{\text{m}} - n_{2} V_{{{\text{m}},2}}^{*} )/n_{1} $$

(15)

and

$$ V_{\phi ,2} = (V_{\text{m}} - n_{1} V_{{{\text{m}},1}}^{*} )/n_{2} $$

(16)

where V _m is the volume of the mixture containing one mole of (cyclopentane + n-alkanol). It can be written as

$$ V_{\text{m}} = V_{\text{m}}^{\text{E}} + x_{1} V_{{{\text{m}},1}}^{*} + x_{2} V_{{{\text{m}},2}}^{*} $$

(17)

Combination of Eqs. 14, 16 and 15, 16 leads to

$$ V_{\phi ,1} = V_{{{\text{m}},1}}^{*} + (V_{\text{m}}^{\text{E}} /x_{1} ) $$

(18)

and

$$ V_{\phi ,2} = V_{{{\text{m}},2}}^{*} + (V_{\text{m}}^{\text{E}} /x_{2} ) $$

(19)

Equations 18 and 19 allow easy calculation of the apparent molar volumes of each component from the experimental excess molar volumes and corresponding mole fractions. Simple graphical extrapolation of V _ϕ,1 to x ₁ = 0 (x ₂ = 1) and of V _ϕ,2 to x ₂ = 0 (x ₁ = 1) gives value of V ⁰_ϕ,1 and V ⁰_ϕ,2 at infinite dilution. These are also the desired partial molar volumes at infinite dilution, represented by $\bar{V}_{{{\text{m}},1}}^{0}$ and $\bar{V}_{{{\text{m}},2}}^{0}$ same as before. The values of partial molar volumes and apparent molar volumes and their values at infinite dilution are reported in Tables 5 and 6, respectively.

Table 5 Values of $\bar{V}_{{{\text{m}},1}}$ × 10⁻⁶/m³ mol⁻¹, $\bar{V}_{{{\text{m}},2}}$ × 10⁻⁶/m³ mol⁻¹, $V_{\phi ,1}$ × 10⁻⁶/m³ mol⁻¹, and V _ϕ,2 × 10⁻⁶/m³ mol⁻¹ for binary mixtures at several temperatures

Table 6 Values of V ^*₁  × 10⁻⁶/m³ mol⁻¹, $\overline{V}_{{{\text{m}},1}}^{0}$ × 10⁻⁶/m³ mol⁻¹, $\overline{V}_{{\phi},{1}}^{0}$ × 10⁻⁶/m³ mol⁻¹, V ^*₂  × 10⁻⁶/m³ mol⁻¹, $\overline{V}_{{{\text{m}},2}}^{0}$ × 10⁻⁶/m³ mol⁻¹ and $\overline{V}_{{\phi},{2}}^{0}$ × 10⁻⁶/m³ mol⁻¹ for binary mixtures at several temperatures

The Flory’s model

The Flory model [30, 31] has been commonly employed to analyze the molar volume of the mixture and the excess molar volume parting from the equation of the state in function of the reduced variables:

$$ \tilde{P}\tilde{v}/\tilde{T} = [\tilde{v}^{1/3} /(\tilde{v}^{1/3} - 1)] - 1/(\tilde{v}T) $$

(20)

where

$$ V^{*} = V/\tilde{v} = V[( 1 { } + \alpha T)/( 1+ \left( { 4/ 3} \right)\alpha T)]^{ 3} $$

(21)

$$ P^{*} = P/\tilde{P} = \, [(\alpha T\tilde{v}^{2} )/\kappa T] $$

(22)

$$ T^{*} = T/\tilde{T} = \tilde{v}^{4/3} /(\tilde{v}^{1/3} - 1) $$

(23)

Theoretical values of dV ^E_m /dT [32] were calculated from the Flory theory using

$$ T({\text{d}}V_{\text{m}}^{\text{E}} /{\text{d}}T) = \left[ {\sum\limits_{i = 1}^{2} {x_{i} V_{i}^{*} [T({\text{d}}\tilde{v}/{\text{d}}T)]} - \left( {\sum\limits_{i = 1}^{2} {x_{i} V_{i}^{*} [T({\text{d}}\tilde{v}/{\text{d}}T)]} } \right)i} \right] $$

(24)

where

$$ T({\text{d}}\tilde{v}/{\text{d}}T) = \tilde{v}(1-\tilde{v}^{ - 1/3} )/[(4/3)\tilde{v}^{ - 1/3} -1] $$

(25)

In the present study, the value of the reduced volume for the liquids and their mixture $\tilde{v}$ was determined from α values of the mixtures using the Eq. 21.

The excess function (∂V ^E_m /∂T)_P was computed by analytical differentiation of Eq. 7 at 298.15 K for each mixture. From (∂V ^E_m /∂T)_P and V ^E_m of this work we also have obtained (∂H ^E/∂P)_T at zero pressure according to the equation:

$$ (\partial H^{\text{E}} /\partial P)_{\text{T}} = V_{\text{m}}^{\text{E}} -T(\partial V_{\text{m}}^{\text{E}} /\partial T)_{\text{P}} $$

(26)

Values for (∂V ^E_m /∂T)_P, and (∂H ^E/∂P)_T, for equimolar mixtures are reported in Table 7.

Table 7 Equimolar values of the excess functions at T = 298.15 K

It is observed from Fig. 1 that the excess molar volumes for all the mixtures at T = 288.15, 298.15 and 308.15 K are positive over the whole composition range. The excess molar volumes decrease with the increase in chain length of the primary and secondary alcohols. This supports our earlier results reported or cyclopentane + 1-alkanol systems [2]. The magnitude of V ^E_m value increases as we move from propan-1-ol [2] to propan-2-ol and butan-1-ol to butan-2-ol. For the systems, cyclopentane with primary and secondary alcohols, the excess molar volume increase with decrease in the chain length of alcohol, this increase suggest that dipole–dipole interactions are weak in lower alcohol owing to decrease in their polarizability [33] with decreased chain length.

It is observed from Table 2 that u increases with increase in the concentration of cyclopentane in cyclopentane (1) + propan-2-ol (2) systems while for other two binary mixtures viz. cyclopentane (1) + butan-1-ol (2) and cyclopentane (1) + butan-2-ol (2) u decreases. The increase in u with x ₁ indicate significant interaction between molecules. It is observed from Tables 3, 4 and Figs. 2, 3 that K ^E_S,m and L ^E_f shows positive deviations for all mixtures over the whole composition range at all temperatures. For the same value of x ₁ the absolute values of K ^E_S,m and L ^E_f for mixtures decrease with decrease in chain length of primary and secondary alcohols. The magnitude of K ^E_S,m and L ^E_f increases with increase in temperature for all systems studied at all three temperatures. The deviations in these functions from rectilinear dependence on mole fraction indicate the extent of interaction between unlike molecules. For the same values of x ₁, the absolute values of K ^E_S,m and L ^E_f for the mixtures fall in the order: butan-1-ol < propan-2-ol < butan-2-ol, which means that values increase with the increase in chain length of secondary alcohol and on changing the position of hydroxyl group, i.e. on branching. Further, the values increase with the increase on temperature for the all the mixtures studied. Positive values of K ^E_S,m mean that the mixture is more compressible than the corresponding ideal mixture and, likewise, L ^E_f is positive, suggesting weaker interactions among the molecules which is in accordance with the positive values of excess molar volumes.

From Table 6, it is observed that partial molar volumes of cyclopentane at infinite dilution $\bar{V}_{{{\text{m}},1}}^{0}$ in alkanols are greater than the corresponding V ^*₁ values of pure cyclopentane. Thus, the difference in values $(\bar{V}_{{{\text{m}},1}}^{0} - V_{1}^{*} )$ are positive, suggesting the expansion in volume of the mixture on mixing which may be attributed to the non-specific interactions between cyclopentane and alkanol molecules. It is also observed that all of the $\bar{V}_{{{\text{m}},2}}^{0} ,$ i.e. partial molar volumes of alkanols in cyclopentane are greater than corresponding molar volumes V ^*₂ of n-alkanol which may suggest that alkanol molecules are not able to fit into the empty spaces in cyclopentane which results in positive excess molar volumes. Apparent molar volumes at infinite dilution $\bar{V}_{\phi ,1}^{0}$ for cyclopentane in alkanol are higher than corresponding molar volume V ^*₁ of pure cyclopentane. This suggests the idea that apparent molar volume of cyclopentane is actually the molar volume of cyclopentane and additional volume that arises from the rupture of interaction between the mixture components. The difference between $\bar{V}_{\phi ,1}^{0}$ and V ^*₁ increases as we from primary alkanol to secondary alkanol and with decrease in chain length of alkanol which constrained the structure formation in these mixtures and increases the excess molar volumes. This observation and positive values of V ^E_m for these mixtures suggest that structure breaking effect between like molecules exceeds the structure formation between unlike molecules. Dispersion interactions between cyclopentane and alkanol increases with decrease in chain length of alkanol, i.e. from 1-butanol to 1-propanol. Repulsive interactions are relatively strong in cyclopentane + 2-propanol as observed from V ^E_m data. Further, the difference between $\overline{V}_{{\phi},{2}}^{0}$ and V ^*₂ are smaller in the case of 1-butanol as compared to 2-butanol which indicates more expansion means more positive V ^E_m for cyclopentane + 2-butanol mixture.

It is observed from Table 7 that the values obtained for (∂V ^E_m /∂T)_P are positive for all the systems and are in agreement with the values of V ^E_m at T = 298.15 K. The values of (∂H ^E/∂P)_T are negative at equimolar concentration, for all cyclopentane + alkanol systems. The values of (∂V ^E_m /∂T)_P and (∂H ^E/∂P)_T have similar variation with the n-alkanol but with opposite sign. The values obtained from Flory’s theory are greater than the experimental values. The difference between theoretical and experimental values is higher in case of cyclopentane + 2-butanol systems. The values of (∂V ^E_m /∂T)_P decrease with increase in the chain length, i.e. from 2-propanol to 2-butanol and with branching, i.e. from 1-butanol to 2-butanol. The mixing quantities (∂V ^E_m /∂T)_P and (∂H ^E/∂P)_T are an indicator of nonrandomness or order in the solution [34–36]. (∂V ^E_m /∂T)_P values are positive for all the cyclopentane + alkanol systems so it is expected that destruction of order during mixing is not important as positive contribution of (∂V ^E_m /∂T)_P implies the nonrandomness or order in the solution. Randomness in solution implies a negative contribution to (∂V ^E_m /∂T)_P. An analysis of the results shows that out of three systems, cyclopentane + 2-propanol has more positive values of (∂V ^E_m /∂T)_P which implies that it has very less tendency to break the order or to create the randomness in the solution on mixing.