Introduction

A cure kinetic study of polymeric resin can be carried out in a calorimeter analysis, operating by two models: isothermal and non-isothermal. A way to estimate the kinetic parameters using any experimental data is the use of an objective function to be minimized. The algorithms frequently used to find the minimum are deterministic, but the application of the heuristic algorithms to estimate cure kinetic parameters have become a good way. Among these algorithms, the Particle Swarm Optimization (PSO) [1] has been extensively applied in parameter estimation. One important detail of these algorithms is that the knowledge of the objective function gradients and the initial parameter guesses are not necessary. Although a higher number of the objective function evaluation is necessary, this characteristic can be used to determine the parameter confidence limits.

Many authors have studied the kinetic parameter estimation of polymeric resin using both isothermal and non-isothermal data coming from DSC [2–7]. Kissinger [8], Borchardt and Daniels [9], and Ozawa [10] methods are the main ones used to estimate kinetic parameter by using non-isothermal data found in the literature [11–17]. However, Kissinger and Ozawa methods are generally applied to determine only the activation energy from experimental data.

The estimated activation energy and pre-exponential factor using isothermal and non-isothermal experimental data have values in agreement in the literature [18, 19], however, some papers have found differences among the kinetic parameters values using different analysis modes [11, 20–23]. The use of the energy balance in kinetic parameter estimation of epoxy resins was studied in isothermal case [24]. Thus, in this contribution, this procedure was applied to non-isothermal data and the PSO was applied to build the confidence regions of all estimated parameters.

Theoretical

Kinetic models

The main models used to express the cure kinetic for a polymeric resin shows the form:

$$ {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} = K_{1} f(\alpha ) $$
(1)

where dα/dt is the cure kinetic rate, α is the curing degree of the resin, t is the curing time, and K 1 is the temperature-dependent rate constant given by Arrhenius equation:

$$ K_{1} = K_{1} (T) = A_{1} e^{{ - {\frac{{E_{1} }}{RT}}}} $$
(2)

where E 1 is the curing activation energy, T is the absolute temperature, A 1 is the pre-exponential factor, and R is the universal gas constant.

The cure kinetic expression for epoxy resins is based on the autocatalytic model [25], Eq. 3:

$$ f(\alpha ,T) = (1 + K_{2} \alpha^{m} )(1 - \alpha )^{n} $$
(3)

where m and n represent the catalytic and autocatalytic natures of the reaction, respectively, and K 2 follows the Arrhenius equation.

The ultimate reaction heat can be calculated through the area under the curve of the released reaction heat rate; but in this paper, this constant was estimated along with the kinetic parameters (E 1, E 2, A 1, A 2, m, n). The measured value of ultimate reaction heat is found by an integration method (commonly through the area under the experimental heat flow). This method can insert error in the parameter value because the area depends on chosen points, on the integration method, etc. For degree of cure, the analysis is similar because it can be found by the same way. Thus, it is important to avoid intermediate calculus using experimental data, minimizing so error propagation. For that, in the present paper, the adjustment is achieved using experimental data coming from DSC without any manipulation. The degree of cure and the ultimate reaction heat are calculated during the estimation process through the mass and energy balances in DSC.

Mathematical modeling

The kinetic model proposed by Kamal and Sourour [25], Eq. 4, was adopted herein.

$$ {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} = \left( {K_{1} + K_{2} \cdot \alpha^{m} } \right) \cdot \left( {1 - \alpha } \right)^{n} $$
(4)

where

$$ K_{2} = K_{2} (T) = A_{2} e^{{ - {\frac{{E_{2} }}{RT}}}} $$

Because of the correlation among the parameters, it was inserted in the mathematical system a dimensionless variables. This transformation and an appropriated reference temperature lead the estimation with lower correlation [26]. In terms of dimensionless variables, Eq. 4 is expressed by Eq. 5:

$$ r(\alpha ,\Theta ) = {\frac{{{\text{d}}\alpha }}{{{\text{d}}\varsigma}}} = \left[ {e^{{\left( {\xi_{1} + {\frac{{\sigma_{1} \Theta }}{1 + \Theta }}} \right)}} + e^{{\left( {\xi_{2} + {\frac{{\sigma_{2} \Theta }}{1 + \Theta }}} \right)}} \alpha^{m} } \right] \cdot \left( {1 - \alpha } \right)^{n} \quad {\text{with}}\;\alpha (0) = 0 $$
(5)

\( \varsigma = {\frac{t}{\tau }} \), \( \sigma_{i} = {\frac{{E_{i} }}{{RT_{0} }}} \), \( \Theta = \left( {{\frac{{T - T_{0} }}{{T_{0} }}}} \right) \), \( \xi_{i} = \ln (\tau A_{i} ) - \sigma_{i} \), where T 0 is a reference temperature and τ is a reference time for integration.

Six parameters must be estimated to define the cure kinetics. The dimensionless parameters are related to dimension parameters by the following expressions:

$$ E_{i} = \sigma_{i} RT_{0} \quad A_{i} = (e^{{\xi_{i} + \sigma_{i} }} )/\tau $$

Particle swarm optimization

The PSO is an optimization algorithm based on the social behavior of an animal collection. This algorithm uses information about the best solution found by each particle and all particles. Kennedy and Eberhart [27] proposed the first approach to this technique which can be mathematically described by Eqs. 6 and 7.

$$ v_{{}}^{k + 1} = wv_{{}}^{k} + c_{1} r_{1} \left( {x_{\text{local}}^{k} - x^{k} } \right) + c_{2} r_{2} \left( {x_{\text{global}}^{k} - x^{k} } \right) $$
(6)
$$ x_{{}}^{k + 1} = x_{{}}^{k} + v_{{}}^{k + 1} $$
(7)

where v is the particle pseudovelocity vector; x is the particle position vector; \( x_{\text{local}}^{k} \) and \( x_{\text{global}}^{k} \) are the best solutions found by each particle and by all particles, respectively; r 1 and r 2 are two random numbers in the range [0,1]; c 1 and c 2 are the search parameters and superscript k denotes the iteration index. The parameter w is calculated by \( w = w_{i} + \left( {w_{f} - w_{i} } \right){\frac{i}{{n_{\text{iter}} }}} \), with w f and w i as the weight parameters, which control the method convergence, and n iter is the number of iterations. More details about the application of this algorithm can be found elsewhere [24].

Experimental data

The system used was an epoxy resin, diglicidyl ether of bisphenol-A (DGEBA), with a commercial name of DER 331, and a hardener, triethylenetetramine (TETA), both from Dow Chemical Company. The epoxy equivalent weight was 183 g/eq DGEBA and TETA were used as received, without further purification. A ratio of 13% (stoichiometric ratio) was used. DGEBA was vigorously mixed with the appropriate amount of TETA for about 1 min, at room temperature.

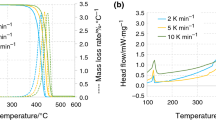
Non-isothermal experiments were run in a Perkin-Elmer, DSC model Diamond. The heating rates, ϕ, on the experiments were 5, 10, 15, and 20 K min−1. Approximately, 10 mg of the mixture were encapsulated in a standard aluminum sample pan. The instrument was calibrated using indium as a standard. The gas used was nitrogen at 20 mL min−1. More details can be found elsewhere [28].

Mathematical modeling

The energy balance of the sample inside the calorimeter was taken into consideration. A convective loss was also considered in the system. Thus, considering a sample inside the calorimeter, in the non-isothermal case, we can write an energy balance as

$$ [{\text{Accumulation}}\;{\text{rate}}] = [{\text{in/out}}\;{\text{net}}\;{\text{rate}}] + [{\text{generation}}\;{\text{rate}}] - [{\text{convective}}\;{\text{loss}}] $$

In non-isothermal case, considering c p and m e constant, the energy balance is:

$$ m_{\text{e}} c_{p} {\frac{{{\text{d}}T}}{{{\text{d}}t}}} = m_{\text{e}} \left( { - \Updelta H} \right)R_{\alpha } + Q - hA(T - T_{\infty } ) $$
(8)

where Q is heat rate leaving DSC, (−∆H) is the ultimate reaction heat of system, m e is the sample mass, c p is the sample specific heat, h is the heat transfer coefficient, A is the heat transfer area, T ∞ is the ambient temperature, and R α is a cure kinetic expression.

The last term of right side is related to convective loss in the process. In a dimensionless form, we can write Eq. 8 as

$$ {\frac{{{\text{d}}\Theta }}{{{\text{d}}\varsigma }}} = \eta r_{\alpha } + q - \gamma (\Theta - \Theta_{\infty } ) $$
(9)

and

$$ {\frac{{{\text{d}}\Theta }}{{{\text{d}}\varsigma }}} = \beta \,\quad {\text{with}}\;\,\Theta (0) = \Theta_{0} $$
(10)
$$ {\frac{{{\text{d}}\alpha }}{{{\text{d}}\varsigma }}} = r_{\alpha } = \left[ {e^{{\left( {\xi_{1}^{{}} + {\frac{{\sigma_{1} \Theta }}{1 + \Theta }}} \right)}} + e^{{\left( {\xi_{2}^{{}} + {\frac{{\sigma_{2} \Theta }}{1 + \Theta }}} \right)}} \alpha^{m} } \right]\left( {1 - \alpha } \right)^{n} \quad {\text{with}}\;\,\alpha (0) = \alpha_{0} $$
(11)

where η is the dimensionless reaction heat, η = (−ΔH)/c p T 0, q is the dimensionless heat rate, q = Qτ/m e c p T 0, β is the dimensionless heating rate, β = ϕτ/T 0, γ is the dimensionless heat transfer coefficient, γ = hAτ/(m e c p ), τ is the reference time, ς = t/τ, Θ is the dimensionless temperature, Θ = (T − T 0)/T 0, and T 0 is the reference temperature.

Results and discussion

The system composed by Eqs. 9, 10, and 11 is an index 1 differential–algebraic equation (DAE) system and it can be solved by an appropriated numerical package. In the present paper, the code DASSL [29] was applied to find the variables used in the estimation process.

In order to estimate the kinetic parameter (E 1, E 2, A 1, A 2, m, n) and the ultimate reaction heat, the ESTIMA [30], which is a computational package composed by heuristic algorithm (swarm) and a deterministic algorithm (Gauss–Newton), was applied to find the minimum of objective function described by Eq. 12.

$$ f = \sum\limits_{i = 1}^{{N_{\exp } }} {\left( {q_{\text{estimated}}^{i} - q_{\exp }^{i} } \right)}^{2} $$
(12)

The value of ultimate reaction heat was estimated along with the kinetic parameters in the present paper as described by Pagano et al. [24]. This procedure reduces estimation errors as the objective function is directly associated with the released reaction heat rate. Table 1 has the dimensionless parameters and Fig. 1 shows the comparison between experimental and estimated values of heat flow obtained by applying this methodology. A good prediction was achieved for all experiments data, although the results coming from lower heating rate (5 K min−1) showed a small difference in the beginning of analysis.

Table 1 Estimated dimensionless parameters
Full size table
Fig. 1
figure 1

Experimental and estimated values of heat flow for the reactional system DGEBA/TETA in stoichiometric ratio for different heating rates a 5 K min−1, b 10 K min−1, c 15 K min−1, and d 20 K min−1

Full size image

Owing to importance of knowledge of the estimated parameter certainty, the confidence regions of all parameters were determined. It was considered a confidence level of 95% and the square error function described by Eq. 12. The parameter set that composes the confidence region was chosen according to Eq. 13, as suggested by Schwaab et al. [31]

$$ C_{R} (p) \le C_{R} (p^{*})\left( {1 + {\frac{{n_{p} }}{{n - n_{p} }}}F_{{n_{p} ,n - n_{p} }}^{1 - \delta } } \right) $$
(13)

where p* is a vector that contains the best parameters, p is a vector with parameters that will be tested, n p is the number of parameters, n is the total number of data and \( F_{{n_{p} ,n - n_{p} }}^{1 - \delta } \) is the F-distribution with n p and n − n p degrees of freedom and a confidence level of 1 − δ. More details of this procedure can be found elsewhere [31].

The application of this approach to isothermal data was done in a previous work and similar results were obtained [24]. The confidence regions for each estimated parameter in the non-isothermal case can be seen in Fig. 2a–d.

Fig. 2
figure 2

Confidence regions from estimated parameters using non-isothermal data: a activation energies, b pre-exponential factors, c reaction order, and d dimensionless heating rate and heat transfer coefficient. The cross refers to the estimated parameter values

Full size image

One of hypothesis used in parameter estimation is the absence of correlation among the parameters to be estimated. If that hypothesis is true, the confidence region must have a symmetrical and elliptical shape. Considering these observations, some points must be highlighted about the results showed in Fig. 2. First, the confidence regions show an angle to the main axes because the estimated parameters are correlated. Other point is related to the region shape; we can see that the elliptical region is a bad approximation for these confidence regions. Lastly, the estimated parameters, the crosses in Fig. 2a–d, are not in the geometric center of the regions as expected in linear models. Thus, the use of the energy balance claims to be a good methodology to estimate cure kinetic parameters of non-isothermal experiments.

Conclusions

A differential–algebraic approach was applied to estimate the kinetic parameters of epoxy resin. The released reaction heating rates measured in DSC were directly used as variable to be adjusted. This approach was very suitable to parameter estimation and an excellent agreement between experimental and predicted data was achieved. The application of the PSO algorithm to minimize objective function was especially suitable for estimation purposes and, at the same time, allowed the construction of correspondent confidence regions for the estimated parameters. The ultimate reaction heat, obtained by numerical integration of the reaction heating rate conducted isothermically in DSC experiments, lies outside the confidence region of the reaction heat estimated in the proposed method. This fact, along with the high quality of the parameter adjustments, indicates that the proposed methodology is more reliable. It must be pointed out that the use of dimensionless variables and an appropriate reference temperature increase their accuracy because this procedure results in a low parameter correlation.