Introduction

Thermal analysis [thermogravimetry (TG), derivative thermogravimetry (DTG), differential thermal analysis (DTA), differential scanning calorimetry (DSC), etc.] is widely utilized for the determination of the kinetic parameters for reactions with at least one solid reactant from isothermal and non-isothermal data. Recently much attention has been given to determining the validity of the kinetic parameters obtained in this fashion [1–3], especially those obtained using non-isothermal methods. The modelling of solid state reactions is frequently based on a differential equation derived in an analogous fashion from homogeneous chemical kinetics [4, 5]. For the thermal oxidation of graphite by oxygen it reads

$$ {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} = k(T)\,f(\alpha )\,{\rm P}_{{{\text{O}}_{2} }}^{r} $$
(1)

Here α is the dimensionless degree of reaction or conversion which is defined as follows:

$$ \alpha = {\frac{{m_{0} - m}}{{m_{0} }}} $$
(2)

where m 0 is the starting mass and m is the mass of the sample at time, t, or temperature, T. Since the sample under consideration here is highly pure nuclear grade graphite with zero ash content, the starting mass is the full weight of the original sample and the final measured value for the mass is zero. The function f(α) is the reaction model or conversion function applicable to the situation at hand (see Table 1). \( {\rm P}_{{O_{2} }} \) is the partial pressure of the oxygen and r is the reaction order in oxygen. Assuming that the gas behaves ideally, this factor can be further subdivided into the expression:

$$ {\rm P}_{{O_{ 2} }} = y_{{O_{2} }} {\rm P} $$
(3)

where \( y_{{O_{2} }} \)is the mole fraction of oxygen in the reactant gas and P is the system pressure. There are some doubts as to the correct form and temperature dependence of the reaction rate constant, k(T) [8, 9]. Usually though a simple Arrhenius temperature dependence is assumed:

$$ k(T) = k_{0} \exp \left( {{\frac{{ - E_{\text{A}} }}{\text{RT}}}} \right) $$
(4)

This leads to the complete expression:

$$ {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} = k_{0} \exp \left( { - {\frac{{E_{\text{A}} }}{\text{RT}}}} \right)\,f(\alpha )y_{{{\text{O}}_{2} }}^{r} {\rm P}^{r} $$
(5)

The isothermal case represents the simplest situation for kinetic evaluations. As can be seen from Eq. 5, by plotting dα/dt against α at constant oxygen potential but different temperatures, the curves would represent the conversion function, f(α), only scaled by a constant factor, its magnitude dictated by the Arrhenius expression. By choosing an arbitrary fixed value for α and constructing an Arrhenius plot, the activation energy for the reaction can be easily determined. This is only valid if the conversion function is temperature independent.

Table 1 Selected kinetic models for solid state reactions [6, 7]
Full size table

The experimental difficulties associated with the execution of precise isothermal experiments with gas–solid reactions are well known [10]. It is often easier to control experimental conditions using temperature-programmed thermal analysis with linear temperature ramping:

$$ T(t) = T_{0} + \beta t $$
(6)

Under these conditions, assuming that the heating rates are not excessive and other limitations (i.e. mass and heat transfer, measurement lag, localized gas depletion, concentration gradients, etc.) do not become active, Eq. 5 should still apply. For the non-isothermal experiments, if the remaining constants are known it should be possible to reconstruct the conversion function again by plotting dα/dt, divided by some factor (as determined by the measured temperature and the Arrhenius expression), against α.

The difficulty associated with both isothermal and non-isothermal approaches is the correct choice of the form of the conversion function. The approach mentioned above is largely empirical with no consideration of the underlying mechanism which governs the conversion function. It solely focuses on the validity of the assumption that Eq. 5 is applicable to both isothermal and non-isothermal scenarios and aims to find a single coherent model which describes a wide range of experimental conditions.

In this paper we explore the application of both isothermal and non-isothermal analyses to the oxidation kinetics of a powdered natural graphite sample which displays somewhat unusual behaviour for what one expects to be contracting flakes. In general, the study of graphite oxidation kinetics has been limited to ranges within the first 0–20% of conversion with very few studies focusing on the entire range of conversions. Thus no single kinetic model for the conversion function is generally established for powdered graphite, to aid comparisons of the observed graphite behaviour with known kinetic models for solid state reactions, some relevant models given in Table 1 are plotted in Fig. 1.

Fig. 1
figure 1

Selected kinetic models from Table 1 (scaled to fit figure) (A) nucleation and growth (n = 2.3), (B) phase boundary reaction (n = 2), (c) autocatalysis (n = 2, m = 0.5)

Full size image

Experimental

The oxidation kinetics of a proprietary sample of natural graphite recommended for use in nuclear applications were characterized using both isothermal and non-isothermal TG analysis, using a TA Instruments SDT Q600 simultaneous DSC/TGA machine. Samples were placed in alumina pans and, for the non-isothermal runs, they were heated to 1000 °C at scan rates of 1, 3 and 10 °C/min in instrument grade (IG) air flowing at 50 mL/min. During the isothermal runs the samples were heated at a scan rate of 10 °C/min in nitrogen (IG) flowing at 250 mL/min to temperatures between 600 and 700 °C and then the purge gas was switched to oxygen (IG) at 200 mL/min. No pre-treatment of the samples was done. In addition, inductively coupled plasma-mass spectrometry (ICP-MS) and scanning electron microscope imaging (on a JEOL 840 SEM) was used to characterize the natural graphite.

Results

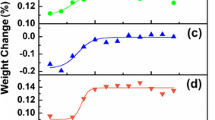
The results for the isothermal and non-isothermal runs are shown in Figs. 2 and 3, respectively. Shown in Fig. 4 is the SEM image for the as received graphite, while in Fig. 5 an image of the partially oxidized graphite sample (roughly 20% mass loss) is presented. The ICP-MS compositional analysis for the sample was obtained for iron, sodium, cobalt, nickel, vanadium and boron; these results are shown in Table 2.

Fig. 2
figure 2

a Isothermal mass loss curves, b isothermal conversion rate

Full size image
Fig. 3
figure 3

a Non-isothermal mass loss curves, b non-isothermal conversion rate

Full size image
Fig. 4
figure 4

SEM for as received graphite sample

Full size image
Fig. 5
figure 5

SEM for partially oxidized natural graphite at ca. 20% conversion

Full size image
Table 2 ICP-MS data for natural graphite sample
Full size table

Modelling

The activation energy of the graphite can be calculated as described earlier, using the isothermal Arrhenius plots at an arbitrarily chosen conversion. However, for this investigation the procedure was repeated at regular intervals of conversion (Δα = 0.005) for the entire burn-off curve and the result is shown in Fig. 6, along with the RMS error in percentage. From the figure one can see there is a larger error in the calculated values for the activation energy at low conversions (α < 0.1) and there is a much larger spread in the values obtained for higher conversions (α > 0.65). This is due to the uncertainty of the data in these regions compared to central conversions where any external effects (e.g. due to transients in the furnace) have had time to establish equilibrium and no longer affect the reaction, while at higher conversions minor secondary effects may become more pronounced due to the small amount of sample which remains. For that reason the average value for the activation energy was taken over the region: 0.1 < α < 0.65; and was found to be 155 kJ/mol. This value is slightly lower than the value of 188 kJ/mol reported by Zaghib et al. [11] for natural graphite powder, but it is important to note that their powder was pretreated at 1200 °C and the rate parameters were determined only from the initial slope of the weight loss curve.

Fig. 6
figure 6

Activation energy estimation

Full size image

Recently much attention has been given in the literature [12, 13] to the significance of the activation energy obtained in this fashion from thermal analysis for the reactions of solid reagents. For the reagent under consideration the factors affecting the reliability of the activation energy are assumed to be fairly small since the reagent is very pure and no phase change or reagent transitions are known to occur. Furthermore, because no a priori assumptions are made regarding the shape of the conversion function it seems reasonable to assume that these effects will be automatically incorporated into this function and the activation energy purely serves to scale the reaction rate as a function of the measured reaction temperature.

The reaction order was obtained from the literature [14, 15] as r = 0.55 and is assumed to be independent of burn-off for the graphite under consideration. The mole fraction of oxygen in air was assumed to be 0.21 and the system pressure was assumed to remain constant during all the experiments. This fully specifies all the constants required for Eq. 5 with the exception of the factor \( k_{0} {\rm P}^{r} \). Some rearrangement of Eq. 5 yields:

$$ {\frac{d\alpha }{dt}}\left[ {\exp \left( { - {\frac{{E_{A} }}{RT}}} \right)y_{{O_{2} }}^{r} } \right]^{ - 1} = k_{0} {\rm P}^{r} f(\alpha ) $$
(7)

Plotting the left hand side of Eq. 7 against α for all the experiments, should yield the same curve. To obtain a representative curve, all the experimental curves could be averaged to yield a single curve. Then by picking a value for the factor \( k_{0} {\rm P}^{r} \), the curve can be further scaled to give 0 ≤ f(α) ≤ 1. The result of this procedure is shown in Fig. 7. However, only the data for the isothermal experiments at 600 and 612 °C and the non-isothermal experiments at scan rates of 1 and 3 °C/min were used to calculate the average conversion function. The remaining datasets were excluded to later ascertain the models’ predictive capability on two datasets which were not utilized in any way during the model fabrication. The final conversion function is plotted in Fig. 8 and the look-up table is supplied in Appendix 1. As the result of some experimentation and the search for an analytical expression to describe the attained conversion function, it was found that the small secondary peak at very high α values (primarily observed in the isothermal data, see Fig. 2b), was superfluous in accounting for the apparent bimodal nature of the non-isothermal data. Thus to keep the model simple and allow a clear illustration of this point via the model predictions it was decided to completely remove the second peak from the model and approximate the high conversion (>0.9) segment of the curve as shown in Fig. 8.

Fig. 7
figure 7

Average conversion function prediction from isothermal and non-isothermal data

Full size image
Fig. 8
figure 8

Approximate conversion function used in model

Full size image

It is interesting to note (although not clearly visible in Fig. 7) that for the non-isothermal data the conversion function has a predicted non-zero starting value. However, the dynamic nature of the gas changing during an isothermal run, where inert atmosphere is changed to oxidizing, means that the isothermal reaction rate appears to start at zero when the oxidizing gas flow is started. This raises the question whether the initial acceleration of the reaction rate to the peak value for the isothermal data is in fact caused by the dynamic effect of the oxidizing gas gradually replacing the inert atmosphere. However, the fact that the non-isothermal data, in which no gas change was done and the sample was in an oxidizing atmosphere from the start, also exhibits this acceleration illustrates that this peak behaviour is in fact the true behaviour. Thus, strictly speaking, only the initial starting value for the isothermal is incorrect and should in fact have a non-zero value.

This value can be found by step testing the oxygen partial pressure to obtain its dynamic response, then using this model to calculate the true gas composition (which was assumed to be constant in the model calculation) the reaction rate curve can be compensated for this effect. This was done for the TG machine used in the experiments, using a mass spectrometer to measure the gas compositions. However since the conversion function used in the model is already an average of the isothermal and non-isothermal data the additional accuracy afforded by this approach was found to be insignificant and it was subsequently left out of the model to keep the approach simple.

The complete model was then used in Microsoft Excel® to predict the reaction rate as a function of temperature if a monotonically increasing temperature ramp was imposed on the model. The result is shown in Fig. 9. The model’s performance is adequate given the crude nature of the analysis. Crucially, it manages to predict the bimodal nature of the reaction rate curve during a non-isothermal experiment. The model was also used to predict the isothermal TG runs; these results are shown in Fig. 10. In both figures the additional datasets which were not utilized in the modelling are shown to illustrate the predictive capabilities of the model.

Fig. 9
figure 9

Non-isothermal conversion model (solid lines represent the model predictions and empty markers are the experimental data)

Full size image
Fig. 10
figure 10

Isothermal conversion model (solid lines represent the model predictions and empty markers are the experimental data)

Full size image

Thus both the isothermal and non-isothermal data are modelled adequately over a wide temperature range using a unique conversion function and most notably only a single value for the activation energy.

Discussion

The apparent bimodal nature of the reaction rate curve for the natural graphite is clearly visible from Fig. 3b, where dα/dT is plotted against T. Initially the reaction rate accelerates as the onset temperature is passed, however, in all cases this is followed by a period where the reaction rate slows down (identified as the first mode) and then gradually accelerates again. The rate again reaches a maximum (identified as the second mode) followed by a sharp decline in rate as the particles are consumed. This behaviour leads one to contemplate the possibility that the natural graphite is composed of two distinct reaction processes, which are activated at different stages during the experiment, thus leading to the observed dual reaction peaks. However, if they are different reactions, one would expect them to have different activation energies and if they are occurring in parallel, the magnitude of the peaks, relative to each other, would change at different temperatures. However, as can be seen from Fig. 2b this is clearly not the case. In addition, the fact that the graphite can be accurately modelled across a wide range of temperatures using only a single value for the activation energy supports the conclusion that there is only one reaction process, albeit with a very distinctive conversion function.

At this point it is critical to distinguish between the clear double peaks observed in the non-isothermal data (Fig. 3b) and the large primary peak and a small secondary peak observed in the isothermal data (Fig. 2b). It should be clear from the modelling that the secondary peak in the isothermal data is not responsible for the second peak observed in the non-isothermal experiments, since the model excludes this peak and is still capable of modelling the dual peaks observed in the non-isothermal data. On the contrary, the secondary peak is caused by a combination of the temperature ramp imposed on the sample and the non-zero value of the conversion function at high conversions (0.75–0.9).

This conclusion is further rationalized by considering the possible use of the autocatalysis expression given in Table 1, i.e. f(α) = α m(1 − α)n, to approximate the conversion function. As can be seen from Fig. 11, the model provides an adequate description of the conversion function up to conversions of 50%, but critically beyond this point the autocatalysis curve decays to zero. If this conversion function is utilized in the model to predict any of the non-isothermal experiments, the model is found to be unable to predict the bimodal behaviour and a very poor prediction is obtained, as shown in Fig. 12.

Fig. 11
figure 11

Autocatalytic conversion function comparison

Full size image
Fig. 12
figure 12

Non-isothermal conversion model using an autocatalytic conversion function

Full size image

The natural graphite conversion function has a rather unexpected shape (see Fig. 2b) for the conversion function of particles which appear to simply be contracting flakes or disks (compare to curve B in Fig. 1), by means of visual inspection of Fig. 4. After an initial acceleration in reaction rate (from Fig. 2b this seems to correlate to a conversion of 10%), the reaction rate rapidly declines, followed by a slowing of the decline at conversions of between 50% and 80% (at this point the shape of the curve is reminiscent of that predicted by nucleation and growth or autocatalysis expressions in Table 1).

Since the experiments were conducted close to the oxidation onset temperature (roughly 550 °C, as ascertained from Fig. 3b) and the powder consists of fairly small particles (mean particle diameter is 20 μm), diffusional limitations were ignored for the modelling and only kinetic factors were considered.

From the ICP-MS data in Table 2, the presence of trace amounts of known catalysts [16, 17] for graphite oxidation is observed. The random catalytic roughening observed by McKee and Chatterji [18] for sodium is consistent with the ICP analysis and the almost fractal-like roughening observed for the partially oxidized natural graphite sample shown in Fig. 5. The surface roughening effect of the catalyst cannot be discounted and would explain the acceleration in reaction rate of natural graphite as seen in Fig. 2b, up to roughly 10% conversion, since more active sites are created until a maximum surface roughness is achieved.

The model suggested by Ranish and Walker [19] for surface roughening due to the presence of metallic catalysts was applied to the natural graphite under consideration; an example of a conversion function derived from this model is given in Fig. 13. It was found that, whilst this model could account for the initial surface roughening via an increase in active sites and subsequently the reaction rate, it is unable to account for the steep decay in the reaction rate after the peak surface roughening is achieved and due to the underlying assumptions in the model, the predictions conform to the disk shaped phase boundary controlled kinetic model at high conversions. In fact, for a phase boundary controlled reaction no simple geometric model was found that could account for the shape of the natural graphite conversion function between 20% and 80% conversion.

Fig. 13
figure 13

Conversion function derived from Ranish and Walker [19]

Full size image

Another effect to be considered is the possibility of catalyst deactivation, which may account for the sharp drop in reaction rate beyond the peak value. However, surface roughening was found to persist up to conversions as high as 90% (at which point the fractal nature of the roughening becomes even more apparent as can be seen in the SEM image shown in Fig. 14) which implies that the catalyst is still active at this late stage of oxidation.

Fig. 14
figure 14

SEM for partially oxidized natural graphite at 90% conversion

Full size image

Conclusions

Despite the unexpected shape of the conversion function for a proprietary sample of flake-like natural graphite, it is possible to model both isothermal and non-isothermal oxidation behaviour by assuming a simple Arrhenius type temperature dependence and by constructing a look-up table for the conversion function based on either isothermal or non-isothermal data. The model performs acceptably for a wide range of temperatures (between 500 and 900 °C) in oxygen and air as well as providing good accuracy across the entire conversion range.

The approach used in this paper to model the gas–solid reaction of graphite and oxygen, provides a consistent framework to test the validity of complementary isothermal and non-isothermal data for a specific solid state reaction.

Potential causes for the unexpected behaviour include catalytic surface roughening as a result of the presence of trace metallic impurities. But no cause was found which could account for the behaviour across the entire range of conversions. Ultimately a comprehensive physical explanation of the mechanism underlying the conversion function, i.e. geometry, autocatalysis, diffusion, etc. and a fully analytical model have not yet been found to fit the oxidation behaviour of the graphite sample under investigation. The determination of such a model is the objective of ongoing research.