Introduction

The dry-type pyrometallurgical process of spent nuclear fuel is more attractive than the conventional wet method in respect of economical efficiency and waste quantity. In addition, resistance to nuclear proliferation is improved with the dry process, since the purity of extracted Pu in this process is relatively low. Thus, the pyroprocessing technology has raised hopes for the treatment of spent nuclear fuel without concerns of nuclear proliferation [1].

The central process of pyroprocessing for separating actinides from fission products (FPs) is the electrorefining step [2, 3]. The electrorefining process is carried out in the electrolytic cell that contains a molten eutectic chloride salt (LiCl–KCl) as an electrolyte operated at 773 K under an argon atmosphere [4]. In order to develop a pyroprocessor with high proliferation-resistance, high decontamination factor, as well as good throughput, it is important to have a capability for predicting electrochemical behavior of various constituents within a processor. In order to achieve a high process rate, it is essential to take into account a detailed geometry effect and reaction kinetics.

Attempts to make a 3-dimensional multi-physics model for an electrorefiner is a challenging task as they must solve a system of coupled non-linear equations with the added complication that the governing equation set changes under different physical situations and operational conditions at a current driven cell. A suitable technique has been desirable to represent the electro-fluid dynamic behavior for an electrorefining process. The application of computational fluid dynamic (CFD) methodology to modeling a molten-salt electrochemical system has spurred significantly progress including 3-dimensional capabilities [5].

In this study, an implementation of the electro-fluid analysis within a CFD framework is carried out to simulate the electrorefining process. In an electrorefiner geometry, the comprehensive approach and algorithm for representing the more realistic electro-fluid features are described.

Model development

Computational fluid dynamic model

The CFD model is 3-dimensional throughout the electrolyte field in an electrorefining cell, as shown in Fig. 1. The CFD model is set up within the ANSYS CFX-11.0 framework [6]. The electrolyte fluid flow of the electrolytic process is assumed to be well represented by the incompressible Navier–Stokes equation:

$$ \rho {\frac{\partial u}{\partial t}} + \rho u\nabla u = - \nabla P + \mu \nabla^{2} u + S_{u} $$
(1)
Fig. 1
figure 1

Schematic of a molten salt electrorefiner for a computational model

Full size image

where, u is the velocity, t is the time, μ is the turbulent viscosity, P is the pressure, ρ is the electrolyte density and S u represents momentum source for forced convection such as electrolyte stirring. Together with the continuity equation:

$$ \rho (\nabla \cdot u) = 0 $$
(2)

and the concentration (C) equation with external mass source (S C ):

$$ \rho {\frac{\partial C}{\partial t}} + \rho \nabla \cdot (uC) = \rho \nabla \cdot (D_{C} \nabla C) + S_{C} $$
(3)

where D C is the mass diffusivity.

A scalar transport equation is used to describe the transport of the reactive ion from the bulk to the electrode surface. The choice of spatial coordinate and the boundary conditions depend on the electrode geometry.

Electrochemical reaction rate

The polarization equation is necessary to express the dependence of the local rate of the reaction on the various concentrations and on the potential jump at the interface. It is common to use the Butler–Volmer equation of electrode kinetics for this form of metal/ion systems [7, 8]. The local current density (i) distribution on the electrode surface is modeled by the following equation:

$$ i = i_{0} \left[ {{\frac{{C_{O}^{S} }}{{C_{O}^{bulk} }}}{ \exp }\left( { - {\frac{\alpha F}{RT}}\eta } \right) - {\frac{{C_{R}^{S} }}{{C_{R}^{bulk} }}}{ \exp }\left( {{\frac{(1 - \alpha )F}{RT}}\eta } \right)} \right] $$
(4)

where F is the Faraday’s constant, R is the gas constant, η is the overpotential, α and k 0 are kinetic parameters, superscripts s and bulk are the locations at the electrode surface and bulk electrolyte, subscripts O and R are the oxidized and reduced species, and i 0 is the exchange current density:

$$ i_{0} = nk^{0} F\left( {C_{O}^{bulk} } \right)^{1 - \alpha } \left( {C_{R}^{bulk} } \right)^{\alpha } $$
(5)

where n is the ionic valence. This equation is a modified-type Butler–Volmer equation that includes terms of concentration overpotential as commonly used.

Boundary condition

A scalar transport equation is solved for the concentration of the ionic species, with source/sink (S C ) at the appropriate anode and cathode boundary based on Faraday’s law. The electric boundary conditions include the specification of a current flux equivalent to an applied current through the electrodes. The boundary conditions for the ionic species for the source/sink at the wall of electrodes are calculated as follows:

$$ S_{C} = \pm {\frac{i}{nF}} $$
(6)

On the anode side, a positive flux is applied, while a negative flux of a same size is applied on the cathode. No slip boundary (friction) conditions are enforced upon at all solid walls, whilst a free slip (no friction) boundary condition is applied at the top free surface.

The anodic dissolution and cathodic deposition at the electrode surface are given by the Butler–Volmer equation. Current density in this kinetic relation is a function of the ratio of local surface concentration to bulk concentration of reacting ions \( \left( {C^{S} /C^{Bulk} } \right) \) and electrode surface overpotential (η). Assuming that we impose a specific voltage drop E Cell across the electrodes, the overall voltage balance may be written as:

$$ E_{Cell} = E_{{{\text{U}}^{3 + } / {\text{U}}}}^{0} + \phi_{\text{ohm}} + \eta_{a} + \eta_{c} $$
(7)

Here \( E_{Cell} \) is the difference between the applied cell voltage and the thermodynamic equilibrium cell voltage (\( E_{{{\text{U}}^{3 + } / {\text{U}}}}^{0} \)). \( \phi_{\text{ohm}} \) is the ohmic voltage drop, \( \eta_{a} \) and \( \eta_{c} \) are the voltage drops due to activation polarization (i.e., kinetic effects) and concentration polarization (due to concentration gradients between the electrode surface and the bulk electrolyte) respectively.

Computational algorithm

The calculation is implemented through the user Fortran program links in the CFX-11.0 solver. A user Fortran source is compiled and linked into a platform of specific shared library. The shared library is dynamically loaded at a runtime. The local current density is calculated from the concentration gradient obtained from the latest solution fields for the locations on which the subroutine is currently operating. Then a linear solver of the CFX-11.0 runs for a coefficient loop until its solution satisfies the convergence criteria of the equation residuals.

Results and discussion

According to the above-mentioned approach, a simple electrorefiner was modeled. The vessel consists of an anode basket of a cruciform arrangement and a steel cathode submerged in a molten LiCl–KCl eutectic containing approximately 8 wt% of U. Table 1 shows the properties of the LiCl–KCl eutectic used in the study. The molten salt electrolyte is mixed during the electrorefining process by the rotating cathode (50 rpm clockwise) and anode basket assemblies (50 rpm clockwise). The operational conditions, physical properties and kinetic parameters for the electrorefining analysis are summarized in Table 2.

Table 1 Data of the molten eutectic salt (LiCl–KCl) used as an electrorefiner electrolyte [9]
Full size table
Table 2 Parameters and thermodynamic data used in the calculation at 773 K [9]
Full size table

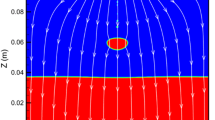
Figure 2 shows a pattern of velocity stream lines exhibiting a fully developed fluid behavior. This is due to that a salt electrolyte is stirred and mixed during the electrorefining process mainly by the rotating anode assemblies of fuel dissolution baskets. Both walls of electrode surfaces are defined to consider a wall friction by assuming an appropriate roughness height (0.01 m). These roughnesses specified are the equivalent dendrite growth on the cathode and coarse surface of anode baskets for a no-slip wall velocity option in the k-epsilon turbulence model [6].

Fig. 2
figure 2

Schematic of electrorefiner exhibiting a fully developed fluid behavior

Full size image

The concentration profiles of ionic reacting species U is shown between the both electrodes in Fig. 3. As expected, U ion depletion near the cathode surface and generation from the anode are depicted under this convective turbulent condition. It is shown that the concentration distribution of U in the bulk electrolyte region is almost uniform.

Fig. 3
figure 3

Concentration profiles of ionic reacting species U between both electrodes

Full size image

Here we suppose that the only one electrochemical reaction taking place at the anode is dissolution of U metal, that is:

$$ {\text{U}} \to {\text{U}}^{3 + } + 3 {\text{e}}^{ - } \quad \quad E_{{{\text{U}}^{3 + } / {\text{U}}}}^{ 0} = - 1.244\,{\text{V}}\;{\text{vs}} .\;{\text{Ag}}^{ + } / {\text{Ag}}^{ 0} $$

where, \( E_{{{\text{U}}^{3 + } / {\text{U}}}}^{0} \) is the standard potential of reaction. At the cathode, the reduction deposition takes place at a given applied current. The electrotransport rate of U from anode to cathode could be limited by decreased reactant concentration near the cathode surface. In this calculation, an initial estimate of the potentials is automatically generated from the value of \( E_{{{\text{U}}^{3 + } / {\text{U}}}}^{0} \) at each of the electrodes.

In an electrorefining cell, all of the potentials in the electrolyte solution must fall between the potentials imposed on the anode and cathode. This principle is used in making the estimates and adjustments of the electrode potential reflected with overpotential at a given current density. Ohmic overpotential is the loss associated with resistance to electron transport in the electrolyte region. For a given applied current, magnitude of this overpotential is dependent on the path of the electron.

The diffusion overpotentials is related to the concentration gradient near the electrodes. It is found that the concentration gradient at the electrode surface is proportional to the applied current over a wide current range up to around the limiting current density. Figure 4 depicts the local current density distribution along the electrode surface in case of coupled computation with the concentration gradient. The effects of electrolyte concentration are taken into account. It is found that a higher local potential is arisen from a lower ionic concentration at the electrode surface. In order to maintain the given current density, a higher overpotential is necessary for the compensation of the ionic reactant depletion.

Fig. 4
figure 4

Current density distribution coupling U concentration gradient between both electrodes

Full size image

The current density required to drive the electrochemical reaction is generally a function of the overpotential. Because of U ion depletion near the electrode surface, concentration overpotential altered the shape of the current density curve at electrode potentials.

In Figure 5, the cell potential distribution between the electrodes is plotted with account taken of applied current density. These include ohmic potential drop and surface overpotential. It is found that the ohmic potential drop is larger than surface overpotential in this calculation condition using the concentration-dependent Butler–Volmer kinetics.

Fig. 5
figure 5

Calculated cell potential variation with applied current density

Full size image

Conclusions

A three-dimensional computational electro-fluid dynamics model of an electrorefining cell was developed on a CFD framework. This model provides valuable information about the transport phenomena inside the cell such as concentration distribution, potential distribution, overpotential distribution, and local current distribution. A unique feature of this model is the implementation of the potential-to-current algorithm that allows for a more realistic spatial variation of the electrochemical kinetics. The computational procedure involves the coupling of the potential field with the ionic species concentration field. Rather than assuming a constant surface overpotential over the electrode surface, the spatial variation of the cathode surface overpotential is computed locally, resulting in improved prediction of the local current density distribution. The current density distribution patterns are found to vary with applied current conditions. Future work will focus on a benchmark test for this unique approach with available experimental data from an aqueous electroplating cell.