1 Introduction

In this paper, we describe a path following algorithm based both on the central path and on the Levenberg–Marquardt (LM) trajectories for solving the problem of minimizing a convex and continuously differentiable function on a bounded polyhedron with nonempty algebraic interior.

The objective of this work is to show that, near the analytic center, the trajectories share the same tangent, which will allow one the construction of a procedure to initialize an interior point path following algorithm for solving the problem from a point on the LM trajectory. This procedure assumes that the analytic center is known, which is the case in trust region subproblems.

In Sect. 2, we define both trajectories. In Sect. 3, we describe trust region subproblems, in which we apply our procedure. In Sects. 4 and 5, we establish primal-dual relations between the trajectories and, in Sects. 6 and 7, we present our procedure and numerical results. In Sect. 8, we give some conclusions.

2 The Trajectories

Consider the problem

$$ \mbox{minimize } f(x)\quad\mbox{s.t. } Ax=b,\ x\geq0, $$
(1)

where \(f:\mathbb{R}^{n}\rightarrow\mathbb{R}\) is a convex and continuously differentiable function, \(A\in\mathbb{R}^{m\times n}\) and \(b\in\mathbb{R}^{m}\). We denote the feasible set by \(\varOmega:=\{x\in\mathbb{R}^{n}|Ax=b, x\geq0\}\) and the set of algebraic interior points by Ω 0:={x∈Ω|x>0}.

We assume that Ω is bounded and Ω 0≠∅. Then, the logarithmic barrier function \(x\in\varOmega^{0}\mapsto p_{\log}(x) :=-\sum_{i=1}^{n}\log(x_{i})\) is well-defined, as well as the analytic center of Ω, χ=argmin{p log(x)∣x∈Ω 0} (see [1]).

To simplify the treatment, we assume that

$$\chi=e=(1,1,\ldots,1)\in \mathbb {R}^n. $$

This assumption is made without any loss of generality, as we now show: given the problem

$$ \mbox{minimize } f_0(w) \quad \mbox{s.t. } A_0w=b,\ w\geq0, $$
(2)

with the same hypotheses as above but with analytic center w AN >0, the format (1) is obtained by defining \(W_{AN}:=\operatorname{diag}(w_{AN})\) and scaling the problem by setting w:=W AN x, A:=A 0 W AN and for \(x\in \mathbb {R}^{n} \), f(x):=f 0(W AN x). The scaled problem inherits the convexity of the original one because W AN is positive definite, and now the analytic center becomes χ=e, because w AN =W AN e.

The objective function of (1) will be modified to f(x)+μp(x) by penalty terms in two ways:

  1. (a)

    with the logarithmic barrier p log, which determines the primal central path

    $$\mu>0\mapsto x_{\log}(\mu)=\mathop {\mathrm {argmin}}_{x\in\varOmega^0} f(x)+\mu p_{\log}(x). $$
  2. (b)

    with the LM regularization

    $$x\in \mathbb {R}^n\mapsto p_{LM}(x):=\|x-e\|^2 /2 , $$

    which defines the primal LM trajectory

    $$ \mu>0\mapsto x_{LM}(\mu)=\mathop {\mathrm {argmin}}\bigl\{ f(x)+\mu p_{LM}(x)\mid Ax=b, x\in \mathbb {R}^n\bigr\} . $$
    (3)

The idea of this quadratic penalization goes back to [2, 3].

The central path is contained in Ω 0 and is scale-independent, while the LM trajectory is scale-dependent and is in general not contained in Ω. Points on the LM trajectory may be easy to compute, but are in general feasible only for large values of μ.

3 Trust Region Subproblems

Our main motivation comes from the solution of trust region subproblems with the shape

$$\mbox{minimize } \bigl\{ m(d) \mid Ad=b, \|d\|\leq\Delta\bigr\} , $$

where m(⋅) is convex quadratic and Δ>0. If the Euclidean norm is used, the minimizers are points on the LM trajectory, which may be easy to compute. The infinity norm gives larger trust regions, which are very convenient whenever box constraints are present in the original problem.

The box-constrained trust region subproblem is stated in the format (1) as follows: consider the convex quadratic program

$$ \begin{array}{l@{\quad}l} \mbox{minimize} &\displaystyle \biggl[\frac{1}{2} (\bar{z}+d)^\top\bar{Q} (\bar{z}+d)+\bar{c}^\top(\bar{z}+d) \biggr] \\ \mbox{s.t.} & \bar{A} d=0, -u \leq d \leq u, \end{array} $$
(4)

where \(\bar{Q}\in\mathbb{R}^{\bar{n}\times\bar{n}}\) is symmetric and positive semidefinite, \(\bar{z}, \bar{c}\in\mathbb{R}^{\bar{n}}\), \(u\in\mathbb {R}_{++}^{\bar{n}}\) and \(\bar{A}\in\mathbb{R}^{\bar{m}\times\bar{n}}\). The logarithmic barrier function for this problem is

$$-u<d<u \mapsto -\sum_{i=1}^{\bar{n}} \log(u_i-d_i) -\sum_{i=1}^{\bar{n}} \log(u_i+d_i), $$

and its minimizer, the analytic center of the feasible set, is d=0.

The following reformulation of Problem (4) is based on the change of variables z:=u+d and w:=u−d:

$$ \begin{array}{l@{\quad}l} \mbox{minimize} &\displaystyle \biggl[\frac{1}{2} z^\top\bar{Q} z+\bigl(\bar{c}+\bar{Q}(\bar{z}-u)\bigr)^\top z \biggr] \\ \mbox{s.t.} & \left [ \begin{array}{c@{\quad}c} \bar{A} & 0 \\ I & I \end{array} \right ] \left [ \begin{array}{c} z \\ w \end{array} \right ]=\left [ \begin{array}{c} \bar{A}u \\ 2u \end{array} \right ] \\ & z,w \geq0. \\ \end{array} $$
(5)

Defining \(U:=\operatorname{diag}(u)\) and \(x:=(U^{-1}z,U^{-1}w)\in \mathbb {R}^{2\bar{n}}\), we rewrite Problem (5) as

$$ \begin{array}{l@{\quad}l} \mbox{minimize} &\displaystyle \biggl[\frac{1}{2} x^\top Qx +c^\top x \biggr] \\ \mbox{s.t.} & Ax=b,\ x \geq0, \end{array} $$
(6)

where , , and .

One can easily check that (6) inherits the convexity of (4) and that these problems are in an obvious correspondence with respect to optimality, due to our change of variables. Moreover, we have that \(e\in \mathbb {R}^{n}\), with \(n:=2\bar{n}\), is the analytic center of the compact polyhedron \(\varOmega:=\{x\in \mathbb {R}^{n}|Ax=b\mbox{ and }x\geq0\}\).

The following straightforward facts on the geometry of the trajectories are shown in Fig. 1:

  1. (i)

    For μ>0, d LM (μ)=argmin{m(d)∣Ad=0,∥d∥≤∥d LM (μ)∥}, i.e., d LM (μ) is the minimizer of m(⋅) in an Euclidean trust region around 0. These trust regions are contained in the box for large values of μ, and in general d LM (μ) is infeasible for small μ.

  2. (ii)

    For μ>0, d log(μ)=argmin{m(d)∣Ad=0,p log(d)≤p log(d log(μ))}, i.e., d log(μ) minimizes m(⋅) in a log-barrier trust region around 0. These trust regions are feasible and approach the feasible set as μ decreases, while d log(μ) converges to an optimal solution of (4).

Fig. 1
figure 1

The trajectories

Full size image

Figure 1 shows the evolution of the trajectories and trust regions for an example with a unit box and non-interior optimal solution. The figures at left and right show respectively the trust regions for large and small values of μ. For large values of μ the trust regions are very similar, as well as the trajectories. As μ decreases, the trajectories branch out.

Remark 3.1

Although this is not a subject of this paper, such log-barrier trust regions may be used in trust region methods for convex programming, avoiding the need for solving (4) precisely.

4 Preliminaries

In this section, we define the primal-dual versions of the central path and LM trajectories and neighborhoods of the central path. Consider the Karush–Kuhn–Tucker (KKT) conditions of Problem (1), given by

$$\begin{aligned} &P_{\mathcal{K}(A)} \bigl(\nabla f(x)-s \bigr)=0 \end{aligned}$$
(7)
$$\begin{aligned} &Ax =b,\quad x \geq0,\quad s \geq0 \end{aligned}$$
(8)
$$\begin{aligned} &x\cdot s =0, \end{aligned}$$
(9)

where P is the Euclidean projection operator, \(x\cdot s:=(x_{1}s_{1},\dots,x_{n}s_{n})\in \mathbb {R}^{n}\) is the Hadamard product and \(\mathcal{K}(A):=\{x\in \mathbb {R}^{n}|Ax=0\}\). Due to convexity, these conditions are necessary and sufficient for optimality of (1).

We say that a strictly positive pair \((x,s)\in \mathbb {R}^{n}_{++}\times \mathbb {R}^{n}_{++}\) is an interior feasible primal-dual point associated with (1), if it satisfies both the Lagrange condition (7) and (8). We denote by Γ ∘ the set of all interior feasible primal-dual points, i.e.,

$$\varGamma^\circ:=\bigl\{ (x,s)\in \mathbb {R}_{++}^n\times \mathbb {R}^n_{++}|Ax=b,P_{\mathcal {K}(A)} \bigl(\nabla f(x)-s \bigr)=0 \bigr\} . $$

4.1 The Primal-Dual Central Path

The primal-dual central path associated with Problem (1) is the curve

$$\mu>0\mapsto\bigl(x_{CP}(\mu),s_{CP}(\mu)\bigr)\in \varGamma^\circ\quad\mbox{such that } x_{CP}(\mu)\cdot s_{CP}(\mu)=\mu e. $$

Under our hypotheses, [4] ensures that the central path is well defined, and it is consistent with the former definition of primal central path, as x log(μ)=x CP (μ) for μ>0. The primal central path {x CP (μ)|μ>0} converges to an optimal solution of Problem (1) as μ→0+. For related results under weaker assumption, see [5]. For primal-dual convergence properties of the central path we refer the reader to [6]. In this paper we are interested in the features of the central path close to the analytic center, i.e., when μ is large.

4.2 Neighborhoods of the Central Path

Sequences generated by path following algorithms [7–9] remain in the proximity of the central path along the iterates, in the sense described by proximity measures. The proximity measure we are going to use in the theoretical treatment is defined by

$$ (x,s)\in\varGamma^\circ, \mu>0 \mapsto \sigma(x,s,\mu):= \biggl\Vert \frac{x\cdot s}{\mu}-e\biggr\Vert . $$
(10)

Clearly, (x,s)∈Γ ∘ is the central point associated with μ>0 if and only if σ(x,s,μ)=0.

Low complexity path following algorithms compute sequences (x k ,s k ,μ k ) such that σ(x k ,s k ,μ k )≤ρ, where ρ is a fixed positive tolerance. These points belong to a neighborhood of the central path

$$\mathcal{N}_2(\rho):=\displaystyle \bigl\{ (x,s,\mu)\in \varGamma^\circ \times R_{++}\mid\sigma(x,s,\mu)\leq \rho \bigr\} . $$

Practical algorithms (with a higher proved complexity) use a larger neighborhood, defined by (see [10, Chap. 5]):

$$\mathcal{N}_{-\infty}(\rho):= \biggl\{ (x,s,\mu)\in\varGamma^\circ \times R_{++}\biggm| \frac{x_i s_i}{\mu}\geq1-\rho,\forall i=1,\dots,n \biggr\} . $$

This neighborhood will be used in our implementation. For a study of other proximity measures, see [11].

The next lemma shows than one can easily get an interior feasible primal-dual point with its primal part being the analytic center.

Lemma 4.1

Let s e (μ):=∇f(e)+μe. Then, for all sufficiently large μ>0, we have (e,s e (μ))∈Γ ∘. Moreover, σ(e,s e (μ),μ)=μ −1∥∇f(e)∥.

Proof

The proof that (e,s e (μ))∈Γ ∘ for all large μ>0 is straightforward. Now, note that

$$\begin{aligned} \sigma\bigl(e,s_e(\mu),\mu\bigr) =&\biggl\Vert \frac{e\cdot(\nabla f(e)+\mu e)}{\mu }-e \biggr\Vert \\ =&\biggl\Vert \frac{\nabla f(e)}{\mu}+e-e\biggr\Vert = \mu^{-1}\bigl\| \nabla f(e)\bigr\| . \end{aligned}$$

 □

Note that, for large values of μ, the point (e,s e (μ)) is centralized.

4.3 The Primal-Dual LM Trajectory

Consider the primal LM trajectory x LM defined in (3).

In our construction, it is easy to verify that for a given μ>0, x LM (μ) can be obtained solving the problem in (3) with p LM replaced by the penalization \(\frac{1}{2}\|\cdot\|^{2}\).

For convenience, we define the dual LM trajectory by taking

$$s_{LM}(\mu):=\mu\bigl(2\chi-x_{LM}(\mu)\bigr), \quad \mbox{for each } \mu>0. $$

This will allow us to relate the primal-dual trajectories in the next section.

5 Primal-Dual Relations Between the LM and the Central Path Trajectories

The first lemma in this section describes properties of the trajectory associated with a general strongly convex penalty function, and will be used to establish primal relations between the central path and the LM trajectory.

5.1 An Auxiliary Result

For each μ>0 consider the problem

$$ \mbox{minimize } \bigl[f(x)+\mu p(x) \bigr],\quad \mbox{s.t. } Ax=b, $$
(11)

where \(p:\mathbb{R}^{n}\rightarrow\mathbb{R}\cup\{\infty\}\) is a strongly convex function.

Lemma 5.1

Let \(\bar{x}\) be the minimizer of p subject to Ax=b and suppose that p is twice continuously differentiable with a locally Lipschitz Hessian ∇2 p(⋅) at \(\bar{x}\). Assume also that \(\nabla^{2} p(\bar{x})=I\). Then, considering that x(μ) denotes the solution of the optimization problem (11), with μ>0, it follows that:

  1. (i)

    The trajectory \(\{x(\mu)\in\mathbb{R}^{n}|\mu>0\}\) is well defined and \(\lim_{\mu\to\infty} x(\mu)=\bar{x}\);

  2. (ii)

    x(μ) minimizes f in the convex trust region \(\{ x\in\mathbb{R}^{n}|p(x)\leq p(x(\mu)), Ax=b\}\) and μ>0↦p(x(μ)) is a non-increasing function;

  3. (iii)

    \(\lim_{\mu\to\infty}\mu ( x(\mu)-\bar{x} )=-P_{\mathcal{K}(A)}(\nabla f(\bar{x}))\).

Proof

For any μ>0, the function f+μp is strongly convex. Hence, (11) has the unique solution x(μ). In particular, \(\{x(\mu)\in\mathbb{R}^{n}|\mu >0\}\) is well defined. From the definition of x(μ) and \(\bar{x}\) we have, for all μ≥1, that

$$\begin{aligned} f\bigl(x(\mu)\bigr)+p\bigl(x(\mu)\bigr)-p(\bar{x})&\leq f\bigl(x(\mu)\bigr)+\mu \bigl(p\bigl(x(\mu)\bigr)-p(\bar{x}) \bigr) \\ &\leq f(\bar{x})+\mu \bigl(p(\bar{x})-p(\bar{x}) \bigr)= f(\bar{x}). \end{aligned}$$

This inequality, together with the compactness of the level sets of f+p, implies that \(\{x(\mu)\in\mathbb{R}^{n}|\mu\geq1\}\) is bounded. Consequently, {f(x(μ))} μ≥1 must be bounded. Therefore, the second inequality leads to

$$\lim_{\mu\rightarrow\infty}\mu\bigl( p\bigl(x(\mu)\bigr)-p(\bar{x})\bigr)< \infty. $$

Hence,

$$\lim_{\mu\rightarrow\infty} p\bigl(x(\mu)\bigr)-p(\bar{x})=0. $$

Then, the strong convexity of p guarantees that

$$\lim_{\mu\rightarrow\infty} x(\mu)=\bar{x}, $$

proving (i).

The KKT conditions of (11), necessary and sufficient due to convexity, read as follows:

$$\begin{aligned} P_{\mathcal{K} (A)} \bigl(\nabla f \bigl(x(\mu)\bigr)+\mu\nabla p \bigl(x(\mu)\bigr) \bigr) =&0; \end{aligned}$$
(12)
$$\begin{aligned} A \bigl(x(\mu) \bigr) =&b. \end{aligned}$$
(13)

From (12) and (13) we conclude that x(μ) minimizes f in the convex set \(\{x\in\mathbb{R}^{n}|p(x)\leq p(x(\mu)), Ax=b\}\). Moreover, the Lagrange multiplier correspondent to the inequality constraint is μ. Now take 0<μ 2<μ 1. Then,

$$\begin{aligned} f \bigl(x(\mu_2) \bigr)+\mu_2p \bigl(x( \mu_2) \bigr) \leq& f \bigl(x(\mu_1) \bigr)+ \mu_2p \bigl(x(\mu_1) \bigr), \\ f \bigl(x(\mu_1) \bigr)+\mu_1p \bigl(x( \mu_1) \bigr) \leq& f \bigl(x(\mu_2) \bigr)+ \mu_1p \bigl(x(\mu_2) \bigr). \end{aligned}$$

Adding these inequalities we get p(x(μ 1))≤p(x(μ 2)), proving (ii).

Note that, if for some \(\bar{\mu}>0\) we have \(x(\bar{\mu})=\bar{x}\), then the strong convexity of p and (ii) guarantee that \(x(\mu)=\bar{x}\) for every \(\mu>\bar{\mu}\). In this case, (12) implies (iii). Therefore, let us assume from now on that \(x(\mu)\neq\bar{x}\) for all μ>0. From Taylor’s formula we have that

$$ p(x)-p(\bar{x})-\nabla{p(\bar{x})}^\top(x-\bar{x})- \frac{1}{2}(x-\bar{x})^\top\nabla^2p(\bar{x}) (x-\bar{x})=o\bigl(\Vert x-\bar{x}\Vert ^2\bigr), $$
(14)

with

$$\lim_{x\to\bar{x}}\frac{o(\|x-\bar{x}\|^2)}{\|x-\bar{x}\|^2}=0. $$

Moreover, from the local Lipschitz continuity of ∇2 p around \(\bar{x}\), we know that there exist L>0 and δ>0, so that for all \(x\in \mathcal{B}(\bar{x}, \delta)\) it holds that

$$ \bigl\Vert v(x)\bigr\Vert \leq L \Vert x - \bar{x}\Vert ^2, $$
(15)

where

$$v(x):=\nabla p(x)-\nabla p(\bar{x})-\underbrace{\nabla^2 p(\bar{x})}_{I} (x-\bar{x}). $$

Since \(\bar{x}\) is the minimizer of p subject to Ax=b, we conclude that \(\nabla p(\bar{x})\) is orthogonal to \(\mathcal{K}(A)\). Then, taking also (14) and \(\nabla^{2}p(\bar{x})=I\) into account, we get

$$ p\bigl(x(\mu)\bigr)-p(\bar{x})=\bigl\| x(\mu)-\bar{x}\bigr\| ^2 \biggl(\frac{1}{2}+\frac{o(\|x(\mu)-\bar{x}\|^2)}{\|x(\mu)-\bar{x}\|^2} \biggr) $$
(16)

for all μ sufficiently large. Due to (13) and the feasibility of \(\bar{x}\), it follows that \(x(\mu) - \bar{x}\in\mathcal{K}(A)\), for all μ>0. Then, using the linearity of \(P_{\mathcal{K}(A)}\) and (12) we obtain

$$\begin{aligned} 0&=P_{\mathcal{K}(A)} \bigl(\nabla f\bigl(x(\mu)\bigr)+\mu\nabla p \bigl(x(\mu)\bigr) \bigr) \\ &=P_{\mathcal{K}(A)} \bigl(\nabla f\bigl(x(\mu)\bigr)+\mu\nabla p(\bar{x})+\mu \bigl(x(\mu)-\bar{x}\bigr)+\mu v\bigl(x(\mu)\bigr) \bigr) \\ &=P_{\mathcal{K}(A)}\bigl(\nabla f\bigl(x(\mu)\bigr)\bigr)+\mu P_{\mathcal{K}(A)} \bigl(\nabla p(\bar{x})\bigr)+\mu P_{\mathcal{K}(A)}\bigl(x(\mu)-\bar{x} \bigr) \\ &\quad{}+P_{\mathcal {K}(A)}\bigl(\mu v\bigl(x(\mu)\bigr)\bigr) \\ &=P_{\mathcal{K}(A)}\bigl(\nabla f\bigl(x(\mu)\bigr)\bigr)+\mu\bigl(x(\mu)-\bar{x} \bigr)+ P_{\mathcal {K}(A)}\bigl(\mu v\bigl(x(\mu)\bigr)\bigr). \end{aligned}$$
(17)

In order to finish the proof we will show that lim μ→∞ μv(x(μ))=0. Note that the definition of x(μ) implies that

$$0\leq\mu\bigl(p\bigl(x(\mu)\bigr)-p(\bar{x})\bigr) \leq f(\bar{x})-f\bigl(x(\mu) \bigr). $$

Using (i) we get

$$ \lim_{\mu\to\infty}\mu\bigl(p\bigl(x(\mu)\bigr)-p(\bar{x}) \bigr)=0. $$
(18)

Now, multiplying (16) by μ and taking limits, we obtain

$$ \lim_{\mu\rightarrow\infty}\mu\bigl\Vert x(\mu)-\bar{x}\bigr\Vert ^2=0. $$
(19)

Using (15) we conclude that lim μ→∞ μv(x(μ))=0. This fact, combined with (17), implies (iii). □

One can trivially check that p log and p LM satisfy the hypotheses of Lemma 5.1 with \(\bar{x}=\chi=e\). Note also that \(P_{\mathcal{K}(A)}(e)=0\).

Hence, item (ii) of Lemma 5.1 implies that x LM (μ) and x CP (μ) minimize f subject to Ax=b in the Euclidean ball centered at χ=e with radius ∥x LM (μ)∥ and in the level set \(\{x\in \mathbb {R}^{n}|p_{\log}(x)\leq p_{\log}(x_{CP}(\mu))\}\), respectively.

5.2 Our Theorem

Theorem 5.1

It holds that:

  1. (i)

    \(P_{\mathcal{K}(A)} (\nabla f(x_{LM}(\mu))-s_{LM}(\mu) )=0\) for all μ>0;

  2. (ii)

    σ(x LM (μ),s LM (μ),μ)≤∥x LM (μ)−χ∥2, where σ is the proximity measure given in (10);

  3. (iii)

    the LM trajectory and the central path associated with (1) are tangent at χ=e;

  4. (iv)

    for all μ>0 sufficiently large, \((x_{LM}(\mu), s_{LM}(\mu))\in \mathbb {R}^{n}\times \mathbb {R}^{n}\) is an interior feasible primal-dual point associated with (1).

Proof

From the linearity of \(P_{\mathcal{K}(A)}\) and the definition of x LM (μ) and s LM (μ), we conclude that

$$\begin{aligned} &P_{\mathcal{K}(A)} \bigl(\nabla f\bigl(x_{LM}(\mu)\bigr)-s_{LM}( \mu) \bigr) \\ &\quad=P_{\mathcal{K}(A)} \bigl(\nabla f\bigl(x_{LM}(\mu)\bigr)+\mu x_{LM}(\mu) -2\mu\chi \bigr) \\ &\quad=P_{\mathcal{K}(A)} \bigl(\nabla f\bigl(x_{LM}(\mu)\bigr)+\mu x_{LM}(\mu) \bigr) -2\mu P_{\mathcal{K}(A)} ( \chi ) \\ &\quad=0-2\mu P_{\mathcal{K}(A)}(e)=0. \end{aligned}$$

This proves (i). Let us now prove (ii).

Considering the definition of the proximity measure σ given in (10) and remembering that χ=e, we conclude that

$$\begin{aligned} \sigma\bigl(x_{LM}(\mu),s_{LM}(\mu),\mu\bigr)&:=\biggl\Vert \frac{x_{LM}(\mu)\cdot s_{LM}(\mu)}{\mu}-e\biggr\Vert \\ &=\bigl\Vert x_{LM}(\mu)\cdot\bigl(2\chi-x_{LM}(\mu) \bigr)-e\bigr\Vert \\ &=\bigl\Vert \bigl(\chi+\bigl(x_{LM}(\mu)-\chi\bigr)\bigr)\cdot \bigl(\chi- \bigl(x_{LM}(\mu)-\chi\bigr)\bigr)-e\bigr\Vert \\ &=\bigl\Vert \bigl(x_{LM}(\mu)-\chi\bigr)\cdot\bigl(x_{LM}( \mu)-\chi\bigr)\bigr\Vert \\ &\leq\bigl\Vert x_{LM}(\mu)-\chi\bigr\Vert ^2. \end{aligned}$$

Taking into account that p log and p LM satisfy the hypotheses of Lemma 5.1, item (iii) follows directly from item (iii) in Lemma 5.1.

Due to item (i), and the fact that Ax LM (μ)=b, we only need to check the positivity of x LM (μ) and s LM (μ) in order to prove (iv). But this follows for sufficiently large μ>0, since χ=e>0 and lim μ→∞ x LM (μ)=χ. □

Our theorem says basically that the primal-dual LM trajectory {(x LM (μ),s LM (μ))|μ>0} is given by interior primal-dual feasible points associated with Problem (1) (for all μ sufficiently large) that lie close to the primal-dual central path in terms of the proximity measure σ. Furthermore, the primal LM trajectory is tangent to the central path at the analytic center χ=e. We established these results for a general convex continuously differentiable function f.

6 Interior Point Scheme

We now present a scheme for solving Problem (1) composed of two phases: Phase 1 follows the primal-dual LM trajectory until a point near the central path is found; an interior point path following method is then started at this point. Phase 1 will stop when a point in a neighborhood \(\mathcal{N}(\rho) \) is found, where ρ is a proximity constant, usually ρ<1 and \(\mathcal{N}=\mathcal{N}_{2} \) or \(\mathcal{N}=\mathcal {N}_{-\infty} \). In the algorithm below we start following the LM trajectory at a given value μ 0 and increase it.

Phase 1: Primal-Dual LM Path Following

Set k:=0 and choose μ 0>0, ρ>0 and β>1;

REPEAT

Compute the solution x LM (μ) of (3) with μ:=μ k and define \(s_{LM}(\mu_{k}):=\mu_{k} (2\underbrace{\chi}_{e}-x_{LM}(\mu_{k}))\);

IF \((x_{LM}(\mu_{k}), s_{LM}(\mu_{k}))\notin\mathcal{N}(\rho)\), set μ k+1:=βμ k , k=k+1.

ELSE set \((\hat{x},\hat{s})=(x_{LM}(\mu_{k}), s_{LM}(\mu_{k})) \) and stop.

Phase 2: Path Following Scheme

Choose and implement a primal-dual interior point method taking \((\hat{x}, \hat{s})\) as the initial point.

Due to Theorem 5.1 this scheme is well defined and may be applied to any problem in the format (1).

6.1 Our Theorem Applied to Convex Quadratic Programming

Theorem 5.1 is specially interesting when f is quadratic. In this case, one can calculate points on the LM trajectory by solving linear systems of equations. Indeed, if \(f:\mathbb {R}^{n}\rightarrow \mathbb {R}\) is a convex quadratic function given by

$$f(x):=\frac{1}{2}x^\top Q x+c^\top x $$

where \(c\in \mathbb {R}^{n}\) and \(Q\in \mathbb {R}^{n\times n}\) is positive semidefinite, then the KKT conditions of Problem (3) that define the LM trajectory read as follows:

$$ \left [ \begin{array}{c@{\quad}c} Q+\mu I & A^\top\\ A & 0 \end{array} \right ]\left [ \begin{array}{c} x \\ \lambda \end{array} \right ]=\left [ \begin{array}{c} -c \\ b \end{array} \right ]. $$
(20)

For each μ>0 this system is always solvable and its unique solution is x LM (μ). Uniqueness in λ is ensured if, and only if, A is full rank.

So, in the quadratic case, Phase 1 turns out to be easily implementable, since the primal-dual LM trajectory is defined by means of the linear system (20).

7 Numerical Experiments

We generate instances of Problem (4) for different values of \(\bar{n} \) and \(\bar{m} \), and solve them by an infeasible path following interior point algorithm using three different primal-dual starting points: the point given by our scheme, the Mehrotra starting point [12], and the analytic center χ=e with a dual variable s e (μ) given by Lemma 4.1 for a large value of μ. Since the analytic center is known, we shall see that the third choice is always better than the second.

Each test problem with given \(\bar{n} \) and \(\bar{m} \) is constructed as follows:

  • \(\bar{A} \) is an m×n matrix with random entries in [−1,1].

  • \(\bar{Q} \) is obtained by the following procedure: let D be a diagonal matrix with random entries in [1,1000], and M a unitary random matrix (constructed using the Matlab routine qr). Now \(\bar{Q}=MDM^{\top}\) is a randomly generated Hessian matrix with eigenvalues \(\operatorname{diag}(D) \).

The objective function is given by \(( x - x^{*} )^{\top}\bar{Q}( x - x^{*})/2 \), where the global minimizer x ∗ is obtained by projecting a random vector into the null space of \(\bar{A} \) and then adjusting it so that ∥x ∗∥∞=1.2. This choice is done to stress the nonlinearity in the examples: if x ∗ is in the unit box, the minimization becomes too easy; if its norm is large, the LM trajectory becomes nearly straight, again too easy.

We do not elaborate on the search along the LM trajectory, studied in non-linear programming texts like [13]. For our series of examples we used the simple strategy of setting \(\mu_{0}=\hat{\mu}/2 \), where \(\hat{\mu}\) is the parameter value obtained by the previous example (μ 0=1 for the first example in the series). This is a usual scheme in trust region algorithms for non-linear programming.

We used Matlab R2012a to implement the infeasible path-following method for convex quadratic programming presented in [14]. The tolerance for optimality is fixed at 10−8 and the barrier parameter is reduced by a factor of 10 at each iteration. As a measure of performance we used the number of iterations necessary for convergence.

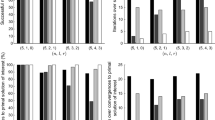
Table 1 lists the results for 56 problems: for each value of \(\bar{n}\) in the first column and four values of \(\bar{m}\), we run the three strategies. The column LM displays the number of iterations Phase 1/Phase 2 of our scheme; columns M and AC correspond to the number of iterations of the interior point method using respectively the Mehrotra starting point and the analytic center.

Table 1 Number of iterations for the interior point method using the LM starting point, the Mehrotra starting point and the analytic center
Full size table

From the table we see that for this choice of quadratic objectives, our scheme spares about 3 iterations from the interior point algorithm. This may be very significant in trust region algorithms, in which there is no need for a high precision in the solution of Problem (4).

8 Conclusions

The main goal of this paper is to show how the primal-dual LM and central trajectories are related for general linearly constrained convex programming problems, and then to develop an initialization technique for path following methods based on this relationship.

We believe that the main application of this is in trust region methods for non-linear programming based on trust regions defined by level sets of the barrier penalty function, which are contained in the unit box, as we remarked in Sect. 2.

Initial numerical experiments indicate that our initialization technique spares about 3 iterations from the interior point algorithm. More robust numerical experiments should be carried out on a larger collection of relevant problems where the analytic center is known. In particular, the algorithm should be tested on trust region subproblems from general non-linear solvers.