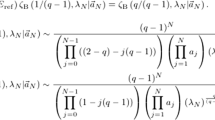Entropic Fluctuations in Thermally Driven Harmonic Networks

Abstract

We consider a general network of harmonic oscillators driven out of thermal equilibrium by coupling to several heat reservoirs at different temperatures. The action of the reservoirs is implemented by Langevin forces. Assuming the existence and uniqueness of the steady state of the resulting process, we construct a canonical entropy production functional $S^t$ which satisfies the Gallavotti–Cohen fluctuation theorem. More precisely, we prove that there exists $\kappa _c>\frac{1}{2}$ such that the cumulant generating function of $S^t$ has a large-time limit $e(\alpha )$ which is finite on a closed interval $[\frac{1}{2}-\kappa _c,\frac{1}{2}+\kappa _c]$, infinite on its complement and satisfies the Gallavotti–Cohen symmetry $e(1-\alpha )=e(\alpha )$ for all $\alpha \in {\mathbb {R}}$. Moreover, we show that $e(\alpha )$ is essentially smooth, i.e., that $e'(\alpha )\rightarrow \mp \infty$ as $\alpha \rightarrow \tfrac{1}{2}\mp \kappa _c$. It follows from the Gärtner–Ellis theorem that $S^t$ satisfies a global large deviation principle with a rate function I(s) obeying the Gallavotti–Cohen fluctuation relation $I(-s)-I(s)=s$ for all $s\in {\mathbb {R}}$. We also consider perturbations of $S^t$ by quadratic boundary terms and prove that they satisfy extended fluctuation relations, i.e., a global large deviation principle with a rate function that typically differs from I(s) outside a finite interval. This applies to various physically relevant functionals and, in particular, to the heat dissipation rate of the network. Our approach relies on the properties of the maximal solution of a one-parameter family of algebraic matrix Riccati equations. It turns out that the limiting cumulant generating functions of $S^t$ and its perturbations can be computed in terms of spectral data of a Hamiltonian matrix depending on the harmonic potential of the network and the parameters of the Langevin reservoirs. This approach is well adapted to both analytical and numerical investigations.

1 Introduction

Boundary driven mechanical systems are paradigmatic in nonequilibrium statistical mechanics. Existence and uniqueness of nonequilibrium steady states have been extensively studied for a variety of such systems: harmonic [47] and anharmonic [5] crystals, 1-dimensional chains of anharmonic oscillators [6, 8, 21–24, 65], rotors [11, 12] and other Hamiltonian systems [9, 26, 49, 50]. More general Hamiltonian networks have been considered in [10, 27, 52]. In this paper, we shall study stochastically driven networks of harmonic oscillators which are the simplest models in the last category. The questions of existence and uniqueness of the steady state is well understood in such systems. Estimates of the rate of relaxation to the steady state are also available [1, 66]. The focus of this work is on the concept of entropy production and its fluctuations, although our approach can be extended to cover the fluctuations of energy/entropy fluxes between individual heat reservoirs and the network. The universal fluctuation relations satisfied by the entropy production rate (or phase-space contraction rate) in transient [20, 25] and stationary [31, 32] processes have been one of the central issues in the recent developments of nonequilibrium statistical mechanics. Various approaches to these relations have been proposed in the literature and we refer the reader to [13, 14, 39, 40, 48, 51, 61, 69] for reviews and detailed discussions. The interested reader should also consult [67], where fluctuation relations are derived for boundary driven anharmonic chains, and [41] for a discussion of these topics in the framework of Gaussian dynamical systems. For theoretical and experimental works dealing specifically with mechanically driven harmonic systems we refer the reader to [36, 37, 44].

In this paper we follow the scheme advocated in [39, 40] and fully elaborated in [38]. The details are as follows.

Consider a probability space $(\Omega ,\mathcal{P},\mathbb {P})$ equipped with a measurable involution $\Theta :\Omega \rightarrow \Omega$. Suppose that the measures $\mathbb {P}$ and $\widetilde{\mathbb {P}}=\mathbb {P}\circ \Theta$ are equivalent. We define the canonical entropic functional of the quadruple $(\Omega ,\mathcal{P},\mathbb {P},\Theta )$ by

$$\begin{aligned} S(\omega )=\log \frac{\mathrm {d}\mathbb {P}}{\mathrm {d}\widetilde{\mathbb {P}}}(\omega ), \end{aligned}$$

(1.1)

and denote by P the law of this random variable under $\mathbb {P}$. Since

$$\begin{aligned} S\circ \Theta (\omega ) =\log \frac{\mathrm {d}\mathbb {P}\circ \Theta }{\mathrm {d}\widetilde{\mathbb {P}}\circ \Theta }(\omega ) =\log \frac{\mathrm {d}\widetilde{\mathbb {P}}}{\mathrm {d}\mathbb {P}}(\omega ) =-S(\omega ), \end{aligned}$$

(1.2)

the support of P is symmetric w.r.t. the origin. It reduces to $\{0\}$ whenever $\widetilde{\mathbb {P}}=\mathbb {P}$. In the opposite case the symmetry $\Theta$ is broken and the well known fact that the relative entropy of $\mathbb {P}$ w.r.t. $\widetilde{\mathbb {P}}$, given by

$$\begin{aligned} \mathrm{Ent}(\mathbb {P}|\widetilde{\mathbb {P}})=-\int _\Omega S(\omega )\mathbb {P}(\mathrm {d}\omega ) =-\int _{{\mathbb {R}}}sP(\mathrm {d}s) \end{aligned}$$

is strictly negative (it vanishes iff $\mathbb {P}=\widetilde{\mathbb {P}}$) shows that the law P favors positive values of S. To obtain a more quantitative statement of this fact, it is useful to consider Rényi’s relative $\alpha$-entropy

$$\begin{aligned} \mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}}) =\log \int _\Omega \mathrm {e}^{\alpha S(\omega )}\widetilde{\mathbb {P}}(\mathrm {d}\omega ). \end{aligned}$$

Note that $\mathrm{Ent}_0(\mathbb {P}|\widetilde{\mathbb {P}})=\mathrm{Ent}_1(\mathbb {P}|\widetilde{\mathbb {P}})=0$, and since the function ${\mathbb {R}}\ni \alpha \mapsto \mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}})$ is convex by Hölder’s inequality, one has $\mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}})\le 0$ for $\alpha \in [0,1]$. It is straightforward to check that $\mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}})$ is a real-analytic function of $\alpha$ on some open interval containing ]0, 1[ and infinite on the (possibly empty) complement of its closure. In particular, it is strictly convex on its analyticity interval.

From the definition of $\widetilde{\mathbb {P}}$ and Relation (1.2) we deduce

$$\begin{aligned} \mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}}) \!=\!\log \int _\Omega \mathrm {e}^{\alpha S\circ \Theta (\omega )}\mathbb {P}(\mathrm {d}\omega ) =\log \int _\Omega \mathrm {e}^{-\alpha S(\omega )}\mathbb {P}(\mathrm {d}\omega ) =\log \int _\Omega \mathrm {e}^{-\alpha S(\omega )}\frac{\mathrm {d}\mathbb {P}}{\mathrm {d}\widetilde{\mathbb {P}}}(\omega ) \widetilde{\mathbb {P}}(\mathrm {d}\omega ), \end{aligned}$$

(1.3)

and the definition of S yields

$$\begin{aligned} \log \int _\Omega \mathrm {e}^{-\alpha S(\omega )}\frac{\mathrm {d}\mathbb {P}}{\mathrm {d}\widetilde{\mathbb {P}}}(\omega ) \widetilde{\mathbb {P}}(\mathrm {d}\omega ) =\log \int _\Omega \mathrm {e}^{(1-\alpha ) S(\omega )}\widetilde{\mathbb {P}}(\mathrm {d}\omega ) =\mathrm{Ent}_{1-\alpha }(\mathbb {P}|\widetilde{\mathbb {P}}). \end{aligned}$$

It follows that Rényi’s entropy satisfies the symmetry relation

$$\begin{aligned} \mathrm{Ent}_{1-\alpha }(\mathbb {P}|\widetilde{\mathbb {P}})=\mathrm{Ent}_{\alpha }(\mathbb {P}|\widetilde{\mathbb {P}}), \end{aligned}$$

(1.4)

which, in applications to dynamical systems, will turn into the so-called Gallavotti–Cohen symmetry. The second equality in Eq. (1.3) allows us to express Rényi’s entropy in terms of the law P as

$$\begin{aligned} \mathrm{Ent}_\alpha (\mathbb {P}|\widetilde{\mathbb {P}})=e(\alpha ) =\log \int _{\mathbb {R}}\mathrm {e}^{-\alpha s}P(\mathrm {d}s). \end{aligned}$$

Note that, up to the sign of $\alpha$, $e(\alpha )$ is the the cumulant generating function of the random variable S. Denoting by $\widetilde{P}$ the law of $-S$ under $\mathbb {P}$, the symmetry (1.4) leads to

$$\begin{aligned} \int _{\mathbb {R}}\mathrm {e}^{\alpha s}\widetilde{P}(\mathrm {d}s) =\int _{\mathbb {R}}\mathrm {e}^{-\alpha s}P(\mathrm {d}s) =\int _{\mathbb {R}}\mathrm {e}^{-(1-\alpha )s}P(\mathrm {d}s) =\int _{\mathbb {R}}\mathrm {e}^{\alpha s}\mathrm {e}^{-s}P(\mathrm {d}s), \end{aligned}$$

from which we obtain

$$\begin{aligned} \frac{\mathrm {d}\widetilde{P}}{\mathrm {d}P}(s)=\mathrm {e}^{-s} \end{aligned}$$

(1.5)

on the common support of P and $\widetilde{P}$. Thus, negative values of S are exponentially suppressed by the universal weight $\mathrm {e}^{-s}$. In the physics literature such an identity is called a fluctuation relation or a fluctuation theorem for the quantity described by S. Most often S is a measure of the power injected in a system or of the rate at which it dissipates heat in some thermostat. The equivalent symmetry of the cumulant generating function $e(\alpha )$ of S which follows from the symmetry (1.4) of Rényi’s entropy

$$\begin{aligned} e(1-\alpha )=e(\alpha ) \end{aligned}$$

(1.6)

is referred to as the Gallavotti–Cohen symmetry. The name symmetry function is sometimes given to

$$\begin{aligned} \mathfrak {s}(s)=\log \frac{\mathrm {d}P}{\mathrm {d}\widetilde{P}}(s). \end{aligned}$$

In terms of this function, the fluctuation relation is expressed as

$$\begin{aligned} \mathfrak {s}(s)=s. \end{aligned}$$

The above-mentioned fact that

$$\begin{aligned} 0=\mathrm{Ent}_1(\mathbb {P}|\widetilde{\mathbb {P}})=\log \int _{\mathbb {R}}\mathrm {e}^{-s}P(\mathrm {d}s), \end{aligned}$$

rewritten as

$$\begin{aligned} \int _{\mathbb {R}}\mathrm {e}^{-s}P(\mathrm {d}s)=1, \end{aligned}$$

(1.7)

constitute the associated Jarzynski identity and the strict negativity of relative entropy

$$\begin{aligned} 0<-\mathrm{Ent}(\mathbb {P}|\widetilde{\mathbb {P}})=\int sP(\mathrm {d}s), \end{aligned}$$

(1.8)

becomes Jarzynski’s inequality.

In all known applications of the above scheme to nonequilibrium statistical mechanics, the space $(\Omega ,\mathcal{P},\mathbb {P})$ describes the space-time statistics of the physical system under consideration over some finite time interval [0, t] (in the following, we shall denote by a superscript or a subscript the dependence of various objects on the length t of the considered time interval). The involution $\Theta ^t$ is related to time-reversal and the canonical entropic functional $S^t$ to entropy production or phase space contraction. The fluctuation relation (1.5) is a fingerprint of time-reversal symmetry breaking and the strict inequality in (1.8) is a signature of nonequilibrium.

The practical implementation of our scheme to nonequilibrium statistical mechanics requires 4 distinct steps which will structure our treatment of thermally driven harmonic networks. In order to clearly formulate the purpose of each of these steps, we illustrate the procedure at hand on a very simple model of electrical RC-circuit described in Fig. 1. We shall not provide detailed proofs of our claims in this example since they all reduce to elementary calculations. We refer the reader to [74] for a detailed physical analysis and to [30] for experimental verification of the fluctuation relations for this system.

Step 1: Construction of the canonical entropic functional

Fig. 1

A parallel RC circuit is fed with a constant current I. The resistor R is in contact with a heat bath at temperature T. The Johnson–Nyquist thermal noise in this resistor generates a fluctuating electromotive force V which contributes to the potential difference $U=RI_R+V$ driving the capacitor C

The internal energy of the circuit of Fig. 1 is stored in the electric field within the capacitor and is given by

$$\begin{aligned} E=\frac{z^2}{2C}, \end{aligned}$$

(1.9)

where z denotes the charge on the plate of the capacitor and C is the capacitance. The equation of motion for z is

$$\begin{aligned} \dot{z}_t=I-\frac{z_t}{RC}+\frac{V_t}{R}, \end{aligned}$$

where I is the constant current fed into the circuit and $V_t$ the electromotive force (emf) generated by the Johnson–Nyquist thermal noise within the resistor R. Integrating the equation of motion gives

$$\begin{aligned} z_t=\mathrm {e}^{-t/RC}z_0+ \left( 1-\mathrm {e}^{-t/RC}\right) RCI+\frac{1}{R}\int _0^t\mathrm {e}^{-(t-s)/RC}V_s\mathrm {d}s. \end{aligned}$$

(1.10)

To simplify our discussion (and to avoid stochastic integrals and the technicalities related to time-reversal), we shall assume that $V_t$ has the form

$$\begin{aligned} \frac{V_t}{R}=\sum _{k=1}^\infty \xi _k\delta (t-k\tau ), \end{aligned}$$

where $\tau \ll \tau _0=RC$ and $\xi _k$ denotes a sequence of i.i.d. centered Gaussian random variables with variance $\sigma ^2$. Sampling the charge at times $n\tau +0$ yields a sequence $z_0,z_1,z_2,\ldots$ satisfying the recursion relation

$$\begin{aligned} z_{k+1}=\eta z_k+(1-\eta ){\overline{z}}+\xi _{k+1}, \end{aligned}$$

where ${\overline{z}}=I\tau _0$ and $\eta =\mathrm {e}^{-\tau /\tau _0}$. According to (1.10), the charge between two successive kicks is given by

$$\begin{aligned} z_{k\tau +s}=\mathrm {e}^{-s/\tau _0}z_k+\left( 1-\mathrm {e}^{-s/\tau _0}\right) {\overline{z}},\quad s\in ]0,\tau [. \end{aligned}$$

(1.11)

Assuming $z_0$ to be independent of $\{\xi _k\}$, the sequence $z_0,z_1,z_2\ldots$ is a Markov chain with transition kernel

$$\begin{aligned} p(z'|z)=\frac{1}{\sqrt{2\pi \sigma ^2}} \mathrm {e}^{-(z'-\eta z-(1-\eta ){\overline{z}})^2/2\sigma ^2}. \end{aligned}$$

(1.12)

One easily checks that the unique invariant measure for this chain has the pdf

$$\begin{aligned} p_\mathrm{st}(z)=\frac{1}{\sqrt{2\pi \sigma ^2/(1-\eta ^2)}}\, \mathrm {e}^{-(z-{\overline{z}})^2(1-\eta ^2)/2\sigma ^2}. \end{aligned}$$

(1.13)

In the case $I=0$ (no external forcing), according to the zero${}^\mathrm{th}$ law of thermodynamics, the system should relax to its thermal equilibrium at the temperature T of the heat bath. Thus, in this case the invariant measure should be the equilibrium Gibbs state of the circuit at temperature T which, by (1.9), has the pdf

$$\begin{aligned} p_\mathrm{eq}(z)=\frac{1}{\sqrt{2\pi k_BTC}}\, \mathrm {e}^{-z^2/2k_BTC}, \end{aligned}$$

$k_B$ denoting Boltzmann’s constant. This requirement fixes the value of variance of $\xi _k$’s and

$$\begin{aligned} \sigma ^2=k_BTC\left( 1-\eta ^2\right) . \end{aligned}$$

One can show (see Sect. 8 in [3]) that, in the limit $\tau \rightarrow 0$, the covariance of the fluctuating emf $V_t$ converges to

$$\begin{aligned} \langle V_sV_t\rangle =2k_BTR\delta (s-t), \end{aligned}$$

in accordance with the Johnson–Nyquist formula ([55], see also [73, Sect. IX.2]). For $I\not =0$, Eq. (1.13) describes a nonequilibrium steady state (NESS) of the system. In the following, we shall consider the stationary Markov chain started with the invariant measure and denote by $\langle \,\cdot \,\rangle _\mathrm{st}$ the corresponding expectation.

The pdf of a finite segment $Z_n=(z_0,\ldots ,z_n)\in {\mathbb {R}}^{n+1}$ of the stationary process is given by

$$\begin{aligned} p_n(Z_n)=p(z_n|z_{n-1})\cdots p(z_1|z_0)p_\mathrm{st}(z_0), \end{aligned}$$

(1.14)

which is the Gaussian measure on ${\mathbb {R}}^{n+1}$ with mean and covariance

$$\begin{aligned} \langle z_k\rangle _\mathrm{st}={\overline{z}},\qquad \langle z_kz_j\rangle _\mathrm{st} -\langle z_k\rangle _\mathrm{st}\langle z_j\rangle _\mathrm{st} =k_BTC\mathrm {e}^{-|k-j|\tau /\tau _0}. \end{aligned}$$

We chose the involution $\Theta :{\mathbb {R}}^{n+1}\rightarrow {\mathbb {R}}^{n+1}$ to be the composition of charge conjugation $z\mapsto -z$ with time-reversal of the Markov chain,

$$\begin{aligned} \Theta :(z_0,\ldots ,z_n)\mapsto (-z_n,\ldots ,-z_0). \end{aligned}$$

The time-reversed process is the Markov chain which assigns the weight (1.14) to the reversed segment $\Theta (Z_n)$. Thus, the transition kernel ${\tilde{p}}(z'|z)$ and invariant measure ${\tilde{p}}_\mathrm{st}(z)$ of the time-reversed process must satisfy

$$\begin{aligned} {\tilde{p}}(-z_0|-z_1)\cdots {\tilde{p}}(-z_{n-1}|-z_n) {\tilde{p}}_\mathrm{st}(-z_n) =p(z_n|z_{n-1})\cdots p(z_1|z_0)p_\mathrm{st}(z_0) \end{aligned}$$

(1.15)

for all $n\ge 1$ and $Z_n\in {\mathbb {R}}^{n+1}$. For $n=1$, this equation becomes

$$\begin{aligned} {\tilde{p}}(-z_0|-z_1){\tilde{p}}_\mathrm{st}(z_1)=p(z_1|z_0)p_\mathrm{st}(z_0). \end{aligned}$$

(1.16)

Integrating both sides over $z_1$ gives

$$\begin{aligned} {\tilde{p}}_\mathrm{st}(-z_0)=p_\mathrm{st}(z_0), \end{aligned}$$

from which we further deduce

$$\begin{aligned} {\tilde{p}}(-z_0|-z_1) =p(z_1|z_0)\frac{p_\mathrm{st}(z_0)}{p_\mathrm{st}(z_1)}. \end{aligned}$$

One then easily checks that (1.15) is indeed satisfied for all $n\ge 1$. Note that in the case $I=0$ one has

$$\begin{aligned} p(-z'|-z)=p(z'|z),\qquad p_\mathrm{st}(z)=p_\mathrm{st}(-z), \end{aligned}$$

and it follows that ${\tilde{p}}(z'|z)=p(z'|z)$, Eq. (1.16) turning into the detailed balance condition. In this case, the time-reversed process coincides with the direct one: in thermal equilibrium, the time-reversal symmetry holds. However, in the nonequilibrium case $I\not =0$, time-reversal invariance is broken and ${\tilde{p}}_\mathrm{st}(z)\not =p_\mathrm{st}(z)$.

We are now ready to describe the canonical entropic functional. Applying our general scheme to the marginal $\mathbb {P}^{n\tau }$ of the finite segment $Z_n$ (which has the pdf $p_n$), we can write (1.1) as

$$\begin{aligned} S^{n\tau } =\log \frac{\mathrm {d}\mathbb {P}^{n\tau }}{\mathrm {d}\widetilde{\mathbb {P}}^{n\tau }}(Z_n) =\log \frac{p_n(Z_n)}{p_n(\Theta (Z_n))}&=\log \frac{p(z_n|z_{n-1})\cdots p(z_1|z_0)p_\mathrm{st}(z_0)}{p(-z_0|-z_1)\cdots p(-z_{n-1}|-z_n)p_\mathrm{st}(-z_n)}\\&=\sum _{k=0}^{n-1}\log \frac{p(z_{k+1}|z_k)}{p(-z_k|-z_{k+1})} +\log \frac{p_\mathrm{st}(z_0)}{p_\mathrm{st}(-z_n)}. \end{aligned}$$

Eqs. (1.12) and (1.13) yield

$$\begin{aligned} \log \frac{p(z'|z)}{p(-z|-z')}= & {} -\frac{1}{k_BTC}\left( \frac{z^{\prime 2}}{2}-\frac{z^2}{2} -\frac{1-\eta }{1+\eta }(z+z'){\overline{z}}\right) ,\\ \log \frac{p_\mathrm{st}(z_0)}{p_\mathrm{st}(-z_n)}= & {} \frac{1}{k_BTC}\left( \frac{z_n^2}{2}-\frac{z_0^2}{2} +(z_0+z_n){\overline{z}}\right) , \end{aligned}$$

from which we deduce

$$\begin{aligned} S^{n\tau }=\frac{1}{k_BT} \left[ \frac{1-\eta }{1+\eta }\sum _{k=0}^{n-1}z_k +\frac{z_n+\eta z_0}{1+\eta } \right] \frac{2{\overline{z}}}{C}. \end{aligned}$$

Step 2: Deriving a large deviation principle

From a more mathematical point of view, as stressed by Gallavotti–Cohen [31, 32], the interesting question is whether the entropic functional $S^t$ satisfies a large deviation principle in the limit $t\rightarrow \infty$. More precisely, is it possible to control the large fluctuations of $S^t$ by a rate function ${\mathbb {R}}\ni s\mapsto I(s)$ such that

$$\begin{aligned} \mathbb {P}\left[ \frac{1}{t} S^t\in \mathcal{S}\right] \approx \mathrm {e}^{-t\inf _{s\in \mathcal{S}}I(s)}, \end{aligned}$$

as $t\rightarrow \infty$ for any open set $\mathcal{S}\subset {\mathbb {R}}$ ? Moreover, does this rate function satisfy the relation

$$\begin{aligned} I(-s)=I(s)+s, \end{aligned}$$

(1.17)

which is the limiting form of (1.5), for all $s\in {\mathbb {R}}$ ? Finally, can one relate this rate function to the large-time asymptotics of Rényi’s entropy via a Legendre transformation

$$\begin{aligned} I(s)=\sup _{\alpha \in {\mathbb {R}}} \left( \alpha s-e(-\alpha )\right) ,\qquad e(\alpha )=\limsup _{t\rightarrow \infty } \frac{1}{t}\mathrm{Ent}_\alpha (\mathbb {P}^t|\widetilde{\mathbb {P}}^t), \end{aligned}$$

as suggested by the theory of large deviations? To illustrate these points, we return to our simple example.

For this very particular system, the fluctuation relation (1.5) essentially fixes the law of the random variable $S^{n\tau }$. Indeed, since $S^{n\tau }$ is Gaussian under the law of the stationary process (as a linear combination of Gaussian random variables $\xi _k$), its pdf $P^{n\tau }$ is completely determined by the mean ${\overline{s}}_n$ and variance $\sigma _n^2$ of $S^{n\tau }$. A simple calculation based on (1.5) shows that $\sigma _n^2=2{\overline{s}}_n$, whence it follows that

$$\begin{aligned} P^{n\tau }(s)=\frac{1}{\sqrt{4\pi {\overline{s}}_n}}\mathrm {e}^{-(s-{\overline{s}}_n)^2/4{\overline{s}}_n^2}, \end{aligned}$$

(1.18)

where we set

$$\begin{aligned} {\overline{s}}_n=\langle S^{n\tau }\rangle _\mathrm{st} =\frac{1}{k_BT}\left( \frac{1-\eta }{1+\eta }n+1\right) \frac{2{\overline{z}}^2}{C}. \end{aligned}$$

We conclude that

$$\begin{aligned} e_{n\tau }(\alpha )=\mathrm{Ent}_\alpha (\mathbb {P}^{n\tau }|\widetilde{\mathbb {P}}^{n\tau }) =\log \int \mathrm {e}^{-\alpha s}P^{n\tau }(s)\mathrm {d}s =-\alpha (1-\alpha ){\overline{s}}_n, \end{aligned}$$

(1.19)

and hence

$$\begin{aligned} e(\alpha )= \lim _{n\rightarrow \infty }\frac{1}{n\tau }e_{n\tau }(\alpha ) =-\alpha (1-\alpha ){\overline{s}},\qquad {\overline{s}}=\frac{1}{k_BT}\frac{1-\eta }{1+\eta }\frac{2{\overline{z}}^2}{C\tau }. \end{aligned}$$

A direct calculation using (1.18) implies that, for any open set $\mathcal{S}\subset {\mathbb {R}}$,

$$\begin{aligned} \mathbb {P}^{n\tau }\left[ \frac{S^{n\tau }}{n\tau }\in \mathcal{S}\right] \approx \mathrm {e}^{-n\tau \inf _{s\in \mathcal{S}}I(s)}\quad \text{ as } n\rightarrow \infty , \end{aligned}$$

where the rate function

$$\begin{aligned} I(s)=\sup _\alpha (\alpha s-e(-\alpha ))=\frac{(s-{\overline{s}})^2}{4{\overline{s}}} \end{aligned}$$

satisfies the fluctuation relation (1.17). The large-time symmetry function for $S^{n\tau }$ is

$$\begin{aligned} \mathfrak {s}(s)=I(-s)-I(s)=s. \end{aligned}$$

Step 3: Relating the canonical entropic functional to a relevant dynamical or thermodynamical quantity

Denoting by $U_t=z_t/C$ the voltage and using (1.10), the work performed on the system by the external current I in the period $]k\tau ,(k+1)\tau [$ is equal to

$$\begin{aligned} \delta W_k =\int _0^\tau U_t I\mathrm {d}t=\int _0^\tau \frac{z_t}{C} I\mathrm {d}t =(1-\eta )\frac{{\overline{z}} z_k}{C}-(1-\tau /\tau _0-\eta )\frac{{\overline{z}}^2}{C}. \end{aligned}$$

Thus, we can rewrite

$$\begin{aligned} \frac{S^{n\tau }}{n\tau }=\frac{1}{k_BT}\left[ \frac{2}{1+\eta } (w_{n}-{\overline{w}})+2\frac{1-\eta }{1+\eta }\frac{\tau _0}{\tau }{\overline{w}} +\frac{1}{n}\frac{2{\overline{z}}}{C\tau } \frac{z_n+\eta z_0}{1+\eta } \right] , \end{aligned}$$

where

$$\begin{aligned} w_n=\frac{W^{n\tau }}{n\tau },\qquad W^{n\tau }=\sum _{k=0}^{n-1}\delta W_k, \qquad {\overline{w}}=\langle w_n\rangle _\mathrm{st} =\frac{{\overline{z}}^2}{C\tau _0}=RI^2. \end{aligned}$$

$W^{n\tau }$ is the work performed by the external current during the period $[0,n\tau ]$. Accordingly, $w_n$ is the average injected power and ${\overline{w}}$ is its expected stationary value. It follows from the first law of thermodynamics that the heat dissipated by the resistor R in the thermostat during the interval $[0,n\tau +0[$ is given by

$$\begin{aligned} Q^{n\tau }=-\left( \frac{z_n^2}{2C}-\frac{z_0^2}{2C}\right) +W^{n\tau }, \end{aligned}$$

and so we may also write

$$\begin{aligned} \frac{S^{n\tau }}{n\tau } =\frac{1}{k_BT}\left[ \frac{2}{1+\eta } (q_n-{\overline{q}})+2\frac{1-\eta }{1+\eta }\frac{\tau _0}{\tau }{\overline{q}} +\frac{1}{n}\left( \frac{2{\overline{z}}}{C\tau } \frac{z_n+\eta z_0}{1+\eta } +\frac{z_n^2-z_0^2}{C\tau (1+\eta )}\right) \right] , \end{aligned}$$

where

$$\begin{aligned} q_n=\frac{Q^{n\tau }}{n\tau },\qquad {\overline{q}}=\langle q_n\rangle _\mathrm{st}={\overline{w}}, \end{aligned}$$

denote the average dissipated power and its expected stationary value.

Thus, up to a multiplicative and additive constant and a “small” (i.e., formally $\mathcal{O}(n^{-1})$) correction, $S^{n\tau }/n\tau$ is the time averaged power injected in the system by the external forcing and the time averaged power dissipated into the heat reservoir during the time period $[0,n\tau +0[$.

Step 4: Deriving a large deviation principle for physically relevant quantities

The problem encountered here stems from the fact that the relation between $S^t$ and a physically relevant quantity (denoted by $\mathfrak {S}^t$) typically involves some “boundary terms”, which depend on the state of the system at the initial time 0 and final time t. In cases where these boundary terms are uniformly bounded as $t\rightarrow \infty$, one finds that $\mathfrak {S}^t$ satisfies the same large deviation principle as $S^t$. This is what happens, for example, in strongly chaotic dynamical systems over a compact phase space (e.g., under the Gallavotti–Cohen chaotic hypothesis); we refer the reader to [40, Sect. 10] for a discussion of this case. However, unbounded boundary terms can compete with the tails of the law of $S^t$, which may lead to complications, as our example shows.

Given the Gaussian nature of $w_n$, it is an easy exercise to show that the entropic functional directly related to work and defined by

$$\begin{aligned} \frac{\mathfrak {S}_\mathrm{w}^{n\tau }}{n\tau } =\frac{S^{n\tau }}{n\tau }-\frac{1}{n}\frac{1}{k_BT} \frac{2{\overline{z}}}{C\tau }\frac{z_n+\eta z_0}{1+\eta } =\frac{1}{k_BT}\left[ \frac{2}{1+\eta } (w_n-{\overline{w}})+2\frac{1-\eta }{1+\eta }\frac{\tau _0}{\tau }{\overline{w}}\right] , \end{aligned}$$

has a cumulant generating function which satisfies

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n\tau } \log \langle \mathrm {e}^{-\alpha \mathfrak {S}_\mathrm{w}^{n\tau }}\rangle _\mathrm{st}=e(\alpha ), \end{aligned}$$

for all $\alpha \in {\mathbb {R}}$. It follows that $\mathfrak {S}_\mathrm{w}^{n\tau }$ satisfies the very same large deviation estimates as $S^{n\tau }$. However, note that unlike function (1.19), the finite-time cumulant generating function $\log \langle \mathrm {e}^{-\alpha \mathfrak {S}_\mathrm{w}^{n\tau }}\rangle _\mathrm{st}$ does not satisfy the Gallavotti–Cohen symmetry (1.6). Only in the large time limit do we recover this symmetry. A simple change of variable allows us to write down the cumulant generating function of the work $W^{n\tau }$,

$$\begin{aligned} e_\mathrm{work}(\alpha )=\lim _{n\rightarrow \infty }\frac{1}{n\tau }\log \langle \mathrm {e}^{-\alpha W^{n\tau }/k_BT}\rangle _\mathrm{st}=-\alpha \left( 1-\alpha \frac{1-\eta ^2}{2\tau /\tau _0}\right) \frac{{\overline{w}}}{k_BT}. \end{aligned}$$

We conclude that the work $W^{n\tau }$ satisfies the large deviations estimate

$$\begin{aligned} \mathbb {P}^{n\tau }\left[ \frac{1}{n\tau }\frac{W^{n\tau }}{k_BT}\in \mathcal{W}\right] \approx \mathrm {e}^{-n\tau \inf _{w\in \mathcal{W}} I_\mathrm{work}(w)} \end{aligned}$$

for all open sets $\mathcal{W}\subset {\mathbb {R}}$ with the rate function

$$\begin{aligned} I_\mathrm{work}(w)=\frac{1}{4}\left( w-\frac{{\overline{w}}}{k_BT}\right) ^2\frac{k_BT}{{\overline{w}}} \frac{2\tau /\tau _0}{1-\eta ^2}. \end{aligned}$$

The symmetry function for work is thus

$$\begin{aligned} \mathfrak {s}_\mathrm{work}(w) =I_\mathrm{work}(-w)-I_\mathrm{work}(w)=\frac{2\tau /\tau _0}{1-\eta ^2}w. \end{aligned}$$

Note that, as the kick period $\tau$ approaches zero, we recover the universal fluctuation relation (1.17), i.e., $\mathfrak {s}_\mathrm{work}(w)=w$.

Consider now the entropic functional

$$\begin{aligned} \frac{\mathfrak {S}_\mathrm{h}^{n\tau }}{n\tau }= & {} \frac{S^{n\tau }}{n\tau }-\frac{1}{n}\frac{1}{k_BT}\left( \frac{2{\overline{z}}}{C\tau }\frac{z_n+\eta z_0}{1+\eta } +\frac{z_n^2-z_0^2}{C\tau (1+\eta )}\right) \nonumber \\= & {} \frac{1}{k_BT}\left[ \frac{2}{1+\eta } (q_n-{\overline{q}})+2\frac{1-\eta }{1+\eta }\frac{\tau _0}{\tau }{\overline{q}}\right] , \end{aligned}$$

(1.20)

related to the dissipated heat. The explicit evaluation of a Gaussian integral shows that its cumulant generating function is given by

$$\begin{aligned} \frac{1}{n\tau }\log \langle \mathrm {e}^{-\alpha \mathfrak {S}_\mathrm{h}^{n\tau }}\rangle _\mathrm{st} =\left\{ \begin{array}{ll} \displaystyle e(\alpha )-\frac{1}{2n\tau }\left[ \log \left( 1-\frac{\alpha ^2}{\alpha _n^2}\right) +\frac{a_n\alpha +b_n}{\alpha _n^2-\alpha ^2}\alpha ^3 \right] &{}\text{ if } |\alpha |<\alpha _n;\\ +\infty &{}\text{ otherwise }; \end{array} \right. \end{aligned}$$

where $a_n$ and $b_n$ are bounded (in fact converging) sequences and

$$\begin{aligned} \alpha _n=\frac{1}{2}\frac{1+\eta }{(1-\eta ^{2n})^{\frac{1}{2}}}. \end{aligned}$$

The divergence of the cumulant generating function for $|\alpha |\ge \alpha _n$ is of course due to the competition between the tail of the Gaussian law $p_n$ and the quadratic terms in $\mathfrak {S}^{n\tau }_\mathrm{h}$.

Note that the sequence $\alpha _n$ is monotone decreasing to its limit

$$\begin{aligned} \alpha _\mathrm{c}=\frac{1+\eta }{2}, \end{aligned}$$

and it follows that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n\tau } \log \left\langle \mathrm {e}^{-\alpha \mathfrak {S}_\mathrm{h}^{n\tau }}\right\rangle _\mathrm{st} =\left\{ \begin{array}{l@{\quad }l} e(\alpha )&{}\text{ if } |\alpha |<\alpha _\mathrm{c};\\ +\infty &{}\text{ if } |\alpha |>\alpha _\mathrm{c}. \end{array} \right. \end{aligned}$$

The unboundedness of the boundary terms involving $z_0^2$ and $z_n^2$ in (1.20) leads to a breakdown of the Gallavotti–Cohen symmetry for $|\alpha -\frac{1}{2}|>|\alpha _\mathrm{c}-\frac{1}{2}|$. More dramatically, the limiting cumulant generating function is not steep, i.e., its derivative fails to diverge as $\alpha$ approaches ${\pm }\alpha _\mathrm{c}$. Under such circumstances, the derivation of a global large deviation principle for nonlinear dynamical systems is a difficult problem which remains largely open and deserves further investigations. For linear systems, however, as shown in [41], it is sometimes possible to exploit the Gaussian nature of the process to achieve this goal. Indeed, following the strategy developped in Sect. 3.4, one can show that $\mathfrak {S}_\mathrm{h}^{n\tau }$ satisfies a large deviation principle with rate function

$$\begin{aligned} I_\mathrm{h}(s)=\sup _{|\alpha |<\alpha _\mathrm{c}}(\alpha s-e(-\alpha )) =\left\{ \begin{array}{l@{\quad }l} I(s_-)+(s-s_-)I'(s_-)&{}\text{ for } s<s_-;\\ I(s)&{}\text{ for } s\in [s_-,s_+];\\ I(s_+)+(s-s_+)I'(s_+)&{}\text{ for } s>s_+; \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} s_-=-e'(\alpha _c)=-\eta {\overline{s}},\qquad s_+=-e'(-\alpha _c)=(2+\eta ){\overline{s}}. \end{aligned}$$

Performing a simple change of variable, we conclude that the cumulant generating function of the heat $Q^{n\tau }$ satisfies

$$\begin{aligned} e_\mathrm{heat}(\alpha )=\lim _{n\rightarrow \infty }\frac{1}{n\tau }\log \langle \mathrm {e}^{-\alpha Q^{n\tau }/k_BT}\rangle _\mathrm{st}= \left\{ \begin{array}{c@{\quad }c} e_\mathrm{work}(\alpha )&{}\text{ for } |\alpha |<1;\\ +\infty &{}\text{ for } |\alpha |>1. \end{array} \right. \end{aligned}$$

The corresponding large deviations estimate reads

$$\begin{aligned} \mathbb {P}^{n\tau }\left[ \frac{1}{n\tau }\frac{Q^{n\tau }}{k_BT}\in \mathcal{Q}\right] \approx \mathrm {e}^{-n\tau \inf _{q\in \mathcal{Q}}I_\mathrm{heat}(q)} \end{aligned}$$

for all open sets $\mathcal{Q}\subset {\mathbb {R}}$ with the rate function

$$\begin{aligned} I_\mathrm{heat}(q)=\sup _{|\alpha |<1}(\alpha q-e_\mathrm{heat}(-\alpha )) =I_\mathrm{h}\left( \frac{2}{1+\eta }q+2\frac{1-\tau /\tau _0-\eta }{1+\eta } \frac{\tau _0}{\tau }\frac{{\overline{q}}}{k_BT}\right) , \end{aligned}$$

which satisfies what is called in the physics literature an extended fluctuation relation [15, 16, 28, 29, 33–35, 54, 72] with the symmetry function

$$\begin{aligned} \mathfrak {s}_\mathrm{heat}(q)=I_\mathrm{heat}(-q)-I_\mathrm{heat}(q) =\left\{ \begin{array}{l@{\quad }l} \displaystyle 2q\frac{q_++q_-}{q_+-q_-}&{}\text{ for } 0\le q\le -q_-;\\ \displaystyle -\frac{q^2-2qq_++q_-^2}{q_+-q_-}&{} \text{ for } -q_-<q\le q_+;\\ q_++q_-&{}\text{ for } q>q_+; \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} q_-=-\frac{RI^2}{k_BT}\left( \frac{1-\eta ^2}{\tau /\tau _0}-1\right) ,\qquad q_+=\frac{RI^2}{k_BT}\left( \frac{1-\eta ^2}{\tau /\tau _0}+1\right) . \end{aligned}$$

Thus, the linear behavior persists for small fluctuations $|q|\le |q_{-}|$, but saturates to the constant values ${\mp }({q_{+}}+{q_{-}})$ for $|q| > q_{+}$, the crossover between these two regimes being described by a parabolic interpolation. Note also that, as the kick period $\tau$ approaches zero, $q_{\mp }\rightarrow (1\mp 2){\overline{q}}/k_{B}T$. In this limit the symmetry function ${\mathfrak {s}_\mathrm{heat}}(q)$ agrees with the conclusions of [74] (see Fig. 2). $\square$

Fig. 2

The symmetry functions (i.e., twice the odd part of the rate function) of work and heat for the circuit of Fig. 1 in the limit $\tau \rightarrow 0$ (the unit on the abscissa is $RI^{2}/k_{B}T$)

As this example shows, the main problem in understanding the mathematical status and physical implications of fluctuation relations in oscillator networks and other boundary driven Hamiltonian systems stems from the lack of compactness of phase space and its consequence: the unboundedness of the observable describing the energy transfers between the system and the reservoirs [i.e., the last term in the right-hand side of Eq. (1.20)]. We will show that one can achieve complete control of these boundary terms by an appropriate change of drift (a Girsanov transformation) in the Langevin equation describing the dynamics of harmonic networks. This change is parametrized by the maximal solution of a one-parameter family of algebraic Riccati equation naturally associated to deformations of the Markov semigroup of the system. For a network of N oscillators, our approach reduces the calculation of the limiting cumulant generating function of the canonical functional $S^t$ and its perturbations by quadratic boundary terms to the determination of some spectral data of the $4N\times 4N$ Hamiltonian matrix of the above-mentioned Riccati equations. Combining this asymptotic information with Gaussian estimates of the finite time cumulant generating functions, we are able to derive a global large deviation principle for arbitrary quadratic boundary perturbations of $S^t$. We stress that our scheme is completely constructive and well suited to numerical calculations.

The remaining parts of this paper are organized as follows. In Sect. 2 we introduce a general class of harmonic networks and the stochastic processes describing their nonequilibrium dynamics. Section 3 contains our main results. There, we consider more general framework and study the large time asymptotics of the entropic functional $S^t$ canonically associated to stochastic differential equations with linear drift satisfying some structural constraints (fluctuation–dissipation relations). We prove a global large deviation principle for this functional and show, in particular, that it satisfies the Gallavotti–Cohen fluctuation theorem. We then consider perturbations of $S^t$ by quadratic boundary terms and show that they also satisfy a global large deviation principle. This applies, in particular, to the heat released by the system in the reservoirs. We turn back to harmonic networks in Sect. 4 where we apply our results to specific examples. Finally, Sect. 5 collects the proofs of our results.

2 The Model

We consider a collection of one-dimensional harmonic oscillators indexed by a finite set $\mathcal{I}$. The configuration space ${\mathbb {R}}^\mathcal{I}$ is endowed with its Euclidean structure and the phase space $\Xi ={\mathbb {R}}^\mathcal{I}\oplus {\mathbb {R}}^\mathcal{I}$ is equipped with its canonical symplectic 2-form $\mathrm {d}p\wedge \mathrm {d}q$. The Hamiltonian is given by

$$\begin{aligned} \Xi \ni (p,q)\mapsto h(p,q)=\tfrac{1}{2}|p|^2+\tfrac{1}{2}|\omega q|^2, \end{aligned}$$

(2.1)

where $|\cdot |$ is the Euclidean norm and $\omega : {\mathbb {R}}^\mathcal{I}\rightarrow {\mathbb {R}}^\mathcal{I}$ is a non-singular linear map. Time-reversal of the Hamiltonian flow of h is implemented by the anti-symplectic involution of $\Xi$ given by

$$\begin{aligned} \theta :(p,q)\mapsto (-p,q). \end{aligned}$$

(2.2)

We consider the stochastic perturbation of the Hamiltonian flow of h obtained by coupling a non-empty subset of the oscillators, indexed by $\partial \mathcal{I}\subset \mathcal{I}$, to Langevin heat reservoirs. The reservoir coupled to the ith oscillator is characterized by two parameters: its temperature $\vartheta _i>0$ and its relaxation rate $\gamma _i>0$. We encode these parameters in two linear maps: a bijection $\vartheta :{\mathbb {R}}^{\partial \mathcal{I}}\rightarrow {\mathbb {R}}^{\partial \mathcal{I}}$ and an injection $\iota :{\mathbb {R}}^{\partial \mathcal{I}}\rightarrow {\mathbb {R}}^\mathcal{I}={\mathbb {R}}^{\partial \mathcal{I}}\oplus {\mathbb {R}}^{\mathcal{I}\setminus \partial \mathcal{I}}$ defined by

$$\begin{aligned} \vartheta : (u_i)_{i\in \partial \mathcal{I}}\mapsto (\vartheta _iu_i)_{i\in \partial \mathcal{I}},\qquad \iota : (u_i)_{i\in \partial \mathcal{I}}\mapsto (\sqrt{2\gamma _i}u_i)_{i\in \partial \mathcal{I}}\oplus 0. \end{aligned}$$

The external force acting on the ith oscillator has the usual Langevin form

$$\begin{aligned} f_i(p,q)=(2\gamma _i\vartheta _i)^\frac{1}{2}\dot{w}_i-\gamma _ip_i, \end{aligned}$$

(2.3)

where the $\dot{w}_i$ are independent white noises.

In mathematically more precise terms, we shall deal with the dynamics described by the following system of stochastic differential equations

$$\begin{aligned} \mathrm {d}q(t)=p(t)\mathrm {d}t,\quad \mathrm {d}p(t)=-\left( \tfrac{1}{2}\iota \iota ^*p(t)+\omega ^*\omega q(t)\right) \mathrm {d}t +\iota \vartheta ^\frac{1}{2}\mathrm {d}w(t), \end{aligned}$$

(2.4)

where ${}^*$ denotes conjugation w.r.t. the Euclidean inner products and w is a standard ${\mathbb {R}}^{\partial \mathcal{I}}$-valued Wiener process over the canonical probability space $(W,\mathcal{W},\mathbb {W})$. We denote by $\{\mathcal{W}_t\}_{t\ge 0}$ the associated natural filtration.

To the Hamiltonian (2.1) we associate the graph $\mathcal{G}=(\mathcal{I},\mathcal{E})$ with vertex set $\mathcal{I}$ and edges

$$\begin{aligned} \mathcal{E}=\{\{i,j\}\subset \mathcal{I}\,|\,(\omega ^*\omega )_{ij}\not =0\}. \end{aligned}$$

To avoid trivialities, we shall always assume that $\mathcal{G}$ is connected.

As explained in the introduction, we shall construct the canonical entropic functional of the process (p(t), q(t)) and relate it to the heat released by the network into the thermal reservoir. We end this section with a calculation of the latter quantity.

Applying Itô’s formula to the Hamiltonian h we obtain the expression

$$\begin{aligned} \mathrm {d}h(p(t),q(t)) =\sum _{i\in \partial \mathcal{I}}\gamma _i\left( \vartheta _i-p_i(t)^2\right) \mathrm {d}t +(2\gamma _i\vartheta _i)^\frac{1}{2}p_i(t)\mathrm {d}w_i(t) \end{aligned}$$

which describes the change in energy of the system. The ith term on the right-hand side of this identity is the work performed on the network by the ith Langevin force (2.3). Since these Langevin forces describe the action of heat reservoirs, we shall identify

$$\begin{aligned} \delta Q_i(t)=\gamma _i\left( \vartheta _i-p_i(t)^2\right) \mathrm {d}t +(2\gamma _i\vartheta _i)^\frac{1}{2}p_i(t)\mathrm {d}w_i(t) \end{aligned}$$

(2.5)

with the heat injected in the network by the ith reservoir. A direct application of the fundamental thermodynamic relation between heat and entropy leads to consider $\mathrm {d}S_i(t)=-\vartheta _i^{-1}\delta Q_i(t)$ as the entropy dissipated into the ith reservoir. Accordingly, the total entropy dissipated in the reservoirs during the time interval [0, t] is given by the functional

$$\begin{aligned} \mathfrak {S}^t=-\sum _{i\in \partial \mathcal{I}}\int _0^t\frac{\delta Q_i(s)}{\vartheta _i} =\sum _{i\in \partial \mathcal{I}}\int _0^t\left( -(2\gamma _i\vartheta _i^{-1})^\frac{1}{2}p_i(s)\mathrm {d}w_i(s) -\gamma _i(1-\vartheta _i^{-1}p_i(s)^2)\mathrm {d}s\right) . \end{aligned}$$

(2.6)

For a lack of better name, we shall call the physical quantity described by this functional the thermodynamic entropy (TDE), in order to distinguish it from various information theoretic entropies that will be introduced latter.

3 Abstract Setup and Main Results

It turns out that a large part of the analysis of the process (2.4) and its entropic functionals is independent of the details of the model and relies only on its few structural properties. In this section we recast the harmonic networks in a more abstract framework, retaining only the structural properties of the original system which are necessary for our analysis.

Notations and Conventions Let E and F be real or complex Hilbert spaces. L(E, F) denotes the set of (continuous) linear operators $A:E\rightarrow F$ and $L(E)=L(E,E)$. For $A\in L(E,F)$, $A^*\in L(F,E)$ denotes the adjoint of A, $\Vert A\Vert$ its operator norm, $\mathrm{Ran}\,A\subset F$ its range and $\mathrm{Ker}\,A\subset E$ its kernel. We denote the spectrum of $A\in L(E)$ by $\mathrm{sp}(A)$. A is non-negative (resp. positive), written $A\ge 0$ (resp. $A>0$), if it is self-adjoint and $\mathrm{sp}(A)\in [0,\infty [$ (resp. $\mathrm{sp}(A)\subset ]0,\infty [$). We write $A\ge B$ whenever $A-B\in L(E)$ is non-negative. The relation $\ge$ defines a partial order on L(E). The controllable subspace of a pair $(A,Q)\in L(E)\times L(F,E)$ is the smallest A-invariant subspace of E containing $\mathrm{Ran}\,Q$. We denote it by $\mathcal{C}(A,Q)$. If $\mathcal{C}(A,Q)=E$, then (A, Q) is said to be controllable. We denote by ${\mathbb {C}}_\mp$ the open left/right half-plane. $A\in L(E)$ is said to be stable/anti-stable whenever $\mathrm{sp}(A)\subset {\mathbb {C}}_\mp$.

We start by rewriting the equation of motion (2.4) in a more compact form. Setting

$$\begin{aligned} x=\left[ \begin{array}{c} p\\ \omega q \end{array} \right] ,\qquad A= \left[ \begin{array}{c@{\quad }c} -\frac{1}{2}\iota \iota ^*&{}-\omega ^*\\ \omega &{}0 \end{array} \right] ,\qquad Q=\left[ \begin{array}{c} \iota \\ 0 \end{array} \right] \vartheta ^\frac{1}{2}, \end{aligned}$$

(3.1)

Equation (2.4) takes the form

$$\begin{aligned} \mathrm {d}x(t)=Ax(t)\mathrm {d}t+Q\mathrm {d}w(t), \end{aligned}$$

(3.2)

and functional (2.6) becomes

$$\begin{aligned} \mathfrak {S}^t =-\int _0^t\vartheta ^{-1}Q^*x(s)\cdot \mathrm {d}w(s) +\tfrac{1}{2}\int _0^t|\vartheta ^{-1}Q^*x(s)|^2\mathrm {d}s -\tfrac{1}{2} t\,\mathrm{tr}(Q\vartheta ^{-1}Q^*). \end{aligned}$$

(3.3)

Note that the vector field Ax splits into a conservative (Hamiltonian) part $\Omega x$ and a dissipative part $-\Gamma x$ defined by

$$\begin{aligned} \Omega&=\tfrac{1}{2}(A-A^*)=\left[ \begin{array}{c@{\quad }c} 0&{}-\omega ^*\\ \omega &{}0 \end{array} \right] , \end{aligned}$$

(3.4)

$$\begin{aligned} \Gamma&=-\tfrac{1}{2}(A+A^*)=\tfrac{1}{2} Q\vartheta ^{-1}Q^*. \end{aligned}$$

(3.5)

These operators satisfy the relations

$$\begin{aligned} \Omega ^*=\theta \Omega \theta =-\Omega ,\qquad \Gamma ^*=\theta \Gamma \theta =\Gamma . \end{aligned}$$

(3.6)

The solution of the Cauchy problem associated to (3.2) with initial condition $x(0)=x_0$ can be written explicitly as

$$\begin{aligned} x(t)=\mathrm {e}^{tA}x_0+\int _0^t\mathrm {e}^{(t-s)A}Q\mathrm {d}w(s). \end{aligned}$$

(3.7)

This relation defines a family of $\Xi$-valued Markov processes indexed by the initial condition $x_0\in \Xi$. This family is completely characterized by the data

$$\begin{aligned} (A,Q,\vartheta ,\theta )\in L(\Xi )\times L(\partial \,\Xi ,\Xi ) \times L(\partial \,\Xi )\times L(\Xi ), \end{aligned}$$

(3.8)

where $\Xi$ and $\partial \,\Xi$ are finite-dimensional Euclidean vector spaces and $(A,Q,\vartheta ,\theta )$ is subject to the following structural constraints:

(3.9)

In the remaining parts of Sect. 3, we shall consider the family of processes (3.7), which are strong solutions of SDE (3.2), associated with the data (3.8) satisfying (3.9).

Remark 3.1

The concrete models of the previous section fit into the abstract setup defined by (3.2), (3.8), and (3.9) with $\mathrm{Ker}\,(A-A^*)=\{0\}$ and $\theta Q=-Q$. We have weakened the first condition and included the case $\theta Q=+Q$ in (3.9) in order to encompass the quasi-Markovian models introduced in [23, 24]. There, the Langevin reservoirs are not directly coupled to the network, but to additional degrees of freedom described by dynamical variables $r\in {\mathbb {R}}^\mathcal{J}$, where $\mathcal{J}$ is a finite set. The augmented phase space of the network is $\Xi ={\mathbb {R}}^\mathcal{J}\oplus {\mathbb {R}}^\mathcal{I}\oplus {\mathbb {R}}^\mathcal{I}$, and $\partial \,\Xi ={\mathbb {R}}^\mathcal{J}$. The equations of motion take the form (3.2) with

$$\begin{aligned} x=\left[ \begin{array}{c} r\\ p\\ \omega q \end{array} \right] ,\qquad A=\left[ \begin{array}{c@{\quad }c@{\quad }c} -\frac{1}{2}\iota \iota ^*&{}-\Lambda ^*&{}0\\ \Lambda &{}0&{}-\omega ^*\\ 0&{}\omega &{}0 \end{array} \right] ,\qquad Q=\left[ \begin{array}{c} \iota \\ 0\\ 0 \end{array} \right] \vartheta ^{\frac{1}{2}}, \end{aligned}$$

where $\iota :{\mathbb {R}}^\mathcal{J}\rightarrow {\mathbb {R}}^\mathcal{J}$ is bijective and $\Lambda :{\mathbb {R}}^\mathcal{J}\rightarrow {\mathbb {R}}^\mathcal{I}$ injective. The time reversal map in this case is given by

$$\begin{aligned} \theta =\left[ \begin{array}{c@{\quad }c@{\quad }c} I&{}0&{}0\\ 0&{}-I&{}0\\ 0&{}0&{}I \end{array} \right] . \end{aligned}$$

Writing the system internal energy as $H(x)=\frac{1}{2}|p|^2+\frac{1}{2}|\omega q|^2+\frac{1}{2}|r|^2$, the calculation of the previous section yields the following formula for the total entropy dissipated into the reservoirs

$$\begin{aligned} \mathfrak {S}^t+ \tfrac{1}{2}|\vartheta ^{-\frac{1}{2}}r(t)|^2-\tfrac{1}{2}|\vartheta ^{-\frac{1}{2}}r(0)|^2, \end{aligned}$$

(3.10)

where $\mathfrak {S}^t$ is given by (3.3).

Let $\mathcal{P}(\Xi )$ be the set of Borel probability measures on $\Xi$ and denote by $P^t(x,\,\cdot \,)\in \mathcal{P}(\Xi )$ the transition kernel of the process (3.7). For bounded or non-negative measurable functions f on $\Xi$ and $\nu \in \mathcal{P}(\Xi )$ we write

$$\begin{aligned} \nu (f)=\int f(x)\nu (\mathrm {d}x),\quad f_t=P^tf=\int P^t(\,\cdot \,,\mathrm {d}y)f(y),\quad \nu _t=\nu P^t=\int \nu (\mathrm {d}y)P^t(y,\,\cdot \,), \end{aligned}$$

so that $\nu (f_t)=\nu _t(f)$. A measure $\nu$ is invariant if $\nu _t=\nu$ for all $t\ge 0$. We denote the actions of time-reversal by

$$\begin{aligned} \widetilde{f}=\Theta f=f\circ \theta ,\qquad \widetilde{\nu }=\nu \Theta =\nu \circ \theta , \end{aligned}$$

so that $\nu (\widetilde{f})=\widetilde{\nu }(f)$. A measure $\nu$ is time-reversal invariant if $\widetilde{\nu }=\nu$. The generator L of the Markov semigroup $P^t$ acts on smooth functions as

$$\begin{aligned} L=\tfrac{1}{2}\nabla \cdot B\nabla +Ax\cdot \nabla , \end{aligned}$$

(3.11)

where

$$\begin{aligned} B=QQ^*. \end{aligned}$$

(3.12)

We further denote by $\mathbb {P}_{x_0}$ the induced probability measure on the path space $C({\mathbb {R}}^+,\Xi )$ and by $\mathbb {E}_{x_0}$ the associated expectation. Considering $x_0$ as a random variable, independent of the driving Wiener process w and distributed according to $\nu \in \mathcal{P}(\Xi )$, we denote by $\mathbb {P}_\nu$ and $\mathbb {E}_\nu$ the induced path space measure and expectation. In the language of statistical mechanics, functions f on $\Xi$ are the observables of the system, $\nu$ is its initial state, and the flow $t\mapsto \nu _t$ describes its time evolution. Invariant measures thus correspond to steady states of the system.

The following result is well known (see Chapter 6 in the book [18] and the papers [27, 52]). For the reader convenience, we provide a sketch of its proof in Sect. 5.1.

Theorem 3.2

• (1) Under the above hypotheses, the operator

  $$\begin{aligned} M:=\int _0^\infty e^{sA}Be^{sA^*}\mathrm {d}s \end{aligned}$$

  is well defined and non-negative, and its restriction to $\mathrm{Ran}\,M$ satisfies the inequality

  $$\begin{aligned} \vartheta _\mathrm{min}=\min \mathrm{sp}(\vartheta ) \le M\big |_{\mathrm{Ran}\,M}\le \max \mathrm{sp}(\vartheta )=\vartheta _\mathrm{max}. \end{aligned}$$

  (3.13)

  Moreover, the centred Gaussian measure $\mu$ with covariance M is invariant for the Markov processes associated with (3.2).

• (2) The invariant measure $\mu$ is unique iff the pair (A, Q) is controllable. In this case, the mixing property holds in the sense that, for any $f\in L^1(\Xi ,\mathrm {d}\mu )$, we have

  $$\begin{aligned} \lim _{t\rightarrow +\infty }P^tf=\mu (f), \end{aligned}$$

  where the convergence holds in $L^1(\Xi ,\mathrm {d}\mu )$ and uniformly on compact subsets of $\Xi$.

• (3) Let x(t) be defined by relation (3.7), in which the initial condition $x_0$ is independent of w and is distributed as $\mu$. Then x(t) is a centred stationary Gaussian process. Moreover, its covariance operator defined by the relation $(\eta _1,K(t,s)\eta _2)=\mathbb {E}_\mu \bigl \{(x(t),\eta _1)(x(s),\eta _2)\bigr \}$ has the form

  $$\begin{aligned} K(t,s)= e^{(t-s)_+A}M e^{(t-s)_-A^*}. \end{aligned}$$

  (3.14)

Remark 3.3

In the harmonic network setting, if $\vartheta =\vartheta _0 I$ for some $\vartheta _0\in ]0,\infty [$ (i.e., the reservoirs are in a joint thermal equilibrium at temperature $\vartheta _0$), then it follows from (3.13) that $M=\vartheta$, which means that $\mu$ is the Gibbs state at temperature $\vartheta _0$ induced by the Hamiltonian h.

In the sequel, we shall assume without further notice that process (3.7) has a unique invariant measure $\mu$, i.e., that the following hypothesis holds:

Assumption (C) The pair (A, Q) is controllable.

Remark 3.4

To make contact with [52], note that in terms of Stratonovich integral the TDE functional (3.3) is given by

$$\begin{aligned} \mathfrak {S}^t= -\int _0^t\vartheta ^{-1}Q^*x(s)\circ \mathrm {d}w(s) +\tfrac{1}{2}\int _0^t|\vartheta ^{-1}Q^*x(s)|^2\mathrm {d}s. \end{aligned}$$

This identity is a standard result of stochastic calculus (see, e.g., Sect. II.7 in [58]) and is used as a definition of the entropy current in [52].

3.1 Entropies and Entropy Production

In this section we introduce information theoretic quantities which play an important role in our approach to fluctuation relations. We briefly discuss their basic properties and in particular their relations with the TDE $\mathfrak {S}^t$.

Let $\nu _1$ and $\nu _2$ be two probability measures on the same measurable space. If $\nu _1$ is absolutely continuous w.r.t. $\nu _2$, the relative entropy of the pair $(\nu _1, \nu _2)$ is defined by

$$\begin{aligned} \mathrm{Ent}(\nu _1|\nu _2)=-\int \log \left( \frac{\mathrm {d}\nu _1}{\mathrm {d}\nu _2}\right) \mathrm {d}\nu _1. \end{aligned}$$

We recall that $\mathrm{Ent}(\nu _1|\nu _2)\in [-\infty ,0]$, with $\mathrm{Ent}(\nu _1|\nu _2)=0$ iff $\nu _1=\nu _2$ (see, e.g., [56]).

Suppose that $\nu _1$ and $\nu _2$ are mutually absolutely continuous. For $\alpha \in {\mathbb {R}}$, the Rényi [60] relative $\alpha$-entropy of the pair $(\nu _1, \nu _2)$ is

$$\begin{aligned} \mathrm{Ent}_\alpha (\nu _1|\nu _2)=\log \int \left( \frac{\mathrm {d}\nu _1}{\mathrm {d}\nu _2}\right) ^\alpha \mathrm {d}\nu _2. \end{aligned}$$

The function ${\mathbb {R}}\ni \alpha \mapsto \mathrm{Ent}_\alpha (\nu _1|\nu _2)\in ]-\infty ,\infty ]$ is convex. It is non-positive on [0, 1], vanishes for $\alpha \in \{0,1\}$, and is non-negative on ${\mathbb {R}}\setminus ]0,1[$. It is real analytic on ]0, 1[ and vanishes identically on this interval iff $\nu _1=\nu _2$. Finally,

$$\begin{aligned} \mathrm{Ent}_{1-\alpha }(\nu _1|\nu _2)=\mathrm{Ent}_\alpha (\nu _2|\nu _1) \end{aligned}$$

(3.15)

for all $\alpha \in {\mathbb {R}}$.

Let $\nu \in \mathcal{P}(\Xi )$ be such that $\nu (|x|^2)<\infty$ (recall that in our abstract framework the Hamiltonian is $h(x)=\frac{1}{2}|x|^2$). The Gibbs–Shannon entropy of $\nu _t=\nu P^t$ is defined by

$$\begin{aligned} S_\mathrm{GS}(\nu _t)=-\int \log \left( \frac{\mathrm {d}\nu _t}{\mathrm {d}x}\right) \nu _t(\mathrm {d}x). \end{aligned}$$

(3.16)

The Gibbs–Shannon entropy is finite for all $t>0$ (see Lemma 5.4 (1) below) and is a measure of the internal entropy of the system at time t.

To formulate our next result (see Sect. 5.2 for its proof) we define

$$\begin{aligned} \mathcal{P}_{+}(\Xi )=\left\{ \nu \in \mathcal{P}(\Xi )\,\bigg |\, \int \mathrm {e}^{\frac{1}{2} m|x-a|^2}\nu (\mathrm {d}x)<\infty \text { for some }m>0\text { and }a\in \Xi \right\} . \end{aligned}$$

Note that any Gaussian measure on $\Xi$ belongs to $\mathcal{P}_+(\Xi )$.

Proposition 3.5

Let a non-negative operator $\beta \in L(\Xi )$ be such that¹

$$\begin{aligned} \beta Q=Q\vartheta ^{-1},\qquad \theta \beta \theta =\beta . \end{aligned}$$

(3.17)

Define the quadratic form

$$\begin{aligned} \sigma _\beta (x)=\tfrac{1}{2} x\cdot \Sigma _\beta x,\qquad \Sigma _\beta =[\Omega ,\beta ], \end{aligned}$$

(3.18)

and a reference measure $\mu _\beta$ on $\Xi$ by

$$\begin{aligned} \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x)=\mathrm {e}^{-\frac{1}{2}|\beta ^\frac{1}{2} x|^2}. \end{aligned}$$

(3.19)

Then the following assertions hold.

• (1) $\mu _\beta \Theta =\mu _\beta$ and $\Theta \sigma _\beta =-\sigma _\beta$.

• (2) Let $L^\beta$ denote the formal adjoint of the Markov generator (3.11) w.r.t. the inner product of the Hilbert space $L^2(\Xi ,\mu _\beta )$. Then

  $$\begin{aligned} \Theta L^\beta \Theta =L+\sigma _\beta . \end{aligned}$$

  (3.20)

• (3) The TDE (3.3) can be written as

  $$\begin{aligned} \mathfrak {S}^t=-\int _0^t\sigma _\beta (x(s))\mathrm {d}s +\log \frac{\mathrm {d}\mu _{\beta }}{\mathrm {d}x}(x(t)) -\log \frac{\mathrm {d}\mu _{\beta }}{\mathrm {d}x}(x(0)). \end{aligned}$$

  (3.21)

• (4) Suppose that Assumption (C) holds. Then for any $\nu \in \mathcal{P}_+(\Xi )$ the de Bruijn relation

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\mathrm{Ent}(\nu _t|\mu ) =\tfrac{1}{2} \nu _t\left( |Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }|^2\right) \end{aligned}$$

  (3.22)

  holds for t large enough. In particular, $\mathrm{Ent}(\nu _t|\mu )$ is non-decreasing for large t.

• (5) Under the same assumptions

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\left( S_\mathrm{GS}(\nu _t)+\mathbb {E}_{\nu }[\mathfrak {S}^t]\right) =\tfrac{1}{2}\nu _t \left( |Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu _\beta }|^2\right) \end{aligned}$$

  (3.23)

  holds for t large enough.

Remark 3.6

Part (2) states that our system satisfies a generalized detailed balance condition as defined in [24] (see also [6]).

Let us comment on the physical interpretation of Part (3) in the harmonic network setting. Let $\mathcal{I}=\cup _{k\in K}\mathcal{I}_k$ be a partition of the network and denote by $\pi _k$ the orthogonal projection on ${\mathbb {R}}^\mathcal{I}$ with range ${\mathbb {R}}^{\mathcal{I}_k}$. Defining

$$\begin{aligned} h_k(p,q)=\tfrac{1}{2}|\pi _kp|^2+\tfrac{1}{2}|\omega \pi _kq|^2,\qquad v_{k,l}(q)=\tfrac{1}{2}q\cdot (\pi _k\omega ^*\omega \pi _l +\pi _l\omega ^*\omega \pi _k)q, \end{aligned}$$

for $k,l\in K$, we decompose the network into |K| clusters $\mathcal{R}_k$ with internal energy $h_k$, interacting through the potentials $v_{k,l}$. Denote by

$$\begin{aligned} {\tilde{h}}_k(p,q)=h_k(p,q)+\tfrac{1}{2}\sum _{l\not =k}v_{k,l}(q) \end{aligned}$$

the total energy stored in $\mathcal{R}_k$. Assume that all the reservoirs attached to $\mathcal{R}_k$, if any, are at the same temperature, i.e.,

$$\begin{aligned} i\in \mathcal{I}_k\cap \partial \mathcal{I}\Rightarrow \vartheta \iota ^*\pi _k=\vartheta _i\iota ^*\pi _k, \end{aligned}$$

(3.24)

and for $k\in K$ let $\beta _k\ge 0$ be such that $\beta _k=\vartheta _i^{-1}$ whenever $i\in \mathcal{I}_k\cap \partial \mathcal{I}$ (see Fig. 3). Defining the non-negative operator $\beta$ by

$$\begin{aligned} \tfrac{1}{2}x\cdot \beta x=\sum _{k\in K}\beta _k{\tilde{h}}_k(p,q), \end{aligned}$$

(3.25)

we observe that (3.17) holds as a consequence of (3.24) and the time-reversal invariance of ${\tilde{h}}_k$. The corresponding reference measure $\mu _\beta$ is, up to irrelevant normalization, a local Gibbs measure where each cluster $\mathcal{R}_k$ is in equilibrium at the inverse temperatures $\beta _k$.

Itô’s formula yields the local energy balance relation

$$\begin{aligned} \mathrm {d}{\tilde{h}}_k(x(t)) =-\tfrac{1}{4}p(t)\cdot (\pi _k\omega ^*\omega -\omega ^*\omega \pi _k)q(t)\mathrm {d}t +\sum _{i\in \mathcal{I}_k\cap \partial \mathcal{I}}\delta Q_i(t), \end{aligned}$$

(3.26)

where $\delta Q_i(t)$ is given by (2.5). The last term on the right-hand side of this identity is the total heat injected into subsystem $\mathcal{R}_k$ by the reservoirs attached to it. Thus, we can identify

$$\begin{aligned} \mathfrak {j}_k(t)=\sum _{l\not =k}\mathfrak {j}_{k\rightarrow l}(t),\qquad \mathfrak {j}_{k\rightarrow l}(t) =\tfrac{1}{4}p(t)\cdot (\pi _k\omega ^*\omega \pi _l -\pi _l\omega ^*\omega \pi _k)q(t), \end{aligned}$$

Fig. 3

A partition of the network. Black disks represents heat reservoirs. In this situation one has, $\beta _1^{-1}=\vartheta _1=\vartheta _3$, $\beta _2^{-1}=\vartheta _4=\vartheta _5=\vartheta _6$, $\beta _4^{-1}=\vartheta _2$. $\beta _3\ge 0$ and $\beta _5\ge 0$ arbitrary

with the total flux of energy flowing out of $\mathcal{R}_k$ into its environment which is composed of the other subsystems $\mathcal{R}_{l\not =k}$. Multiplying Eq. (3.26) with $\beta _k$, summing over k, integrating over [0, t] and comparing the result with (2.6) we obtain

$$\begin{aligned} \mathfrak {S}^t=-\sum _{k\in K}\beta _k\int _0^t\mathfrak {j}_k(t)\mathrm {d}t +\log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x(t))-\log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x(0)). \end{aligned}$$

Comparison with (3.21) yields

$$\begin{aligned} \sigma _\beta (x(t))=\sum _{k\in K}\beta _k\mathfrak {j}_k(t) =\tfrac{1}{2}\sum _{k\not =l}(\beta _k-\beta _l)\mathfrak {j}_{k\rightarrow l}(t), \end{aligned}$$

which, according to the heat-entropy relation, is the total inter-cluster entropy flux. Two different ways of partitioning the system and assigning reference local temperatures to each subsystems leads to total entropy dissipation which only differs by a boundary term

$$\begin{aligned} \sigma _\beta (x(t))-\sigma _{\beta '}(x(t)) =\sum _{k\in K}\beta _k \mathfrak {j}_k(t) -\sum _{k\in K'}\beta '_k \mathfrak {j'}_k(t) =\frac{\mathrm {d}}{\mathrm {d}t}\log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}\mu _{\beta '}}(x(t)), \end{aligned}$$

provided the local inverse temperatures $\beta _k$, $\beta _k'$ are consistent with the temperatures of the reservoirs.

Equation (3.23) can be read as an entropy balance equation. Its left-hand side is the sum of the rate of increase of the internal Gibbs–Shannon entropy of the system and of the TDE flux leaving the system. Thus, the quantity on the right-hand side of Eq. (3.23) can be interpreted as the total entropy production rate of the process. Using Eqs. (3.16) and (3.21), we can rewrite Eq. (3.23) as

$$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\mathbb {E}_{\nu }[\mathrm{Ep}(\nu ,t)] =\nu _t\left( -\sigma _\beta )+\frac{\mathrm {d}\ }{\mathrm {d}t}\mathrm{Ent}(\nu _t|\mu _\beta \right) =\tfrac{1}{2}\nu _t\left( |Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu _\beta }|^2\right) , \end{aligned}$$

(3.27)

where the entropy production functional $\mathrm{Ep}$ is defined by

$$\begin{aligned} \mathrm{Ep}(\nu ,t)&=-\int _0^t\sigma _\beta (x(s))\mathrm {d}s-\log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu _\beta }(x(t)) +\log \frac{\mathrm {d}\nu }{\mathrm {d}\mu _\beta }(x(0))\nonumber \\&=\mathfrak {S}^t-\log \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x(t)) +\log \frac{\mathrm {d}\nu }{\mathrm {d}x}(x(0)). \end{aligned}$$

(3.28)

In the physics literature, the quantity

$$\begin{aligned} \varsigma _\mathrm{stoch}(t)=-\log \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x(t)), \end{aligned}$$

is sometimes called stochastic entropy (see, e.g., [69, Sect. 2.4]). In the case $\nu =\mu$, i.e., for the stationary process, stochastic entropy does not contribute to the expectation of $\mathrm{Ep}(\mu ,t)$, and Eq. (3.28) yields

$$\begin{aligned} \frac{1}{t}\mathbb {E}_{\mu }[\mathrm{Ep}(\mu ,t)] =\frac{1}{t}\mathbb {E}_{\mu }[\mathfrak {S}^t] =-\mu (\sigma _\beta ), \end{aligned}$$

(3.29)

so that (3.27) reduces to

$$\begin{aligned} -\mu (\sigma _\beta ) =\tfrac{1}{2}\mu \left( |Q^*\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}\mu _\beta }|^2\right) , \end{aligned}$$

(3.30)

where the right-hand side is the steady state entropy production rate. In the following, we set

$$\begin{aligned} \mathrm{ep}=-\mu (\sigma _\beta ). \end{aligned}$$

(3.31)

By (3.29) this quantity is independent of the choice of $\beta \in L(\Xi )$ satisfying Conditions (3.17). The relation (3.30) shows that $\mathrm{ep}\ge 0$. Computing the Gaussian integral on the right-hand side of (3.30) yields

$$\begin{aligned} \mathrm{ep}=\tfrac{1}{2}\mathrm{tr}(\vartheta ^{-1}(MQ-Q\vartheta )^*M^{-1}(MQ-Q\vartheta )\vartheta ^{-1}) =\tfrac{1}{2}\Vert M^{-\frac{1}{2}}(MQ-Q\vartheta )\vartheta ^{-\frac{1}{2}}\Vert _2^2, \end{aligned}$$

(3.32)

where $\Vert \cdot \Vert _2$ denotes the Hilbert–Schmidt norm. Thus, $\mathrm{ep}>0$ iff $MQ-Q\vartheta \not =0$. By Remark 3.3, the latter condition implies in particular that the eigenvalues of $\vartheta$ (i.e., the temperatures $\vartheta _i$) are not all equal. Part (2) of the next proposition provides a converse. For the proof see Sect. 5.3.

Proposition 3.7

• (1)    $\mathrm{ep}=0\Leftrightarrow MQ=Q\vartheta \Leftrightarrow [\Omega ,M]=0\Leftrightarrow \mu \Theta =\mu .$ In particular, the steady state entropy production rate vanishes iff the steady state $\mu$ is time-reversal invariant and invariant under the (Hamiltonian) flow $\mathrm {e}^{t\Omega }$.

• (2) Let $\vartheta _1,\vartheta _2$ be two distinct eigenvalues of $\vartheta$ and denote by $\pi _1,\pi _2$ the corresponding spectral projections. If $\mathcal{C}(\Omega ,Q\pi _1)\cap \mathcal{C}(\Omega ,Q\pi _2)\not =\{0\}$, then $\mathrm{ep}>0$.

Remark 3.8

The time-reversal invariance $\mu \Theta =\mu$ of the steady state is equivalent to $\theta M\theta =M$. For Markovian harmonic networks, the latter condition is easily seen to imply

$$\begin{aligned} \mu (p_i q_j)=0,\qquad (i,j\in \mathcal{I}), \end{aligned}$$

i.e., the statistical independence of simultaneous positions and momenta. In the quasi-Markovian case, $\theta M\theta =M$ implies

$$\begin{aligned} \mu (p_i q_j)=\mu (p_ir_k)=\mu (q_jr_k)=0,\qquad (i,j\in \mathcal{I}, k\in \mathcal{J}). \end{aligned}$$

3.2 Path Space Time-Reversal

Given $\tau >0$, the space-time statistics of the process (3.7) in the finite period $[0,\tau ]$ is described by $(\mathfrak {X}^\tau ,\mathcal{X}^\tau ,\mathbb {P}_\nu ^\tau )$, where $\mathbb {P}_\nu ^\tau$ is the measure induced by the initial law $\nu \in \mathcal{P}(\Xi )$ on the path-space $\mathfrak {X}^\tau =C([0,\tau ],\Xi )$ equipped with its Borel $\sigma$-algebra $\mathcal{X}^\tau$. Path space time-reversal is given by the involution

$$\begin{aligned} \Theta ^\tau :\varvec{x}=\{x(t)\}_{t\in [0,\tau ]}\mapsto \varvec{\tilde{x}}=\{\theta x(\tau -t)\}_{t\in [0,\tau ]} \end{aligned}$$

of $\mathfrak {X}^\tau$. The time reversed path space measure $\widetilde{\mathbb {P}}_\nu ^\tau$ is defined by

$$\begin{aligned} \widetilde{\mathbb {P}}_\nu ^\tau =\mathbb {P}_\nu ^\tau \circ \Theta ^\tau . \end{aligned}$$

Since

$$\begin{aligned} \widetilde{\mathbb {E}}_\nu ^\tau [f(x(0))] =\mathbb {E}_\nu ^\tau [f(\theta x(\tau ))]=\nu P^\tau \Theta (f), \end{aligned}$$

(3.33)

$\widetilde{\mathbb {P}}_\nu ^\tau$ describes the statistics of the time reversed process $\varvec{\tilde{x}}$ started with the law $\nu P^\tau \Theta$. It is therefore natural to compare it with $\mathbb {P}_{\nu P^\tau \Theta }^\tau$. The following result (proved in Sect. 5.4) provides a connection between the functional $\mathrm{Ep}(\,\cdot \,,\tau )$ and time-reversal of the path space measure.

Set

$$\begin{aligned} \mathcal{P}^1_{\mathrm {loc}}(\Xi )=\left\{ \zeta \in \mathcal{P}(\Xi )\,\bigg |\, \frac{\mathrm {d}\zeta }{\mathrm {d}x}+ \left| \nabla \frac{\mathrm {d}\zeta }{\mathrm {d}x}\right| \in L^2_\mathrm{loc}(\Xi ,\mathrm {d}x) \right\} . \end{aligned}$$

Proposition 3.9

For any $\tau >0$ and any $\nu \in \mathcal{P}^1_{\mathrm {loc}}(\Xi )$, $\widetilde{\mathbb {P}}_\nu ^\tau$ is absolutely continuous w.r.t. $\mathbb {P}_{\nu P^\tau \Theta }^\tau$ and

$$\begin{aligned} \log \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau } =\mathrm{Ep}(\nu ,\tau )\circ \Theta ^\tau =-\mathfrak {S}^\tau -\log \frac{\mathrm {d}\nu _\tau }{\mathrm {d}x}(\theta x(0)) +\log \frac{\mathrm {d}\nu }{\mathrm {d}x}(\theta x(\tau )). \end{aligned}$$

(3.34)

Remark 3.10

The above result is a mathematical formulation of [52, Sect. 3.1] in the framework of harmonic networks. Rewriting (3.34) as

$$\begin{aligned} \log \frac{\mathrm {d}\mathbb {P}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau \circ \Theta ^\tau } =\mathrm{Ep}(\nu ,\tau ) =\mathfrak {S}^\tau +\log \frac{\mathrm {d}\nu }{\mathrm {d}x}(x(0))-\log \frac{\mathrm {d}\nu _\tau }{\mathrm {d}x}(x(\tau )), \end{aligned}$$

we obtain Eq. (3.12) of [52]. Proposition 3.9 is a consequence of Girsanov formula, the generalized detailed balance condition (3.20), and the fact that the time-reversed process $\varvec{\tilde{x}}$ is again a diffusion. Apart from the last fact, which was proven in [57], the main technical difficulty in its proof is to check the martingale property of the exponential of the right-hand side of (3.34).

Remark 3.11

It is an immediate consequence of Eq. (5.13) below that $\nu P^\tau \in \mathcal{P}^1_{\mathrm {loc}}(\Xi )$ for any $\nu \in \mathcal{P}(\Xi )$ and $\tau >0$.

Equipped with Eq. (3.34) it is easy to transpose the relative entropies formulas of the previous section to path space measures. As a first application, let us compute the relative entropy of $\mathbb {P}_{\eta \Theta }^\tau$ w.r.t. $\widetilde{\mathbb {P}}_\nu ^\tau$:

$$\begin{aligned} \mathrm{Ent}\left( \widetilde{\mathbb {P}}_\nu ^\tau |\mathbb {P}_{\eta \Theta }^\tau \right)&=\widetilde{\mathbb {E}}_\nu ^\tau \left[ -\log \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\eta \Theta }^\tau }\right] =\widetilde{\mathbb {E}}_\nu ^\tau \left[ -\log \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau } +\log \frac{\mathrm {d}\mathbb {P}_{\eta \Theta }^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau }\right] \\&=\widetilde{\mathbb {E}}_\nu ^\tau \left[ -\mathrm{Ep}(\nu ,\tau )\circ \Theta ^\tau +\log \frac{\mathrm {d}\eta }{\mathrm {d}\nu _\tau }(\theta x(0))\right] =-\mathbb {E}_\nu ^\tau \left[ \mathrm{Ep}(\nu ,\tau )\right] +\mathrm{Ent}(\nu _\tau |\eta ). \end{aligned}$$

If $\nu \in \mathcal{P}_+(\Xi )$ then (3.27) yields

$$\begin{aligned} -\mathrm{Ent}\left( \widetilde{\mathbb {P}}_\nu ^\tau |\mathbb {P}_{\nu P^\tau \Theta }^\tau \right) =\mathbb {E}_\nu ^\tau \left[ \mathrm{Ep}(\nu ,\tau )\right] =\tfrac{1}{2}\int _0^\tau \nu _t\left( |Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu _\beta }|^2\right) \mathrm {d}t, \end{aligned}$$

which, according to the previous section, is the entropy produced by the process during the period $[0,\tau ]$. Setting $\nu =\mu$, we obtain

$$\begin{aligned} -\mathrm{Ent}\left( \widetilde{\mathbb {P}}_\mu ^\tau |\mathbb {P}_{\mu \Theta }^\tau \right) =\mathrm {ep}(\mu )\tau . \end{aligned}$$

Together with Proposition 3.7(1), this relation proves

Theorem 3.12

The following statements are equivalent:

• (1) $\mathbb {P}_{\mu }^\tau \circ \Theta ^\tau =\mathbb {P}_\mu ^\tau$ for all $\tau >0$, i.e., the stationary process (3.7) is reversible.

• (2) $\mathbb {P}_{\mu }^\tau \circ \Theta ^\tau =\mathbb {P}_\mu ^\tau$ for some $\tau >0$.

• (3) $\mathrm{ep}=0$.

3.3 The Canonical Entropic Functional

We are now in position to deal with the first step in our scheme: the construction of the canonical entropic functional $S^\tau$ associated to $(\mathfrak {X}^\tau ,\mathcal{X}^\tau ,\mathbb {P}_\mu ^\tau ,\Theta ^\tau )$. By Proposition 3.9, Rényi’s relative $\alpha$-entropy per unit time of the pair ($\mathbb {P}_\mu ^\tau , \widetilde{\mathbb {P}}_\mu ^\tau )$,

$$\begin{aligned} \mathrm{Ent}_\alpha \left( \mathbb {P}_\mu ^\tau |\widetilde{\mathbb {P}}_\mu ^\tau \right) =\log \mathbb {E}_\mu \left[ \mathrm {e}^{-\alpha S^\tau }\right] , \end{aligned}$$

is the cumulant generating function of

$$\begin{aligned} S^\tau =\log \frac{\mathrm {d}\mathbb {P}_\mu ^\tau }{\mathrm {d}\widetilde{\mathbb {P}}_\mu ^\tau } =\mathfrak {S}^\tau -\log \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x(\tau )) +\log \frac{\mathrm {d}\mu }{\mathrm {d}x}(x(0)). \end{aligned}$$

(3.35)

In the following, we shall set

$$\begin{aligned} e_\tau (\alpha ) =\frac{1}{\tau }\log \mathbb {E}_\mu \left[ \mathrm {e}^{-\alpha S^\tau }\right] , \end{aligned}$$

(3.36)

which, by construction, satisfies the Gallavotti–Cohen symmetry $e_\tau (1-\alpha )=e_\tau (\alpha )$.

Before formulating our main result on the large time asymptotics of $e_\tau (\alpha )$, we need several technical facts which will be proved in Sect. 5.5.

Theorem 3.13

Suppose that Assumption (C) holds.

• (1) For $\beta \in L(\Xi )$ satisfying Conditions (3.17), the map

  $$\begin{aligned} {\mathbb {R}}\ni \omega \mapsto E(\omega ) =Q^*(A^*-\mathrm {i}\omega )^{-1}\Sigma _\beta (A+\mathrm {i}\omega )^{-1}Q \end{aligned}$$

  (3.37)

  takes values in the self-adjoint operators on the complexification of $\partial \Xi$. As such, it is continuous and independent of the choice of $\beta$.

• (2) Set

  $$\begin{aligned} \varepsilon _-=\min _{\omega \in {\mathbb {R}}}\min \mathrm{sp}(E(\omega )),\qquad \varepsilon _+=\max _{\omega \in {\mathbb {R}}}\max \mathrm{sp}(E(\omega )),\qquad \kappa _c=\frac{1}{\varepsilon _+}-\frac{1}{2}. \end{aligned}$$

  The following alternative holds: either $\kappa _c=\infty$ in which case $E(\omega )=0$ for all $\omega \in {\mathbb {R}}$, or $\frac{1}{2}<\kappa _c<\infty$, $\varepsilon _-<0$, $0<\varepsilon _+<1$, and

  $$\begin{aligned} \frac{1}{\varepsilon _-}+\frac{1}{\varepsilon _+}=1. \end{aligned}$$

• (3) Set $\mathfrak {I}_c=]\frac{1}{2}-\kappa _c,\frac{1}{2}+\kappa _c[\, =\,]\frac{1}{\varepsilon _-},\frac{1}{\varepsilon _+}[$. The function

  $$\begin{aligned} e(\alpha )= -\int _{-\infty }^{\infty }\log \det \left( I-\alpha E(\omega )\right) \frac{\mathrm {d}\omega }{4\pi } \end{aligned}$$

  (3.38)

  is analytic on the cut plane $\mathfrak {C}_c=({\mathbb {C}}\setminus {\mathbb {R}})\cup \mathfrak {I}_c$. It is convex on the open interval $\mathfrak {I}_c$ and extends to a continuous function on the closed interval ${\overline{\mathfrak {I}}}_c$. It further satisfies

  $$\begin{aligned} e(1-\alpha )=e(\alpha ) \end{aligned}$$

  (3.39)

  for all $\alpha \in \mathfrak {C}_c$,

  $$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} e(\alpha )\le 0&{}\text{ for } \alpha \in [0,1];\\ e(\alpha )\ge 0&{}\text{ for } \alpha \in {\overline{\mathfrak {I}}}_c\setminus ]0,1[;\\ \end{array} \right. \end{aligned}$$

  and in particular $e(0)=e(1)=0$. Moreover

  $$\begin{aligned} \mathrm{ep}=-e'(0)=e'(1), \end{aligned}$$

  and either $\mathrm{ep}=0$, $\kappa _c=\infty$, and $e(\alpha )$ vanishes identically, or $\mathrm{ep}>0$, $\kappa _c<\infty$, $e(\alpha )$ is strictly convex on ${\overline{\mathfrak {I}}}_c$, and

  $$\begin{aligned} \lim _{\alpha \downarrow \frac{1}{2}-\kappa _c}e'(\alpha )=-\infty , \qquad \lim _{\alpha \uparrow \frac{1}{2}+\kappa _c}e'(\alpha )=+\infty . \end{aligned}$$

  (3.40)

• (4) If $\mathrm{ep}>0$, then there exists a unique signed Borel measure $\varsigma$ on ${\mathbb {R}}$, supported on ${\mathbb {R}}{\setminus }\mathfrak {I}_c$, such that

  $$\begin{aligned} \int \frac{|\varsigma |(\mathrm {d}r)}{|r|}<\infty , \end{aligned}$$

  and

  $$\begin{aligned} e(\alpha )=-\int \log \left( 1-\frac{\alpha }{r}\right) \varsigma (\mathrm {d}r). \end{aligned}$$

• (5) For $\alpha \in {\mathbb {R}}$ define

  $$\begin{aligned} K_\alpha =\left[ \begin{array}{c@{\quad }c} -A_\alpha &{}QQ^*\\ C_\alpha &{}A_\alpha ^*\end{array}\right] , \end{aligned}$$

  (3.41)

  where

  $$\begin{aligned} A_\alpha =(1-\alpha )A-\alpha A^*,\qquad C_\alpha =\alpha (1-\alpha )Q\vartheta ^{-2}Q^*. \end{aligned}$$

  (3.42)

  For all $\omega \in {\mathbb {R}}$ and $\alpha \in {\mathbb {R}}$ one has

  $$\begin{aligned} \det (K_\alpha -\mathrm {i}\omega )=|\det (A+\mathrm {i}\omega )|^2\det (I-\alpha E(\omega )). \end{aligned}$$

  Moreover, for $\alpha \in \mathfrak {I}_c$,

  $$\begin{aligned} e(\alpha ) =\frac{1}{4}\mathrm{tr}(Q\vartheta ^{-1}Q^*) -\frac{1}{4}\sum _{\lambda \in \mathrm{sp}(K_\alpha )}|\mathrm{Re}\,\lambda |\, m_\lambda , \end{aligned}$$

  (3.43)

  where $m_\lambda$ denotes the algebraic multiplicity of $\lambda \in \mathrm{sp}(K_\alpha )$.

Remark 3.14

We shall prove, in Proposition 5.5(11), that

$$\begin{aligned} \kappa _c\ge \kappa _0=\frac{1}{2} \frac{\vartheta _{\mathrm {max}}+\vartheta _{\mathrm {min}}}{\vartheta _{\mathrm {max}}-\vartheta _{\mathrm {min}}}. \end{aligned}$$

(3.44)

This lower bound is sharp, i.e., there are networks for which equality holds [see Theorem 4.2(3)].

Remark 3.15

It follows from (3.44) that $\kappa _c=\infty$ for harmonic networks at equilibrium, i.e., whenever $\vartheta _\mathrm{min}=\vartheta _\mathrm{max}=\vartheta _0>0$. Up to the controllability assumption of Proposition 3.7(2), these are the only examples with $\kappa _c=\infty$ (see also Remark 5.6 and Sect. 4).

Remark 3.16

Remark 2 after Theorem 2.1 in [41] applies to Part (4) of Theorem 3.13.

In the sequel it will be convenient to consider the following natural extension of the function $e(\alpha )$.

Definition 3.17

The function

$$\begin{aligned} {\mathbb {R}}\ni \alpha \mapsto e(\alpha )\in ]-\infty ,+\infty ] \end{aligned}$$

is given by (3.38) for $\alpha \in {\overline{\mathfrak {I}}}_c$ and $e(\alpha )=+\infty$ for $\alpha \in {\mathbb {R}}{\setminus }{\overline{\mathfrak {I}}}_c$.

This definition makes ${\mathbb {R}}\ni \alpha \mapsto e(\alpha )$ an essentially smooth closed proper convex function (see [62]).

The main result of this section relates the spectrum of the matrix $K_\alpha$, through the function $e(\alpha )$, to the large time asymptotics of the Rényi entropy (3.36) and the cumulant generating function of the canonical entropic functional $S^t$.

Proposition 3.18

Under Assumption (C) and with Definition 3.17 one has

$$\begin{aligned} \lim _{\tau \rightarrow \infty }e_\tau (\alpha )=e(\alpha ), \end{aligned}$$

(3.45)

for all $\alpha \in {\mathbb {R}}$.

A closer look at the proof of Proposition 3.18 in Sect. 5.7 gives more. For any $x\in \Xi$ and $\alpha \in {\overline{\mathfrak {I}}}_c$

$$\begin{aligned} \lim _{\tau \rightarrow \infty }\mathbb {E}_x\left[ \mathrm {e}^{-\alpha S^\tau -\tau e(\alpha )}\right] =f_\alpha (x)=c_\alpha \mathrm {e}^{-\frac{1}{2} x\cdot T_\alpha x}, \end{aligned}$$

see [53, Sect. 20.1.5] and references therein. The functions $\alpha \mapsto c_\alpha \in [0,\infty [$ and $\alpha \mapsto T_\alpha \in L(\Xi )$ are real analytic on $\mathfrak {I}_c$, continuous on ${\overline{\mathfrak {I}}}_c$, $c_\alpha >0$ for $\alpha \in \mathfrak {I}_c$, and $T_\alpha >M^{-1}$ for $\alpha \in {\overline{\mathfrak {I}}}_c$. Moreover, the convergence also holds in $L^1(\Xi ,\mathrm {d}\mu )$ and is exponentially fast for $\alpha \in \mathfrak {I}_c$. For $\alpha \in {\overline{\mathfrak {I}}}_c$ and as $\tau \rightarrow \infty$, one has

$$\begin{aligned} e_\tau (\alpha )=e(\alpha )+\frac{1}{\tau }g_\tau (\alpha ) =e(\alpha )+\frac{1}{\tau }\left( \log \mu (f_\alpha ) +\mathcal {O}\left( \mathrm {e}^{-\epsilon (\alpha )\tau }\right) \right) , \end{aligned}$$

where $\epsilon (\alpha )>0$ for $\alpha \in \mathfrak {I}_c$. However, $c_\alpha$ vanishes on $\partial \mathfrak {I}_c$ and hence the “prefactor” $g_\tau (\alpha )$ diverges as $\alpha \rightarrow \partial \mathfrak {I}_c$. Nevertheless, (3.45) holds because

$$\begin{aligned} -\infty =\lim _{\tau \rightarrow \infty }\lim _{\alpha \rightarrow \partial \mathfrak {I}_c} \frac{1}{\tau }g_\tau (\alpha )\not = \lim _{\alpha \rightarrow \partial \mathfrak {I}_c}\lim _{\tau \rightarrow \infty } \frac{1}{\tau }g_\tau (\alpha )=0. \end{aligned}$$

Like in our introductory example, the occurrence of singularities in the “prefactor” $g_\tau (\alpha )$ is related to the tail of the law of $S^t$. This phenomenon was observed by Cohen and van Zon in their study of the fluctuations of the work done on a dragged Brownian particle and its heat dissipation [15] (see also [16, 72] for more detailed analysis). In their model, which is closely related to ours, the cumulant generating function of the dissipated heat $e_\tau (\alpha )$ diverges for $\alpha ^2\ge (1-\mathrm {e}^{-2\tau })^{-1}$ and hence

$$\begin{aligned} \lim _{\tau \rightarrow \infty }e_\tau (\alpha )=+\infty \quad \text{ for } |\alpha |>1. \end{aligned}$$

This leads to a breakdown of the Gallavotti–Cohen symmetry and to an extended fluctuation relation. We will come back to this point in the next section and see that this is a general feature of the TDE functional $\mathfrak {S}^t$ [see Eq. (3.64) below]. Proposition 3.18 and Theorem 3.13(3) show that the canonical entropic functional $S^t$ does not suffer from this defect: its limiting cumulant generating function $e(\alpha )$ satisfies Gallavotti–Cohen symmetry for all $\alpha \in {\mathbb {R}}$.

3.4 Large Deviations of the Canonical Entropic Functional

We now turn to Step 2 of our scheme. We recall some fundamental results on the large deviations of a family $(\xi _t)_{t\ge 0}$ of real-valued random variables (the Gärtner–Ellis theorem, see, e.g., [17, Theorem V.6]). We shall focus on the situations relevant for our discussion of entropic fluctuations. We refer the reader to [17, 19] for more general exposition.

By Hölder’s inequality, the cumulant generating function

$$\begin{aligned} {\mathbb {R}}\ni \alpha \mapsto \Lambda _t(\alpha ) =\frac{1}{t}\log \mathbb {E}[\mathrm {e}^{\alpha \xi _t}]\in ]-\infty ,\infty ], \end{aligned}$$

is convex and vanishes at $\alpha =0$. It is finite on some (possibly empty) open interval and takes the value $+\infty$ on the (possibly empty) interior of its complement.

Remark 3.19

The above definition follows the convention used in the mathematical literature on large deviations. Note, however, that in the previous section we have adopted the convention of the physics literature on entropic fluctuations where the cumulant generating function of an entropic functional $\xi _t$ is defined by $\alpha \mapsto t^{-1}\log \mathbb {E}[\mathrm {e}^{-\alpha \xi _t}]$. This clash of conventions is the origin of various minus signs occurring in Theorems 3.20 and 3.28 below.

The function

$$\begin{aligned} {\mathbb {R}}\ni \alpha \mapsto \Lambda (\alpha )=\limsup _{t\rightarrow \infty }\Lambda _t(\alpha ) =\lim _{t\rightarrow \infty }\sup _{s\ge t}\Lambda _s(\alpha )\in [-\infty ,\infty ] \end{aligned}$$

is convex and vanishes at $\alpha =0$. Let D be the interior of its effective domain $\{\alpha \in {\mathbb {R}}\,|\,\Lambda (\alpha )<\infty \}$, and assume that $0\in D$. Then D is a non-empty open interval, $\Lambda (\alpha )>-\infty$ for all $\alpha \in {\mathbb {R}}$, and the function $D\ni \alpha \mapsto \Lambda (\alpha )$ is convex and continuous. The Legendre transform

$$\begin{aligned} \Lambda ^*(x)=\sup _{\alpha \in {\mathbb {R}}}(\alpha x-\Lambda (\alpha )) =\sup _{\alpha \in {\overline{D}}}(\alpha x-\Lambda (\alpha )) \end{aligned}$$

is convex and lower semicontinuous, as supremum of a family of affine functions. Moreover, $\Lambda (0)=0$ implies that $\Lambda ^*$ is non-negative. The large deviation upper bound

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}\left[ \frac{1}{t}\xi _t\in C\right] \le -\inf _{x\in C}\Lambda ^*(x) \end{aligned}$$

(3.46)

holds for all closed sets $C\subset {\mathbb {R}}$.

Assume, in addition, that on some finite open interval $0\in D_0=]\alpha _-,\alpha _+[\subset D$ the function $D_0\ni \alpha \mapsto \Lambda (\alpha )$ is real analytic and not linear. Then $\Lambda$ is strictly convex and its derivative $\Lambda '$ is strictly increasing on $D_0$. We denote by $x_\mp$ the (possibly infinite) right/left limits of $\Lambda '(\alpha )$ at $\alpha =\alpha _\mp$. By convexity,

$$\begin{aligned} \Lambda (\alpha )\ge \Lambda (\alpha _0)+(\alpha -\alpha _0)\Lambda '(\alpha _0) \end{aligned}$$

(3.47)

for any $\alpha _0\in D_0$ and $\alpha \in {\mathbb {R}}$, and

$$\begin{aligned} \Lambda (\alpha _\pm )\ge \Lambda _\pm =\lim _{D_0\ni \alpha \rightarrow \alpha _\pm }\Lambda (\alpha ). \end{aligned}$$

Since $\Lambda ^*$ is non-negative, it follows that $\Lambda ^*(\Lambda '(0))=0$. One easily shows that (3.47) also implies

$$\begin{aligned} \Lambda ^*(x)=\sup _{\alpha \in D_0}(\alpha x-\Lambda (\alpha )) \end{aligned}$$

for $x\in E=]x_-,x_+[$. If the limit

$$\begin{aligned} \lim _{t\rightarrow \infty }\Lambda _t(\alpha ) \end{aligned}$$

exists for all $\alpha \in D_0$, then it coincides with $\Lambda (\alpha )$, and the large deviation lower bound

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}\left[ \frac{1}{t}\xi _t\in O\right] \ge -\inf _{x\in O\cap E}\Lambda ^*(x) \end{aligned}$$

(3.48)

holds for all open sets $O\subset {\mathbb {R}}$. Note that in cases where $x_-=-\infty$ and $x_+=+\infty$ one has $E={\mathbb {R}}$ and convexity implies $\Lambda (\alpha )=+\infty$ for $\alpha \in {\mathbb {R}}\setminus [\alpha _-,\alpha _+]$.

We shall say that the family $(\xi _t)_{t\ge 0}$ satisfies a local LDP on E with rate function $\Lambda ^*$ if (3.46) holds for all closed sets $C\subset {\mathbb {R}}$ and (3.48) holds for all open sets $O\subset {\mathbb {R}}$. If the latter holds with $E={\mathbb {R}}$, we say that this family satisfies a global LDP with rate function $\Lambda ^*$.

By the above discussion, Proposition 3.18 and Theorem 3.13(3) immediately yield:

Theorem 3.20

Suppose that Assumption (C) holds. Then, under the law $\mathbb {P}_\mu$, the family $(S^t)_{t\ge 0}$ satisfies a global LDP with rate function (see Fig. 4)

$$\begin{aligned} I(s)=\sup _{-\alpha \in \mathfrak {I}_c}(\alpha s-e(-\alpha )). \end{aligned}$$

(3.49)

Fig. 4

The cumulant generating function $e(\alpha )$ and the rate function I(s) for the canonical entropic functional of a harmonic network satisfying Assumption (C) and $\mathrm{ep}>0$. Notice the bias due to the symmetry $I(-s)=I(s)+s$

It follows from the Gallavotti–Cohen symmetry (3.39) that the function ${\mathbb {R}}\ni s\mapsto I(s)+\frac{1}{2} s\in [0,\infty ]$ is even, i.e., the universal fluctuation relation

$$\begin{aligned} \mathfrak {s}(s)=I(-s)-I(s)=s, \end{aligned}$$

(3.50)

holds for all $s\in {\mathbb {R}}$.

Remark 3.21

If $\mathrm{ep}>0$, then the strict convexity and analyticity of the function $e(\alpha )$ stated in Theorem 3.13(3) imply that the rate function I(s) is itself real analytic and strictly convex. Denoting by $s\mapsto \ell (s)$ the inverse of the function $\alpha \mapsto -e'(-\alpha )$, we derive

$$\begin{aligned} I(s)=s\ell (s)-e(-\ell (s)),\qquad I'(s)=\ell (s), \end{aligned}$$

and the Gallavotti–Cohen symmetry translates to $\ell (-s)+\ell (s)=-1$.

3.5 Intermezzo: A Naive Approach to the Cumulant Generating Function of ${{\mathfrak {S}}^t}$

Before dealing with perturbations of the functional $S^t$, we briefly digress from the main course of our scheme in order to better motivate what will follow. We shall try to compute the cumulant generating function of the TDE functional $\mathfrak {S}^t$ by a simple Perron-Frobenius type argument.

By Itô calculus, for any $f\in C^2(\Xi )$ one has

$$\begin{aligned}&\mathrm {d}(\mathrm {e}^{-\alpha \mathfrak {S}^t}f(x(t)))\\&\quad =\mathrm {e}^{-\alpha \mathfrak {S}^t}\left[ (L_\alpha f)(x(t))\mathrm {d}t +\left( Q^*(\nabla f)(x(t))+\alpha \vartheta ^{-1}Q^*x(t)f(x(t))\right) \cdot \mathrm {d}w(t) \right] , \end{aligned}$$

where

$$\begin{aligned} L_\alpha =\tfrac{1}{2}\left( \nabla \cdot B\nabla +2A_\alpha x\cdot \nabla -x\cdot C_\alpha x+\alpha \mathrm{tr}(Q\vartheta ^{-1}Q^*)\right) \end{aligned}$$

is the deformation of the Fokker–Planck operator (3.11), and $A_\alpha$, B, $C_\alpha$ are given by (3.12), (3.42). Note that the structural relations (3.9) imply

$$\begin{aligned} \Theta L_\alpha \Theta =L^*_{1-\alpha }, \end{aligned}$$

(3.51)

where $L_\alpha ^*$ denotes the formal adjoint of $L_\alpha$. Assuming $L_\alpha$ to have a non-vanishing spectral gap, a naïve application of Girsanov formula leads to

$$\begin{aligned} \mathbb {E}_\mu \left[ \mathrm {e}^{-\alpha \mathfrak {S}^t}\right] =\mu (\mathrm {e}^{tL_\alpha }1) =\mathrm {e}^{t\lambda _\alpha }\left( \mu (\Psi _\alpha )\int \Psi _{1-\alpha }(x)\mathrm {d}x +o(1)\right) ,\quad (t\rightarrow \infty ). \end{aligned}$$

(3.52)

where $\Psi _\alpha$ is the properly normalized eigenfunction of $L_\alpha$ to its dominant eigenvalue $\lambda _\alpha$. It follows that

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {E}_\mu \left[ \mathrm {e}^{-\alpha \mathfrak {S}^t}\right] =\lambda _\alpha , \end{aligned}$$

the Gallavotti–Cohen symmetry $\lambda _{1-\alpha }=\lambda _\alpha$ being a direct consequence of (3.51).

Given the form of $L_\alpha$, the Gaussian Ansatz

$$\begin{aligned} \Psi _\alpha (x)=\mathrm {e}^{-\frac{1}{2} x\cdot X_\alpha x}\qquad \end{aligned}$$

is mandatory. Insertion into the eigenvalue equation $L_\alpha \Psi _\alpha =\lambda _\alpha \Psi _\alpha$ leads to the following equation for the real symmetric matrix $X_\alpha$,

$$\begin{aligned} X_\alpha BX_\alpha -X_\alpha A_\alpha -A_\alpha ^*X_\alpha -C_\alpha =0, \end{aligned}$$

(3.53)

while the dominant eigenvalue is given by

$$\begin{aligned} \lambda _\alpha =\tfrac{1}{2}\left( \alpha \mathrm{tr}(Q\vartheta ^{-1}Q^*) -\mathrm{tr}(BX_\alpha )\right) . \end{aligned}$$

(3.54)

There are two difficulties with this naïve argument. The first one is that it is far from obvious that Girsanov theorem applies here. The second one is again related to the “prefactor” problem. In fact we shall see that Eq. (3.53) does not have positive definite solutions for $\alpha \le 0$, making the right-hand side of (3.52) infinite for $\alpha \ge 1$. Nevertheless, the above calculation reveals Eq. (3.53) and (3.54) which will play a central role in what follows.

3.6 More Entropic Functionals

In this section we deal with step 3 of our scheme. The main result, Proposition 3.22 below, concerns the large time behavior of cumulant generating functions of the kind

$$\begin{aligned} {\mathbb {R}}\ni \alpha \mapsto g_t(\alpha ) =\frac{1}{t}\log \mathbb {E}_\nu \left[ \mathrm {e}^{-\alpha [S^t+\Phi (x(t))-\Psi (x(0))]}\right] , \end{aligned}$$

where $\Phi$ and $\Psi$ are quadratic forms on the phase space $\Xi$,

$$\begin{aligned} \Phi (x)=\tfrac{1}{2} x\cdot Fx,\qquad \Psi (x)=\tfrac{1}{2} x\cdot Gx, \end{aligned}$$

(3.55)

and the initial measure $\nu \in \mathcal{P}(\Xi )$ is Gaussian. We then apply this result to some entropic functionals of physical interest:

• (1) The steady state TDE (recall Eq. (3.35)),

  $$\begin{aligned} \mathfrak {S}^t=S^t+\log \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x(t)) -\log \frac{\mathrm {d}\mu }{\mathrm {d}x}(x(0)), \end{aligned}$$

  (3.56)

  with $\nu =\mu$.

• (2) The steady state TDE for quasi-Markovian networks (3.10) which we can rewrite as

  $$\begin{aligned} \mathfrak {S}^t_\mathrm{qM} =\mathfrak {S}^t+\tfrac{1}{2}|\vartheta ^{-1/2}\pi _Q x(t)|^2 -\tfrac{1}{2}|\vartheta ^{-1/2}\pi _Q x(0)|^2, \end{aligned}$$

  (3.57)

  where $\pi _Q$ denotes the orthogonal projection to $\mathrm{Ran}\,Q=\partial \Xi$, with $\nu =\mu$.

• (3) Transient TDEs, i.e., the functionals $\mathfrak {S}^t$ and $\mathfrak {S}_\mathrm{qM}^t$, but in the transient process started with a Dirac measure $\nu =\delta _{x_0}$.

• (4) The steady state entropy production functional

  $$\begin{aligned} \mathrm{Ep}(\mu ,t)=S^t+\log \frac{\mathrm {d}\mu \Theta }{\mathrm {d}\mu }(x(t)) \end{aligned}$$

  with $\nu =\mu$.

• (5) The canonical entropic functional for the transient process, started with the non-degenerate Gaussian measure $\nu \in \mathcal{P}(\Xi )$,

  $$\begin{aligned} S^t_\nu \!=\!\log \frac{\mathrm {d}\mathbb {P}_\nu ^t}{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^t} \!=\!\log \frac{\mathrm {d}\mathbb {P}_\mu ^t}{\mathrm {d}\widetilde{\mathbb {P}}_\mu ^t} +\log \frac{\mathrm {d}\mathbb {P}_\nu ^t}{\mathrm {d}\mathbb {P}_\mu ^t} -\log \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^t}{\mathrm {d}\widetilde{\mathbb {P}}_\mu ^t} =S^t-\log \frac{\mathrm {d}\nu }{\mathrm {d}\mu }(\theta x(t))+\log \frac{\mathrm {d}\nu }{\mathrm {d}\mu }(x(0)). \end{aligned}$$

To formulate our general result, we need some facts about the matrix equation (3.53).

Define a map $\mathcal{R}_\alpha :L(\Xi )\rightarrow L(\Xi )$ by

$$\begin{aligned} \mathcal{R}_\alpha (X)= X BX-X A_\alpha -A_\alpha ^*X-C_\alpha , \end{aligned}$$

(3.58)

where $A_\alpha$, B and $C_\alpha$ are defined by (3.12) and (3.42). The equation $\mathcal{R}_\alpha (X)=0$ is an algebraic Riccati equation for the unknown self-adjoint $X\in L(\Xi )$. We refer the reader to the monographs [2, 46] for an in depth discussion of such equations.

A solution X of the Riccati equation is called minimal (maximal) if it is such that $X\le X'$ ($X\ge X'$) for any other solution $X'$ of the equation. We shall investigate the Riccati equation in Sect. 5.6. At this point we just mention that, under Assumption (C), it has a unique maximal solution $X_\alpha$ for any $\alpha \in {\overline{\mathfrak {I}}}_c$, with the special values

$$\begin{aligned} X_0=0,\qquad X_1=\theta M^{-1}\theta . \end{aligned}$$

(3.59)

Proposition 3.22

Suppose that Assumption (C) is satisfied and let $\nu$ be the Gaussian measure on $\Xi$ with mean a and covariance $N\ge 0$. Denote by $P_\nu$ the orthogonal projection on $\mathrm{Ran}\,N$ and by $\widehat{N}$ the inverse of the restriction of N to its range. Let $F,G\in L(\Xi )$ be self-adjoint and define $\Phi$, $\Psi$ by (3.55).

• (1) For $t>0$ the function

  $$\begin{aligned} {\mathbb {R}}\ni \alpha \mapsto g_t(\alpha )= \frac{1}{t}\log \mathbb {E}_\nu \left[ \mathrm {e}^{-\alpha (S^t+\Phi (x(t))-\Psi (x(0)))}\right] \end{aligned}$$

  is convex. It is finite and real analytic on some open interval $\mathfrak {I}_t=]\alpha _-(t),\alpha _+(t)[\ni 0$ and infinite on its complement. Moreover, the following alternatives hold:

  • Either $\alpha _-(t)=-\infty$ or $\lim _{\alpha \downarrow \alpha _-(t)}g_t'(\alpha )=-\infty$.

  • Either $\alpha _+(t)=+\infty$ or $\lim _{\alpha \uparrow \alpha _+(t)}g_t'(\alpha )=+\infty$.

• (2) Set

  $$\begin{aligned} \mathfrak {I}_+&=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\, \theta X_{1-\alpha }\theta +\alpha (X_1+F)>0\},\\ \mathfrak {I}_-&=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\, \widehat{N}+P_\nu (X_\alpha -\alpha (G+\theta X_1\theta ))|_{\mathrm{Ran}\,N}>0\}, \end{aligned}$$

  with the proviso that $\mathfrak {I}_-={\overline{\mathfrak {I}}}_c$ whenever $N=0$. Then $\mathfrak {I}_\infty =\mathfrak {I}_-\cap \mathfrak {I}_+$ is a (relatively) open subinterval of ${\overline{\mathfrak {I}}}_c$ containing 0.

• (3) If $X_1+F>0$ and either $N=0$ or $\widehat{N}+P_\nu (X_1-\theta X_1\theta -G)|_{\mathrm{Ran}\,N}>0$, then $[0,1]\subset \mathfrak {I}_\infty$.

• (4) For $\alpha \in \mathfrak {I}_\infty$ one has

  $$\begin{aligned} \lim _{t\rightarrow \infty }g_t(\alpha )=e(\alpha ). \end{aligned}$$

  (3.60)

• (5) Set $\alpha _-=\inf \mathfrak {I}_\infty <0$ and $\alpha _+=\sup \mathfrak {I}_\infty >0$. Then,

  $$\begin{aligned} \lim _{t\rightarrow \infty }\alpha _\pm (t)=\alpha _\pm , \end{aligned}$$

  (3.61)

  and for any $\alpha \in {\mathbb {R}}\setminus [\alpha _-,\alpha _+]$,

  $$\begin{aligned} \lim _{t\rightarrow \infty }g_t(\alpha )=+\infty . \end{aligned}$$

  (3.62)

Remark 3.23

The existence and value of the limit (3.60) for $\alpha \in \partial \mathfrak {I}_\infty$ is a delicate problem whose resolution requires additional information on the two subspaces

$$\begin{aligned} \mathrm{Ker}\,(\theta X_{1-\alpha }\theta +\alpha (X_1+F)),\qquad \mathrm{Ker}\,(\widehat{N}+P_\nu (X_\alpha -\alpha (G+\theta X_1\theta ))|_{\mathrm{Ran}\,N}) \end{aligned}$$

at the points $\alpha \in \partial \mathfrak {I}_\infty$. Since, as we shall see in the next section, this question is irrelevant for the large deviations properties of the functional $S^t+\Phi (x(t))-\Psi (x(0))$, we shall not discuss it further.

Remark 3.24

We shall see in Sect. 5.6 that the maximal solution $X_\alpha$ of the Riccati equation is linked to the function $e(\alpha )$ through the identity $e(\alpha )=\lambda _\alpha$, where $\lambda _\alpha$ is given by Eq. (3.54). Thus, the large time behavior of the function $\alpha \mapsto g_t(\alpha )$ is completely characterized by the maximal solution $X_\alpha$ through this formula and the two numbers $\alpha _\pm$. Riccati equations play an important role in various areas of engineering mathematics, e.g., control and filtering theory. For these reasons, very efficient algorithms are available to numerically compute their maximal/minimal solutions. Hence, our approach is well designed for numerical investigation of concrete models.

Steady State Dissipated TDE According to Eqs. (3.56) and (3.59), the case of TDE dissipation in the stationary process corresponds to the choice

$$\begin{aligned} \widehat{N}=\theta X_1\theta ,\qquad F=-X_1,\qquad G=-\theta X_1\theta , \end{aligned}$$

and it follows directly from Proposition 5.5(2) and (4) below that

$$\begin{aligned} \mathfrak {I}_+=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_{1-\alpha }>0\}=[\tfrac{1}{2}-\kappa _c,1[. \end{aligned}$$

Setting $\alpha _-=\inf \{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_\alpha +\theta X_1\theta >0\}$, we have either $\alpha _-\in ]\tfrac{1}{2}-\kappa _c,0[$ and

$$\begin{aligned} \mathfrak {I}_\infty =]\alpha _-,1[, \end{aligned}$$

or $\alpha _-=\tfrac{1}{2}-\kappa _c$ and

$$\begin{aligned} \mathfrak {I}_\infty =[\alpha _-,1[. \end{aligned}$$

Suppose that $\tfrac{1}{2}-\kappa _c\le -1$ and let $\alpha \in [\tfrac{1}{2}-\kappa _c,-1]$. From Proposition 5.5(10) we deduce that $X_\alpha \le \alpha X_1$. Since $X_1=\theta M^{-1}\theta >0$, it follows that

$$\begin{aligned} X_\alpha +\theta X_1\theta \le \alpha X_1+\theta X_1\theta =\alpha (X_1-\theta X_1\theta )+(1+\alpha )\theta X_1\theta \le \alpha (\theta M^{-1}\theta -M^{-1}). \end{aligned}$$

(3.63)

Observe that the right-hand side of this inequality is odd under conjugation by $\theta$. Moreover, Proposition 3.7(1) implies that it vanishes iff $\mathrm{ep}=0$. It follows that $\mathrm{sp}(X_\alpha +\theta X_1\theta )\cap ]-\infty ,0]\not =\emptyset$. Thus, we can conclude that one always has $\alpha _+=1$ and $\alpha _-\ge -1$, with strict inequality whenever $\mathrm{ep}>0$.

By Proposition 3.22,

$$\begin{aligned} e_\mathrm{TDE,st}(\alpha )= \lim _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {E}_\mu [ \mathrm {e}^{-\alpha \mathfrak {S}^t}] =\left\{ \begin{array}{l@{\quad }l} e(\alpha )&{}\text {for }\alpha \in ]\alpha _-,1[\\ +\infty &{}\text {for }\alpha \not \in [\alpha _-,1]. \end{array} \right. \end{aligned}$$

(3.64)

An explicit evaluation of the resulting Gaussian integral further shows that

$$\begin{aligned} e_\mathrm{TDE,st}(1) =\lim _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {E}_\mu [\mathrm {e}^{-\mathfrak {S}^t}] =\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*)>0. \end{aligned}$$

The Gallavotti–Cohen symmetry is broken in the sense that it fails outside the interval ]0, 1[, in particular $e_\mathrm{TDE,st}(0)=e(0)=0<e_\mathrm{TDE,st}(1)$. Note also that

$$\begin{aligned} \liminf _{\alpha \rightarrow 1}e_\mathrm{TDE,st}(\alpha )=e(1)=0<e_\mathrm{TDE,st}(1) <\limsup _{\alpha \rightarrow 1}e_\mathrm{TDE,st}(\alpha )=+\infty , \end{aligned}$$

i.e., the limiting cumulant generating function for TDE dissipation rate in the stationary process is neither lower semicontinuous nor upper semicontinuous.

Remark 3.25

We shall see in Sect. 5.6 (see Remark 5.6) that in the case of thermal equilibrium, i.e., $\vartheta =\vartheta _0I$ for some $\vartheta _0\in ]0,\infty [$, one has $X_\alpha =\alpha \vartheta _0I$ and hence $X_{-1}+\theta X_1\theta =0$. Thus, in this case, $\alpha _-=-1$ and since $e(\alpha )$ vanishes identically by Proposition 3.13(3),

$$\begin{aligned} e_\mathrm{TDE,st}(\alpha )=\left\{ \begin{array}{l@{\quad }l} 0&{}\text {for }|\alpha |<1\\ +\infty &{}\text {for }|\alpha |>1. \end{array} \right. \end{aligned}$$

Remark 3.26

According to Eq. (3.57), for quasi-Markovian networks the steady-state TDE dissipation corresponds to

$$\begin{aligned} \widehat{N}=\theta X_1\theta ,\qquad F=-X_1+\pi _Q\vartheta ^{-1}\pi _Q,\qquad G=\theta (-X_1+\pi _Q\vartheta ^{-1}\pi _Q)\theta . \end{aligned}$$

Since $\theta \pi _Q=\pm \pi _Q=\pi _Q\theta$, one has

$$\begin{aligned}{}[0,1[\subset \mathfrak {I}_+=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\, X_{1-\alpha }+\alpha \pi _Q\vartheta ^{-1}\pi _Q>0\} \subset [\tfrac{1}{2}-\kappa _c,1[, \end{aligned}$$

provided $\partial \Xi \not =\Xi$. The inequality (3.63) yields

$$\begin{aligned} (I-\pi _Q)(X_\alpha +\theta X_1\theta -\alpha \pi _Q\vartheta ^{-1}\pi _Q)(I-\pi _Q) \le \alpha (I-\pi _Q)(\theta M^{-1}\theta -M^{-1})(I-\pi _Q), \end{aligned}$$

for $\tfrac{1}{2}-\kappa _c\le \alpha \le -1$. From the Lyapunov equation (5.4) one easily deduces that

$$\begin{aligned} (I-\pi _Q)(\theta M^{-1}\theta -M^{-1})(I-\pi _Q)=0 \end{aligned}$$

iff $\theta M\theta =M$ so that the above argument still applies and (3.64) holds with $\mathfrak {S}^t$ replaced by $\mathfrak {S}_\mathrm{qM}^t$ and $\alpha _-\ge -1$ with strict inequality whenever $\mathrm{ep}>0$.

Transient Dissipated TDE Consider now the functional $\mathfrak {S}^t$ for the process started with the Dirac measure $\nu =\delta _{x_0}$ for some $x_0\in \Xi$. This corresponds to

$$\begin{aligned} N=0,\qquad F=-X_1,\qquad G=-\theta X_1\theta , \end{aligned}$$

and in this case

$$\begin{aligned} \mathfrak {I}_+=[\tfrac{1}{2}-\kappa _c,1[,\qquad \mathfrak {I}_-={\overline{\mathfrak {I}}}_c, \end{aligned}$$

and hence $\mathfrak {I}_\infty =[\tfrac{1}{2}-\kappa _c,1[$. Proposition 3.22 yields a cumulant generating function

$$\begin{aligned} e_\mathrm{TDE,tr}(\alpha )= \lim _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {E}_{x_0}[ \mathrm {e}^{-\alpha \mathfrak {S}^t}] =\left\{ \begin{array}{l@{\quad }l} e(\alpha )&{}\text {for }\alpha \in ]\tfrac{1}{2}-\kappa _c,1[\\ +\infty &{}\text {for }\alpha \not \in [\tfrac{1}{2}-\kappa _c,1], \end{array} \right. \end{aligned}$$

(3.65)

which does not depend on the initial condition $x_0$.

Remark 3.27

For quasi-Markovian networks it may happen that $\mathfrak {I}_\infty =]\alpha _-,1[$ with $\alpha _->\tfrac{1}{2}-\kappa _c$. For later reference, let us consider the case² $\kappa _c=\kappa _0$ (recall Remark 3.14). We deduce from Proposition 5.5(12) that

$$\begin{aligned} X_{1-\alpha }+\alpha \pi _Q\vartheta ^{-1}\pi _Q \ge \frac{1-\alpha }{\vartheta _\mathrm{max}}(I-\pi _Q) +\frac{\Delta }{\vartheta _\mathrm{min}\vartheta _\mathrm{max}} \left( \alpha -\frac{1}{2}+\kappa _0\right) \pi _Q>0, \end{aligned}$$

for $\alpha \in [\tfrac{1}{2}-\kappa _0,0]$. Thus, in this case we have $\mathfrak {I}_\infty =[\tfrac{1}{2}-\kappa _c,1[$ as in the Markovian case.

Steady State Entropy Production Rate Motivated by [52], where the functional $\mathrm{Ep}(\mu ,t)$ plays a central role, we shall also investigate the large time asymptotics of its cumulant generating function

$$\begin{aligned} e_{\mathrm{ep},t}(\alpha ) =\frac{1}{t}\log \mathbb {E}_\mu \left[ \mathrm {e}^{-\alpha \mathrm{Ep}(\mu ,t)}\right] , \end{aligned}$$

in the stationary process. We observe that this function coincides with a Rényi relative entropy, namely

$$\begin{aligned} e_{\mathrm{ep},t}(\alpha ) =\mathrm{Ent}_\alpha \left( \widetilde{\mathbb {P}}_{\mu \Theta }^t|\mathbb {P}_\mu ^t\right) , \end{aligned}$$

so that the symmetry (3.15) yields

$$\begin{aligned} e_{\mathrm{ep},t}(1-\alpha ) =\mathrm{Ent}_\alpha \left( \mathbb {P}_\mu ^t|\widetilde{\mathbb {P}}_{\mu \Theta }^t\right) =\mathrm{Ent}_\alpha \left( \widetilde{\mathbb {P}}_{\mu }^t|\mathbb {P}_{\mu \Theta }^t\right) =\frac{1}{t}\log \mathbb {E}_{\mu \Theta }\left[ \mathrm {e}^{-\alpha \mathrm{Ep}(\mu \Theta ,t)}\right] . \end{aligned}$$

The large time behavior of $e_{\mathrm{ep},t}(\alpha )$ follows from Proposition 3.22 with the choice

$$\begin{aligned} \widehat{N}=\theta X_1\theta ,\qquad F=\theta X_1\theta -X_1,\qquad G=0. \end{aligned}$$

Thus,

$$\begin{aligned} \mathfrak {I}_+=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_{1-\alpha }+\alpha X_1>0\},\qquad \mathfrak {I}_-=\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_{\alpha }+(1-\alpha )\theta X_1\theta >0\}, \end{aligned}$$

and since we can write $X_\alpha +(1-\alpha )\theta X_1\theta =\theta (Y_{1-\alpha }+W_{1-\alpha })\theta$ with $Y_{1-\alpha }=X_{1-\alpha }+\theta X_\alpha \theta$ and $W_{1-\alpha }=(1-\alpha )X_1-X_{1-\alpha }$, it follows from Proposition 5.5(10) that

$$\begin{aligned} \mathfrak {I}_\infty =\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_{1-\alpha }+\alpha X_1>0\}. \end{aligned}$$

In particular the limit

$$\begin{aligned} e_\mathrm{ep}(\alpha )=\lim _{t\rightarrow \infty }e_{\mathrm{ep},t}(\alpha ), \end{aligned}$$

coincides with $e(\alpha )$ for all $\alpha \in {\mathbb {R}}$ iff the following condition holds:

Condition (R) $X_{1-\alpha }+\alpha X_1>0$ for all $\alpha \in {\overline{\mathfrak {I}}}_c$.

This condition involves maximal solutions of two algebraic Riccati equations. Except in some special cases [see Proposition 5.5(12)], its validity is not ensured by general principles (the known comparison theorems for Riccati equations do not apply) and we shall leave it as an open question. We will come back to it in Sect. 4 in context of concrete examples.

Transient Canonical Entropic Functional Assuming for simplicity that the covariance N of the initial condition $\nu \in \mathcal{P}(\Xi )$ is positive definite, Proposition 3.22 applies to the cumulant generating function of $S_\nu ^t$ with

$$\begin{aligned} \widehat{N}=N^{-1},\qquad F=\theta G\theta =\theta N^{-1}\theta -X_1. \end{aligned}$$

It follows that

$$\begin{aligned} \mathfrak {I}_\infty =\{\alpha \in {\overline{\mathfrak {I}}}_c\,|\,X_\alpha +(1-\alpha )N^{-1}>0 \text{ and } X_{1-\alpha }+\alpha N^{-1}>0\}, \end{aligned}$$

so that $\alpha _-=1-\alpha _+=\tfrac{1}{2}-\kappa _\nu$ for some $\kappa _\nu >\tfrac{1}{2}$ and

$$\begin{aligned} e_\nu (\alpha )=\lim _{t\rightarrow \infty }\frac{1}{t}\mathbb {E}_\nu \left[ \mathrm {e}^{-\alpha S_\nu ^t}\right] =\left\{ \begin{array}{l@{\quad }l} e(\alpha )&{}\text {for }|\alpha -\frac{1}{2}|<\kappa _\nu ;\\ +\infty &{}\text {for }|\alpha -\frac{1}{2}|>\kappa _\nu . \end{array} \right. \end{aligned}$$

Note that by the construction of $S_\nu ^t$ the Gallavotti–Cohen symmetry holds for all times. One has $\kappa _\nu =\kappa _c$ and hence $e_\nu (\alpha )=e(\alpha )$ for all $\alpha \in {\mathbb {R}}$, provided

$$\begin{aligned} (\kappa _c-\tfrac{1}{2})X_{\frac{1}{2}+\kappa _c}^{-1}<N <-(\kappa _c+\tfrac{1}{2})X_{\frac{1}{2}-\kappa _c}^{-1}. \end{aligned}$$

3.7 Extended Fluctuation Relations

We finally deal with the 4$^\mathrm{th}$ and last step of our scheme: we derive an LDP for the the entropic functionals considered in the previous section and illustrate its use in obtaining extended fluctuation relations for various physical quantities of interest. We start with a complement to the discussion of Sect. 3.4.

In most cases relevant to entropic functionals of harmonic networks, the generating function $\Lambda$ is real analytic and strictly convex on a finite interval $D_0=]\alpha _-,\alpha _+[$, is infinite on ${\mathbb {R}}\setminus [\alpha _-,\alpha _+]$, and the interval $E=]x_-,x_+[$ is finite. In such cases $\Lambda _\pm$ are both finite and (3.47) implies that the Legendre transform of $\Lambda$ is given by

$$\begin{aligned} \Lambda ^*(x)=\sup _{\alpha \in {\mathbb {R}}}(\alpha x-\Lambda (\alpha ))=\left\{ \begin{array}{l@{\quad }l} x\alpha _--\Lambda _-&{}\text{ for } x\le x_-;\\ x\ell (x)-\Lambda (\ell (x)) &{}\text{ for } x\in ]x_-,x_+[;\\ x\alpha _+-\Lambda _+&{}\text{ for } x\ge x_+; \end{array} \right. \end{aligned}$$

where $\ell :E\rightarrow D_0$ is the reciprocal function to $\Lambda '$. Thus, $\Lambda ^*$ is real analytic on E, affine on ${\mathbb {R}}\setminus E$ and $C^1$ on ${\mathbb {R}}$. The Gärtner–Ellis theorem only provides a local LDP on E for which the affine branches of $\Lambda ^*$ are irrelevant. However, exploiting the Gaussian nature of the underlying measure $\mathbb {P}$, it is sometimes possible to extend this local LDP to a global one, with the rate function $\Lambda ^*$. Inspired by the earlier work of Bryc and Dembo [4], we have recently obtained such an extension for entropic functionals of a large class of Gaussian dynamical systems [41]. The next result is an adaptation of the arguments in [4, 41] and applies to the functional

$$\begin{aligned} \xi _t=S^t+\Phi (x(t))-\Psi (x(0)), \end{aligned}$$

under the law $\mathbb {P}_\nu$, with the hypothesis and notations of Proposition 3.22. We set (recall (3.40))

$$\begin{aligned} \eta _-=\left\{ \begin{array}{l@{\quad }l} -\infty &{}\text{ if } \alpha _+=\frac{1}{2}+\kappa _c;\\ -e'(\alpha _+)&{}\text{ if } \alpha _+<\frac{1}{2}+\kappa _c; \end{array} \right. \qquad \eta _+=\left\{ \begin{array}{l@{\quad }l} +\infty &{}\text{ if } \alpha _-=\frac{1}{2}-\kappa _c;\\ -e'(\alpha _-)&{}\text{ if } \alpha _->\frac{1}{2}-\kappa _c. \end{array} \right. \end{aligned}$$

Theorem 3.28

• (1) If Assumption (C) holds then, under the law $\mathbb {P}_\nu$, the family $(\xi _t)_{t\ge 0}$ satisfies a global LDP with the rate function

  $$\begin{aligned} J(s)=\left\{ \begin{array}{ll} I(\eta _-)-(s-\eta _-)\alpha _+= -s\alpha _+-e(\alpha _+)&{}\quad \text{ for } s\le \eta _-;\\ I(s)&{} \quad \text{ for } s\in ]\eta _-,\eta _+[;\\ I(\eta _+)-(s-\eta _+)\alpha _-= -s\alpha _--e(\alpha _-)&{}\quad \text{ for } s\ge \eta _+; \end{array} \right. \end{aligned}$$

  (3.66)

  where I(s) is given by (3.49). In particular, if $\mathrm{ep}>0$, then it follows from the strict convexity of I(s) that

  $$\begin{aligned} J(-s)-J(s)<I(-s)-I(s)=s, \end{aligned}$$

  for $s>\max (-\eta _-,\eta _+)$.

• (2) Under the same assumptions, the family $(\xi _t)_{t\ge 0}$ satisfies the Central Limit Theorem: For any Borel set $\mathcal{E}\subset {\mathbb {R}}$,

  $$\begin{aligned} \lim _{t\rightarrow \infty }\mathbb {P}_\nu \left[ \frac{\xi _t-\mathbb {E}_\nu [\xi _t]}{\sqrt{ta}}\in \mathcal{E}\right] ={\mathrm n}_1(\mathcal{E}), \end{aligned}$$

  where $a=e''(0)$ and $\mathrm {n}_1$ denotes the centered Gaussian measure on ${\mathbb {R}}$ with variance 1.

If $\mathfrak {I}_\infty ={\overline{\mathfrak {I}}}_c$, then we are in the same situation as in Sect. 3.4 and $\xi _t$ has the same large fluctuations as the canonical entropic functional $S^t$. In particular it also satisfies the Gallavotti–Cohen fluctuation theorem. However, in the more likely event that $\mathfrak {I}_\infty$ is strictly smaller than ${\overline{\mathfrak {I}}}_c$, then (see Fig. 5) the function $g(\alpha )=\limsup _{t\rightarrow \infty }g_t(\alpha )$ only coincides with $e(\alpha )$ on $]\alpha _-,\alpha _+[$ and the rate function J(s) differs from I(s) outside the closure of the interval $]\eta _-,\eta _+[$. Unless $\alpha _-=1-\alpha _+$ (in which case $\eta _-=-\eta _+$ and $J(-s)-J(s)=s$ for all $s\in {\mathbb {R}}$) the Gallavoti-Cohen symmetry is broken and the universal fluctuation relation (3.50) fails. The symmetry function $\mathfrak {s}(s)=J(-s)-J(s)$ then satisfies an “extended fluctuation relation”.

Fig. 5

The cumulant generating function $g(\alpha )=\limsup _{t\rightarrow \infty }g_t(\alpha )$ and the rate function J(s) for the functionals $(\xi _t)_{t\ge 0}$ of Theorem 3.28

Combining Theorem 3.28 with the results of Sect. 3.6 we obtain global LDPs for steady state and transient dissipated TDE. Let us discuss their features in more detail.

Steady State Dissipated TDE Assuming $\mathrm{ep}>0$, we have $-1<\alpha _{\mathrm {TDE,st}-}<0$ and $\alpha _{\mathrm {TDE,st}+}=1$, hence $\eta _{\mathrm {TDE,st}-}=-e'(1)=-\mathrm{ep}$ and $\eta _{\mathrm {TDE,st}+}=-e'(\alpha _{\mathrm {TDE,st}-})>\mathrm{ep}$. In this case, the symmetry function is

$$\begin{aligned} \mathfrak {s}_\mathrm{TDE,st}(s)=\left\{ \begin{array}{l@{\quad }l} s&{}\text{ for } 0\le s\le \mathrm{ep};\\ s-I(s)&{}\text{ for } \mathrm{ep}\le s\le \eta _{\mathrm {TDE,st}+};\\ e(\alpha _{\mathrm {TDE,st}-})+(1+\alpha _{\mathrm {TDE,st}-})s&{} \text{ for } s\ge \eta _{\mathrm {TDE,st}+}; \end{array} \right. \end{aligned}$$

and in particular $\mathfrak {s}_\mathrm{TDE,st}(s)<s$ for $s>\mathrm{ep}$. The slope of the affine branch of $\mathfrak {s}_\mathrm{TDE,st}$ satisfies

$$\begin{aligned} \mathfrak {s}_\mathrm{TDE,st}'(s)=1+\alpha _{\mathrm {TDE,st}-} \in ]0,1[,\quad (s\ge \eta _{\mathrm {TDE,st}+}), \end{aligned}$$

so that $s\mapsto \mathfrak {s}_\mathrm{TDE,st}(s)$ is strictly increasing.

In the equilibrium case ($\vartheta _\mathrm{min}=\vartheta _\mathrm{max}$) one has $\alpha _{\mathrm {TDE,st}\mp }=\mp 1$ and $e(\alpha )$ vanishes identically. Hence the rate function for steady state dissipated TDE is the universal function

$$\begin{aligned} J_\mathrm{TDE,st}(s)=|s|, \end{aligned}$$

and $\mathfrak {s}_\mathrm{TDE,st}(s)=0$ for all $s\in {\mathbb {R}}$.

Transient Dissipated TDE Assuming again $\mathrm{ep}>0$, we have $\alpha _{\mathrm {TDE,tr}-}=\frac{1}{2}-\kappa _c$ and $\alpha _{\mathrm {TDE,tr}+}=1$, so that $\eta _{\mathrm {TDE,tr}-}=-e'(1)=-\mathrm{ep}$ and $\eta _{\mathrm {TDE,tr}+}=-e'(\tfrac{1}{2}-\kappa _c)=+\infty$. The symmetry function reads

$$\begin{aligned} \mathfrak {s}_\mathrm{TDE,tr}(s)=\left\{ \begin{array}{l@{\quad }l} s&{}\text{ for } 0\le s\le \mathrm{ep};\\ s-I(s)&{}\text{ for } s\ge \mathrm{ep}; \end{array} \right. \end{aligned}$$

which coincides with the steady state heat dissipation for $0\le s\le \eta _{\mathrm {TDE,st}+}$. However, the strict concavity of the function $s-I(s)$ implies

$$\begin{aligned} \mathfrak {s}_\mathrm{TDE,tr}(s)<\mathfrak {s}_\mathrm{TDE,st}(s) \end{aligned}$$

for all $s>\eta _{\mathrm {TDE,st}+}$. By Remark 3.21,

$$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}s}(s-I(s))=1-\ell (s)=0 \end{aligned}$$

iff $s=-e'(-1)>-e'(0)=\mathrm{ep}$. Thus, whenever $\tfrac{1}{2}-\kappa _c<-1$ ³ the function $[0,\infty [\ni s\mapsto \mathfrak {s}_\mathrm{TDE,tr}(s)$ has a unique maximum at $s=-e'(-1)$, and the concavity of $s-I(s)$ implies that $\mathfrak {s}_\mathrm{TDE,tr}$ becomes negative for large enough s. In the opposite case where $\tfrac{1}{2}-\kappa _c>-1$ the symmetry function $\mathfrak {s}_\mathrm{TDE,tr}$ is strictly monotone increasing (see Fig. 7 in Sect. 4.1 for an explicit example of this somewhat surprising fact.)

4 Examples

In this section we turn back to harmonic networks in the setup of Sect. 2. We denote by $\{\delta _i\}_{i\in \mathcal{I}}$ the canonical basis of the configuration space ${\mathbb {R}}^\mathcal{I}$.

We start with two general facts which reduce the phase space controllability condition (C) and the non-vanishing of $\mathrm{ep}$ to configuration space controllability (see Sect. 5.10 for a proof).

Lemma 4.1

• (1) If $\mathrm{Ker}\,\omega =\{0\}$, then (A, Q) is controllable iff $(\omega ^*\omega ,\iota )$ is controllable.

• (2) Denote by $\pi _i$, $i\in \partial \mathcal{I}$, the orthogonal projection on $\mathrm{Ker}\,(\vartheta -\vartheta _i)$. Let $\mathcal{C}_i=\mathcal{C}(\omega ^*\omega ,\iota \pi _i)$. If there exist $i,j\in \partial _\mathcal{I}$ such that $\vartheta _i\not =\vartheta _j$ and $\mathcal{C}_i\cap \mathcal{C}_j\not =\{0\}$, then $\mathrm {ep}(\mu )>0$.

Fig. 6

A triangular network and a contour plot of $1/\kappa _c$ as function of the parameters (u, v). See the text for details

4.1 A Triangular Network

Consider the triangular network of Fig. 6 where $\mathcal{I}={\mathbb {Z}}_6$ and $\partial \mathcal{I}={\mathbb {Z}}_6\setminus 2{\mathbb {Z}}_6$ (the indices arithmetic is modulo 6). The potential

$$\begin{aligned} \tfrac{1}{2} q\cdot \omega ^2q=\tfrac{1}{2}\sum _{i\in \mathcal{I}}q_i^2+a\sum _{i\in \mathcal{I}}q_iq_{i+1} +b\sum _{i\in \partial \mathcal{I}}q_{i}q_{i+2}, \end{aligned}$$

is positive definite provided $|a|<\frac{1}{2}$ and $2a^2-\frac{1}{2}<b<1-4a^2$. One easily checks that $a\not =0$ implies $\mathrm{Ran}\,\iota \vee \mathrm{Ran}\,\omega ^2\iota ={\mathbb {R}}^\mathcal{I}$. Thus Assumption (C) is verified under these conditions. Noting that $\delta _2\in \mathcal{C}_1\cap \mathcal{C}_3$, we conclude that $\mathrm{ep}>0$ if $\vartheta _1\not =\vartheta _3$. By symmetry, $\mathrm{ep}>0$ iff

$$\begin{aligned} \Delta =\vartheta _\mathrm{max}-\vartheta _\mathrm{min}>0. \end{aligned}$$

We shall fix the parameters of the model to the following values

$$\begin{aligned} a=\frac{1}{2\sqrt{2}},\qquad b=\frac{1}{4},\qquad \gamma _1=\gamma _3=\gamma _5=1, \qquad \underline{\vartheta }=\frac{1}{|\partial \mathcal{I}|}\sum _{i\in \partial \mathcal{I}}\vartheta _i, \end{aligned}$$

the “relative temperatures” being parametrized by

$$\begin{aligned} \vartheta _1=\underline{\vartheta }(1-u),\quad \vartheta _3=\underline{\vartheta }(1+\tfrac{1}{2}(u+3v)),\quad \vartheta _5=\underline{\vartheta }(1+\tfrac{1}{2}(u-3v)). \end{aligned}$$

Under these constraints, the simplex $\{(u,v)\,|\,0\le u\le 1,0\le v\le u\}$ is a fundamental domain for the action of the symmetry group $S_3$ of the network which corresponds to $\vartheta _\mathrm{min}=\vartheta _1$, $\vartheta _\mathrm{max}=\vartheta _3$. Factoring $\vartheta =\underline{\vartheta }\hat{\vartheta }$, one easily deduces from (3.37) that the matrix $E(\omega )$ and hence the cumulant generating function $e(\alpha )$ do not depend on $\underline{\vartheta }$. We have performed our numerical calculations with $\underline{\vartheta }=1$. The thermodynamic drive of the system is the ratio $\varrho =\Delta /\underline{\vartheta }=\frac{3}{2}(u+v)\in [0,3]$.

Figure 6 shows the reciprocal of $\kappa _c$ as a function of (u, v). It was obtained by numerical calculation of the eigenvalues of the Hamiltonian matrix $K_\alpha$. The lower-left and upper-right corners of the plot correspond to $\varrho =0$ and $\varrho =3$ respectively. Its right edge is the singular limit $\vartheta _\mathrm{min}=0$. Our results are compatible with the two limiting behaviors

$$\begin{aligned} \lim _{\varrho \downarrow 0}\kappa _c=\infty ,\qquad \lim _{\vartheta _\mathrm{min}\downarrow 0}\kappa _c=\tfrac{1}{2}. \end{aligned}$$

The first limit, which corresponds to thermal equilibrium $\vartheta _\mathrm{min}=\vartheta _\mathrm{max}=\underline{\vartheta }$, follows from the lower bound (3.44). Computing the generating function $e(\alpha )$ from Eq. (3.43), and its Legendre transform, we have obtained the symmetry function $\mathfrak {s}_\mathrm{TDE,tr}(s)$ for transient TDE dissipation at three points on the line $v=0.3(1-u)$ where $\kappa _c=1.4, 1.5$ and 1.6 respectively. The result, displayed in Fig. 7 confirm our discussion in Sect. 3.7.

Fig. 7

The numerically computed rate function $J_\mathrm{TDE,tr}(s)$ and the corresponding symmetry function $\mathfrak {s}_\mathrm{TDE,tr}(s)$ for the transient TDE dissipation of the triangular network (both the argument s and the value of these functions are in the units of the corresponding steady state entropy production rate $\mathrm{ep}$)

Solving the Riccati equation (3.58) one can investigate the validity of Condition (R). Figure 8 shows a plot of $\min \mathrm{sp}(X_{1-\alpha }+\alpha X_1)$ as function of (u, v) and a few sections along the lines $v=1+m(u-1)$. It appears that Condition (R) is clearly satisfied for all temperatures.

Fig. 8

Contour plot of $\min \mathrm{sp}(X_{1-\alpha }+\alpha X_1)$ as function of (u, v) and some sections along the lines $v=1+m(u-1)$ for the triangular network

4.2 Jacobi Chains

In our framework, a chain of L oscillators with nearest neighbour interactions coupled to heat baths at its two ends (see Fig. 9) is described by $\mathcal{I}=\{1,\ldots ,L\}$, $\partial \mathcal{I}=\{1,L\}$, and the potential energy

$$\begin{aligned} \tfrac{1}{2}|\omega q|^2=\tfrac{1}{2}\sum _{i=1}^Lb_iq_i^2 +\sum _{i=1}^{L-1}a_i q_i q_{i+1}, \end{aligned}$$

(4.1)

where, without loss of generality, we may assume $\omega$ to be self-adjoint. We parametrize the temperature and relaxation rates of the baths by

$$\begin{aligned} {\overline{\vartheta }}=\tfrac{1}{2}(\vartheta _1+\vartheta _L),\qquad \Delta =|\vartheta _L-\vartheta _1|,\qquad {\overline{\gamma }}=\sqrt{\gamma _1\gamma _L},\qquad \delta =\log \frac{\gamma _1}{\gamma _L},\qquad \kappa _0=\frac{{\overline{\vartheta }}}{\Delta }, \end{aligned}$$

and introduce the parity operator

$$\begin{aligned} \begin{array}{lccc} \mathcal{S}:&{}{\mathbb {R}}^\mathcal{I}&{}\rightarrow &{}{\mathbb {R}}^\mathcal{I}\\ &{}(q_i)_{i\in \mathcal{I}}&{}\mapsto &{}(q_{L+1-i})_{i\in \mathcal{I}}. \end{array} \end{aligned}$$

Fig. 9

A linear chain coupled to two heat baths

To formulate our main result (see Sect. 5.11 for its proof) we state

Assumption (J)  $\omega >0$ and ${\hat{a}}=a_1a_2\cdots a_{L-1}\not =0.$

Assumption (S)  The chain is symmetric, i.e., $[\mathcal{S},\omega ^2]=0$ and $\delta =0$.

Theorem 4.2

Under Assumption (J), the following hold for the harmonic chain with potential (4.1):

• (1) Assumption (C) is satisfied.

• (2) If $\Delta \not =0$, then the covariance of the steady state $\mu$ satisfies

  $$\begin{aligned} \vartheta _{\mathrm {min}}<M<\vartheta _{\mathrm {max}}, \end{aligned}$$

  and $\mathrm{ep}>0$.

• (3) If Assumption (S) also holds, then $\displaystyle \kappa _c=\kappa _0$ and Condition (R) is satisfied.

Remark 4.3

For a class of symmetric quasi-Markovian anharmonic chains, Rey-Bellet and Thomas have obtained in [67] a local LDP for various entropic functionals of the form $S^t+\Psi (x(t))-\Psi (x(0))$ under the law $\mathbb {P}_{x_0}$, $x_0\in \Xi$. In view of their Hypothesis (H1) (more precisely, the condition $k_2\ge k_1\ge 2$), their results should apply in particular to harmonic chains satisfying Assumptions (J) and (S). They proved that the cumulant generating function of these functionals are finite and satisfy the Gallavotti–Cohen symmetry on the interval $]\frac{1}{2}-\kappa _0,\frac{1}{2}+\kappa _0[$. The lower bound of this interval is consistent with Part (4) of Theorem 4.2 and Remark 3.27, whereas the upper bound is different from our conclusions in Sect. 3.7 on the transient TDE. There, we found that the cumulant generating function diverges for $\alpha >1$. In view of this, it appears that the analysis of [67] does not apply to the harmonic case.

Remark 4.4

We believe that Condition (S) is essential for Part (4) since the proof indicates that for non-symmetric chains $\kappa _c>\kappa _0$ is generic. Figure 10 shows a plot of $\kappa _c$ vs $\delta$ for a homogeneous chain with $L=4$, $b_i=1$, $a_i=\frac{1}{2}$, ${\overline{\gamma }}=2$, ${\overline{\vartheta }}=4$ and $\Delta =2$.

Fig. 10

The critical value $\kappa _c/\kappa _0$ as a function of $\delta$ for an homogeneous chain

5 Proofs

Even though the processes induced by Eq. (3.2) take values in a real vector space, it will be sometimes more convenient to work with complex vector spaces. With this in mind, we start with some general remarks and notational conventions concerning complexifications.

Let E be a real Hilbert space with inner product $\langle \,\cdot \,,\,\cdot \,\rangle$. We denote by ${\mathbb {C}}E=\{x+\mathrm {i}y\,|\,x,y\in E\}$ the complexification of E. This complex vector space inherits a natural Hilbertian structure with inner product

$$\begin{aligned} (x+\mathrm {i}y,u+\mathrm {i}v) =\langle x,u\rangle +\langle y,v\rangle +\mathrm {i}\langle x,v\rangle -\mathrm {i}\langle y,u\rangle . \end{aligned}$$

We denote by $|\cdot |$ the induced norm. Any $A\in L(E,F)$ extends to an element of $L({\mathbb {C}}E,{\mathbb {C}}F)$ which we denote by the same symbol: $A(x+\mathrm {i}y)=Ax+\mathrm {i}Ay$. If A is a self-adjoint/non-negative/positive element of L(E), then this extension is a self-adjoint/non-negative/positive element of $L({\mathbb {C}}E)$. The conjugation $\mathcal{C}_E:x+\mathrm {i}y\mapsto x-\mathrm {i}y$ is a norm-preserving involution of ${\mathbb {C}}E$. For $z\in {\mathbb {C}}E$ and $A\in L({\mathbb {C}}F,{\mathbb {C}}E)$ we set ${\overline{z}}=\mathcal{C}_E z$ and ${\overline{A}}=\mathcal{C}_E A\mathcal{C}_F$. We identify E with the set $\{z\in {\mathbb {C}}E\,|\,{\overline{z}}=z\}$ of real elements of ${\mathbb {C}}E$. Likewise, L(F, E) is identified with the set $\{A\in L({\mathbb {C}}F,{\mathbb {C}}E)\,|\,{\overline{A}}=A\}$ of real elements of $L({\mathbb {C}}F,{\mathbb {C}}E)$. A subspace $V\subset {\mathbb {C}}E$ is real if it is invariant under $\mathcal{C}_E$. V is real iff there exists a subspace $V_0\subset E$ such that $V={\mathbb {C}}V_0$. If $A\in L({\mathbb {C}}F,{\mathbb {C}}E)$ is real, then $\mathrm{Ran}\,A$ and $\mathrm{Ker}\,A$ are real subspaces of ${\mathbb {C}}E$ and ${\mathbb {C}}F$. Finally, we note that if $(A,Q)\in L(E)\times L(F,E)$, then the controllability subspace of the corresponding pair in $L({\mathbb {C}}E)\times L({\mathbb {C}}F,{\mathbb {C}}E)$ is the real subspace ${\mathbb {C}}\mathcal{C}(A,Q)\subset {\mathbb {C}}E$. In particular (A, Q) is controllable as a pair of ${\mathbb {R}}$-linear maps iff it is controllable as a pair of ${\mathbb {C}}$-linear maps.

Note that

$$\begin{aligned} \xi (t)=\int _0^t\mathrm {e}^{(t-s)A}Q\mathrm {d}w(s) \end{aligned}$$

(5.1)

is a centered Gaussian random variable with covariance

$$\begin{aligned} M_t=\int _0^t\mathrm {e}^{sA}QQ^*\mathrm {e}^{sA^*}\mathrm {d}s. \end{aligned}$$

(5.2)

The next lemma concerns some elementary properties of this operator.

Lemma 5.1

Assume that $(A,Q,\vartheta ,\theta )\in L(\Xi )\times L(\partial \Xi ,\Xi )\times L(\partial \Xi )\times L(\Xi )$ satisfies the structural relations (3.9) and let $M_t$ be given by Eq. (5.2).

• (1) $\mathrm{Ran}\,M_t=\mathcal{C}(A,Q)$ for all $t>0$.

• (2) The subspace $\mathcal{C}(A,Q)$ is invariant for both A and $A^*$, and $\mathrm{sp}(A|_{\mathcal{C}(A,Q)}),\mathrm{sp}(A^*|_{\mathcal{C}(A,Q)})\subset {\mathbb {C}}_-$. In particular, there exist constants $C\ge 1$ and $\delta '\ge \delta >0$ such that

  $$\begin{aligned} C^{-1}\mathrm {e}^{-\delta ' t}|x|\le |\mathrm {e}^{tA}x|\le C\mathrm {e}^{-\delta t}|x|\quad \text{ for } x\in \mathcal{C}(A,Q), \end{aligned}$$

  and the function $t\mapsto M_t$ converges to a limit M as $t\rightarrow +\infty$.

• (3) $\mathrm{Ran}\,M=\mathcal{C}(A,Q)=\mathcal{C}(A^*,Q)$.

• (4) $A|_{\mathcal{C}(A,Q)^\bot }=-A^*|_{\mathcal{C}(A,Q)^\bot }$ and $\mathrm {e}^{tA}|_{\mathcal{C}(A,Q)^\bot }$ is unitary.

• (5) The following inequality holds for all $t\ge 0:$

  $$\begin{aligned} \vartheta _\mathrm{min}(I-\mathrm {e}^{tA}\mathrm {e}^{tA^*})\le M_t \le \vartheta _\mathrm{max}(I-\mathrm {e}^{tA}\mathrm {e}^{tA^*})\le \vartheta _\mathrm{max}. \end{aligned}$$

  (5.3)

  In particular,

  $$\begin{aligned} \vartheta _\mathrm{min}\le M|_{\mathrm{Ran}\,M}\le \vartheta _\mathrm{max}, \end{aligned}$$

  and if all the reservoirs are at the same temperature $\vartheta _0$, then $M|_{\mathrm{Ran}\,M}=\vartheta _0$.

• (6) $M-M_t=\mathrm {e}^{tA}M\mathrm {e}^{tA^*}\ge 0$ and $(M-M_t)|_{\mathrm{Ran}\,M}>0$.

• (7) M satisfies the Lyapunov equation

  $$\begin{aligned} AM+MA^*+QQ^*=0. \end{aligned}$$

  (5.4)

• (8) If (A, Q) is controllable, then $\mathrm{Ran}\,M=\Xi$ and M is the only solution of (5.4). Moreover, for any $\tau >0$ there exists a constant $C_\tau$ such that

  $$\begin{aligned} 0<M_t^{-1}-M^{-1}\le C_\tau \mathrm {e}^{-2\delta t} \quad \text{ for } \text{ all }\quad t\ge \tau . \end{aligned}$$

Proof

• (1) Fix $t>0$. From the relation

  $$\begin{aligned} x\cdot M_tx=\int _0^t|Q^*\mathrm {e}^{sA^*}x|^2\mathrm {d}s \end{aligned}$$

  we deduce that $\mathrm{Ker}\,M_t=\cap _{s\in [0,t]}\mathrm{Ker}\,Q^*\mathrm {e}^{sA^*}$. This relation is easily seen to be equivalent to

  $$\begin{aligned} \mathrm{Ker}\,M_t=\bigcap _{n\ge 0}\mathrm{Ker}\,Q^*A^{*n}, \end{aligned}$$

  (5.5)

  and hence to

  $$\begin{aligned} \mathrm{Ran}\,M_t=\bigvee _{n\ge 0}\mathrm{Ran}\,A^nQ. \end{aligned}$$

  (5.6)

  The right-hand side of the last relation is included in any A-invariant subspace containing $\mathrm{Ran}\,Q$, and therefore coincides with the controllability subspace $\mathcal{C}(A,Q)$.

• (2) The invariance of the subspace $\mathcal{C}(A,Q)$ under A follows from the definition. To prove its invariance under $A^*$, it suffices to recall the relation

  $$\begin{aligned} A+A^*=-Q\vartheta ^{-1}Q^*. \end{aligned}$$

  (5.7)

  We now prove that the spectra of the restrictions of A and $A^*$ to $\mathcal{C}(A,Q)$ are subsets of ${\mathbb {C}}_-$. It suffices to consider the case of A. Pick $\alpha \in \mathrm{sp}(A)$ and let $z\in {\mathbb {C}}\Xi \setminus \{0\}$ be a corresponding eigenvector. It follows from (5.7) that

  $$\begin{aligned} 2\mathrm{Re}\,\alpha |z|^2=(z,(A+A^*)z)=-|\vartheta ^{-1/2}Q^*z|^2, \end{aligned}$$

  which implies $\mathrm{Re}\,\alpha \le 0$. If $\mathrm{Re}\,\alpha =0$, then $Q^*z=0$ and (5.7) yields $A^*z=-\alpha z$ which further implies $Q^*A^{*n}z=(-\alpha )^nQ^*z=0$ for all $n\ge 0$. Eq. (5.5) then gives $z\in \mathrm{Ker}\,M_t$ and so $\mathrm{sp}(A|_{\mathrm{Ran}\,M_t})\subset {\mathbb {C}}_-$. The remaining statements are elementary consequences of this fact and the observation that $M_t$ vanishes on $\mathcal{C}(A,Q)^\bot$.

• (3) The proof of the relation $\mathrm{Ran}\,M=\mathcal{C}(A,Q)$ is exactly the same as that of (1). The relation $\mathcal{C}(A,Q)=\mathcal{C}(A^*,Q)$ is a simple consequence of (5.7).

• (4) Combining (5.5) with (5.7), we deduce $\mathrm{Ker}\,(A+A^*)=\mathrm{Ker}\,Q^*\supset \mathcal{C}(A,Q)^\bot$. Thus A and $-A^*$ coincide on $\mathcal{C}(A,Q)^\bot$.

• (5) From Eq. (5.7) we deduce

  $$\begin{aligned} \int _0^t\mathrm {e}^{sA}Q\vartheta ^{-1}Q^*\mathrm {e}^{sA^*}\mathrm {d}s =-\int _0^t\frac{\mathrm {d}\ }{\mathrm {d}s}\mathrm {e}^{sA}\mathrm {e}^{sA^*}\mathrm {d}s=I-\mathrm {e}^{tA}\mathrm {e}^{tA^*}, \end{aligned}$$

  from which we infer

  $$\begin{aligned} \vartheta _\mathrm{max}^{-1}M_t\le I-\mathrm {e}^{tA}\mathrm {e}^{tA^*} \le \vartheta _\mathrm{min}^{-1}M_t. \end{aligned}$$

  This is equivalent to (5.3). Restricting these inequalities to $\mathcal{C}(A,Q)$ and taking the limit $t\rightarrow \infty$ yields the desired result.

• (6) The first assertion follows directly from the definition of M and the group property of $\mathrm {e}^{tA}$. The second assertion is a consequence of Parts (3) and (5) which imply

  $$\begin{aligned} (M-M_t)|_{\mathrm{Ran}\,M}=\mathrm {e}^{tA}M\mathrm {e}^{tA^*}|_{\mathrm{Ran}\,M} \ge \vartheta _{\mathrm {min}}\mathrm {e}^{tA}\mathrm {e}^{tA^*}|_{\mathrm{Ran}\,M}>0. \end{aligned}$$

• (7) Follows from Part (6) and Eq. (5.2) by differentiation.

• (8) Any solution N of (5.4) is easily seen to satisfy

  $$\begin{aligned} N-M_t=\mathrm {e}^{tA}N\mathrm {e}^{tA^*}\quad \text{ for } \text{ all } t\ge 0. \end{aligned}$$

  Letting $t\rightarrow +\infty$ and using the exponential decay of $\mathrm {e}^{tA}$ and $\mathrm {e}^{tA^*}$ [see (2) in the case $\mathcal{C}(A,Q)=\Xi$], we see that $N=M$. The second assertion follows from the identity

  $$\begin{aligned} M_t^{-1}-M^{-1}=M_t^{-1}(M-M_t)M^{-1} \end{aligned}$$

  and the inequalities $M_t\ge c_\tau >0$ for $t\ge \tau$ and $\Vert M_t-M\Vert \le Ce^{-2\delta t}$ for $t\ge 0$.

$\square$

5.1 Sketch of the Proof of Theorem 3.2

(1) The fact that M is well defined and satisfies (3.13) was established in Lemma 5.1. Let us prove the invariance of $\mu$.

We fix a random variable $x_0$ that is independent of w and is distributed by the law $\mu$. We wish to show that the law of the process

$$\begin{aligned} x(t)=\mathrm {e}^{t A}x_0+\xi (t), \end{aligned}$$

(5.8)

where $\xi$ is given by (5.1), coincides with $\mu$ for all $t\ge 0$. To this end, we note that both terms in (5.8) are centred Gaussian random variables with covariances $\mathrm {e}^{tA}M\mathrm {e}^{tA^*}$ and $M_t$, respectively. Since they are independent, x(t) is also a centred Gaussian random variable with covariance $\mathrm {e}^{tA}M\mathrm {e}^{tA^*}+M_t$. This operator coincides with M in view of Lemma 5.1(6). Hence, the law of x(t) coincides with $\mu$.

(2) If the pair (A, Q) is controllable, then for any initial condition $x_0$ independent of w the corresponding solution (5.8) converges in law to $\mu$. It follows that $\mu$ is the only invariant measure. On the other hand, if the pair (A, Q) is not controllable, then, by Lemma 5.1, the subspace $\mathrm{Ker}\,M=\mathcal{C}(A,Q)^\bot \not =\{0\}$ is invariant for the group $\{\mathrm {e}^{t A}\}$, whose restriction to it is a unitary. The latter has infinitely many invariant measures (e.g., the normalized Lebesgue measure on any sphere $\{x\in \mathcal{C}(A,Q)^\bot \,|\,|x|=R\}$ is invariant).

To prove the mixing property, we write

$$\begin{aligned} P^tf(x)=\mathbb {E}f\bigr (\mathrm {e}^{t A}x+\xi (t)\bigr )=\int _{\Xi } f(y)\mathrm{n}_t(x,y)\,\mathrm {d}y, \end{aligned}$$

where $\mathrm{n}_t(x,y)$ denotes the density of the Gaussian measure with mean value $\mathrm {e}^{t A}x$ and covariance $M_t$:

$$\begin{aligned} \mathrm{n}_t(x,y)=\det (2\pi M_t)^{-1/2} \exp \Bigl \{-\frac{1}{2}\,\bigl (y-\mathrm {e}^{tA}x,M_t^{-1}(y-\mathrm {e}^{tA}x\bigr )\Bigr \}. \end{aligned}$$

The required convergence follows now from assertions (6) and (8) of Lemma 5.1 and the Lebesgue theorem on dominated convergence.

(3) The fact that process (3.7) is centred and Gaussian follows from linearity of the equation. Let us calculate its covariance operator K(t, s). It is a straightforward to check that a stationary solution of (3.2) defined on the whole real line can be written as

$$\begin{aligned} {\hat{\xi }}(t)=\int _{-\infty }^t\mathrm {e}^{(t-r)A}Q\mathrm {d}w(r), \end{aligned}$$

where w(t) stands for a two-sided ${\mathbb {R}}^{\partial \mathcal{I}}$-valued Brownian motion. Assuming without loss of generality that $t>s$, for any $\eta _1,\eta _2\in \Xi$ we write

$$\begin{aligned} (\eta _1,K(t,s)\eta _2)&=\mathbb {E}\bigl \{(\hat{\xi }(t),\eta _1\bigr )\bigl (\hat{\xi }(s),\eta _2\bigr )\bigr \}\\&=\mathbb {E}\biggl \{\int _{-\infty }^t\bigl (\mathrm {e}^{(t-r)A}Q\mathrm {d}w(r),\eta _1\bigr )\, \int _{-\infty }^s\bigl (\mathrm {e}^{(s-r)A}Q\mathrm {d}w(r),\eta _2\bigr )\biggr \}\\&=\int _{-\infty }^s\bigl (Q^*\mathrm {e}^{(t-r)A^*}\eta _1,Q^*\mathrm {e}^{(s-r)A^*}\eta _2\bigr )\mathrm {d}r\\&=\int _0^{+\infty }\bigl (\eta _1,\mathrm {e}^{(t-s+u)A}QQ^*\mathrm {e}^{uA^*}\eta _2\bigr )\mathrm {d}u=(\eta _1,\mathrm {e}^{tA}M\eta _2). \end{aligned}$$

This implies the required relation (3.14) and completes the proof of Theorem 3.2. $\square$

For later use, we now formulate and prove two other auxiliary results. We start with a few technical facts. Consider the scale of spaces

$$\begin{aligned} \mathfrak {H}_+\subset \mathfrak {H}\subset \mathfrak {H}_-, \end{aligned}$$

where $\mathfrak {H}=L^2({\mathbb {R}})\otimes {\mathbb {C}}\Xi$, $\mathfrak {H}_+$ is the Sobolev space $H^1({\mathbb {R}})\otimes {\mathbb {C}}\Xi$, and $\mathfrak {H}_-=H^{-1}({\mathbb {R}})\otimes {\mathbb {C}}\Xi$ is its dual w.r.t. the duality induced by the inner product of $\mathfrak {H}$. To simplify notations, we shall also use the symbols $\mathfrak {H}$, $\mathfrak {H}_\pm$ to denote the corresponding real Hilbert spaces (the meaning should remain clear from the context). For $x\in \mathfrak {H}$, we denote by

$$\begin{aligned} {\hat{x}}(\omega )=\int x(s)\mathrm {e}^{-\mathrm {i}\omega s}\mathrm {d}s \end{aligned}$$

its Fourier transform. Since, under Assumption (C), A is stable, we can use

$$\begin{aligned} \Vert x\Vert _\pm =\left( \int |(A-\mathrm {i}\omega )^{\pm 1} {\hat{x}}(\omega )|^2\frac{\mathrm {d}\omega }{2\pi }\right) ^{\frac{1}{2}} \end{aligned}$$

as norms on $\mathfrak {H}_\pm$. For $\tau >0$, we denote by $\Pi _\tau$ the operator of multiplication with the characteristic function of the interval $[0,\tau ]$. Thus, $\Pi _\tau$ is an orthogonal projection in $\mathfrak H$ whose range $\mathfrak {H}_\tau$ will be identified with the Hilbert space $L^2([0,\tau ])\otimes {\mathbb {C}}\Xi$.

Lemma 5.2

Under Assumption (C) the following hold.

• (1) The Volterra integral operator

  $$\begin{aligned} (Rx)(s)=\int _{-\infty }^s\mathrm {e}^{(s-s')A}x(s')\mathrm {d}s' \end{aligned}$$

  maps isometrically $\mathfrak {H}_-$ onto $\mathfrak {H}$ and $\mathfrak {H}$ onto $\mathfrak {H}_+$. By duality, its adjoint

  $$\begin{aligned} (R^*x)(s)=\int _s^\infty \mathrm {e}^{(s'-s)A^*}x(s')\mathrm {d}s', \end{aligned}$$

  has the same properties.

• (2) $\Pi _\tau R$ is Hilbert–Schmidt, with norm

  $$\begin{aligned} \Vert \Pi _\tau R\Vert _2=\left( \tau \int _0^\infty \mathrm{tr}(\mathrm {e}^{tA^*}\mathrm {e}^{tA})\mathrm {d}t\right) ^{\frac{1}{2}}. \end{aligned}$$

• (3) For $t_0\in [0,\tau ]$, the Hilbert–Schmidt norm of the map $R_{t_0}:\mathfrak {H}\rightarrow \Xi$ defined by $R_{t_0}x=(Rx)(t_0)$ is given by

  $$\begin{aligned} \Vert R_{t_0}\Vert _2=\left( \int _0^{t_0}\mathrm{tr}(\mathrm {e}^{tA^*}\mathrm {e}^{tA})\mathrm {d}t\right) ^{\frac{1}{2}}. \end{aligned}$$

Proof

• (1) Follows from our choice of the norms on $\mathfrak {H}_\pm$ and the fact that $(Rx)^{\,\widehat{}}(\omega )=(\mathrm {i}\omega -A)^{-1}{\hat{x}}(\omega )$.

• (2) $\Pi _\tau R$ is an integral operator with kernel $1_{[0,\tau ]}(s)\theta (s-s')\mathrm {e}^{(s-s')A}$, where $1_{[0,\tau ]}$ denotes the characteristic function of the interval $[0,\tau ]$ and $\theta$ the Heaviside step function. Its Hilbert–Schmidt norm is given by

  $$\begin{aligned} \Vert \Pi _\tau R\Vert _2^2= \int _0^\tau \mathrm {d}s\int _{-\infty }^s\mathrm {d}s'\, \mathrm{tr}(\mathrm {e}^{(s-s')A^*}\mathrm {e}^{(s-s')A}) =\tau \int _0^\infty \mathrm {d}t\, \mathrm{tr}(\mathrm {e}^{tA^*}\mathrm {e}^{tA}). \end{aligned}$$

• (3) Follows from a simple calculation.

$\square$

Given $\tau >0$, consider the process $\{x(t)\}_{t\in [0,\tau ]}$ started with a Gaussian measure $\nu \in \mathcal{P}(\Xi )$. Let $a\in \Xi$ be the mean of $\nu$ and $0\le N\in L(\Xi )$ its covariance. Denote by $(\,\cdot \,|\,\cdot \,)$ the inner product of $\mathfrak {H}_\tau$.

Lemma 5.3

Let $T_\tau :\Xi \ni v\mapsto \mathrm {e}^{sA}v\in \mathfrak {H}_\tau$ and define

$$\begin{aligned} \mathcal{D}_\tau =\left[ \begin{array}{cc} T_\tau N^{\frac{1}{2}}&\Pi _\tau RQ \end{array}\right] : \Xi \oplus \partial \mathfrak {H}\rightarrow \mathfrak {H}_\tau , \end{aligned}$$

where $\partial \mathfrak {H}=L^2({\mathbb {R}})\otimes \partial \Xi$, and the operator Q acts on $\partial \mathfrak {H}$ by the relation $(Qy)(t) =Qy(t)$ for $t\in {\mathbb {R}}$. Then, under Assumption (C), the following properties hold for any $\tau >0$:

• (1) $\mathcal{D}_\tau$ is Hilbert–Schmidt and has a unique continuous extension to $\Xi \oplus \mathfrak {H}_-$.

• (2) $\mathcal{K}_\tau =\mathcal{D}_\tau \mathcal{D}_\tau ^*$ is a non-negative trace class operator on $\mathfrak {H}_\tau$ with integral kernel

  $$\begin{aligned} \mathcal{K}_\tau (s,s')=\mathrm {e}^{(s-s')_+A}(\mathrm {e}^{(s\wedge s')A}N\mathrm {e}^{(s\wedge s')A^*} +M_{s\wedge s'})\mathrm {e}^{(s-s')_-A^*}, \end{aligned}$$

  (5.9)

  and there exists a constant $C_\nu$, depending on A, B and N but not on $\tau$, and such that

  $$\begin{aligned} \mathcal{K}_\tau \le C_\nu ,\qquad \Vert \mathcal{K}_\tau \Vert _1\le C_\nu \tau , \end{aligned}$$

  where $\Vert \cdot \Vert _1$ denotes the trace norm.

• (3) The process $\{x(t)\}_{t\in [0,\tau ]}$ is Gaussian with mean $T_\tau a$ and covariance $\mathcal{K}_\tau$, i.e.,

  $$\begin{aligned} \mathbb {E}_\nu [\mathrm {e}^{\mathrm {i}(x|u)}]=\mathrm {e}^{\mathrm {i}(T_\tau a|u)-\frac{1}{2}(u|\mathcal{K}_\tau u)} \end{aligned}$$

  (5.10)

  for all $u\in \mathfrak {H}_\tau$.

Proof

• (1) $T_\tau$ is clearly finite rank and it follows from Lemma 5.2(2) that the operator $\mathcal{D}_\tau$ is Hilbert–Schmidt. Lemma 5.2(1) further implies that it extends by continuity to $\Xi \oplus \mathfrak {H}_-$.

• (2) It follows immediately that

  $$\begin{aligned} \mathcal{K}_\tau =\mathcal{D}_\tau \mathcal{D}_\tau ^*=T_\tau NT_\tau ^*+\Pi _\tau RQQ^*R^*\Pi _\tau |_{\mathfrak {H}_\tau } \end{aligned}$$

  (5.11)

  is non-negative and trace class. Formula (5.9) can be checked by an explicit calculation. Defining the function $u\in \mathfrak {H}_\tau$ to be zero outside $[0,\tau ]$, we can invoke Plancherel’s theorem to translate (5.11) into

  $$\begin{aligned} (u|\mathcal{K}_\tau u)=\left| \int _{-\infty }^{\infty }N^\frac{1}{2}(A^*+\mathrm {i}\omega )^{-1} {\hat{u}}(\omega )\frac{\mathrm {d}\omega }{2\pi }\right| ^2 +\int _{-\infty }^{\infty }|Q^*(A^*+\mathrm {i}\omega )^{-1} {\hat{u}}(\omega )|^2\frac{\mathrm {d}\omega }{2\pi }. \end{aligned}$$

  By Lemma 5.1, Assumption (C) implies $\mathrm{sp}(A)\cap \mathrm {i}{\mathbb {R}}=\emptyset$ and we conclude that

  $$\begin{aligned} \mathcal{K}_\tau \le \int _{-\infty }^{\infty }\Vert N^\frac{1}{2}(A^*+\mathrm {i}\omega )^{-1}\Vert ^2 \frac{\mathrm {d}\omega }{2\pi }+\sup _{\omega \in {\mathbb {R}}}\Vert Q^*(A^*+\mathrm {i}\omega )^{-1}\Vert ^2 <\infty . \end{aligned}$$

  Finally, it is well known [70, Theorem 3.9] that the trace norm of a non-negative trace class integral operator with continuous kernel $\mathcal{K}_\tau (s,s')$ is given by

  $$\begin{aligned} \Vert \mathcal{K}_\tau \Vert _1=\mathrm{tr}(\mathcal{K}_1)=\int _0^\tau \mathrm{tr}(\mathcal{K}_\tau (s,s))\mathrm {d}s =\int _0^\tau \mathrm{tr}(\mathrm {e}^{sA}N\mathrm {e}^{sA^*}+M_s)\mathrm {d}s\le \tau \left( C\,\mathrm{tr}(N)+\mathrm{tr}(M)\right) , \end{aligned}$$

  where C depends only on A.

• (3) By Eq. (3.7) we have, for $u\in \mathfrak {H}_\tau$,

  $$\begin{aligned} (x|u)&=(T_\tau x(0)|u)+\int _0^\tau \left[ \int _0^t\mathrm {e}^{(t-s)A}Q\,\mathrm {d}w(s)\right] \cdot u(t)\mathrm {d}t\\&=x(0)\cdot T_\tau ^*u+\int _0^\tau Q^*(R^*u)(s)\cdot \mathrm {d}w(s) \end{aligned}$$

  so that

  $$\begin{aligned} \mathbb {E}_\nu [\mathrm {e}^{\mathrm {i}(x|u)}] =\mathbb {W}[\mathrm {e}^{\mathrm {i}\int _0^\tau Q^*(R^*u)(s)\cdot \mathrm {d}w(s)}] \int \mathrm {e}^{\mathrm {i}x\cdot T_\tau ^*u}\nu (\mathrm {d}x). \end{aligned}$$

  Evaluating Gaussian integrals we get

  $$\begin{aligned} \int \mathrm {e}^{\mathrm {i}x\cdot T_\tau ^*u}\nu (\mathrm {d}x) =\mathrm {e}^{\mathrm {i}a\cdot T_\tau ^*u-\frac{1}{2} T_\tau ^*u\cdot NT_\tau ^*u} =\mathrm {e}^{\mathrm {i}(T_\tau a|u)-\frac{1}{2} (u|T_\tau NT_\tau ^*u)}, \end{aligned}$$

  and

  $$\begin{aligned} \mathbb {W}[\mathrm {e}^{\mathrm {i}\int _0^\tau Q^*(R^*u)(s)\cdot \mathrm {d}w(s)}]= \mathrm {e}^{-\frac{1}{2}(u|RQQ^*R^*u)}, \end{aligned}$$

  which provide the desired identity.

$\square$

5.2 Proof of Proposition 3.5

We start with some results on the Markov semigroup

$$\begin{aligned} (P^tf)(x)=\int f(\mathrm {e}^{tA}x+M_t^{\frac{1}{2}}y)\mathrm{n}(\mathrm {d}y). \end{aligned}$$

(5.12)

For a multi-index $\alpha =(\alpha _1,\alpha _2,\ldots )\in {\mathbb {N}}^{\dim \Xi }$ and $p\in [1,\infty ]$ set

$$\begin{aligned} |\alpha |=\sum _i\alpha _i,\qquad \partial ^\alpha =\prod _i\partial _{x_i}^{\alpha _i}, \end{aligned}$$

and define

$$\begin{aligned} \mathcal{A}^p=\left\{ \psi \in C^\infty (\Xi )\,\bigg |\, |\partial ^\alpha \psi | \in L^p(\Xi ,\mathrm {d}\mu )\text { for all }\alpha \in {\mathbb {N}}^{\dim \Xi } \right\} . \end{aligned}$$

Lemma 5.4

Suppose that Assumption (C) holds.

• (1) For any $\nu \in \mathcal{P}(\Xi )$ and $t>0$, $\nu _t$ is absolutely continuous w.r.t. Lebesgue measure. Its Radon-Nikodym derivative

  $$\begin{aligned} \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x) =\det (2\pi M_t)^{-\frac{1}{2}}\int \mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}y)|^2}\nu (\mathrm {d}y) \end{aligned}$$

  (5.13)

  is strictly positive and $S_\mathrm {GS}(\nu _t)>-\infty$. Moreover, if $\nu (|x|^2)<\infty$, then $S_\mathrm {GS}(\nu _t)<\infty$.

• (2) For any $\nu \in \mathcal{P}(\Xi )$, any $t>0$, and any multi-index $\alpha$,

  $$\begin{aligned} \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}x}\in L^1(\Xi ,\mathrm {d}x)\cap L^\infty (\Xi ,\mathrm {d}x). \end{aligned}$$

• (3) For $t>0$, $\widetilde{M}_t=M-\mathrm {e}^{t\widetilde{A}}M\mathrm {e}^{t\widetilde{A}^*}>0$, and

  $$\begin{aligned} \widetilde{M}_t^{-1}=M^{-1}+\mathrm {e}^{tA^*}M_t^{-1}\mathrm {e}^{tA}. \end{aligned}$$

  (5.14)

• (4) $P^t$ is a contraction semigroup on $L^p(\Xi ,\mathrm {d}\mu )$ for any $p\in [1,\infty ]$. Its adjoint w.r.t. the duality $\langle f|g\rangle _\mu =\mu (fg)$ is given by

  $$\begin{aligned} (P^{t*}\psi )(x)=\int \psi (\mathrm {e}^{t\widetilde{A}}x+\widetilde{M}_t^\frac{1}{2}y) \mathrm{n}(\mathrm {d}y). \end{aligned}$$

  (5.15)

  In particular, $P^{t*}$ is positivity improving.

• (5) For all $t>0$, $P^{t*}L^\infty (\Xi ,\mathrm {d}\mu )\subset \mathcal{A}^\infty$.

• (6) For $p\in [1,\infty [$, $\mathcal{A}^p$ is a core of the generator of $P^{t*}$ on $L^p(\Xi ,\mathrm {d}\mu )$ and this generator acts on $\psi \in \mathcal{A}^p$ as

  $$\begin{aligned} L^*\psi =\frac{1}{2}\nabla \cdot B\nabla \psi +\widetilde{A}x\cdot \nabla \psi . \end{aligned}$$

  (5.16)

• (7) For $\nu \in \mathcal{P}_+(\Xi )$ and $p\in [1,\infty [$ there exists $t_{\nu ,p}>0$ such that $\frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }\in \mathcal{A}^p$ for all $t>t_{\nu ,p}$.

• (8) For $\nu \in \mathcal{P}_+(\Xi )$ there exist $t_{\nu ,\infty }>0$, $C_\nu$ and $\delta _\nu >0$ such that

  $$\begin{aligned} \left| \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\right| \le C_\nu \mathrm {e}^{-\delta _\nu t}(1+|x|^2) \end{aligned}$$

  for $t\ge t_{\nu ,\infty }$.

Proof

• (1) We deduce from Eq. (5.12) that for any bounded measurable function f on $\Xi$ one has

  $$\begin{aligned} \nu _t(f)= & {} \nu (P^t f)=\int f(\mathrm {e}^{tA}x+M_t^\frac{1}{2}y)\nu (\mathrm {d}x)\mathrm{n}(\mathrm {d}y)\\= & {} \det (2\pi M_t)^{-\frac{1}{2}}\int f(y)\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(y-\mathrm {e}^{tA}x)|^2}\nu (\mathrm {d}x)\mathrm {d}y, \end{aligned}$$

  from which we conclude that $\nu _t$ is absolutely continuous w.r.t. Lebesgue measure with Radon-Nikodym derivative given by Eq. (5.13). It follows immediately that

  $$\begin{aligned} \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)\le \det (2\pi M_t)^{-\frac{1}{2}}, \end{aligned}$$

  which implies the lower bound

  $$\begin{aligned} S_\mathrm{GS}(\nu _t)\ge \frac{1}{2}\log \det (2\pi M_t)>-\infty . \end{aligned}$$

  To derive an upper bound, let r be such that $B_r=\{x\in \Xi \,|\,|x|<r\}$ satisfies $\nu (B_r)>\frac{1}{2}$. Then one has

  $$\begin{aligned} \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)&\ge \frac{1}{2}\det (2\pi M_t)^{-\frac{1}{2}} \inf _{z\in B_r}\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}z)|^2}\\&\ge \frac{1}{2}\det (2\pi M_t)^{-\frac{1}{2}} \mathrm {e}^{-\frac{1}{2}\Vert M_t^{-1}\Vert \sup _{z\in B_r}|(x-\mathrm {e}^{tA}z)|^2}\\&\ge \frac{1}{2}\det (2\pi M_t)^{-\frac{1}{2}} \mathrm {e}^{-\frac{1}{2}\Vert M_t^{-1}\Vert (|x|+R\Vert \mathrm {e}^{tA}\Vert )^2}, \end{aligned}$$

  from which we conclude that

  $$\begin{aligned} \log \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)\ge -C_t(1+|x|^2) \end{aligned}$$

  for some constant $C_t>0$, and hence

  $$\begin{aligned} S_\mathrm{GS}(\nu _t)\le C_t(1+\nu (|x|^2)). \end{aligned}$$

• (2) From Eq. (5.13) we deduce that

  $$\begin{aligned} \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)= \int p_{\alpha ,t}(x-\mathrm {e}^{tA}y)\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}y)|^2} \nu (\mathrm {d}y), \end{aligned}$$

  where $p_{\alpha ,t}$ denotes a polynomial whose coefficients are continuous functions of $t\in ]0,\infty [$. It follows that

  $$\begin{aligned} \sup _{x\in \Xi }\left| \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)\right| \le \sup _{z\in \Xi }|p_{\alpha ,t}(z)|\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}z|^2}<\infty , \end{aligned}$$

  and

  $$\begin{aligned} \int \left| \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}x}(x)\right| \mathrm {d}x \le \int |p_{\alpha ,t}(z)|\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}z|^2}\mathrm {d}z<\infty . \end{aligned}$$

• (3) From Lemma 5.1(5) we get

  $$\begin{aligned} \mathrm {e}^{tA^*}M^{-1}\mathrm {e}^{tA}=(M+\mathrm {e}^{-tA}M_t\mathrm {e}^{-tA^*})^{-1}<M^{-1}. \end{aligned}$$

  The strict positivity of $\widetilde{M}_t$ follows from

  $$\begin{aligned} \widetilde{M}_t=M-M(\mathrm {e}^{tA^*}M^{-1}\mathrm {e}^{tA})M>M-MM^{-1}M=0. \end{aligned}$$

  Using again Lemma 5.1(5), it is straightforward to check the last statement of Part (3).

• (4) For $f\in L^1(\Xi ,\mathrm {d}\mu )$ we have

  $$\begin{aligned} \Vert P^tf\Vert _{L^1(\Xi ,\mathrm {d}\mu )}= \mu (|P^tf|)\le \mu (P^t|f|)=\mu (|f|)=\Vert f\Vert _{L^1(\Xi ,\mathrm {d}\mu )}. \end{aligned}$$

  The representation (5.12) shows that $P^t$ is a contraction on $L^\infty (\Xi ,\mathrm {d}\mu )$. The Riesz-Thorin interpolation theorem yields that $P^t$ is a contraction on $L^p(\Xi ,\mathrm {d}\mu )$ for all $p\in [1,\infty ]$. To get a representation of the adjoint semigroup $P^{t*}$, we start again with Eq. (5.12),

  $$\begin{aligned} \langle \psi |P^tf\rangle _\mu&=\int \psi (y)f(\mathrm {e}^{tA}y+M_t^\frac{1}{2} x)\mathrm{n}(\mathrm {d}x)\mu (\mathrm {d}y)\\&=\int \psi (y)f(\mathrm {e}^{tA}y+ x) \frac{\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}x|^2}}{\det (2\pi M_t)^\frac{1}{2}} \frac{\mathrm {e}^{-\frac{1}{2}|M^{-\frac{1}{2}}y|^2}}{\det (2\pi M)^\frac{1}{2}}\mathrm {d}x\mathrm {d}y\\&=\int \psi (y)f(x) \frac{\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}y)|^2}}{\det (2\pi M_t)^\frac{1}{2}} \frac{\mathrm {e}^{-\frac{1}{2}|M^{-\frac{1}{2}}y|^2}}{\det (2\pi M)^\frac{1}{2}}\mathrm {d}x\mathrm {d}y\\&=\int \psi (y)f(x) \frac{\mathrm {e}^{-\frac{1}{2}|M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}y)|^2}}{\det (2\pi M_t)^\frac{1}{2}} \mathrm {e}^{\frac{1}{2}(|M^{-\frac{1}{2}}x|^2-|M^{-\frac{1}{2}}y|^2)}\mu (\mathrm {d}x)\mathrm {d}y, \end{aligned}$$

  to conclude that

  $$\begin{aligned} (P^{t*}\psi )(x)=\det (2\pi M_t)^{-\frac{1}{2}}\int \mathrm {e}^{-\phi _t(x,y)}\psi (y)\mathrm {d}y, \end{aligned}$$

  where, taking (5.14) into account,

  $$\begin{aligned} \phi _t(x,y)=\frac{1}{2} x\cdot (M_t^{-1}-M^{-1})x+\frac{1}{2}y\cdot \widetilde{M}_t^{-1}y -\mathrm {e}^{tA^*}M_t^{-1}x\cdot y. \end{aligned}$$

  Using Lemma 5.1(5) and (5.14) one shows that

  $$\begin{aligned} \phi _t(x,\mathrm {e}^{t\widetilde{A}}x+z) =\frac{1}{2} z\cdot \widetilde{M}_t^{-1}z, \end{aligned}$$

  (5.17)

  which leads to

  $$\begin{aligned} (P^{t*}\psi )(x)=\det (2\pi M_t)^{-\frac{1}{2}} \int \mathrm {e}^{-\frac{1}{2}|\widetilde{M}_t^{-\frac{1}{2}}z|^2} \psi (\mathrm {e}^{t\widetilde{A}}x+z)\mathrm {d}z. \end{aligned}$$

  Noticing that $M_t=(I-\mathrm {e}^{tA}\mathrm {e}^{t\widetilde{A}})M$ and $\widetilde{M}_t=(I-\mathrm {e}^{t\widetilde{A}}\mathrm {e}^{tA})M$ we conclude that $\det (M_t)=\det (\widetilde{M}_t)$ and Eq. (5.15) follows.

• (5) Rewriting Eq. (5.15) as

  $$\begin{aligned} (P^{t*}\psi )(x)=\det (2\pi M_t)^{-\frac{1}{2}} \int \mathrm {e}^{-\frac{1}{2}|\widetilde{M}_t^{-\frac{1}{2}}(z-\mathrm {e}^{t\widetilde{A}}x)|^2} \psi (z)\mathrm {d}z, \end{aligned}$$

  (5.18)

  we derive that for any multi-index $\alpha$,

  $$\begin{aligned} (\partial ^\alpha P^{t*}\psi )(x)= \int p_{\alpha ,t}(z-\mathrm {e}^{t\widetilde{A}}x) \mathrm {e}^{-\frac{1}{2}|\widetilde{M}_t^{-\frac{1}{2}}(z-\mathrm {e}^{t\widetilde{A}}x)|^2} \psi (z)\mathrm {d}z, \end{aligned}$$

  where $p_{\alpha ,t}$ is a polynomial whose coefficients are continuous functions of $t\in ]0,\infty [$. For $\psi \in L^\infty (\Xi ,\mathrm {d}\mu )$ this yields

  $$\begin{aligned} \left\| \partial ^\alpha P^{t*}\psi \right\| _{L^\infty (\Xi ,\mathrm {d}\mu )} \le \Vert \psi \Vert _{L^\infty (\Xi ,\mathrm {d}\mu )}\int |p_{\alpha ,t}(z)| \mathrm {e}^{-\frac{1}{2}|\widetilde{M}_t^{-\frac{1}{2}}z|^2}\mathrm {d}z, \end{aligned}$$

  where the integral on the right-hand side is finite for all $t>0$.

• (6) $\mathcal{A}^p$ is dense in $L^p(\Xi ,\mathrm {d}\mu )$ for $p\in [1,\infty [$. For $\psi \in \mathcal{A}^p$, Eq. (5.15) yields

  $$\begin{aligned} (\partial ^\alpha P^{t*}\psi )(x)&=\sum _{|\alpha '|=|\alpha |}C_{\alpha ,\alpha '}(t) \int (\partial ^{\alpha '}\psi )(\mathrm {e}^{t\widetilde{A}}x+\widetilde{M}_t^\frac{1}{2}y) \mathrm{n}(\mathrm {d}y)\\&=\sum _{|\alpha '|=|\alpha |}C_{\alpha ,\alpha '}(t) (P^{t*}\partial ^{\alpha '}\psi )(x), \end{aligned}$$

  where the $C_{\alpha ,\alpha '}$ are continuous functions of t. As a consequence of Part (4), $\mathcal{A}^p$ invariant under the semigroup $P^{t*}$ and Part (6) follows from the core theorem (Theorem X.49 in [64]) and a simple calculation.

• (7) Assuming $\nu (\mathrm {e}^{m|x-a|^2/2})<\infty$, we deduce from Eq. (5.13) that for any $m'<m$

  $$\begin{aligned} \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)=\det (M^{-1}M_t)^{-\frac{1}{2}} \int \mathrm {e}^{-\phi _t(x,y)}\nu '(\mathrm {d}y), \end{aligned}$$

  where

  $$\begin{aligned} \phi _t(x,y)=\frac{1}{2}\left( |M_t^{-\frac{1}{2}}(x-\mathrm {e}^{tA}y)|^2+m'|y-a|^2-|M^{-\frac{1}{2}}x|^2\right) , \end{aligned}$$

  and $\nu '$ is such that $\nu '(\mathrm {e}^{\epsilon |x-a|^2})<\infty$ for $\epsilon >0$ small enough. It follows that

  $$\begin{aligned} \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x) =\int p_{\alpha ,t}(x,y)\mathrm {e}^{-\phi _t(x,y)}\nu '(\mathrm {d}y), \end{aligned}$$

  where $p_{\alpha ,t}$ is a polynomial of degree $|\alpha |$ whose coefficients are continuous functions of $t\in ]0,\infty [$. An elementary calculation shows that

  $$\begin{aligned} \phi _t(x)= \inf _{y\in \Xi }\phi _t(x,y)&=\left| M_t^{-\frac{1}{2}}x\right| ^2-\left| M^{-\frac{1}{2}}x\right| ^2+m'|a|^2\\&\quad -\left| \left( m'+\mathrm {e}^{tA^*}M_t^{-1}\mathrm {e}^{tA}\right) ^{-\frac{1}{2}}\left( m'a+\mathrm {e}^{tA^*}M_t^{-1}x\right) \right| ^2, \end{aligned}$$

  and since $\int |p_{\alpha ,t}(x,y)|\nu '(\mathrm {d}y)\le C_{\alpha ,t}(1+|x|^{2|\alpha |})$ for some constant $C_{\alpha ,t}$ we have

  $$\begin{aligned} \left| \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\right| \le C_{\alpha ,t}\left( 1+|x|^{2|\alpha |}\right) \mathrm {e}^{-\phi _t(x)}. \end{aligned}$$

  This gives the estimate

  $$\begin{aligned} \left\| \partial ^\alpha \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }\right\| _{L^p(\Xi ,\mathrm {d}\mu )}^p \le C_{\alpha ,t}^p \int \left( 1+|x|^{2|\alpha |}\right) ^p\mathrm {e}^{-p\left( \phi _t(x)+\frac{1}{2p}|M^{-\frac{1}{2}}x|^2\right) }\mathrm {d}x, \end{aligned}$$

  where the last integral is finite provided the quadratic form

  $$\begin{aligned} \left| M_t^{-\frac{1}{2}}x\right| ^2-\left( 1-p^{-1}\right) \left| M^{-\frac{1}{2}}x\right| ^2 -\left| \left( m'+\mathrm {e}^{tA^*}M_t^{-1}\mathrm {e}^{tA}\right) ^{-\frac{1}{2}}\mathrm {e}^{tA^*}M_t^{-1}x\right| ^2 \end{aligned}$$

  is positive definite. Since $M_t^{-1}-M^{-1}>0$, this holds if

  $$\begin{aligned} M_t^{-1}\mathrm {e}^{tA}\left( m'+\mathrm {e}^{tA^*}M_t^{-1}\mathrm {e}^{tA}\right) ^{-1}\mathrm {e}^{tA^*}M_t^{-1} \le \frac{1}{p} M^{-1}. \end{aligned}$$

  Finally, the last inequality holds for large t since the left-hand side is exponentially small as $t\rightarrow \infty$.

• (8) By Lemma 5.1(1), $\Vert \mathrm {e}^{tA}\Vert =\mathcal{O}(\mathrm {e}^{-\delta t})$ as $t\rightarrow \infty$. Repeating the previous analysis with $m'=\mathrm {e}^{-\delta t}$ we get, for large enough $t>0$,

  $$\begin{aligned} \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\le \frac{1}{2}\mathrm{tr}(\log M-\log M_t) +\log \int \mathrm {e}^{\frac{1}{2}m'|x-a|^2}\nu (\mathrm {d}x)-\phi _t(x). \end{aligned}$$

  One easily shows that $\mathrm{tr}(\log M-\log M_t)=\mathcal{O}(\mathrm {e}^{-2\delta t})$ and $|\phi _t(x)|=\mathcal{O}(\mathrm {e}^{-\delta t})(1+|x|^2)$. Finally, since

  $$\begin{aligned} \int \mathrm {e}^{\frac{1}{2}m'|x-a|^2}\nu (\mathrm {d}x)=1+\mathcal{O}(m') \end{aligned}$$

  as $m'\rightarrow 0$, we derive the upper bound

  $$\begin{aligned} \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\le \mathcal{O}(\mathrm {e}^{-\delta t})(1+|x|^2). \end{aligned}$$

  To get a lower bound we set $m'=0$ and note that the ball $B_{t}=\{x\in \Xi \,|\,m|x-a|^2\le \delta t\}$ satisfies

  $$\begin{aligned} 1-\nu (B_t)&=\int _{\Xi \setminus B_t}\nu (\mathrm {d}x) \le \int _{\Xi \setminus B_t}\mathrm {e}^{-m|x-a|^2} \mathrm {e}^{m|x-a|^2}\nu (\mathrm {d}x) \le \mathrm {e}^{-\delta t}\int \mathrm {e}^{m|x-a|^2}\nu (\mathrm {d}x)\\&=\mathcal{O}(\mathrm {e}^{-\delta t}). \end{aligned}$$

  Since $\log M>\log M_t$ we get

  $$\begin{aligned} \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\ge -\sup _{y\in B_t}\phi _t(x,y)+\log (\nu (B_t)). \end{aligned}$$

  It is straightforward to check that

  $$\begin{aligned} \sup _{y\in B_t}\phi _t(x,y)=\mathcal{O}(\mathrm {e}^{-\delta t})(1+\mathcal{O}(t^\frac{1}{2}))(1+|x|^2), \end{aligned}$$

  and therefore

  $$\begin{aligned} -\log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }(x)\le \mathcal{O}(\mathrm {e}^{-\epsilon t})(1+|x|^2) \end{aligned}$$

  for any $\epsilon <\delta$.

$\square$

We are now ready to prove Proposition 3.5. Writing the polar decomposition $Q=V(Q^*Q)^{\frac{1}{2}}$, the existence of $\beta \in L(\Xi )$ satisfying (3.17) easily follows from the structural relations $[\vartheta ,Q^*Q]=0$ and $\theta Q=\pm Q$.

(1) Follows from Condition (3.17) and Eq. (3.6).

(2) From Eq. (3.11) we deduce that the formal adjoint of L w.r.t. the inner product of $L^2(\Xi ,\mathrm {d}x)$ is

$$\begin{aligned} L^T=\frac{1}{2}\nabla \cdot B\nabla -\nabla \cdot Ax. \end{aligned}$$

It follows from the structural relations (3.9) and Condition (3.17) that

$$\begin{aligned} L^\beta&=\mathrm {e}^{\frac{1}{2}|\beta ^\frac{1}{2}x|^2}L^T\mathrm {e}^{-\frac{1}{2}|\beta ^\frac{1}{2}x|^2} =\frac{1}{2}(\nabla -\beta x)\cdot B(\nabla -\beta x)-(\nabla -\beta x)\cdot Ax\\&=\frac{1}{2}\nabla \cdot B\nabla -(A+Q\vartheta ^{-1}Q^*)x\cdot \nabla -\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*+A+A^*)\\&\quad +\frac{1}{2}x\cdot (Q\vartheta ^{-2}Q^*+\beta A+A^*\beta )x\\&=\frac{1}{2}\nabla \cdot B\nabla +A^*x\cdot \nabla -\sigma _\beta (x). \end{aligned}$$

The desired identity thus follows from (3.9) and Part (1).

(3) The Itô formula gives

$$\begin{aligned} \mathrm {d}\left( \tfrac{1}{2}x(t)\cdot Cx(t)\right)&=x(t)\cdot C\mathrm {d}x(t) +\tfrac{1}{2}\mathrm{tr}(CB)\mathrm {d}t\\&=\tfrac{1}{2}x(t)\cdot (CA+A^*C)x(t)\mathrm {d}t +\tfrac{1}{2}\mathrm{tr}(CB)\mathrm {d}t+x(t)\cdot CQ\mathrm {d}w(t). \end{aligned}$$

Therefore, since $\log \tfrac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x)=-\tfrac{1}{2}x\cdot \beta x$, we have

$$\begin{aligned} \mathrm {d}\log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x_t) =-\tfrac{1}{2}x(t)\cdot (\beta A+A^*\beta )x(t)\mathrm {d}t -\tfrac{1}{2}\mathrm{tr}(\beta QQ^*)\mathrm {d}t-x(t)\cdot \beta Q\mathrm {d}w(t). \end{aligned}$$

Using (3.17) and the decomposition $A=\Omega -\frac{1}{2}Q^*\vartheta ^{-1}Q$, we deduce

$$\begin{aligned} \mathrm {d}\log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x_t)&=\frac{1}{2}x(t)\cdot (\Omega \beta -\beta \Omega )x(t)\mathrm {d}t +\frac{1}{2}|Q^*\beta x(t)|^2\mathrm {d}t\\&\quad -\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*)\mathrm {d}t-Q^*\beta x(t)\cdot \mathrm {d}w(t), \end{aligned}$$

and, observing that $\nabla \log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}(x)=-\beta x$, the result follows from Eq. (3.3) and Condition (3.17).

(4) Let $\nu \in \mathcal{P}_+(\Xi )$ and denote by $\psi _t$ the density of $\nu _t$ w.r.t. $\mu$. By Lemma 5.4, $\psi _t$ is a strictly positive element of $\mathcal{A}^2$ for large enough t. For $\epsilon >0$ we have $\log \epsilon \le \log (\psi _t+\epsilon )\le \psi _t+\epsilon -1$, and hence $\log (\psi _t+\epsilon )\in L^2(\Xi ,\mathrm {d}\mu )$. Thus, $s_\epsilon (\psi _t)=-\psi _t\log (\psi _t+\epsilon )\in L^1(\Xi ,\mathrm {d}\mu )$, and the monotone convergence theorem yields

$$\begin{aligned} \mathrm{Ent}(\nu _t|\mu )=\lim _{\epsilon \downarrow 0}\mu (s_\epsilon (\psi _t)). \end{aligned}$$

From

$$\begin{aligned} s_\epsilon (\psi _t(x))-s_\epsilon (\psi _s(x)) =\int _s^ts_\epsilon '(\psi _u(x))(L^*\psi _u)(x)\mathrm {d}u \end{aligned}$$

we infer

$$\begin{aligned} \mu (s_\epsilon (\psi _t))-\mu (s_\epsilon (\psi _s)) =\int _s^t\langle s_\epsilon '(\psi _u)|L^*\psi _u\rangle _\mu \mathrm {d}u. \end{aligned}$$

Since $\psi _u$ and $s_\epsilon '(\psi _u)=-1-\log (\psi _u+\epsilon )+\epsilon (\psi _u+\epsilon )^{-1}$ are elements of $\mathcal{A}^2$ we can integrate by parts, using Eq. (5.16), to get

$$\begin{aligned} \langle s_\epsilon '(\psi _u)|L^*\psi _u\rangle _\mu =\langle f_\epsilon (\psi _u)||Q^*\nabla \psi _u|^2\rangle _\mu +\langle g_\epsilon (\psi _u)|(\widetilde{A}-A)x\cdot \nabla \psi _u\rangle _\mu , \end{aligned}$$

where

$$\begin{aligned} f_\epsilon (\psi )=\frac{1}{2}\frac{\psi +2\epsilon }{(\psi +\epsilon )^2}, \qquad g_\epsilon (\psi )=\frac{1}{2}\frac{\epsilon ^2}{(\psi +\epsilon )^2}. \end{aligned}$$

Since $f_\epsilon \ge 0$ and decreases as a function of $\epsilon$, the monotone convergence theorem yields

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \int _s^t\langle f_\epsilon (\psi _u)||Q^*\nabla \psi _u|^2\rangle _\mu \mathrm {d}u= & {} \frac{1}{2}\int _s^t\langle \psi _u^{-1}||Q^*\nabla \psi _u|^2\rangle _\mu \mathrm {d}u\\= & {} \frac{1}{2}\int _s^t\nu _u(|Q^*\nabla \log \psi _u|^2)\mathrm {d}u. \end{aligned}$$

Since $0<g_\epsilon \le \frac{1}{2}$, the dominated convergence theorem gives

$$\begin{aligned} \lim _{\epsilon \downarrow 0} \int _s^t\langle g_\epsilon (\psi _u)| (\widetilde{A}-A)x\cdot \nabla \psi _u\rangle _\mu \mathrm {d}u=0. \end{aligned}$$

We conclude that for s sufficiently large and $t>s$

$$\begin{aligned} \mathrm{Ent}(\nu _t|\mu )-\mathrm{Ent}(\nu _s|\mu ) =\lim _{\epsilon \downarrow 0}(\mu (s_\epsilon (\psi _t))-\mu (s_\epsilon (\psi _s))) =\frac{1}{2}\int _s^t\nu _u(|Q^*\nabla \log \psi _u|^2)\mathrm {d}u, \end{aligned}$$

and Eq. (3.22) follows.

(5) Equation (3.3) gives

$$\begin{aligned} \mathbb {E}_\nu [\mathfrak {S}^t] =\frac{1}{2}\int _0^t\nu _s\left( \left| Q^*\nabla \log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}\right| ^2 \right) \mathrm {d}s-\frac{1}{2} t\,\mathrm{tr}(Q\vartheta ^{-1}Q^*). \end{aligned}$$

Since $S_\mathrm{GS}(\nu _t)=\mathrm{Ent}(\nu _t|\mu )+\nu _t(\varphi )$, where

$$\begin{aligned} \varphi (x)=-\log \frac{\mathrm {d}\mu }{\mathrm {d}x}(x) =\frac{1}{2}\left| M^{-\frac{1}{2}}x\right| ^2+\frac{1}{2}\log \det (2\pi M), \end{aligned}$$

Equation (3.22) implies

$$\begin{aligned}&\frac{\mathrm {d}\ }{\mathrm {d}t}(S_\mathrm{GS}(\nu _t)+\mathbb {E}_\nu [\mathfrak {S}^t])\\&\quad =\nu _t\left( \frac{1}{2}\left| Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }\right| ^2 +L\varphi +\frac{1}{2}\left| Q^*\nabla \log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}\right| ^2 -\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*)\right) . \end{aligned}$$

A simple calculation yields $L\varphi =-\frac{1}{2}|Q^*\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}x}|^2 +\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*)$ and hence

$$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}(S_\mathrm{GS}(\nu _t)+\mathbb {E}_\nu [\mathfrak {S}^t])&=\frac{1}{2}\nu _t\left( \left| Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu }\right| ^2 +\left| Q^*\nabla \log \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}\right| ^2 -\left| Q^*\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}x}\right| ^2 \right) \\&=\frac{1}{2}\nu _t\left( \left| Q^*\nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}\mu _\beta }\right| ^2\right) +\nu _t\left( \nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}x}\cdot B\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}\mu _\beta }\right) . \end{aligned}$$

An integration by parts shows that

$$\begin{aligned} \nu _t\left( \nabla \log \frac{\mathrm {d}\nu _t}{\mathrm {d}x}\cdot B\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}\mu _\beta }\right)&=-\nu _t\left( \nabla \cdot B\nabla \log \frac{\mathrm {d}\mu }{\mathrm {d}\mu _\beta }\right) =\mathrm{tr}\left( B(M^{-1}-\beta )\right) , \end{aligned}$$

and, since $BM^{-1}-B\beta =-A-MAM^{-1}+A+A^*$, we have $\mathrm{tr}(B(M^{-1}-\beta ))=0$. The result follows.

5.3 Proof of Proposition 3.7

(1) Since the first equivalence is provided by (3.32), it suffices to show the sequence of implications

$$\begin{aligned} MQ=Q\vartheta \Rightarrow [\Omega ,M]=0\Rightarrow \mu \Theta =\mu \Rightarrow \mathrm{ep}=0. \end{aligned}$$

(5.19)

Writing $\Omega =A+\frac{1}{2} Q\vartheta ^{-1}Q^*$ and invoking Lemma 5.1(6) (the covariance of the steady state satisfies the Lyapunov equation $B+AM+MA^*=0$) one easily derives

$$\begin{aligned}{}[\Omega ,M]=\frac{1}{2}\left( (MQ-Q\vartheta )\vartheta ^{-1}Q^*+Q\vartheta ^{-1}(MQ-Q\vartheta )^*\right) , \end{aligned}$$

which proves the first implication in (5.19). The last identity, rewritten as $[A-A^*,M]=0$, further implies that

$$\begin{aligned} 0&=AM+MA^*+B=A^*M+MA+B =\theta A\theta M+M\theta A^*\theta +\theta B\theta \\&=\theta (A\theta M\theta +\theta M\theta A^*+B)\theta , \end{aligned}$$

from which we deduce that $\theta M\theta$ is also solution of the Lyapunov equation. Lemma 5.1(7) allows us to conclude that $\theta M\theta =M$ which is clearly equivalent to $\mu \Theta =\mu$ and proves the second implication in (5.19). Finally, from (3.29) we deduce that if $\mu \Theta =\mu$, then

$$\begin{aligned} \mathrm{ep}&=-\mu (\sigma _\beta )=-\frac{1}{2}\mathrm{tr}(M[\Omega ,\beta ]) =\frac{1}{2}\mathrm{tr}(\beta [\Omega ,M])\\&=\frac{1}{2}\mathrm{tr}(\theta \beta [\Omega ,M]\theta ) =\frac{1}{2}\mathrm{tr}(\beta [\theta \Omega \theta ,\theta M\theta ]) =-\frac{1}{2}\mathrm{tr}(\beta [\Omega ,\theta M\theta ])=-\mathrm{ep}, \end{aligned}$$

which gives the last implication.

(2) Let $\vartheta _1,\vartheta _2\in \mathrm{sp}(\vartheta )$ be such that $\vartheta _1\not =\vartheta _2$ and $\mathcal{C}_{\vartheta _1}\cap \mathcal{C}_{\vartheta _2}\ni u\not =0$. Assume that $\mathrm{ep}=0$. By Part (1) this implies $MQ=Q\vartheta$ and $[\Omega ,M]=0$. By construction, there exist polynomials $f_1$, $f_2$ and vectors $v_1,v_2\in \Xi$ such that

$$\begin{aligned} f_1(\Omega )Q\pi _{\vartheta _1}v_1=u=f_2(\Omega )Q\pi _{\vartheta _2}v_2. \end{aligned}$$

The first equality in the above formula yields

$$\begin{aligned} Mu=Mf_1(\Omega )Q\pi _{\vartheta _1}v_1=f_1(\Omega )MQ\pi _{\vartheta _1}v_1 =f_1(\Omega )Q\vartheta \pi _{\vartheta _1}v_1 =\vartheta _1f_1(\Omega )Q\pi _{\vartheta _1}v_1=\vartheta _1 u. \end{aligned}$$

Similarly, the second one yields $Mu=\vartheta _2 u$. Since $u\not =0$, this contradicts the assumption $\vartheta _1\not =\vartheta _2$.

5.4 Proof of Proposition 3.9

Let $\tau >0$, $\nu \in \mathcal{P}^1_{\mathrm {loc}}(\Xi )$, set

$$\begin{aligned} \psi _t=\frac{\mathrm {d}\nu _{\tau -t}}{\mathrm {d}x}, \end{aligned}$$

and note that since $\psi _\tau +|\nabla \psi _\tau |\in L^2_{\mathrm {loc}}(\Xi ,\mathrm {d}x)$, it follows from Lemma 5.4 that

$$\begin{aligned} \int _0^\tau \left( \Vert f\psi _t\Vert _2^2+\Vert f\nabla \psi _t\Vert _2^2\right) \mathrm {d}t <\infty \end{aligned}$$

(5.20)

for all $f\in C_0^\infty (\Xi )$. We consider the process $\varvec{x}=\{x(t)\}_{t\in [0,\tau ]}$ which is the solution of the SDE (3.2) with initial law $\nu$. By Theorem 2.1 in [57], the estimate (5.20) implies that the process ${\overline{\varvec{x}}}=\{{\overline{x}}_t\}_{t\in [0,\tau ]}$ with ${\overline{x}}_t=x_{\tau -t}$ is a diffusion satisfying the SDE

$$\begin{aligned} \mathrm {d}{\overline{x}}(t)={\overline{b}}({\overline{x}}(t),t)\mathrm {d}t+Q\mathrm {d}{\overline{w}}(t) \end{aligned}$$

with initial law $\nu P^\tau$, drift ${\overline{b}}(x,t)=-Ax+B\nabla \log \psi _t(x)$, and a standard $\partial \,\Xi$-valued Wiener process ${\overline{w}}(t)$. Since $\theta Q=\mp Q$, the time-reversed process $\varvec{\widetilde{x}}=\Theta ^\tau (\varvec{x}) =\{\theta {\overline{x}}(t)\}_{t\in [0,\tau ]}$ satisfies

$$\begin{aligned} \mathrm {d}\widetilde{x}(t) =\widetilde{b}(\widetilde{x}(t),t)\mathrm {d}t+Q\mathrm {d}\widetilde{w}(t) \end{aligned}$$

with initial law $\nu P^\tau \Theta$, drift $\widetilde{b}(x,t)=\theta {\overline{b}}(\theta x,t)$, and standard Wiener process $\widetilde{w}(t)=\mp {\overline{w}}(t)$. Using the structural relations (3.9) and $A+A^*=-QQ^*\beta$ we derive

$$\begin{aligned} \widetilde{b}(x,t)=Ax+QQ^*\nabla \log \phi _t(x),\qquad \phi _t=\Theta \left( \frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}\right) ^{-1}\psi _t, \end{aligned}$$

and conclude that we can rewrite the original SDE (3.2) as

$$\begin{aligned} \mathrm {d}x(t)=\widetilde{b}(x(t),t)\mathrm {d}t+Q(\mathrm {d}w(t)-Q^*\nabla \log \phi _t(x(t))\mathrm {d}t). \end{aligned}$$

(5.21)

Set

$$\begin{aligned} \eta (t)=\int _0^tQ^*\nabla \log \phi _s(x(s))\cdot \mathrm {d}w(s), \end{aligned}$$

and let $Z(t)=\mathcal{E}(\eta )(t)$ denote its stochastic exponential. We claim that

$$\begin{aligned} \mathbb {E}_{\nu P^\tau \Theta }^\tau [Z(t)]=1 \end{aligned}$$

(5.22)

for all $t\in [0,\tau ]$. Delaying the proof of this claim and applying Girsanov theorem we conclude that

$$\begin{aligned} w(t)-\int _0^tQ^*\nabla \log \phi _s(x(s))\mathrm {d}s \end{aligned}$$

is a standard Wiener process under the law $\mathbb {E}_{\nu P^\tau \Theta }^\tau [Z(\tau )\,\cdot \,]$, so that Eq. (5.21) implies

$$\begin{aligned} \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau }=Z(\tau ). \end{aligned}$$

(5.23)

Using Itô calculus, one derives from Eq. (3.2) that

$$\begin{aligned} Q^*\nabla \log \phi _t(x(t))\cdot \mathrm {d}w(t)&=\mathrm {d}\log \phi _t(x(t))-((\partial _t+L)\log \phi _t)(x(t))\mathrm {d}t\\&=\mathrm {d}\log \phi _t(x(t)) -\left( \frac{(\partial _t+L)\phi _t}{\phi _t}(x(t)) -\tfrac{1}{2}|Q^*\nabla \log \phi _t(x(t))|^2\right) \mathrm {d}t, \end{aligned}$$

from which we obtain

$$\begin{aligned} \eta (t)-\tfrac{1}{2}[\eta ](t) =\log \phi _t(x(t))-\log \phi _0(x(0)) -\int _0^t\left( \frac{(\partial _s+L)\phi _s}{\phi _s}\right) (x(s))\mathrm {d}s. \end{aligned}$$

The generalized detailed balance condition (3.20) further yields

$$\begin{aligned} (\partial _s+L)\phi _s=-\sigma _\beta \phi _s, \end{aligned}$$

so that

$$\begin{aligned} \eta (t)-\tfrac{1}{2}[\eta ](t) =\log \frac{\mathrm {d}\nu _{\tau -t}}{\mathrm {d}\mu _\beta }(\theta x(t)) -\log \frac{\mathrm {d}\nu _{\tau }}{\mathrm {d}\mu _\beta }(\theta x(0)) +\int _0^t\sigma _\beta (x(s))\mathrm {d}s, \end{aligned}$$

from which we conclude that

$$\begin{aligned} Z(t)=\exp \left[ \eta (t)-\tfrac{1}{2}[\eta ](t)\right] =\left( \frac{\mathrm {d}\nu _{\tau }}{\mathrm {d}\mu _\beta }(\theta x(0))\right) ^{-1} \frac{\mathrm {d}\nu _{\tau -t}}{\mathrm {d}\mu _\beta }(\theta x(t)) \exp \left( \int _{0}^t\sigma _\beta (x(s))\mathrm {d}s \right) , \end{aligned}$$

(5.24)

and in particular that $Z(\tau )=\exp (\mathrm{Ep}(\nu ,\tau ))\circ \Theta ^\tau$. From (5.23) we finally get

$$\begin{aligned} \frac{\mathrm {d}\widetilde{\mathbb {P}}_\nu ^\tau }{\mathrm {d}\mathbb {P}_{\nu P^\tau \Theta }^\tau } =\exp [\mathrm{Ep}(\nu ,\tau )]\circ \Theta ^\tau . \end{aligned}$$

It remains to prove the claim (5.22). Set $\zeta =\nu P^\tau \Theta$ and observe that it suffices to show that $\mathbb {E}_\zeta [Z(t)]\ge 1$ for $t\in [0,\tau ]$ since $\mathbb {E}_\zeta [Z(t)]\le 1$ is a well known property of the stochastic exponential. The proof of this fact relies on a sequence of approximations.

The inequality $\mathbb {E}_\zeta [Z(t)]\le 1$ gives that for $s,s',t\in [0,\tau ]$ and bounded measurable f, g one has

$$\begin{aligned} |\mathbb {E}_\zeta [Z(t)f(x(s))g(x(s'))]|\le \Vert f\Vert _\infty \Vert g\Vert _\infty . \end{aligned}$$

(5.25)

Here and in the following we denote by $\Vert \cdot \Vert _p$ the norm of $L^p(\Xi ,\mathrm {d}x)$. The duality between $L^p(\Xi ,\mathrm {d}x)$ and $L^q(\Xi ,\mathrm {d}x)$ will be written $\langle \,\cdot \,|\,\cdot \,\rangle$. Next, we note that Eq. (5.24) implies

$$\begin{aligned}&\mathbb {E}_\zeta [Z(t)g(x(0))f(x(t))]\\&\quad =\mathbb {E}_\zeta \left[ \left( \frac{\mathrm {d}\nu _{\tau }}{\mathrm {d}\mu _\beta }(\theta x(0))\right) ^{-1} g(x(0))\frac{\mathrm {d}\nu _{\tau -t}}{\mathrm {d}\mu _\beta }(\theta x(t))f(x(t)) \exp \left( \int _{0}^t\sigma _\beta (x(s))\mathrm {d}s \right) \right] \\&\quad =\int g(x)\chi (x) \mathbb {E}_x\left[ \chi (x(t))^{-1}\psi _t(\theta x(t))f(x(t))\mathrm {e}^{V(t)} \right] \mathrm {d}x=\langle g|\chi P_\sigma ^t\chi ^{-1}\widetilde{\psi }_t f\rangle , \end{aligned}$$

where we have set

$$\begin{aligned} V(t)=\int _{0}^t\sigma _\beta (x(s))\mathrm {d}s,\qquad \chi =\frac{\mathrm {d}\mu _\beta }{\mathrm {d}x}, \qquad \widetilde{\psi }_t=\Theta \psi _t, \end{aligned}$$

and

$$\begin{aligned} (P_\sigma ^tf)(x)=\mathbb {E}_x[\mathrm {e}^{V(t)}f(x(t))]. \end{aligned}$$

It follows from the estimate (5.25) that $\Vert \chi P_\sigma ^t\chi ^{-1}\widetilde{\psi }_t f\Vert _1\le \Vert f\Vert _\infty$. For $n,m>0$ we define

$$\begin{aligned} \sigma _{n,m}(x)=\left\{ \begin{array}{ll} -n&{}\text { if }\sigma _\beta (x)\le -n;\\ \sigma _\beta (x)&{}\text { if } -n\le \sigma _\beta (x)\le m;\\ m&{}\text { if }\sigma _\beta (x)\ge m; \end{array}\right. \qquad \sigma _{m}(x)=\left\{ \begin{array}{ll} \sigma _\beta (x)&{}\text { if } \sigma _\beta (x)\le m;\\ m&{}\text { if }\sigma _\beta (x)\ge m; \end{array}\right. \end{aligned}$$

and set

$$\begin{aligned} V_{n,m}(t)=\int _0^t\sigma _{n,m}(x(s))\mathrm {d}s,\qquad V_{m}(t)=\int _0^t\sigma _{m}(x(s))\mathrm {d}s. \end{aligned}$$

Since

$$\begin{aligned} \lim _{n\rightarrow \infty }\sigma _{n,m}(x)&=\sigma _m(x),&\sigma _{n,m}(x)&\le m\\ \lim _{m\rightarrow \infty }\sigma _m(x)&=\sigma _\beta (x),&\sigma _m(x)&\le \sigma _\beta (x), \end{aligned}$$

for all $x\in \Xi$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\mathrm {e}^{V_{n,m}(t)}&=\mathrm {e}^{V_m(t)},&\mathrm {e}^{V_{n,m}(t)}&\le \mathrm {e}^{mt},\\ \lim _{m\rightarrow \infty }\mathrm {e}^{V_{m}(t)}&=\mathrm {e}^{V(t)},&\mathrm {e}^{V_{m}(t)}&\le \mathrm {e}^{V(t)}, \end{aligned}$$

$\mathbb {P}_{\zeta }$-almost surely. Hence, the dominated convergence theorem yields

$$\begin{aligned}&\left\langle g|\chi P_\sigma ^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle \\&\quad =\mathbb {E}_{\zeta }\left[ \chi (x(0))\widetilde{\psi }_{0}(x(0))^{-1}g(x(0)) \chi (x(t))^{-1}\widetilde{\psi }_t(x(t))f(x(t))\mathrm {e}^{V(t)}\right] \\&\quad =\lim _{m\rightarrow \infty }\lim _{n\rightarrow \infty } \mathbb {E}_{\nu _{\tau -t}}\left[ \chi (x(0))\widetilde{\psi }_{0}(x(0))^{-1}g(x(0)) \chi (x(t))^{-1}\widetilde{\psi }_t(x(t))f(x(t))\mathrm {e}^{V_{n,m}(t)}\right] \\&\quad =\lim _{m\rightarrow \infty }\lim _{n\rightarrow \infty } \left\langle g|\chi P_{\sigma _{n,m}}^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle , \end{aligned}$$

where, by the Feynman–Kac formula,

$$\begin{aligned} \left( P_{\sigma _{n,m}}^tf\right) (x)=\mathbb {E}_x\left[ \mathrm {e}^{V_{n,m}(t)}f(x(t))\right] =\left( \mathrm {e}^{t(L+\sigma _{n,m})}f\right) (x) \end{aligned}$$

defines a quasi-bounded semigroup on $L^2(\Xi ,\mathrm {d}x)$. In the following, we assume that $f\in C_0^\infty (\Xi )$ is non-negative. It follows from Eq. (5.13) that $\chi ^{-1}\widetilde{\psi }_t f\in C_0^\infty (\Xi )\subset \mathrm{Dom}\,(L)=\mathrm{Dom}\,(L+\sigma _{n,m})$ and we can write

$$\begin{aligned} \left\langle g|\chi P_{\sigma _{n,m}}^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\left\langle g|\widetilde{\psi }_t f\right\rangle +\int _0^t\left\langle g | \chi (L+\sigma _{n,m})P_{\sigma _{n,m}}^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle \mathrm {d}s. \end{aligned}$$

Denote by $L^T$ the adjoint of L on $L^2(\Xi ,\mathrm {d}x)$ which acts on $C_0^\infty (\Xi )$ as $L^T=\frac{1}{2}\nabla \cdot B\nabla -\nabla \cdot Ax$. Assuming $g\in C_0^\infty$, we get

$$\begin{aligned} \left\langle g|\chi P_{\sigma _{n,m}}^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\nu _{\tau -t}\Theta (gf)+\int _0^t\left\langle \chi ^{-1}\left( L^T+\sigma _{n,m}\right) \chi g |\chi P_{\sigma _{n,m}}^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle \mathrm {d}s. \end{aligned}$$

The generalized detailed balance condition (3.20) yields

$$\begin{aligned} \chi ^{-1}L^T\chi g=\Theta (L+\sigma _\beta )\Theta g =(\Theta L\Theta -\sigma _\beta )g, \end{aligned}$$

and it follows that

$$\begin{aligned} \left\langle \chi ^{-1}\left( L^T+\sigma _{n,m}\right) \chi g |\chi P_{\sigma _{n,m}}^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\left\langle (\Theta L\Theta +\sigma _{n,m}-\sigma _\beta ) g |\chi P_{\sigma _{n,m}}^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle . \end{aligned}$$

Since g is compactly supported, if n and m are sufficiently large we have $(\sigma _{n,m}-\sigma _\beta ) g=0$ and so

$$\begin{aligned} \left\langle g|\chi P_{\sigma _{n,m}}^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\nu _{\tau -t}\Theta (gf)+\int _0^t\left\langle \Theta L\Theta g |\chi P_{\sigma _{n,m}}^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle \mathrm {d}s. \end{aligned}$$

Taking the limits $n\rightarrow \infty$ and $m\rightarrow \infty$ we get that

$$\begin{aligned} \left\langle g|\chi P_{\sigma }^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\nu _{\tau -t}\Theta (fg)+\int _0^t\left\langle \Theta L\Theta g |\chi P_{\sigma }^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle \mathrm {d}s \end{aligned}$$

holds for all $f,g\in C_0^\infty (\Xi )$. For $k>0$ set

$$\begin{aligned} g_k(x)=\left( 1+\mathrm {e}^{|x|^2/2k}\right) ^{-1}, \end{aligned}$$

and let $\rho \in C_0^\infty ({\mathbb {R}})$ be such that $0\le \rho \le 1$, $\rho '\le 0$, $\rho (x)=1$ for $x\le 0$ and $\rho (x)=0$ for $x\ge 1$. Define $g_{k,r}\in C_0^\infty (\Xi )$ by $g_{k,r}(x)=g_k(x)\rho (\langle x\rangle -r)$. One easily checks that

$$\begin{aligned} \lim _{r\rightarrow \infty }\Vert g_{k,r}-g_k\Vert _\infty +\Vert L(g_{k,r}-g_k)\Vert _\infty =0, \end{aligned}$$

and noticing that $g_k$ and $g_{k,r}$ are $\Theta$-invariant, it follows that

$$\begin{aligned} \left\langle g_k|\chi P_{\sigma }^t\chi ^{-1}\widetilde{\psi }_t f\right\rangle =\nu _{\tau -t}\Theta (g_kf)+\int _0^t\left\langle \Theta L g_k |\chi P_{\sigma }^s\chi ^{-1}\widetilde{\psi }_t f\right\rangle \mathrm {d}s. \end{aligned}$$

Using the fact that

$$\begin{aligned} (Lg_k)(x)\ge -\frac{1}{8k}\mathrm{tr}(B), \end{aligned}$$

and the monotone convergence theorem we conclude that

$$\begin{aligned} \langle 1|\chi P_{\sigma }^t\chi ^{-1}\widetilde{\psi }_t f\rangle&=\lim _{k\rightarrow \infty }\langle g_k|\chi P_{\sigma }^t\chi ^{-1} \widetilde{\psi }_t f\rangle \\&\ge \lim _{k\rightarrow \infty }\nu _{\tau -t}\Theta (g_kf) -\frac{1}{8k}\mathrm{tr}(B)\int _0^t\langle 1 |\chi P_{\sigma }^s\chi ^{-1}\widetilde{\psi }_t f\rangle \mathrm {d}s =\nu _{\tau -t}(f). \end{aligned}$$

Finally, letting f converge to 1 monotonically, we deduce

$$\begin{aligned} \mathbb {E}_\zeta [Z(t)]=\lim _{f\nearrow 1}\mathbb {E}_\zeta [Z(t)f(x(t))] =\lim _{f\nearrow 1}\langle 1|\chi P_{\sigma }^t\chi ^{-1} \widetilde{\psi }_t f\rangle \ge \lim _{f\nearrow 1}\nu _{\tau -t}(f)=\nu _{\tau -t}(1)=1. \end{aligned}$$

This completes the proof of the claim (5.22).

5.5 Proof of Theorem 3.13

(1) We start with some algebraic preliminaries. For $\omega \in {\mathbb {R}}$, set

$$\begin{aligned} R(\omega )=\vartheta ^{-1}Q^*(A+\mathrm {i}\omega )^{-1}Q,\qquad U(\omega )=I+R(\omega ), \end{aligned}$$

and note that since the matrices A, Q and $\vartheta$ are real one has

$$\begin{aligned} \mathcal{C}R(\omega )\mathcal{C}=R(-\omega ),\qquad \mathcal{C}U(\omega )\mathcal{C}=U(-\omega ), \end{aligned}$$

(5.26)

where $\mathcal{C}$ denotes complex conjugation on ${\mathbb {C}}\partial \Xi$. Further note that

$$\begin{aligned} \det (U(\omega ))=\det (I+(A+\mathrm {i}\omega )^{-1}Q\vartheta ^{-1}Q^*) =\frac{\det (A^*-\mathrm {i}\omega )}{\det (A+\mathrm {i}\omega )}, \end{aligned}$$

from which we deduce that

$$\begin{aligned} |\det (U(\omega ))|=1. \end{aligned}$$

(5.27)

From the relations

$$\begin{aligned} \left( I+\vartheta ^{-1}Q^*(A-\mathrm {i}\omega )^{-1}Q\right) ^{-1}&=I-\left( I+\vartheta ^{-1}Q^*(A-\mathrm {i}\omega )^{-1}Q\right) ^{-1} \vartheta ^{-1}Q^*(A-\mathrm {i}\omega )^{-1}Q\\&=I-\vartheta ^{-1}Q^*\left( I+(A-\mathrm {i}\omega )^{-1}Q\vartheta ^{-1}Q^*\right) ^{-1}(A-\mathrm {i}\omega )^{-1}Q\\&=I-\vartheta ^{-1}Q^*\left( A-\mathrm {i}\omega +Q\vartheta ^{-1}Q^*\right) ^{-1}Q\\&=I+\vartheta ^{-1}Q^*(A^*+\mathrm {i}\omega )^{-1}Q\\&=I+\vartheta ^{-1}Q^*\theta (A^*+\mathrm {i}\omega )^{-1}\theta Q\\&=I+\vartheta ^{-1}Q^*(A+\mathrm {i}\omega )^{-1}Q=I+R(\omega ) \end{aligned}$$

we also get

$$\begin{aligned} U(-\omega )^{-1}=U(\omega ). \end{aligned}$$

(5.28)

Writing

$$\begin{aligned} E(\omega )&=Q^*(A^*-\mathrm {i}\omega )^{-1} \left( (-A^*-\frac{1}{2} Q\vartheta ^{-1}Q^*+\mathrm {i}\omega )\beta +\beta (-A-\frac{1}{2} Q\vartheta ^{-1}Q^*-\mathrm {i}\omega )\right) \\&\qquad \times (A+\mathrm {i}\omega )^{-1}Q\\&=Q^*\left( -(A^*-\mathrm {i}\omega )^{-1}\beta -\beta (A+\mathrm {i}\omega )^{-1} -(A^*-\mathrm {i}\omega )^{-1}Q\vartheta ^{-2}Q^*(A+\mathrm {i}\omega )^{-1} \right) Q\\&=-R(\omega )-R(\omega )^*-R(\omega )^*R(\omega ) =I-(I+R(\omega ))^*(I+R(\omega ))\\&=I-U(\omega )^*U(\omega ), \end{aligned}$$

shows that $E(\omega )$ is indeed independent of the choice of $\beta$. The continuity of $\omega \mapsto E(\omega )$ follows from Assumption (C) and Lemma 5.1(1) which ensures that $\mathrm {i}{\mathbb {R}}\cap \mathrm{sp}(A)=\emptyset$.

(2) Invoking Relation (5.28) we infer

$$\begin{aligned} E(\omega )=I-U(\omega )^*U(\omega ) =U(\omega )^*(U(-\omega )^*U(-\omega )-I)U(\omega ) =-U(\omega )^*E(-\omega )U(\omega ), \end{aligned}$$

and

$$\begin{aligned} I-\alpha E(\omega )&=U(\omega )^*\left( U(-\omega )^*U(-\omega )+\alpha E(-\omega )\right) U(\omega )\\&=U(\omega )^*(I-(1-\alpha )E(-\omega ))U(\omega ). \end{aligned}$$

Combining the last identity with Eq. (5.26) and (5.27) yields

$$\begin{aligned} \det (I-\alpha E(\omega ))=\overline{\det (I-(1-{\overline{\alpha }})E(\omega ))}. \end{aligned}$$

(5.29)

The simple estimate $\Vert (A+\mathrm {i}\omega )^{-1}\Vert _2\le c(1+\omega ^2)^{-\frac{1}{2}}$ implies

$$\begin{aligned} \Vert E(\omega )\Vert _1\in L^1({\mathbb {R}},\mathrm {d}\omega ),\qquad \lim _{\omega \rightarrow \pm \infty }\Vert E(\omega )\Vert =0. \end{aligned}$$

(5.30)

Thus, the eigenvalues of $E(\omega )$, which are continuous functions of $\omega$, tend to zero as $\omega \rightarrow \pm \infty$. Since (5.29) implies that $I-E(\omega )$ is unimodular, $1\not \in \mathrm{sp}(E(\omega ))$ for any $\omega \in {\mathbb {R}}$ and we conclude that $E(\omega )<1$ for all $\omega \in {\mathbb {R}}$. From (5.29) we further deduce that the elements of $\mathrm{sp}(E(\omega ))\setminus \{0\}$ can be paired as $(\varepsilon ,\varepsilon ')$ with $0<\varepsilon <1$ and $\varepsilon '=-\varepsilon /(1-\varepsilon )<0$. Moreover, since the function $]0,1[\ni \varepsilon \mapsto -\varepsilon /(1-\varepsilon )$ is monotone decreasing, one has

$$\begin{aligned} \varepsilon _-(\omega )=\min \mathrm{sp}(E(\omega )) =-\frac{\varepsilon _+(\omega )}{1-\varepsilon _+(\omega )},\qquad \varepsilon _+(\omega )=\max \mathrm{sp}(E(\omega )). \end{aligned}$$

Thus, the following alternative holds: either

$$\begin{aligned} \varepsilon _-=\min _{\omega \in {\mathbb {R}}}\varepsilon _-(\omega )=0 =\max _{\omega \in {\mathbb {R}}}\varepsilon _+(\omega )=\varepsilon _+, \end{aligned}$$

and hence $E(\omega )=0$ for all $\omega \in {\mathbb {R}}$, or

$$\begin{aligned} \varepsilon _+\in ]0,1[,\qquad \varepsilon _-=-\frac{\varepsilon _+}{1-\varepsilon _+}\in ]0,-\infty [, \end{aligned}$$

and hence

$$\begin{aligned} \frac{1}{\varepsilon _-}+\frac{1}{\varepsilon _+}=1. \end{aligned}$$

This proves Part (2).

(3) By Part (2), $\det (I-\alpha E(\omega ))\not =0$ for $\alpha \in \mathfrak {C}_c$ and hence the function

$$\begin{aligned} \mathfrak {C}_c\ni \alpha \mapsto \log \det (I-\alpha E(\omega )) \end{aligned}$$

is analytic. Moreover, an elementary analysis shows that for any compact subset $K\subset \mathfrak {C}_c$ there is a constant $C_K$ such that

$$\begin{aligned} \sup _{\alpha \in K}\Vert E(\omega )(I-\alpha E(\omega ))^{-1}\Vert _1 \le C_K \Vert E(\omega )\Vert _1. \end{aligned}$$

For any $\alpha \in \mathfrak {C}_c$ one has

$$\begin{aligned} \log \det (I-\alpha E(\omega )) =-\int _0^\alpha \mathrm{tr}(E(\omega )(I-\gamma E(\omega ))^{-1})\mathrm {d}\gamma , \end{aligned}$$

and since the integration path from 0 to $\alpha$ lies in $\mathfrak {C}_c$ there is a constant $C_\alpha <\infty$ such that

$$\begin{aligned} |\log \det (I-\alpha E(\omega ))|\le C_\alpha \,\Vert E(\omega )\Vert _1. \end{aligned}$$

By (5.30) and Fubini’s theorem

$$\begin{aligned} e(\alpha )=-\int _{-\infty }^{\infty } \log \det (I-\alpha E(\omega ))\frac{\mathrm {d}\omega }{4\pi } =\int _0^\alpha \left( \int _{-\infty }^{\infty }\mathrm{tr}(E(\omega )(I-\gamma E(\omega ))^{-1})\frac{\mathrm {d}\omega }{4\pi }\right) \mathrm {d}\gamma . \end{aligned}$$

It follows that $\mathfrak {C}_c\ni \alpha \mapsto e(\alpha )$ is analytic and that

$$\begin{aligned} e'(\alpha ) =\int _{-\infty }^{\infty } \mathrm{tr}(E(\omega )(I-\alpha E(\omega ))^{-1})\frac{\mathrm {d}\omega }{4\pi }, \end{aligned}$$

$$\begin{aligned} e''(\alpha ) =\int _{-\infty }^{\infty } \mathrm{tr}(E(\omega )(I-\alpha E(\omega ))^{-1}E(\omega )(I-\alpha E(\omega ))^{-1} )\frac{\mathrm {d}\omega }{4\pi }. \end{aligned}$$

Since $I-\alpha E(\omega )>0$ for $\alpha \in \mathfrak {I}_c$, the last formula shows in particular that $e''(\alpha )\ge 0$ for $\alpha \in \mathfrak {I}_c$, and so the function $\mathfrak {I}_c\ni \alpha \mapsto e(\alpha )$ is convex. Going back to the alternative of Part (2), we conclude that either $e(\alpha )$ vanishes identically, or is strictly convex on $\mathfrak {I}_c$. The symmetry $e(1-\alpha )=e(\alpha )$ follows from Eq. (5.29) and, since $e(0)=e(1)=0$, convexity implies that $e(\alpha )\le 0$ for $\alpha \in [0,1]$ and $e(\alpha )\ge 0$ for $\alpha \in \mathfrak {I}_c\setminus [0,1]$. By Plancherel’s theorem

$$\begin{aligned} \int _{-\infty }^{\infty }(A+\mathrm {i}\omega )^{-1}QQ^*(A^*-\mathrm {i}\omega )^{-1} \frac{\mathrm {d}\omega }{2\pi }=\int _0^\infty \mathrm {e}^{tA}QQ^*\mathrm {e}^{tA^*}\mathrm {d}t=M, \end{aligned}$$

and so

$$\begin{aligned} e'(0)&=-e'(1)=\int _{-\infty }^{\infty } \mathrm{tr}\left( \Sigma _\beta (A+\mathrm {i}\omega )^{-1}QQ^*(A^*-\mathrm {i}\omega )^{-1}\right) \frac{\mathrm {d}\omega }{4\pi }\\&=\frac{1}{2}\mathrm{tr}(\Sigma _\beta M)=\mu (\sigma _\beta )=-\mathrm{ep}. \end{aligned}$$

Assume that $\varepsilon _+>0$. By Lemma 5.1(1), A is stable and hence $E(\omega )$ is an analytic function of $\omega$ in a strip $|\mathrm{Im}\,\omega |<\delta$. By (5.30) there is a compact subset K of this strip such that $\varepsilon _+(\omega )<\varepsilon _+$ for all $\omega \in {\mathbb {R}}\setminus K$. By regular perturbation theory the eigenvalues of $E(\omega )$ are analytic in K, except for possibly finitely many exceptional points where some of these eigenvalues cross. Thus, there is a strip $\mathcal S=\{\omega \,|\,|\mathrm{Im}\,(\omega )|<\delta '\}$ such that all exceptional points of $E(\omega )$ in $\mathcal S\cap K$ are real. Since $E(\omega )$ is self-adjoint for $\omega \in {\mathbb {R}}$, its eigenvalues are analytic at these exceptional points (see, e.g., [43, Theorem 1.10]). We conclude that the eigenvalues of $E(\omega )$ are analytic in $\mathcal S\cap K$. It follows that the function ${\mathbb {R}}\ni \omega \mapsto \varepsilon _+(\omega )$ reaches its maximum $\varepsilon _+$ on a finite subset $\mathcal{M}\subset K\cap {\mathbb {R}}$. To each $\mathfrak {m}\in \mathcal{M}$ let us associate $\delta _\mathfrak {m}>0$, to be chosen later, in such a way that the intervals $O_\mathfrak {m}=]\mathfrak {m}-\delta _\mathfrak {m},\mathfrak {m}+\delta _\mathfrak {m}[$ are pairwise disjoint. Setting

$$\begin{aligned} e_\mathfrak {m}(\alpha ) =-\int \limits _{O_\mathfrak {m}}\log \det (I-\alpha E(\omega ))\frac{\mathrm {d}\omega }{4\pi } =-\sum _j\int \limits _{O_\mathfrak {m}}\log (1-\alpha \varepsilon _j(\omega )) \frac{\mathrm {d}\omega }{4\pi }, \end{aligned}$$

(5.31)

where the sum runs over all repeated eigenvalues of $E(\omega )$, we can decompose

$$\begin{aligned} e(\alpha )=\sum _{\mathfrak {m}\in \mathcal{M}}e_\mathfrak {m}(\alpha )+e_\mathrm{reg}(\alpha ), \end{aligned}$$

where the function $\alpha \mapsto e_\mathrm{reg}(\alpha )$ is analytic at $\alpha =\frac{1}{2}+\kappa _c$. Since $\mathfrak {I}_c\ni \alpha \mapsto e(\alpha )$ is convex, to prove that it has a continuous extension to $\alpha =\tfrac{1}{2}+\kappa _c$ and that its derivative diverges to $+\infty$ as $\alpha \uparrow \tfrac{1}{2}+\kappa _c$, it suffices to show that for all $\mathfrak {m}\in \mathcal{M}$ the function $e_\mathfrak {m}(\alpha )$ remains bounded and its derivative diverges to $+\infty$ in this limit. The same argument links the behavior of $e(\alpha )$ and $e'(\alpha )$ as $\alpha \downarrow \tfrac{1}{2}-\kappa _c$ to the minima of $\varepsilon _-(\omega )$, and we shall only consider the case $\alpha \uparrow \tfrac{1}{2}+\kappa _c$.

Let $\mathfrak {m}\in \mathcal{M}$ and consider an eigenvalue $\varepsilon (\omega )$ of $E(\omega )$ which takes the maximal value $\varepsilon _+$ at $\omega =\mathfrak {m}$. There is an integer $n\ge 1$ and a function f, analytic at $\mathfrak {m}$, such that $f(\mathfrak {m})>0$ and

$$\begin{aligned} \varepsilon (\omega )=\varepsilon _+-(\omega -\mathfrak {m})^{2n}f(\omega ). \end{aligned}$$

Moreover, we can chose $\delta _\mathfrak {m}>0$ such that f is analytic in $O_\mathfrak {m}$ and

$$\begin{aligned} \inf _{\omega \in O_\mathfrak {m}}f(\omega )>0,\qquad \sup _{\omega \in O_\mathfrak {m}}f(\omega )<\infty ,\qquad \inf _{\omega \in O_\mathfrak {m}}\varepsilon (\omega )>0. \end{aligned}$$

Setting

$$\begin{aligned} \eta =\left( \frac{1}{\alpha }-\varepsilon _+\right) ^{\tfrac{1}{2n}} =\left( \frac{\frac{1}{2}+\kappa _c-\alpha }{(\frac{1}{2}+\kappa _c)\alpha }\right) ^{\tfrac{1}{2n}}, \end{aligned}$$

so that $\eta \downarrow 0 \Leftrightarrow \alpha \uparrow \tfrac{1}{2}+\kappa _c$, we can write

$$\begin{aligned} 1-\alpha \varepsilon (\omega ) =\alpha \eta ^{2n} \left( 1+\left( \frac{\omega -\mathfrak {m}}{\eta }\right) ^{2n}f(\omega )\right) =\alpha (\omega -\mathfrak {m})^{2n} \left( \left( \frac{\eta }{\omega -\mathfrak {m}}\right) ^{2n}+f(\omega )\right) \end{aligned}$$

and since

$$\begin{aligned} \int \limits _{|\omega -\mathfrak {m}|\le \eta }&\log \left[ \alpha \eta ^{2n}\left( 1+\left( \frac{\omega -\mathfrak {m}}{\eta }\right) ^{2n}f(\omega ) \right) \right] \mathrm {d}\omega =\mathcal {O}(\eta \log \eta ),\\ \int \limits _{\eta \le |\omega -\mathfrak {m}|\le \delta _\mathfrak {m}}&\log \left[ \alpha (\omega -\mathfrak {m})^{2n}\left( \left( \frac{\eta }{\omega -\mathfrak {m}}\right) ^{2n} +f(\omega )\right) \right] \mathrm {d}\omega =\mathcal {O}(1), \end{aligned}$$

as $\eta \downarrow 0$, it follows that

$$\begin{aligned} \int \limits _{O_\mathfrak {m}}\log (1-\alpha \varepsilon (\omega ))\mathrm {d}\omega =\mathcal {O}(1) \end{aligned}$$

as $\alpha \uparrow \tfrac{1}{2}+\kappa _c$. Since the contributions to the sum on the right-hand side of Eq. (5.31) arising from eigenvalues of $E(\omega )$ that do not reach the maximal value $\varepsilon _+$ at $\mathfrak {m}$ are analytic at $\alpha =\tfrac{1}{2}+\kappa _c$, it follows that $e_\mathfrak {m}(\alpha )$ remains bounded as $\alpha \uparrow \tfrac{1}{2}+\kappa _c$.

Let us now consider the derivative $e_\mathfrak {m}'(\alpha )$. Setting $\eta =\tfrac{1}{2}+\kappa _c-\alpha$, we can write

$$\begin{aligned} \int \limits _{O_\mathfrak {m}} \frac{\varepsilon (\omega )}{1-\alpha \varepsilon (\omega )}\mathrm {d}\omega =\int \limits _{O_\mathfrak {m}} \left( \eta +\frac{f(\omega )}{\varepsilon (\omega )\varepsilon _+}(\omega -\mathfrak {m})^{2n}\right) ^{-1}\mathrm {d}\omega . \end{aligned}$$

Since

$$\begin{aligned} D=\sup _{\omega \in O_\mathfrak {m}} \frac{f(\omega )}{\varepsilon (\omega )\varepsilon _+}>0, \end{aligned}$$

we get

$$\begin{aligned} \int \limits _{O_\mathfrak {m}} \frac{\varepsilon (\omega )}{1-\alpha \varepsilon (\omega )}\mathrm {d}\omega \ge 2\int _0^{\delta _\mathfrak {m}}\frac{\mathrm {d}\omega }{\eta +\omega ^{2n}D} \ge C\eta ^{-1+\tfrac{1}{2n}}\rightarrow \infty , \end{aligned}$$

as $\eta \downarrow 0$. Since again the contributions of the eigenvalues of $E(\omega )$ which do not reach the maximal value $\varepsilon _+$ at $\mathfrak {m}$ are analytic at $\alpha =\tfrac{1}{2}+\kappa _c$, it follows that $e_\mathfrak {m}'(\alpha )\rightarrow \infty$ as $\alpha \uparrow \tfrac{1}{2}+\kappa _c$.

(4) For any bounded continuous function $f:[\varepsilon _-,\varepsilon _+]\rightarrow {\mathbb {C}}$ one has

$$\begin{aligned} \left| \int _{-\infty }^{\infty } \mathrm{tr}(E(\omega )f(E(\omega )))\frac{\mathrm {d}\omega }{4\pi }\right| \le \Vert f\Vert _\infty \int _{-\infty }^{\infty }\Vert E(\omega )\Vert _1\frac{\mathrm {d}\omega }{4\pi }. \end{aligned}$$

Hence, by the Riesz-Markov representation theorem there is a regular signed Borel measure $\varrho$ on $[\varepsilon _-,\varepsilon _+]$ such that

$$\begin{aligned} \int _{-\infty }^{\infty } \mathrm{tr}(E(\omega )f(E(\omega )))\frac{\mathrm {d}\omega }{4\pi } =\int f(\varepsilon )\varrho (\mathrm {d}\varepsilon ), \end{aligned}$$

and

$$\begin{aligned} \int |\varrho |(\mathrm {d}\varepsilon ) \le \int _{-\infty }^{\infty }\Vert E(\omega )\Vert _1\frac{\mathrm {d}\omega }{4\pi }<\infty . \end{aligned}$$

For $\alpha \in \mathfrak {C}_c$ the function

$$\begin{aligned} f_\alpha :[\varepsilon _-,\varepsilon _+]\ni \varepsilon \mapsto -\frac{1}{\varepsilon }\log (1-\alpha \varepsilon ) \end{aligned}$$

is continuous and we can write

$$\begin{aligned} e(\alpha )=-\int _{-\infty }^{\infty } \mathrm{tr}(E(\omega )f_\alpha (E(\omega )))\frac{\mathrm {d}\omega }{4\pi } =\int f_\alpha (\varepsilon )\mathrm {d}\varrho (\varepsilon ). \end{aligned}$$

(5.32)

We can now proceeds as the proof of Theorem 2.4(2) in [41].

(5) We start with some simple consequences of Assumption (C). The reader is referred to Sect. 4 of [46] for a short introduction to the necessary background material. Since $A_\alpha =A+\alpha Q\vartheta ^{-1}Q^*$, the pair $(A_\alpha ,Q)$ is controllable for all $\alpha$. The relation $A_\alpha ^*=-A_{1-\alpha }$ shows that the same is true for the pair $(A_\alpha ^*,Q)$. Thus, one has

$$\begin{aligned} \bigcap _{n\ge 0}\mathrm{Ker}\,(Q^*A_\alpha ^n) =\bigcap _{n\ge 0}\mathrm{Ker}\,(Q^*A_\alpha ^{*n})=\{0\} \end{aligned}$$

(5.33)

for all $\alpha$. This implies that if $Q^*u=0$ and $(A_\alpha -z)u=0$ or $(A_\alpha ^*-z)u=0$, then $u=0$, i.e., no eigenvector of $A_\alpha$ or $A_\alpha ^*$ is contained in $\mathrm{Ker}\,Q^*$.

Assume that $z\in \mathrm{sp}(A_\alpha )$ and let $u\not =0$ be a corresponding eigenvector. Since

$$\begin{aligned} A_\alpha +A_\alpha ^*=2(\alpha -\tfrac{1}{2})Q\vartheta ^{-1}Q^*, \end{aligned}$$

taking the real part of $(u,(A_\alpha -z)u)=0$ yields

$$\begin{aligned} (\alpha -\tfrac{1}{2})|\vartheta ^{-\frac{1}{2}}Q^*u|^2=\mathrm{Re}\,z|u|^2. \end{aligned}$$

Thus, controllability of $(A_\alpha ,Q)$ implies $\mathrm{sp}(A_\alpha )\subset {\mathbb {C}}_\pm$ for ${\pm }(\alpha -\frac{1}{2})>0$.

For $\alpha \in {\mathbb {R}}\setminus \{\frac{1}{2}\}$ and $\omega \in {\mathbb {R}}$, Schur’s complement formula yields

$$\begin{aligned} \det (K_\alpha -\mathrm {i}\omega ) =\frac{\det \left( I+\alpha (1-\alpha )Q^*(A_\alpha ^*-\mathrm {i}\omega )^{-1} Q\vartheta ^{-2}Q^*(A_\alpha +\mathrm {i}\omega )^{-1}Q\right) }{\det \left( (A_\alpha +\mathrm {i}\omega )^{-1}\right) \det \left( (A_\alpha ^*-\mathrm {i}\omega )^{-1}\right) }, \end{aligned}$$

and using the relations

$$\begin{aligned} (A_\alpha +\mathrm {i}\omega )^{-1}&=(A+\mathrm {i}\omega )^{-1}(I+\alpha Q\vartheta ^{-1}Q^*(A+\mathrm {i}\omega )^{-1})^{-1},\\ (A_\alpha ^*-\mathrm {i}\omega )^{-1}&=(I+\alpha (A^*-\mathrm {i}\omega )^{-1}Q\vartheta ^{-1}Q^*)^{-1} (A^*-\mathrm {i}\omega )^{-1}, \end{aligned}$$

one easily derives

$$\begin{aligned} \det (K_\alpha -\mathrm {i}\omega )=|\det (A+\mathrm {i}\omega )|^2\det (I-\alpha E(\omega )). \end{aligned}$$

(5.34)

Writing Eq. (3.41) as

$$\begin{aligned} K_\alpha =\left[ \begin{array}{c@{\quad }c} -A&{}QQ^*\\ 0&{}A^*\end{array}\right] +\left[ \begin{array}{c@{\quad }c} -\alpha Q\vartheta ^{-1}Q^*&{}0\\ \alpha (1-\alpha ) Q\vartheta ^{-2}Q^*&{}\alpha Q\vartheta ^{-1}Q^*\end{array}\right] , \end{aligned}$$

one derives that the identity (5.34), as the equality between two polynomials, extends to all $\alpha \in {\mathbb {C}}$.

By Part (2), we conclude that $\mathrm{sp}(K_\alpha )\cap \mathrm {i}{\mathbb {R}}=\emptyset$ for $\alpha \in \mathfrak {C}_c$. It follows from the regular perturbation theory that the spectral projection $P_\alpha$ of $K_\alpha$ for the part of its spectrum in the open right half-plane is an analytic function of $\alpha$ in the cut plane $\mathfrak {C}_c$ (see, e.g., [43, Sect. II.1]). For $\alpha \in {\mathbb {R}}$, $K_\alpha$ is ${\mathbb {R}}$-linear on the real vector space $\Xi \oplus \Xi$. Thus, its spectrum is symmetric w.r.t. the real axis. Observing that $JK_\alpha +K_\alpha ^*J=0$, where J is the unitary operator

$$\begin{aligned} J=\left[ \begin{array}{c@{\quad }c} 0&{}I\\ -I&{}0 \end{array}\right] , \end{aligned}$$

we conclude that the spectrum of $K_\alpha$ is also symmetric w.r.t. the imaginary axis. It follows that for $\alpha \in \mathfrak {I}_c$

$$\begin{aligned} \frac{1}{2}\sum _{\lambda \in \mathrm{sp}(K_\alpha )}|\mathrm{Re}\,\lambda |\,m_\lambda =\mathrm{tr}(P_\alpha K_\alpha ). \end{aligned}$$

(5.35)

Denoting the resolvent of $K_\alpha$ by $T_\alpha (z)=(z-K_\alpha )^{-1}$, we have

$$\begin{aligned} P_\alpha =\oint _{\Gamma _+}T_\alpha (z)\frac{\mathrm {d}z}{2\pi \mathrm {i}}, \end{aligned}$$

where $\Gamma _+\subset {\mathbb {C}}_+$ is a Jordan contour enclosing $\mathrm{sp}(K_\alpha )\cap {\mathbb {C}}_+$ which can be chosen so that it also encloses $\mathrm{sp}(-A)=\mathrm{sp}(K_0)\cap {\mathbb {C}}_+$. Thus, we can rewrite (5.35) as

$$\begin{aligned} \frac{1}{2}\sum _{\lambda \in \mathrm{sp}(K_\alpha )}|\mathrm{Re}\,\lambda |\,m_\lambda =\oint _{\Gamma _+}z\tau _\alpha (z)\frac{\mathrm {d}z}{2\pi \mathrm {i}}, \end{aligned}$$

with $\tau _\alpha (z)=\mathrm{tr}(T_\alpha (z))$.

An elementary calculation yields the following resolvent formula

$$\begin{aligned} T_\alpha (z)&=T_0(z)\\&\quad +\left[ \begin{array}{l@{\quad }l} -\alpha r(z)QD(z)(I+R^\circledast (z))\vartheta ^{-1}Q^*r(z) &{}r(z)Q(I-D(z))Q^*r^\circledast (z)\\ -\lambda r^\circledast (z)Q\vartheta ^{-1}(I+R(z))D(z)\vartheta ^{-1}Q^*r^\circledast (z) &{}\alpha r^\circledast (z)Q\vartheta ^{-1}(I+R(z))D(z)Q^*r^\circledast (z) \end{array}\right] , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rclrcl} r(z)&{}=&{}(A+z)^{-1}, &{}r^\circledast (z)&{}=&{}(A^*-z)^{-1},\\ R(z)&{}=&{}\vartheta ^{-1}Q^*r(z)Q, &{}\quad R^\circledast (z)&{}=&{}Q^*r^\circledast (z)Q\vartheta ^{-1}, \end{array} \end{aligned}$$

and

$$\begin{aligned} D(z)=\left( I+\alpha (R(z)+R^\circledast (z)+R^\circledast (z)R(z))\right) ^{-1}. \end{aligned}$$

It follows that

$$\begin{aligned} \tau _\alpha (z)=\tau _0(z)+\mathrm{tr}\left( D(z)\alpha \partial _z((I+R^\circledast (z))(I+R(z))\right) . \end{aligned}$$

Thus, for small enough $\alpha \in {\mathbb {C}}$ and $z\in \Gamma _+$ we have

$$\begin{aligned} \tau _\alpha (z)=\tau _0(z)+\partial _z\log \det \left( I+\alpha (R(z)+R^\circledast (z)+R^\circledast (z)R(z))\right) . \end{aligned}$$

Since

$$\begin{aligned} T_0(z)=\left[ \begin{array}{c@{\quad }c} r(z)&{}-r(z)QQ^*r^\circledast (z)\\ 0&{}-r^\circledast (z) \end{array}\right] , \end{aligned}$$

the fact that $\Gamma _+$ encloses $\mathrm{sp}(-A)\subset {\mathbb {C}}_+$ but no point of $\mathrm{sp}(A^*)\subset {\mathbb {C}}_-$ implies

$$\begin{aligned} \oint _{\Gamma _+}z\,\tau _0(z)\frac{\mathrm {d}z}{2\pi \mathrm {i}} =\oint _{\Gamma _+}z\,\mathrm{tr}\left( (z+A)^{-1}+(z-A^*)^{-1}\right) \frac{\mathrm {d}z}{2\pi \mathrm {i}}=-\mathrm{tr}(A)=\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*), \end{aligned}$$

and hence

$$\begin{aligned} \oint _{\Gamma _+}z\tau _\alpha (z)\frac{\mathrm {d}z}{2\pi \mathrm {i}} =\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*) -\oint _{\Gamma _+}\log \det (I+\alpha (R(z)+R^\circledast (z) +R^\circledast (z)R(z)))\frac{\mathrm {d}z}{2\pi \mathrm {i}}. \end{aligned}$$

Noting that

$$\begin{aligned} R(z)+R^\circledast (z)+R^\circledast (z)R(z) =-Q^*(A^*-z)^{-1}\Sigma _\beta (A+z)^{-1}Q, \end{aligned}$$

and deforming the contour $\Gamma _+$ to the imaginary axis (which is allowed due to the decay of the above expression as $|z|\rightarrow \infty$) yields

$$\begin{aligned} \mathrm{tr}(K_\alpha P_\alpha ) =\tfrac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*) +\int _{-\infty }^{\infty }\log \det (I-\alpha E(\omega ))\frac{\mathrm {d}\omega }{2\pi }. \end{aligned}$$

Since both sides of the last identity are analytic functions of $\alpha$, this identity extends to all $\alpha \in \mathfrak {C}_c$ and the proof of Theorem 3.13 is complete.

5.6 The Algebraic Riccati Equation

This section is devoted to the study the algebraic Riccati equation

$$\begin{aligned} \mathcal{R}_\alpha (X)= X BX-X A_\alpha -A_\alpha ^*X-C_\alpha =0 \end{aligned}$$

which plays a central role in the proof of Proposition 3.18. We summarize our results in the following proposition.

Proposition 5.5

Under Assumption (C) the following hold:

• (1) For $\alpha \in \mathfrak {I}_c$ the Riccati equation $\mathcal{R}_\alpha (X)=0$ has a unique maximal solution which we denote by $X_\alpha$. It also has a unique minimal solution, which is given by $-\theta X_{1-\alpha }\theta$. Moreover,

  $$\begin{aligned} D_\alpha =A_\alpha -BX_\alpha \end{aligned}$$

  is stable and

  $$\begin{aligned} Y_\alpha =X_\alpha +\theta X_{1-\alpha }\theta >0. \end{aligned}$$

• (2) The function $\mathfrak {I}_c\ni \alpha \mapsto X_\alpha \in L(\Xi )$ is real analytic, concave, and satisfies

  $$\begin{aligned} \left\{ \begin{array}{l@{\quad }l@{\quad }l} X_\alpha <0&{}\text {for}&{}\alpha \in ]\frac{1}{2}-\kappa _c,0[;\\ X_\alpha >0&{}\text {for}&{}\alpha \in ]0,\frac{1}{2}+\kappa _c[. \end{array} \right. \end{aligned}$$

  (5.36)

  $Moreover, X_0=0$ and $X_1=\theta M^{-1}\theta$.

• (3) If, for some $\alpha \in {\overline{\mathfrak {I}}}_c$, $X\in L(\Xi )$ is a self-adjoint solution of $\mathcal{R}_\alpha (X)=0$ and $\mathrm{sp}(A_\alpha -BX)\subset \overline{{\mathbb {C}}}_-$, then X is the unique maximal solution of $\mathcal{R}_\alpha (X)=0$.

• (4) If $\kappa _c<\infty$, then the limits

  $$\begin{aligned} X_{\frac{1}{2}-\kappa _c}=\lim _{\alpha \downarrow \frac{1}{2}-\kappa _c}X_\alpha ,\qquad X_{\frac{1}{2}+\kappa _c}=\lim _{\alpha \uparrow \frac{1}{2}+\kappa _c}X_\alpha , \end{aligned}$$

  exist and are non-singular. They are the maximal solutions of the corresponding limiting Riccati equations $\mathcal{R}_{\frac{1}{2}\pm \kappa _c}(X_{\frac{1}{2}\pm \kappa _c})=0$.

• (5) If $X\in L(\Xi )$ is self-adjoint and satisfies $\mathcal{R}_\alpha (X)\le 0$ for some $\alpha \in {\overline{\mathfrak {I}}}_c$, then $X\le X_\alpha$.

• (6) For all $\alpha \in {\overline{\mathfrak {I}}}_c$ the pair $(D_\alpha ,Q)$ is controllable and $\mathrm{sp}(D_\alpha )=\mathrm{sp}(K_\alpha )\cap \overline{{\mathbb {C}}}_-$. Moreover, for any $\beta \in L(\Xi )$ satisfying Conditions (3.17) one has

  $$\begin{aligned} e(\alpha )=\frac{1}{2}\mathrm{tr}\left( D_\alpha +\frac{1}{2} Q\vartheta ^{-1}Q^*\right) =-\frac{1}{2}\mathrm{tr}(Q^*(X_\alpha -\alpha \beta )Q). \end{aligned}$$

  (5.37)

• (7) For $t>0$ set

  $$\begin{aligned} M_{\alpha ,t}=\int _0^t\mathrm {e}^{sD_\alpha }B\mathrm {e}^{sD_\alpha ^*}\mathrm {d}s>0. \end{aligned}$$

  Then for all $\alpha \in {\overline{\mathfrak {I}}}_c$

  $$\begin{aligned} \lim _{t\rightarrow \infty }M_{\alpha ,t}^{-1} =\inf _{t>0}M_{\alpha ,t}^{-1} =Y_\alpha \ge 0, \end{aligned}$$

  and $\mathrm{Ker}\,(Y_\alpha )$ is the spectral subspace of $D_\alpha$ corresponding to its imaginary eigenvalues.

• (8) Set $\Delta _{\alpha ,t}=M_{\alpha ,t}^{-1}-Y_\alpha$. For all $\alpha \in {\overline{\mathfrak {I}}}_c$, one has

  $$\begin{aligned} \mathrm {e}^{tD_\alpha ^*}M_{\alpha ,t}^{-1}\mathrm {e}^{tD_\alpha } =\theta \Delta _{1-\alpha ,t}\theta , \end{aligned}$$

  (5.38)

  and

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \det (\Delta _{\alpha ,t}) =4e(\alpha )-\mathrm{tr}(Q\vartheta ^{-1}Q^*). \end{aligned}$$

  In particular, for $\alpha \in \mathfrak {I}_c$, $\Delta _{\alpha ,t}\rightarrow 0$ exponentially fast as $t\rightarrow \infty$.

• (9) Let $\widetilde{D}_\alpha =\theta D_{1-\alpha }\theta$. Then

  $$\begin{aligned} Y_\alpha \mathrm {e}^{t\widetilde{D}_\alpha }=\mathrm {e}^{tD_\alpha ^*} Y_\alpha \end{aligned}$$

  for all $\alpha \in {\overline{\mathfrak {I}}}_c$ and $t\in {\mathbb {R}}$.

• (10) Let $W_\alpha =\alpha X_1-X_\alpha$. Then

  $$\begin{aligned} \left\{ \begin{array}{l@{\quad }l@{\quad }l} W_\alpha \le 0&{}\text {for}&{}|\alpha -\frac{1}{2}|\le \frac{1}{2};\\ W_\alpha \ge 0&{}\text {for}&{}\frac{1}{2}\le |\alpha -\frac{1}{2}|\le \kappa _c; \end{array} \right. \end{aligned}$$

  and $Y_\alpha +W_\alpha >0$ for all $\alpha \in {\overline{\mathfrak {I}}}_c$.

• (11) Set ${\overline{\vartheta }}=\tfrac{1}{2}(\vartheta _\mathrm{max}+\vartheta _\mathrm{min})$ and $\Delta =\vartheta _\mathrm{max}-\vartheta _\mathrm{min}$. Then the following lower bound holds

  $$\begin{aligned} \kappa _c\ge \kappa _0=\frac{{\overline{\vartheta }}}{\Delta }>\frac{1}{2}. \end{aligned}$$

  Moreover, the maximal solution satisfies

  $$\begin{aligned} X_\alpha \ge \left\{ \begin{array}{l@{\quad }l} \alpha \vartheta _\mathrm{min}^{-1}&{}\text{ for } \alpha \in [\tfrac{1}{2}-\kappa _0,0];\\ \alpha \vartheta _\mathrm{max}^{-1}&{}\text{ for } \alpha \in [0,\frac{1}{2}+\kappa _0]. \end{array} \right. \end{aligned}$$

  (5.39)

• (12) Assume that $\kappa _c=\kappa _0$ and that the steady state covariance satisfies the strict inequalities [recall (3.13)]

  $$\begin{aligned} \vartheta _\mathrm{min}<M<\vartheta _\mathrm{max}. \end{aligned}$$

  Then Condition (R) is satisfied.

Remark 5.6

In the equilibrium case $\vartheta _\mathrm{min}=\vartheta _\mathrm{max}=\vartheta _0$ it follows from Part (11) that $\kappa _c=\infty$. One easily checks that in this case

$$\begin{aligned} X_\alpha =\alpha \vartheta _0^{-1}I,\qquad \theta X_{1-\alpha }\theta =(1-\alpha )\vartheta _0^{-1}I,\qquad Y_\alpha =\vartheta _0^{-1}I,\qquad W_\alpha =0,\qquad D_\alpha =A. \end{aligned}$$

Proof

For the reader convenience, we have collected the well known results on algebraic Riccati equations needed for the proof in the Appendix.

We denote by $\mathcal{H}$ the complex Hilbert space ${\mathbb {C}}\Xi \oplus {\mathbb {C}}\Xi$ on which the Hamiltonian matrix $K_\alpha$ acts and introduce the unitary operators

$$\begin{aligned} \Theta =\left[ \begin{array}{c@{\quad }c} 0&{}\theta \\ \theta &{}0 \end{array}\right] , \end{aligned}$$

acting on the same Hilbert space. We have already observed in the proof of Theorem 3.13 that for $\alpha \in {\mathbb {R}}$ the spectrum of $K_\alpha$ is symmetric w.r.t. the real axis and the imaginary axis. The time-reversal covariance relations

$$\begin{aligned} \theta A_\alpha \theta =A_\alpha ^*=-A_{1-\alpha },\qquad \theta B\theta =B^*=B,\qquad \theta C_\alpha \theta =C_\alpha ^*=C_\alpha =C_{1-\alpha }, \end{aligned}$$

(5.40)

which follow easily from the definitions of the operators $A_\alpha$, B, $C_\alpha$ [recall Eq. (3.1), (3.12) and (3.42)], further yield $\Theta K_\alpha -K_{1-\alpha }^*\Theta =0$ which implies

$$\begin{aligned} \mathrm{sp}(K_\alpha )=\mathrm{sp}(K_{1-\alpha }). \end{aligned}$$

(5.41)

• (1) By Theorem 3.13(5), $\mathrm{sp}(K_\alpha )\cap \mathrm {i}{\mathbb {R}}=\emptyset$ for $\alpha \in \mathfrak {I}_c$ and the existence and uniqueness of the minimal/maximal solution of $\mathcal{R}_\alpha (X)=0$ follows from Corollary 6.3. The relation between minimal and maximal solutions follows from the identity

  $$\begin{aligned} \mathcal{R}_\alpha (\theta X\theta )=\theta \mathcal{R}_{1-\alpha }(-X)\theta , \end{aligned}$$

  which is a direct consequence of Eq. (5.40). The maximal solution $X_\alpha$ is related to the spectral subspace $\mathcal{H}_-(K_\alpha )$ of $K_\alpha$ for the part of its spectrum in the open left half-plane ${\mathbb {C}}_-$ by

  $$\begin{aligned} \mathcal{H}_-(K_\alpha )=\mathrm{Ran}\,\left[ \begin{array}{c}I\\ X_{\alpha }\end{array}\right] , \end{aligned}$$

  (5.42)

  see Sect. A.3. In particular $\mathrm{sp}(D_\alpha )=\mathrm{sp}(K)\cap {\mathbb {C}}_-$. The matrix $Y_\alpha =X_\alpha -\theta X_{1-\alpha }\theta$ is called the gap of the equation $\mathcal{R}_\alpha (X)=0$. It is obviously non-negative. It has the remarkable property that for any solution X, $\mathrm{Ker}\,(Y_\alpha )$ is the spectral subspace of $A_\alpha -BX$ for the part of its spectrum in $\mathrm {i}{\mathbb {R}}$ [Theorem 6.7(1)]. Since $\mathrm{sp}(D_\alpha )\subset {\mathbb {C}}_-$, we must have $Y_\alpha >0$.

• (2) One deduces from Eq. (5.42) that the spectral projection of $K_\alpha$ for the part of its spectrum in ${\mathbb {C}}_+$ is given by

  $$\begin{aligned} P_\alpha =\left[ \begin{array}{c}I\\ X_\alpha \end{array}\right] Y_\alpha ^{-1} \left[ \begin{array}{l@{\quad }l}\theta X_{1-\alpha }\theta&I\end{array}\right] =\left[ \begin{array}{ll}I-Y_\alpha ^{-1}X_\alpha &{}Y_\alpha ^{-1}\\ X_\alpha (I-Y_\alpha ^{-1}X_\alpha )&{}X_\alpha Y_\alpha ^{-1} \end{array}\right] . \end{aligned}$$

  As already noticed in the proof of Theorem 3.13, $P_\alpha$ is an analytic function of $\alpha$ in the cut plane $\mathfrak {C}_c\supset \mathfrak {I}_c$. It follows that $Y_\alpha ^{-1}$ and $X_\alpha Y_\alpha ^{-1}$ are real analytic on $\mathfrak {I}_c$. The same holds for $Y_\alpha$ and $X_\alpha =X_\alpha Y_\alpha ^{-1}Y_\alpha$. To prove concavity we shall invoke the implicit function theorem to compute the first and second derivatives $X'_\alpha$ and $X''_\alpha$ of the maximal solution. To this end, we must show that the derivative $D\mathcal{R}_\alpha$ of the map $X\mapsto \mathcal{R}_\alpha (X)$ at $X=X_\alpha$ is injective. A simple calculation shows that

  $$\begin{aligned} D\mathcal{R}_\alpha : Z\mapsto -ZD_\alpha -D_\alpha ^*Z. \end{aligned}$$

  By (1) one has $\mathrm{sp}(D_\alpha )\subset {\mathbb {C}}_-$ for $\alpha \in \mathfrak {I}_c$. It follows that for any $L\in L(\Xi )$ the Lyapunov equation $D\mathcal{R}_\alpha Z=L$ has the unique solution

  $$\begin{aligned} Z=\int _0^\infty \mathrm {e}^{tD_\alpha ^*}L\,\mathrm {e}^{tD_\alpha }\mathrm {d}t \end{aligned}$$

  (see, e.g., Sect. 5.3 in [46]). This ensures the applicability of the implicit function theorem and a straightforward calculation yields the following expressions valid for all $\alpha \in \mathfrak {I}_c$:

  $$\begin{aligned} X_\alpha '&=\int _0^\infty \mathrm {e}^{tD_\alpha ^*} \left( X_\alpha B\beta +\beta BX_\alpha +(1-2\alpha )\beta B\beta \right) \mathrm {e}^{tD_\alpha }\mathrm {d}t, \end{aligned}$$

  (5.43)
  $$\begin{aligned} X_\alpha ''&=-2\int _0^\infty \mathrm {e}^{tD_\alpha ^*}(X_\alpha '-\beta ) B(X_\alpha '-\beta )\mathrm {e}^{tD_\alpha }\mathrm {d}t. \end{aligned}$$

  (5.44)

  From (5.44) we deduce $X_\alpha ''\le 0$ which yields concavity. We shall now prove the inequalites (5.36), using again the Lyapunov equation. Indeed, one can rewrite the Riccati equation $\mathcal{R}_\alpha (X_\alpha )=0$ in the following two distinct forms:

  $$\begin{aligned} X_\alpha A_\alpha +A_\alpha ^*X_\alpha&=X_\alpha BX_\alpha -C_\alpha , \end{aligned}$$

  (5.45)
  $$\begin{aligned} X_\alpha D_\alpha +D_\alpha ^*X_\alpha&=-X_\alpha BX_\alpha -C_\alpha . \end{aligned}$$

  (5.46)

  Recall that Condition (C) implies $\mathrm{sp}(A_\alpha )\subset {\mathbb {C}}_-$ for $\alpha <0$ [as established at the beginning of the proof of Theorem 3.13(5)]. It follows from Eq. (5.45) that

  $$\begin{aligned} X_\alpha =-\int _0^\infty \mathrm {e}^{tA_\alpha ^*} (X_\alpha BX_\alpha -C_\alpha )\mathrm {e}^{tA_\alpha }\mathrm {d}t \le \alpha (1-\alpha ) \int _0^\infty \mathrm {e}^{tA_\alpha ^*}Q\vartheta ^{-2}Q^*\mathrm {e}^{tA_\alpha }\mathrm {d}t. \end{aligned}$$

  (5.47)

  Since $(A_\alpha ^*,Q)$ is controllable, we can conclude that $X_\alpha <0$ for $\alpha \in ]\frac{1}{2}-\kappa _c,0[$. Similarly, for $\alpha >1$, $\mathrm{sp}(A_\alpha )\subset {\mathbb {C}}_+$ and Eq. (5.45) leads to

  $$\begin{aligned} X_\alpha =\int _0^\infty \mathrm {e}^{-tA_\alpha ^*} (X_\alpha BX_\alpha -C_\alpha )\mathrm {e}^{-tA_\alpha }\mathrm {d}t \ge \alpha (\alpha -1) \int _0^\infty \mathrm {e}^{-tA_\alpha ^*}Q\vartheta ^{-2}Q^*\mathrm {e}^{-tA_\alpha }\mathrm {d}t. \end{aligned}$$

  (5.48)

  Controllability again yields $X_\alpha >0$ for $\alpha \in ]1,\frac{1}{2}+\kappa _c[$. Finally, for $\alpha \in ]0,1[$ we use Eq. (5.46) and the fact that $D_\alpha$ is stable [established in Part (1)] to obtain

  $$\begin{aligned} X_\alpha =\int _0^\infty \mathrm {e}^{tD_\alpha ^*} (X_\alpha BX_\alpha +C_\alpha )\mathrm {e}^{tD_\alpha }\mathrm {d}t \ge \alpha (1-\alpha ) \int _0^\infty \mathrm {e}^{tD_\alpha ^*}Q\vartheta ^{-2}Q^*\mathrm {e}^{tD_\alpha }\mathrm {d}t. \end{aligned}$$

  It follows that $X_\alpha \ge 0$ for $\alpha \in ]0,1[$. To show that $X_\alpha >0$, let $u\in \mathrm{Ker}\,X_\alpha$. From (5.45) we infer $(u,C_\alpha u)=0$ and hence $u\in \mathrm{Ker}\,C_\alpha =\mathrm{Ker}\,Q^*$. Using (5.45) again, we deduce $A_\alpha u\in \mathrm{Ker}\,X_\alpha$. Thus, we conclude that $u\in \mathrm{Ker}\,Q^*A_\alpha ^n$ for all $n\ge 0$ and (5.33) yields that $u=0$. From $X_0=\lim _{\alpha \uparrow 0}X_\alpha \le 0$ and $X_0=\lim _{\alpha \downarrow 0}X_\alpha \ge 0$, we deduce $X_0=0$. To prove the last assertion, we deduce from (5.45) and identities $A_1=-A^*=-\theta A\theta$, $C_1=0$, that $\widehat{M}=\theta X_1^{-1}\theta$ satisfies the Lyapunov equation $A\widehat{M}+\widehat{M}A^*+B=0$. Since A is stable, this equation has a unique solution and Lemma 5.1(5) yields $\widehat{M}=M$.

• (3) is a well known property of the Riccati equation [Theorem 6.6(3)].

• (4) Since $X_\alpha$ is concave and vanishes at $\alpha =0$, the function $\alpha \mapsto X_\alpha -\alpha X_0'$ is monotone decreasing/increasing for $\alpha$ negative/positive. Thus, to prove the existence of the limits $X_{\frac{1}{2}\pm \kappa _c}$ it suffices to show that the set $\{X_\alpha \,|\,\alpha \in \mathfrak {I}_c\}$ is bounded in $L(\Xi )$. For positive $\alpha$, this follows directly from Part (2) which implies $0\le X_\alpha \le \alpha X_0'$. For negative $\alpha$, taking the trace on both sides of the first equality in Eq. (5.47) and using the fact that $C_\alpha \le 0$, we obtain

  $$\begin{aligned} \mathrm{tr}(X_\alpha )=-\int _0^\infty \mathrm{tr}((X_\alpha BX_\alpha -C_\alpha ) \mathrm {e}^{tA_\alpha ^*}\mathrm {e}^{tA_\alpha })\mathrm {d}t \ge -\mathrm{tr}(X_\alpha BX_\alpha -C_\alpha )\int _0^\infty \Vert \mathrm {e}^{tA_\alpha }\Vert ^2\mathrm {d}t. \end{aligned}$$

  Thus, an upper bound on $\mathrm{tr}(X_\alpha BX_\alpha -C_\alpha )$ will conclude the proof. Taking the trace of Riccati’s equation yields

  $$\begin{aligned} \mathrm{tr}(X_\alpha BX_\alpha -C_\alpha )=\mathrm{tr}(X_\alpha (A_\alpha +A_\alpha ^*)) =(2\alpha -1)\mathrm{tr}(X_\alpha Q\vartheta ^{-1}Q^*) \le \frac{2\alpha -1}{\vartheta _\mathrm {min}}\mathrm{tr}(\widehat{X}_\alpha ), \end{aligned}$$

  where $\widehat{X}_\alpha =Q^*X_\alpha Q$. Combining the last inequality with the estimate

  $$\begin{aligned} \mathrm{tr}(\widehat{X}_\alpha )^2\le |\partial \mathcal{I}|\mathrm{tr}(\widehat{X}_\alpha ^2) =|\partial \mathcal{I}|\mathrm{tr}(Q^*X_\alpha QQ^*X_\alpha Q) \le |\partial \mathcal{I}|\,\Vert Q\Vert ^2\mathrm{tr}(X_\alpha BX_\alpha ) \end{aligned}$$

  yields a quadratic inequality for $\mathrm{tr}(\widehat{X}_\alpha )$ which gives

  $$\begin{aligned} \mathrm{tr}(\widehat{X}_\alpha )\ge -(1-2\alpha )|\partial \mathcal{I}|\,\Vert Q\Vert ^2\vartheta _\mathrm {min}^{-1}. \end{aligned}$$

  Summing up, we have obtained the required lower bound

  $$\begin{aligned} \mathrm{tr}(X_\alpha )\ge -(1-2\alpha )^2|\partial \mathcal{I}|\, \Vert Q\Vert ^2\vartheta _\mathrm {min}^{-2} \int _0^\infty \Vert \mathrm {e}^{tA_\alpha }\Vert ^2\mathrm {d}t. \end{aligned}$$

  By continuity, we clearly have $\mathcal{R}_{\frac{1}{2}\pm \kappa _c}(X_{\frac{1}{2}\pm \kappa _c})=0$. Continuity also implies that $\mathrm{sp}(D_{\frac{1}{2}\pm \kappa _c})\subset \overline{{\mathbb {C}}}_-$ and the maximality of $X_{\frac{1}{2}\pm \kappa _c}$ follows from Part (3). Since $C_{\frac{1}{2}\pm \kappa _c}\le 0$, the fact that $X_{\frac{1}{2}\pm \kappa _c}$ is regular follows from the same argument we have used to prove the regularity of $X_\alpha$ for $\alpha \in ]0,1[$.

• (5) is another well known property of the Riccati equation [Theorem 6.7(3)].

• (6) Since $D_\alpha =A+Q(\alpha \vartheta ^{-1}Q^*-Q^*X_\alpha )$, the controllability of $(D_\alpha ,Q)$ follows from that of (A, Q). The relation between $\mathrm{sp}(K_\alpha )$ and $\mathrm{sp}(D_\alpha )$ is a direct consequence of the relation

  $$\begin{aligned} -K_\alpha \left[ \begin{array}{c}I\\ X_{\alpha }\end{array}\right] = \left[ \begin{array}{c}I\\ X_{\alpha }\end{array}\right] D_\alpha , \end{aligned}$$

  which follows from Eq. (5.42). Formula (5.37) is obtained by combining this information with Eq. (3.43). The last assertion is deduced from controllability of $(D_\alpha ,Q)$ in the same way as in the proof of Lemma 5.1(1).

• (7) To prove the existence of the limit, we note that (6) implies that for any $\alpha \in {\overline{\mathfrak {I}}}_c$ and $t_0>0$ the function $[t_0,\infty [\ni t\mapsto M_{\alpha ,t}^{-1}$ takes strictly positive values and is bounded and decreasing. Thus, we have

  $$\begin{aligned} Z_\alpha = \lim _{t\rightarrow \infty }M_{\alpha ,t}^{-1}=\inf _{t>0}M_{\alpha ,t}^{-1}\ge 0. \end{aligned}$$

  Since $M_{\alpha ,t}^{-1}$ is easily seen to satisfy the differential Riccati equation

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}M_{\alpha ,t}^{-1}= -\left( M_{\alpha ,t}^{-1}BM_{\alpha ,t}^{-1}+M_{\alpha ,t}^{-1}D_\alpha +D_\alpha ^*M_{\alpha ,t}^{-1}\right) , \end{aligned}$$

  (5.49)

  it follows that for any $t>0$ and $\tau \ge 0$

  $$\begin{aligned} M_{\alpha ,t}^{-1}-M_{\alpha ,t+\tau }^{-1} =\int _0^\tau \left( M_{\alpha ,t+s}^{-1}BM_{\alpha ,t+s}^{-1} +M_{\alpha ,t+s}^{-1}D_\alpha +D_\alpha ^*M_{\alpha ,t+s}^{-1}\right) \mathrm {d}s. \end{aligned}$$

  Letting $t\rightarrow \infty$, we conclude that $Z_\alpha$ satisfies

  $$\begin{aligned} Z_\alpha BZ_\alpha +Z_\alpha D_\alpha +D_\alpha ^*Z_\alpha =0. \end{aligned}$$

  (5.50)

  Expressing the last equation in terms of $V_\alpha =\theta (Z_\alpha -X_\alpha )\theta$ and using (5.40), we derive $\mathcal{R}_{1-\alpha }(V_\alpha )=0$. By a well known property of Lyapunov equation (see, e.g., Theorem 4.4.2 in [46]), one has $\mathrm{sp}(D_\alpha +BM_{\alpha ,t}^{-1})\subset {\mathbb {C}}_+$ for all $t>0$, which implies $\mathrm{sp}(D_\alpha +BZ_\alpha )\subset {\overline{{\mathbb {C}}}}_+$. Since $D_\alpha +BZ_\alpha =-\theta (A_{1-\alpha }-BV_\alpha )\theta$, we have $\mathrm{sp}(A_{1-\alpha }-BV_\alpha )\subset \overline{{\mathbb {C}}}_-$. From Part (3) we conclude that $V_\alpha$ is the maximal solution to the Riccati equation $\mathcal{R}_{1-\alpha }(X)=0$, i.e., that $V_\alpha =X_{1-\alpha }$. Thus,

  $$\begin{aligned} Z_\alpha =X_\alpha +\theta X_{1-\alpha }\theta =Y_\alpha , \end{aligned}$$

  is the gap of the Riccati equation. It is a well known property of this gap that $\mathrm{Ker}\,(Y_\alpha )$ is the spectral subspace of $D_\alpha$ associated to its imaginary eigenvalues [Theorem 6.7(1)].

• (8) Combining (5.49) and (5.50), one shows that $\Delta _{\alpha ,t}=M_{\alpha ,t}^{-1}-Y_\alpha$ satisfies the differential Riccati equation

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\Delta _{\alpha ,t}=-\Delta _{\alpha ,t}B\Delta _{\alpha ,t} +\Delta _{\alpha ,t}\widetilde{D}_\alpha +\widetilde{D}_\alpha ^*\Delta _{\alpha ,t}, \end{aligned}$$

  (5.51)

  where $\widetilde{D}_\alpha =-(A_\alpha +B\theta X_{1-\alpha }\theta ) =\theta D_{1-\alpha }\theta$. Since

  $$\begin{aligned} \Delta _{\alpha ,t}^{-1}=(I-M_{\alpha ,t}Y_\alpha )^{-1}M_{\alpha ,t}, \end{aligned}$$

  we further have $\lim _{t\rightarrow 0}\Delta _{\alpha ,t}^{-1}=0$. We deduce that $S_{\alpha ,t}=\Delta _{\alpha ,t}^{-1}$ satisfies the linear Cauchy problem

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}S_{\alpha ,t} =B-\widetilde{D}_\alpha S_{\alpha ,t} -S_{\alpha ,t}\widetilde{D}_\alpha ^*,\qquad S_{\alpha ,0}=0, \end{aligned}$$

  whose solution is easily seen to be given by

  $$\begin{aligned} S_{\alpha ,t}&=\int _0^t\mathrm {e}^{-s\widetilde{D}_\alpha }B\mathrm {e}^{-s\widetilde{D}_\alpha ^*}\mathrm {d}s =\theta \left( \int _0^t\mathrm {e}^{-sD_{1-\alpha }}B\mathrm {e}^{-sD_{1-\alpha }^*}\mathrm {d}s \right) \theta \\&=\theta \mathrm {e}^{-tD_{1-\alpha }}\left( \int _0^t\mathrm {e}^{sD_{1-\alpha }} B\mathrm {e}^{sD_{1-\alpha }^*}\mathrm {d}s \right) \mathrm {e}^{-tD_{1-\alpha }^*}\theta \\&=\theta \mathrm {e}^{-tD_{1-\alpha }}M_{1-\alpha ,t}\mathrm {e}^{-tD_{1-\alpha }^*}\theta . \end{aligned}$$

  We thus conclude that

  $$\begin{aligned} \Delta _{\alpha ,t} =\theta \mathrm {e}^{tD_{1-\alpha }^*}M_{1-\alpha ,t}^{-1}\mathrm {e}^{tD_{1-\alpha }}\theta , \end{aligned}$$

  which immediately yields (5.38). Since $\Delta _{\alpha ,t}$ is strictly positive for $t>0$, we infer from Eq. (5.51) that

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\log \det (\Delta _{\alpha ,t})&=\mathrm{tr}(\dot{\Delta }_{\alpha ,t}\Delta _{\alpha ,t}^{-1}) =-\mathrm{tr}(\Delta _{\alpha ,t}B-{\tilde{D}}_\alpha -{\tilde{D}}_\alpha ^*)\\&=-\mathrm{tr}(Q^*\Delta _{\alpha ,t}Q)+2\mathrm{tr}(D_{1-\alpha }). \end{aligned}$$

  By Part (3) and Theorem 3.13(5), we have

  $$\begin{aligned} \mathrm{tr}(D_{1-\alpha })&=-\frac{1}{2}\sum _{\lambda \in \mathrm{sp}(K_{1-\alpha })}|\mathrm{Re}\,\lambda |m_\lambda =2e(1-\alpha )-\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*)\\&=2e(\alpha )-\frac{1}{2}\mathrm{tr}(Q\vartheta ^{-1}Q^*). \end{aligned}$$

  Since $\Delta _{\alpha ,t}\rightarrow 0$ for $t\rightarrow \infty$, given $\epsilon >0$ there exists $t_0>0$ such that

  $$\begin{aligned} 4e(\alpha )-\mathrm{tr}(Q\vartheta ^{-1}Q^*) -\epsilon \le \frac{\mathrm {d}\ }{\mathrm {d}t}\log \det (\Delta _{\alpha ,t}) \le 4e(\alpha )-\mathrm{tr}(Q\vartheta ^{-1}Q^*) \end{aligned}$$

  for all $t>t_0$. It is straightforward to derive from these estimates that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \det (\Delta _{\alpha ,t}) =4e(\alpha )-\mathrm{tr}(Q\vartheta ^{-1}Q^*). \end{aligned}$$

• (9) Using (5.40), one rewrites the Riccati equation (5.50) as

  $$\begin{aligned} D_\alpha ^*Y_\alpha&=-Y_\alpha (D_\alpha +BY_\alpha ) =-Y_\alpha (A_\alpha +B(Y_\alpha -X_\alpha ))\\&=-Y_\alpha (A_\alpha +B\theta X_{1-\alpha }\theta ) =-Y_\alpha \theta (-A_{1-\alpha }+BX_{1-\alpha })\theta \\&=Y_\alpha \theta D_{1-\alpha }\theta =Y_\alpha \widetilde{D}_\alpha . \end{aligned}$$

  Thus, the result immediately follows from the fact that

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}t}\,\mathrm {e}^{tD_\alpha ^*}Y_\alpha \mathrm {e}^{-t\widetilde{D}_\alpha } =\mathrm {e}^{tD_\alpha ^*} (D_\alpha ^*Y_\alpha -Y_\alpha \widetilde{D}_\alpha ) \mathrm {e}^{-t\widetilde{D}_\alpha }=0. \end{aligned}$$

• (10) For any $u\in \Xi$ we infer from Parts (2) and (4) that the function $\alpha \mapsto (u,W_\alpha u)$ is convex, real analytic on the interval $\mathfrak {I}_c$, and continuous on its closure. Since it vanishes for $|\alpha -\frac{1}{2}|=\frac{1}{2}$ one has either $(u,W_\alpha u)=0$ for all $\alpha \in {\overline{\mathfrak {I}}}_c$ or $(u,W_\alpha u)<0$ for $|\alpha -\frac{1}{2}|<\frac{1}{2}$ and $(u,W_\alpha u)>0$ for $\frac{1}{2}<|\alpha -\frac{1}{2}|\le \kappa _c$. This proves the first assertion. Since $Y_\alpha +W_\alpha =\alpha X_1+\theta X_{1-\alpha }\theta$, we deduce from Part (2) that $Y_\alpha +W_\alpha >0$ for $|\alpha -\frac{1}{2}|\le \frac{1}{2}$. Consider now $\frac{1}{2}<|\alpha -\frac{1}{2}|\le \kappa _c$. If $u\in \Xi$ is such that $(u,W_\alpha u)>0$, then Part (7) yields $(u,(Y_\alpha +W_\alpha )u)>0$. Thus, it remains to consider the case of $u\in \Xi$ such that $(u,W_\alpha u)=0$ for all $\alpha \in {\overline{\mathfrak {I}}}_c$. Using (5.44) we get that

  $$\begin{aligned} (u,W_\alpha ''u) =-(u,X_\alpha ''u) =2\int _0^\infty |Q^*(X_\alpha '-\beta )\mathrm {e}^{tD_\alpha }u|^2\mathrm {d}t=0 \end{aligned}$$

  for $\alpha \in \mathfrak {I}_c$. Since $QQ^*(X_\alpha '-\beta )=-D_\alpha '$, this further implies $D_\alpha '\mathrm {e}^{tD_\alpha }u=0$ for all $(\alpha ,t)\in \mathfrak {I}_c\times {\mathbb {R}}$. Duhamel’s formula

  $$\begin{aligned} \frac{\mathrm {d}\ }{\mathrm {d}\alpha }\mathrm {e}^{tD_\alpha }u =\int _0^t\mathrm {e}^{(t-s)D_\alpha }D_\alpha '\mathrm {e}^{sD_\alpha }u\,\mathrm {d}s=0 \end{aligned}$$

  allows us to conclude that $\mathrm {e}^{tD_\alpha }u=\mathrm {e}^{tD_0}u=\mathrm {e}^{tA}u$, a relation which extends by continuity to all $(\alpha ,t)\in {\overline{\mathfrak {I}}}_c\times {\mathbb {R}}$. Thus,

  $$\begin{aligned} \lim _{t\rightarrow \infty }\mathrm {e}^{tD_\alpha }u=\lim _{t\rightarrow \infty }\mathrm {e}^{tA}u=0, \end{aligned}$$

  which, using (7) again, further implies that $u\not \in \mathrm{Ker}\,(Y_\alpha )$ and hence $(u,(Y_\alpha +W_\alpha )u)=(u,Y_\alpha u)>0$.

• (11) For $\lambda \in {\mathbb {R}}$, one has

  $$\begin{aligned} \mathcal{R}_\alpha (\lambda I)=Q\vartheta ^{-1} \left( \lambda \vartheta -(\alpha -1)\right) \left( \lambda \vartheta -\alpha \right) \vartheta ^{-1}Q^*, \end{aligned}$$

  so that $\mathcal{R}_\alpha (\lambda I)\le 0$ iff $\alpha -1\le \lambda \vartheta \le \alpha$. It follows that $\mathcal{P}=\{(\alpha ,\lambda )\in {\mathbb {R}}^2\,|\,\mathcal{R}_\alpha (\lambda I)\le 0\}$ is the closed parallelogram limited by the 4 lines (see Fig. 11)

  $$\begin{aligned} \lambda =\frac{\alpha }{\vartheta _\mathrm{max}},\quad \lambda =\frac{\alpha }{\vartheta _\mathrm{min}},\quad \lambda =\frac{\alpha -1}{\vartheta _\mathrm{max}},\quad \lambda =\frac{\alpha -1}{\vartheta _\mathrm{min}}. \end{aligned}$$

  The projection of $\mathcal{P}$ on the $\alpha$-axis is the closed interval $[\tfrac{1}{2}-\kappa _0,\tfrac{1}{2}+\kappa _0]$. Thus, Theorem 6.5 implies that the Riccati equation has a self-adjoint solution for all $\alpha \in [\tfrac{1}{2}-\kappa _0,\tfrac{1}{2}+\kappa _0]$. By Theorem 6.6(2) it also has a maximal solution $X_\alpha$ which, by Theorem 6.7(3), satisfies the lower bound (5.39). From this lower bound we further deduce that for $\alpha \in [0,\tfrac{1}{2}+\kappa _0[$, the gap satisfies

  $$\begin{aligned} Y_\alpha =X_\alpha +\theta X_{1-\alpha }\theta \ge \frac{\alpha }{\vartheta _\mathrm{max}}+\frac{1-\alpha }{\vartheta _\mathrm{min}} =\frac{\Delta }{\vartheta _\mathrm{max} \vartheta _\mathrm{min}}\left( \tfrac{1}{2}+\kappa _0-\alpha \right) >0. \end{aligned}$$

  Since $\mathrm{Ker}\,Y_{\frac{1}{2}+\kappa _c}\not =\{0\}$ by Parts (6) and (7), we conclude that $\kappa _c\ge \kappa _0$.

• (12) The concavity of $R_\alpha =X_\alpha +(1-\alpha )X_1$ and the fact that $R_0=R_1=X_1>0$ imply that for $|\alpha -\frac{1}{2}|\le \frac{1}{2}$ one has $R_\alpha \ge X_1>0$. For $\frac{1}{2}<\alpha -\frac{1}{2}\le \kappa _0$, Part (11) gives $X_\alpha \ge \alpha \vartheta _{\mathrm {max}}^{-1}$. Since $M>\vartheta _\mathrm{min}$, Part (2) yields $X_1=\theta M^{-1}\theta <\vartheta _{\mathrm {min}}^{-1}$ and hence

  $$\begin{aligned} R_\alpha >\frac{\alpha }{\vartheta _{\mathrm {max}}} +\frac{1-\alpha }{\vartheta _{\mathrm {min}}} =\frac{\kappa _0-(\alpha -\frac{1}{2})}{\Delta (\kappa _0^2-\tfrac{1}{4})}\ge 0. \end{aligned}$$

  The case $-\kappa _0\le \alpha -\frac{1}{2}<-\frac{1}{2}$ is similar.

$\square$

Fig. 11

The parallelogram $\mathcal{P}$

5.7 Proof of Proposition 3.18

5.7.1 A Girsanov Transformation

By Proposition 5.5, for $\alpha \in {\overline{\mathfrak {I}}}_c$ we have $A=D_\alpha +QQ^*(X_\alpha -\alpha \beta )$, and we can rewrite the equation of motion (3.2) as

$$\begin{aligned} \mathrm {d}x(t)=D_\alpha x(t)\mathrm {d}t+Q\mathrm {d}w_\alpha (t), \end{aligned}$$

(5.52)

where

$$\begin{aligned} w_\alpha (t)=w(t)-\int _0^tQ^*(\alpha \beta -X_\alpha )x(s)\mathrm {d}s. \end{aligned}$$

Let $Z_\alpha (t)$ be the stochastic exponential of the local martingale

$$\begin{aligned} \eta _\alpha (t)=\int _0^tQ^*(\alpha \beta -X_\alpha )x(s)\cdot \mathrm {d}w(s). \end{aligned}$$

Combining the Riccati equation with the relations $\beta QQ^*=QQ^*\beta =Q\vartheta ^{-1}Q$ and $\beta QQ^*\beta =Q\vartheta ^{-2}Q^*$, we derive

$$\begin{aligned} \frac{1}{2}|Q^*(\alpha \beta -X_\alpha )x|^2 =-\alpha \sigma _\beta (x)-(\alpha \beta -X_\alpha )x\cdot Ax, \end{aligned}$$

and we can write the quadratic variation of $\eta _\alpha$ as

$$\begin{aligned} \frac{1}{2}[\eta _\alpha ](t)=-\alpha \int _0^t\sigma _\beta (x(s))\mathrm {d}s -\int _0^t(\alpha \beta -X_\alpha )x(s)\cdot Ax(s)\mathrm {d}s. \end{aligned}$$

Hence

$$\begin{aligned} \eta _\alpha (t)-\frac{1}{2}[\eta _\alpha ](t) =\int _0^t(\alpha \beta -X_\alpha )x(s)\cdot \mathrm {d}x(s) +\alpha \int _0^t\sigma _\beta (x(s))\mathrm {d}s. \end{aligned}$$

The Itô calculus and Proposition 3.5(3) give

$$\begin{aligned} \eta _\alpha (t)-\frac{1}{2}[\eta _\alpha ](t) =-\left( \lambda _\alpha t +\alpha \mathfrak {S}^t+\chi _\alpha (x(t))-\chi _\alpha (x(0))\right) , \end{aligned}$$

with $\lambda _\alpha =\frac{1}{2}\mathrm{tr}(QQ^*(\alpha \beta -X_\alpha ))$ and

$$\begin{aligned} \chi _\alpha (x)=\frac{1}{2} x\cdot X_\alpha x. \end{aligned}$$

Finally, we note that Proposition 5.5(6) yields

$$\begin{aligned} \lambda _\alpha =-\frac{1}{2}\mathrm{tr}(Q^*(X_\alpha -\alpha \beta )Q)=e(\alpha ). \end{aligned}$$

Lemma 5.7

The process

$$\begin{aligned} Z_\alpha (t)=\mathcal{E}(\eta _\alpha )(t) =\mathrm {e}^{-\left[ e(\alpha ) t+\alpha \mathfrak {S}^t +\chi _\alpha (x(t))-\chi _\alpha (x(0))\right] } \end{aligned}$$

(5.53)

is a $\mathbb {P}_x$-martingale for all $x\in \Xi$.

Proof

We wish to apply the Girsanov theorem; see Sect. 3.5 in [42]. However, it is not clear that the Novikov condition is satisfied on a given finite interval. To overcome this difficulty, we follow the argument used in the proof of Corollary 5.14 in [42, Chapter 3].

Fix $\tau >0$. By Lemma 5.3, $\{x(t)-\mathrm {e}^{tA}x\}_{t\in [0,\tau ]}$ is a centered Gaussian process under the law $\mathbb {P}_x$. Since

$$\begin{aligned} \int _{s}^{s'}|Q^*(\alpha \beta -X_\alpha )x(t)|^2\mathrm {d}t\le C|s-s'|\left( |x|^2+\sup _{t\in [0,\tau ]}|x(t)-\mathrm {e}^{tA}x|^2\right) \end{aligned}$$

for some constant C, Fernique’s theorem implies that there exists $\delta >0$ such that

$$\begin{aligned} \mathbb {E}_x\left[ \exp \left( \frac{1}{2}\int _{s}^{s'} |Q^*(\alpha \beta -X_\alpha )x(t)|^2\mathrm {d}t\right) \right] <\infty , \end{aligned}$$

provided $0\le s\le s'\le \tau$ and $s'-s<\delta$. Novikov criterion implies that under the same conditions,

$$\begin{aligned}&\mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(s')}{\mathcal{E}(\eta _\alpha )(s)}\bigg |\mathcal{W}_s \right] \\&\quad =\mathbb {E}_x\left[ \exp \left( \int _s^{s'}Q^*(\alpha \beta -X_\alpha )x(t)\cdot \mathrm {d}w(t) -\frac{1}{2}\int _s^{s'}|Q^*(\alpha \beta -X_\alpha )x(t)|^2 \mathrm {d}t\right) \bigg |\mathcal{W}_s\right] \!=\!1. \end{aligned}$$

For $0\le s\le s'\le s''\le \tau$, $s'-s<\delta$ and $s''-s'<\delta$ we deduce

$$\begin{aligned} \mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(s'')}{\mathcal{E}(\eta _\alpha )(s)}\bigg |\mathcal{W}_s\right]&=\mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(s'')}{\mathcal{E}(\eta _\alpha )(s')} \frac{\mathcal{E}(\eta _\alpha )(s')}{\mathcal{E}(\eta _\alpha )(s)} \bigg |\mathcal{W}_s\right] \\&=\mathbb {E}_x\left[ \mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(s'')}{\mathcal{E}(\eta _\alpha )(s')}\bigg |\mathcal{W}_{s'}\right] \frac{\mathcal{E}(\eta _\alpha )(s')}{\mathcal{E}(\eta _\alpha )(s)} \bigg |\mathcal{W}_s\right] \\&=\mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(s')}{\mathcal{E}(\eta _\alpha )(s)} \bigg |\mathcal{W}_s\right] =1, \end{aligned}$$

and an induction argument gives

$$\begin{aligned} \mathbb {E}_x\left[ \mathcal{E}(\eta _\alpha )(\tau )\right] =\mathbb {E}_x\left[ \frac{\mathcal{E}(\eta _\alpha )(\tau )}{\mathcal{E}(\eta _\alpha )(0)}\bigg |\mathcal{W}_0\right] =1. \end{aligned}$$

Since $\tau >0$ is arbitrary, the proof is complete.$\square$

The previous lemma allows us to apply Girsanov theorem and to conclude that $\{w_\alpha (t)\}_{t\in [0,\tau ]}$ is a standard Wiener process under the law $\mathbb {Q}_{\alpha ,\nu }^\tau [\,\cdot \,]=\mathbb {E}_\nu [Z_\alpha (\tau )\,\cdot \,]$. This change of measure will be our main tool in the next section.

5.7.2 Completion of the Proof

From Eq. (3.35) and the results of the previous section we deduce that for $\alpha \in {\overline{\mathfrak {I}}}_c$,

$$\begin{aligned} e_t(\alpha )&=\frac{1}{t}\log \mathbb {E}_\mu \left[ \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x(t))\right) ^\alpha \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(x(0))\right) ^{-\alpha } \mathrm {e}^{-\alpha \mathfrak {S}^t} \right] \\&=\frac{1}{t}\log \mathbb {E}_\mu \left[ Z_\alpha (t) \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x(t))\right) ^\alpha \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(x(0))\right) ^{-\alpha } \mathrm {e}^{-\chi _\alpha (x(0))+\chi _\alpha (x(t))+e(\alpha )t} \right] \\&=e(\alpha )+\frac{1}{t}\log \mathbb {Q}_{\alpha ,\mu }^t\left[ \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x(t))\right) ^\alpha \left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(x(0))\right) ^{-\alpha } \mathrm {e}^{-\chi _\alpha (x(0))+\chi _\alpha (x(t))} \right] , \end{aligned}$$

where $\chi _\alpha (x)=\frac{1}{2} x\cdot X_\alpha x$. Denoting by $Q_\alpha ^t$ the Markov semigroup associated with Eq. (5.52), we can write

$$\begin{aligned} e_t(\alpha )=e(\alpha ) +\frac{1}{t}\log \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle , \end{aligned}$$

where

$$\begin{aligned} \eta _\alpha (x)=\left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(x)\right) ^{1-\alpha } \mathrm {e}^{-\chi _\alpha (x)},\qquad \xi _{\alpha }(x)=\left( \frac{\mathrm {d}\mu }{\mathrm {d}x}(\theta x)\right) ^{\alpha } \mathrm {e}^{\chi _\alpha (x)}. \end{aligned}$$

(5.54)

Thus, to prove Eq. (3.45) we must show that the “prefactor” $\langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle$ satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle =0. \end{aligned}$$

To this end, let us note that the Markov semigroup for (3.7) can be written as

$$\begin{aligned} (P^tf)(x)=\int _{\mathcal{X}}f(\mathrm {e}^{tA}x+M_t^\frac{1}{2} y)\mathrm{n}(\mathrm {d}y), \end{aligned}$$

(5.55)

where $\mathrm n$ denotes the centered Gaussian measure on $\mathcal{X}$ with covariance I. For $\alpha \in {\overline{\mathfrak {I}}}_c$, this yields the representation

$$\begin{aligned} (Q_\alpha ^tf)(x)=\det (2\pi M_{\alpha ,t})^{-\frac{1}{2}}\int \mathrm {e}^{-\frac{1}{2}|M_{\alpha ,t}^{-\frac{1}{2}}(y-\mathrm {e}^{tD_\alpha }x)|^2}f(y)\mathrm {d}y. \end{aligned}$$

(5.56)

Using Eq. (5.54), a simple calculation leads to

$$\begin{aligned} \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle&=\det (2\pi M_{\alpha ,t})^{-\frac{1}{2}}\det (2\pi M)^{-\frac{1}{2}} \int \mathrm {e}^{-\frac{1}{2}z\cdot N_{\alpha ,t}z} \mathrm {d}z\\&=\det (M_{\alpha ,t}^{-1})^{\frac{1}{2}}\det (M^{-1})^{\frac{1}{2}} \det (N_{\alpha ,t})^{-\frac{1}{2}}, \end{aligned}$$

provided

$$\begin{aligned} N_{\alpha ,t} =\left[ \begin{array}{lc} \theta (Y_{1-\alpha }+W_{1-\alpha }+\Delta _{1-\alpha ,t})\theta &{}-\mathrm {e}^{tD_\alpha ^*}M_{\alpha ,t}^{-1}\\ -M_{\alpha ,t}^{-1}\mathrm {e}^{tD_\alpha }&{} Y_\alpha +W_\alpha +\Delta _{\alpha ,t} \end{array}\right] \end{aligned}$$

is positive definite. By Schur’s complement formula, we have

$$\begin{aligned} \det (N_{\alpha ,t})=\det (Y_\alpha +W_\alpha +\Delta _{\alpha ,t}) \det (Y_{1-\alpha }+W_{1-\alpha }+\Delta _{1-\alpha ,t}-T_{\alpha ,t}), \end{aligned}$$

where

$$\begin{aligned} T_{\alpha ,t}=\theta \left( \mathrm {e}^{tD_\alpha ^*}M_{\alpha ,t}^{-\frac{1}{2}}\right) M_{\alpha ,t}^{-\frac{1}{2}} (Y_\alpha +W_\alpha +\Delta _{\alpha ,t})^{-1} M_{\alpha ,t}^{-\frac{1}{2}}\left( M_{\alpha ,t}^{-\frac{1}{2}}\mathrm {e}^{tD_\alpha }\right) \theta . \end{aligned}$$

It follows that

$$\begin{aligned} \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle= & {} \left( \det (M)\det (M_{\alpha ,t}) \det (Y_\alpha +W_\alpha +\Delta _{\alpha ,t})\right. \\&\left. \times \det (Y_{1-\alpha }+W_{1-\alpha } +\Delta _{1-\alpha ,t}-T_{\alpha ,t})\right) ^{-\frac{1}{2}}. \end{aligned}$$

For any $\alpha \in {\overline{\mathfrak {I}}}_c$, Proposition 5.5 implies that $Y_\alpha +W_\alpha >0$ while, as $t\rightarrow \infty$, $M_{\alpha ,t}^{-\frac{1}{2}}\searrow Y_\alpha ^\frac{1}{2}$, $\Delta _{\alpha ,t}\searrow 0$ and $\Vert M_{\alpha ,t}^{-\frac{1}{2}}\mathrm {e}^{tD_\alpha }\Vert \searrow 0$ monotonically (and exponentially fast for $\alpha \in \mathfrak {I}_c$ ). It follows that

$$\begin{aligned} f(\alpha )= \lim _{t\rightarrow \infty }\langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle =\left( \frac{\det (Y_\alpha )}{ \det (M) \det (Y_\alpha +W_\alpha ) \det (Y_{1-\alpha }+W_{1-\alpha })}\right) ^{\frac{1}{2}}. \end{aligned}$$

(5.57)

For $\alpha \in \mathfrak {I}_c$, $Y_\alpha >0$, and we conclude that

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle =0. \end{aligned}$$

(5.58)

Consider now the limiting cases $\alpha =\frac{1}{2}\pm \kappa _c$. We shall denote by C and r generic positive constants which may vary from one expression to the other. Since $Y_\alpha$ is singular, one has $\log \det (M_{\alpha ,t}^{-1})\rightarrow -\infty$. However, the obvious estimate $\Vert \mathrm {e}^{tD_\alpha }\Vert \le C(1+t)^r$ implies $M_{\alpha ,t}\le C(1+t)^r$ and hence $M_{\alpha ,t}^{-1}\ge C(1+t)^{-r}$ from which we conclude that

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \det (M_{\alpha ,t}^{-1})=0. \end{aligned}$$

(5.59)

It follows that (5.58) also holds in the limiting cases $\alpha =\frac{1}{2}\pm \kappa _c$.

By Hölder’s inequality ${\mathbb {R}}\ni \alpha \mapsto e_t(\alpha )$ is a convex function. The above analysis shows that it is a proper convex function differentiable on $\mathfrak {I}_c$ for any $t>0$, and such that $\lim _{t\rightarrow \infty }e_t(\alpha )=e(\alpha )$ for $\alpha \in \mathfrak {I}_c$. Since $\lim _{\alpha \uparrow \frac{1}{2}+\kappa _c}e'(\alpha )=+\infty$ by Theorem 3.13(3), the fact that

$$\begin{aligned} \lim _{t\rightarrow \infty }e_t(\alpha )=+\infty \end{aligned}$$

for $\alpha \in {\mathbb {R}}\setminus {\overline{\mathfrak {I}}}_c$ is a consequence of the following lemma and the symmetry (3.39).

Lemma 5.8

Let $(f_t)_{t>0}$ be a family of proper convex functions $f_t:{\mathbb {R}}\rightarrow ]-\infty ,\infty ]$ with the following properties:

• (1) For each $t>0$, $f_t$ is differentiable on ]a, b[.

• (2) The limit $f(\alpha )=\lim _{t\rightarrow \infty }f_t(\alpha )$ exists for $\alpha \in ]a,b[$ and is differentiable on ]a, b[.

• (3) $\lim _{\alpha \uparrow b}f'(\alpha )=+\infty$.

Then, for all $\alpha >b$, one has $\lim _{t\rightarrow \infty }f_t(\alpha )=+\infty$.

Proof

By convexity, for any $\gamma \in ]a,b[$ and any $\alpha \in {\mathbb {R}}$ one has

$$\begin{aligned} f_t(\alpha )\ge f_t(\gamma )+(\alpha -\gamma )f_t'(\gamma ), \end{aligned}$$

and Properties (1) and (2) further imply

$$\begin{aligned} \lim _{t\rightarrow \infty }f_t'(\gamma )=f'(\gamma ). \end{aligned}$$

It follows that

$$\begin{aligned} \liminf _{t\rightarrow \infty }f_t(\alpha )\ge f(\gamma )+(\alpha -\gamma )f'(\gamma ). \end{aligned}$$

(5.60)

As a limit of a family of convex functions, f is convex on ]a, b[ and, hence, $\inf _{\gamma \in ]a,b[}f(\gamma )>-\infty$. Thus, Property (3) and Inequality (5.60) yield

$$\begin{aligned} \liminf _{t\rightarrow \infty }f_t(\alpha )\ge \liminf _{\gamma \uparrow b} f(\gamma )+(\alpha -\gamma )f'(\gamma )=+\infty \quad \text{ for } \text{ all } \alpha >b. \end{aligned}$$

$\square$

5.8 Proof of Proposition 3.22

(1) The required properties of the function $g_t(\alpha )$ are consequences of more general results concerning integrals of exponentials of quadratic forms with respect to a Gaussian measure on an infinite-dimensional space. However, we shall derive here more detailed information about $g_t(\alpha )$ which will be used later (see the proof of Theorem 3.28).

We shall invoke Lemmata 5.2 and 5.3, and use the notations introduced in their proofs. By Proposition 3.5, we can write

$$\begin{aligned} g_t(\alpha )=\frac{1}{t}\log \int \mathrm {e}^{-\frac{\alpha }{2}(x|\mathcal{L}_t x)}\gamma _t(\mathrm {d}x), \end{aligned}$$

where $\gamma _t$ is the Gaussian measure on $\mathfrak {H}_t$ with mean $T_t a$ and covariance $\mathcal{K}_t=\mathcal{D}_t\mathcal{D}_t^*$. The convexity of $g_t$ is a consequence of Hölder’s inequality. The operator $\mathcal{L}_t$, given by

$$\begin{aligned} (\mathcal{L}_t x)(s)=-\Sigma _\beta x(s) +\delta (s-t)(F+X_1-\beta )x(t)-\delta (s)(G+\theta X_1\theta -\beta )x(0), \end{aligned}$$

(5.61)

maps $\mathfrak {H}_+$ to $\mathfrak {H}_-$ in such a way that $(x|\mathcal{L}_t y)=(\mathcal{L}_t x|y)$ for all $x,y\in \mathrm{Ran}\,\mathcal{D}_t$. It follows that the operator $\mathcal{S}_t=\mathcal{D}_t^*\mathcal{L}_t\mathcal{D}_t$ acting in the space $\Xi \oplus \partial \mathfrak {H}$ is self-adjoint, and a simple calculation shows that $\mathcal{S}_t-\mathcal{D}_t^*[\beta ,\Omega ]\mathcal{D}_t$ is finite rank, so that $\mathcal{S}_t$ is trace class. Using explicit formulas for Gaussian measures, we derive

$$\begin{aligned} g_t(\alpha )=-\frac{1}{2t}\log \det (I+\alpha \mathcal{S}_t) -\frac{\alpha }{2t}(T_ta|\mathcal{L}_tT_ta) +\frac{\alpha ^2}{2t}(\mathcal{D}_t^*\mathcal{L}_tT_ta|(I+\alpha \mathcal{S}_t)^{-1} \mathcal{D}_t^*\mathcal{L}_tT_ta) \end{aligned}$$

(5.62)

if $I+\alpha \mathcal{S}_t>0$, and $g_t(\alpha )=+\infty$ otherwise. Set $s_-(t)=\min \mathrm{sp}(\mathcal{S}_t)\le 0$, $s_+(t)=\max \mathrm{sp}(\mathcal{S}_t)\ge 0$, and

$$\begin{aligned} \alpha _-(t)=\left\{ \begin{array}{c@{\quad }l} -s_+(t)^{-1}&{}\text{ if } s_+(t)>0;\\ -\infty &{}\text{ if } s_+(t)=0; \end{array} \right. \qquad \alpha _+(t)=\left\{ \begin{array}{c@{\quad }l} -s_-(t)^{-1}&{}\text{ if } s_-(t)<0;\\ +\infty &{}\text{ if } s_-(t)=0; \end{array} \right. \end{aligned}$$

so that $I+\alpha \mathcal{S}_t>0$ iff $\alpha \in \mathfrak {I}_t=]\alpha _-(t),\alpha _+(t)[$. Analyticity of $g_t$ on $\mathfrak {I}_t$ follows from the Fredholm theory (e.g., see [70]), and a simple calculation yields

$$\begin{aligned} \begin{array}{ll} g_t'(\alpha )=&{}-\frac{1}{2t}\mathrm{tr}((I+\alpha \mathcal{S}_t)^{-1}\mathcal{S}_t) -\frac{1}{2t}(T_ta|\mathcal{L}_tT_ta)\\ &{}+\,\frac{\alpha }{2t}(\mathcal{D}_t^*\mathcal{L}_tT_ta| \left( (I+\alpha \mathcal{S}_t)^{-1}+(I+\alpha \mathcal{S}_t)^{-2}\right) \mathcal{D}_t^*\mathcal{L}_tT_ta). \end{array} \end{aligned}$$

(5.63)

Suppose $\alpha _+(t)<\infty$ and denote by $P_-$ the spectral projection of $\mathcal{S}_t$ associated to its minimal eigenvalue $s_-(t)<0$. By the previous formula, for any $\alpha \in [0,\alpha _+(t)[$ one has

$$\begin{aligned} g_t'(\alpha )\ge \frac{1}{2t}\frac{\mathrm{tr}(P_-)}{\alpha _+(t)-\alpha } -\frac{1}{2t}\mathrm{tr}((I+\alpha \mathcal{S}_t)^{-1}\mathcal{S}_t(I-P_-)) -\frac{1}{2t}(T_ta|\mathcal{L}_tT_ta), \end{aligned}$$

which implies that $g_t'(\alpha )\rightarrow +\infty$ as $\alpha \rightarrow \alpha _+(t)$. The analysis of the lower bound $\alpha _-(t)$ is similar.

(2) Is a simple consequence of the continuity and concavity of the maps

$$\begin{aligned}&{\overline{\mathfrak {I}}}_c\ni \alpha \mapsto F_\alpha =\theta X_{1-\alpha }\theta +\alpha (X_1+F),\\&{\overline{\mathfrak {I}}}_c\ni \alpha \mapsto G_\alpha =\widehat{N}+P_\nu (X_\alpha -\alpha (G+\theta X_1\theta ))|_{\mathrm{Ran}\,(N)}, \end{aligned}$$

and the fact that $F_0=\theta X_1\theta >0$ and $G_0=\widehat{N}+P_\nu X_1|_{\mathrm{Ran}\,N}>0$.

(3) If $X_1+F>0$ and $\widehat{N}+P_\nu (X_1-G-\theta X_1\theta )|_{\mathrm{Ran}\,N}>0$, then we also have $F_1>0$ and $G_1>0$ and the result is again a consequence of the concavity of $F_\alpha$ and $G_\alpha$.

(4) Proceeding as in the proof of Proposition 3.18, we start from the expression

$$\begin{aligned} g_t(\alpha ) =e(\alpha )+\frac{1}{t}\log \langle \eta _\alpha |Q_\alpha ^t\xi _\alpha \rangle , \end{aligned}$$

where

$$\begin{aligned} \eta _\alpha (\mathrm {d}x) =\mathrm {e}^{-\frac{1}{2} x\cdot (X_\alpha -\alpha (G+\theta X_1\theta ))x}\nu (\mathrm {d}x),\qquad \xi _\alpha (x)=\mathrm {e}^{-\frac{1}{2} x\cdot (-X_\alpha +\alpha (F+X_1))x}. \end{aligned}$$

Setting

$$\begin{aligned} C_{\alpha ,t}=\left[ \begin{array}{c@{\quad }c} G_\alpha +P_\nu \theta \Delta _{1-\alpha ,t}\theta |_{\mathrm{Ran}\,N} &{}-P_\nu \mathrm {e}^{tD_\alpha ^*}M_{\alpha ,t}^{-1}\\ -M_{\alpha ,t}^{-1}\mathrm {e}^{tD_\alpha }|_{\mathrm{Ran}\,N}&{} F_\alpha +\Delta _{\alpha ,t} \end{array}\right] , \end{aligned}$$

$$\begin{aligned} c_{\alpha ,t}=\tfrac{1}{2} a\cdot (X_\alpha -\alpha (G+\theta X_1\theta )+\theta \Delta _{1-\alpha ,t}\theta )a,\\ b_{\alpha ,t}=\left[ \begin{array}{c} P_\nu (X_\alpha -\alpha (G+\theta X_1\theta )+\theta \Delta _{1-\alpha ,t}\theta ) a\\ -M_{\alpha ,t}^{-1}\mathrm {e}^{tD_\alpha }a \end{array}\right] , \end{aligned}$$

evaluation of a Gaussian integral leads to

$$\begin{aligned} \langle \eta _\alpha |Q_\alpha ^t\xi _\alpha \rangle&=\det (2\pi \widehat{N}^{-1})^{-\frac{1}{2}}\det (2\pi M_{\alpha ,t})^{-\frac{1}{2}} \int _{\mathrm{Ran}\,(N)\oplus \Xi } \mathrm {e}^{-\frac{1}{2}z\cdot C_{\alpha ,t}z-z\cdot b_{\alpha ,t}-c_{\alpha ,t}} \mathrm {d}z\\&=\det (\widehat{N}^{\frac{1}{2}})\det (M_{\alpha ,t})^{-\frac{1}{2}} \det (C_{\alpha ,t})^{-\frac{1}{2}} \,\mathrm {e}^{\frac{1}{2}b_{\alpha ,t}\cdot C_{\alpha ,t}^{-1}b_{\alpha ,t} -c_{\alpha ,t}},\nonumber \end{aligned}$$

(5.64)

provided $C_{\alpha ,t}>0$. By Schur’s complement formula, the last condition is equivalent to

$$\begin{aligned} F_\alpha +\Delta _{\alpha ,t}>0,\qquad G_\alpha +P_\nu \theta \Delta _{1-\alpha ,t}\theta |_{\mathrm{Ran}\,N}-T_{\alpha ,t}>0, \end{aligned}$$

where

$$\begin{aligned} T_{\alpha ,t}=P_\nu \left( \mathrm {e}^{tD_\alpha ^*}M_{\alpha ,t}^{-\frac{1}{2}}\right) M_{\alpha ,t}^{-\frac{1}{2}} \left( F_\alpha +\Delta _{\alpha ,t}\right) ^{-1} M_{\alpha ,t}^{-\frac{1}{2}}\left( M_{\alpha ,t}^{-\frac{1}{2}}\mathrm {e}^{tD_\alpha }\right) \bigg |_{\mathrm{Ran}\,N}. \end{aligned}$$

Moreover, one has

$$\begin{aligned} \det (C_{\alpha ,t}) =\det (F_\alpha +\Delta _{\alpha ,t}) \det (G_\alpha +P_\nu \theta \Delta _{1-\alpha ,t}\theta |_{\mathrm{Ran}\,N}-T_{\alpha ,t}). \end{aligned}$$

For $\alpha \in \mathfrak {I}_\infty$, it follows from Proposition 5.5 that

$$\begin{aligned} \lim _{t\rightarrow \infty }T_{\alpha ,t}=0, \end{aligned}$$

and $F_\alpha +\Delta _{\alpha ,t}$ and $G_\alpha +P_\nu \theta \Delta _{1-\alpha ,t}\theta |_{\mathrm{Ran}\,N}-T_{\alpha ,t}$ are both positive definite for large t. As in the proof of Proposition 3.18 we can conclude that

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \langle \eta _\alpha |Q_\alpha ^t\xi _{\alpha }\rangle =0. \end{aligned}$$

(5) Suppose that $\alpha _+<\frac{1}{2}+\kappa _c$. If $\alpha \in ]\alpha _+,\frac{1}{2}+\kappa _c]$, then the matrix $C_{\alpha ,t}$ acquires a negative eigenvalue as t increases. Consequently, the integral in (5.64) diverges and $g_t(\alpha )=+\infty$ for large t, proving (3.62). The case $\alpha _->\frac{1}{2}-\kappa _c$ and $\alpha \in [\frac{1}{2}-\kappa _c,\alpha _-[$ is similar. Suppose now that $\alpha _+=\frac{1}{2}+\kappa _c$. Since $e'(\alpha )\rightarrow \infty$ as $\alpha \uparrow \frac{1}{2}+\kappa _c$ by Theorem 3.13(3), Lemma 5.8 applies to $g_t$ and yields (3.62) again. The same argument works in the case $\alpha _-=\frac{1}{2}-\kappa _c$.

Combined with Parts (1) and (4), the above analysis shows that for any $\alpha <\alpha _+$ one has $\alpha _+(t)\ge \alpha$ for large enough t while for any $\alpha >\alpha _+$, $\alpha _+(t)\le \alpha$ for large enough t. We deduce

$$\begin{aligned} \alpha _+\le \liminf _{t\rightarrow \infty }\alpha _+(t) \le \limsup _{t\rightarrow \infty }\alpha _+(t)\le \alpha _+, \end{aligned}$$

and (3.61) follows.$\square$

5.9 Proof of Theorem 3.28

We use the notation of Proposition 3.22 and its proof. We start with a few technical facts that will be used in the proof.

Lemma 5.9

Assume that Condition (C) holds and that $\mathrm{ep}>0$. Then, for some constants $c>0$ and $T>0$, the following hold true.

• (1) $\Vert \mathcal{S}_t\Vert \le c$ and $\Vert \mathcal{S}_t\Vert _1\le ct$ for $t\ge T$.

• (2) The function $g_t(\alpha )$ has an analytic continuation from $\mathfrak {I}_t$ to the cut plane ${\mathbb {C}}\setminus (]-\infty ,\alpha _-(t)]\cup [\alpha _+(t),\infty ])$. Moreover, for any compact subset $K\subset {\mathbb {C}}\setminus (]-\infty ,\alpha _-]\cup [\alpha _+,\infty ])$ there is $T_K>0$ such that

  $$\begin{aligned} \sup _{\begin{array}{c} \alpha \in K\\ t\ge T_K \end{array}}\left| g_t(\alpha )\right| <\infty . \end{aligned}$$

• (3) For $t\ge T$ the interval $\mathfrak {I}_t$ is finite and is mapped bijectively to ${\mathbb {R}}$ by the function $g_t'$. In the following, we set

  $$\begin{aligned} \alpha _{s,t}=(g_t^{\prime })^{-1}(s) \end{aligned}$$

  for $t\ge T$ and $s\in {\mathbb {R}}$.

• (4) Let

  $$\begin{aligned} s_\pm =\lim _{\mathfrak {I}_\infty \ni \alpha \rightarrow \alpha _\pm }e'(\alpha ), \end{aligned}$$

  and suppose that $s\in ]-\infty ,s_-]$ (resp. $s\in [s_+,+\infty [$). Then we have

  $$\begin{aligned} \lim _{t\rightarrow \infty }\alpha _{s,t}=\alpha _- \text{(resp. } \alpha _+\text{) }, \qquad \liminf _{t\rightarrow \infty }g_t(\alpha _{s,t})\ge e(\alpha _-) \text{(resp. } e(\alpha _+)\text{) }. \end{aligned}$$

  (5.65)

• (5) For $t\ge T$ and $s\in ]-\infty ,s_-]\cup [s_+,+\infty [$, let

  $$\begin{aligned} \mathfrak {M}_{s,t}=\frac{1}{t}\mathcal{S}_t(I+\alpha _{s,t}\mathcal{S}_t)^{-1},\qquad b_{s,t}=\frac{1}{t}(I+\alpha _{s,t}\mathcal{S}_t)^{-\frac{3}{4}}\mathcal{D}_t^*\mathcal{L}_t T_ta. \end{aligned}$$

  The operator $\mathfrak {M}_{s,t}$ is trace class on $\Xi \oplus \partial \mathfrak {H}$, with trace norm

  $$\begin{aligned} \Vert \mathfrak {M}_{s,t}\Vert _1\le c+|s|, \end{aligned}$$

  and $b_{s,t}\in \Xi \oplus \partial \mathfrak {H}$ is such that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\Vert b_{s,t}\Vert =0. \end{aligned}$$

Proof

• (1) Writing (5.61) as

  $$\begin{aligned} (\mathcal{L}_tx)(s)=L^{(1)}x(s)+\delta (s-t)L^{(2)}x(t)+\delta (s)L^{(3)}x(0) \end{aligned}$$

  with $L^{(j)}\in L(\Xi )$, we decompose $\mathcal{S}_t=\mathcal{D}_t^*\mathcal{L}_t\mathcal{D}_t=\mathcal{S}_t^{(1)}+\mathcal{S}_t^{(2)}+\mathcal{S}_t^{(3)}$. Lemma 5.3(4) yields

  $$\begin{aligned} \Vert \mathcal{S}_t^{(1)}\Vert \le \Vert L^{(1)}\Vert \,\Vert \mathcal{D}_t\Vert ^2=\Vert L^{(1)}\Vert \,\Vert \mathcal{K}_t\Vert \le c_1, \end{aligned}$$
  $$\begin{aligned} \Vert \mathcal{S}_t^{(1)}\Vert _1=\mathrm{tr}(\mathcal{D}_t^*|L^{(1)}|\mathcal{D}_t) \le \Vert L^{(1)}\Vert \mathrm{tr}(\mathcal{D}_t\mathcal{D}_t^*) =\Vert L^{(1)}\Vert \Vert \mathcal{K}_t\Vert _1\le c_1 t, \end{aligned}$$

  for $t\ge 0$. A simple calculation further gives $\mathcal{S}_t^{(2)}=\widetilde{\mathcal{D}}_t^*L^{(2)}\widetilde{\mathcal{D}}_t$, $\mathcal{S}_t^{(3)}=\widetilde{\mathcal{D}}_0^*L^{(3)}\widetilde{\mathcal{D}}_0$, where

  $$\begin{aligned} \widetilde{\mathcal{D}}_s=\left[ \begin{array}{cc} \mathrm {e}^{sA}N^{\frac{1}{2}}&R_sQ \end{array} \right] . \end{aligned}$$

  It follows from Lemma 5.2(3) that

  $$\begin{aligned} \Vert \mathcal{S}_t^{(2)}\Vert \le \Vert \mathcal{S}_t^{(2)}\Vert _1&=\mathrm{tr}(\widetilde{\mathcal{D}}_t^*|L^{(2)}|\widetilde{\mathcal{D}}_t) \le \Vert L^{(2)}\Vert \mathrm{tr}(\widetilde{\mathcal{D}}_t\widetilde{\mathcal{D}}_t^*)\\&=\Vert L^{(2)}\Vert \mathrm{tr}(\mathrm {e}^{tA}N\mathrm {e}^{tA^*}+R_tQQ^*R_t^*)\le c_2, \end{aligned}$$

  and

  $$\begin{aligned} \Vert \mathcal{S}_t^{(3)}\Vert \le \Vert \mathcal{S}_t^{(3)}\Vert _1=\mathrm{tr}(\widetilde{\mathcal{D}}_0^*|L^{(3)}|\widetilde{\mathcal{D}}_0) \le \Vert L^{(3)}\Vert \mathrm{tr}(\widetilde{\mathcal{D}}_0\widetilde{\mathcal{D}}_0^*) =\Vert L^{(3)}\Vert \mathrm{tr}(N)\le c_3, \end{aligned}$$

  for $t\ge 0$. We conclude that $\Vert \mathcal{S}_t\Vert \le c_1+c_2+c_3$ and $\Vert \mathcal{S}_t\Vert _1\le (c_1+c_2+c_3)t$ for $t\ge 1$.

• (2) Since $g_t(0)=0$ for all $t>0$, it suffices to show that the function $g_t'$ has the claimed properties. By definition,

  $$\begin{aligned} {\mathbb {C}}\setminus (]-\infty ,\alpha _-(t)]\cup [\alpha _+(t),\infty ]) \subset \{\alpha \in {\mathbb {C}}\,|\,-\alpha ^{-1}\not \in \mathrm{sp}(\mathcal{S}_t)\}, \end{aligned}$$

  (5.66)

  and the analyticity of $g'_t$ on this set follows directly from Eq. (5.63). Let $K\subset {\mathbb {C}}\setminus (]-\infty ,\alpha _-]\cup [\alpha _+,\infty ])$ be compact. By Proposition 3.22(5) and (6) there exists $T_K\ge T$ such that

  $$\begin{aligned} \mathrm{dist}(K,]-\infty ,\alpha _-(t)]\cup [\alpha _+(t),\infty ])\ge \delta >0 \end{aligned}$$

  (5.67)

  for all $t\ge T_K$. By Part (1), $\Vert \alpha \mathcal{S}_t\Vert \le \frac{1}{2}$ so that $\Vert (I+\alpha \mathcal{S}_t)^{-1}\Vert \le 2$ for all $t\ge T$ and all $\alpha \in {\mathbb {C}}$ satisfying $|\alpha |\le (2c)^{-1}$. By the spectral theorem, it follows from (5.66) and (5.67) that

  $$\begin{aligned} \Vert (I+\alpha \mathcal{S}_t)^{-1}\Vert \le \frac{2c}{\delta } \end{aligned}$$

  for all $t\ge T_K$ and all $\alpha \in K$ such that $|\alpha |\ge (2c)^{-1}$. Hence $\Vert (I+\alpha \mathcal{S}_t)^{-1}\Vert$ is bounded on K uniformly in $t\ge T_K$. The boundedness of $g'_t$ now easily follows from Eq. (5.63) and Part (1).

• (3) By Part (5) of Proposition 3.22, if $T>0$ is large enough then the interval $\mathfrak {I}_t$ is finite for all $t\ge T$. By Part (1) of the same Proposition, the function $g_t'$ is strictly increasing on $\mathfrak {I}_t$ and maps this interval onto ${\mathbb {R}}$.

• (4) We consider $s\ge s_+$, the case $s\le s_-$ is similar. Since $\alpha _{s,t}\in \mathfrak {I}_t$, Part (5) of Proposition 3.22 gives

  $$\begin{aligned} \underline{\alpha }= \liminf _{t\rightarrow \infty }\alpha _{s,t}\le \limsup _{t\rightarrow \infty }\alpha _{s,t}\le \lim _{t\rightarrow \infty }\alpha _+(t)=\alpha _+. \end{aligned}$$

  Suppose that $\underline{\alpha }<\alpha _+$. Invoking convexity, we deduce from the definition of $\alpha _{s,t}$ and Part (4) of Proposition 3.22

  $$\begin{aligned} s=\liminf _{t\rightarrow \infty }g_t'(\alpha _{s,t})\le \liminf _{t\rightarrow \infty }g_t'(\underline{\alpha })=e'(\underline{\alpha }). \end{aligned}$$

  The strict convexity of $e(\alpha )$ leads to $s\le e'(\underline{\alpha })<s_+$ which contradicts our hypothesis and yields the first relation in (5.65). To prove the second one, notice that for any $\gamma \in [0,\alpha _+[$ one has $\gamma <\alpha _{s,t}\le \alpha _+(t)$ provided t is large enough. By convexity

  $$\begin{aligned} g_t(\alpha _{s,t}) \ge g_t(\gamma )+(\alpha _{s,t}-\gamma )g_t'(\gamma ) \ge g_t(\gamma )+(\alpha _{s,t}-\gamma )g_t'(0), \end{aligned}$$

  and letting $t\rightarrow \infty$ yields

  $$\begin{aligned} \liminf _{t\rightarrow \infty }g_t(\alpha _{s,t})\ge e(\gamma )+(\alpha _+-\gamma )e'(0). \end{aligned}$$

  Taking $\gamma \rightarrow \alpha _+$ gives the desired inequality.

• (5) We consider $s\ge s_+$, the case $s\le s_-$ is again similar. By Part (3), if $T>0$ is large enough then $\alpha _{s,t}\in ]0,\alpha _+(t)[\subset \mathfrak {I}_t$ for all $t\ge T$. Since $I+\alpha \mathcal{S}_t>0$ for $\alpha \in \mathfrak {I}_t$, Part (1) allows us to conclude

  $$\begin{aligned} \Vert \mathfrak {M}_{s,t}^+\Vert _1=\frac{1}{t}\mathrm{tr}\left( \mathcal{S}_t^+(I+\alpha _{s,t}\mathcal{S}_t^+)^{-1}\right) \le \frac{1}{t}\Vert \mathcal{S}_t^+\Vert _1\le \frac{1}{t}\Vert \mathcal{S}_t\Vert _1\le c. \end{aligned}$$

  By Eq. (5.63) and the definition of $\alpha _{s,t}$ we have

  $$\begin{aligned} s&=-\frac{1}{2}\mathrm{tr}(\mathfrak {M}_{s,t})-\frac{1}{2t}a\cdot T_t^*\mathcal{L}_t T_ta\\&\quad +\frac{t\alpha _{s,t}}{2}\left( b_{s,t}\big | \left( (I+\alpha _{s,t}\mathcal{S}_t)^{\frac{1}{2}}+(I+\alpha _{s,t}\mathcal{S}_t)^{-\frac{1}{2}}\right) b_{s,t}\right) , \end{aligned}$$

  from which we deduce

  $$\begin{aligned} \Vert \mathfrak {M}_{s,t}^-\Vert _1&=s+\Vert \mathfrak {M}_{s,t}^+\Vert _1+\frac{1}{t}a\cdot T_t^*\mathcal{L}_t T_ta\nonumber \\&\quad -t\alpha _{s,t}\left( b_{s,t}\big | \left( (I+\alpha _{s,t}\mathcal{S}_t)^{\frac{1}{2}}+(I+\alpha _{s,t}\mathcal{S}_t)^{-\frac{1}{2}}\right) b_{s,t}\right) . \end{aligned}$$

  (5.68)

  One easily checks that

  $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\Vert T_t^*\mathcal{L}_t T_t\Vert =0, \end{aligned}$$

  so that $\Vert \mathfrak {M}_{s,t}^-\Vert _1\le s+2c$ and hence $\Vert \mathfrak {M}_{s,t}\Vert _1=\Vert \mathfrak {M}_{s,t}^-\Vert _1+\Vert \mathfrak {M}_{s,t}^+\Vert _1\le |s|+3c$ for t large enough. Finally, from (5.68) we derive

  $$\begin{aligned} \Vert b_{s,t}\Vert ^2&\le \frac{1}{2}\left( b_{s,t}\big | \left( (I+\alpha _{s,t}\mathcal{S}_t)^{\frac{1}{2}}+(I+\alpha _{s,t}\mathcal{S}_t)^{-\frac{1}{2}}\right) b_{s,t}\right) \\&\le \frac{1}{2t\alpha _{s,t}} \left( s+\frac{1}{2}\mathrm{tr}(\mathfrak {M}_{s,t})+\frac{1}{2t}a\cdot T_t^*\mathcal{L}_tT_ta \right) , \end{aligned}$$

  from which we conclude that $\Vert b_{s,t}\Vert \rightarrow 0$ as $t\rightarrow \infty$.

$\square$

(1) By Proposition 3.22(4) one has

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {E}_\nu [\mathrm {e}^{\alpha \eta _t}]=e(-\alpha ), \end{aligned}$$

for $-\alpha \in \mathfrak {I}_\infty$. By the Gärtner–Ellis theorem, the local LDP holds on the interval $]\eta _-,\eta _+[$ with the rate function

$$\begin{aligned} I(s)=\sup _{\alpha \in {\mathbb {R}}}(\alpha s-e(-\alpha )). \end{aligned}$$

Note that $I(s)=\sup _{\alpha \in \mathfrak {I}_\infty }(\alpha s-e(-\alpha ))$ for $s\in ]\eta _-,\eta _+[$. To prove that the global LDP holds we must show that for all open sets $O\subset {\mathbb {R}}$

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}_\nu \left[ \frac{\eta _t}{t}\in O\right] \ge -\inf _{s\in O}J(s). \end{aligned}$$

By a simple and well known argument (see, e.g., [17, Sect. V.2]), it suffices to show that for any $s\in {\mathbb {R}}$

$$\begin{aligned} \lim _{\epsilon \downarrow 0}\liminf _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}_\nu \left[ |\hat{\eta }_t|<\epsilon \right] \ge -J(s), \end{aligned}$$

where $\hat{\eta }_t=\frac{\eta _t}{t}-s$. The latter holds for any $s\in ]\eta _-,\eta _+[$ by the Gärtner–Ellis theorem. Next, we observe that whenever $\alpha _\pm =\frac{1}{2}\pm \kappa _c$, then by Proposition 3.22(4) we have $\eta _\pm =\pm \infty$. Thus, it suffices to consider the cases where $\alpha _->\frac{1}{2}-\kappa _c$ or/and $\alpha _+<\frac{1}{2}+\kappa _c$. We shall only discuss the second case, the analysis of the first one is similar.

Fix $s\le \eta _-$ and set $\alpha _t=-\alpha _{-s,t}$ so that $g'_t(-\alpha _t)=-s$ and, by Lemma 5.9(3),

$$\begin{aligned} \lim _{t\rightarrow \infty }\alpha _t=-\alpha _+,\qquad \liminf _{t\rightarrow \infty }g_t(-\alpha _t)\ge e(\alpha _+). \end{aligned}$$

(5.69)

Defining the tilted probability $\widehat{\mathbb {P}}_\nu ^t$ on $C([0,t],\Xi )$ by

$$\begin{aligned} \frac{\mathrm {d}\widehat{\mathbb {P}}^t_\nu }{\mathrm {d}\mathbb {P}_\nu ^t} =\mathrm {e}^{\alpha _t\eta _t-tg_t(-\alpha _t)}, \end{aligned}$$

we immediately get the estimate

$$\begin{aligned} \mathbb {P}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] \ge \mathrm {e}^{-t(s\alpha _t+\epsilon |\alpha _t|-g_t(-\alpha _t))} \widehat{\mathbb {P}}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] , \end{aligned}$$

and hence,

$$\begin{aligned} \frac{1}{t}\log \mathbb {P}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] \ge g_t(-\alpha _t)-s\alpha _t-\epsilon |\alpha _t| +\frac{1}{t}\log \widehat{\mathbb {P}}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] . \end{aligned}$$

(5.70)

We claim that for any sufficiently small $\epsilon >0$,

$$\begin{aligned} p_\epsilon =\liminf _{t\rightarrow \infty }\widehat{\mathbb {P}}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] >0. \end{aligned}$$

(5.71)

Using (5.69) we derive from (5.70) that

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] \ge e(\alpha _+)+s\alpha _+-\epsilon |\alpha _+|, \end{aligned}$$

provided $\epsilon >0$ is small enough. Letting $\epsilon \downarrow 0$, we finally get

$$\begin{aligned} \lim _{\epsilon \downarrow 0}\liminf _{t\rightarrow \infty }\frac{1}{t}\log \mathbb {P}_\nu ^t\left[ |\hat{\eta }_t|<\epsilon \right] \ge e(\alpha _+)+s\alpha _+, \end{aligned}$$

which, in view of (3.66), is the desired relation.

Thus, it remains to prove our claim (5.71). To this end, note that for $\lambda \in {\mathbb {R}}$,

$$\begin{aligned} \widehat{\mathbb {E}}_\nu ^t\left[ \mathrm {e}^{-\mathrm {i}\lambda \hat{\eta }_t}\right] =\mathbb {E}_\nu ^t\left[ \mathrm {e}^{(\alpha _t-\mathrm {i}\lambda /t)\eta _t-tg_t(-\alpha _t) -\mathrm {i}\lambda g_t'(-\alpha _t)}\right] =\mathrm {e}^{t(g_t(-\alpha _t+\mathrm {i}\lambda /t)-g_t(-\alpha _t) -\mathrm {i}g_t'(-\alpha _t)\lambda /t)}, \end{aligned}$$

and a simple calculation using Eq. (5.62), (5.63) yields

$$\begin{aligned} \widehat{\mathbb {E}}_\nu ^t\left[ \mathrm {e}^{-\mathrm {i}\lambda \hat{\eta }_t}\right] =\left( \det (I+\mathrm {i}\lambda \mathfrak {M}_{-s,t})^{-1} \mathrm {e}^{\mathrm {i}\lambda \mathrm{tr}(\mathfrak {M}_{-s,t}) -\lambda ^2(b_{-s,t}|(I+\mathrm {i}\lambda \mathfrak {M}_{-s,t})^{-1}b_{-s,t})}\right) ^{\frac{1}{2}}. \end{aligned}$$

(5.72)

Let $\mathcal{S}({\mathbb {R}},\Xi )$ be the Schwartz space of rapidly decaying $\Xi$-valued smooth functions on ${\mathbb {R}}$ and $\mathcal{S}'({\mathbb {R}},\Xi )$ its dual w.r.t. the inner product of $\mathfrak {H}$. Denote by $\hat{\gamma }$ the centered Gaussian measure on $\mathcal{K}_-=\Xi \oplus \mathcal{S}'({\mathbb {R}},\Xi )$ with covariance I and let

$$\begin{aligned} \widetilde{\eta }_t(k)=-\frac{1}{2}(k|\mathfrak {M}_{-s,t}k-2b_{-s,t}). \end{aligned}$$

By Lemma 5.9(5), $|\hat{\eta }_t(k)|<\infty$ for $\hat{\gamma }$-a.e. $k\in \mathcal{K}_-$ and

$$\begin{aligned} {\overline{\eta }}_t= \int \widetilde{\eta }_t(k)\hat{\gamma }(\mathrm {d}k)=-\frac{1}{2}\mathrm{tr}(\mathfrak {M}_{-s,t}). \end{aligned}$$

It follows that for $\lambda \in {\mathbb {R}}$,

$$\begin{aligned} \int \mathrm {e}^{-\mathrm {i}\lambda (\hat{\eta }_t(k)-{\overline{\eta }}_t)}\hat{\gamma }(\mathrm {d}k) =\left( \det (I+\mathrm {i}\lambda \mathfrak {M}_{-s,t})^{-1} \mathrm {e}^{\mathrm {i}\lambda \mathrm{tr}(\mathfrak {M}_{-s,t}) -\lambda ^2(b_{-s,t}|(I+\mathrm {i}\lambda \mathfrak {M}_{-s,t})^{-1}b_{-s,t})} \right) ^{\frac{1}{2}}, \end{aligned}$$

and comparison with (5.72) allows us to conclude that the law of $\hat{\eta }_t$ under $\widehat{\mathbb {P}}_\nu ^t$ coincides with the one of $\widetilde{\eta }_t-{\overline{\eta }}_t$ under $\hat{\gamma }$, so that

$$\begin{aligned} p_\epsilon =\liminf _{t\rightarrow \infty }\hat{\gamma } \left[ |\widetilde{\eta }_t-{\overline{\eta }}_t| <\epsilon \right] . \end{aligned}$$

For $m>0$ let $P_m$ denote the spectral projection of $\mathfrak {M}_{s,t}$ for the interval $[-m,m]$ and define

$$\begin{aligned} \zeta _t^<(k)&=-\frac{1}{2}(P_m k|\mathfrak {M}_{-s,t}k-2b_{-s,t}) +\frac{1}{2}\mathrm{tr}(P_m\mathfrak {M}_{-s,t}),\\ \zeta _t^>(k)&=-\frac{1}{2}((I-P_m) k|\mathfrak {M}_{-s,t}k-2b_{-s,t}) +\frac{1}{2}\mathrm{tr}((I-P_m)\mathfrak {M}_{-s,t}), \end{aligned}$$

so that $\widetilde{\eta }_t-{\overline{\eta }}_t=\zeta _t^<+\zeta _t^>$ and $\hat{\gamma }[\zeta _t^<]=\hat{\gamma }[\zeta _t^>]=0$. Since $\zeta _t^<$ and $\zeta _t^>$ are independent under $\hat{\gamma }$, we have

$$\begin{aligned} p_\epsilon \ge \liminf _{t\rightarrow \infty } \hat{\gamma }\left[ |\zeta _t^<|<\epsilon /2\right] \hat{\gamma }\left[ |\zeta _t^>|<\epsilon /2\right] . \end{aligned}$$

(5.73)

The Chebyshev inequality gives

$$\begin{aligned} \hat{\gamma }\left[ |\zeta _t^<|<\epsilon /2\right] =1-\hat{\gamma }\left[ |\zeta _t^<|\ge \epsilon /2\right] \ge 1-\frac{4}{\epsilon ^2}\hat{\gamma }\left[ |\zeta _t^<|^2\right] . \end{aligned}$$

Choosing $m=\frac{1}{3}(c+|s|)\epsilon ^2$, the estimate

$$\begin{aligned} \hat{\gamma }\left[ |\zeta _t^<|^2\right]&=\frac{1}{2}\mathrm{tr}(P_m\mathfrak {M}_{s,t}^2)+\Vert P_mb_{s,t}\Vert ^2\\&\le \frac{1}{2}\Vert P_m\mathfrak {M}_{s,t}\Vert \,\Vert \mathfrak {M}_{s,t}\Vert _1+\Vert b_{s,t}\Vert ^2 \le \frac{m}{2}(c+|s|)+\Vert b_{s,t}\Vert ^2, \end{aligned}$$

together with Lemma 5.9(5) shows that

$$\begin{aligned} \liminf _{t\rightarrow \infty }\hat{\gamma }\left[ |\zeta _t^<|<\epsilon /2\right] \ge 1-\frac{2m}{(c+|s|)\epsilon ^2}=\frac{1}{3}. \end{aligned}$$

To deal with the second factor on the right-hand side of (5.73) we first note that $(I-P_m)|\mathfrak {M}_{s,t}|\ge m(I-P_m)$, so that, using again Lemma 5.9(5),

$$\begin{aligned} N_m=\mathrm{tr}(I-P_m)\le \frac{1}{m}\mathrm{tr}((I-P_m)|\mathfrak {M}_{s,t}|)\le \frac{\Vert \mathfrak {M}_{s,t}\Vert _1}{m} \le \frac{c+|s|}{m}=\frac{3}{\epsilon ^2}. \end{aligned}$$

Setting

$$\begin{aligned} \epsilon _j=\frac{|\mu _j|}{c+|s|}\epsilon ,\qquad (j=1,\ldots ,N_m), \end{aligned}$$

where the $\mu _j$ denote the repeated eigenvalues of $(I-P_m)\mathfrak {M}_{s,t}$ we have $\sum _j\epsilon _j\le \epsilon$ and hence, passing to an orthonormal basis of eigenvectors of $(I-P_m)\mathfrak {M}_{s,t}$, we obtain

$$\begin{aligned} \hat{\gamma }\left[ |\zeta _t^>|<\epsilon /2\right]&=\mathrm{n}_{N_m}\left[ \left| \sum _{j=1}^{N_m}\mu _jk_j^2-2b_jk_j-\mu _j\right|<\epsilon \right] \\&\ge \prod _{j=1}^{N_m}\mathrm{n}_1\left[ \left| k^2-2\frac{b_j}{\mu _j}k-1\right| <\frac{\epsilon _j}{|\mu _j|}\right] , \end{aligned}$$

where $\mathrm{n}_N$ denotes the centered Gaussian measure of unit covariance on ${\mathbb {R}}^N$ and the $b_j\in {\mathbb {R}}$ are such that $|b_j|\le \Vert b_{s,t}\Vert$. An elementary analysis shows that if $|b|\le 1$ and $0<\delta \le 1$, then

$$\begin{aligned} \mathrm{n}_1\left[ |k^2-2bk-1|<\delta \right] \ge \frac{\delta }{\mathrm {e}\sqrt{6\pi }}. \end{aligned}$$

Thus, provided $\epsilon <c+|s|$, we can conclude that

$$\begin{aligned} \liminf _{t\rightarrow \infty }\hat{\gamma }\left[ |\zeta _t^>|<\epsilon /2\right] \ge \left( \frac{\epsilon }{\mathrm {e}(c+|s|)\sqrt{6\pi }}\right) ^{3\epsilon ^{-2}}>0, \end{aligned}$$

which shows that $p_\epsilon >0$ and concludes the proof of Part (2).

(2) According to Bryc’s lemma (see [7] or [39, Sect. 4.8.4]) the Central Limit Theorem for the family $(\eta _t)_{t>0}$ holds, provided that the generating function $g_t$ has an analytic continuation to the disc $D_\epsilon =\{\alpha \in {\mathbb {C}}\,|\,|\alpha |<\epsilon \}$ for some $\epsilon >0$ and satisfies the estimate

$$\begin{aligned} \sup _{\begin{array}{c} \alpha \in D_\epsilon \\ t>t_0 \end{array}}|g_t(\alpha )|<\infty , \end{aligned}$$

for some $t_0>0$. These properties clearly follow from Lemma 5.9 (2).

5.10 Proof of Lemma 4.1

(1) Let

$$\begin{aligned} \mathcal{C}=\bigvee _{j\ge 0}\mathrm{Ran}\,(\omega ^*\omega )^{j}\iota \end{aligned}$$

be the controllable subspace of $(\omega ^*\omega ,\iota )$. From (3.1) and (3.4) we derive

$$\begin{aligned} \Omega ^{2j} Q=(-1)^j\left[ \begin{array}{c} (\omega ^*\omega )^{j}\iota \\ 0 \end{array}\right] \vartheta ^\frac{1}{2}, \end{aligned}$$

and hence

$$\begin{aligned} \bigvee _{j\ge 0}\mathrm{Ran}\,(\Omega ^{2j} Q)=\mathcal{C}\oplus \{0\}. \end{aligned}$$

The last relation and $\Omega (\mathcal{C}\oplus \{0\})=\{0\}\oplus \omega ^*\mathcal{C}$ yield that the controllable subspace of $(\Omega ,Q)$ is $\mathcal{C}\oplus \omega ^*\mathcal{C}$. Since $A=\Omega -\frac{1}{2} Q\vartheta ^{-1}Q^*$, (A, Q) has the same controllable subspace. Finally, since $\mathrm{Ker}\,\omega =\{0\}$, we conclude that $\mathcal{C}\oplus \omega ^*\mathcal{C}=\Xi$ iff $\mathcal{C}={\mathbb {R}}^\mathcal{I}$.

(2) The same argument yields $\mathcal{C}(\Omega ,Q\pi _i)=\mathcal{C}_i\oplus \omega ^*\mathcal{C}_i$. Thus if $0\not =u\in \mathcal{C}_i\cap \mathcal{C}_j$, we have $0\not =u\oplus 0\in \mathcal{C}(\Omega ,Q\pi _i)\cap \mathcal{C}(\Omega ,Q\pi _j)$ and the result follows from Proposition 3.7 (2).

5.11 Proof of Theorem 4.2

(1) By assumption (J), the Jacobi matrix

$$\begin{aligned} \omega ^2=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} b_1&{}a_1&{}0&{}0&{}\cdots &{}0&{}0\\ a_1&{}b_2&{}a_2&{}0&{}&{}0&{}0\\ 0&{}a_2&{}b_3&{}a_3&{}&{}0&{}0\\ \vdots &{}&{}\ddots &{}\ddots &{}\ddots &{}&{}\vdots \\ 0&{}0&{}0&{}\ddots &{}\ddots &{}a_{L-2}&{}0\\ 0&{}0&{}0&{}0&{}\ddots &{}b_{L-1}&{}a_{L-1}\\ 0&{}0&{}0&{}0&{}\cdots &{}a_{L-1}&{}b_L \end{array}\right] , \end{aligned}$$

is positive and $a_i\not =0$ for all $i\in \mathcal{I}$. Denote by $\{\delta _i\}_{i\in \mathcal{I}}$ the canonical basis of ${\mathbb {R}}^\mathcal{I}$. Starting with the obvious fact that $\mathrm{Ran}\,(\iota )=\mathrm {span}(\{\delta _i\,|\,i\in \partial \mathcal{I}\})$, a simple induction yields

$$\begin{aligned} \bigvee _{0\le j\le k}\mathrm{Ran}\,(\omega ^{2j}\iota ) =\mathrm {span}(\{\delta _i\,|\,\mathrm{dist}(i,\partial \mathcal{I})\le k\}). \end{aligned}$$

Hence the pair $(\omega ^2,\iota )$ is controllable.

(2) The argument in the proof of Part (1) yields $\mathcal{C}_1=\mathcal{C}_L={\mathbb {R}}^\mathcal{I}$ and the first statement follows directly from Proposition 3.7(2). To prove the second one, we may assume that $\vartheta _{\mathrm {min}}=\vartheta _1$ and $\vartheta _{\mathrm {max}}=\vartheta _L$. From Theorem 3.2(3) we already know that $\vartheta _1\le M\le \vartheta _L$ and that

$$\begin{aligned} M-\vartheta _1=\vartheta _1\int _0^\infty \mathrm {e}^{tA}Q (\vartheta _1^{-1}-\vartheta ^{-1})Q^*\mathrm {e}^{tA^*}\mathrm {d}t. \end{aligned}$$

Since $\vartheta _1^{-1}-\vartheta ^{-1}\ge 0$ it follows that

$$\begin{aligned} \mathrm{Ker}\,(M-\vartheta _1)\subset \bigcap _{n\ge 0}\mathrm{Ker}\,(\vartheta _1^{-1}-\vartheta ^{-1})Q^*A^{*n} =\left( \bigvee _{n\ge 0}A^nQ\delta _1\right) ^\perp =\mathcal{C}_1^\perp =\{0\}, \end{aligned}$$

which implies $M-\vartheta _1>0$. A similar argument shows that $\vartheta _2-M>0$.

(3) Set $\kappa =\alpha -\frac{1}{2}$ and $\kappa _0=\frac{{\overline{\vartheta }}}{\Delta }>\frac{1}{2}$. Writing

$$\begin{aligned} \mathrm {i}\nu -K_\alpha= & {} \left[ \begin{array}{c@{\quad }c} \Omega +\mathrm {i}\nu &{}0\\ 0&{}\Omega +\mathrm {i}\nu \end{array}\right] +\left[ \begin{array}{c@{\quad }c} Q\vartheta ^{-\frac{1}{2}}&{}0\\ 0&{}Q\vartheta ^{-\frac{1}{2}} \end{array}\right] \left[ \begin{array}{c@{\quad }c} \kappa &{}-\vartheta \\ (\kappa ^2-\frac{1}{4})\vartheta ^{-1}&{}-\kappa \end{array}\right] \\&\times \left[ \begin{array}{c@{\quad }c} \vartheta ^{-\frac{1}{2}}Q^*&{}0\\ 0&{}\vartheta ^{-\frac{1}{2}}Q^*\end{array}\right] , \end{aligned}$$

one derives $\det (\mathrm {i}\nu -K_\alpha )=\det (\Omega +\mathrm {i}\nu )^2\det (I+\Sigma (\mathrm {i}\nu ))$, where

$$\begin{aligned} \Sigma (z)=\left[ \begin{array}{c@{\quad }c} \kappa R(z)&{}-R(z)\vartheta \\ (\kappa ^2-\frac{1}{4})R(z)\vartheta ^{-1}&{}-\kappa R(z) \end{array}\right] ,\qquad R(z)=\vartheta ^{-\frac{1}{2}}Q^*(\Omega +z)^{-1}Q\vartheta ^{-\frac{1}{2}}. \end{aligned}$$

(5.74)

A simple calculation further gives

$$\begin{aligned} \det (\Omega +\mathrm {i}\nu )=\det (\omega ^2-\nu ^2),\qquad R(\mathrm {i}\nu )=\mathrm {i}\nu \iota ^*(\omega ^2-\nu ^2)^{-1}\iota . \end{aligned}$$

Denote by $D(\nu ^2)$ the adjugate of $\omega ^2-\nu ^2$. Expressing $(\omega ^2-\nu ^2)^{-1}$ with Cramer’s formula and observing that $D_{1L}(\nu ^2)=D_{L1}(\nu ^2)={\hat{a}}$, we get

$$\begin{aligned} R(\mathrm {i}\nu )=\frac{2{\overline{\gamma }}\mathrm {i}\nu }{d(\nu ^2)}\left[ \begin{array}{c@{\quad }c} b(\nu ^2)\mathrm {e}^{\frac{1}{2}\delta }&{}{\hat{a}}\\ {\hat{a}}&{}c(\nu ^2)\mathrm {e}^{-\frac{1}{2}\delta } \end{array}\right] , \end{aligned}$$

(5.75)

where

$$\begin{aligned} b(\nu ^2)=D_{11}(\nu ^2),\qquad c(\nu ^2)=D_{LL}(\nu ^2),\qquad d(\nu ^2)=\det (\omega ^2-\nu ^2), \end{aligned}$$

are polynomials in $\nu ^2$ with real coefficients. Inserting (5.75) into (5.74), an explicit calculation of $\det (I+\Sigma (\mathrm {i}\nu ))$ yields

$$\begin{aligned} \det (\mathrm {i}\nu -K_\alpha )&= \left( d(\nu ^2)+({\overline{\gamma }}\nu )^2\frac{b(\nu ^2)c(\nu ^2)-{\hat{a}}^2}{d(\nu ^2)}\right) ^2 \\&\quad +({\overline{\gamma }}\nu )^2\left( \mathrm {e}^{\delta /2}b(\nu ^2)-\mathrm {e}^{-\delta /2}c(\nu ^2)\right) ^2 -4{\hat{a}}^2\frac{\kappa ^2-\kappa _0^2}{\kappa _0^2-\frac{1}{4}}({\overline{\gamma }}\nu )^2. \end{aligned}$$

By the Desnanot–Jacobi identity,

$$\begin{aligned} \frac{b(\nu ^2)c(\nu ^2)-{\hat{a}}^2}{d(\nu ^2)}=\det (\widetilde{\omega ^2}-\nu ^2) ={\tilde{d}}(\nu ^2), \end{aligned}$$

where $\widetilde{\omega ^2}$ is the matrix obtained from $\omega ^2$ by deleting its first and last rows and columns. Thus, we finally obtain

$$\begin{aligned} \det (\mathrm {i}\nu -K_\alpha )&= \left( d(\nu ^2)+({\overline{\gamma }}\nu )^2{\tilde{d}}(\nu ^2)\right) ^2 +({\overline{\gamma }}\nu )^2 \left( \mathrm {e}^{\delta /2}b(\nu ^2)-\mathrm {e}^{-\delta /2}c(\nu ^2)\right) ^2\\&\quad -4{\hat{a}}^2\frac{\kappa ^2-\kappa _0^2}{\kappa _0^2-\frac{1}{4}}({\overline{\gamma }}\nu )^2, \end{aligned}$$

where b, c, d and ${\tilde{d}}$ are polynomials with real coefficients. Since $d(0)=\det (\omega ^2)>0$, $K_\alpha$ is regular for all $\alpha \in {\mathbb {R}}$ and we can rewrite the eigenvalue equation as

$$\begin{aligned} g(\nu ^2)=\frac{\kappa ^2-\kappa _0^2}{\kappa _0^2-\frac{1}{4}}, \end{aligned}$$

(5.76)

where the rational function

$$\begin{aligned} g(x)=\frac{1}{4{\hat{a}}^2}\left[ \frac{(d(x)+{\overline{\gamma }}^2x{\tilde{d}}(x))^2}{{\overline{\gamma }}^2x} +\left( \mathrm {e}^{\delta /2}b(x)-\mathrm {e}^{-\delta /2}c(x)\right) ^2\right] \end{aligned}$$

has real coefficients, a simple pole at 0, a pole of order 2L at infinity and is non-negative on $]0,\infty [$. It follows that

$$\begin{aligned} \kappa _c=\sqrt{\kappa _0^2+g_0(\kappa _0^2-\frac{1}{4})}, \end{aligned}$$

where

$$\begin{aligned} g_0=\min _{x\in ]0,\infty [}g(x). \end{aligned}$$

Since $\kappa _0>\frac{1}{2}$, we conclude that $\kappa _c\ge \kappa _0$, with equality iff $g_0=0$.

Under Assumption (S) the polynomials b and c coincide and $\delta =0$. Thus, $g_0=0$ iff the polynomial

$$\begin{aligned} f(x)=d(x)+{\overline{\gamma }}^2x{\tilde{d}}(x) \end{aligned}$$

(5.77)

has a positive zero. If L is odd, then this property follows immediately from the fact that

$$\begin{aligned} f(0)=\det (\omega ^2)>0,\qquad f(x)=(-x)^L+\mathcal {O}(x^{L-1})<0\quad (x\rightarrow \infty ). \end{aligned}$$

A more elaborate argument is needed in the case of even L. We shall invoke the deep connection between spectral analysis of Jacobi matrices and orthogonal polynomials. We refer the reader to [71] for a detailed introduction to this vast subject.

Let $\rho$ be the spectral measure of $\omega ^2$ for the vector $\delta _1$. The argument in the proof of Part (1) shows that $\delta _1$ is cyclic for $\omega ^2$. Thus, $\omega ^2$ is unitarily equivalent to multiplication by x on $L^2({\mathbb {R}},\rho (\mathrm {d}x))$ and in this Hilbert space $\delta _1$ is represented by the constant polynomial $p_0=1$. Starting with $\delta _2=a_1^{-1}(\omega ^2-b_1)\delta _1=p_1(\omega ^2)\delta _1$, a simple induction shows that there are real polynomials $\{p_k\}_{k\in \{0,\ldots ,L-1\}}$ satisfying the recursion

$$\begin{aligned} a_kp_{k-1}(x)+(b_{k+1}-x)p_k(x)+a_{k+1}p_{k+1}(x)=0, \quad (k\in \{0,\ldots ,L-2\},p_{-1}=0,p_0=1), \end{aligned}$$

(5.78)

and such that $\delta _k=p_{k-1}(\omega ^2)\delta _1$. Thus, these polynomials form an orthonormal basis of $L^2({\mathbb {R}},\rho (\mathrm {d}x))$ such that

$$\begin{aligned} \langle \delta _k|(\omega ^2-x)^{-1}\delta _j\rangle =\int \frac{p_{k-1}(\lambda )p_{j-1}(\lambda )}{\lambda -x}\rho (\mathrm {d}\lambda ). \end{aligned}$$

(5.79)

For $1\le j\le k\le L$, define

$$\begin{aligned} d_{[j,k]}(x)=\det (x-J_{[j,k]}),\qquad J_{[j,k]}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} b_j&{}a_j&{}0&{}0&{}\cdots &{}0&{}0\\ a_j&{}b_{j+1}&{}a_{j+1}&{}0&{}&{}0&{}0\\ 0&{}a_{j+1}&{}b_{j+2}&{}a_{j+2}&{}&{}0&{}0\\ \vdots &{}&{}\ddots &{}\ddots &{}\ddots &{}&{}\vdots \\ 0&{}0&{}0&{}\ddots &{}\ddots &{}a_{k-2}&{}0\\ 0&{}0&{}0&{}0&{}\ddots &{}b_{k-1}&{}a_{k-1}\\ 0&{}0&{}0&{}0&{}\cdots &{}a_{k-1}&{}b_k \end{array}\right] . \end{aligned}$$

Laplace expansion of the determinant $P_{k+1}(x)=d_{[1,k+1]}(x)$ on its last row yields the recursion

$$\begin{aligned} P_{k+1}(x)=(x-b_{k+1})P_k(x)-a_k^2P_{k-1}(x). \end{aligned}$$

Comparing this relation with (5.78) one easily deduces

$$\begin{aligned} a_1\cdots a_k\, p_k(x)=P_k(x),\quad (k\in \{1,\ldots ,L-1\}), \qquad d(x)=P_L(x). \end{aligned}$$

(5.80)

Polynomials of the second kind $\{q_k\}_{k\in \{0,\ldots L-1\}}$ associated to the measure $\rho$ are defined by

$$\begin{aligned} q_k(x)=\int \frac{p_k(\lambda )-p_k(x)}{\lambda -x}\rho (\mathrm {d}x). \end{aligned}$$

(5.81)

Note in particular that $q_0(x)=0$ and $q_1(x)=a_1^{-1}$. Applying the recursion relation (5.78) to both sides of this definition, we obtain

$$\begin{aligned} a_kq_{k-1}(x)\!+\!(b_{k+1}-x)q_k(x)+a_{k+1}q_{k+1}(x) \!=\!\int p_k(\lambda )\rho (\mathrm {d}\lambda )=0,\quad (k\in \{1,\ldots ,L-2\}). \end{aligned}$$

Set ${\tilde{q}}_k(x)=a_1q_{k+1}(x)$ and observe that these polynomials satisfy the recursion

$$\begin{aligned}&a_{k+1}{\tilde{q}}_{k-1}(x)+(b_{k+2}-x){\tilde{q}}_k(x)+a_{k+2}{\tilde{q}}_{k+1}(x)=0,\\&\quad (k\in \{0,\ldots ,L-3\},{\tilde{q}}_{-1}=0,{\tilde{q}}_0=1). \end{aligned}$$

Comparing this Cauchy problem with (5.78) and repeating the argument leading to (5.80) we deduce that $a_2\cdots a_{k+1}\,{\tilde{q}}_k(x)=d_{[2,k+1]}(x)$, so that

$$\begin{aligned} a_1\cdots a_k\,q_k(x)=d_{[2,k]}(x),\qquad (k\in \{2,\ldots ,L-1\}). \end{aligned}$$

In particular, we can rewrite Definition (5.77) as

$$\begin{aligned} f(x)=P_L(x)+{\overline{\gamma }}^2xq_{L-1}(x). \end{aligned}$$

(5.82)

Taking now Assumption (S) into account we derive from (5.79) that for any $z\in {\mathbb {C}}\setminus \mathrm{sp}(\omega ^2)$,

$$\begin{aligned} \int \frac{|p_{L-1}(\lambda )|^2}{\lambda -z}\rho (\mathrm {d}\lambda )&=\langle \delta _L|(\omega ^2-z)^{-1}\delta _L\rangle =\langle \mathcal{S}\delta _1|(\omega ^2-z)^{-1}\mathcal{S}\delta _1\rangle \\&=\langle \delta _1|(\omega ^2-z)^{-1}\delta _1\rangle =\int \frac{\rho (\mathrm {d}\lambda )}{\lambda -z}, \end{aligned}$$

from which we conclude that $|p_{L-1}(\lambda )|=1$ for all $\lambda \in \mathrm{sp}(\omega ^2)$. Denote by $\lambda _L\ge \lambda _{L-1}\ge \cdots \ge \lambda _1$ the eigenvalues of $\omega ^2=J_{[1,L]}$ and by $\mu _{L-1}\ge \mu _{L-2}\ge \cdots \ge \mu _1$ that of $J_{[1,L-1]}$. It is a well known property of Jacobi matrices (or equivalently of orthogonal polynomials) that

$$\begin{aligned} \lambda _L<\mu _{L-1}<\lambda _{L-1}<\cdots<\mu _{1}<\lambda _1 \end{aligned}$$

(see Fig. 12). These interlacing inequalities and the previously established property allow us to conclude that

$$\begin{aligned} p_{L-1}(\lambda _j)=(-1)^j,\qquad p_{L-1}'(\lambda _1)<0. \end{aligned}$$

Fig. 12

The zeros of the polynomials $P_L$ and $p_{L-1}$ interlace

From Eq. (5.82) and Definition (5.81), we deduce

$$\begin{aligned} f(\lambda _1)&={\overline{\gamma }}^2\lambda _1\left( p_{L-1}'(\lambda _1)\rho (\{\lambda _1\}) +\sum _{j=2}^{L-1} \frac{p_{L-1}(\lambda _1)-p_{L-1}(\lambda _j)}{\lambda _1-\lambda _j} \rho (\{\lambda _j\}) \right) \\&={\overline{\gamma }}^2\lambda _1\left( p_{L-1}'(\lambda _1)\rho (\{\lambda _1\}) -2\sum _{j=1}^{\frac{1}{2} L-1} \frac{\rho (\{\lambda _{2j}\})}{\lambda _1-\lambda _{2j}} \right) <0, \end{aligned}$$

which, together with $f(0)>0$, shows that f has a positive root.

By Proposition 5.5(12), the validity of Condition (R) follows from Part (2) and the fact that $\kappa _c=\kappa _0$.

Appendix: Basic Theory of the Algebraic Riccati Equation

In this appendix, for the reader convenience we briefly expose the basic results on algebraic Riccati equation used in this work. We refer the reader to [2, 46, 68] for detailed expositions and proofs.

Let $\mathfrak {h}$ be a d-dimensional complex Hilbert space. We denote by $(\,\cdot \,,\,\cdot \,)$ the inner product of $\mathfrak {h}$. We equip the vector space $\mathcal{H}=\mathfrak {h}\oplus \mathfrak {h}$ with the Hilbertian structure induced by $\mathfrak {h}$ and the symplectic form

$$\begin{aligned} \omega (x\oplus y,x'\oplus y')=(x\oplus y,J(x'\oplus y'))=(x,y')-(y,x'). \end{aligned}$$

The symplectic complement of $\mathcal{V}\subset \mathcal{H}$ is the subspace $\mathcal{V}^\omega =\{v\,|\,\omega (u,v)=0 \text{ for } \text{ all } u\in \mathcal{V}\}$. A subspace $\mathcal{V}\subset \mathcal{H}$ is isotropic if $\mathcal{V}\subset \mathcal{V}^\omega$ and Lagrangian if $\mathcal{V}=\mathcal{V}^\omega$. $\mathcal{V}$ is Lagrangian iff it is isotropic and d-dimensional. For $Y,Z\in L(\mathfrak {h})$, we denote by $Y\oplus Z$ the element of $L(\mathfrak {h},\mathcal{H})$ defined by $(Y\oplus Z)x=Yx\oplus Zx$. In the block-matrix notation,

$$\begin{aligned} Y\oplus Z=\left[ \begin{array}{cc} Y\\ Z \end{array}\right] ,\qquad (Y\oplus Z)^*=\left[ \begin{array}{cc} Y^*&Z^*\end{array}\right] . \end{aligned}$$

The graph of $X\in L(\mathfrak {h})$ is the d-dimensional subspace of $\mathcal{H}$ defined by

$$\begin{aligned} \mathcal{G}(X)=\mathrm{Ran}\,G_X,\quad G_X=I\oplus X. \end{aligned}$$

A subspace $\mathcal{V}\subset \mathcal{H}$ is a graph iff $\mathcal{V}\cap (\{0\}\oplus \mathfrak {h})=\{0\oplus 0\}$.

The algebraic Riccati equation associated to the triple (A, B, C) of elements of $L(\mathfrak {h})$ is the following quadratic equation for the unknown self-adjoint $X\in L(\mathfrak {h})$:

$$\begin{aligned} \mathcal{R}(X)=XBX-XA-A^*X-C=0. \end{aligned}$$

(6.1)

In the following, we shall assume that C is self-adjoint, that $B\ge 0$ and that the pair (A, B) is controllable. We denote by $\mathfrak {R}(A,B,C)$ the set of self-adjoint elements of $L(\mathfrak {h})$ satisfying Eq. (6.1), which we can also write as

$$\begin{aligned} \mathcal{R}(X)= G_X^*L G_X =0,\qquad L=\left[ \begin{array}{cc} C&{}A^*\\ A&{}-B^*\end{array}\right] . \end{aligned}$$

1.1 Existence of Self-Adjoint Solutions

The Hamiltonian associated to the Riccati equation (6.1) is the unique element of $L(\mathcal{H})$ such that $(u,Lv)=\omega (u,Kv)$ for all $u,v\in \mathcal{H}$. One easily checks that

$$\begin{aligned} K=\left[ \begin{array}{cc} -A&{}B\\ C&{}A^*\end{array}\right] . \end{aligned}$$

Note that since $L=L^*$, K is $\omega$-skew adjoint:

$$\begin{aligned} \omega (u,Kv)+\omega (Ku,v)=\omega (u,Kv)-\omega (v,Ku)=(u,Lv)-(v,Lu)=0. \end{aligned}$$

(6.2)

The first result we recall is a characterization of the set $\mathfrak {R}(A,B,C)$.

Theorem 6.1

(Theorem 7.2.4 in [46]) The map $X\mapsto \mathcal{G}(X)$ is a bijection from $\mathfrak {R}(A,B,C)$ onto the set of K-invariant Lagrangian subspaces of $\mathcal{H}$.

The following are elementary symplectic geometric properties of projections:

Lemma 6.2

• (1) The range of a projection $P\in L(\mathcal{H})$ is isotropic iff $P^*JP=0$ and Lagrangian iff $I-P=J^*P^*J$.

• (2) Denote by $P_\kappa$ the spectral projection of K for $\kappa \in \mathrm{sp}(K)$. Then $JP_\kappa J^*=P_{-{\overline{\kappa }}}^*$ and in particular $\mathrm{Ran}\,P_\kappa$ is isotropic iff $\kappa \not \in \mathrm {i}{\mathbb {R}}$.

• (3) Let $\Sigma \subset \mathrm{sp}(K)$ be such that $\Sigma \cap (-{\overline{\Sigma }})=\emptyset$. Then the spectral subspace of K for $\Sigma$ is isotropic.

Note that $JK+K^*J=0$, which implies that the spectrum of K, including multiplicities, is symmetric w.r.t. the imaginary axis. If $\mathrm{sp}(K)\cap \mathrm {i}{\mathbb {R}}=\emptyset$, then the spectral subspace of K for $\Sigma =\mathrm{sp}(K)\cap {\mathbb {C}}_+$ is d-dimensional and hence, by Lemma 6.2(3), Lagrangian. Thus, Theorem 6.1 yields (see Theorems 7.2.4 and 7.5.1 in [46])

Corollary 6.3

If $\mathrm{sp}(K)\cap \mathrm {i}{\mathbb {R}}=\emptyset$, then $\mathfrak {R}(A,B,C)\not =\emptyset$.

Remark 6.4

In cases where $\mathrm{sp}(K)\cap \mathrm {i}{\mathbb {R}}\not =\emptyset$, and under our controllability assumption, a necessary and sufficient condition for the existence of self-adjoint solution is that all Jordan blocks of K corresponding to eigenvalues in $\mathrm {i}{\mathbb {R}}$ are even-dimensional. For the Riccati equations arising in our analysis of harmonic networks, the singular case $\mathrm{sp}(K_\alpha )\cap \mathrm {i}{\mathbb {R}}\not =\emptyset$ only occurs at the boundary points $\alpha =\frac{1}{2}\pm \kappa _c$. There, the existence of solutions follows by continuity [Part (4) of Theorem 5.5].

Another powerful criterion for the existence of self-adjoint solutions is the following

Theorem 6.5

(Theorem 9.1.1 in [46]) If there exists a self-adjoint $X\in L(\mathfrak {h})$ such that $\mathcal{R}(X)\le 0$, then $\mathfrak {R}(A,B,C)\not =\emptyset$.

1.2 Extremal Solutions

The set $\mathfrak {R}(A,B,C)$ inherits the partial order of $L(\mathfrak {h})$. A minimal/maximal solution of (6.1) is a minimal/maximal element of $\mathfrak {R}(A,B,C)$. Clearly, a minimal/maximal solution, if it exists, is unique.

Theorem 6.6

Assume that $\mathfrak {R}(A,B,C)\not =\emptyset$.

• (1) $\mathfrak {R}(A,B,C)$ is compact.

• (2) $\mathfrak {R}(A,B,C)$ contains a minimal element $X_-$ and a maximal element $X_+$. In the following, we set

  $$\begin{aligned} D_\mp =A-BX_\mp . \end{aligned}$$

• (3) $X\in \mathfrak {R}(A,B,C)$ is minimal/maximal iff $\mathrm{sp}(A-BX)\subset \overline{{\mathbb {C}}}_\pm$.

• (4) $\mathfrak {R}(A,B,C)=X_-+\mathfrak {R}(D_-,B,0)=X_+-\mathfrak {R}(-D_+,B,0)$.

Parts (2) and (3) are stated as Theorems 7.5.1 in [46]. Part (4) follows from simple algebra. Since $X\mapsto \mathcal{R}(X)$ is continuous, $\mathfrak {R}(A,B,C)$ is closed. Its boundedness follows from from Part (4) and the fact that

$$\begin{aligned} \Vert X-X_-\Vert _1=\mathrm{tr}(X-X_-)\le \mathrm{tr}(X_+-X_-), \end{aligned}$$

for all $X\in \mathfrak {R}(A,B,C)$. The Heine-Borel theorem thus yields Part (1).

1.3 The Gap

In this section, we assume that $\mathfrak {R}(A,B,C)\not =\emptyset$ and use the notations introduced in Theorem 6.6.

The gap of the Riccati equation (6.1) is the non-negative element of $L(\mathfrak {h})$ defined by

$$\begin{aligned} Y=X_+-X_-. \end{aligned}$$

We set $\mathcal{K}=\mathrm{Ker}\,Y$, so that $\mathcal{K}^\perp =\mathrm{Ran}\,Y$. For $X\in L(\mathfrak {h})$, we define

$$\begin{aligned} D_X=A-BX. \end{aligned}$$

Theorem 6.7

• (1) For any $X\in \mathfrak {R}(A,B,C)$, $\mathcal{K}$ is the spectral subspace of $D_X$ for $\mathrm{sp}(D_X)\cap \mathrm {i}{\mathbb {R}}$ and $\mathcal{K}^\perp$ is the spectral subspace of $D_X^*$ for $\mathrm{sp}(D_X^*)\setminus \mathrm {i}{\mathbb {R}}$. Moreover, $D_X|_\mathcal{K}$ is independent of $X\in \mathfrak {R}(A,B,C)$.

• (2) The map $X\mapsto \mathrm{Ker}\,X$ is a bijection from $\mathfrak {R}(D_-,B,0)$ onto the set of all $D_-$-invariant subspaces containing the spectral subspace of $D_-$ to the part of its spectrum in $\mathrm {i}{\mathbb {R}}$. Moreover, $X\le X'$ iff $\mathrm{Ker}\,X'\subset \mathrm{Ker}\,X$.

• (3) If $\mathcal{R}(X)\le 0$ for some self-adjoint $X\in L(\mathfrak {h})$, then $X_-\le X\le X_+$.

• (4) If $\mathcal{R}(X)<0$ for some self-adjoint $X\in L(\mathfrak {h})$, then $\mathrm{sp}(K)\cap \mathrm {i}{\mathbb {R}}=\emptyset$.

The first and last Assertions of Part (1) is Theorem 7.5.3 in [46]. The second Assertion is dual to the first one. Part (2) is a special case of Theorem 1 and Part (3) is Theorem 14(b) in [68]. Part (4) is the first assertion of Theorem 9.1.3 in [46].

Note that Theorem 6.1 implies that for $X\in \mathfrak {R}(A,B,C)$ one has

$$\begin{aligned} -KG_X=G_XD_X, \end{aligned}$$

so that $\mathrm{sp}(D_X)=\mathrm{sp}(-K|_{\mathcal{G}(X)})$. Whenever $\mathrm{sp}(K)\cap \mathrm {i}{\mathbb {R}}=\emptyset$, it follows that $\mathrm{sp}(D_X)\cap \mathrm {i}{\mathbb {R}}=\emptyset$ and hence $\mathcal{K}=\{0\}$ and $Y>0$. By Part (3) of Theorem 6.6, we further have $\mathrm{sp}(D_+)\subset {\mathbb {C}}_-$ so that $G_{X_+}$ is the spectral subspace of K to the part of its spectrum in ${\mathbb {C}}_-$.

1.4 Real Riccati Equations and Real Solutions

In this section, we assume that $\mathcal{E}$ is a d-dimensional real Hilbert space and (A, B, C) a triple of elements of $L(\mathcal{E})$ such that (A, B) is controllable, $B\ge 0$, and C self-adjoint.

Denote by $\mathfrak {h}={\mathbb {C}}\mathcal{E}$ the complexification of $\mathcal{E}$ equipped with its natural Hilbertian structure and conjugation $\mathcal{C}$. The ${\mathbb {C}}$-linear extensions of A, B and C to $\mathfrak {h}$ (which we denote by the same symbols) are such that (A, B) is controllable, $B\ge 0$, and C is self-adjoint on $\mathfrak {h}$. Let $\mathfrak {R}(A,B,C)$ be the set of self-adjoint solutions of (6.1), interpreted as a Riccati equation in $L(\mathfrak {h})$, and define

$$\begin{aligned} \mathfrak {R}_{\mathbb {R}}(A,B,C)=\{X\in \mathfrak {R}(A,B,C)\,|\,X={\overline{X}}\}. \end{aligned}$$

Clearly, $\mathfrak {R}_{\mathbb {R}}(A,B,C)$ is the set of real self-adjoint solutions of (6.1) viewed as a Riccati equation on $L(\mathcal{E})$.

Theorem 6.8

• (1) If $\mathfrak {R}(A,B,C)\not =\emptyset$, then its minimal/maximal element is real and hence coincides with the minimal/maximal element of $\mathfrak {R}_{\mathbb {R}}(A,B,C)$.

• (2) Under the same assumption, the gap $Y=X_+-X_-$ is real and so is $\mathcal{K}=\mathrm{Ker}\,Y$.

• (3) For any $X\in \mathfrak {R}_{\mathbb {R}}(A,B,C)$, $\mathcal{K}$ is the spectral subspace of $D_X$ for $\mathrm{sp}(D_X)\cap \mathrm {i}{\mathbb {R}}$ and $\mathcal{K}^\perp$ is the spectral subspace of $D_X^*$ for $\mathrm{sp}(D_X^*)\setminus \mathrm {i}{\mathbb {R}}$. Moreover, $D_X|_\mathcal{K}$ is independent of $X\in \mathfrak {R}(A,B,C)$.

To prove Part (1), note that $\overline{X}\in \mathfrak {R}(A,B,C)$ whenever $X\in \mathfrak {R}(A,B,C)$. In particular, one has $\overline{X}_+\in \mathfrak {R}(A,B,C)$ and hence $X_+-\overline{X}_+\ge 0$. It follows that

$$\begin{aligned} \Vert X_+-\overline{X}_+\Vert _1=\mathrm{tr}(X_+-\overline{X}_+)=\mathrm{tr}(X_+-X_+^*)=0. \end{aligned}$$

The remaining statements are simple consequences of the reality of $X_\pm$.