1 Introduction

The generalized Langevin equation (GLE) approach [40], which is also known as the memory function method, provides an effective tool to analyze the phenomena of Brownian motion and anomalous diffusion. The approach has a solid theoretical background. The equation has been derived from a microscopic equilibrium system [28, 36] and from an incompressible fluid described by the fluctuating hydrodynamics [15] and shown to hold for a broad class of stochastic processes [37]. Reduction to the Langevin equation has been demonstrated on microscopic scales [18] and on hydrodynamic scales [15]. Generalization to nonequilibrium systems has also been considered [20]. In addition, the GLE is versatilely applicable to interpret experimental data over a broad range of time scales. Theoretical predictions on Brownian motion at short time scales have been experimentally confirmed by single-particle tracking techniques in the framework of the GLE [30]. A model based on the GLE and the fractional Gaussian noise has been used to explain subdiffusion dynamics in the conformational fluctuation of a protein molecule [27] and a phenomenological model, which combines the Basset force and the generalized Stokes force, has been proposed for the hydrodynamic and subdiffusive motion of a tracer in a viscoelastic medium [13].

There are two types of the GLE approach. In the first approach, diffusion and velocity relaxation of a tracer particle are investigated through the deterministic GLE, which is formally derived by the projection operator technique [28, 36]. Two essential quantities are the memory function and the autocorrelation function of the fluctuating force. They are related by the fluctuation-dissipation theorem [28, 36], and several methods have been proposed to determine these functions from trajectory realizations [6, 24, 33, 39]. The temporal behavior of the velocity autocorrelation function and the mean square displacement function is explained by the memory function [25, 39, 48]. In addition, whether the diffusion is normal or anomalous is determined by the tail behavior of the memory function [23, 35]; only if the time integral of the memory function converges to a positive value, the diffusion is normal. On the other hand, the second approach employs the stochastic GLE, where the fluctuating force in the deterministic GLE is replaced by an independent random noise process. Considering that the relationship between the fluctuating force and the velocity is complicated in the deterministic GLE, the stochastic GLE is more easily investigated analytically and numerically and used in stochastic modeling. For a Gaussian random process (such as the Gaussian colored noise or the fractional Gaussian noise) and a certain analytic form of the memory function (such as exponential and power-law decaying functions), plenty of analytic results are available [8, 26, 38, 40, 45, 47]. Also, one can use standard numerical techniques to generate sample trajectories of the stochastic GLE [3, 40].

If the mass of a tracer particle is much larger than that of a fluid particle, the time scale of the movement of the former is correspondingly larger than that of the latter. Due to large time scale separation, the motion of the Brownian particle is approximately described by a Markovian process (i.e., the Langevin equation) [41]. Complete time scale separation would occur in the Brownian limit, where the Brownian particle has an infinite mass. Microscopically, this corresponds to the frozen dynamics, where the Brownian particle is fixed and the fluid particles move under the presence of the Brownian particle. The force autocorrelation function of this dynamics provides information not only for the macroscopic Markovian description through the adiabatic approximation but also for the microscopic description of systems in the near-Brownian-limit regime. The friction coefficient in the Langevin equation is calculated from the time integral of the frozen dynamics force autocorrelation function. As the mass \(M\) of the Brownian particle increases, the autocorrelation function of the fluctuating force converges to the frozen-dynamics force autocorrelation function and, by the fluctuation-dissipation theorem, the Brownian limit of the memory function, which we will call the limit memory function, is also obtained by the frozen dynamics [12]. An asymptotic expression for the velocity autocorrelation function with respect to \(M\) is available in terms of the limit memory function [22].

In this paper, we investigate Brownian motion in a confined Rayleigh gas through the deterministic GLE. The Rayleigh gas is a simplified model consisting of a heavy Brownian particle and a surrounding ideal gas, where elastic collisions of the Brownian particle with gas particles are usually assumed. Owing to the noninteracting bath assumption, hydrodynamic effects of the surrounding fluid become suppressed whereas the effects of direct interaction between the Brownian particle and gas particles become dominant. The unconfined Rayleigh gas has been extensively studied by analytic means. It has been proved that the motion of the Brownian particle converges to the Ornstein–Uhlenbeck process in the Brownian limit [9, 42]. The friction coefficient [11, 14, 21, 34] and the velocity autocorrelation function [17, 32] have been obtained by various techniques. The convergence proofs have also been given for the systems generalized in the following ways: the Brownian particle has a convex shape and rotates [10]; the space is confined by a wall [4]; there are several Brownian particles and the elastic collisional dynamics is replaced by dynamics under a continuous interaction potential [29]. In a confined Rayleigh gas, a gas particle can perform a series of collisions alternately with the Brownian particle and the boundary wall. As a result, the interaction between the Brownian particle and the ideal gas becomes complicated and a long-time tail in the memory function is expected to emerge. Although a tail is also present in the memory function in the unconfined case, it decays exponentially and its magnitude becomes negligible when the mass of the Brownian particle is sufficiently large [17]. Hence, by investigating the long-time tail in the memory function of the confined case, we discuss the effects of confinement in the Rayleigh gas. More specifically, we observe the power-law tail and investigate its dependence on system parameters such as the dimensionality of the space and the size of confinement. In addition, we investigate the effects of the stochastic thermal wall satisfying Maxwell boundary condition [43, 44]. However, we note that the confinement effects observed in our model are different in nature from those on Brownian motion in a liquid, where hydrodynamic interactions play an important role [5, 19, 46].

We use both an analytical approach and molecular dynamics (MD) simulation approach in a complementary way, which have been employed to investigate the memory function of the unconfined Rayleigh gas with a continuous interaction potential function [21]. From the analytical approach, we obtain an expression for the limit memory function by using an analytic expression of the frozen dynamics force autocorrelation function. In the frozen dynamics of the Rayleigh gas model, the dynamics of each gas particle becomes decoupled from those of the other gas particles and, thus, each relevant physical quantity is written as an ensemble average of a functional of the single-gas-particle trajectory. On the other hand, from the MD simulation approach, we investigate the system with a finite-mass Brownian particle and/or the stochastic thermal walls. However, in general, analyzing the tail of a time correlation function by means of MD simulations is not so straightforward due to the difficulty in accurately estimating the time correlation function over a large time interval. In this case, analytic results for the limiting situation are very helpful for guiding the MD simulation approach. In turn, we also confirm the analytic results by the MD simulation results.

In order to make full use of analytic features, we consider a cube of fixed orientation as the Brownian particle rather than a spherical shape. We shall see that by assuming all collisions are elastic, the diffusions along the directions other than the transverse direction to the channel become identical to the unconfined case and decoupled from the one along the transverse direction in the Brownian limit. Since the generalization to a higher-dimensional space is straightforward, we consider a hypercube in \(d\)-dimensional space with \(d\ge 2\). A similar setting of the system (a hypercube in a half space confined by a single wall) has been considered in the mathematical proof for the convergence of the diffusion process [4]. A sufficient condition for the convergence has been given in terms of the velocity distribution of gas particles. For the three-dimensional equilibrium ideal gas, which satisfies the condition, the diffusion process in the Brownian limit becomes the Ornstein–Uhlenbeck-type process with a position-dependent friction coefficient. However, it has been pointed out that the condition does not hold in the two-dimensional equilibrium case, which suggests the possibility of failure in converging to normal diffusion. We shall see that the tail of the memory kernel decays like \(t^{-1}\) in the two-dimensional case with the elastic walls, which implies anomalous diffusion.

The rest of the paper is organized as follows. In Sect. 2, we explain the system. In Sect. 3, we present analytic results. In Sect. 4, we show MD simulation results. In Sect. 5, we provide the derivation of two analytic results: the GLE and the frozen dynamics force autocorrelation function. In Sect. 6, we present a summary and discussion.

2 System

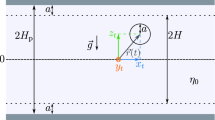
We consider the \(d\)-dimensional space with \(d\ge 2\) and denote the coordinates of a point as \((x_1,x_2,\ldots ,x_d)\). Two parallel walls normal to the \(x_d\)-axis are located at \(x_d=h_\pm \). In the space between the two walls, a hypercube with sides \(L_1\), \(L_2\), \(\ldots \), \(L_d\) is placed. We fix the orientation of the cube so that the edges with length \(L_i\) (\(i=1,2,\ldots ,d\)) are parallel to the \(x_i\)-axes, respectively. Then, two faces of the cube are parallel to the walls. Depending on their \(x_d\)-coordinates, we call the two walls as the upper and lower walls and the two faces of the hypercube as the upper and lower faces. We also call the direction parallel to the \(x_d\)-axis as the transverse direction (to the channel). The remaining space between the walls is filled with an ideal gas. We denote the mass of a gas particle as \(m\) and the number density of the gas as \(a\), respectively. For the geometry of the walls and the hypercube for \(d=3\), see Fig. 1a.

Fig. 1
figure 1

In panel a, the geometry of the system is depicted for the three-dimensional case. For the definitions of the symbols, see the text. In panel b, a trajectory of a gas particle colliding alternatively with the (purely elastic) upper wall and the upper face of the fixed cube is depicted

Full size image

We first explain the dynamics of the system with a finite-mass hypercube and elastic walls. For the frozen dynamics and the stochastic thermal walls, see below. We denote the mass of the hypercube as \(M\) and assume that it collides with a gas particle elastically. When a gas particle with velocity \((v_1,v_2,\ldots ,v_d)\) collides with the hypercube with velocity \((V_1,V_2,\ldots ,V_d)\) through one of the faces normal to the \(x_i\)-axis, the \(i\)th velocity components of the gas particle and the hypercube become

$$\begin{aligned} v_i \rightarrow v_i-\frac{2M}{m+M}(v_i-V_i),\quad V_i \rightarrow V_i+\frac{2m}{m+M}(v_i-V_i), \end{aligned}$$
(1)

respectively, and the other components do not change. When a gas particle collides with one of the elastic walls, its velocity \((v_1,v_2,\ldots ,v_d)\) becomes \((v_1,v_2,\ldots ,-v_d)\). We assume that gas particles do not interact among themselves.

In addition, we introduce a harmonic potential to the hypercube along the transverse direction. By denoting the force constant as \(k\), the hypercube located at \((X_1,X_2,\ldots ,X_d)\) experiences the linear restoring force \((0,0,\ldots ,-k X_d)\). In order to avoid the direct interaction of the hypercube with the walls, we assume that \(k\) is sufficiently large so that there is almost no chance for it to reach the walls. We note that in the Brownian limit considered in Ref. [4] (i.e., \(m\rightarrow 0\) while the mass and the size of the cube are kept fixed and the number density and the velocity distribution of the ideal gas are appropriately scaled), it has been proved that the cube never reaches the wall. We also note that a similar experimental setting (i.e., a particle under a harmonic potential, which is suspended in a liquid confined by a wall) has been employed to investigate confined colloidal diffusion at hydrodynamic scales by the optical trap technique [5, 19, 46].

We assume that the system is in equilibrium and obeys the Boltzmann distribution. We denote the inverse temperature of the system by \(\beta =(k_\mathrm {B}T)^{-1}\). We call this dynamics (i.e., with the finite-mass hypercube under the harmonic potential) full dynamics.

Frozen dynamics In this dynamics, the hypercube is assumed to have an infinite mass so that it is held fixed at given position regardless of elastic collisions with gas particles. If a gas particle with velocity \((v_1,v_2,\ldots ,v_d)\) collides with a face normal to the \(x_i\)-axis, the \(i\)th component becomes \(-v_i\) and the other components do not change. We denote the distances between the upper wall and the upper face and between the lower wall and the lower face as \(\Delta _+\) and \(\Delta _-\), see Fig. 1a. We note that, in the frozen dynamics, neither \(M\) nor \(k\) is defined and the separation distances \(\Delta _\pm \) are given as parameters.

Thermal walls We employ a stochastic thermal wall model satisfying the Maxwell boundary condition [43, 44]. We first explain the thermalizing procedure of the gas-particle velocity at the walls. If a gas particle collides with one of the walls, the particle is instantly released from the wall with a randomly sampled velocity \((v_1,v_2,\ldots ,v_d)\) from the following distributions

$$\begin{aligned}&\psi _\parallel (v_i)=\sqrt{\frac{\beta m}{2\pi }}e^{-\frac{1}{2}\beta m v_i^2},\quad i=1,2,\ldots ,d-1,\end{aligned}$$
(2a)
$$\begin{aligned}&\psi _\perp (v_d)=\beta m|v_d|e^{-\frac{1}{2}\beta m v_d^2}, \end{aligned}$$
(2b)

where \(\psi _\perp (v_d)\) is defined for \(v_d>0\) at the lower wall and for \(v_d<0\) at the upper wall. Then, we define the accommodation factor \(0\le \phi \le 1\), which is the probability that gas particles are thermalized when colliding with the walls. We call the cases \(\phi =0\) and \(\phi =1\), respectively, purely elastic and fully thermalizing walls.

3 Analytic Results

Throughout this section, we only consider the purely elastic walls so that every collision occurring in the system is elastic and the dynamics is deterministic. We present analytic results as follows. We first consider the full dynamics and present the form of the GLE for the finite-mass hypercube in Sect. 3.1. Then, we investigate its Brownian limit. We provide an analytic expression of the frozen dynamics force autocorrelation function and investigate its power-law decaying tail in Sect. 3.2. We obtain the limit memory function in Sect. 3.3. We discuss the Langevin description and obtain its position-dependent friction coefficients in Sect. 3.4. We present the derivation of the GLE and the frozen dynamics force autocorrelation function in Sect. 5.

3.1 GLE

By using the Mori projection method [36, 40], we show in Sect. 5.1 that the position \(\mathbf {X}=(X_1,X_2,\ldots ,X_d)\) and velocity \(\mathbf {V}=(V_1,V_2,\ldots ,V_d)\) of the hypercube having mass \(M\) satisfy the following GLE:

$$\begin{aligned}&\dot{X}_i(t)=V_i(t),\end{aligned}$$
(3a)
$$\begin{aligned}&M\dot{V}_i(t)=-\int _0^t K_i (t-s) V_i(s) ds + F^+_i(t),\quad i=1,2,\ldots ,d-1,\end{aligned}$$
(3b)
$$\begin{aligned}&\dot{X}_d(t)=V_d(t),\end{aligned}$$
(3c)
$$\begin{aligned}&M\dot{V}_d(t)=-k X_d(t)-\int _0^t K_d (t-s)V_d(s) ds + F^+_d(t), \end{aligned}$$
(3d)

where the memory function \(K_i(t)\) and the fluctuating force \(F_i^+(t)\) satisfy the fluctuation-dissipation relation

$$\begin{aligned}&K_i(t)=\beta \left\langle F_i^+(0)F_i^+(t)\right\rangle ,\quad i=1,2,\ldots ,d,\end{aligned}$$
(4a)
$$\begin{aligned}&\left\langle F_i^+(0)F_j^+(t)\right\rangle =0,\quad \text{ for } i\ne j. \end{aligned}$$
(4b)

In addition, the fluctuating force is uncorrelated with \(X_d(0)\) and \(\mathbf {V}(0)\):

$$\begin{aligned}&\left\langle X_d(0)F_i^+(t)\right\rangle =0,\quad i=1,2,\ldots ,d,\end{aligned}$$
(5a)
$$\begin{aligned}&\left\langle V_i(0)F_j^+(t)\right\rangle =0,\quad i,j=1,2,\ldots ,d. \end{aligned}$$
(5b)

We note that since \(\mathbf {V}(t)\) changes discontinuously whenever it collides with gas particles, its time derivative \(\dot{\mathbf {V}}(t)=\frac{1}{M}\mathbf {F}(t)\) is understood as a formal derivative containing a series of Dirac delta functions and so is the fluctuating force. We also note that Eq. (3) is exact and equivalent to the original time evolution equation although, in general, it cannot be used to generate sample trajectories because the fluctuating force is very complicatedly related with \(\mathbf {X}\) and \(\mathbf {V}\).

In order to derive the GLE, we make the assumption that the harmonic potential is so stiff that the direct interaction between the hypercube and the walls is negligible. In Sect. 5.1.1, we show that in this case the following equilibrium distribution of the hypercube along the transverse direction can be assumed:

$$\begin{aligned} \rho (X_d)=\sqrt{\frac{\beta k}{2\pi }}e^{-\frac{1}{2}\beta k X_d^2}. \end{aligned}$$
(6)

Since this distribution becomes exactly valid in the case that the hypercube is subject to a harmonic potential but suspended in an unbounded ideal gas, Eq. (3) is exact in the latter case.

3.2 Frozen Dynamics Force Autocorrelation Function

Denoting the force exerted on the fixed hypercube by the ideal gas as \(\mathbf {F}_0=(F_{0,1}, F_{0,2}, \ldots , \) \(F_{0,d})\), we derive the following analytic expression for the frozen dynamics force autocorrelation in Sect. 5.2:

$$\begin{aligned}&\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle =\frac{8a}{\beta }\sqrt{\frac{2m}{\pi \beta }}\left( \prod _{\begin{array}{c} j=1\\ j\ne i \end{array}}^d L_j\right) \delta (t),\quad i=1,2,\ldots ,d-1,\end{aligned}$$
(7a)
$$\begin{aligned}&\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle = \frac{8a}{\beta }\sqrt{\frac{2m}{\pi \beta }} \left( \prod _{j=1}^{d-1} L_j\right) \delta (t)+I_2^+(t)+I_2^-(t). \end{aligned}$$
(7b)

Here, \(I_2^\pm (t)=I_2(t;\Delta _\pm )\), where

$$\begin{aligned}&I_2(t;\Delta )=A(t;\Delta ) \prod _{i=1}^{d-1} B(t;L_i),\end{aligned}$$
(8a)
$$\begin{aligned}&A(t;\Delta )=4am^2\sum _{n=1}^\infty \frac{(2n\Delta )^4}{t^5}\varphi \left( \frac{2n\Delta }{t}\right) ,\end{aligned}$$
(8b)
$$\begin{aligned}&B(t;L) =L\; \mathrm {erf}\left( \frac{L}{t}\sqrt{\frac{\beta m}{2}}\right) -t\sqrt{\frac{2}{\pi \beta m}}\left( 1-e^{-\frac{\beta m L^2}{2t^2}}\right) , \end{aligned}$$
(8c)

with \(\varphi (v)=\sqrt{\frac{\beta m}{2\pi }}e^{-\frac{\beta m}{2}v^2}\) and \(\mathrm {erf}(x)=\frac{2}{\sqrt{\pi }}\int _0^x e^{-y^2} dy\). The longitudinal-direction force autocorrelation functions \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) (\(i=1,2,\ldots ,d-1\)) contain only a delta functionFootnote 1. This indicates that the effects of collisions are instantaneous and uncorrelated as in the unbounded case. On the other hand, the transverse-direction force autocorrelation function \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) contains also slowly decaying parts \(I_2^+(t)\) and \(I_2^-(t)\), which result from repeated collisions with the upper and lower wall, respectively. As \(\Delta \rightarrow \infty \), \(I_2^\pm (t)\) becomes zero and we retrieve the unbounded case.

We make the following observations on the time profile of \(I_2(t;\Delta )\). It is zero at \(t=0\) and nonnegative for all \(t\). At short times, it has very small values until it exhibits a sharp increase and attains a maximum, and then it monotonically decreases to zero. The short-time behavior of \(I_2(t;\Delta )\) is explained by that it takes time for a gas particle to collide again with the hypercube. Hence, the time when the maximum value appears is of the order of \(\Delta / \left\langle \left| v_d\right| \right\rangle \). On the other hand, at large time \(t\), \(A(t;\Delta )\) and \(B(t;L)\) become

$$\begin{aligned}&A(t;\Delta )\approx \frac{2am^2}{\Delta }\int _0^\infty y^4 \varphi (y) dy = \frac{3a}{\beta ^2\Delta },\end{aligned}$$
(9a)
$$\begin{aligned}&B(t;L)\approx \frac{L^2}{t}\sqrt{\frac{\beta m}{2\pi }}. \end{aligned}$$
(9b)

Hence, we obtain

$$\begin{aligned} I_2(t;\Delta )\approx \frac{3a}{\beta ^2}\left( \frac{\beta m}{2\pi }\right) ^{\frac{d-1}{2}}\frac{L_1^2 L_2^2\cdots L_{d-1}^2}{t^{d-1}\Delta }, \end{aligned}$$
(10)

and observe that the tail decays like \(t^{-(d-1)}\). In addition, we observe that at large times the magnitude of the tail is inversely proportional to the separation distance \(\Delta \) and proportional to the square of the area of the upper or lower face.

In Fig. 2, the time profile of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) is shown for the two-dimensional case. If the hypercube is fixed at the center of the channel (i.e., \(\Delta _+=\Delta _-=\Delta \)), \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle =\frac{2}{\beta }\gamma _d^*\delta (t)+2I_2(t;\Delta )\) and we observe the shape of \(I_2(t;\Delta )\). Otherwise, the tail may have two local maxima as a result of superposing \(I_2(t;\Delta _+)\) and \(I_2(t;\Delta _-)\).

Fig. 2
figure 2

The frozen dynamics force autocorrelation function for the transverse direction to the channel in the two-dimensional case. The width of the channel is 6 (i.e., \(h_\pm =\pm 3\)) and the hypercube has sides \(L_1=L_2=1\) and is fixed at \(X_d=0\) (i.e., \(\Delta _\pm =2.5\)) in panel a and at \(X_d=-1\) (i.e., \(\Delta _+=3.5\) and \(\Delta _-=1.5\)). The other parameters are given as \(m=a=\beta =1\). The analytic result (depicted by the dashed line), see Eq. (7b), is compared with the frozen dynamics MD simulation result (depicted by the solid line). The error bars correspond to statistical errors with two standard deviations. The long-time asymptotic result, see Eq. (10), is also plotted by the dotted line. In the inset of panel b, the time profiles of \(I_2^\pm (t)=I_2(t;\Delta _\pm )\), see Eq. (8), are plotted

Full size image

3.3 Limit Memory Function

As the mass of the Brownian particle increases, the memory function \(K_i(t)\) defined in Eq. (3) converges to the limit memory function \(K_i^\mathrm {BL}(t)\), where BL stands for the Brownian limit \(M\rightarrow \infty \). Compared with the free Brownian case in an unbounded space, where a simple relation \(K_i^\mathrm {BL}(t)=\beta \left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) holds, the frozen dynamics force autocorrelation function depends on the position of the hypercube (through the separation distance \(\Delta _\pm \)) and the limit memory function \(K_i^\mathrm {BL}(t)\) is expected to be expressed as the average of \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) over the equilibrium distribution of the hypercube. By assuming

$$\begin{aligned} K_i^{\mathrm {BL}}(t)=\beta \int \rho (X_d) \left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle dX_d \end{aligned}$$
(11)

and using Eq. (7), we obtain the limit memory function as follows:

$$\begin{aligned}&K_i^{\mathrm {BL}}(t)=2\gamma ^*_i\delta (t),\quad i=1,2,\ldots ,d-1,\end{aligned}$$
(12a)
$$\begin{aligned}&K_d^{\mathrm {BL}}(t)=2\gamma ^*_d\delta (t)+\tilde{K}_d^\mathrm {BL}(t), \end{aligned}$$
(12b)

where

$$\begin{aligned}&\gamma ^*_i = 4a\sqrt{\frac{2m}{\pi \beta }}\prod _{\begin{array}{c} j=1\\ j\ne i \end{array}}^d L_j,\quad i=1,2,\ldots ,d,\end{aligned}$$
(13)
$$\begin{aligned}&\tilde{K}_d^\mathrm {BL}(t)=\beta \int \rho (X_d) \left[ I_2(t;\Delta _+)+I_2(t;\Delta _-)\right] dX_d. \end{aligned}$$
(14)

We note that the separation distances \(\Delta _\pm \) are functions of \(X_d\) defined as \(\Delta _+=h_+ - X_d-\frac{1}{2}L_d\) and \(\Delta _- = X_d-\frac{1}{2}L_d-h_-\), see Fig. 1a. In addition, by letting \(\Delta \rightarrow \infty \), we see that \(\gamma _i^*\) is the friction coefficient of the unbounded case. Rather than analytically investigating the convergence of \(K_i(t)\) to \(K_i^\mathrm {BL}(t)\) in the Brownian limit or the validity of Eq. (11), numerical validation by using MD simulations is performed, see Fig. 7.

3.4 Langevin Description

Based on the adiabatic approximation due to time scale separation, the following Langevin equation is proposed in the Brownian limit:

$$\begin{aligned}&\dot{X}_i(t)=V_i(t),\end{aligned}$$
(15a)
$$\begin{aligned}&M\dot{V}_i(t)=-\gamma _i^* V_i(t)+\Gamma _i(t),\quad i=1,2,\ldots ,d-1,\end{aligned}$$
(15b)
$$\begin{aligned}&\dot{X}_d(t)=V_d(t),\end{aligned}$$
(15c)
$$\begin{aligned}&M\dot{V}_d(t)=-kX_d(t)-\gamma _d(X_d) V_i(t)+\Gamma _d(t), \end{aligned}$$
(15d)

where \(\gamma _i^*\) and \(\gamma _d(X_d)\) are the friction coefficients in the corresponding directions and \(\Gamma _i(t)\) (\(i=1,2,\ldots ,d\)) is Gaussian white noise.

For the longitudinal directions (\(i=1,2,\ldots ,d-1\)), \(\gamma _i^*\) is expressed by Eq. (13) from \(\gamma _i^*=\beta \int _0^\infty \left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) and the noise correlation is correspondingly given as \(\left\langle \Gamma _i(t)\Gamma _j(t')\right\rangle =\frac{2\gamma _i^*}{\beta }\delta _{ij}\delta (t-t')\). Hence, the Langevin description in these directions is identical to the unbounded case. On the other hand, for the transverse direction, since \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) depends on the position of the hypercube through \(X_d\), \(\gamma _d(X_d)\) becomes a position-dependent friction coefficient. For \(d=2\), since the time integral of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) diverges from Eq. (10), the Langevin description fails and anomalous diffusion is expected. For \(d\ge 3\), we have

$$\begin{aligned} \gamma _d(X_d) = \gamma _d^* + \delta \gamma (\Delta _+) + \delta \gamma (\Delta _-),\quad \text{ where } \quad \delta \gamma (\Delta )=\beta \int _0^\infty I_2(t;\Delta ) dt. \end{aligned}$$
(16)

We note that due to the presence of the walls, \(\gamma _d\) depends on the separation distances \(\Delta _\pm \) and becomes larger than the unconfined one. In case of normal diffusion, \(\Gamma _d(t)\) is given as \(\sqrt{\frac{2\gamma _d(X_d)}{\beta }}\dot{W}_t\), where \(W_t\) is the standard Wiener process independent of \(\Gamma _i(t)\).

An asymptotic expression of \(\delta \gamma (\Delta )\) for large \(\Delta \) is obtained as follows. As \(\Delta \) becomes larger, it takes longer time for a gas particle to recollide with the wall and the time interval where \(A(t;\Delta )\) attains considerable values appears later. In this case, we approximate \(I_2(t;\Delta )\) in Eq. (8a) by replacing \(B(t;L)\) with its long-time asymptotic expression given in Eq. (9b). Then, by integrating this with respect to \(t\), we obtain

$$\begin{aligned} \delta \gamma (\Delta )\approx 64am^2\beta \left( \frac{\beta m}{2\pi }\right) ^{d/2}\frac{L_1^2 L_2^2\cdots L_{d-1}^2}{\Delta ^{d-1}}\sum _{n=1}^\infty \frac{1}{n^{d-1}}\int _0^\infty y^{d+2}e^{-2\beta m y^2}dy. \end{aligned}$$
(17)

From Eq. (17), we see that for \(d=2\), \(\delta \gamma (\Delta )\) diverges and for higher \(d\), it is proportional to \(\Delta ^{-(d-1)}\). For \(d=3\), Eq. (17) becomes

$$\begin{aligned} \delta \gamma (\Delta )\approx \frac{a\sqrt{2\pi m\beta }}{3}\frac{L_1^2 L_2^2}{\Delta ^2}. \end{aligned}$$
(18)

In Fig. 3, the dependence of \(\delta \gamma (\Delta )\) on \(\Delta \) is plotted for \(d=3\) and compared with Eq. (18).

Fig. 3
figure 3

Log–log plot of the increment \(\delta \gamma (\Delta )\) in the transverse-direction friction coefficient \(\gamma _d\) due to the wall separated by distance \(\Delta \), see Eq. (16), versus \(\Delta \). The result is obtained from the three-dimensional case and the other parameters are given as \(L_1=L_2=1\), and \(m=a=\beta =1\). The asymptotic expression of \(\delta \gamma (\Delta )\) for large \(\Delta \), see Eq. (18), is also plotted by the dotted line

Full size image

Before closing this section, we obtain the friction coefficient \(\gamma _{d-\mathrm {sphere}}\) of a \(d\)-dimensional hypersphere by using the analytic expression of \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \). We note that its \(\delta \)-weight is proportional to the area of corresponding face and that the contribution of the collisions on an area element is uncorrelated with that on the other area elements. Hence, we can define its density \(\overline{\langle \mathbf {F}_0(0)\cdot \mathbf {F}_0(t) \rangle } = \frac{4a}{\beta }\sqrt{\frac{2m}{\pi \beta }}\delta (t)\) per unit area, from which the friction coefficient \(\gamma _{d\mathrm {-sphere}}\) for a hypersphere of radius \(R\) in the unbounded \(d\)-dimensional space is obtained. By denoting the area of the hypersphere as \(S_{d-1}(R)\), we have \(\left\langle \mathbf {F}_0(0)\cdot \mathbf {F}_0(t) \right\rangle = \overline{\left\langle \mathbf {F}_0(0)\cdot \mathbf {F}_0(t) \right\rangle } S_{d-1}(R)\). From the relation \(\gamma =\frac{\beta }{d}\int _0^\infty \langle {\mathbf {F}}_0(0)\cdot {\mathbf {F}}_0(t) \rangle dt\) for the isotropic case [18], we obtain

$$\begin{aligned} \gamma _{d\mathrm {-sphere}} = 2a \frac{\pi ^{(d-1)/2}}{\Gamma \left( \frac{d}{2}+1\right) } \sqrt{\frac{2m}{\beta }}R^{d-1}. \end{aligned}$$
(19)

This general formula coincides with the previous results for \(d=2\) and 3 [11, 14, 21, 32, 34] and even for \(d=1\) [7]. We also note that a similar argument can be applied to the computation of the friction coefficient of a convex body [10].

4 MD Simulation Results

In this section, we present MD simulation results for the frozen and full dynamics of the two- and three-dimensional confined Rayleigh gas. In Sect. 4.1, we explain the MD procedures as well as the simulation parameters. In Sect. 4.2, we confirm the analytic results for the frozen dynamics and investigate the effects of the thermal walls. In Sect. 4.3, we observe the memory function of the finite-mass hypercube under the harmonic potential.

4.1 MD Procedures

Physical Parameters For the two-dimensional system, a square with \(L_1=L_2=1\) in a channel of width \(H_\mathrm {channel}=6\) (i.e., \(h_\pm =\pm 3\)) is considered. In order to mimic an infinite channel, the length of the channel is set as \(L_\mathrm {channel}=100\) and periodic boundary condition is imposed along the direction of the channel axis. The mass \(m\) of a gas particle and the inverse temperature \(\beta \) and number density \(a\) of the ideal gas are chosen as \(m=\beta =a=1\). In the frozen dynamics, the hypercube is fixed in the middle of the channel (i.e., \(\Delta _\pm =2.5\)) and the accommodation factor \(\phi \) of the thermal walls is varied from \(\phi =0\) (purely elastic) to \(\phi =1\) (fully thermalizing). The hypercube fixed at \(X_d=-1\) (i.e., \(\Delta _+=3.5\) and \(\Delta _-=1.5\)) is also simulated with \(\phi =0\). In the full dynamics, the force constant \(k\) of the harmonic potential is chosen as \(k=4\), 6, and 8 and the mass \(M\) of the square is chosen as \(M=10\), 20, 50, 100, 200, and 500. Only the purely elastic walls are considered. For the frozen dynamics of the three-dimensional system, a cube with \(L_1=L_2=L_3=1\) in a channel with \(H_\mathrm {channel}=6\) is considered and periodic boundary condition with \(L_\mathrm {channel}=100\) is imposed to the \(x_1\)- and \(x_2\)-axes. While the same values \(m=\beta =1\) are used, \(a=0.01\) is used to reduce the mean number of the gas particles. The value of \(\phi \) is varied from \(\phi =0\) to \(\phi =1\).

In order to investigate the case of a single-wall system, we additionally simulate the frozen dynamics of the two- and three-dimensional systems with larger values of \(H_\mathrm {channel}=12\), 24, and 48 but with \(\Delta _+=2.5\) fixed and observe \(\left\langle F_+(0)F_+(t)\right\rangle \). When we increase the volume of the system, we correspondingly decrease the value of \(a\) so that the mean number of the gas particles remains the same, which is for computational convenience. Since the frozen dynamics force autocorrelation is linearly proportional to \(a\), we normalize it by \(a\) before comparison.

Generating Initial Configurations For the frozen dynamics, the initial configuration of the ideal gas is sampled from Eq. (42). In other words, the number of the gas particles is sampled from the Poisson distribution with mean \(a(H_\mathrm {channel}L_\mathrm {channel} - L_1 L_2)\) for \(d=2\) and \(a(H_\mathrm {channel}L_\mathrm {channel}^2 - L_1 L_2 L_3)\) for \(d=3\). Then, the position and velocity of each gas particle are sampled from the uniform distribution and the Maxwell–Boltzmann distribution, respectively. For the full dynamics, the initial position \((X_1,X_2,\ldots ,X_d)\) of the hypercube is determined as follows: \(X_1=\cdots =X_{d-1}=0\) and \(X_d\) is sampled from Eq. (6). Its velocity is sampled from the Maxwell–Boltzmann distribution. Then, the initial configuration of the ideal gas is sampled as in the frozen dynamics case.

Calculating Trajectories For the MD simulations of the frozen dynamics, a standard event-driven algorithm for hard-core systems [1, 2] is employed. In other words, we repeat the following procedure: calculate the next collision time from the smallest collision time among all possible collisions; move all particles forward until collision occurs; implement collision dynamics for the colliding gas particle. For the MD simulation with the finite-mass hypercube under the harmonic potential, where an event/time-driven hybrid method should be used in order to properly handle with the collisional dynamics as well as the dynamics under the continuous potential, the collision Verlet algorithm [16] is employed. The basic idea is to approximate the continuous dynamics between the collisions by the Verlet map. In our case (i.e., under the harmonic potential), the collision time between the hypercube and a gas particle under the Verlet map is formally solved for and thus the next collision time is accurately estimated without employing any iterative solver.

Evaluating Forces and Time Correlation Functions In frozen dynamics, the force \(\mathbf {F}_0(t)\) on the fixed hypercube at time \(t\) is calculated from the average force in the time interval \([t,t+\Delta t]\) (i.e., the impulse divided by \(\Delta t\)). Every time step, each component of \(\mathbf {F}_0(n\Delta t)\) is calculated and, for the transverse direction, \(F_+(n\Delta t)\) and \(F_-(n\Delta t)\) are separately calculated. In full dynamics, the total force \(\mathbf {F}(t)\) is obtained from the sum of the harmonic force \((0,\ldots ,0,-k X_d(t))\) and the average force due to the collisions in the time interval \([t,t+\Delta t]\). Every time step, \(\mathbf {F}(n\Delta t)\) is calculated along with the trajectory \((\mathbf {X}(n\Delta t),\mathbf {V}(n\Delta t))\).

Using a standard technique to estimate time correlation functions [2], the following time correlation functions are calculated: \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) and \(\left\langle F_\pm (0)F_\pm (t)\right\rangle \) for the frozen dynamics and the auto/cross-correlation functions among \(\mathbf {X}(t)\), \(\mathbf {V}(t)\), and \(\mathbf {F}(t)\) for the full dynamics. The \(\delta \)-weights in the force autocorrelation functions are separately estimated as follows. For each collision with the faces normal to the \(x_i\)-axis, we calculate the square of the momentum change of the colliding gas particle. From the sum of these values divided by the total simulation time, we estimate the \(\delta \)-weight in the force autocorrelation function of the \(x_i\)-component of the force.

The procedures to calculate the force and the \(\delta \)-weight in the force autocorrelation function are elaborated by considering the frozen dynamics. For the full dynamics, the procedures are essentially the same. In the frozen dynamics, the force \(F_{0,i}(t)\) is expressed as

$$\begin{aligned} F_{0,i}(t)=-\sum _k \Delta p_{i,k}\delta (t-\tau _k), \end{aligned}$$
(20)

where \(\Delta p_{i,k}\) and \(\tau _k\) are, respectively, the momentum change of a colliding gas particle in the \(x_i\)-direction and the collision time at \(k\)th collision. The force at the time step \(n\Delta t\) is estimated as

$$\begin{aligned} F_{0,i}^\mathrm {MD}(n\Delta t) =\frac{1}{\Delta t}\int _{n\Delta t}^{(n+1)\Delta t}F_{0,i}(t)dt=-\frac{1}{\Delta t}\sum _{\tau _k\in [n\Delta t,(n+1)\Delta t)}\Delta p_{i,k}. \end{aligned}$$
(21)

The force autocorrelation function \(\left\langle F_{0,i}(0)F_{0,i}(n\Delta t)\right\rangle \) is evaluated from \(F_{0,i}^\mathrm {MD}(t)\) except the point \(n=0\) where the delta function affects the value. The expression for the \(\delta \)-weight in \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) is obtained from the following time average expression:

$$\begin{aligned}&\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \mathop {=}\limits ^{\mathcal {T}\rightarrow \infty } \frac{1}{\mathcal {T}}\int _0^\mathcal {T} F_{0,i}(\tau )F_{0,i}(\tau +t) d\tau \nonumber \\&=\frac{1}{\mathcal {T}}\sum _{\tau _k\in [0,\mathcal {T}]}\sum _l \Delta p_{i,k}\Delta p_{i,l}\delta (t+\tau _k-\tau _l). \end{aligned}$$
(22)

Here, the last equality is obtained by substituting Eq. (20) and integrating the delta function \(\delta (\tau -\tau _k)\). Hence, the \(\delta \)-weight is estimated from \(\frac{1}{\mathcal {T}}\sum _{\tau _k\in [0,\mathcal {T}]}\Delta p_{i,k}^2\).

Calculating the Memory Function Next, we explain how to evaluate the transverse-direction memory function \(K_d(t)\). For the other directions, the same procedure with \(k=0\) can be applied. In principle, we need to solve the following Volterra equation for \(K_d(t)\):

$$\begin{aligned} \left\langle V_d(0)F_d(t)\right\rangle = -\,k\left\langle V_d(0)X_d(t)\right\rangle -\int _0^t K_d(s)\left\langle V_d(0)V_d(t-s)\right\rangle ds. \end{aligned}$$
(23)

This is obtained by multiplying \(V_d(0)\) to Eq. (3d) and taking ensemble average with Eq. (5b). One expected difficulty we encounter in the collisional dynamics is that the memory function contains a \(\delta \)-peak, which should be handled with care separately from the continuous part. In addition, since Eq. (23) is the first kind Volterra equation, its solution is numerically unstable. To resolve these issues, we convert Eq. (23) into its second kind equation by differentiating with respect to \(t\):

$$\begin{aligned} \left\langle F_d(0)F_d(t)\right\rangle =k M \left\langle V_d(0)V_d(t)\right\rangle +\frac{1}{\beta }K_d(t)+\int _0^t K_d(s)\left\langle V_d(0)F_d(t-s)\right\rangle ds. \end{aligned}$$
(24)

Then, we decompose \(\left\langle F_d(0)F_d(t)\right\rangle \) and \(K_d(t)\) into the \(\delta \)-peaks and continuous parts:

$$\begin{aligned} \left\langle F_d(0)F_d(t)\right\rangle =a_1\delta (t)+a_2(t),\quad K_d(t)=b_1\delta (t)+b_2(t). \end{aligned}$$
(25)

By substituting Eq. (25) into Eq. (24) and equating the \(\delta \)-peaks and continuous parts, we obtain

$$\begin{aligned} b_1=\beta a_1, \end{aligned}$$
(26)
$$\begin{aligned} \begin{array}{l@{\quad }l} \frac{1}{\beta }b_2(t) &{}+\displaystyle \int _0^t b_2(s)\left\langle V_d(0)F_d(t-s)\right\rangle ds\\ &{}=a_2(t)-kM\left\langle V_d(0)V_d(t)\right\rangle -\frac{1}{2}b_1\left\langle V_d(0)F_d(t)\right\rangle . \end{array} \end{aligned}$$
(27)

The numerical procedure to calculate the \(\delta \)-peak and continuous part of \(K_d(t)\) is summarized as follows. By using the \(\delta \)-weight \(a_1\) of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \), which is estimated from MD simulation as described above, \(b_1\) is determined by Eq. (26). Then, the continuous part \(b_2(t)\) of \(K_d(t)\) is obtained from numerically solving Eq. (27). The convolution integral is discretized by the trapezoidal rule and the values of \(b_2(n\Delta t)\) is successively obtained for \(n=1,2,\ldots \) [31, 39].

Numerical Parameters Each trajectory is calculated up to time \(T_\mathrm {sim}=10^3\) with \(\Delta t=0.01\). The time correlation functions are calculated up to time \(T_\mathrm {corr}\) from each trajectory and their ensemble averages are obtained from \(N_\mathrm {sample}\) samples. Correspondingly, the memory function is calculated up to time \(T_\mathrm {corr}\). The values of \(T_\mathrm {corr}\) and \(N_\mathrm {sample}\) are chosen as follows: for the two-dimensional frozen dynamics, \(T_\mathrm {corr}=20\), \(N_\mathrm {sample}=2^{20}\approx 10^6\); for the three-dimensional frozen dynamics, \(T_\mathrm {corr}=10\), \(N_\mathrm {sample}=2^{20}\approx 10^6\); for the two-dimensional full dynamics, \(T_\mathrm {corr}=100\), \(N_\mathrm {sample}=2^{18}\approx 2.6\times 10^5\) or \(T_\mathrm {corr}=250\), \(N_\mathrm {sample}=2^{17}\approx 1.3\times 10^5\) (only used in the computations for Fig. 10).

4.2 Frozen Dynamics Results

We first observe MD simulation results with purely elastic walls, by which we can numerically confirm our analytic results presented in Sect. 3.2. For the two-dimensional system with the parameters given in Sect. 4.1, the estimated values of the \(\delta \)-weights in \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) (\(i=1,2\)) coincide with the theoretical value. The ratio of the statistical errors to the theoretical value is estimated as \(1\times 10^{-4}\). The MD result for the tail part of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) also agrees very well with the analytic result, see Fig. 2. The statistical error at the maximum of the tail is estimated as \(7\times 10^{-3}\) of the theoretical value. Similarly, for the three-dimensional system, excellent agreement of the MD results with the analytic results is observed. The ratios of the statistical errors to the theoretical values are estimated as \(5\times 10^{-4}\) for the \(\delta \)-weights and 0.06 for the maximum value of the tail, respectively.

Now we observe the effects of the thermal walls. While the \(\delta \)-weight of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) does not depend on the accommodation factor \(\phi \), the tail part has the following dependence on \(\phi \). As the stochastic character of the walls increases (i.e., \(\phi \) increases), the tail appears at a later time and decays faster. In addition, its maximum has a smaller value and appears at a later time. In Fig. 4, the time profiles of the tail for the two extreme cases \(\phi =0\) and \(\phi =1\) are compared for \(d=2\). The tail behavior with faster decay and smaller maximum can be explained by that the repeated collision pattern is destroyed and randomized when the colliding particle is thermalized by the wall. The time delay in the appearance of the tail can be understood as follows. The time when the tail appears is related with the time for a gas particle to recollide with the hypercube. Specifically, the time when the tail is about to appear and increase is related with the recollisions of gas particles with large velocities in the transverse direction. If these particles are thermalized, their new velocities tend to be smaller and thus it takes more time for them to recollide with the wall.

Fig. 4
figure 4

For the two-dimensional systems with two values of the accommodation factor \(\phi =0\) (purely repulsive) and \(\phi =1\) (fully thermalizing), the time profiles of the frozen dynamics force autocorrelation function \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \) for the transverse direction are plotted by the dashed and solid lines, respectively. The separation distances are \(\Delta _+=\Delta _-=2.5\). In the inset, negative values in the tail of the fully thermalizing case are shown with the error bars corresponding to two standard deviations

Full size image

One more interesting observation is that under the thermal walls, the tail exhibits negative values as shown in the inset of Fig. 4. We note that this is possible only when \(F_+\) and \(F_-\) are correlated. Actually, under the thermal walls, there is a nonzero probability that a gas particle collides sequentially with the upper face, the upper wall, the lower wall, and the lower face, which contributes to the correlation of \(F_+\) and \(F_-\). Hence, the superposition of the wall effects separately calculated from \(F_+\) and \(F_-\), see Eq. (7b), is no more valid.

We also investigate the long-time tail decay behavior under the thermal wall and compare it with the purely elastic wall case, i.e., \(t^{-(d-1)}\). As described above, the long-time decay also becomes faster as \(\phi \) increases. By sufficiently increasing the separation distance \(\Delta _-\) from the lower wall, we mimic the system with a single wall and investigate the long-time decay of \(I_2^+(t)\) or \(\left\langle F_+(0)F_+(t)\right\rangle -\left\langle F_+\right\rangle ^2\). As shown in Fig. 5, under the fully thermalizing wall, the tail is observed to decay like \(t^{-3}\) for \(d=2\) and \(t^{-5}\) for \(d=3\). Under the stochastic walls, the tail is also observed in the longitudinal-direction force autocorrelation function. However, the magnitude is much smaller than the transverse direction, and the decaying exponent cannot be estimated due to relatively large statistical errors.

Fig. 5
figure 5

For the two- and three-dimensional systems with the fully thermalizing walls, where the hypercube is located near the upper wall (\(\Delta _+=2.5\)) but far from the lower wall (\(\Delta _-=44.5\)), the long-time decays of the autocorrelation function of \(F_+\) is observed through the log–log plot of the normalized \(I_2^+(t)\) versus \(t\). Error bars correspond to the statistical errors with two standard deviations. For comparison, the decays of \(t^{-3}\) and \(t^{-5}\) are also plotted

Full size image

4.3 Full Dynamics Results

From the two-dimensional full-dynamics simulations, we mainly observe the memory function \(K_i^M(t)\) in the \(x_i\)-direction, where the superscript \(M\) indicates the mass of the hypercube. As we increase \(M\), we compare this function with the corresponding limit memory function \(K_i^\mathrm {BL}(t)\) to confirm the analytic expression of \(K_i^\mathrm {BL}(t)\), see Eq. (12), and investigate the convergence behaviors of \(K_i^M(t)\) to \(K_i^\mathrm {BL}(t)\). We decompose \(K_i^M(t)\) as the sum of the \(\delta \)-peak and tail parts: \(K_i^M(t)=2\gamma _i^{M,\delta }\delta (t)+\tilde{K}_i^M(t)\). We added the superscript \(\delta \) in the \(\delta \)-weight to emphasize that it is obtained from the \(\delta \)-peak rather than the time integral of \(K_i^M(t)\). We first observe the \(\delta \)-peak in the memory function and then the tail part.

For both longitudinal and transverse directions to the channel (i.e., \(i=1,2\)), we observe that \(\gamma _i^{M,\delta }\) has a smaller value than \(\gamma _i^*\) and converges to \(\gamma _i^*\) as \(M\) increases. We also observe that \(\gamma _1^{M,\delta }/L_2\) and \(\gamma _2^{M,\delta }/L_1\) have the (statistically) same value for a wide range of values of \(M\). Although this would be quite expected in the free unbounded case, this implies, in our case, that the \(\delta \)-peak depends neither on the confined geometry nor on the external potential as long as the surrounding ideal gas stays in the identical equilibrium state. In Fig. 6, the deviation \(\gamma _i^{M,\delta }-\gamma _i^*\) is plotted versus \(M\), where a clear linear dependence on \(M^{-1}\) is shown. Hence, we observe

$$\begin{aligned} \gamma _i^{M,\delta }=\gamma _i^* - \mathrm {O}(M^{-1}),\quad i=1,2,\ldots ,d. \end{aligned}$$
(28)
Fig. 6
figure 6

For various values of the mass \(M\) of the hypercube in the two-dimensional system, the \(\delta \)-weights \(\gamma _i^{M,\delta }\) in the memory functions \(K_i^{M}(t)\) are estimated and their deviations from the Brownian-limit values \(\gamma _i^*\) in the unbounded case are plotted versus \(M\) in the log–log plot with the error bars corresponding to two standard deviations. The force constant of the harmonic potential is \(k=4\). For comparison, \(M^{-1}\) is also plotted

Full size image

Now we observe the convergence of the tail part \(\tilde{K}_d^M(t)\). In Fig. 7, the time profiles of \(\tilde{K}_d^M(t)\) are plotted for various values of \(M\). For sufficiently large values of \(M\), the tail has a similar shape to the limit memory function; after achieving the maximum, the tail monotonically decreases. From these results, we confirm the convergence of \(\tilde{K}_d^M(t)\) to \(\tilde{K}_d^\mathrm {BL}(t)\); as \(M\) increases, the magnitude of the tail increases and it becomes closer to \(\tilde{K}_d^\mathrm {BL}(t)\). Then, we investigate the scaling behavior of the deviation \(\tilde{K}_d^M(t)-\tilde{K}_d^\mathrm {BL}(t)\) with respect to the mass \(M\). In Fig. 8, the following form of scaling behavior is tested

$$\begin{aligned} \tilde{K}_d^M(t)\approx \tilde{K}_d^\mathrm {BL}(t)+\frac{1}{\sqrt{M}}g\left( \frac{t}{\sqrt{M}}\right) . \end{aligned}$$
(29)

From the coincidence of the scaled curves, Eq. (29) is confirmed and the shape of the function \(g(t)\) is obtained.

Fig. 7
figure 7

The time profiles of the transverse-direction memory function \(K_d^M(t)\) are plotted for various values of \(M\). The force constant of the harmonic potential is \(k=4\). For comparison, the limit memory function \(K_d^\mathrm {BL}(t)\) is plotted by the dashed line

Full size image

For the other values of the force constant \(k\), we similarly observe the convergence. In Fig. 9, the time profiles of \(\tilde{K}_d^M(t)\) with the largest value of \(M=500\) are compared with those of the corresponding \(\tilde{K}_d^\mathrm {BL}(t)\) for various values of \(k\). For each value of \(k\), two time profiles show clear agreement, which confirms again Eq. (12). As \(k\) increases, the tail appears later. This is because the hypercube tends to stay in the middle of the channel under a stiffer harmonic potential and thus it takes more time for a gas particle to recollide with either the upper or lower face. For the chosen values of \(k\), the decaying parts of the tail are quite similar.

Fig. 8
figure 8

The deviation of the memory function \(K_d^M(t)\) from the limit memory function \(K_d^\mathrm {BL}(t)\) is plotted versus \(t\). For three values of the mass \(M\) of the hypercube, the magnitude of the deviations and time are scaled with respect to \(\sqrt{M}\), see Eq. (29). Since the time profiles of \(K^M_d(t)\) are calculated up to time 100 in all cases, the time domains of the scaled curves become shorter as \(M\) increases. The force constant of the harmonic potential is \(k=4\)

Full size image
Fig. 9
figure 9

The time profile of the transverse-direction memory function \(K_d^M(t)\) are plotted for three values of the force constant \(k\). The mass of the hypercube is \(M = 500\). For comparison, corresponding time profiles of the limit memory function \(K_d^\mathrm {BL}(t)\) are plotted by the dashed lines

Full size image

We finally report that a slow oscillation is observed after the main peak of the tail for small values of \(M\). We first check whether it is a numerically spurious one. We note that insufficient sample averaging of the time correlation functions may cause a spurious oscillatory tail as follows. When we determine the value of \(K_d^M(n\Delta t)\) from Eq. (27), we use estimated values of the \(\delta \)-weight and estimated time correlation functions up to time \(n\Delta t\), which contain statistical errors. As a result, the solution also accumulates errors. In this case, the error in the solution satisfies a similar Volterra equation [31] and thus it is proportional to the statistical errors in the input values. We observe that the use of insufficient sample average causes a spurious oscillatory tail, the magnitude and phase of which may be very different among independent realizations. This unfavorable effects of course can be reduced by increasing the size of sample average, which, however, seriously increases computational cost. By increasing the sample size, we rule out the possibility that numerically originated spurious oscillation dominates the long-time tail. In Fig. 10, the slow oscillations in \(K_d^M(t)\) are shown for small values of \(M\). We observe that the period is inversely proportional to \(\sqrt{k}\) and the magnitude is proportional to \(\sqrt{k}\). In addition, we observe that as \(M\) increases, the magnitude decreases and the period increases. Due to the computational limitations, however, quantitative analysis is not systematically performed.

Fig. 10
figure 10

The time profiles of \(K_d^M(t)\) are plotted up to time 250 for three sets of values \((M,k)\): (10,4) (squares), (10,8) (circles), and (20,4) (triangles). Error bars correspond to the statistical errors with two standard deviations

Full size image

5 Derivation

5.1 GLE

In order to derive Eqs. (3)–(5), we use the Mori projection method [36, 40]. Since the Mori projection operator is defined in terms of equilibrium average, we discuss the equilibrium distribution of the hypercube and the ensemble averages of relevant quantities in Sect. 5.1.1. We present the standard form of the GLE obtained from the Mori projection method in Sect. 5.1.2. Then, we show how this equation is reduced to Eq. (3) in our specific case in Sect. 5.1.3.

5.1.1 Equilibrium Distribution and Average

We assume the system is in equilibrium and follows the Boltzmann distribution. The equilibrium distribution of the hypercube is expressed as

$$\begin{aligned} \rho _\mathrm {eq}(\mathbf {X},\mathbf {V}) =\rho _1(X_1,X_2,\ldots ,X_{d-1})\rho _2(X_d)\rho _\mathbf {V}(\mathbf {V}) \end{aligned}$$
(30)

and \(\rho _1\) and \(\rho _\mathbf {V}\) follow the uniform and Maxwell–Boltzmann distribution, respectively. The approximation of \(\rho _2(X_d)\) by \(\rho (X_d)\) defined in Eq. (6) for large \(k\) is explained as follows. Suppose that a repulsive interaction potential \(U\) between the hypercube and the walls is imposed and it depends on the separation distance from a wall with short cutoff distance \(\epsilon \). Then, \(\rho _2(X_d)\) is expressed as

$$\begin{aligned} \rho _2(X_d)\propto e^{-\beta \left[ \frac{1}{2}kX_d^2+U\left( h_+-X_d-\frac{1}{2}L_d\right) +U\left( X_d-\frac{1}{2}L_d-h_-\right) \right] } \end{aligned}$$
(31)

for \(X_d\in \left( h_-+\frac{1}{2}L_d,h_+-\frac{1}{2}L_d\right) \). If \(k\) is sufficiently large that the probability of the hypercube being in the interaction range of \(U\) is negligible, \(\rho _2(X_d)\) is approximated by \(\rho (X_d)\). Hence, the validity depends on the distances \(|h_\pm \mp \epsilon |\) as well as \(k\) and \(\beta \). Actually, the assumption becomes exactly valid as \(h_\pm \rightarrow \pm \infty \), which corresponds to the case that the hypercube is subject to the harmonic potential but suspended in an unbounded ideal gas.

From Eq. (30) with \(\rho _2(X_d)\) replaced by \(\rho (X_d)\), we obtain the following equilibrium averages, which are used in Sect. 5.1.3:

$$\begin{aligned} \begin{array}{l@{\quad }l} &{}\left\langle V_i^2\right\rangle =\left( \beta M\right) ^{-1},\quad \left\langle V_i F_i\right\rangle =0,\quad \text{ for } i=1,2,\ldots ,d,\\ &{}\left\langle X_d^2\right\rangle =\left( \beta k\right) ^{-1},\quad \left\langle X_d V_d\right\rangle =0,\quad \left\langle X_d F_d\right\rangle =-\beta ^{-1}, \end{array} \end{aligned}$$
(32)

where \(\mathbf {F}=(F_1,F_2,\ldots ,F_d)\equiv M\dot{\mathbf {V}}\). The other ensemble averages containing two quantities from different directions (e.g., \(\left\langle X_d V_1 \right\rangle \)) are all zero.

Ensemble averages containing the force need some discussion. In a collisional dynamics, \(\left\langle V_i(0)F_i(t)\right\rangle \) has a jump discontinuity at \(t=0\), which can be seen from that its time derivative \(-\frac{1}{M}\left\langle F_i(0)F_i(t)\right\rangle \) has a delta function due to elastic collisions. Hence, \(\left\langle V_iF_i\right\rangle \) is actually undefined. This is also explained by that the velocity of the hypercube discontinuously changes whenever a collision occurs and thus \(\left\langle V_i(0)F_i(0+)\right\rangle \) and \(\left\langle V_i(0)F_i(0-)\right\rangle \) are different. On the other hand, in a system under a continuous interaction potential, \(\left\langle V_i(0)F_i(t)\right\rangle \) is continuous \(t=0\) and \(\left\langle V_iF_i\right\rangle =0\) from \(\left\langle V_i(0)F_i(-t)\right\rangle =-\left\langle V_i(0)F_i(t)\right\rangle \). By considering that our system is obtained as a limit where a continuous repulsive potential becomes an infinite potential barrier, we formally define \(\left\langle V_iF_i\right\rangle =0\). The average \(\left\langle X_d F_d\right\rangle \) is obtained from that the conditional expectation of \(F_d\) given \(X_d\) is \(-k X_d\) and thus \(\left\langle X_d F_d\right\rangle =-k\left\langle X_d^2\right\rangle \).

5.1.2 Mori Projection

For a phase variable \(\mathbf {A}=(A_1,A_2,\ldots ,A_n)^T\) defined on a Hamiltonian system, the Mori projection operators are defined as

$$\begin{aligned} \mathcal {P}(\bullet )=\left\langle \,\bullet \,\mathbf {A}^*\right\rangle \left\langle \mathbf {A}\mathbf {A}^*\right\rangle ^{-1}\mathbf {A},\quad \mathcal {Q}=\mathcal {I}-\mathcal {P}, \end{aligned}$$
(33)

where subscripts \(^T\) and \(^*\) denote the transpose and the conjugate transpose, respectively, and \(\mathcal {I}\) is the identity operator. The time evolution equation of \(\mathbf {A}\), \(\dot{\mathbf {A}}(t)=i\mathcal {L}\mathbf {A}(t)\), where \(i\mathcal {L}\) is the Liouville operator of the system, is cast into the following GLE:

$$\begin{aligned} \frac{d}{dt}\mathbf {A}(t)=i\mathbf {\Omega }\mathbf {A}(t)-\int _0^t \mathbf {K}(t-s)\mathbf {A}(s)ds+\mathbf {B}(t), \end{aligned}$$
(34)

where the frequency matrix \(i\mathbf {\Omega }\), the fluctuating force vector \(\mathbf {B}(t)\), and the memory function matrix \(\mathbf {K}(t)\) are defined as

$$\begin{aligned}&i\mathbf {\Omega }=\left\langle (i\mathcal {L}\mathbf {A})\mathbf {A}^*\right\rangle \left\langle \mathbf {A}\mathbf {A}^*\right\rangle ^{-1},\end{aligned}$$
(35a)
$$\begin{aligned}&\mathbf {B}(t)=e^{\mathcal {Q}i\mathcal {L}t}\mathcal {Q}i\mathcal {L}\mathbf {A}(0),\end{aligned}$$
(35b)
$$\begin{aligned}&\mathbf {K}(t)=\left\langle \mathbf {B}(t)\mathbf {B}^*(0)\right\rangle \left\langle \mathbf {A}\mathbf {A}^*\right\rangle ^{-1}. \end{aligned}$$
(35c)

Since \(\mathcal {P}\mathbf {B}(t)=0\), the following condition holds:

$$\begin{aligned} \left\langle \mathbf {B}(t)\mathbf {A}^*(0)\right\rangle =0, \end{aligned}$$
(36)

which implies every pair of a component of \(\mathbf {A}(0)\) and that of \(\mathbf {B}(t)\) is uncorrelated.

5.1.3 Derivation of Eqs. (3)–(5)

We apply the results in Sect. 5.1.2 to phase variable \(\mathbf {A}=(X_d,V_1,V_2,\ldots ,V_d)^T\). A technical difficulty of including \(X_i\) (\(i=1,2,\ldots ,d-1\)) is that \(\left\langle X_i^2\right\rangle \) is not clearly defined. Since Eq. (3b) for \(\dot{V}_i(t)\) (\(i=1,2,\ldots ,d-1\)) does not contain \(X_i(t)\), Eq. (3a) for \(\dot{X}_i(t)\) can be included after obtaining Eqs. (3b)–(3d).

The frequency matrix \(i\mathbf {\Omega }\) is calculated from Eq. (35a). By substituting Eq. (32) into \(\left\langle (i\mathcal {L}\mathbf {A})\mathbf {A}^*\right\rangle \) and \(\left\langle \mathbf {A}\mathbf {A}^*\right\rangle \), \(i\mathbf {\Omega }\) becomes a matrix containing two nonzero elements \((i\mathbf {\Omega })_{1,d}=1\) and \((i\mathbf {\Omega })_{d,1}=-\frac{k}{M}\). Hence, we obtain

$$\begin{aligned} i\mathbf {\Omega }\mathbf {A}(t)=\left( V_d,0,0,\ldots ,-\frac{k}{M}X_d\right) . \end{aligned}$$
(37)

Many components of \(\mathbf {K}(t)\) and the first component of \(\mathbf {B}(t)\) become zero in our case, as seen in Eq. (3). Although the resulting equation is consistent with physical intuition, showing this without relying on it is not straightforward. It is because \(\mathbf {K}(t)\) is defined through the fluctuation-dissipation relation, Eq. (35c), in terms of the orthogonal dynamics \(\mathbf {B}(t)\). We first consider the simplest case \(d=2\) and show which components of \(\mathbf {K}(t)\) and \(\mathbf {B}(t)\) are nonzero. Then, we discuss the general case and derive Eqs. (3)–(5).

For \(d=2\), the GLE is written as

(38)

where the subscripts in the matrix and vectors indicate the time that their components are evaluated. Since \(\dot{X}_2=V_2\), the first component of vector equation (38) becomes

$$\begin{aligned} \int _0^t K_{11}(s)X_2(t-s)ds+ \int _0^t K_{12}(s)V_1(t-s)ds+ \int _0^t K_{13}(s)V_2(t-s)ds+ B_1(t)=0. \end{aligned}$$
(39)

By multiplying \(X_2(0)\), \(V_1(0)\), and \(V_2(0)\) and taking average, we have

$$\begin{aligned}&\int _0^t K_{11}(s)\left\langle X_2(0)X_2(t-s)\right\rangle ds+ \int _0^t K_{13}(s)\left\langle X_2(0)V_2(t-s)\right\rangle ds=0,\end{aligned}$$
(40a)
$$\begin{aligned}&\int _0^t K_{12}(s)\left\langle V_1(0)V_1(t-s)\right\rangle ds=0,\end{aligned}$$
(40b)
$$\begin{aligned}&\int _0^t K_{11}(s)\left\langle V_2(0)X_2(t-s)\right\rangle ds+ \int _0^t K_{13}(s)\left\langle V_2(0)V_2(t-s)\right\rangle ds=0. \end{aligned}$$
(40c)

Here, we have used Eq. (36). Differentiating Eq. (40a) with respect to \(t\) and adding Eq. (40c), we obtain \(\left\langle X_2^2\right\rangle K_{11}(t)=0\) and thus \(K_{11}(t)=K_{13}(t)=0\). From Eq. (40b), we have \(K_{12}(t)=0\). Hence, we have \(B_1(t)=0\) and the first component of the vector equation becomes \(\dot{X}_2=V_2\), as expected. For the other components, the same procedure is applicable to show that \(K_{21}(t)=K_{23}(t)=K_{31}(t)=K_{32}(t)=0\). Therefore, only \(K_{22}(t)\) and \(K_{33}(t)\) are nonzero components. In addition, from Eq. (35c), we have \(K_{22}(t)=\beta M\left\langle B_2(0)B_2(t)\right\rangle \), \(K_{33}(t)=\beta M\left\langle B_3(0)B_3(t)\right\rangle \), \(\left\langle B_2(0)B_3(t)\right\rangle =\left\langle B_3(0)B_2(t)\right\rangle =0\). From Eq. (36), we also have \(\left\langle X_2(0)B_i(t)\right\rangle =\left\langle V_1(0)B_i(t)\right\rangle =\left\langle V_2(0)B_i(t)\right\rangle =0\) for \(i=2,3\).

For the \(d\)-dimensional case, we can similarly show (i) \(K_{ii}(t)\) and \(B_i(t)\) (\(i=2,3,\ldots ,d+1\)) are nonzero; (ii) \(K_{ii}(t)=\beta M\left\langle B_i(0)B_i(t)\right\rangle \); (iii) \(\left\langle B_{i}(0)B_{j}(t)\right\rangle =0\) for \(i\ne j\); (iv) \(\left\langle X_d(0)B_i(t)\right\rangle =0\) (\(i=2,3,\ldots ,d+1\)); and (v) \(\left\langle V_i(0)B_j(t)\right\rangle =0\) (\(i=1,2,\ldots ,d\) and \(j=2,3,\ldots ,d+1\)). Eq. (3) is obtained by defining \(K_i(t)\) and \(F^+_i(t)\) (\(i=1,2,\ldots ,d\)) in Eq. (3) as \(M K_{i+1,i+1}(t)\) and \(M B_{i+1}(t)\), respectively. Then, Eqs. (4) and (5) are obtained from (ii)–(v).

5.2 Frozen Dynamics Force Autocorrelation Function

In this section, we derive the analytic expression for \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) (\(i=1,2,\ldots ,d)\) given in Eq. (7). For the frozen dynamics with the purely elastic walls and the fixed hypercube of the upright orientation, we make the following observations, which our derivation is based on:

  1. (i)

    if a gas particle collides with a face, it never collides with the other faces;

  2. (ii)

    repeated collisions with the hypercube are possible only when a gas particle collides with the upper or lower face;

  3. (iii)

    \(F_{0,i}(t)\) is attributed to the collisions with the faces normal to the \(x_i\)-axis.

For the schematic of the repeated collisions in the case of \(d=3\), see Fig. 1b.

From observations (i) and (iii) and \(\left\langle F_{0,i}\right\rangle =0\) (\(i=1,2,\ldots ,d\)) by symmetry, all cross-correlations \(\left\langle F_{0,i}(0)F_{0,j}(t)\right\rangle \) (\(i\ne j\)) become zero. From observation (ii), \(\left\langle F_{0,i}(0)F_{0,i}(t)\right\rangle \) (\(i=1,2,\ldots ,d-1\)) contains only a \(\delta \)-peak. We also note that the form of the \(\delta \)-weight is the same as that of \(\left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle \). In fact, by taking the separation distances \(\Delta _\pm \) to infinity, we have \(I_2^\pm (t)\rightarrow 0\) and retrieve the unconfined case. Hence, in what follows, we only derive Eq. (7b). To this end, we decompose the force \(F_{0,d}=F_+ + F_-\), where \(F_+\) and \(F_-\) are the forces on the upper and lower faces, respectively. By using that \(F_+\) and \(F_-\) are uncorrelated, we have

$$\begin{aligned} \left\langle F_{0,d}(0)F_{0,d}(t)\right\rangle = \left\langle F_+(0)F_+(t)\right\rangle + \left\langle F_-(0)F_-(t)\right\rangle +2\left\langle F_+\right\rangle \left\langle F_-\right\rangle . \end{aligned}$$
(41)

In Sect. 5.2.1, we explain in detail the geometry and initial configuration of the system in the frozen dynamics. In Sect. 5.2.2, we express \(\left\langle F_+\right\rangle \) and \(\left\langle F_+(0)F_+(t)\right\rangle \) as ensemble averages of functionals of the single-gas-particle trajectory. In Sect. 5.2.3, we analyze the single-gas-particle trajectories contributing to the ensemble averages. In Sect. 5.2.4, we obtain analytic expressions for \(\left\langle F_\pm \right\rangle \) and \(\left\langle F_\pm (0)F_\pm (t)\right\rangle \) and, thus, Eq. (7b).

5.2.1 Geometry and Initial Configuration

Since translating the system does not affect the frozen dynamics, we assume that the upper wall is located at \(x_d=\Delta _+\) and the upper face of the fixed hypercube is on the plane \(x_d=0\). Furthermore, we assume that the domain of the upper face on the plane is denoted as \((0,L_1)\times (0,L_2)\times \cdots \times (0,L_{d-1})\). For the case \(d=3\), see Fig. 1b.

We assume that the system is initially at equilibrium and the initial configuration of the system is described by the Poisson field as follows. By denoting the position and velocity of a gas particle as \(\mathbf {x}=(x_1,x_2,\ldots ,x_d)\) and \(\mathbf {v}=(v_1,v_2,\ldots ,v_d)\), respectively, the probability that a gas particle is found in the volume element \(d\mathbf {x}d\mathbf {v}\) is given as

$$\begin{aligned} \lambda (d\mathbf {x},d\mathbf {v}) =a\left( \prod _{i=1}^d \varphi (v_i) dx_idv_i \right) \mathbb {I}_{\mathrm {geom}}(\mathbf {x}), \end{aligned}$$
(42)

where \(\varphi (v)=\sqrt{\frac{\beta m}{2\pi }}e^{-\frac{\beta m}{2}v^2}\) and \(\mathbb {I}_{\mathrm {geom}}(\mathbf {x})\) is 1 if \(\mathbf {x}\) is in the geometrically accessible region (i.e., outside the hypercube and between the walls) and otherwise 0. In other words, the gas particles are distributed uniformly outside the hypercube with the number density \(a\) and their velocities following the Maxwell–Boltzmann distribution.

5.2.2 Reduction to Single-Gas-Particle Properties

Since the dynamics of each gas particle is decoupled from those of the other gas particles in the frozen dynamics, we express \(\left\langle F_+\right\rangle \) and \(\left\langle F_+(0)F_+(t)\right\rangle \) in terms of a single particle quantity. By denoting the \(x_d\)-component of the force exerted on the upper face by the gas particle with initial condition \((\mathbf {x},\mathbf {v})\) as \(f_+(t;\mathbf {x},\mathbf {v})\), these quantities are expressed as

$$\begin{aligned}&\left\langle F_+\right\rangle =\int f_+(0;\mathbf {x},\mathbf {v})\lambda (d\mathbf {x},d\mathbf {v}),\end{aligned}$$
(43)
$$\begin{aligned}&\left\langle F_+(0)F_+(t)\right\rangle =\int f_+(0;\mathbf {x},\mathbf {v})f_+(t;\mathbf {x},\mathbf {v})\lambda (d\mathbf {x},d\mathbf {v})+\left\langle F_+\right\rangle ^2. \end{aligned}$$
(44)

These expressions are obtained as follows. By denoting the initial configuration of the ideal gas as \(\left\{ \mathbf {x}^{(\alpha )},\mathbf {v}^{(\alpha )}\right\} _{\alpha =1}^\infty \), we define the corresponding measure \(\mu (d\mathbf {x},d\mathbf {v})=\sum _{\alpha =1}^\infty \delta (\mathbf {x}-\mathbf {x}^{(\alpha )})\delta (\mathbf {v}-\mathbf {v}^{(\alpha )})d\mathbf {x}d\mathbf {v}\). Since the initial configuration is given as the Poisson field with mean \(\lambda (d\mathbf {x},d\mathbf {v})\), we have \(\left\langle \mu (d\mathbf {x},d\mathbf {v})\right\rangle =\lambda (d\mathbf {x},d\mathbf {v})\). Hence, from \(F_+(t)=\int f_+(t;\mathbf {x},\mathbf {v})\mu (d\mathbf {x},d\mathbf {v})\), we obtain Eq. (43). We obtain Eq. (44) by using the decomposition \(\mu (d\mathbf {x},d\mathbf {v})=\lambda (d\mathbf {x},d\mathbf {v})+\tilde{\mu }(d\mathbf {x},d\mathbf {v})\) and applying the following Itô isometry for \(\tilde{\mu }(d\mathbf {x},d\mathbf {v})\)

$$\begin{aligned} \left\langle \int f_+(0)\tilde{\mu }(d\mathbf {x},d\mathbf {v}) \int f_+(t)\tilde{\mu }(d\mathbf {x},d\mathbf {v}) \right\rangle =\int f_+(0)f_+(t) \lambda (d\mathbf {x},d\mathbf {v}). \end{aligned}$$
(45)

As in Eq. (45), we suppress the dependence on \((\mathbf {x},\mathbf {v})\) unless needed.

5.2.3 Meaningful Trajectories

In Eqs. (43) and (44), we note that we only need to consider gas particles colliding with the upper face instantaneously (i.e., at \(t=0\)). However, in order to properly handle with the \(\delta \)-character in \(f_+(0)\), we consider all gas particles colliding first with the upper face. By introducing the indicator function \(\mathbb {I}(A)\), which is 1 if the condition \(A\) is valid and otherwise 0, these particles are characterized by the following function:

$$\begin{aligned} \mathbb {I}_0(\mathbf {x},\mathbf {v})=\mathbb {I}\left( 0<x_d<\Delta _+,v_d<0\right) \prod _{i=1}^{d-1}\mathbb {I}\left( 0<x_i-\frac{x_d}{v_d}v_i<L_i \right) \!. \end{aligned}$$
(46)

For the gas particle satisfying \(\mathbb {I}_0=1\), the collision time is given as \(\tau _0=-x_d/v_d\) and \(f_+(t)\) is expressed as

$$\begin{aligned} f_+(t)= 2mv_d\left[ \mathbb {I}_0\delta (t-\tau _0)+\sum _{n=1}^\infty \mathbb {I}_n\delta (t-\tau _n)\right] \!, \end{aligned}$$
(47)

where \(\mathbb {I}_n\) indicates whether the \((n+1)\)th collision with the upper face occurs and \(\tau _n\) is the corresponding collision time.

5.2.4 \(\left\langle F_\pm \right\rangle \) and \(\left\langle F_\pm (0)F_\pm (t)\right\rangle \)

Calculating \(\left\langle F_+\right\rangle \) is straightforward. We first integrate \(f_+(0)=-2mv_d^2\mathbb {I}_0\delta (x_d)\) with respect to \(x_d\) and obtain \(\int f_+(0)dx_d=-2mv_d^2\bar{\mathbb {I}}_0\), where

$$\begin{aligned} \bar{\mathbb {I}}_0=\mathbb {I}(v_d<0)\prod _{i=1}^{d-1}\mathbb {I}(0<x_i<L_i). \end{aligned}$$
(48)

We note that integrating \(\delta (x_d)\) led us to take the limit \(x_d\rightarrow 0\) for the remaining terms and the overbar notation was introduced for this limit. By further integrating with respect to \((x_1,x_2,\cdots ,x_{d-1})\) and \(\mathbf {v}\), we obtain

$$\begin{aligned} \left\langle F_+\right\rangle =-2m (a L_1 L_2 \cdots L_{d-1}) \int _{-\infty }^0 v_d^2 \varphi (v_d)dv_d =-\frac{a}{\beta }L_1 L_2 \cdots L_{d-1}. \end{aligned}$$
(49)

We note that \(\left\langle F_+\right\rangle \) does not depend on the separation distance \(\Delta _+\).

Now we obtain an analytic expression for \(\left\langle F_+(0)F_+(t)\right\rangle \). As we did for \(f_+(0)\) above, we first integrate \(f_+(0)f_+(t)\) with respect to \(x_d\) and obtain

$$\begin{aligned} \int f_+(0)f_+(t)dx_d =-4m^2v_d^3\left[ \bar{\mathbb {I}}_0\delta (t)+\sum _{n=1}^\infty \bar{\mathbb {I}}_n\delta (t-\bar{\tau }_n)\right] \!, \end{aligned}$$
(50)

where

$$\begin{aligned} \bar{\mathbb {I}}_n=\bar{\mathbb {I}}_0\prod _{i=1}^{d-1}\mathbb {I}\left( 0<x_i-\frac{2n\Delta _+ v_i}{v_d}<L_i\right) \!,\quad \bar{\tau }_n=-\frac{2n\Delta _+}{v_d}. \end{aligned}$$
(51)

We note that \(\bar{\mathbb {I}}_n\) checks whether the gas particle collides with the upper face of the hypercube instantaneously at \(t=0\) and then has further \(n\) successive collisions. From Eq. (50), the integration of \(f_+(0)f_+(t)\) with respect to \(\lambda (d\mathbf {x},d\mathbf {v})\) is decomposed into two parts as follows:

$$\begin{aligned} \int f_+(0)f_+(t) \lambda (d\mathbf {x},d\mathbf {v})=I_1\delta (t)+I^+_2(t). \end{aligned}$$
(52)

We note that the \(\delta \)-peak is attributed to the instantaneous collision whereas the tail part \(I^+_2(t)\) is due to the repeated collisions. We obtain the intensity of the \(\delta \)-peak as follows:

$$\begin{aligned} I_1 =-4m^2(a L_1 L_2 \cdots L_{d-1})\int _{-\infty }^0 v_d^3\varphi (v_d)dv_d =\frac{4a}{\beta }\sqrt{\frac{2m}{\pi \beta }}L_1 L_2\cdots L_{d-1}. \end{aligned}$$
(53)

Calculating the tail part is more involved since the domain of integration with respect to \((x_1,x_2,\ldots ,x_{d-1})\) and \((v_1,v_2,\ldots ,v_{d-1})\) is restricted by \(\bar{\mathbb {I}}_n=1\). \(I^+_2(t)\) is expressed as

$$\begin{aligned} I^+_2(t)=-4am^2\sum _{n=1}^\infty \int _{-\infty }^0 dv_d\; \delta \left( t+\frac{2n\Delta _+}{v_d}\right) v_d^3\varphi (v_d) \prod _{i=1}^{d-1} J_{i,n}(v_d,t), \end{aligned}$$
(54)

where

$$\begin{aligned} J_{i,n}(v_d,t) = \int _0^{L_i} dx_i \int _{\frac{v_d x_i}{2n\Delta _+}}^{-\frac{v_d(L_i-x_i)}{2n\Delta _+}}dv_i \varphi (v_i). \end{aligned}$$
(55)

By using \(\delta \left( t+\frac{2n\Delta _+}{v_d}\right) =\frac{2n\Delta _+}{t^2}\delta \left( v_d+\frac{2n\Delta _+}{t}\right) \), we perform the integration with respect to \(v_d\) and finally obtain \(I^+_2(t)=I_2(t;\Delta _+)\).

For the force \(F_-\), we follow the same procedure to obtain \(\left\langle F_-\right\rangle =-\left\langle F_+\right\rangle \) and similar expressions to Eqs. (44) and (52) with all plus subscripts replaced with minus ones and \(I_2^-(t)=I_2(t;\Delta _-)\). By substituting them into Eq. (41), we finally obtain Eq. (7b).

6 Summary and Discussion

We have systematically investigated Brownian motion of the \(d\)-dimensional hypercube in the slit-pore through the analytical and computational analysis of its memory function. The hypercube interacts with the surrounding ideal gas particles via elastic collisions. To avoid direct interaction with the walls, the hypercube is also subject to a stiff harmonic potential along the transverse direction to the channel.

In the analytic approach, for the case where the hypercube has a finite mass and every collision in the system is elastic, we have obtained the GLE [Eqs. (3)–(5)] from the Mori projection method. Then, we have obtained the limit memory function [Eq. (12)] from the analytic expression of the frozen dynamics force autocorrelation function [Eq. (7)] through the adiabatic approximation [Eq. (11)]. From the emergence of the power-law decaying (\(t^{-(d-1)}\)) tail in the transverse direction [Eq. (10)], we have observed the anomalous diffusion for \(d=2\) and the increase in the position-dependent friction coefficient for \(d=3\) [Eqs. (16) and (18)].

In the MD simulation approach, we have numerically verified our analytic results by observing the convergence of the finite-mass memory function to the limit memory function. We have also observed its converging behaviors [Eqs. (28)–(29)]. In addition, the effects of stochastic thermal walls have been investigated. We have observed that the superposition of wall effects is no more valid and that the long-time decay of the transverse-direction memory function due to a single wall becomes faster (\(t^{-3}\) for \(d=2\) and \(t^{-5}\) for \(d=3\)).

We have used these two approaches in a complementary way. Elastic collisions introduce a series of delta functions in the force on the hypercube. Hence, handling the force properly with care is required in the analytic approach. Moreover, results obtained by using delta functions cannot be rigorously justified. Our analytic results possessing the following issues have been numerically verified by MD simulations: application of the Mori GLE to collisional dynamics, formal definition of \(\left\langle V_i F_i\right\rangle =0\), approximation of \(\rho (X_d)\), adiabatic approximation [Eq. (11)], convergence of the memory function. In addition, by MD simulations, we have observed the system with the finite-mass hypercube and/or thermal walls, which is not easily investigated by the analytic approach. On the other hand, we have developed the numerical procedure to calculate the \(\delta \)-weight and continuous part of the memory function from MD trajectories and verified it with the analytic results.

The deviation of the finite-mass memory function from its limit memory function is related with how inaccurate the adiabatic approximation is for a given value of mass \(M\). We have observed that the scaling behavior of the deviation with respect to \(M\) is different from the free unbounded case [18, 22]. In the free unbounded case, the leading term in the deviation is attributed to nonzero velocity of the Brownian particle, which we believe is also true in our case. Compared with the free unbounded case, where the linear dependence on the velocity disappears by the isotropy of the system, we expect that this linear dependence does not disappear in our case, which may be related with the \(\sqrt{M}\)-dependence of the tail deviation (note that the velocity is \(\mathrm {O}(M^{-1/2})\) from the equipartition theorem). Another possible origin of the deviation is the coupling with the harmonic force. For small values of \(M\), we have clearly observed that the memory function contains a slow oscillation and its magnitude and period depend on the force constant \(k\) as well as the mass \(M\). We expect that for larger value of \(M\) this oscillatory tail is still present although it is computationally difficult to clearly characterize it due to its small magnitude and its large period.

Finally, we discuss the fixed upright orientation of the hypercube. As demonstrated in this paper, it allows enormous analytic tractability for the analysis of the frozen dynamics. The trajectories of gas particles become simple and the effects of the two purely elastic walls can be separately considered and superimposed. Using these properties, we have obtained the analytic expressions and expected anomalous diffusion in the two-dimensional case. As mentioned in Sect. 1, our results explain why the convergence to normal diffusion has not been proved for the two-dimensional case in Ref. [4]. However, we think that the \(t^{-1}\) decay behavior may be singular in the sense that under any tilted orientations faster decay is expected. It is because the repeated collisions with the same patterns are no more possible under these orientations. In addition, the regular collision patterns are also easily destroyed by the thermal walls, which causes faster decay. Regarding the effects of geometric shape, we are currently investigating the Brownian motion of a disk and a sphere in a slit pore with thermal walls and the effects of confinement with thermal walls and we will present our results in the future publication.