1 Introduction

The ability of biodiesel to contribute to the solutions of problems and concerns from air pollution, global warming, environmental improvements and other sustainability issues, has led to its widespread production. The bio-fuel so produced has resulted in the abundant availability of bio-glycerol, a by-product of the biodiesel industry [1]. This bio-glycerol finds an application in the etherification of 2-methylpropan-2-ol to produce tert-butyl ethers of glycerol (high content of the di-ethers), which are potential alternatives to diesel fuel, with high gasoline octane booster capabilities [2, 3]. 2-Methylpropan-2-ol, being an important etherification reagent, has a major dehydration issue, mainly due to the formation of a minimum boiling azeotrope with water that restricts its industrial applicability [4, 5]. Among the various alternatives, extractive distillation with the aid of glycols as an entrainer is a promising method for the dehydration of 2-methylpropan-2-ol [6, 7]. Ethane-1,2-diol is found to dehydrate 2-methylpropan-2-ol efficiently, due to its water-like hydrogen bond network structure and lower molar mass.

In the design of extractive distillation, knowledge of phase equilibrium data at ambient and low pressures is vital to establish appropriate relation between temperature and pressure as well as to determine the capacity of the solvent [8, 9]. Further, the volumetric properties of liquid mixtures provide information about the character the of the solute–solute, solvent–solvent and solute–solvent pair interactions in a mixture. The properties also shed light on packing effects which arise due to different sizes of the molecules [10, 11].

A literature survey reveals that various thermo-physical properties of the systems 2-methylpropan-2-ol + water, water + ethane-1,2-diol and 2-methylpropan-2-ol + water + ethane-1,2-diol have been reported [5, 6, 12,13,14,15,16]. However, to the best of our knowledge, there is no report of data for the phase equilibria of the binary system 2-methylpropan-2-ol + ethane-1,2-diol and so this system has been studied in the present work. Additionally, the densities \( (\rho ) \) and refractive index values \( (n_{\text{D}} ) \) have been measured and the excess molar volumes (\( V_{\text{m}}^{\text{E}} ) \), deviations in molar refractivity \( (\Delta R) \) and partial molar volumes \( \left( {\bar{V}_{1} \; {\text{and}} \; \bar{V}_{2} } \right) \) are calculated. The phase equilibria of 2-methylpropan-2-ol + ethane-1,2-diol were measured at sub-atmospheric (19.99, 39.99, 59.99, 78.79 kPa) and local atmospheric pressure of 94.99 kPa over the entire composition range. The activity coefficient models, Wilson [17] and NRTL [18] models for activity coefficient were used to model the experimental phase equilibrium data. Non-linear regression analysis was performed using the generalized reduced gradient optimization technique, to find out the optimum binary interaction parameters for the binary mixture. The universal functional activity coefficient model (UNIFAC) was employed to predict the bubble temperature of the 2-methylpropan-2-ol + ethane-1,2-diol mixtures.

The densities, refractive indices and the derived excess properties of the binary mixtures of 2-methylpropan-2-ol + ethane-1,2-diol were measured at 303.15, 313.15, 323.15, and 333.15 K under local atmospheric pressure of 94.99 kPa over the entire composition range. The derived excess properties; excess molar volumes \( (V_{\text{m}}^{\text{E}} ) \) and deviations in molar refractivity \( (\Delta R) \) were correlated with the Redlich–Kister polynomial equation [19]. Generally, the refractive index values are measured at sodium D light wavelength i.e. 589.3 nm, however, the refractive index values at other wavelengths (404.7, 435.8, 486.1, 546.1, 587.6, 632.8, 644.0 and 706.5) nm were also explored, since it is convenient in the field of optics and for processes that are phase matched [20]. Furthermore, to predict the refractive indices of the binary liquid mixtures, the Lorentz–Lorentz (L–L), Weiner (W), Gladstone–Dale (G–D), Argo-Biot relation (A-B) and Heller (H) theoretical mixing rules were applied and the deviations are reported in terms of average percentage deviation [21,22,23]. The Prigogine–Flory–Patterson theory was used to predict the excess molar volumes of binary mixtures of 2-methylpropan-2-ol + ethane-1,2-diol.

2 Experimental Section

2.1 Materials

2-Methylpropan-2-ol (>99.5 mass%, AR) provided by Sigma–Aldrich, India was dried over molecular sieves (Aldrich, type 4Å, 1.6 mm pellets) and ethane-1,2-diol (>99.5 mass%, AR) was provided by SD Fine Chemical Ltd, India. The solvents were double distilled to remove trace impurities and were stored in desiccators to prevent moisture absorption. The water content of these chemicals was measured using a Karl Fischer titrator, Metrohm 797. The final purities of 2-methylpropan-2-ol and ethane-1,2-diol were analyzed using Shimadzu Gas Chromatograph, GC-17A, with with a flame ionization detector and an Agilent CP-Wax 57 CB column (0.53 mm × 25 m) at 373 K initially, followed by a ramping of 10 K per minute to 473 K. The injector and detector temperature was maintained at 423 K. The sample analyses were carried out in triplicate. The specifications (density and refractive index) of the pure components used in the present study have been measured at different temperatures and compared to those of literature values in Table 1 [24,25,26,27,28,29,30,31,32].

Table 1 Specifications of the chemicals and comparison of refractive index (n D) and density (ρ) of pure components with the literature data
Full size table

2.2 Isobaric Phase Equilibria Measurements

The phase equilibria were measured using a Sweitoslawski-type ebulliometer, similar to that described by Hala et al. [33]. A detailed description of the construction of the experimental setup and the procedure followed in the present study was described by Kumari et al. [34]. The Sweitoslawski-type ebulliometer is connected to a vacuum pump and a nitrogen gas cylinder, along with a closed end U-tube mercury in-line manometer to maintain the pressure within 0.50 kPa of the desired value. The pressure was adjusted manually using the needle valve of the gas cylinder or by opening the bypass line of the vacuum pump. A Lutron barometer, PHB-318, was used to measure the local atmospheric pressure. A high precision WIKA digital thermometer, Model CTH6200 calibrated by point-to-point by comparison to a WIKA hand-held calibrator, Model CEP3000, was used for measuring the equilibrium temperatures with an accuracy of 0.01 K. The thermometer is placed in the thermo-well containing glycerol to measure the equilibrium temperature of the mixture impinging on the thermo-well from the Cottrell tube of the ebulliometer. The samples used were prepared gravimetrically using a Shimadzu balance, AUW120D which can record weights with an uncertainty of 0.00001 g and thereafter charged into the ebulliometer. The average uncertainty in the measurement of mole fractions were determined to be 5 × 10−5.

In accordance with the Hala et al. [33], the mixture is placed into the ebulliometer and vacuum is gradually applied. The heating rate is slowly increased and adjusted to produce the required boil-up rate, so that a drop count of about 30 drops per minute is achieved. The equilibrium temperature is recorded after the system reaches a steady-state condition, judged by the constancy of temperature and uniformity of the drop rate over at least 30 min. The phase equilibrium experiment was initially performed at the lowest pressure and after the measurement of the equilibrium temperature, the vacuum was released and pressure regulated to the next higher value to be studied. Experimental phase equilibrium data were measured at constant pressures of 19.99, 39.99, 59.99, 78.79 and 94.99 kPa and the standard uncertainty in pressure was found to be 0.50 kPa.

2.3 Volumetric Property and Molar Refractivity Measurements

The densities and refractive indices of the 2-methylpropan-2-ol + ethane-1,2-diol binary mixtures were measured using a Rudolph Research analytical automatic densitometer (Model DDM 2911) and Schmidt + Haensch refractometer (Model DSR λ), respectively. The densitometer and refractometer were switched on an hour prior to the start of experimentation to allow the instruments to stabilize. A regular calibration of the instruments was carried out with the standard samples provided by the manufacturers to ensure the accuracy of measurements. The U-tube of the densitometer was cleaned with acetone and the air pump was switched on to remove the solvent. Thereafter, the temperature of the densitometer was increased to 353.15 K and left for almost 15 min to remove the traces of solvent. The traces were also removed by the air pump and density of air is measured at 353.15 and 293.15 K. This procedure was repeated until the air density conformed to the standard values at the corresponding temperatures. Then, the sample tube was rinsed with the sample to be measured. After the measurements, the same procedure was followed to clean the sample U-tube.

For the measurement of refractive indices, the housing or sample well of the instrument was cleaned with acetone to remove any impurities. Subcequently, it was rinsed with a small amount of the sample, whose refractive index is to be measured. The measurement was performed by placing the required amount of sample to the well at the desired temperature. The uncertainties in measurements of density and refractive index were determined to be 0.00125 g·cm−3 and 0.00150, respectively. The densities and refractive index values of the binary mixture were measured at 303.15, 313.15, 323.15 and 333.15 K over the entire composition range at a local atmospheric pressure of 94.99 kPa.

3 Results and Discussion

3.1 Isobaric Phase Equilibria

The experimental isobaric phase equilibrium data for the 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) binary system were measured at sub-atmospheric pressures of 19.99, 39.99, 59.99, 78.79 and local atmospheric pressure of 94.99 kPa and are reported in Table 2. The vapor phase mole fraction (\( y_{1} \)) of 2-methylpropan-2-ol was predicted using the non-random two liquid activity (NRTL) coefficient model and the results are included in Table 2. It can be observed that with an increase in the mole fraction of 2-methylpropan-2-ol, the bubble point temperature also increased. Moreover, the mixture did not show any azeotropic behavior. The pure component data and the Antoine constants used for vapor pressure calculations are reported in Table 3 [35,36,37]. The equilibrium data were correlated with the activity coefficient (Wilson and NRTL) and UNIFAC predictive models.

Table 2 Experimental and derived phase equilibrium data of 2-methylpropan-2-ol (1) + 1,2 dihydroxyethane (2) at different pressures using the NRTL model
Full size table
Table 3 Physical properties and Antoine constants for pure components
Full size table
$$ {\text{Wilson model}}:\,\,\ln \gamma_{\text{i}} = \ln \left( {x_{i} + \varLambda_{ij} x_{j} } \right) + x_{j} \left[ {\left\{ {\frac{{\varLambda_{ij} }}{{\varLambda_{ij} x_{j} + x_{i} }}} \right\} - \left\{ {\frac{{\varLambda_{ij} }}{{\varLambda_{ij} x_{i} + x_{j} }}} \right\}} \right] $$
(1)
$$ {\text{NRTL Model}}:\ln \gamma_{i} = x_{j}^{2} \left\{ {\tau_{li} \left( {\frac{{G_{ji} }}{{G_{ji} x_{j} + x_{i} }}} \right)^{2} + \left( {\frac{{G_{ij} \tau_{ij} }}{{\left( {x_{i} + x_{i} G_{ij} } \right)^{2} }}} \right)} \right\} $$
(2)

where \( G_{ij} = { \exp }\left( { - \alpha_{ij} \tau_{ij} } \right), \quad \tau_{ij} = a_{ij} + \frac{{b_{ij} }}{T} \),\(\, \tau_{ij} \ne \tau_{ji} \), and \( \alpha_{ij} = \alpha_{ji}\, \) where \( T \) is the absolute temperature, \( x_{i} \, {\text{is the mole fraction, and}}\,\gamma_{i} \) is the activity coefficient of component \( i \).\( \,\varLambda_{ij} \) is the binary interaction parameter for the Wilson model, \( \alpha_{ij} \) is the non-randomness factor, \( \tau_{ij} \) is the binary interaction energy parameter and \( G_{ji} \) is the local binary parameter for the NRTL model.

$$ {\text{UNIFAC model}}:\ln \gamma_{i} = \ln \gamma_{i}^{\text{C}} + \ln \gamma_{i}^{\text{R}} $$
(3)

where \( \ln \gamma_{i}^{\text{C}} \) and \( \ln \gamma_{i}^{\text{R}} \) are the combinatorial and residual components of the activity for the ith molecule:

$$ \ln \gamma_{i}^{\text{C}} = \ln \frac{{\phi_{i} }}{{x_{i} }} + \frac{z}{2}q_{i} \ln \frac{{\theta_{i} }}{{x_{i} }} + l_{i} \frac{{\phi_{i} }}{{x_{i} }}\sum\limits_{j} {x_{j} l_{j} } $$
(4)

where \( \theta_{i} \),\( \phi_{i} \) and \( l_{i} \) are the molar weighted segment, area fractional components and a compound parameter of coordination number z, for the ith molecule in the system.

$$ l_{i} = \frac{z}{2}\left( {r_{i} - q_{i} } \right) - \left( {r_{i} - 1} \right); z = 10;\theta_{i} = \frac{{q_{i} x_{i} }}{{\mathop \sum \nolimits_{j} q_{j} x_{j} }} ; \phi_{i} = \frac{{r_{i} x_{i} }}{{\mathop \sum \nolimits_{j} r_{j} x_{j} }} $$
(5)

where, \( q_{i} \) and \( r_{i} \) are calculated from the group surface area and volume contibutions.

$$ { \ln }\gamma_{i}^{\text{R}} = \mathop \sum \limits_{k}^{n} v_{k}^{(i)} [\ln \varGamma_{k} - \ln \varGamma_{k}^{\left( i \right)} ] $$
(6)

where  \( \ln \varGamma_{k} \)  is the activity of an isolated group in a solution consisting only of molecules of type \( i \). The total pressure equation used in the calculations for the binary data reduction by Barker’s method is as follows:

$$ p_{\text{cal}} /{\text{kPa}} = (p_{1}^{0} / {\text{KPa}})x_{1} \gamma_{1} F_{1 } + (p_{1}^{0} / {\text{KPa}})x_{2} \gamma_{2} F_{2} $$
(7)

where \( p_{i}^{0 }\, {\text{indicates}} \) the vapor pressures of the pure components, \( x_{i} \) is the liquid-phase mole fractions, and \( \gamma_{i} \) is the activity coefficient. According to Reid et al. [38] the vapor phase non-ideality correction factor, \( F_{i} \) in Eq. 7, is close to unity for low and ambient pressures. Hence Eq. 7 can be reduced as:

$$ p_{\text{cal}} /{\text{kPa}} = (p_{1}^{0} / {\text{kPa}})x_{1} \gamma_{1} + (p_{1}^{0} / {\text{kPa}})x_{2} \gamma_{2} $$
(8)

The optimum binary interaction parameters of the activity coefficient models were obtained by minimizing the following objective function \( \varPhi \) based on Generalized Reduced Gradient (GRG) optimization technique as described by Edgar and Himmelblau [39].

$$ \varPhi = \left( {\frac{{p_{\text{cal}} - p_{ \exp } }}{{p_{ \exp } }}} \right)^{2} $$
(9)

The results of the correlations of the experimental data with the local composition models (Wilson and NRTL) and that predicted by the UNIFAC group contribution method [40, 41] are presented in Table 4. The deviations in bubble temperatures predicted by the different models from the experimental values are expressed in terms of root mean square deviation (RMSD). The results showed that the deviations obtained from the predicted values of UNIFAC model were substantially larger. Among the models used in the study, the 2-methylpropan-2-ol + ethane-1,2-diol binary system was best represented by the NRTL model, followed closely by the Wilson activity coefficient model. These results can be observed from Fig. 1, where the phase equilibrium data have been plotted with modeled values of NRTL and UNIFAC model at 19.99 and 94.99 kPa. Further, the optimum model parameters were used to calculate the activity coefficients \( (\gamma_{1} \; {\text{and}} \; \gamma_{2 } ) \) and excess Gibbs energy (\( G^{\text{E}} \)). It was observed from the activity coefficients in Table 2 that the system 2-methylpropan-2-ol(1) + ethane-1,2-diol (2) exhibits non-ideal behavior with positive deviations from Raoult’s law, which was mainly attributed to the presence of strong hydrogen bonding. Also, the excess Gibbs energies of the mixtures were found to be positive. The plot of \( G^{\text{E}} \) as the function of mole fraction of the more volatile component is presented in Fig. 2. The plot shows that \( G^{\text{E}} \) is symmetric with respect to the mole fraction for the mixture of 2-methylpropan-2-ol and ethane-1,2-diol, which indicates the highly non-ideal behavior of the binary mixtures. The excess Gibbs energy was observed to be positive over the entire composition range with maxium value at \( x_{1} \) = 0.5.

Table 4 Binary interaction parameters of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) at various pressures based on Wilson, NRTL and UNIFAC models
Full size table
Fig. 1
figure 1

Phase equilibrium data of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) experimental data at pressure p: 19.99 kPa, filled square; 94.99 kPa, filled triangle; solid curve (dashed lines), fitted to NRTL model; (filled circles), predicated by UNIFAC

Full size image
Fig. 2
figure 2

Excess Gibbs energy \( G^{\text{E}} \) as a function of the mole fraction of the first component for the binary mixture formed by 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) at 19.99 kPa, filled square; 39.99 kPa, filled circle; 59.99 kPa, filled triangle; 78.79 kPa, filled inverted triangle; 94.99 kPa, filled diamond

Full size image

3.2 Volumetric Properties and Molar Refractivity

Volumetric properties reflect the intermolecular interactions between the components studied. In the 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) mixtures 1–1, 1–2 and 2–2 hydrogen bonding plays an imperative role and fluctuations in the volume depend on the relative energies of the hydrogen bonds. 2-Methylpropan-2-ol consists a hydrophilic –OH group that is able to form strong hydrogen bonds with molecules of ethane-1,2-diol and three hydrophobic –CH3 groups that display solvophobic effects, which strengthen the interactions of solvent molecules in the solvation shell [42]. Ethane-1,2-diol has a water-like hydrogen bond network with inter and intramolecular hydrogen bonds. The number of weakly polar methylene groups is equal to the number of hydroxyl groups and thereby have a considerable influence on the volumetric properties with the association of hydrogen bond. Further, it exhibits 27 different conformations and, depending on the temperature and aggregation state, it exists in gauche- and trans-conformations with the predominance of gauche at room temperature and atmospheric pressure conditions [43].

The experimental volumetric properties and densities of the 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) binary system were measured at 303.15, 313.15, 323.15 and 333.15 K at local atmospheric pressure of 94.99 kPa over the entire composition are summarized in Table 5. The derived property, excess molar volumes \( (V_{\text{m}}^{\text{E}} ) \) for the present binary mixtures at different molar compositions, were evaluated according to the following equation:

$$ V_{\text{m}}^{\text{E}} = x_{1} M_{1} \left( {1/\rho - 1/\rho_{1} } \right) + x_{2} M_{2} \left( {1/\rho - 1/\rho_{2} } \right) $$
(10)
Table 5 Densities, \( \rho \) (g·cm−3) of 2-methylpropan-2-ol (1) + ethane-1,2-diol at different temperatures (T/K) at 94.99 kPa
Full size table

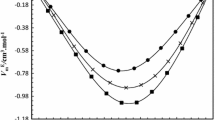
where \( x_{1} , x_{2 } \) are the mole fractions, \( M_{1} , M_{2} \) are the molecular weights and \( \rho_{1, } \rho_{2} \) are the densities of pure 2-methylpropan-2-ol (1) and ethane-1,2-diol (2), respectively; \( \rho \) is the density of the mixture. The excess molar volumes \( (V_{\text{m}}^{\text{E}} ) \) of the binary mixtures were found to be negative over the entire composition range as illustrated in Fig. 3. The negative values of excess molar volumes reflect the strong intermolecular interactions and the packing effect between 2-methylpropan-2-ol and 1, 2-dihydroxyethane. It is also clear from Fig. 3 that, with an increase in the temperature of the mixture, the intermolecular interactions strengthen, which leads to the more negative values of the excess molar volumes \( (V_{\text{m}}^{\text{E}} ) \) with a minimum at \( x_{1} = 0.58 \) and 333.15 K.

Fig. 3
figure 3

Excess molar volume \( V_{\text{m}}^{\text{E}} \) of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) at constant temperature: experimental data at 303.15 K, filled square; 313.15 K, filled circle; 323.15 K, filled triangle; 333.15 K, filled inverted triangle; solid curve—calculated from Redlich–Kister parameters

Full size image

The experimental refractive index (n) of the 2-methylpropan-2-ol + ethane-1,2-diol system were measured at different wavelengths (404.7, 435.8, 486.1, 546.1, 587.6, 589.3, 632.8, 644.0 and 706.5 nm) for the binary mixtures at 303.15, 313.15, 323.15 and 333.15 K over the entire compositions at local atmospheric pressure and are reported in Table 6. Instead of deviations in refractive index, the deviations in molar refractivity \( (\Delta R) \) are evaluated, since this provides the electronic perturbation of molecular orbital resulting from mixing the components [44]. The deviations in molar refractivity \( (\Delta R) \) have been evaluated by following equation [45]:

Table 6 Refractive indices \( n_{\lambda } \) of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) for different wavelengths and temperaturesa
Full size table
$$ \Delta R\left( {{\text{cm}}^{3} \cdot{\text{ mol}}^{ - 1} } \right) = R_{\text{m}} - \mathop \sum \limits_{i} \varphi_{i} R_{i}. $$
(11)

The Lorentz–Lorenz equation was used to investigate R m values for the binary mixture:

$$ R_{\text{m}} = \left( {\frac{{n_{\lambda }^{2} - 1}}{{n_{\lambda }^{2} + 2}}} \right)\left( {\frac{{\mathop \sum \nolimits_{i} x_{i} M_{i} }}{{\rho_{\text{m}} }}} \right) $$
(12)
$$ R_{i} = \left( {\frac{{n_{\lambda ,i}^{2} - 1}}{{n_{\lambda ,i}^{2} + 2}}} \right)\left( {\frac{{M_{i} }}{{\rho_{i} }}} \right) $$
(13)
$$ \varphi_{i} = \frac{{x_{i} V_{i} }}{{\mathop \sum \nolimits_{k} x_{k} V_{k} }} $$
(14)

where n λ abd n λ,i are the refractive index values of the mixture and pure components, respectively, and \( \varphi_{i} \) are the volume fractions of 2-methylpropan-2-ol + ethane-1,2-diol. The deviations in the molar refractivity \( (\Delta R) \) at 589.3 nm (sodium D line) was evaluated and found to be negative over the entire range of composition; this is shown in Fig. 4. The negative values of \( \Delta R \) indicate greater dispersive forces in the mixtures than pure components and become more negative with increasing temperature.

Fig. 4
figure 4

Deviation in molar reflectivity \( \Delta R \) of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) at: 303.15 K; filled square, 313.15 K; filled circle, 323.15 K; filled triangle, 333.15 K; filled inverted triangle, Solid curve—calculated from Redlich–Kister parameters and (dashed lines) standard error bar

Full size image

The excess molar volumes (\( V_{\text{m}}^{\text{E}} ) \) and deviations in molar refractivity \( (\Delta R) \) were modeled with Redlich–Kister equation:

$$ V_{\text{m}}^{\text{E}} / \Delta R = x_{2} (1 - x_{2} )\mathop \sum \limits_{i = 0}^{i = n} A_{i} \left( {1 - 2x_{2} } \right)^{i}. $$
(15)

The order of the polynomial is determined based on the F-test. The deviations in experimental and predicted values of \( V_{\text{m}}^{\text{E}} \) or \( \Delta R \) was calculated using the equation stated below:

$$ \sigma = \left[\mathop \sum \nolimits \left( {(V_{\text{m}}^{\text{E}} / \Delta R)_{ \exp } - (V_{\text{m}}^{\text{E}} \; or \; \Delta R)_{\text{cal}} } \right)^{2} / (N - \left( {n + 1} \right))\right]^{0.5} $$
(16)

where \( N \) is the total number of experimental points, \( n \) is the order of the polynomial and \( n + 1 \) is a number of coefficients \( (A_{i} ) \). The Redlich–Kister parameters for excess molar volumes \( (V_{\text{m}}^{\text{E}} ) \) and molar refractivity \( (\Delta R) \) with their standard error σ\( (V_{\text{m}}^{\text{E}} / \Delta R) \) and the overall standard deviations at each temperature are summarized in Table 7. The correlation results for \( V_{\text{m}}^{\text{E}} \) and \( \Delta R \) using the Redlich–Kister equation are relatively good and are graphically presented in Figs. 3 and 4, respectively.

Table 7 Redlich–Kister parameters, standard deviation (SD) and error (σ) for excess molar volumes (\( V_{\text{m}}^{\text{E}} \)) and deviations in molar refractivity \( (\Delta R) \) of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) at different temperatures
Full size table

Additionally, the measured refractive indices were further considered using the Lorentz–Lorenz, Wiener, Heller, Gladstone–Dale and Arago–Biot mixing models [44,45,46,47,48]. These rules are based on the electromagnetic theory of light, which treats the molecules as dipoles or assemblies of dipoles in an external field [49]. The following equations were used for the prediction of the refractive index of binary mixtures:

$$ {\text{Lorentz}}{-}{\text{Lorenz }}\left( {{\text{L}}{-}{\text{L}}} \right){\text{ relation}}:n_{\lambda }^{2} - 1/n_{\lambda }^{2} + 2 = \left( {n_{\lambda ,1}^{2} - 1/n_{\lambda ,1}^{2} + 2} \right)\varphi_{1} + \left( {n_{\lambda ,2}^{2} - 1/n_{\lambda ,2}^{2} + 2} \right)\varphi_{2} $$
(17)
$$ {\text{Wiener }}\left( {\text{W}} \right){\text{ relation}}:n_{\lambda }^{2} - n_{\lambda ,1}^{2} /n_{\lambda }^{2} + 2n_{\lambda ,1}^{2} = \left( {n_{\lambda ,2}^{2} - n_{\lambda ,1}^{2} /n_{\lambda ,2}^{2} - 2n_{\lambda ,1}^{2} } \right)\varphi_{2} $$
(18)
$$ {\text{Heller }}\left( {\text{H}} \right){\text{ relation}}:n_{\lambda } - n_{\lambda ,1} /n_{\lambda ,1} = \frac{3}{2}\left( {\left( {n_{\lambda ,2} /n_{\lambda ,1} } \right)^{2} - 1/\left( {n_{\lambda ,2} /n_{\lambda ,1} } \right)^{2} + 2} \right)\varphi_{2} $$
(19)
$$ {\text{Gladstone}}{-}{\text{Dale }}\left( {{\text{G}}{-}{\text{D}}} \right){\text{ relation}}:n_{\lambda } - 1/\rho = \left( {n_{\lambda ,1} - 1/\rho_{1} } \right) w_{1} + \left( {n_{\lambda ,2} - 1/\rho_{2} } \right) w_{2} $$
(20)
$$ {\text{Arago}}{-}{\text{Biot }}\left( {{\text{A}}{-}{\text{B}}} \right){\text{ relation}}:n_{\lambda } = n_{\lambda ,1} \varphi_{1} + n_{\lambda ,2} \varphi_{2} $$
(21)

where \( w_{1} \) and \( w_{2} \) are the weight fractions of component 1 and 2, respectively.

The average percentage deviation (APD) obtained from these models is presented in Table 8. The G–D model resulted in the lowest deviation. It was also observed that the Arago–Biot relation had similar deviations to the Lorentz–Lorenz relation at all the temperatures studied. Positive deviations were observed for all the mixing rules considered. In general, for binary systems, the dispersion and dipolar interactions are inactive where deviations are found to be positive [44].

Table 8 Average percentage deviations in mixing rules of 2-methylpropan-2-ol(1) + ethane-1,2-diol (2) at different temperatures
Full size table

Furthermore, the partial molar volumes \( (\bar{V}_{1} \) and \( \bar{V}_{2} \)) of 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) system were calculated by differentiation of Eq. 15 with respect to \( x_{2} \) (sixth order polynomial) and the combination of differentiation resulted in Eqs. 22 and 23:

$$ \bar{V}_{1} = V_{1}^{0} + V_{\text{m}}^{\text{E}} - x_{2} (\partial V_{\text{m}}^{\text{E}} /\partial x_{2} ) $$
(22)
$$ \bar{V}_{2} = V_{2}^{0} + V_{\text{m}}^{\text{E}} + (1 - x_{2} )(\partial V_{\text{m}}^{\text{E}} /\partial x_{2} ) $$
(23)

where \( V_{1}^{0} \) and \( V_{2}^{0} \) are molar volumes of pure components 1 and 2, respectively. The derived equations for the calculation of partial molar volumes are:

$$\bar{V}_{1} = ~V_{1}^{0} + ~x_{2}^{2} \sum \limits_{{i = 0}}^{{i = n}} A_{i} ~(1 - 2x_{2} )^{i} + 2x_{2}^{2} ~(1 - x_{2} ) \sum \limits_{{i = 0}}^{{i = n}} A_{i} (i)~(1 - 2x_{2} )^{{i - 1}} $$
(24)
$$ \bar{V}_{2} = ~V_{2}^{0} + ~(1 - x_{2} )^{2} \sum \limits_{{i = 0}}^{{i = n}} A_{i} ~(1 - 2x_{2} )^{i} - 2x_{2} ~\left( {1 - x_{2} } \right) \sum \limits_{{i = 0}}^{{i = n}} A_{i} \left( i \right)\left( {1 - 2x_{2} } \right)^{{i - 1}}. $$
(25)

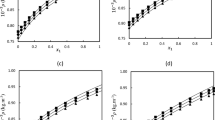
The results for the derived volumetric properties, partial molar volumes for 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) with respect to the mole fraction of 2-methylpropan-2-ol, are shown in Fig. 5a and b.

Fig. 5
figure 5

Dependences of partial molar volumes \( \bar{V}_{1} ,\bar{V}_{2} \) for 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) mixtures, respectively, at different temperatures: 303.15 K, filled square; 313.15 K, filled circle; 323.15 K, filled triangle; 333.15 K, filled inverted triangle

Full size image

The partial molar volume of 2-methylpropan-2-ol (\( \bar{V}_{1} \)) increases with increasing 2-methylpropan-2-ol concentration, while the partial molar volume of ethane-1,2-diol \( (\bar{V}_{2} ) \) decreased over the entire temperature range under consideration. The variation in partial molar volumes \( (\bar{V}_{1} \) and \( \bar{V}_{2} ) \) for both the components was prominent at higher temperatures as is evident from Fig. 5. The increase in temperature decreases in the average length of the H-bond of 2-methylpropan-2-ol and increases the translatory motion. The sharp decrease in the partial molar volumes for ethane-1,2-diol \( (\bar{V}_{2} ) \) is primarily due to the contributions of intra- and intermolecular H-bonds amongst the total intermolecular interactions in the 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) system. The addition of a small quantity of 2-methylpropan-2-ol to ethane-1,2-diol lowers the contribution from intramolecular H-bonds in ethane-1,2-diol and increases the contribution from its intermolecular H-bonds.

3.3 Prigogine–Flory–Patterson (PFP) Theory

For estimation and analysis of excess molar volumes, the Prigogine–Flory–Patterson (PFP) theory has been used. Patterson and coworkers have presented a detailed discussion of the PFP theory [48]. This theory establishes the relative importance of different contributions to the experimental excess molar volumes. The PFP theory considers \( V_{\text{m}}^{\text{E}} \) as a sum of three contributions: an interactional term calculated from the interactional parameter (\( \chi_{12} \)), a free volume contribution and a p* term reflecting a pressure contribution, which arises from the differences in the internal pressures, and the reduced volumes of the pure components and is directly proportional to \( \left( {\bar{\upsilon }_{1} - \bar{\upsilon }_{2} } \right)\left( {p_{1}^{*} - p_{2}^{*} } \right) \). The resulting equation is [50]:

$$ \frac{{V_{\text{m}}^{\text{E}} }}{{V_{1}^{*} x_{1} + x_{2} V_{2}^{*} }} = \frac{{\left( {\bar{\upsilon }^{{\frac{1}{3}}} - 1} \right)\bar{\upsilon }^{{\frac{2}{3}}} \psi_{1} \theta_{2} }}{{\left( {\frac{4}{3}\bar{\upsilon }^{{ - \frac{1}{3}}} - 1} \right)P_{1}^{*} }}\chi_{12} \left( {\text{interactional}} \right) - \frac{{\left( {\bar{\upsilon }_{1} - \bar{\upsilon }_{2} } \right)^{2} \left( {\frac{14}{9}\bar{\upsilon }^{{ - \frac{1}{3}}} - 1} \right)\psi_{1} \psi_{2} }}{{\left( {\frac{4}{3}\bar{\upsilon }^{{ - \frac{1}{3}}} - 1} \right)\bar{\upsilon }}}\left( {\text{Free volume}} \right) + \frac{{\left( {\bar{\upsilon }_{1} - \bar{\upsilon }_{2} } \right)\left( {p_{1}^{*} - p_{2}^{*} } \right)\psi_{1} \psi_{2} }}{{\psi_{1} p_{2}^{*} + \psi_{2} p_{1}^{*} }}(p^{ *}\,{\text{effect}}) $$
(26)

where \( V_{1}^{*} \) is the characteristic volume (\( V_{i}^{*} = \frac{{V_{i} }}{{\bar{\upsilon }_{i} }} \)). The reduced volume, \( \bar{\upsilon }_{i} \), and characteristic pressure, \( p_{i}^{*} \), are calculated according to following equations:

$$ \bar{\upsilon }_{i} = \left( {\frac{{1 + \frac{4}{3}\alpha_{i} T}}{{1 + \alpha_{i} T}}} \right)^{3} $$
(27)
$$ p_{i}^{*} = \frac{{\bar{\upsilon }_{i }^{2} \alpha_{i} T}}{{k_{i} }} $$
(28)

The \( \bar{\upsilon }_{i} \) of a binary mixture in Eq. 27 is approximated by:

$$ \bar{\upsilon } = \psi_{1} \bar{\upsilon }_{1} + \psi_{2} \bar{\upsilon }_{2} $$
(29)

where \( \psi_{i,} \) \( \varPhi_{i} \) and \( \theta_{1} \) represent the molecular contact energy fraction, hard-core volume fraction, and molecular surface site fraction, respectively, and are evaluated as follows:

$$ \psi = 1 - \psi_{2} = \left( {\frac{{\varPhi_{1} p_{1}^{*} }}{{\varPhi_{1} p_{1}^{*} + \varGamma_{2} p_{2}^{*} }}} \right) $$
(30)
$$ \varPhi_{1} = 1 - \theta_{2} = \left( {\frac{{\varPhi_{1} V_{1}^{*} }}{{\varPhi_{1} V_{1}^{*} + \varPhi_{2} V_{2}^{*} }}} \right) $$
(31)
$$ \theta_{1} = 1 - \theta_{2} = \frac{{\varPhi_{1} s_{1} }}{{\varPhi_{1} s_{1} + \varPhi_{2} s_{2} }} $$
(32)

where \( s_{i} \) is the molecular surface to volume ratio, which is determined by the Abe and Flory theory:

$$ \frac{{s_{1} }}{{s_{2} }} = \left( {\frac{{V_{1}^{*} }}{{V_{2}^{*} }}} \right)^{{ - \frac{1}{3}}} $$
(33)

The values of the different parameters of the pure components necessary in the PFP theory (Eq. 26) were obtained using the Flory model and are listed in Table 9. PFP theory requires experimental,\( V_{\text{m}}^{\text{E}} \), thermal expansion coefficient, \( \alpha_{p} \) and isothermal compressibility, \( \kappa_{T} \) and \( \alpha_{p};\) \( \kappa_{T} \) required in the calculation were taken from literature [27, 51, 52]. The values of \( \alpha_{p} , \) \( \kappa_{T} \) at other than 298.15 K were calculated from the following relation [11]:

Table 9 Flory parameters of the pure components at the different temperatures from 303.15 K to 333.15 K
Full size table
$$ \alpha = \alpha_{0} + \alpha_{0}^{2} \left( {7 + 4\alpha_{0} T} \right)\left(\frac{{T - T_{0} }}{3}\right) $$
(34)
$$ \gamma = \gamma_{0} - \gamma_{0} \left( {1 + 2\alpha_{0} T} \right)\left(\frac{{T - T_{0} }}{T}\right), T_{0} = {298.15\, {\text K}}$$
(35)

where \( \kappa_{T} = \frac{{\alpha_{p} }}{\gamma }, \) \( \gamma \) and \( \gamma_{0} \) are the thermal pressure coefficient at the desired temperature and reference temperature, respectively. To predict the \( V_{\text{m}}^{\text{E}} \) according to the PFP theory, the energy interaction parameter, \( \chi_{12} \) was calculated by fitting the Eq. 26 to experimental \( V_{\text{m}}^{\text{E}} \) at equimolar composition. The \( \chi_{12} \) along with three PFP interactional contributions, free volume, p* effect, and experimental and calculated (using PFP theory) \( V_{\text{m}}^{\text{E}} \) values near the equimolar composition are presented in Table 10. Study of the data revealed that the interactional and free volume contributions are positive, whereas \( p^{*} \) (characteristic pressure) contributions are negative for the system studied. For the binary mixtures, the free volume contribution dominates over the other two contributions. Table 9 shows that the characteristic pressure \( p_{i}^{*} \) of ethane-1,2-diol is larger than that of 2-methylpropan-2-ol, while the value of the reduced volume, \( \bar{\upsilon }_{i};\) for 2-methylpropan-2-ol is higher than for ethane-1,2-diol, which results in a negative contribution from the p* term, resulting from the large negative \( \left( {p_{1}^{*} - p_{2}^{*} } \right) \) and positive \( \left( {\bar{\upsilon }_{1} - \bar{\upsilon }_{2} } \right)\; {\text{values}} \). The p* term makes little contribution to \( V_{\text{m}}^{\text{E}} \) for the binary mixtures in comparison with the other terms.

Table 10 Calculated parameters of excess molar volume from the PFP theory with interaction parameter (\( \chi_{12} ) \)
Full size table

Furthermore, the \( \chi_{12} \) value calculated at the equimolar composition was used to check whether the PFP theory can predict \( V_{\text{m}}^{\text{E}} \) correctly over the entire composition range. The theoretical values are plotted in Fig. 6 along with the experimental results. It is clear from the figure that the theoretical results agree adequately with the experimental \( V_{\text{m}}^{\text{E}} \) values in the ethane-1,2-diol rich region, but the agreement is poor at higher mole fractions of 2-methylpropan-2-ol. The discrepancies between theory and experimental values arise at higher mole fraction of 2-methylpropan-2-ol from additional factors that happen through mixing of two components. As Patterson and co-workers suggested that the PFP theory does not consider all the factors existing in a binary mixture, i.e., it turns out the main features of experimental data are represented using only one parameter [50].

Fig. 6
figure 6

Comparison of experimental and theoretical excess molar volume as a function of mole fraction (\( x_{1} ) \) for 2-methylpropan-2-ol (1) + ethane-1,2-diol (2) mixtures: 313.15 K, filled circle solid line calculated using PFP theory

Full size image

4 Conclusions

Isobaric experimental data for 2-methylpropan-2-ol + ethane-1,2-diol were measured at sub-atmospheric and local atmospheric pressures using a modified Sweitoslawski-type ebulliometer. The experimental phase equilibria results are modelled by activity coefficient Wilson and NRTL models to obtain the optimized binary interaction parameters. The lower RMSD values for the NRTL model suggest a better representation of experimental data. Furthermore, density and refractive index values for pure components and the binary mixtures were studied at temperatures from (303.15 to 313) K at 10 K intervals over the entire composition range. The excess properties, excess molar volumes (\( V_{\text{m}}^{\text{E}} ) \), partial molar volumes (\( \bar{V}_{i} \)), and deviations in molar refractivity (\( \Delta R \)) were evaluated to study the effect on these derived properties with varying temperature and molar composition. Excess molar volumes and deviation in molar refractivity were found to be negative at all the temperatures investigated. The negative values of \( V_{\text{m}}^{\text{E}} \) indicate that a more attractive interaction or structural accommodation of components occurred on mixing the components. Moreover, negative values of \( \Delta R \) can be attributed to the dominance of dispersive forces in mixtures compared to those of the pure components. Partial molar volumes of both components showed opposite behavior, i.e., with increasing partial molar volume of 2-methylpropan-2-ol (\( \bar{V}_{1} \)), the partial molar volume of ethane-1,2-diol (\( \bar{V}_{1} \)) decreases. Moreover, different mixing rules were explored to accurately predict the refractive index values of the binary mixture 2-methylpropan-2-ol + ethane-1,2-diol. It was found that the Gladstone–Dale model gives good agreement with the experimental values. The PFP theory correctly represents the main characteristics of experimental excess molar volumes.