A joint order acceptance and scheduling problem with earliness and tardiness penalties considering overtime

Abstract

This paper considers a joint order acceptance and scheduling problem under a general scenario. A manufacturer receives multiple orders with a given revenue, processing time, release date, due date, deadline, and earliness and tardiness penalties. The manufacturer can be seen as a single-machine system. Due to limited capacity, the manufacturer cannot process every order and needs to determine the optimal set of accepted orders and corresponding production schedule such that the total profit is maximized. The manufacturer can extend its capacity with overtime by paying an additional cost. A time-indexed formulation is presented to model the problem. Two exact algorithms are proposed. The first algorithm, denoted by DPIA-GR, is a dynamic programming (DP)-based algorithm that starts by solving a relaxed version of the original model and successively recovers the relaxed constraint until an optimal solution to the original problem is achieved. The second algorithm, denoted by DPIA-LRGR, improves DPIA-GR by incorporating Lagrangian relaxation (LR). The subgradient method is employed to find the optimal Lagrangian multipliers. The relaxed model in DPIA-GR and the LR model in DPIA-LRGR can be represented using a weighted di-graph. Both algorithms are equivalent to finding the longest path in the graph and applying a graph reduction strategy to prevent unnecessary computational time and memory usage. A genetic algorithm (GA) is also proposed to solve large-scale versions of the problem. Numerical experiments show that both DPIA-GR and DPIA-LRGR solve the problem efficiently and outperform CPLEX and GA, but DPIA-LRGR offers better performance.

1 Introduction

Make-to-order (MTO) as a pull-type production strategy has gained considerable popularity in the past decades, which stems from the increasing demand for product variety and customization in today’s market. On the one hand, manufacturers employing MTO benefit from high flexibility and thus can handle a wide variety of product specifications and avoid unnecessary inventory. On the other hand, MTO manufacturers risk insufficient capacity, especially when a spike in demand occurs. This can lead to delays in order delivery time or even order rejections which can result in a decline in customer satisfaction. In such a situation, an MTO manufacturer needs to determine which orders to accept to achieve a high overall revenue; process the orders by following a good schedule, so that the accepted orders are completed at the right times in order to minimize the earliness (i.e., holding cost) and tardiness penalties; and if necessary, extend its capacity by using overtime, which may incur an extra cost. These three decision-making issues, i.e., order acceptance, order scheduling, and overtime usage, have been extensively studied in the past (Hans 1994; Baker and Scudder 1990; Akkan 1996), due to their wide application in practice. However, for an MTO manufacturer, these three problems are highly interrelated and can hardly be separated from one another completely. An order yielding high revenue may need to occupy a large portion of the capacity or come with tight due date and expensive tardiness penalty, which may undermine the overall profit; the usage of overtime depends on whether the profit of the additional orders to accept outweighs the overtime cost, which cannot be determined without considering the production schedule. Hence, order acceptance, scheduling, and overtime usage should be studied integrally.

In the past decade, the joint order acceptance and scheduling (OAS) problem has attracted a great deal of attention (Slotnick 2011). Different variations of the problem have been studied, and various formulations have been proposed. Charnsirisakskul et al. (2004) studied the OAS problem where the objective was to maximize the total revenue minus the manufacturing, holding, and tardiness costs. This model allowed order preemption. Additionally, the manufacturer has the flexibility to choose lead times. A time-indexed mixed-integer linear programming (MILP) model was presented and solved using CPLEX. Nobibon and Leus (2011) considered a generalized OAS problem with tardiness penalty and order preemption. An assignment formulation and a time-indexed formulation were presented. Zhong et al. (2014) studied the OAS problem where orders can only be processed within a number of discontinuous time intervals. The objective is to minimize the make span of all accepted orders minus the penalty caused by order rejection and outsourced orders. Mestry et al. (2011) focused on an OAS problem with multiple resources having regular and non-regular capacities. An MILP model was proposed to formulate the problem.

As a result of the high complexity of the OAS problem, most of the existing papers propose heuristics or meta-heuristic algorithms to solve the problem. Og et al. (2010) studied an OAS problem where orders are defined by their release dates, due dates, deadlines, processing times, sequence-dependent setup times, and revenues, and the manufacturer was regarded as a single machine. They formulated the problem using an MILP model, which can be used to solve problems with up to 15 orders. Three heuristic algorithms, i.e., an iterative sequence first-accept next (ISFAN) algorithm, a dynamic release first-sequence best (RFSB) heuristic, and a modified apparent tardiness cost with setups (m-ATCS) heuristic, were proposed to solve large-sized problems. Cesaret et al. (2012) proposed a tabu search (TS) algorithm to solve the OAS problem where the orders have different release dates, due dates, and sequence-dependent setup times. The numerical experiment shows that the TS algorithm outperforms ISFAN and m-ATCS algorithms in terms of solution quality. Slotnick and Morton (2007) proposed five heuristic algorithms for the OAS problem with minimum total weighted tardiness as the objective. These heuristics include a branch-and-bound (B&B) method using a relaxation bound derived by Vogel’s approximation (RBVA), two beam search methods using RBVA and a relaxed assignment solution, and two myopic heuristic algorithms using Vogel’s approximation and the assignment solution. The first three heuristics are used to solve small-sized problems, while the last two are capable of solving large-sized problems. Rom and Slotnick (2009) developed a genetic algorithm (GA) to solve the OAS problem with tardiness cost. A probabilistic local search was employed. In the computational experiment, the proposed GA showed domination over a myopic heuristic in solution quality and obtained solutions almost as good as exhaustive local search but in a much shorter time. Xiao et al. (2012) studied the OAS problem in a permutation flow shop. A simulated annealing algorithm based on partial optimization was developed to obtain near-optimal solutions. Lin and Ying (2013) developed a modified artificial bee colony (ABC) algorithm for the OAS problem in a two-machine flow shop. The computational results showed that the proposed ABC algorithm produces better solutions than the ISFAN, m-ATCS, and TS algorithms. Chen et al. (2008) presented an OAS problem from hot rolling production in the steel industry. Multiple cost components, such as sequence-dependent transition costs and non-execution penalties, are considered in the model. A hybrid evolutionary algorithm that combines GA and extremal optimization was proposed.

Although heuristics and meta-heuristics are able to solve problems more efficiently, they cannot guarantee optimality. Unfortunately, only a few papers exist that focus on exact algorithms for the OAS problem. Slotnick and Morton (2007) proposed an optimal B&B strategy, which begins with an empty schedule and adds jobs one by one by branching on the job to be accepted and scheduled first. A linear integer relaxation was used for bounding. Nobibon and Leus (2011) studied two B&B strategies to solve the OAS problem with order preemption. The first B&B strategy is based on a hierarchical approach that performs selection and scheduling separately, and the second strategy is similar to the approach proposed by Slotnick and Morton (2007). Mestry et al. (2011) proposed an approximate B&B scheme with Lagrangian relaxation bounds and approximations to remove nodes. The proposed algorithm was shown to solve the problem efficiently with up to 10 candidate orders. Nguyen et al. (2014) improved the basic B&B algorithm by incorporating genetic programming. Computational results show that the enhanced B&B algorithm is more efficient than the basic B&B algorithm and CPLEX solver.

Compared with the existing literature, the contributions of this paper can be summarized as follows. First, this paper examines a generalized version of the OAS problem. In many cases, manufacturers suffer from extra inventory holding cost if an order is completed before its due date. Thus, in addition to tardiness penalties, which has been widely considered in the OAS problem before, this paper takes earliness penalties into account, which further complicates the problem since idle time between consecutive orders may need to be inserted. The specific forms of earliness and tardiness penalties of an order are not restricted in this paper, as long as they depend on the completion time of the order. Moreover, overtime is utilized by many manufacturers when facing insufficient capacity, which helps gain more profit and maintain customer loyalty. However, very few papers can be found considering overtime in the OAS problem. Mestry et al. (2011) proposed a model that allows for overtime capacity, in which each time period represents an aggregated bucket of capacity and multiple orders can be processed in each time period using either regular or overtime capacity. Melchiors et al. (2018) proposed a model where overtime capacity can be used to either process multiple orders simultaneously or speed up the processing time of an order. In this paper, we present a different model of overtime, where regular capacity is available through most of the planning period, and additional overtime capacity is available at the end of the planning period. The form of the overtime cost is not restricted in this paper either, as it can be modeled as any non-decreasing function of time. Additionally, as mentioned above, most papers rely on heuristics or meta-heuristics to solve the OAS problem, and the majority of the papers proposing exact algorithms follow a B&B strategy. In this paper, a time-indexed formulation is presented to model the problem. In addition, two exact dynamic programming (DP)-based algorithms are proposed. Both algorithms are equivalent to finding the longest path in an acyclic graph and applying a graph reduction strategy to prevent unnecessary computational time and memory usage. A GA is also proposed to solve large-scale versions of the problem. Lastly, numerical experiments are used to compare the proposed solution approaches for a linearized version of the problem and show the high efficiency of the two DP-based algorithms.

The rest of the paper is organized as follows. In Sect. 2, the problem statement and the mathematical model are provided. In Sects. 3 and 4, the two exact DP-based algorithms are developed. Section 5 shows some illustrative examples of modifications that can be made to the profit function of each order to account for additional production or overtime costs that can be incurred through various periods in the planning horizon. In Sect. 6, a GA is introduced for a linearized version of the problem and the corresponding MILP model is also formulated. A numerical experiment is presented in Sect. 7 to assess the performance of the mathematical model and the three proposed algorithms. In Sect. 8, we draw some conclusions and indicate some possible future research directions.

2 Problem statement and mathematical formulation

This paper considers a joint order acceptance and scheduling problem under a general scenario, denoted by OASGS. Let $S = \left\{ {1, \ldots ,n} \right\}$ be the set of all orders submitted to a manufacturer. Each order $k \in S$ requires $p_{k}$ time units to process and the manufacturer has a limited capacity, denoted by $T$, to process all the orders. The setup time of an order is counted in its processing time. The revenues among the submitted orders, denoted by $r_{k}$, $k \in S$, are different. The manufacturer needs to determine the set of accepted orders. It is assumed that the manufacturer has a single workstation, which can process at most one order at a time. Each order $k \in S$ comes with a release date $R_{k}$, a due date $d_{k}$, and a deadline $D_{k}$. If an order is accepted, it must be processed within the time window confined by the release date and the deadline. If an order is completed before or after its due date, a penalty is incurred. Hence, the profit of order $k \in S$ is a function of its completion time $t_{k}$, which is denoted by $f_{k} \left( {t_{k} } \right)$. Note that the processing sequence of the accepted orders corresponds to the increasing sequence of their completion times. In order to accept more orders, the manufacturer can use overtime, which results in extra cost. The corresponding overtime cost is denoted by $g\left( {T_{used} } \right)$, where $T_{used}$ is the total number of time units used to process all accepted orders. The objective is to maximize the total profit, which is equal to the total revenue minus the total earliness and tardiness penalties, and overtime cost.

With earliness and tardiness penalties, the completion time of an order should be confined within a time window that guarantees a nonnegative profit. As a common practice, we assume that $f_{k} \left( {t_{k} } \right)$ is a non-increasing function for $t_{k} \in \left[ {R_{k} + p_{k} ,d_{k} } \right]$ and non-decreasing function for $t_{k} \in \left( {d_{k} ,D_{k} } \right]$; and $g\left( {T_{used} } \right)$ is a function equal to 0 for $T_{used} \in \left[ {0,T} \right]$ and a non-decreasing function for $T_{used} > T$. Note that $g\left( {T_{used} } \right)$, for $T_{used} > T$, could be a multi-step function that only increases in steps of size $\Delta t$, where $\Delta t$ could be as small as a single time unit or as large as the duration of an additional shift.

If an order $k$ is accepted, $k \in S$, its completion time $t_{k}$ should satisfy $t_{k}^{lb} \le t_{k} \le t_{k}^{ub}$, where $t_{k}^{lb} = \hbox{max} \left\{ {\hbox{min} \left\{ {t_{k} :f_{k} \left( {t_{k} } \right) \ge 0,t_{k} \ge 0} \right\},R_{k} + p_{k} } \right\}$ is the lower bound of $t_{k}$ and $t_{k}^{ub} = \hbox{min} \left\{ {\hbox{max} \left\{ {t_{k} :f_{k} \left( {t_{k} } \right) - g\left( {t_{k} } \right) \ge 0,t_{k} \ge 0} \right\},D_{k} } \right\}$ is the upper bound of $t_{k}$.

Since each order has an upper bound for its completion time, there also exists an upper bound for $T_{used}$. Let $T_{used}^{ub}$ be an upper bound for the total number of time units used to process all accepted orders; then, $T_{used}^{ub} = \hbox{max} \left\{ {t_{k}^{ub} :k \in S} \right\}$.

The OASGS problem can be modeled using a time-indexed formulation (TIF). In this formulation, $p_{k}$, $R_{k}$, $d_{k}$, $D_{k}$, $k \in S$, and $T$ are assumed to be integer. A set of binary variables are used to determine if an order is completed at a certain time:

$$ z_{k,\tau } = \left\{ \begin{array}{ll} 1,&{\text{if}}\,{\text{order}}\,k\,{\text{is}}\,{\text{selected}}\,{\text{and}}\,{\text{completed}}\,{\text{at}}\,{\text{time}}\,\tau , \hfill \\ 0,& {\text{otherwise,}} \hfill \\ \end{array} \right. \, \tau = t_{k}^{lb} , \ldots ,t_{k}^{ub} ,\;k \in S. $$

The complete model can be formulated as a mixed 0–1 linear program:

$$ {\text{Model}}\;\left( {\text{TIF}} \right):\quad U = \hbox{max} \sum\limits_{k \in S} {\sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } f_{k} \left( \tau \right)} } - C_{O} , $$

(1)

$$ {\text{s}}.{\text{t}}.\quad \sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } } \le 1,\quad k \in S, $$

(2)

$$ \sum\limits_{k \in S} {\sum\limits_{s = \tau }^{{\hbox{min} \left\{ {\tau + p_{k} - 1,t_{k}^{ub} } \right\}}} {z_{k,s} } } \le 1, \, \tau = \mathop {\hbox{min} }\limits_{k \in S} \left\{ {t_{k}^{lb} } \right\}, \ldots ,T_{used}^{ub} , $$

(3)

$$ C_{O} \ge z_{k,\tau } g\left( \tau \right),\quad \tau = \hbox{max} \left\{ {t_{k}^{lb} ,T + 1} \right\}, \ldots ,t_{k}^{ub} ,\quad k \in S, $$

(4)

$$ z_{k,\tau } \in \left\{ {0,1} \right\},\quad \tau = t_{k}^{lb} , \ldots ,t_{k}^{ub} ,\quad k \in S. $$

(5)

In the objective function (1), the first term is the sum of the profit of all the selected orders and the second term $C_{O}$ is the overtime cost. Constraint set (2) ensures that each order is processed at most once. Constraint (3) ensures that no more than one order can be processed at the same time. Note that if order $k$ is selected and stars at time $\tau$, then no other order can be completed in the interval $\left[ {\tau ,\tau + p_{k} - 1} \right]$. Constraint set (4) determines the cost of the overtime needed to process all accepted orders. Constraint set (5) defines the binary variables.

The time-indexed model presented here is somewhat different than other formulations, which typically model the completion time and earliness/lateness of an order as continuous variables. Model (TIF) is introduced in this fashion because it aligns with the solution strategy that is presented, which relies on finding the longest path through a network. The vertices in this network are also time-indexed in this way and represent the completion of an order in that particular time period. The binary decision variables in this formulation align with the construction of the nodes along the optimal path in a graph network. If order $k$ is completed at time $\tau$, then the decision variable associated with this order will be set to 1; otherwise, it will be set to 0. This corresponds to the existence of a node along the optimal path in the graph that is presented in Sect. 3.2.

There are some additional advantages of the proposed model, however. The time-indexed nature of this formulation ensures that even if the earliness and tardiness penalties and overtime costs are nonlinear, they can still be modeled with this formulation. This provides a benefit over other models, in which the earliness (if it is included) and tardiness are continuous variables and are simply assigned a weight (Nobibon and Leus 2011; Og et al. 2010; Slotnick and Morton 2007). Additionally, this allows us to model other types of costs that are associated with scheduling an order to complete at a specified time. An example of this is presented in Sect. 5.

This model allows for idle times between orders, which is a feature that is not included in models that do not consider earliness penalties. In particular, this is due to the nature of constraint set (3) which allows for the possibility of an order to be completed in a time period that is larger than $p_{k}$ time units after the previous order completion. This particular constraint means that the model does not require variables that define the sequence in which orders are processed, a feature which would be required in order to prevent overlapping orders if the completion times are modeled as continuous variables. Nobibon and Leus (2011) provide a time-index formulation that is similar to the model that is presented here, but does not include earliness penalties or overtime. Tanaka et al. (2009) provide a model that uses similar types of constraints; however, their model does not include order acceptance and does not allow for idle times between orders, so the constraints in their model that are similar to constraint sets (2) and (3) are equality constraints.

Finally, the time indices in this model represent individual units of capacity, which means that the completion times, earliness and tardiness can be measured precisely. Some models, such as the one proposed by Charnsirisakskul et al. (2004), define aggregated time periods that contain multiple units of capacity and multiple orders can be scheduled in each period. While the reduced number of time indices in their model provides an advantage in problem size, it does not determine completion times with as much granularity and also can cause problems when it is desired to schedule orders that are initiated at the end of a period and completed at the beginning of the following period.

3 Iterative algorithm based on dynamic programming with graph reduction (DPIA-GR)

If constraint set (2) in Model (TIF) is relaxed, the resulting model can be solved using a DP formulation in $O\left( {nT_{used}^{ub} } \right)$. However, relaxing these constraints may produce an infeasible solution to the original problem because it may contain duplicated orders. To prevent the recurrence of orders, constraint set (2) can be partially recovered on those duplicated orders. The resulting model, as will be shown later, can be solved using a DP formulation in $O\left( {nT_{used}^{ub} 2^{m} } \right)$, where $m$ is the number of orders that are controlled to appear at most once in the optimal sequence. Let $S_{C} \subseteq S$ be the set of such controlled orders.

Each time an order is added to $S_{C}$, the computational effort to solve the partially relaxed model is doubled. Hence, the orders to be controlled should be carefully selected. Since the optimal set of accepted orders is unknown beforehand, a conservative strategy is applied in the proposed algorithm: one order at a time is added to $S_{C}$; once a feasible solution is obtained, it is guaranteed to be an optimal solution to the original model. The relaxed problem can be represented using a weighted di-graph. In order to improve the computational efficiency and reduce the memory usage, a graph reduction process is triggered to delete unnecessary vertices that will never lead to an optimal solution. In this sense, the algorithm presented in this section shares a similar idea with the successive sublimation dynamic programming (SSDP) method (Ibaraki 1987), which was proposed by Ibaraki to solve the single-machine total weighted tardiness (TWT) scheduling problem; however, the TWT problem requires each order to appear exactly once, while our problem allows order rejection, resulting in a different convergence strategy. Additionally, solutions to this problem must also consider overtime and idle times between orders, as a result of the earliness penalties.

3.1 The relaxed model

When constraint set (2), i.e.,

$$ \sum\limits_{{\tau = p_{k} }}^{{t_{k}^{\hbox{max} } }} {z_{k,\tau } } \le 1,\quad k \in S_{C} , $$

(6)

is partially relaxed, the resulting mixed 0–1 linear programming model becomes

$$ {\text{Model}}\;\left( {R\left( {S_{C} } \right)} \right):\quad R\left( {S_{C} } \right) = \hbox{max} \sum\limits_{k \in S} {\sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } f_{k} \left( \tau \right)} } - C_{O} , $$

$$ {\text{s}}.{\text{t}}.\quad \left( 3\right)\;{\text{to}}\;\left( 6\right). $$

Theorem 1

Let $\sigma^{*} \left( {S_{C} } \right)$ be an optimal solution of Model $\left( {R\left( {S_{C} } \right)} \right)$ defined by a sequence of selected orders with the corresponding completion times. If $\sigma^{*} \left( {S_{C} } \right)$ is feasible to Model (TIF), then $\sigma^{*} \left( {S_{C} } \right)$ is also optimal to Model (TIF).

Proof

Since $\sigma^{*} \left( {S_{C} } \right)$ is feasible to Model (TIF), the corresponding objective value, $R\left( {S_{C} } \right)$, satisfies $R\left( {S_{C} } \right) \le U$. Consider an optimal solution to Model (TIF), $\sigma^{*}$, with objective function value $U$. Since $\sigma^{*}$ satisfies (3) to (6), it is feasible to Model (R(S_C)), so $U \le R\left( {S_{C} } \right)$. Therefore, $R\left( {S_{C} } \right) = U$. □

3.2 Graph representation of Model (R(S _C)) and solution procedures

Model (R(S_C)) can be interpreted using a weighted di-graph. Here, we first introduce a dummy order, order 0, to represent one unit of idle time, i.e., $p_{0} = 1$, $f_{0} \left( \tau \right) = 0$, $\tau = 1, \ldots ,T_{used}^{ub}$, and allow the duplication of order 0. For the convenience of presentation, we first define $\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right)$ as a subsequence of orders (including order 0) whose first order starts at time 0 and last order is completed at time $\tau$, $\tau = 1, \ldots ,T_{used}^{ub}$, and $\alpha$ is a vector of binary variables that indicates the occurrences of orders in the controlled set:

$$ \alpha_{{\tilde{k}}} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}}\,{\text{order}}\,\tilde{k}\,{\text{does}}\,{\text{not}}\,{\text{exist}}\,{\text{in}}\,\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right),} \hfill \\ {1,} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right.\tilde{k} \in S_{C} . $$

Then, in the graph, a vertex $v^{\tau ,\alpha }$ represents the existence of $\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right)$. An edge from $v^{{\tau^{\prime},\alpha^{\prime}}}$ to $v^{\tau ,\alpha }$, denoted by $e_{\tau ,\alpha }^{{\tau^{\prime},\alpha^{\prime}}}$, represents an order with processing time $\tau - \tau^{{\prime }}$. For example, $e_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$, $k \in S \cup \left\{ 0 \right\}$, implies that order $k$ starts at time $\tau - p_{k}$ and is completed at time $\tau$. In this case, the subsequence $\sigma_{f}^{{S_{C} }} \left( {\tau - p_{k} ,\alpha^{{\prime }} } \right)$ (corresponding to $v^{{\tau^{\prime} - p_{k} ,\alpha^{\prime}}}$) with order $k$ added to its end forms a new subsequence $\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right)$ (corresponding to $v^{\tau ,\alpha }$). Here, the length of $e_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$, denoted by $d_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$, is defined as the increase of the objective value from $\sigma_{f}^{{S_{C} }} \left( {\tau - p_{k} ,\alpha^{\prime}} \right)$ to $\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right)$, which is calculated as follows:

$$ d_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{{\prime }} }} = f_{k} \left( \tau \right) + \left[ {g\left( {\tau - p_{k} } \right) - g\left( \tau \right)} \right]. $$

(7)

The first term of (7) is the profit of order $k$, and the second term represents the increase of overtime cost. If $k \notin S_{C}$, then the occurrences of controlled orders remain unchanged; hence, $\alpha^{\prime} = \alpha$; otherwise, when $k \in S_{C}$, since order $k$ should appear in the subsequence at most once, $\alpha^{\prime}_{k} = 0$ and $\alpha_{k} = 1$. Since the total number of candidate orders is $n$, for each vertex, there exist at most $n$ adjacent vertices directed to it. In this di-graph, the origin $v^{{0,\bar{0}}}$ is unique; but it can reach up to $n$ neighbors. A path from $v^{{0,\bar{0}}}$ to a vertex $v^{\tau ,\alpha }$ forms a specific sequence of orders, which is exactly $\sigma_{f}^{{S_{C} }} \left( {\tau ,\alpha } \right)$.

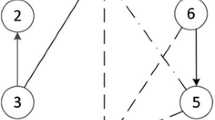
Figure 1 shows the graph of an example with 3 orders and $S_{C} = \left\{ {1,2} \right\}$. The processing times for orders 1, 2, and 3 are 1, 2, and 3, respectively. Further, $t_{1}^{lb} = 1$, $t_{2}^{lb} = 3$, $t_{3}^{lb} = 4$, and $t_{1}^{ub} = 3$, $t_{2}^{ub} = 4$, $t_{3}^{lb} = 5$. Notice that, at the origin $v^{{0,\left( {0,0} \right)^{T} }}$, the only orders that can be selected are the dummy order (order 0) or order 1. If order 0 is selected, edge $e_{{1,\left( {0,0} \right)^{T} }}^{{0,\left( {0,0} \right)^{T} }}$ is followed to reach node $v^{{1,\left( {0,0} \right)^{T} }}$; similarly, when order 1 is chosen, edge $e_{{1,\left( {1,0} \right)^{T} }}^{{0,\left( {0,0} \right)^{T} }}$ is used to get to node $v^{{1,\left( {0,0} \right)^{T} }}$. At time $\tau = 0$, orders 2 and 3 cannot be selected because they would not finish within bounds. Note that order 2 should be completed within the time window (Akkan 1996; Slotnick 2011). There is no vertex $v^{\tau ,\alpha }$ in the graph with $\tau < 3$ and $\alpha_{2} = 1$. Similar situation exists for other orders. The bold path represents a sequence with order 0 processed first, whose processing time spans from $\tau = 0$ to $\tau = 1$, order 1 is processed next from $\tau = 1$ to $\tau = 2$, and order 3 is processed last, starting at $\tau = 2$ and ending at $\tau = 5$.

Fig. 1

Example of a graph presentation of Model (R(S_C))

Model (R(S_C)) is equivalent to finding the longest path in graph $G\left( {V,E} \right)$, where $V$ is the set of vertices reachable from the origin $v^{0,0}$ and $E$ is the set of reachable edges. Clearly, $G\left( {V,E} \right)$ is a directed acyclic graph. Thus, it can be solved using the forward DP algorithm stated below.

Forward DP algorithm for Model (R( S _C )) (DPAR-f)

Optimal value function:

$$ \varphi^{\tau ,\alpha } = {\text{length}}\,{\text{of}}\,{\text{the}}\,{\text{longest}}\,{\text{path}}\,{\text{from}}\;v^{{0,\bar{0}}} \;{\text{to}}\;v^{\tau ,\alpha } , \;\tau = 0, \ldots ,T_{used}^{ub} ,\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} . $$

Recurrence relation:

$$ \varphi^{\tau ,\alpha } = \mathop {\hbox{max} }\limits_{{k \in S \cup \left\{ 0 \right\}}} \left\{ {\psi^{\tau ,\alpha ,k} } \right\},\;\tau = \mathop {\hbox{min} }\limits_{k \in S} \left\{ {t_{k}^{lb} } \right\}, \ldots ,T_{used}^{ub} ,\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} , $$

(8)

where $\psi^{\tau ,\alpha ,k}$ is the length of the longest path from $v^{{0,\bar{0}}}$ to $v^{\tau ,\alpha }$ via $v^{{\tau - p_{k} ,\alpha^{\prime}}}$, which is calculated as follows:

$$ \psi^{\tau ,\alpha ,k} = \varphi^{{\tau - p_{k} ,\alpha^{{\prime }} }} + d_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{{\prime }} }} , $$

(9)

where $\alpha^{{\prime }} = \alpha$ if $k \notin S_{C}$, and $\alpha_{k}^{{\prime }} = 0,\;\alpha_{k} = 1$, and $\alpha_{{\tilde{k}}}^{{\prime }} = \alpha_{{\tilde{k}}}$ for $\tilde{k} \ne k$, $\tilde{k} \in S_{C}$ if $k \in S_{C}$.

Boundary conditions:

$$ \varphi^{{0,\bar{0}}} = 0, $$

(10)

$$ \varphi^{\tau ,\alpha } = - \infty ,\;{\text{for}}\;\tau < 0,\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C}, $$

(11)

$$ \psi^{\tau ,\alpha ,k} = - \infty ,\;{\text{for}}\;\tau = \mathop {\hbox{min} }\limits_{k \in S} \left\{ {t_{k}^{lb} } \right\}, \ldots ,T_{used}^{ub} ,\;\alpha_{k} = 0,\;k \in S_{C} . $$

(12)

Optimal solution:

$$ R\left( {S_{C} } \right) = \hbox{max} \left\{ {\varphi^{\tau ,\alpha } :\tau = 0, \ldots ,T_{used}^{ub} ,\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\tilde{k} \in S_{C} } \right\}. $$

(13)

Theorem 2

DPAR-f finds an optimal solution for Model $\left( {R\left( {S_{C} } \right)} \right)$ in $O\left( {nT_{used}^{ub} 2^{m} } \right)$, where $m = \left| {S_{C} } \right|$.

Proof

(By induction) When $\tau = 0$ and $\alpha = \bar{0}$, no profit is generated, yielding (10). Now, suppose the longest path from $v^{{0,\bar{0}}}$ to $v^{{\tau^{\prime},\alpha }}$, denoted by $\sigma_{f}^{{S_{C} *}} \left( {\tau^{\prime},\alpha } \right)$, has been found for all $\tau^{\prime} < \tau$, $\tau \in \left\{ {1, \ldots ,T_{used}^{ub} } \right\}$, and all possible values of $\alpha$. Let us consider $v^{\tau ,\alpha }$. All adjacent vertices directed to $v^{\tau ,\alpha }$ can be denoted by $v^{{\tau - p_{k} ,\alpha^{\prime}}}$, $k \in S \cup \left\{ 0 \right\}$. The longest path from $v^{{0,\bar{0}}}$ to $v^{\tau ,\alpha }$ via $v^{{\tau - p_{k} ,\alpha^{\prime}}}$ is equal to the longest path from $v^{{0,\bar{0}}}$ to $v^{{\tau - p_{k} ,\alpha^{\prime}}}$ plus the length of $e_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$, yielding (9). Since the longest path from $v^{{0,\bar{0}}}$ to $v^{\tau ,\alpha }$ has to go through a vertex $v^{{\tau - p_{k} ,\alpha^{\prime}}}$ before reaching $v^{\tau ,\alpha }$, the longest path to $v^{\tau ,\alpha }$ can be found by (8). After the longest path to each vertex is obtained, the optimal solution is obtained by (13). In the boundary conditions, equation set (11) guarantees that no order starts before time 0. Equation set (12) prohibits a controlled order to appear more than once. In the recurrence relation, there are generally $T_{used}^{ub}$ values of $\tau$ and $2^{m}$ values of $\alpha$. For each pair of $\tau$ and $\alpha$ values, $\varphi^{\tau ,\alpha }$ is found by checking $\psi^{\tau ,\alpha ,k}$ for all $k \in S \cup \left\{ 0 \right\}$, which is completed in $O\left( n \right)$. Therefore, DPAR-f finds an optimal solution for Model (R($S_{C}$)) in $O\left( {nT_{used}^{ub} 2^{m} } \right)$. □

A path in $G\left( {V,E} \right)$ starting from vertex $v^{\tau ,\alpha }$ can be split into two sub-paths by its adjacent vertex $v^{{\tau + p_{k} ,\alpha^{\prime}}}$. The first sub-path goes from $v^{\tau ,\alpha }$ to $v^{{\tau + p_{k} ,\alpha^{\prime}}}$, and the second path starts from $v^{{\tau + p_{k} ,\alpha^{\prime}}}$ and continues along the rest of the path. Model (R (S_C)) can also be solved using the following backward DP formulation using this simple concept.

Backward DP algorithm for Model (R( S _C )) (DPAR-b)

Optimal value function:

$$ \theta^{\tau ,\alpha } = {\text{length}}\,{\text{of}}\,{\text{the}}\,{\text{longest}}\,{\text{path}}\,{\text{starting}}\,{\text{from}}\;v^{\tau ,\alpha } ,\;\tau = 0, \ldots ,T_{used}^{ub} ,\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} . $$

Recurrence relation:

$$ \theta^{\tau ,\alpha } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{k \in S \cup \left\{ 0 \right\}}} \left\{ {\zeta^{\tau ,\alpha ,k} } \right\},} \hfill & {{\text{if}}\mathop {\hbox{max} }\limits_{{k \in S \cup \left\{ 0 \right\}}} \left\{ {\zeta^{\tau ,\alpha ,k} } \right\} \ge 0,} \hfill \\ { - g\left( \tau \right),} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right. $$

(14)

$$ \tau = 0, \ldots ,\mathop {\hbox{max} }\limits_{k \in S} \left\{ {t_{k}^{ub} - p_{k} } \right\},\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} , $$

where $\zeta^{\tau ,\alpha ,k}$ is the length of the longest path starting from $v^{\tau ,\alpha }$ via $v^{{\tau + p_{k} ,\alpha^{\prime}}}$, which is calculated as follows:

$$ \zeta^{\tau ,\alpha ,k} = d_{{\tau + p_{k} ,\alpha^{\prime}}}^{\tau ,\alpha } + \theta^{{\tau + p_{k} ,\alpha^{\prime}}} , $$

(15)

where $\alpha^{{\prime }} = \alpha$ if $k \notin S_{C}$, and $\alpha_{k}^{{\prime }} = 1,\;\alpha_{k} = 0$, and $\alpha_{{\tilde{k}}}^{{\prime }} = \alpha_{{\tilde{k}}}$ for $\tilde{k} \ne k$, $\tilde{k} \in S_{C}$.

Boundary conditions:

$$ \theta^{\tau ,\alpha } = - \infty ,\;{\text{for}}\;\tau > T_{used}^{ub} ,\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} , $$

(16)

$$ \theta^{{T_{used}^{ub} ,\alpha }} = - g\left( {T_{used}^{ub} } \right),\;\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\},\;\tilde{k} \in S_{C} , $$

(17)

$$ \theta^{{\tau ,\bar{0}}} = - g\left( \tau \right),\;{\text{for}}\;\mathop {\hbox{max} }\limits_{k \in S} \left\{ {t_{k}^{ub} - p_{k} } \right\} < \tau \le T_{used}^{ub} , $$

(18)

$$ \zeta^{\tau ,\alpha ,k} = - \infty ,\;{\text{for}}\;\tau = 0, \ldots ,\mathop {\hbox{max} }\limits_{k \in S} \left\{ {t_{k}^{ub} - p_{k} } \right\},\;\alpha_{k} = 0,\;k \in S_{C} . $$

(19)

Optimal solution:

The optimal objective value is given by:

$$ R\left( {S_{C} } \right) = \theta^{{0,\bar{0}}} . $$

(20)

Theorem 3

DPAR-b finds the optimal solution for Model $(R(S_{C} ))$ in $O\left( {nT_{used}^{ub} 2^{m} } \right)$, where $m = \left| {S_{C} } \right|$.

Proof

No order can start after time $T_{used}^{ub}$, including order 0, yielding (16). An order can end but cannot start at time $T_{used}^{ub}$. Hence, the length of the longest path starting from vertex $v^{{T_{used}^{ub} ,\alpha }}$ is $- g\left( {T_{used}^{ub} } \right)$, yielding (17). Now, suppose we have found the longest paths starting from $v^{{\tau^{{\prime }} ,\alpha^{{\prime }} }}$, for all $\tau^{{\prime }} > \tau$, $\tau = 1, \ldots ,T_{used}^{ub}$, and all possible $\alpha^{{\prime }}$ values, and now we need to find the longest path starting from $v^{\tau ,\alpha }$. Any vertex reachable by $v^{\tau ,\alpha }$ can be denoted by $v^{{\tau + p_{k} ,\alpha^{\prime}}}$, $k \in S \cup \left\{ 0 \right\}$, and if $k \notin S_{C}$, $\alpha^{{\prime }} = \alpha$; otherwise, $\alpha_{k}^{{\prime }} = 1,\;\alpha_{k} = 0$, and $\alpha_{{\tilde{k}}}^{{\prime }} = \alpha_{{\tilde{k}}}$ for $\tilde{k} \ne k$, $\tilde{k} \in S_{C}$. Then, the length of the longest path starting from $v^{\tau ,\alpha }$ via $v^{{\tau + p_{k} ,\alpha^{{\prime }} }}$ is equal to the length of arc $e_{{\tau + p_{k} ,\alpha^{{\prime }} }}^{\tau ,\alpha }$ plus the length of the longest path starting from $v^{{\tau + p_{k} ,\alpha^{{\prime }} }}$, which is equal to $\zeta^{\tau ,\alpha ,k}$ from (15). Equation (14) states that, by enumerating all the vertices $v^{{\tau + p_{k} ,\alpha^{{\prime }} }}$ that can be reached from $v^{\tau ,\alpha }$, and comparing the corresponding $\zeta^{\tau ,\alpha ,k}$, the longest path starting from $v^{\tau ,\alpha }$ that contains at least two vertices is found. If the length of this path is less than 0, then we should not start processing any order at time $\tau$ because the profit of any order would be negative. In this case, the longest path starting from $v^{\tau ,\alpha }$ contains only the vertex itself. Then, considering these two cases, the longest path starting from $v^{\tau ,\alpha }$ is found. Boundary condition (18) states that no order $k \in S$ starts between times $\mathop {\hbox{max} }\limits_{k \in S} \left\{ {t_{k}^{ub} - p_{k} } \right\}$ and $T_{used}^{ub}$. Equation set (19) prevents controlled orders to appear more than once. Since order 0 can be duplicated, it is possible to assume that the longest path in $G\left( {V,E} \right)$ starts from $v^{{0,\bar{0}}}$, yielding (20). For each pair of $\tau$ and $\alpha$ values, $\theta^{\tau ,\alpha }$ can be found by checking $\varsigma^{\tau ,\alpha ,k}$ for all $k \in S \cup \left\{ 0 \right\}$, which is completed in $O\left( n \right)$. Therefore, DPAR-b finds an optimal solution for Model $({\text{R}}(S_{C} ))$ in $O\left( {nT_{used}^{ub} 2^{m} } \right)$. □

Both time and space complexities of DPAR-f and DPAR-b increase exponentially as $\left| {S_{C} } \right|$ grows. When $S_{C} = S$, Model (R(S_C)) is equivalent to Model (TIF). However, $m$ is not necessarily equal to $n$ since not all orders are accepted at the end. The optimal set of accepted orders is unknown before an optimal solution is obtained. Hence, we can start by solving Model (R(S_C)) with $S_{C} = \emptyset$. If the given solution is not feasible to Model (TIF), one duplicated order in the current solution is selected and added to $S_{C}$, and the resulting Model (R(S_C)) is solved. We continue this process until a feasible solution is achieved. In order to improve the computational efficiency and reduce the memory usage, graph reduction is applied to remove unnecessary vertices and the corresponding edges from the graph the model is solved.

3.3 Lower bound generation

Although Model (R(S_C)) may not produce a feasible solution when $S_{C} \subset S$, a lower bound for $U$, denoted by $lb$, can be derived by converting the optimal solution of Model (R(S_C)), denoted by $\sigma$, into a feasible one. In this paper, we adopt a strategy which first removes the duplicated orders except for the one that appears first in the sequence. Then, a DP-based dynasearch algorithm (DPDA) is applied to find a good feasible solution.

The basic idea of the dynasearch algorithm was proposed by Grosso et al. (2004) for the TWT problem. Essentially, it is a local search algorithm using three operators of generalized pairwise interchanges (GPI) to reach a neighborhood, i.e., swap (SWAP), extraction and backward-shifted reinsertion (EBSR), and extraction and forward-shifted reinsertion (EFSR). Let $\sigma$ be a sequence of orders with no inserted idle times: $\sigma_{1} \to k_{1} \to \sigma_{2} \to k_{2} \to \sigma_{3}$, where $k_{1}$ and $k_{2}$ are two different orders and $\sigma_{1}$, $\sigma_{2}$, and $\sigma_{3}$ are subsequences of $\sigma$. Then, the three GPI operators are defined as follows (Grosso et al. 2004):

$$ \begin{aligned} & \sigma_{1} \to k_{1} \to \sigma_{2} \to k_{2} \to \sigma_{3} \mathop \Rightarrow \limits^{{{\text{SWAP}}(k_{1} ,k_{2} )}} \sigma_{1} \to k_{2} \to \sigma_{2} \to k_{1} \to \sigma_{3} , \\ & \sigma_{1} \to k_{1} \to \sigma_{2} \to k_{2} \to \sigma_{3} \mathop \Rightarrow \limits^{{{\text{EBSR}}(k_{1} ,k_{2} )}} \sigma_{1} \to k_{2} \to k_{1} \to \sigma_{2} \to \sigma_{3} , \\ & \sigma_{1} \to k_{1} \to \sigma_{2} \to k_{2} \to \sigma_{3} \mathop \Rightarrow \limits^{{{\text{EFSR}}(k_{1} ,k_{2} )}} \sigma_{1} \to \sigma_{2} \to k_{2} \to k_{1} \to \sigma_{3} . \\ \end{aligned} $$

In the dynasearch algorithm, a locally optimal solution is found iteratively. At a generic stage $s$ of a recursion, we find a locally optimal sequence with $s$ orders through a series of GPI operations. However, to extend the algorithm to the case with inserted idle time, the order completion times should be considered. This paper adapts a scheme similar to the one proposed by Sourd (2006).

Although a feasible sequence $\sigma$ may not contain all the orders because of the capacity constraint, in order to find a good solution, all orders need to be considered as candidates in the neighborhood search. Therefore, $\sigma$ is first extended by arbitrarily allocating all unselected orders after the selected ones, resulting in a full sequence $\sigma^{{\prime }} = \left[ 1 \right] \to \cdots \to \left[ n \right]$, where $\left[ k \right]$ represents the order in the $k$th position of $\sigma^{{\prime }}$. The proposed DP-based dynasearch algorithm (DPDA) finds a good sequence $\sigma^{{\prime \prime }}$ from $\sigma^{{\prime }}$ and uses a DP approach to determine the optimal set of selected orders and their completion times in $\sigma^{{\prime \prime }}$.

Before introducing DPDA, we first present a DP algorithm that determines the optimal set of selected orders and the corresponding completion times given a sequence $\sigma :\left[ 1 \right] \to \cdots \to \left[ s \right]$. The DP algorithm consists of $s$ stages. In each stage $k$, $1 \le k \le s$, we decide whether order $\left[ k \right]$ should be selected if $\tau$ time units are given to process orders [1] to $\left[ k \right]$, $\tau = 0, \ldots ,T_{used}^{ub}$. If order $\left[ k \right]$ is selected, its completion time is also determined. The results of stage $k$ are used to find the optimal solutions in the next stage. The complete DP formulation is provided below.

Forward DP algorithm for a given sequence $\varvec{\sigma}$ (DPA)

Optimal value function:

$F_{k} \left( \tau \right)$:

optimal total profit for a sequence of available orders $[1]$ to $[k]$, given that $\tau$ time units are used to process the selected orders from $[1]$ to $[k]$, $k = 1, \ldots ,s$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$\gamma_{k} \left( \tau \right)$:

binary variable, indicating whether order $\left[ k \right]$ is selected ($\gamma_{k} \left( \tau \right) = 1$) or not ($\gamma_{k} \left( \tau \right) = 0$), given that $\tau$ time units are used to process the selected orders from $[1]$ to $[k]$, $k = 1, \ldots ,s$, $\tau = 0, \ldots ,T_{used}^{ub}$.

Recurrence relation:

$$ F_{k} \left( \tau \right) = \hbox{max} \left\{ {\begin{array}{*{20}c} {f_{\left[ k \right]} \left( \tau \right) + F_{{k{ - }1}} \left( {\tau - p_{\left[ k \right]} } \right) + g\left( {\tau - p_{\left[ k \right]} } \right) - g\left( \tau \right)} \\ {F_{{k{ - }1}} \left( \tau \right)} \\ {F_{k} \left( {\tau - 1} \right) + g\left( {\tau - 1} \right) - g\left( \tau \right)} \\ \end{array} } \right\}, $$

(21)

$$ \gamma_{k} \left( \tau \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}F_{k} \left( \tau \right) = f_{k} \left( \tau \right) + F_{k - 1} \left( {\tau - p_{k} } \right) + g\left( {\tau - p_{k} } \right) - g\left( \tau \right),} \hfill \\ {0,} \hfill & {{\text{if}}\; \, F_{k} \left( \tau \right) = F_{{{\text{k - }}1}} \left( \tau \right)} \hfill \\ {\gamma_{k} \left( {\tau - 1} \right),} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right. $$

(22)

$$ k = 2, \ldots ,s,\;\tau = 1, \ldots ,T_{used}^{ub} . $$

Boundary conditions:

$$ F_{1} \left( \tau \right) = \hbox{max} \left\{ \begin{array}{l} \, f_{\left[ 1 \right]} \left( \tau \right) - g\left( \tau \right) \hfill \\ F_{1} \left( {\tau - 1} \right){ + }g\left( {\tau - 1} \right) - g\left( \tau \right) \hfill \\ \end{array} \right\},\quad \tau = 1, \ldots ,T_{used}^{ub} , $$

(23)

$$ \gamma_{1} \left( \tau \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\; \, F_{1} \left( \tau \right) = f_{\left[ 1 \right]} \left( \tau \right) - g\left( \tau \right)} \hfill \\ {\gamma_{1} \left( {\tau - 1} \right),} \hfill & {{\text{otherwise}},} \hfill \\ \end{array} \tau = 1, \ldots ,T_{used}^{ub} ,} \right. $$

(24)

$$ F_{k} \left( 0 \right) = 0,\quad \gamma_{k} \left( 0 \right) = 0,\quad k = 1, \ldots ,s. $$

(25)

Optimal solution:

$$ {\text{Optimal}}\,{\text{total}}\,{\text{profit}}:\quad \hbox{max} \left\{ {F_{s} (\tau ):\tau = 0, \ldots T_{used}^{ub} } \right\}. $$

Theorem 4

DPA finds the optimal set of selected orders and the corresponding completion time given a sequence $\sigma$ in $O\left( {sT_{used}^{ub} } \right)$.

Proof

At time 0, no order can be completed; hence, the total profit is 0, yielding (25). In stage 1, only order [1] is considered. In (23), the first term in the parenthesis considers the case when order [1] is finished at time $\tau$, and the second term considers the case when the time unit at time $\tau$ is idle. Now, suppose the optimal total profit $F_{k} \left( \tau \right)$ for a sequence of available orders $[1]$ to $[k]$ and $\tau$ time units has been found, $1 \le k \le s$, $\tau = 0, \ldots ,T_{used}^{ub}$. Let us consider stage $k$ and $\tau$ time units, three possible decisions are considered: (i) order [k] is completed at time $\tau$, (ii) order [k] is rejected, and (iii) time unit $\tau$ is idle, $1 \le k \le s$, $\tau = 0, \ldots ,T_{used}^{ub}$. It should be noted that decisions (ii) and (iii) are not mutually exclusive. However, as long as all possible decisions are covered, the optimal solution can be found. For (i), the total profit of orders [1] to [k] is equal to the profit of order [k] plus the optimal total profit of orders [1] to [k − 1], which has been found in stage $k - 1$, subtracted by the increase of overtime cost, yielding the first term in the parenthesis in (21). For (ii), the total profit is the same as that in previous stage, yielding the second term in the parenthesis in (21). For (iii), the total profit is equal to the total profit as that of the previous time unit, subtracted by the difference in overtime cost, yielding the last term in the parenthesis in (21). By comparing the total profit obtained by the three possible decisions, the optimal total profit, given $k$ and $\tau$, is found. Then, the solution for a given sequence $[1]$ to $[s]$ is found by comparing $F_{s} \left( \tau \right)$ for all possible values of $\tau$ in stage $s$. In the recurrence relations, there are $s$ stages; in each stage, there are $T_{used}^{ub}$ values of $\tau$. Hence, the computational complexity of DPA is $O\left( {sT_{used}^{ub} } \right)$. □

DPDA follows a similar idea as DPA to determine the set of selected orders and their completion times but adding GPI operations. Essentially, we start with a sequence with only one order and gradually add orders to the sequence. Each time we add an order to the sequence, we find the best subsequence by searching the neighborhood defined by the GPI operations. Given a sequence of available orders $\sigma$, the following notation will be used in DPDA:

$\sigma_{s}^{*} \left( \tau \right)$:

current best subsequence for the first $s$ orders of $\sigma$, given that $\tau$ time units are used to process these orders, $s = 1, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$F_{s}^{*} \left( \tau \right)$:

total profit of $\sigma_{s}^{*} \left( \tau \right)$, $s = 1, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$\sigma_{s}^{o} \left( \tau \right)$:

subsequence constructed by adding to the end of $\sigma_{s - 1}^{*} \left( \tau \right)$ the $s$th order in $\sigma$, $s = 1, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$F_{s}^{o} \left( \tau \right)$:

optimal total profit of subsequence $\sigma_{s}^{o} \left( \tau \right)$, $s = 1, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$opr\left( {s^{{\prime }} ,s} \right)$:

GPI operation imposed on the $s^{{\prime }}$th and $s$th orders of subsequence $\sigma_{s}^{O} \left( \tau \right)$, $opr\left( {s^{{\prime }} ,s} \right) \in \left\{ {SWAP\left( {s^{{\prime }} ,s} \right),EBSR\left( {s^{{\prime }} ,s} \right),EFSR\left( {s^{{\prime }} ,s} \right)} \right\}$, $s^{{\prime }} = 1, \ldots ,s - 1$, $s = 2, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$\sigma_{s}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( \tau \right)$:

subsequence obtained after operation $opr\left( {s^{{\prime }} ,s} \right)$ is performed on the $s^{{\prime }}$th and $s$th orders of subsequence $\sigma_{s}^{o} \left( \tau \right)$, $opr\left( {s^{{\prime }} ,s} \right) \in \left\{ {SWAP\left( {s^{{\prime }} ,s} \right),EBSR\left( {s^{{\prime }} ,s} \right),EFSR\left( {s^{{\prime }} ,s} \right)} \right\}$, $s^{{\prime }} = 1, \ldots ,s - 1$, $s = 2, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$,

$F_{s}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( \tau \right)$:

optimal total profit of subsequence $\sigma_{s}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( \tau \right)$, $opr\left( {s^{{\prime }} ,s} \right) \in \left\{ {SWAP\left( {s^{{\prime }} ,s} \right),EBSR\left( {s^{{\prime }} ,s} \right),EFSR\left( {s^{{\prime }} ,s} \right)} \right\}$, $s^{{\prime }} = 1, \ldots ,s - 1$, $s = 2, \ldots ,n$, $\tau = 0, \ldots ,T_{used}^{ub}$

Forward DP-based dynasearch algorithm for a given sequence $\varvec{\sigma}$ (DPDA)

• Step 1 (Initialization) Set: $s = 1$, $\sigma_{1}^{*} \left( \tau \right): = \left[ 1 \right]$, $\tau = 0, \ldots ,T_{used}^{ub}$, and calculate $F_{1}^{*} \left( \tau \right)$ as follows:

  $$ \begin{aligned} F_{1}^{*} \left( \tau \right) & = \hbox{max} \left\{ {\begin{array}{*{20}c} { \, f_{\left[ 1 \right]} \left( \tau \right) - g\left( \tau \right)} \\ {F_{1}^{*} \left( {\tau - 1} \right){ + }g\left( {\tau - 1} \right) - g\left( \tau \right)} \\ \end{array} } \right\},\\ \tau & = 1, \ldots ,T_{used}^{ub} . \end{aligned} $$

  (26)

• Step 2 Set $s: = s + 1$. Construct a subsequence $\sigma_{s}^{o} \left( \tau \right): = \sigma_{s - 1}^{*} \left( \tau \right) \to \left[ s \right]$, $\tau = 0, \ldots ,T_{used}^{ub}$, and calculate the corresponding maximum total profit $F_{s}^{o} \left( \tau \right)$ as follows:

  $$ \begin{aligned} F_{s}^{o} \left( \tau \right) & = \hbox{max} \left\{ {\begin{array}{*{20}c} {f_{\left[ s \right]} \left( \tau \right) + F_{s}^{*} \left( {\tau - p_{\left[ s \right]} } \right) + g\left( {\tau - p_{\left[ s \right]} } \right) - g\left( \tau \right)} \\ {F_{s}^{*} \left( \tau \right)} \\ {F_{s}^{o} \left( {\tau - 1} \right) + g\left( {\tau - 1} \right) - g\left( \tau \right)} \\ \end{array} } \right\},\\ \tau & = 1, \ldots ,T_{used}^{ub} . \end{aligned} $$

  (27)

  Perform operation $opr\left( {s^{{\prime }} ,s} \right) \in \{ SWAP\left( {s^{{\prime }} ,s} \right),EBSR\left( {s^{{\prime }} ,s} \right),EFSR\left( {s^{{\prime }} ,s} \right) \}$ on $\sigma_{s}^{o} \left( \tau \right)$ and calculate $F_{s}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( \tau \right)$ for $s^{{\prime }} = 1, \ldots ,s - 1$, $\tau = 1, \ldots ,T_{used}^{ub}$, as follows:

  • (i) For $k = 1, \ldots ,s^{{\prime }} - 1$:

    $$ F_{k}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( {\tau^{{\prime }} } \right) = F_{k}^{*} \left( {\tau^{{\prime }} } \right),\quad \tau^{{\prime }} = 1, \ldots ,\tau . $$

    (28)

  • (ii) For $k = s^{{\prime }} , \ldots ,s$:

    $$ \begin{aligned} & F_{k}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( {\tau^{{\prime }} } \right) \\ &\quad = \hbox{max} \left\{ {\begin{array}{*{20}c} {f_{\left[ k \right]} \left( {\tau^{{\prime }} } \right) + F_{k}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( {\tau^{{\prime }} - p_{\left[ k \right]} } \right) + g\left( {\tau^{{\prime }} - p_{\left[ k \right]} } \right) - g\left( {\tau^{{\prime }} } \right)} \\ {F_{k}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( {\tau^{{\prime }} } \right)} \\ {F_{k}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( {\tau^{{\prime }} - 1} \right) + g\left( {\tau^{{\prime }} - 1} \right) - g\left( {\tau^{{\prime }} } \right)} \\ \end{array} } \right\},\\ \tau^{{\prime }} & = 1, \ldots ,\tau . \end{aligned} $$

    (29)

    Then,

    $$ \begin{aligned} & F_{s}^{*} \left( \tau \right) \\ &\quad = \hbox{max} \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{s^{{\prime }} = 1, \ldots ,s - 1}} F_{s}^{{opr\left( {s^{{\prime }} ,s} \right)}} \left( \tau \right):opr \in \left\{ {SWAP,EBSR,EFSR} \right\}} \\ {F_{s}^{o} \left( \tau \right)} \\ \end{array} } \right\}, \end{aligned} $$

    (30)

    and $\sigma_{s}^{*} \left( \tau \right)$, $\tau = 1, \ldots ,T_{used}^{ub}$, can be determined accordingly.

• Step 3 If $s < n$, go to Step 2; Otherwise, find the optimal total profit:

  $$ \hbox{max} \left\{ {F_{n} \left( \tau \right):\tau = 0, \ldots ,T_{used}^{ub} } \right\}. $$

3.4 Graph reduction

In DPAR-f (DPAR-b), given $S_{C}$, the optimal solution $\sigma_{f}^{\tau ,\alpha }$ $(\sigma_{b}^{\tau ,\alpha } )$ and corresponding objective value, $\varphi^{\tau ,\alpha }$ $(\theta^{\tau ,\alpha } )$ are found for all $\tau = 1, \ldots ,T_{used}^{ub}$, $\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\}$, $\tilde{k} \in S_{C}$. As mentioned before, $\sigma_{f}^{\tau ,\alpha }$ is the subsequence that provides the longest path from $v^{{0,\bar{0}}}$ to $v^{\tau ,\alpha }$ and $\sigma_{b}^{\tau ,\alpha }$ the subsequence that provides the longest path starting from $v^{\tau ,\alpha }$. Thus, the sequence $\sigma_{f}^{\tau ,\alpha } \to \sigma_{b}^{\tau ,\alpha }$ is the longest path passing through $v^{\tau ,\alpha }$, of which the length is $u^{\tau ,\alpha } = \varphi^{\tau ,\alpha } + \theta^{\tau ,\alpha }$. The following theorem identifies the vertices that are never used in a longest path in $G\left( {V,E} \right)$.

Theorem 5

Let $lb$ be a lower bound of the optimal objective value of Model (TIF), i.e., $lb \le U$. If $u^{\tau ,\alpha } < lb$, then there does not exist a longest path in $G\left( {V,E} \right)$ passing $v^{\tau ,\alpha }$.

Proof

(By contradiction) Suppose there exists a longest path in $G\left( {V,E} \right)$ passing through $v^{\tau ,\alpha }$, and $u^{\tau ,\alpha } < lb$. Let $U^{{\prime }}$ be the optimal objective value of Model (TIF) with the following additional constraints:

$$ \sum\limits_{{t = p_{k} }}^{\tau } {z_{k,t} } = 1,\quad \sum\limits_{t = \tau + 1}^{{T_{used}^{ub} }} {z_{k,t} } = 0,\;{\text{if}}\;k \in S_{C} \;{\text{and}}\;\alpha_{k} = 1, $$

(31)

$$ \sum\limits_{{t = p_{k} }}^{\tau } {z_{k,t} } = 0,\quad \sum\limits_{t = \tau + 1}^{{T_{used}^{ub} }} {z_{k,t} } \le 1,\;{\text{if}}\;k \in S_{C} \;{\text{and}}\;\alpha_{k} = 0. $$

(32)

After adding these two sets of constraints, the updated model finds the longest path passing through $v^{\tau ,\alpha }$ and its objective value is exactly $u^{\tau ,\alpha }$, i.e., $U^{{\prime }} { = }u^{\tau ,\alpha }$. By definition of $lb$, we have $lb < U$ and $u^{\tau ,\alpha } < lb$. Also, by our assumption that there exists a longest path passing through $v^{\tau ,\alpha }$, $U = U^{{\prime }} = u^{\tau ,\alpha }$. Then,

$$ u^{\tau ,\alpha } < lb \le U = U^{{\prime }} { = }u^{\tau ,\alpha } \quad \Rightarrow \quad u^{\tau ,\alpha } < u^{\tau ,\alpha } . $$

(33)

Now, we reach a contradiction. Therefore, the original statement holds. □

According to 0, $u^{\tau ,\alpha }$ forms a lower bound for the optimal objective value of Model (TIF), which is calculated as follows:

$$ u^{\tau ,\alpha } = \varphi^{\tau ,\alpha } + \theta^{\tau ,\alpha } - g\left( \tau \right). $$

(34)

In the graph reduction process, we first find $\varphi^{\tau ,\alpha }$ and $\theta^{\tau ,\alpha }$, for all $\alpha_{k} \in \left\{ {0,1} \right\}$, $k \in S_{C}$, $\tau = 1, \ldots ,T_{used}^{ub}$, by executing DPAR-f and DPAR-b once for each node $v^{\tau ,\alpha }$. Therefore, given that $m = \left| {S_{C} } \right|$, the computational complexity of graph reduction process is $O\left( {T_{used}^{ub} 2^{m} } \right)$.

3.5 The overall algorithm and possible improvements

The overall algorithm is provided below.

DP-based iterative algorithm with graph reduction (DPIA-GR)

• Step 1 Initialize: set $S_{C} = \emptyset$.

• Step 2 Solve Model (R(S_C)) using DPAR-f (DPAR-b). Let $\sigma$ be the current optimal sequence. If there exist duplicated orders in $\sigma$, go to Step 3; otherwise, an optimal solution to the original problem is achieved, and stop.

• Step 3 Conduct the graph reduction process to first find $\varphi^{\tau ,\alpha }$ and $\theta^{\tau ,\alpha }$, for all $\alpha_{k} \in \left\{ {0,1} \right\}$, $k \in S_{C}$, $\tau = 1, \ldots ,T_{used}^{ub}$, by executing DPAR-f and DPAR-b. $\sigma$ be the current optimal sequence.

• Step 4 Let order $k^{{\prime }}$ be the order that appears most times in $\sigma^{{\prime }}$ (ties are broken randomly). Set $S_{C} : = S_{C} \cup \left\{ k \right\}$, Go to Step 2.

Theorem 6

DPIA-GR finds an optimal solution for Model $\left( {R\left( {S_{C} } \right)} \right)$ in $O\left( {nT_{used}^{ub} 2^{n} } \right)$.

Proof

In the worst case, we continue to add orders to $S_{C}$ until $S_{C} = S$. In this case, Model (R(S_C)) and Model (TIF) are equivalent and therefore DPIA-GR guarantees to find an optimal solution for Model (TIF). The computational complexity to solve Model (TIF) using DPAR-f (DPAR-b) is $O\left( {nT_{used}^{ub} 2^{n} } \right)$, which is also the overall complexity of DPIA-GR. □

Although the computational complexity of DPIA-GR is non-polynomial, usually, an optimal solution can be obtained before all orders added into $S_{C}$. In other words, DPIA-GR finds an optimal solution for Model (TIF) in $O\left( {nT_{used}^{ub} 2^{m} } \right)$, where $1 \le m \le n$. Even so, the computational effort of DPIA-GR is still large. Therefore, graph reduction plays a critical role to improve the computational efficiency.

4 Iterative algorithm based on dynamic programming and Lagrangian relaxation with graph reduction (DPIA-LRGR)

In DPIA-GR, each time an order is added to $S_{C}$, both time and space complexities of DPAR-f/DPAR-b are doubled in the worst case, which may result in intolerable computational time and memory usage, especially when $m$ is large. In order to overcome this disadvantage, we improve DPIA-GR by incorporating Lagrangian relaxation (LR). The resulting algorithm is denoted by DPIA-LRGR.

In DPIA-LRGR, the LR model of Model (TIF), where the set of job occurrence constraints (constraint set (2)) is relaxed, is solved and an upper bound for the original problem is obtained; meanwhile, a lower bound is derived by generating a feasible solution from the optimal solution of the LR model using the method presented in Sect. 3.3. The subgradient method is applied to find the optimal Lagrangian multipliers (LMs) of the Lagrangian dual (LD) problem. A duality gap may exist between the optimal objective values of the original problem and the upper bound derived by solving the LD model. The set of occurrence constraints for the orders is gradually recovered to enable the bounds to meet. Each time an order is added into $S_{C}$, the graph reduction process described in Sect. 3.4 is executed to improve the computational efficiency. An optimal solution is achieved when the gap vanishes.

To avoid confusion, each time the LMs are updated, it is considered to be an iteration; and each time a new order is added to $S_{C}$, it is considered to be a stage.

4.1 The Lagrangian relaxation model for Model (TIF) and the corresponding DP algorithms

By assigning the LMs, denoted by $\omega_{k}$, $k \in S$, to constraint set (2), the LR model has the following formulation:

$$ \begin{aligned} & {\text{Model}}\;({\text{LR}}\,(\omega ))\quad L\left( \omega \right) \\ &\quad = \hbox{max} \sum\limits_{k \in S} {\sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } f_{k} \left( \tau \right)} } - g\left( {T_{used} } \right) + \sum\limits_{k \in S} {\omega_{k} \left( {1 - \sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } } } \right)} \\ & \quad = \sum\limits_{k \in S} {\sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } \left( {f_{k} \left( \tau \right) - \omega_{k} } \right)} } - g\left( {T_{used} } \right) + \sum\limits_{k \in S} {\omega_{k} } , \\ \end{aligned} $$

(35)

$$ {\text{s}}.{\text{t}}.\quad \left( 3\right)\;{\text{to}}\;\left( 6\right), $$

where $\omega = \left( {\omega_{1} , \ldots ,\omega_{n} } \right)^{T} \ge \overline{0}$. When constraint set (2) is partially recovered, the model becomes:

$$ \begin{aligned} & {\text{Model}}\;({\text{LR}}(S_{C} ,\omega ))\quad L\left( {S_{C} ,\omega } \right) \\ &\quad = \hbox{max} \sum\limits_{k \in S} {\sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } \left( {f_{k} \left( \tau \right) - \omega_{k} } \right)} } - g\left( {T_{used} } \right) + \sum\limits_{k \in S} {\omega_{k} } , \end{aligned} $$

(36)

$$ {\text{s}}.{\text{t}}. \quad \sum\limits_{{\tau = t_{k}^{lb} }}^{{t_{k}^{ub} }} {z_{k,\tau } } \le 1,\quad k \in S_{C} , $$

$$ \left( 3\right)\;{\text{to}}\;\left( 6\right), $$

where $\omega_{k} = 0$, for $k \in S_{C}$. Since Model (LR (ω)) can be seen as a special case of Model (LR(S_C, ω)) with $S_{C} = \emptyset$, in the rest of the paper, we keep the same abbreviation name (LR(S_C, ω)) and notation for the optimal objective function for both models.

Model (LR(S_C, ω)) can also be represented as a weighted di-graph similar to $G\left( {V,E} \right)$; the only difference is that the length of an edge $e_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$, $d_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{\prime}}}$ is calculated as follows:

$$ d_{\tau ,\alpha }^{{\tau - p_{k} ,\alpha^{{\prime }} }} = f_{k} \left( \tau \right) + \left[ {g\left( {\tau - p_{k} } \right) - g\left( \tau \right)} \right] + \omega_{k} . $$

(37)

Let the corresponding di-graph be $G_{LR} \left( {V,E} \right)$. Using DPAR-f (DPAR-b), an optimal solution of Model (LR(S_C, ω)) can be found. In $G_{LR} \left( {V,E} \right)$, we denote $\varPhi^{\tau ,\alpha }$ as the length of the longest path from $v^{{0,\bar{0}}}$ to $v^{\tau ,\alpha }$, and $\varTheta^{\tau ,\alpha }$ as the length of the longest path starting from $v^{\tau ,\alpha }$, $\tau = 0, \ldots ,T_{used}^{ub}$, $\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\}$, $\tilde{k} \in S_{C}$.

The LD model can be formulated as follows:

$$ {\text{Model}}\;\left( {{\text{LD}}\left( {S_{C} } \right)} \right)\quad D\left( {S_{C} } \right) = \hbox{min} \left\{ {L\left( {S_{C} ,\omega } \right):\omega \ge \bar{0}} \right\}. $$

(38)

Theorem 7

Given $S_{C}$ and $S_{C}^{{\prime }}$ , such that $\emptyset \subseteq S_{C} \subset S_{C}^{{\prime }} \subseteq S$ , then $D\left( {S_{C} } \right) \ge D\left( {S_{C}^{{\prime }} } \right) \ge U.$

Proof

Since Model $({\text{LR}}(S_{C}^{{\prime }} ,\omega ))$ is more restricted than Model (LR(S_C, ω)), $L\left( {S_{C} ,\omega } \right) \ge L\left( {S_{C}^{{\prime }} ,\omega } \right)$, for all $\omega \ge \bar{0}$. Further, the feasible regions of Models $(D(S_{C} ))$ and $(D(S_{C}^{{\prime }} ))$ are the same. Therefore, $D\left( {S_{C} } \right) \ge D\left( {S_{C}^{{\prime }} } \right).$ □

4.2 Subgradient procedure

Given $S_{C}$, the objective function of Model (LD(S_C)) is non-differentiable. In this case, the subgradient procedure is applied to minimize the upper bound obtained from Model (LD (S_C)). This paper applies a strategy similar with that proposed by Tanaka et al. (2009). Given $S_{C}$, let the LM vector at the $i$th iteration be $\omega^{{S_{C} ,i}} = \left( {\omega_{1}^{{S_{C} ,i}} , \ldots ,\omega_{n}^{{S_{C} ,i}} } \right)^{T}$. Then, $\omega^{{S_{C} ,i + 1}}$ is obtained as follows:

$$ \omega_{k}^{{S_{C} ,i + 1}} = \hbox{max} \left\{ {0,\omega_{k}^{{S_{C} ,i}} + \pi_{i} \frac{{L\left( {S_{C} ,\omega^{{S_{C} ,i + 1}} } \right) - LB}}{{\sum\limits_{l = 1}^{n} {\left( {1 - \sum\limits_{{\tau = t_{l}^{lb} }}^{{t_{l}^{ub} }} {z_{l,\tau }^{*} \left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} } \right)^{2} } }} \times \left( {1 - \sum\limits_{{\tau = t_{l}^{lb} }}^{{t_{l}^{ub} }} {z_{k,\tau }^{*} \left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} } \right)} \right\},\;k \in S\backslash S_{C} , $$

(39)

$$ \omega_{k}^{{S_{C} ,i + 1}} = 0,\quad k \in S_{C} , $$

(40)

where $LB$ is a lower bound of $U$ generated from the solution of Model $\left( {{\text{LR}}\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} \right)$ using the method introduced in Sect. 3.4, $z_{l,\tau }^{*} \left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)$, $l = 1, \ldots ,n$, $\tau = t_{l}^{lb} , \ldots ,t_{l}^{ub}$, is an optimal solution of Model $\left( {{\text{LR}}\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} \right)$, whose objective value $UB = L\left( {S_{C} ,\omega^{{S_{C} ,i + 1}} } \right)$ is an upper bound of $U$, and $\pi_{i}$ is a controllable parameter representing the step size at iteration $i$, which starts with $\pi_{0} = 1$ and is then set to $\pi_{i + 1} = \pi_{i} /1.2$ at every iteration. For Model $\left( {{\text{LR}}\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} \right)$, $\omega^{{S_{C} ,0}}$ is usually initialized to $\omega^{{S_{C} ,0}} = \overline{0}$. The procedure terminates when the relative gap (RGAP) defined by the best lower and upper bounds is less than a controllable parameter $\varepsilon$, e.g., $\varepsilon = 10^{ - 6}$:

$$ RGAP = \frac{{\left( {UB - LB} \right)}}{LB} < \varepsilon . $$

4.3 Graph reduction

Similar to DPIA-GR, unnecessary vertices are deleted from the graph before the next stage starts. The unnecessary vertices are identified by the following theorem.

Theorem 8

Let $U^{\tau ,\alpha }$ be the maximum objective value of Model $\left( {LR\left( {S_{C} ,\omega } \right)} \right)$ with the additional constraints (31) and (32). If $U^{\tau ,\alpha } < LB$, then, there does not exists an optimal solution of Model (TIF) passing through $v^{\tau ,\alpha }$.

Proof

Similar to the proof of Theorem 5. □

According to 0, $U^{\tau ,\alpha }$ forms an upper bound for the optimal objective value of Model (TIF), which can be calculated as follows:

$$ U^{\tau ,\alpha } = \varPsi^{\tau ,\alpha } + \varTheta^{\tau ,\alpha } - g\left( \tau \right) + \sum\limits_{k \in S} {\omega_{k} } . $$

(41)

In the graph reduction process, we first find $\varPsi^{\tau ,\alpha }$ and $\varTheta^{\tau ,\alpha }$, for all $\tau = 0, \ldots ,T_{used}^{ub}$, $\alpha_{{\tilde{k}}} \in \left\{ {0,1} \right\}$, $\tilde{k} \in S_{C}$, by executing DPAR-f and DPAR-b once for each node $v^{\tau ,\alpha }$. Therefore, given $S_{C}$ and $\omega$, the computational complexity of graph reduction process is $O\left( {T_{used}^{ub} 2^{m} } \right)$.

4.4 Summary of DPIA-LRGR

The steps of the proposed DPIA-LRGR algorithm are provided below.

• Step 1 Set $i = 0$, $S_{C} = \emptyset$, and $\omega^{\emptyset ,0} = \bar{0}$; generate initial sequences of orders using (1) earliest due date first, (2) latest due date first, (3) longest processing time first, (4) shortest processing time first, (5) highest revenue first, (6) highest penalty first, and (7) lowest penalty first; apply DPDA on each generated sequence, and then find the resulting objective function value to get a lower bound $LB$; and set the upper bound $UB = \infty$.

• Step 2 Solve Model $\left( {{\text{LR}}\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)} \right)$ using DPAR-f (DPAR-b); and update the upper bound:

  $$ UB: = \hbox{min} \left\{ {L\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right),UB} \right\}. $$

  (42)

  Update the lower bound if $i$ is a multiple of $I_{U}$ (in other words, the lower bound is updated every $I_{U}$ iterations), where $I_{U}$ is a controllable parameter:

  $$ LB: = \hbox{max} \left\{ {LB^{{\prime }} ,LB} \right\}, $$

  (43)

  where $LB^{\prime}$ is a lower bound derived from the solution of Model (LR $\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)$) using the method described in Sect. 3.3, and meanwhile a feasible solution, denoted by $\sigma_{LB}$, is generated. If

  $$ RGAP: = \frac{{\left( {UB - LB} \right)}}{LB} < \varepsilon , $$

  (44)

  $\sigma_{LB}$ is within a relative gap $\varepsilon$ from the optimal sequence, and stop; if inequality (44) is not satisfied and $UB$ remains unchanged for $I_{L}$ iterations), where $I_{L}$ is a controllable parameter, go to Step 3; otherwise, calculate $\omega^{{S_{C} ,i + 1}}$ using (39) and (40), update $i: = i + 1$, and go to Step 2.

• Step 3 Delete unnecessary vertices: first calculate the upper bound $U^{\tau ,\alpha }$ for all $\tau$ and $\alpha$ values using (41). Delete $v^{\tau ,\alpha }$ from $G_{LR} \left( {V,E} \right)$ if $U^{\tau ,\alpha } < LB$. Update the set of controlled orders: select an order that appears most times in the solution of Model (LR $\left( {S_{C} ,\omega^{{S_{C} ,i}} } \right)$), say, order $k$, and add it into $S_{C}$, i.e., $S_{C} : = S_{C} \cup \left\{ k \right\}$. If there are more than one such orders, select one arbitrarily. Go to Step 2.

5 Modifications to the cost function for period-dependent costs

The profit function of order $k \in S$ in Model (TIF), $f_{k} \left( {t_{k} } \right)$, is a general function of the completion time, $t_{k}$. In the formulation of the model in Sect. 2, we show how this function is used to penalize the earliness and tardiness of the order; however, this function can be used to incorporate other costs that vary based on the time interval that an order is produced or completed. There are often costs associated with production that can vary over time, such as varying utility costs, or costs associated with adding overtime capacity. In the proposed model, we allow for an overtime period at the end of the horizon, but we can use the profit function $f_{k} \left( {t_{k} } \right)$ as an alternate method for modeling overtime. We can think of this cost as an extra cost, given that order $k$ completes at time $t_{k}$, or given that the order is produced over a period of $p_{k}$ time units ending at time $t_{k}$.

Although Model (TIF) only considers overtime at the end of the regular time horizon, we can add costs to model overtime in intermediate time intervals. Consider time units $\tau$ and $\tau^{{\prime }}$, such that $1 < \tau < \tau^{{\prime }} < T$, as shown in Fig. 2 , and let the time interval between $\tau$ and $\tau^{{\prime }}$ be an overtime period that can be used for production of order $k$ with a cost function $h_{k} (\tau_{used} (t_{k} ))$, where $\tau_{used} (t_{k} )$ is the amount of overtime used between $\tau$ and $\tau^{{\prime }}$ for production of order $k$, given that it is completed at time $t_{k}$. We can modify the profit function $f_{k} \left( {t_{k} } \right)$ to $f_{k} \left( {t_{k} } \right) = f_{k}^{{\prime }} \left( {t_{k} } \right) - h_{k} (\tau_{used} (t_{k} ))$, where $f_{k}^{{\prime }} \left( {t_{k} } \right)$ is the component of the function which penalizes earliness and lateness.

Fig. 2

Examples for calculating $\tau_{used} (t_{k} )$

Figure 2 illustrates two special cases that need to be accounted for when calculating $\tau_{used} (t_{k} )$. In case (A) shown in the figure, order $k$ ends after $\tau^{{\prime }}$, but $p_{k}$ is long enough that it must start within the overtime interval, so $\tau_{used} (t_{k} ) = p_{k} - (t_{k} - \tau^{{\prime }} )$. Order $k^{{\prime }}$ ends within the overtime period, so $\tau_{used} (t_{{k^{{\prime }} }} ) = t_{{k^{{\prime }} }} - \tau$. In case (B) from the same figure, the order ends after $\tau^{{\prime }}$, but $p_{k}$ is long enough that it must start before $\tau$, so $\tau_{used} (t_{k} ) = \tau^{{\prime }} - \tau$. Finally, if the order both starts and ends within the overtime period, then $\tau_{used} (t_{k} )$ will be the entire processing time $p_{k}$.

We provide this method as a way to add overtime periods throughout the whole time horizon, instead of the method presented earlier, using the function $g\left( {T_{used} } \right)$, which only models overtime at the end of the regular time horizon. There are two shortcomings with this approach. First, $f_{k} \left( {t_{k} } \right)$ models the cost of overtime used for each individual order, so it cannot incorporate any fixed cost. Second, this model assumes that orders are produced in $p_{k}$ consecutive time units, regardless of whether they are within an overtime period or not. This means that the algorithm cannot choose to avoid overtime costs by starting an order before overtime, pausing production, and then completing it after the overtime finishes.

6 Genetic algorithm and MILP model

In order to test the performance of the DPIA-GR and DPIA-LRGR algorithms, we present two alternative solution methods that can be used for comparisons. The first of these methods is a genetic algorithm, and the second is an MILP implementation of Model (TIF). Let us define $f_{k} \left( {t_{k} } \right)$ and $g\left( {T_{used} } \right)$ for these experiments. It is assumed that the profit of order $k$ as a function of its completion time $t_{k}$, $f_{k} \left( {t_{k} } \right)$, is calculated as follows:

$$ f_{k} \left( {t_{k} } \right) = \left( {\begin{array}{*{20}l} { - \infty ,} \hfill & {{\text{if}}\; \, t_{k} < R_{k} + p_{k} ,} \hfill \\ {r_{k} - c_{k}^{E} \left( {d_{k} - t_{k} } \right),} \hfill & {{\text{if}}\; \, R_{k} + p_{k} \le t_{k} < d_{k} ,} \hfill \\ {r_{k} - c_{k}^{D} \left( {t_{k} - d_{k} } \right),} \hfill & {{\text{if}}\; \, d_{k} \le t_{k} \le D_{k} ,} \hfill \\ { - \infty ,} \hfill & {{\text{if}}\; \, t_{k} > D_{k} .} \hfill \\ \end{array} } \right. $$

(45)

Since an order $k$, $k \in S$, cannot be processed before its release date, $R_{k}$, it cannot be completed before $R_{k} + p_{k}$; when order $k$ is completed before its due date, $d_{k}$, a earliness penalty is incurred, which is a linear function of the earliness with a nonnegative penalty per time unit denoted by $c_{k}^{E}$; when order $k$ is completed after the due date and before the deadline $D_{k}$, a tardiness penalty is triggered, which is equal to the tardiness times a nonnegative penalty per time unit denoted by $c_{k}^{D}$; and order $k$ cannot be completed after its deadline. Figure 3 displays the profit function (45).

Fig. 3

Illustration of $f_{k} \left( {t_{k} } \right)$

The cost of overtime is a function of the total time used $T_{used}$, denoted by $g\left( {T_{used} } \right)$. It consists of a fixed cost and a variable cost and is calculated as follows:

$$ g\left( {T_{used} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if }}T_{used} \le T,} \hfill \\ {C^{O} + c^{O} \left( {T_{used} - T} \right),} \hfill & {{\text{if }}T_{used} > T,} \hfill \\ \end{array} } \right. $$

(46)

where $C^{O}$ is the nonnegative fixed overtime cost and $c^{O}$ is the nonnegative variable overtime cost per time unit. Figure 4 illustrates function $g\left( {T_{used} } \right)$.

Fig. 4

Illustration of $g\left( {T_{used} } \right)$

6.1 Genetic algorithm implementation

A GA is a meta-heuristic optimization approach that searches a solution space in a manner that is inspired by the biology of evolution. In a GA, potential solutions, referred to as individuals or chromosomes, are evaluated as the algorithm searches through the solution space. A set of individuals, called a population, is generated and maintained, as a method to search through the solution space of possible solutions. Members of the population are selected to produce offspring, which will serve to create the population for the next iteration of the algorithm. The current population at each iteration of the algorithm is called a generation. Each individual in the population is assigned a fitness value (in this case, the objective function value) indicating the ability of the individual to compete with other individuals. The fitness value is used to determine the likelihood that a member of a population produces an offspring for the next generation. The reproduction process comprises two steps: called crossover and mutation, which are inspired by biological principles. In order to implement a GA, we need to define the processes that the algorithm will use. Given a particular individual, we need a method to determine its fitness level, i.e., calculate the objective function value for that solution. We also need to define the crossover and mutation processes that are used to create offspring. Finally, the size of the population is set (usually a fixed size across each generation), an initial population is generated, and a stopping criterion is defined. Yoon and Ventura (2002) demonstrated that a GA framework can perform very well for a scheduling problem which aimed to minimize the absolute deviation from order due dates, where orders required a sequence of operations on multiple machines and could be split into sublots. Their problem did not include order acceptance.

6.1.1 MILP models to calculate fitness values

It is common in scheduling problems to define potential solutions in the form of a permutation of the orders in set $S$ (Goldberg and Lingle 1985). Let $\sigma$ be a sequence of the orders in $S$. Define $\sigma_{(j)}$ as the $j$th order in the sequence, so if order $k$, $k \in S$ is the $j$th order in the sequence, then $\sigma_{(j)} = k$. Suppose that the accepted orders in $S$ are scheduled following sequence $\sigma$ (potentially with idle times inserted between them). Given a fixed sequence, and a linear cost structure such as the one defined earlier in this section, we can define a continuous time formulation with order acceptance. The continuous time formulation, fixed sequence model with order acceptance (CTF-FSOA) can be formulated using the following binary variables:

$$ x_{k} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\,{\text{ order}}\, \, k\,{\text{ is}}\,{\text{ accepted}},} \hfill \\ {0,} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right.k \in S, $$

$$ y = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\; \, T_{used} > T,} \hfill \\ {0,} \hfill & {{\text{if}}\; \, T_{used} \le T .} \hfill \\ \end{array} } \right. \, $$

We also define $\lambda$ as the amount of overtime used, i.e., $\lambda = \hbox{max} \{ T_{used} - T,0\}$. We denote variables $e_{k}$ and $l_{k}$ as the earliness and lateness of order $k$, respectively, where $e_{k} = \hbox{max} \{ d_{k} - t_{k} ,0\}$ and $l_{k} = \hbox{max} \{ t_{k} - d_{k} ,0\}$. Finally, we define variables $a_{k}$, the profit of order $k$ if it is accepted, or 0 if it is rejected, $b_{k}^{ + }$ and $b_{k}^{ - }$, which are dummy variables that are set to the negative and positive parts of the profit of order $k$, respectively, if it is rejected, or 0 if it is accepted, and $M$, a large positive number. The model can be formulated as a mixed 0–1 linear program:

$$ {\text{Model}}\;({\text{CTF}} - {\text{FSOA}}):\quad U = \hbox{max} \sum\limits_{k \in S} {a_{k} } - C^{O} y - c^{O} \lambda , $$

(47)

$$ {\text{s}}.{\text{t}}.\quad t_{{\sigma_{(j)} }} - t_{{\sigma_{(j - 1)} }} \ge p_{{\sigma_{(j)} }} x_{{\sigma_{(j)} }} ,\quad j \in \{ 2, \ldots ,n\} , $$

(48)

$$ t_{k} + e_{k} - l_{k} = d_{k} ,\quad k \in S $$

(49)

$$ t_{k} \le T_{used}^{ub} - (T_{used}^{ub} - t_{k}^{ub} )x_{k} ,\quad k \in S $$

(50)

$$ t_{k} \ge t_{k}^{lb} x_{k} ,\quad k \in S $$

(51)

$$ r_{k} - c_{k}^{E} e_{k} - c_{k}^{D} l_{k} = a_{k} - b_{k}^{ - } + b_{k}^{ + } ,\quad k \in S $$

(52)

$$ a_{k} \le M{\kern 1pt} x_{k} ,\quad k \in S $$

(53)

$$ b_{k}^{ - } \le M(1 - x_{k} ),\quad k \in S $$

(54)

$$ t_{\sigma (n)} - \lambda \le T, $$

(55)

$$ \lambda \le (\hbox{max} \{ T_{used}^{ub} - T,0\} )y, $$

(56)

$$ t_{k} ,e_{k} ,l_{k} ,a_{k} ,b_{k} ,c_{k} \ge 0,\;x_{k} \in \{ 0,1\} ,\quad k \in S $$

(57)

$$ \lambda \ge 0,\quad y \in \{ 0,1\} $$

(58)

The objective function (47) is the sum of the contribution of the accepted orders, minus the fixed and variable cost of overtime. Constraint set (48) ensures that if an order is accepted, it does not start until the previous order is completed. Constraint set (49) defines the earliness and lateness of each order. Constraint sets (50) and (51) ensure that each accepted order is scheduled between $t_{k}^{lb}$ and $t_{k}^{ub}$ (recall that these bounds ensure that the order is profitable and scheduled between its release date and deadline). Constraint sets (53) and (54) ensure that $a_{k}$ is only positive if the order is accepted, and $b_{k}^{ - }$ is positive only if the order is rejected. Constraint set (52) sets $a_{k}$ equal to the profit of order $k$ (revenue minus earliness and tardiness penalties) if the order is accepted. If the order $k$ is rejected, then $a_{k}$ is set to zero. Constraint set (52) also ensures that if the profit of rejected order $k$ would be positive, $b_{k}^{ + }$ is set to the lost profit (since $a_{k}$ must be 0), otherwise $b_{k}^{ - }$ is set to the negative of the profit. Constraints (55) and (56) determine if overtime is needed and calculate the amount of overtime that is used. Constraint set (57) and constraint (58) define the completion dates, earliness, lateness, profit-related variables and overtime used as nonnegative and define the binary variables $x_{k}$ and $y$.

Though Model (CTF-FSOA) provides an optimal schedule with optimal order acceptance/rejection, given sequence $\sigma$, in practice, it does not run efficiently enough to be used to determine the fitness of every single member of every single generation in GA. This is largely due to the binary variables $x_{k}$. Instead, order acceptance can be done in an offline heuristic to generate a new sequence of accepted orders $\sigma^{A}$ This sequence contains a subset of accepted orders $S_{A} \subseteq S$. If order $k$, $k \in S_{A}$, is the $j$th order in the sequence, i.e., $\sigma_{(j)}^{A} = k$, then $k$ will be the $j$th order in the schedule, and if $k \notin S_{A}$, then $k$ is not included in $\sigma^{A}$. In this case, we can use a fixed sequence formulation with only one binary variable.

$$ {\text{Model}}\; \, ({\text{CTF}} - {\text{FS}}):\quad U = \hbox{max} \sum\limits_{k \in S} {(r_{k} } - c_{k}^{E} e_{k} - c_{k}^{D} l_{k} ) - C^{O} y - c^{O} \lambda , $$

(59)

$$ {\text{s}}.{\text{t}}.\quad t_{{\sigma_{(j)}^{A} }} - t_{{\sigma_{(j - 1)}^{A} }} \ge p_{{\sigma_{(j)}^{A} }} ,\quad j \in \{ 2, \ldots ,|S_{A} |\} , $$

(60)

$$ t_{k} + e_{k} - l_{k} = d_{k} ,\quad k \in S_{A} $$

(61)

$$ t_{k} \le t_{k}^{ub} ,\quad k \in S_{A} $$

(62)

$$ t_{k} \ge t_{k}^{lb} ,\quad k \in S $$

(63)

$$ t_{{\sigma (|S_{A} |)}} - \lambda \le T, $$

(64)

$$ \lambda \le (\hbox{max} \{ T_{used}^{ub} - T,0\} )y, $$

(65)

$$ t_{k} ,e_{k} ,l_{k} \ge 0,\quad k \in S_{A} $$

(66)

$$ \lambda \ge 0,\quad y \in \{ 0,1\} $$

(67)

The objective function (59) is the revenue of each order, minus the earliness and lateness penalties, and the cost of overtime. Note that if an order is accepted in Model (CTF-FSOA), then variable $a_{k}$ will be equivalent to the expression inside the parentheses in (59). Constraint set (60) ensures that each order does not start until the previous order completes. Constraint set (61) defines the earliness and lateness of each order. Constraint sets (62) and (63) ensure the completion date is between the lower and upper bounds. Constraints (64) and (65) determine if overtime is needed and calculate the amount of overtime that is used. Constraint set (66) and constraint (67) define the completion dates, earliness, lateness and overtime used as nonnegative, and define the binary variable $y$.

In order to determine the fitness level of a member of a population, given a sequence $\sigma$, we first create a tentative schedule by scheduling each order as early as possible such that it is still profitable. This is inspired by a myopic order acceptance technique, proposed by Rom and Slotnick (2009), which was used in another order acceptance problem that did not consider earliness penalties. In order to generate the tentative schedule, we first set $t_{{\sigma_{(1)} }} = t_{{\sigma_{(1)} }}^{lb}$ and add $\sigma_{(1)}$ to $\sigma^{A}$. Then, for $j \in \{ 2, \ldots ,n\}$, we set $t_{{\sigma_{(j)} }} = \hbox{max} \{ t_{{\sigma_{(j')} }}^{{}} + p_{{\sigma_{(j)} }} ,t_{{\sigma_{(j)} }}^{lb} \}$, where $\sigma_{(j')}$ is the most recent order added to $\sigma^{A}$. If $t_{{\sigma_{(j)} }} \le t_{{\sigma_{(j)} }}^{ub},$ then $\sigma_{(j)}$ is appended to the end of $\sigma^{A}$; otherwise, $\sigma_{(j)}$ is rejected. The fitness of $\sigma$ is determined by first using this heuristic to generate $\sigma^{A}$ and then finding the optimal completion dates by solving Model (CTF-FS). At the end of the order selection heuristic, if $t_{{\sigma_{{(|S_{A} |)}}^{A} }} > T$, then Model (CTF-FS) will be forced to use overtime in order to generate a feasible solution. If this is the case, we generate a subsequence $\sigma^{{A^{{\prime }} }}$ that includes only orders $\sigma_{(j)}$, such that $t_{{\sigma_{(j)} }} \le T$, and solve Model (CTF-FS) twice using both $\sigma^{A}$ and $\sigma^{{A^{{\prime }} }}$, and determine the fitness based on the better of the two solutions. Since this method uses a heuristic for order acceptance, we can solve Model (CTF-FSOA) only on the incumbent best solution in the GA. This results in a solution that is potentially near optimal, without having to use an inefficient model for all fitness calculations.

The models that are presented in this section rely on the fact that $f_{k} \left( {t_{k} } \right)$ and $g\left( {T_{used} } \right)$ are linear. If the cost structures are nonlinear, then either they would need to be approximated as a piecewise linear function, or the completion times of the accepted orders would need to be determined using a nonlinear solution method or heuristic. For example, the myopic heuristic used for order acceptance can be modified to more closely approximate an optimal schedule by scheduling the accepted orders with completion times equal to their due dates, and then resolving schedule conflicts by moving overlapping orders either forward or backward in a greedy method that minimizes the resulting earliness or tardiness penalty.

6.1.2 Initializing the population and reproduction

While testing this GA, we started with an initial population comprised of sequences that were randomly generated permutations of the numbers 1 through $n$. The convergence of the GA with this initial population was extremely slow, and the results were far from optimal. We know, however, that in this particular problem the optimal sequence is very likely to be close to a sequence $\sigma^{d}$ which is all orders in $S$ sorted in non-descending order based on their due dates. We can generate an initial population of members that are close to $\sigma^{d}$ in the following way. First, each order $k \in S$, where $k = \sigma_{(j)}^{d}$, is assigned a weight $w_{k} = 2^{n - j}$. As we generate a sequence $\sigma$, the first order $\sigma_{(1)}$ is set to $\tilde{k}$ with a probability of $w_{{\tilde{k}}} /\sum\nolimits_{k \in S} {w_{k} }$. If $\tilde{k}$ is the first order, then the next order $\sigma_{(2)}$ is set to $\tilde{k}^{{\prime }}$ with a probability of $w_{{\tilde{k}^{{\prime }} }} /\sum\nolimits_{{k \in S\backslash \tilde{k}}} {w_{k} }$, and so on. This method of generating an initial population proved to generate final solutions which were closer to optimal.

Once a population is initialized, a reproduction process is used to create offspring for the next generation. When we produce offspring, we wish to combine the data of high fitness individuals in such a way that produces a unique solution with features of the high fitness parents that hopefully results in a high fitness offspring. In order to select individuals to reproduce, the common approach is to weight each individual by its fitness level, then randomly selecting two individuals with a probability equal to their weight divided by the sum of all the weights. These individuals perform a crossover procedure to produce two offspring, and then each offspring has a small chance to have a mutation. This replication process is repeated until the number of offspring is equal to the population size, and then this set of offspring becomes the next generation.

A crossover method is generally designed to take pieces of two individuals and combine them to create two new individuals. A key challenge with scheduling problems is that a crossover process must ensure that when we create a sequence $\sigma$ as an offspring, it does not duplicate any orders, as this would yield an infeasible solution. The crossover method that is commonly used in scheduling problems is called a partially matched crossover (PMX) method, which was first proposed by Goldberg and Lingle (1985). This method uses a two-point crossover, where two points within the chromosome are selected, and the alleles (or orders) in between those points are swapped between the two parents. The resulting sequences become the two offspring. In order to prevent duplicates in the sequence, the alleles in between the crossover points are put in a match table which matches the alleles based on their position in the subsequence that is swapped between both parents. If an offspring sequence is generated so that it has an allele outside of the crossover points which matches an allele between the crossover points, then this would create a duplicate order. In this case, the allele outside the crossover points is replaced by the allele that it is matched with in the match table (the matching allele is an allele that was removed from the offspring during crossover). If an allele is present between the crossover points of both parents, then this allele will not be duplicated, and so a reduction is done to the match table by forming a chain of matches which share alleles. If the alleles at the ends of this chain are unique, then they are placed in the match table, and the other matches are removed.

To illustrate this crossover method, consider two parents, $p_{1}$ and $p_{2}$:

$$ \begin{aligned} & p_{1} = 1 \to 2 \to 3 \to 4 \to 5 \to 6 \to 7 \to 8, \\ & p_{2} = 5 \to 3 \to 2 \to 1 \to 4 \to 8 \to 7 \to 6. \\ \end{aligned} $$

First, we randomly select two positions in the sequence. For example, suppose the crossover points are after the second allele, and after the fifth allele. The crossover subsequences are $3 \to 4 \to 5$ from $p_{1}$, and $2 \to 1 \to 4$ from $p_{2}$. At this point, the offspring $o_{1}$, and $o_{2}$ are as follows:

$$ \begin{aligned} & o_{1} = 1 \to 2 \to 2 \to 1 \to 4 \to 6 \to 7 \to 8, \\ & o_{2} = 5 \to 3 \to 3 \to 4 \to 5 \to 8 \to 7 \to 6. \\ \end{aligned} $$

Notice that neither of these result in feasible solutions, since they both contain duplicated orders. In order to resolve this, we create a match table which matches the alleles in each position between the crossover points, so the matches are $\left( {3,2} \right)$, $\left( {4,1} \right)$ and $\left( {5,4} \right)$. Since 4 appears in both crossover subsequences, we create a chain of matches linked by 4, $\left( {5,4} \right) \leftrightarrow \left( {4,1} \right)$, and then remove both of those matches and form a new match $\left( {5,1} \right)$. Then, we search through the alleles outside of the crossover subsequences, and if they appear in the match table, we replace them with their match (so 5 and 1 would replace each other, as would 3 and 2). The final resulting offspring become:

$$ \begin{aligned} & o_{1} = 5 \to 3 \to 2 \to 1 \to 4 \to 6 \to 7 \to 8, \\ & o_{2} = 1 \to 2 \to 3 \to 4 \to 5 \to 8 \to 7 \to 6. \\ \end{aligned} $$

After crossover, mutation is done on each offspring by an adjacent swap method. Each allele is mutated with a specified mutation probability. If an allele is selected for mutation, it is swapped with the allele that follows it in the sequence. If the last allele is mutated, it is swapped with the first allele.

6.1.3 Stopping criteria

After each generation, the highest fitness member of the generation is compared to the incumbent best solution found so far. If this member has an objective function value that is better than the incumbent, then it is saved as the new incumbent. In this implementation, we then solve the (FSF) model to ensure that the solution is optimal for that particular sequence. The GA is typically stopped after either a fixed number of generations, or if there is little or no improvement over a series of consecutive generations.

6.2 MILP implementation

Another method that can be used to solve this problem is using an MILP formulation. We can implement the MILP using Model (TIF) with $f_{k} \left( {t_{k} } \right)$ defined as it is in (45) and $g\left( {T_{used} } \right)$ as in (46) through the use of an additional binary variable, similar to the variable y in (CTF-FSOA) and (CTF-FS).

7 Numerical experiments

In this section, we present a numerical experiment to assess the performance of the two DP-based algorithms proposed in this paper, and compare them to the GA described in Sect. 6.1 and the MILP defined in Sect. 6.2.

The GA, MILP, DPIA-GR, and DPIA-LRGR algorithms were tested with three problem sizes, i.e., 20, 35, and 50 orders.

7.1 Results

For each problem size, 100 instances were generated using the distributions shown in Table 1. Regarding the DPIA-LRGR parameters, $\varepsilon$ is set to 0.2%; $I_{U}$ to 3; and $I_{L}$ to 10. The GA used a mutation rate of 1%, with a population size of 100 and a stopping criterion of either 2000 generations, or 300 consecutive generations with no improvement to the objective function.

Table 1 Distribution of parameter values

The DPIA-GR and DPIA-LRGR algorithms were coded using C++, the MILP matrices were generated in MATLAB, and solved using CPLEX with the APIs from the CPLEX for MATLAB toolbox. The GA was also coded with MATLAB and the CPLEX for MATLAB toolbox. The MILP solver and three algorithms were run with the same 100 generated instances on an Intel Core i7-4790S 3.20 GHz PC with 16 GB of RAM and 64-bit Windows 10 operating system. The computational results are presented in Table 2. The reported CPU time for the GA is the time that the algorithm took to find the best solution. Since the stopping criteria allow the algorithm to continue for 300 generations without improvement, there are more generations that were evaluated after the best solution was found.

Table 2 Algorithm comparison

The results show that both of the proposed algorithms solve the problem more efficiently, on average, compared to traditional approaches. Also, DPIA-LRGR has higher efficiency than DPIA-GR by approximately a power of 2 for all problem sizes. Further, the deviation of the computational time is relatively comparable. For example, when $n = 50$, the maximal CPU times using DPIA-GR and DPIA-LRGR are 3.25 and 4.40 times larger than the average, respectively, while the maximum is 3.25 times larger than the average for the MILP, and 3.67 times larger for the genetic algorithm. Under all problem sizes, the average CPU times to solve the instances are lowest when using DPIA-LRGR. Furthermore, the results show that the GA is the weakest, not only because it has the longest CPU time (which is compounded by the fact that we need to run more generations after the best solution is found), but also at $n = 50$ it was only able to find the optimal solution once out of the 100 problem instances. At 20 and 35, the genetic algorithm was able to find the optimal solution 43 and 12 times, respectively.

We can see that the growth rate of the GA and MILP is slower than that of DPIA-GR and DPIA-LRGR. When we increase the number of orders from 35 to 50, the CPU time is multiplied by 2.23 and 2.25 for the MILP and GA, respectively, whereas the DPIA-GR and DPIA-LRGR are multiplied by 8.01 and 7.82. Also, the number of variables in the MILP formulation that is used by the GA is much smaller than the number of variables in Model (TIF), and the number of edges in the graphs used by DPIA-GR and DPIA-LRGR, so as a result, it is likely to use far less memory for problems of larger sizes. As such, we can anticipate that the GA will likely be able to find near-optimal solutions to problems that are much larger.

7.2 Relative performance of MILP based on problem parameters

We have seen that for the presented set of parameters, DPIA-LRGR performs the best. These parameters were selected to represent a realistic set of parameters, i.e., the variability of the revenue of each order is relatively low, and correlated with the processing length of the order, and the cost of overtime is generally comparable to the revenue generated by an order. There are different parameter sets on which the MILP performance seems to improve relative to DPIA-GR and DPIA-LRGR. For example, when the revenue associated with each order is more variable, and not correlated with the processing time, it becomes easier to determine which orders should be accepted. If an order has a much higher revenue than another order with a conflicting due date, it is not hard to imagine that the order with the higher revenue will have a variable that is relatively close to 1 in the LP relaxation of the problem, and therefore, the MILP would be able to find a reasonable bound more quickly. Table 3 shows the comparison of the MILP performance with DPIA-GR and DPIA-LRGR, with the same parameters as in Table 1, except the revenue $r_{k}$ was set to ${\text{Uniform}}(1,1000)$. In this case, the performance of the MILP improves relative to the DPIA-GR and DPIA-LRGR algorithms.

Table 3 Algorithm comparison with $r_{k} \sim{\text{Uniform}}\left( {1,1000} \right)$

We can see from Table 3 that in this scenario, the MILP performs better relative to the performance presented in Table 2. The mean CPU time decreased by 47% for the case where $n = 50$. Not only is the MILP performance better, likely due to the factors discussed earlier, but the DPIA-GR and DPIA-LRGR seem to perform worse, with an increase in average CPU time of 81% and 93%, respectively. The increase in CPU time for DPIA-GR and DPIA-LRGR is due, most likely, to the increase in the size of the controlled set $|S_{C} |$. Since the variability of the order revenues is so high, there are likely a set of order with very high revenues compared to the order with close due dates. In this case, it is not surprising that $|S_{C} |$ is higher, on average, because these orders with very high revenues are very profitable to duplicate in the schedule when they are not included in $|S_{C} |$. The GA results seem to also improve in terms of CPU time to find a good solution (reduction of 42% when $n = 50$).

Another factor which seems to improve the MILP is the density of the distribution of due dates. Table 4 shows the performance of the MILP compared to the DPIA-GR and DPIA-LRGR algorithms. In this case, the same parameters from Table 1 were used, except the due dates $d_{k}$ were set to ${\text{Uniform}}(p_{k} ,0.9\sum\nolimits_{k \in S} {p_{k} } )$.

Table 4 Algorithm comparison with $d_{k} \sim {\text{Uniform}}(p_{k} ,0.9\sum\nolimits_{k \in S} {p_{k} } )$

In this case, the performance of the MILP improves, while the GA, DPIA-GR, and DPIA-LRGR seem to be unaffected by the parameter change. Note that if $d_{k} \sim {\text{Uniform}}(p_{k} ,0.8\sum\nolimits_{k \in S} {p_{k} } )$, then every due date is before $T$, and as a result of the delay penalty, the latest upper bound $T_{used}^{ub}$ is only slightly beyond $T$, and so it is very unlikely that using overtime becomes profitable, especially since there is a fixed cost associated with it. In this particular scenario, the decision of whether or not to use overtime becomes relatively trivial.

8 Conclusions and future work

In this paper, we have studied the joint order acceptance and scheduling problem with penalties for earliness and tardiness, where the manufacturer can be seen as a single-machine system with limited capacity to process the orders. Overtime can be used to extend the capacity, which incurs additional cost. The problem has been formulated as a mixed 0–1 linear programming model.

Two exact algorithms, DPIA-GR and DPIA-LRGR, have been developed. DPIA-GR is based on DP. It starts with a relaxed problem where order duplication is allowed, and successively recovers the order occurrence constraint by using a controlled set of orders that cannot be duplicated to tighten the solution space until an optimal solution is found. The relaxed problem can be represented as a weighted di-graph, and the problem is equivalent to finding the longest path in the graph. A DP approach has been applied to find the longest path. To improve the computational efficiency, a graph reduction process has been presented. A DP-based algorithm has also been proposed to find an optimal set of selected orders as well as the corresponding completion times for a given sequence of orders. Based on this algorithm, a dynasearch approach has been employed to convert an infeasible solution produced by the relaxed problem into a feasible one. DPIA-LRGR improves DPIA-GR by incorporating Lagrangian relaxation, which helps prevent order duplication and derive a tighter upper bound. With Lagrangian relaxation, more unnecessary vertices can be removed from the graph and thus the memory usage and computational time is significantly reduced. Numerical experiments have shown that both algorithms solve the problem efficiently, but DPIA-LRGR is faster than DPIA-GR.

Nobibon and Leus (2011) argued that it is unlikely that a constant-factor approximation algorithm can be developed to solve this type of OAS problems. Furthermore, as stated in Sect. 1, Nobibon and Leus proposed two MILP formulations to solve the OAS problem with tardiness penalty and order preemption; one of them is a time-index formulation. Their results show that some of their test problems with 20 orders could not be solved using CPLEX 10.2 within a time limit of 2 h on a Dell Optiplex GX620 personal computer with Pentium R processor with 2.8 GHz clock speed and 1.49 GB RAM. In this work, we have compared the performance of the DPIA-GR and DPIA-LRGR algorithms and found that they outperformed the MILP solver and the GA in our experiments. In this case, the CPU was faster and had much more RAM than the computer used in experiments that were done by Nobibon and Leus. There are some factors that seem to improve the performance of the MILP model; however, these factors tend to be less realistic in practice and lead to problem instances where many of the decisions in the problem become trivial.

Though DPIA-GR and DPIA-LRGR outperform the proposed GA framework, it is expected that the GA will become favorable for problem sizes that are much larger than the ones presented in the experiment, due to the fact that Model (CTF-FS) in GA uses a relatively small number of variables. We also presented a method to generate an initial population with individuals that are likely to be closer to the optimal solution than individuals that are completely random. There are additional potential enhancements that may improve the search power of the algorithm in order to produce solutions that are closer to optimal, such as the modification to the mating process presented by Ventura and Yoon (2013), or a local neighborhood search method for candidate solutions that interchanges the sequence and acceptance/rejection decision of orders, such as the method presented by Thevenin et al. (2015). Finally, modifications to the GA can be made to generalize the formulation for nonlinear cost functions.

The model which was presented in this paper allowed for a period of overtime capacity at the end of the planning horizon. In some cases, a multi-period planning horizon may have multiple periods of available overtime across the planning horizon, such as a third shift at the end of every day, or weekend days over a planning horizon that spans multiple weeks. We have presented a method that can be used to add additional periods throughout the horizon that are available to use as overtime periods; however, this method has some shortcomings in that it cannot model a fixed overtime cost, and it assumes that orders cannot be started before overtime, paused, and then completed after the overtime period using regular capacity. Perhaps additional work can be done to model overtime in a more flexible manner.

In the numerical experiments, we observed that, in some cases, some of the orders in the controlled set are not accepted in the optimal solution, which may lead to unnecessary increase of computational effort. In the future, the method to select the orders to add into the controlled set should be reexamined. Besides, in this paper, our graph reduction strategy aims at unnecessary vertices; another possible extension is to remove unnecessary edges from the graph as well.