Measurements of translation, rotation and strain: new approaches to seismic processing and inversion

Abstract

We propose a novel approach to seismic tomography based on the joint processing of translation, strain and rotation measurements. Our concept is based on the apparent S and P velocities, defined as the ratios of displacement velocity and rotation amplitude, and displacement velocity and divergence amplitude, respectively. To assess the capability of these new observables to constrain various aspects of 3D Earth structure, we study their corresponding finite-frequency kernels, computed with a combination of spectral-element simulations and adjoint techniques. The principal conclusion is that both the apparent S and P velocities are generally sensitive only to small-scale near-receiver structure, irrespective of the type of seismic wave considered. It follows that knowledge of deeper Earth structure would not be required in tomographic inversions for local structure based on the new observables. In a synthetic finite-perturbation test, we confirm the ability of the apparent S and P velocities to directly detect both the location and the sign of shallow lateral velocity variations.

1 Introduction

Thanks to recent technological developments, seismically induced rotation and strain are emerging as new observables that complement the traditional translation recordings. Dynamic strain can be recorded by long-base laser strainmeters (e.g. Agnew and Wyatt 2003), and ring lasers are used for high-precision measurements of rotational ground motions (e.g. Schreiber et al. 2009). Direct and array-derived rotation measurements were compared for ring laser systems (e.g. Suryanto et al. 2006), and recordings of seismically induced strain have been analysed together with seismometer data and theoretical computations by Gomberg and Agnew (1996). For dynamic strain measurements, entire station networks as for example the EarthScope borehole strainmeter array also exist. The testing of portable rotation sensors has started only recently (e.g. Brokešová and Málek 2010; Nigbor et al. 2009; Liu et al. 2009; Wassermann et al. 2009).

While e.g. Mikumo and Aki (1964), Sacks et al.  (1976) and Blum et al. (2010) showed how to derive local phase velocities from acceleration measurements in conjunction with dynamic strain observations, the newly developed rotation sensors have also opened remarkable perspectives in many branches of seismological research: Observations of near-field rotational ground motions induced by swarm quakes (Takeo 2009), and fault ruptures (Wu et al. 2009) are likely to contribute to our understanding of earthquake source processes. As suggested by Pillet et al. (2009), rotation sensors may be used to improve the signal-to-noise ratio of ocean-bottom seismometers.

Also, various methods to infer Earth structure from rotation measurements have recently been proposed: Collocated measurements of translations and rotations were used to estimate local phase velocities (Igel et al. 2005, 2007; Cochard et al. 2006) or to identify the low seismic velocities of sedimentary basins (Wang et al. 2009; Stupazzini et al. 2009). Pham et al. (2009) extracted information about crustal scattering from rotational signals in the coda of P waves. Ferreira and Igel (2009) used full ray-theory modelling to demonstrate a clearly observable effect of near-receiver heterogeneities on rotational motions of Love waves. Following these first successful applications based on single rotational ground motion recordings, the next steps consist in (1) the installation of rotation sensor networks and (2) the incorporation of strain measurements in order to complete the set of seismic observables.

In anticipation of these developments, this paper explores the potentials of future rotation and strain sensor networks in the context of seismic tomography. For this, we investigate an approach to seismic tomography that is based on the joint processing of translation (u _i ), strain ($e_{ij} := \frac{1}{2}(\partial_j u_i + \partial_i u_j)$) and rotation ($\omega_i := \frac{1}{2}\varepsilon_{ijk}\partial_ju_k$) measurements. Following Fichtner and Igel (2009) and Bernauer et al. (2009), we consider the apparent S and P velocities, defined as the ratios of displacement velocity and rotation amplitude, and displacement velocity and divergence amplitude, respectively. Using adjoint techniques and a spectral-element solver of the seismic wave equation (Fichtner et al. 2009; Fichtner 2011), we compute the sensitivity kernels for the apparent P and S velocities. For a 1D model, the sensitivity of the apparent S velocity of S and surface waves is concentrated in the vicinity of the receiver (Fichtner and Igel 2009). In this study, we extend the work of Fichtner and Igel (2009) to P waves and the apparent P velocity. Furthermore, we combine the kernels with a finite-perturbation test indicating that aspects of 3D Earth structure are particularly well constrained by the newly defined observables.

2 The characteristics of a 12-component data set

We begin our developments with the simulation of a 12-component data set that illustrates several characteristic properties of rotation and strain measurements. For the computation of both synthetic seismograms and sensitivity kernels, we use a spectral-element solver of the seismic wave equation (Fichtner et al. 2009; Fichtner 2011). As Earth model, we use the isotropic version of the Preliminary Reference Earth Model (PREM) without viscoelastic dissipation (Dziewonski and Anderson 1981). The seismic wavefield with a dominant period of 20 s is excited by a point source at 400-km depth beneath eastern Indonesia and recorded at 30° epicentral distance, as illustrated in Fig. 1. The explicit source parameters can be found in Appendix. The three-component displacement velocity, three-component rotation and six-component strain corresponding to the previously described setup are displayed in Fig. 2. The symbols θ, ϕ and z denote colatitude, longitude and depth, respectively. The arrival of the direct P wave around 330 s is visible in the radial and vertical components of the displacement velocity v _ϕ and v _z , as well as in the ϕϕ- and zz-components of the strain tensor. P-to-S conversions at the free surface are responsible for the P wave signal in the transverse rotation ω _θ . The clearest S wave arrival at ~600 s is contained in the transverse velocity v _θ , the vertical rotation ω _z and the ϕϕ and θϕ strain components. Love and Rayleigh waves are present roughly from 700 to 800 s.

Fig. 1

Source mechanism and snapshot of the vertical-component wavefield, 200 s after source initiation. The source is located at 400-km depth, 130° E longitude and 0° latitude in eastern Indonesia. The dominant period is 20 s. The receiver is marked by the black dot (100° E longitude, 0° latitude, 0-km depth)

Fig. 2

Synthetic 12-component data set: velocity, rotation and strain are simulated at one single seismic station on Sumatra. The dominant period is 20 s. P and S phases are marked by dashed lines

While the waveforms of the non-zero strain and rotation components strongly depend on the source-receiver geometry, the vanishing components are of a more general nature. In particular, the radial-component rotation—ω _ϕ in our case—is always expected to be zero in a layered medium (Cochard et al. 2006). Furthermore, the free-surface boundary condition forces the strain components e _ϕz and e _θz to zero, which leads us to focus on the diagonal strain components in our subsequent analysis.

3 New observables and their response to 3D Earth structure

While rotation and strain measurements are interesting already by themselves, we wish to go one step further and define new observables from combinations of velocity, strain and rotation. This is motivated by a simple plane wave analysis: Assuming a plane S wave u(x,t) in a homogeneous and isotropic full space, the S velocity β can be expressed as the ratio of velocity and rotation amplitude:

$$ \beta=\frac{1}{2}\frac{|\mathbf{v}|}{|\boldsymbol{\omega}|}\,, $$

(1)

with the time derivative of the displacement field $\mathbf{v}=\dot{\mathbf{u}}$. Similarly, for a plane P wave, the P velocity α is given by

$$\alpha=\frac{|\mathbf{v}|}{|\text{tr}\,\mathbf{e}|}\,. $$

(2)

Due to our restrictive assumptions, Eqs. 1 and 2 are of little practical relevance in heterogeneous media. Nevertheless, a slight generalisation promises to yield rather direct information on the Earth’s S and P velocity structures: Inspired by Eq. 1, we define the apparent S velocity β _a measured at receiver position x ^r as (Fichtner and Igel 2009)

$$ \beta_a(\mathbf{x}^r)=\frac{1}{2}\frac{v(\mathbf{x}^r)}{w(\mathbf{x}^r)}\,, $$

(3)

with the velocity amplitude $v(\mathbf{x}^r)=\sqrt{\int \mathbf{v}^2(\mathbf{x}^r,t)\,dt}$ and the rotation amplitude $w(\mathbf{x}^r)=\sqrt{\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}$. In analogy to Eq. 3, we define the apparent P velocity α _a at the receiver position x ^r as

$$ \alpha_a(\mathbf{x}^r)=\frac{v(\mathbf{x}^r)}{s(\mathbf{x}^r)}\,, $$

(4)

where the symbol s denotes the divergence amplitude $s(\mathbf{x}^r)=\sqrt{\int [\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)]^2\,dt}$. Both definitions, Eqs. 3 and 4, are applicable either to complete seismograms or to isolated waveforms, as discussed in Sect. 4. An exemplary measurement of β _a corresponding to the SH wave phases of the v _θ and ω _z seismograms in Fig. 2 is shown in Fig. 3.

Fig. 3

β _a measurement representing the SH wave phases of the v _θ and $\boldsymbol{\omega}_z$ seismograms in Fig. 2. According to Eq. 3, β _a is calculated via $\frac{1}{2}\sqrt{\int v_{\theta}(\mathbf{x}^r,t)^2dt}/ \sqrt{\int \boldsymbol{\omega}_z(\mathbf{x}^r,t)^2dt}$, while v _θ and $\boldsymbol{\omega}_z$ are restricted to the SH wave windows (grey column)

The apparent S velocity β _a is equal to the S velocity β in the case of a plane S wave in a homogeneous, unbounded and isotropic medium. A similar result holds for the apparent P velocity α _a .

It is at this point important to keep in mind that the apparent P and S velocities α _a and β _a are measurements derived from various seismograms. In contrast, the P and S velocities α and β are material parameters, the 3D variations of which are the target of a tomographic inversion.

Our primary interest is in the response of the previously defined measurements to variations in 3D Earth structure. For this, we consider a generic measurement χ that represents, for instance, the velocity amplitude v(x ^r), the apparent S velocity $\beta_a(\mathbf{x}^r)$ or the apparent P velocity $\alpha_a(\mathbf{x}^r)$. A change in the observable, δχ, that results from a model perturbation δm is given, correct to first order, by

$$ \delta\chi = \int K_m(\chi,\mathbf{x}) \delta m(\mathbf{x})\,d^3\mathbf{x}\,, $$

(5)

where m can be the S velocity β, the P velocity α or any other Earth model parameter. The sensitivity or Fréchet kernel K _m (χ,x) describes how the observable χ is affected by model parameter changes δm at position x in the Earth. In the interest of a succinct notation, we omit the spatial dependence of the kernels from hereon.

In the following, we explore the properties of sensitivity kernels for various rotation- and strain-related observables, including the apparent S and P velocities. This allows us to identify the observable’s capability to constrain different aspects of 3D Earth structure. All kernels are computed with the help of adjoint techniques (e.g. Tarantola 1988; Tromp et al. 2005; Fichtner et al. 2006).

4 Sensitivity kernel gallery

To illustrate the main characteristics of our newly defined observables β _a and α _a , we present a gallery of sensitivity kernels for P, S, Love and Rayleigh waves. This is intended to aid in the development of the physical intuition necessary for the incorporation of β _a and α _a into tomographic inversions.

In the following figures, we show not only the sensitivity kernels for the apparent P and S velocities, K _m (α _a ) and K _m (β _a ), but also for the velocity amplitude, K _m (ν), the rotation amplitude, K _m (w), and the divergence amplitude, K _m (s). This is because K _m (α _a ) and K _m (β _a ) are equal to the differences

$$ K_m(\alpha_a)=K_m(v)-K_m(s)\, $$

(6)

and

$$ K_m(\beta_a)=K_m(v)-K_m(w)\,. $$

(7)

Equations 6 and 7 follow directly from the product rule of differentiation. For a detailed derivation of Eq. 6, we refer to Fichtner and Igel (2009). Equation 7 follows analogously. The necessary technical details for the explicit computation of K _m (v), K _m (s) and K _m (w) can be found in Appendix.

4.1 P wave kernels

In our first series of examples, we consider the direct P wave for the setup described in Figs. 1 and 2. Sensitivity kernels of the velocity amplitude v, the divergence amplitude s and the apparent P velocity α _a are shown in Fig. 4. All kernels are with respect to α, meaning that they describe the first-order response of the respective observable to a change in the P velocity. The velocity amplitude kernel K _α (ν) has the typical cigar shape of a body wave amplitude kernel with negative sensitivity in the first Fresnel zone surrounding the geometric ray path (e.g. Dahlen and Baig 2002). According to Eq. 5, positive perturbations of α located within the region of negative sensitivity reduce the P wave amplitude and vice versa. The broad structure of the divergence amplitude kernel K _α (s) is similar to the velocity amplitude kernel K _α (ν), meaning that both v and s provide nearly identical constraints on 3D Earth structure. As shown in Fig. 5, differences between K _α (ν) and K _α (s) are mostly restricted to the near-receiver region and to the higher Fresnel zones.

Fig. 4

Left column: Vertical slices through the source-receiver plane of the sensitivity kernels for the velocity amplitude v, the divergence amplitude s and the apparent P velocity α _a . All kernels are relative to the P velocity α. K _α (α _a ) is most sensitive to near-receiver structures. Right column: Vertical slices through the source-receiver plane of the rotation amplitude and the apparent S velocity kernels for the 20-s P wave from Fig. 2. K _α (β _a ) is most sensitive to near-receiver structures

Fig. 5

Vertical slices through various sensitivity kernels perpendicular to the source-receiver plane. The slices are close to the receiver in the left panel (a, c, e) and close to the source in the right panel (b, d, f). The velocity and divergence amplitude kernels, K _α (v) and K _α (s), are hardly distinguishable in the source region. Differences are most pronounced around the receiver. Consequently, the α _a kernel K _α (α _a ) = K _α (v) − K _α (s) is largest in the receiver region (left) but vanishes closer to the source (right)

These differences are particularly evident in the apparent P velocity kernel K _α (α _a ), which, according to Eq. 6, is equal to the difference K _α (ν) − K _α (s). The localisation of K _α (α _a ) near the surface and the absence of a broad first Fresnel zone suggest that the apparent P velocity of the direct P wave constrains comparatively small-scale variations of α near the receiver. We furthermore note that K _α (α _a ) is predominantly positive so that increases in α are expected to yield increases in α _a and vice versa. The non-zero sensitivity of α _a directly at the source is confined to a very small volume, meaning that it is practically negligible.

While it is intuitively expected that the apparent P velocity α _a of the direct P wave is sensitive to the P velocity α, the behaviour of the apparent S velocity β _a is less predictable. First, we note that the apparent S velocity of the direct P wave takes a well-defined finite value. This is mostly because the transverse rotation of the P wave (ω _θ in Fig. 2) is non-zero as a result of P-to-S conversions as the P wave reflects off the free surface. Changes in the P velocity α affect the P wave and therefore also lead to perturbations of the converted S wave. This explains why the sensitivity of the rotational signal of the P wave, K _α (w), is significantly different from zero—and in fact very similar to the sensitivity of the displacement amplitude K _α (ν) (Fig. 4). Again, the differences between K _α (ν) and K _α (w) manifest themselves most clearly in the apparent S velocity kernel K _α (β _a ) that is largest near the receiver, similar to K _α (α _a ).

It is a particularly noteworthy observation that the kernels K _α (α _a ) and K _α (β _a ) from Fig. 4 are globally similar but differ significantly from each other in the near-receiver region. This suggests that the apparent P and S velocities provide independent information on the near-receiver P velocity structure. This leads us to conjecture that the combined use of both α _a and β _a in tomographic inversions can improve the resolution of 3D P velocity heterogeneity.

4.2 S wave kernels

The direct P waveform from the previous example is clearly separated from later-arriving phases, which allowed us to study unambiguously defined P wave kernels. S waveforms, in contrast, are more complex and appear in the form of an isolated peak only in the transverse velocity ν _θ and the vertical rotation ω _z . Thus, in the interest of simplicity, we restrict our attention to the measurement of the apparent S velocity β _a , computed from the SH wave phase recorded in the ν _θ and ω _z seismograms in Fig. 2.

The corresponding kernels for the rotation amplitude, K _β (w), the velocity amplitude, K _β (ν), and the apparent S velocity, K _β (β _a ), are displayed in Fig. 6. All kernels are with respect to the S velocity β because the SH wave is practically insensitive to the P velocity α. Except for the slimmer first Fresnel zone that results from the shorter wavelength of S waves compared to P waves, the S wave kernels duplicate the main features of the P wave kernels in Fig. 4. In particular, the large-scale features of K _β (ν) and K _β (w) are nearly identical, meaning that the velocity amplitude and the rotation amplitude of the SH wave do not provide independent constraints on 3D S velocity heterogeneity.

Fig. 6

Vertical slices through the source-receiver plane of sensitivity kernels for the 20-s SH wave shown in Fig. 2. The velocity amplitude kernel at the top and the rotation amplitude kernel in the middle are similar. The apparent S velocity kernel K _β (β _a ) at the bottom pronounces the small differences between K _β (v) and K _β (w)

As for the P wave, the essential benefit comes from the combination of the two measurements, ν and w, into one new observable: the apparent S velocity β _a . The sensitivity of β _a to the S velocity, K _β (β _a ) = K _β (ν) − K _β (w), highlights the differences between K _β (ν) and K _β (w) that can mostly be found within the higher Fresnel zones and near the surface. The apparent S velocity kernel K _β (β _a ) is therefore—similar to the apparent P velocity kernels—only sensitive to comparatively small-scale near-receiver structure. It follows that β _a provides additional information on near-surface structure that is independent of the S velocity at larger distances from the receiver.

4.3 Love wave kernels

For the computation of surface wave sensitivity kernels, we slightly modify our simulation setup: The source is placed at a shallower depth of 50 km, and the dominant period is increased to 50 s. In our study of Love waves, we follow the previous SH wave example and consider only the ν _θ - and ω _z -components. As Love waves are insensitive to the P velocity α, we concentrate on the sensitivity of β _a with respect to β.

Figure 7 demonstrates that the previously observed phenomenon of sensitivity restricted to the near-receiver region is reproduced by Love waves. It follows that Love waves should also be well suited to constrain small-scale variations in β close to the surface. Vertical slices through the sensitivity kernels K _β (ν), K _β (w) and K _β (β _a ) are shown in Fig. 8. As expected, sensitivity for all measurements rapidly decreases away from the surface and practically vanishes below 200-km depth.

Fig. 7

Horizontal slices at 25-km depth through the sensitivity kernels K _β (ν), K _β (w) and K _β (β _a ) for a 50-s Love wave

Fig. 8

Vertical slices for a constant latitude at 0° (left panel) and a constant longitude at 115° (right panel) through the sensitivity kernels K _β (ν), K _β (w) and K _β (β _a ) for a 50-s Love wave. The sensitivity of all measurements, ν, w and β _a , is restricted to the upper 200 km

4.4 Rayleigh wave kernels

To complete the gallery for the most prominent phases in a seismogram, we consider 50-s Rayleigh waves. The setup is identical to the one used for Love waves. Fundamental Rayleigh waves are sensitive to the P velocity α primarily within the crust. We therefore focus on the sensitivity with respect to the S velocity β, displayed in Fig. 9. The velocity and divergence amplitude kernels are based on the ν _ϕ and ν _z velocity components, and the e _ϕϕ and e _zz strain seismograms, respectively. The rotation amplitude kernel contains only the θ-component of the rotation seismogram.

Fig. 9

Horizontal slices at 50-km depth through the sensitivity kernels K _β (ν), K _β (w), K _β (s), K _β (β _a ) and K _β (α _a ) for a 50-s Rayleigh wave

Figure 9 reveals a phenomenon that is similar to the one encountered in Sect. 4.1, where the rotation of the P wave was found to contain information on P velocity structure: The divergence of the Rayleigh wave is affected by heterogeneities in the S velocity, as evidenced by the large non-zero contributions to K _β (s) in Fig. 9. As already expected, the kernels for the apparent P and S velocities, K _β (α _a ) and K _β (β _a ), are restricted to the vicinity of the receiver, with the most important contributions located in the higher Fresnel zones. Furthermore, the spatial patterns of K _β (α _a ) and K _β (β _a ) differ strongly—as in the case of the P wave in Sect. 4.1. This implies that β _a and α _a provide linearly independent constraints on 3D S velocity structure.

5 Perturbation test

In the previous sections, we studied the properties of various observables with the help of sensitivity kernels. The kernel K _β (β _a ), for instance, describes an infinitesimal change of the apparent S velocity, δβ _a , in response to an infinitesimal S velocity perturbation δβ. From a purely mathematical perspective, the kernel corresponds to an exact first derivative. Its physical meaningfulness, however, depends on the linearisability of the observable. How well does a kernel such as K _β (β _a ) describe the finite change Δβ _a that results from a finite S velocity perturbation Δβ?

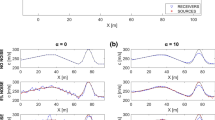
To address this question, we perform a simplistic perturbation test, summarised in Figs. 10 and 11. In terms of demonstrating precisely the nature of the new observables, we abstain from more complex scenarios. For this, we use the complete seismograms from the shallow event of Sects. 4.3 and 4.4 that are clearly dominated by surface waves. The synthetic waveforms are now recorded by a dense array of 720 equally distributed stations shown in Fig. 11a–c in the form of a regular mesh.

Fig. 10

Chequerboard-like S velocity perturbation. The blocks are 2°×2°×200-km wide and are located directly beneath the surface. The perturbation amplitudes are maximum ±10 % relative to PREM

Fig. 11

a Finite relative change of the velocity amplitude ν across the array of 720 receivers. Each gridpoint represents one station. b, c The same as a but for the finite relative changes in the rotation amplitude w and the apparent S velocity β _a

In the first simulation, we compute synthetic velocity, rotation and strain seismograms for the 1D background model PREM (Dziewonski and Anderson 1981). These provide reference values for the velocity amplitude, $v^\text{ref}$, the rotation amplitude, $w^\text{ref}$, and the apparent S velocity, $\beta_a^\text{ref}$. For the second simulation, we add the ±10 % chequerboard-like S velocity perturbation in Fig. 10 to PREM.

The resulting observables $\nu^\text{pert}$, $w^\text{pert}$ and $\beta_a^\text{pert}$ can then be used to compute the finite relative changes $(\nu^\text{pert}-\nu^\text{ref})/\nu^\text{ref}$, $(w^\text{pert}-w^\text{ref})/w^\text{ref}$ and $(\beta_a^\text{pert}-\beta_a^\text{ref})/\beta_a^\text{ref}$ at each station. These are displayed in Fig. 11a–c. The finite response of the velocity amplitude (Fig. 11a) corresponds well to the prediction of the sensitivity kernels K _β (ν) for both body and surface waves that are dominated by negative first Fresnel zones. An increase of β therefore leads to a decrease of ν and vice versa. This explains the approximate anti-correlation of Δβ and ν in the vicinity of the perturbation. The large spatial extent of K _β (ν) is responsible for the significant changes in the velocity amplitude in regions that are far from the actual perturbation. In other words, the spatial pattern of $(\nu^\text{pert}-\nu^\text{ref})/\nu^\text{ref}$ does not allow us to unambiguously identify the location of the S velocity perturbation. The same arguments and conclusions are valid for the rotation amplitude w, shown in Fig. 11b.

The finite perturbations of the apparent S velocity, displayed in Fig. 11c, are localised directly above the S velocity perturbations, with only small tails extending towards the northwest and southwest. This observation is in agreement with the concentration of the β _a kernels in the vicinity of the receiver. We may therefore directly infer both the location and the sign of lateral S velocity perturbations—which was, in fact, the initial motivation for defining the apparent S and P velocities. While the previous example was designed to demonstrate the ability of the apparent S velocity to constrain local heterogeneities, a similar experiment is possible for the apparent P velocity, with nearly identical results.

6 Discussion

The sensitivity kernels for the apparent P and S velocities share two essential properties that are independent of the type of seismic wave considered: (1) the localisation of sensitivity in the vicinity of the receiver and (2) the comparatively strong lateral variations of the kernels that result of the nearly complete absence of sensitivity inside the first Fresnel zone. The advantageous consequence of the first property is that both α _a and β _a contain information about 3D heterogeneities in the direct vicinity of the receiver that is not contaminated by potentially unknown deeper Earth structure.

The rapid oscillations of the α _a and β _a kernels are both an advantage and a drawback. They suggest, on the one hand, that lateral variations smaller than the width of the first Fresnel zone may be resolvable. On the other hand, they are responsible for the small effect of larger scale heterogeneities on the apparent P and S velocities. The relatively large-scale chequerboard-like pattern in Fig. 10, for instance, leads to nearly ±15 % changes in ν and w. However, the effect on β _a is almost a factor of 3 smaller because the positive and negative contributions of K _β (β _a ) in the integral of Eq. 5 tend to cancel. Consequently, high-precision measurements of the new observables α _a and β _a are required. In this context, providing reliable amplitude data is still a challenging task in seismic data acquisition.

The non-zero apparent S velocity of the P wave provides additional constraints on the local P velocity structure. This improvement—as well as its analogue for Rayleigh waves—should also be considered in the context of a multi-parameter inversion for both P and S velocity structure. Apparent velocities in the sense of Eqs. 3 and 4 generally depend on both α and β. The solution of an inverse problem therefore requires either precise prior knowledge on one of the parameters (one-parameter inversion) or a joint inversion (multi-parameter inversion). In both cases, the benefits of incorporating apparent velocities in the inverse problem must be quantified with a proper resolution analysis (Fichtner and Trampert 2011).

The examples in this study are rather specific but should be seen in a broader context. The apparent P and S velocities are just two among infinitely many combinations of translations, rotations and strain that happen to have advantageous properties. One obvious extrapolation would be to construct combinations of measurements that are particularly useful to constrain specific aspects of 3D Earth structure. This could be achieved through the optimisation of a design criterion, e.g. large sensitivity or resolution in a certain region of the Earth. This, however, is clearly beyond the scope of this work.

7 Conclusions

The principal conclusions drawn from this work are as follows: (1) Both the apparent P and S velocities, α _a and β _a , are generally only sensitive to small-scale near-receiver structure—irrespective of the seismic wave considered. These properties result from the different source mechanisms of the adjoint wavefields for velocity, rotation and strain observables (see Appendix). This suggests that measurements of α _a and β _a may be used in tomographic inversion to constrain local structure without requiring knowledge of 3D heterogeneities in the deeper Earth. (2) As a result of P-to-S conversions at the surface, the rotation of the P wave is significantly non-zero. This leads to a strong sensitivity of β _a to the local P velocity α. (3) The sensitivity patterns of K _α (α _a ) and K _α (β _a ) for the P wave are substantially different, meaning that rotation measurements provide independent constraints on the local P velocity structure. (4) Similarly, α _a and β _a for the Rayleigh wave provide independent constraints on the local S velocity. (5) Perturbation tests confirm that finite perturbations in α _a and β _a are indeed well predicted by the sensitivity kernels that only capture the first-order effect. In particular, α _a and β _a only respond to near-receiver heterogeneities. These results pave the way towards tomographic inversions for local Earth structure on the basis of combined translational, rotational and strain measurements.

Appendix: Details for the computation of sensitivity kernels

The forward wavefield is excited by a bandpass filtered Heaviside function between 20 and 200 s. The moment tensor components given in Nm are

$$ \begin{array}{rll} M_{\theta\theta}&=&0.710 \cdot 10^{19}\\[-4pt] M_{\phi\phi}&=&-0.356 \cdot 10^{19}\\[-4pt] M_{zz}&=&-0.355 \cdot 10^{19}\\[-4pt] M_{\theta\phi}&=&0.800 \cdot 10^{19}\\[-4pt] M_{\theta z}&=&0.315 \cdot 10^{19}\\[-4pt] M_{\phi z}&=&-1.150 \cdot 10^{19}. \end{array} $$

The sensitivity kernel K _m (v) is computed via the adjoint source time function

$$ f^v_k(\mathbf{x})=\frac{1}{\int\mathbf{v}^2(\mathbf{x}^r,t)\,dt} \ddot{u}_k(\mathbf{x}^r) \delta(\mathbf{x}-\mathbf{x}^r). $$

The adjoint sources for the sensitivity kernels K _m (w) and K _m (s) are dipolar sources described by the moment tensor M. The explicit moment tensor components for the computation of K _m (w) are

$$ \begin{array}{rll} M_{\theta\theta}&=&0\\ M_{\theta\phi}&=&\frac{1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_z(\mathbf{x}^r,t)\\ M_{\theta z}&=&\frac{-1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_{\phi}(\mathbf{x}^r,t)\\ M_{\phi\theta}&=&\frac{-1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_z(\mathbf{x}^r,t)\\ M_{\phi\phi}&=&0\\ M_{\phi z}&=&\frac{1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_{\theta}(\mathbf{x}^r,t)\\ M_{z \theta}&=&\frac{1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_{\phi}(\mathbf{x}^r,t)\\ M_{z \phi}&=&\frac{-1}{2\int \boldsymbol{\omega}^2(\mathbf{x}^r,t)\,dt}\omega_{\theta}(\mathbf{x}^r,t)\\ M_{zz}&=&0. \end{array} $$

The moment tensor components corresponding to K _m (s) are given by

$$ \begin{array}{rll} M_{\theta\theta}&=&\frac{-1}{\int [\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)]^2\,dt}\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)\\ M_{\theta\phi}&=&0\\ M_{\theta z}&=&0\\ M_{\phi\theta}&=&0\\ M_{\phi\phi}&=&\frac{-1}{\int [\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)]^2\,dt}\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)\\ M_{\phi z}&=&0\\ M_{z \theta}&=&0\\ M_{z \phi}&=&0\\ M_{zz}&=&\frac{-1}{\int [\text{tr}\,\mathbf{e}(\mathbf{x}^r,t)]^2\,dt}\text{tr}\,\mathbf{e}(\mathbf{x}^r,t). \end{array} $$

For a detailed derivation of the adjoint source time functions, we refer to Fichtner and Igel (2009).