Seismometer self-noise estimation using a single reference instrument

Abstract

A new method is presented for the self-noise estimation of a seismometer using a single, side-by-side, reference instrument and taking into consideration the misalignment in the orientation of both seismometers. The self-noise of seismometers is extracted directly from the measurements without using any information relating to the transfer functions. This procedure can be applied if the self-noise of the reference seismometer is well known and defined, or if the self-noise of the reference seismometer is sufficiently below the self-noise of the tested instrument and can be neglected. The latter case applies to this study. An algorithm is also developed where we apply self-noise data in order to determine the orientation misalignment between two seismometers, which is then resolved in three-dimensional space. This new method provides an estimate of the self-noise and can also be used to extract some parameters of the installed seismic system in comparison with the reference seismic system, such as generator constants and seismometer orientation or to eliminate unwanted noise sources, which have their origin in the seismic station’s design. The new technique was applied to the CMG-3ESPC and CMG-40T seismometers, where an STS-2 instrument served as the reference seismometer.

1 Introduction

In recent years, more and more seismic stations that are deployed in local seismic networks use broadband seismometers as a replacement for short-period instruments because of their lower self-noise, larger dynamic range, wider frequency response and more stable electronics.

Local seismic networks have two main goals. The first goal is to inform and alarm local government agencies, media and the community about the basic parameters of an earthquake, such as the hypocenter and the magnitude, and to provide an estimate of its intensity soon after the earthquake has occurred. Another goal of local seismic networks is to detect small earthquakes that do not cause damage but are important for additional geophysical and seismological studies. However, weak signals may be masked or distorted by the instrumental noise.

The noise floor is the sum of all the noise sources and unwanted signals within a seismic recording system and determines the lower limit of seismic signals that can be recorded at a seismic station. The noise floor is bounded by the seismometer, the installation technique and the acquisition unit at the seismic station. While the self-noise of dataloggers can be measured with a short-circuited input, this is not the case for the self-noise measurement of broadband seismometers (Evans et al. 2010). The self-noise of seismometers is usually represented by the power spectral density (PSD) function. The noise specifications of seismometers are given by the manufacturers and are commonly presented as the interval where the self-noise of a particular seismometer is below the U.S. Geological Survey (USGS) new low-noise model (NLNM), (Peterson 1993). This interval is usually provided by the manufacturer as a generic interval for the same type of seismometers. However, the interval may vary between similar instruments. There are also other sources affecting the noise floor at a seismic station, which may have a larger effect than the seismometer itself (e.g., the electronic noise of a power supply, acoustic effects, the EM radiation, etc.). A seismometer’s self-noise information allows the removal or minimizing of these sources of noise. Once the seismometer self-noise is known, these unwanted sources of noise can be eliminated or at least minimized. Such information about a particular seismometer is important for each seismic station where the goal is to observe and detect earthquakes with small magnitudes. The self-noise of a seismometer can be evaluated by using one- (two-sensor test) or two reference seismometers (three-sensor test; Hutt et al. 2009).

The method where the self-noise of a seismometer is quantified by using another (second) reference seismometer is described by Holcomb (1989). Both seismometers need to be placed together and be aligned in the same way, so it can be assumed they record the same ground motion. The practical usage of this approach is limited as a result of two sources of error: the transfer function uncertainty, and the imperfect alignment of the instruments. (Holcomb 1989, 1990).

In this approach, even small inaccuracies in the transfer functions of seismometers can cause relatively large errors in the calculated self-noise levels (Holcomb 1989). So this approach can only be applied when the transfer functions of both seismometers are the same, or they are different but known with high accuracy, or when the reference seismometer has a known transfer function and is noise-free while the system under evaluation is noisy and has an unknown transfer function (Wielandt 2002). In the case of a three-sensor test (Sleeman et al. 2006; Hutt et al. 2009), two seismometers are placed close to the tested one and with the same orientation. There is no need to know the transfer functions of either of them and also an assumption of noise-free instruments is not required. But in this case, a three-acquisition system and three seismometers are needed, making this approach more complicated and expensive.

In the above-mentioned procedures, the effect of sensor misalignment (Holcomb 1990) is not canceled out and is usually visible in the frequency band around the peak amplitude of the secondary microseism. In the case of a higher seismic noise, the sensor misalignment can also affect the calculation of self-noise, so seismometers need to be oriented in the same direction to within 0.1° (Hutt et al. 2009), which is not always possible.

After considering the discussed problems, we have developed an algorithm to estimate the self-noise of a tested seismometer using a single reference seismometer where the transfer function uncertainty and the sensor misalignment do not affect the results. Using this technique, the information regarding the transfer function is not needed, and the possible misalignment is not critical, because it can be calculated and taken into consideration. The requirement is that the self-noise of the reference seismometer is below the self-noise of the tested sensor or the self-noise of the reference seismometer is similar to the self-noise of the tested sensor, but well known and defined.

2 Self-noise measurement

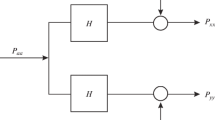
The following mathematical description of the model is presented first in a one-dimensional approach where two linear systems, representing seismometers, are both fed by a common input signal. The system to be evaluated is depicted in Fig. 1, where the index ‘q’ represents the seismometer under investigation and the index ‘r’ represents the reference seismometer.

Fig. 1

Simple 1D model for the seismometer self-noise measurement. The common input signal is ‘x’. The outputs are y _q and y _r

The output y _q of the seismometer ‘q’ is the convolution of the input signal x with the transfer function h _q of the seismometer ‘q’ adding the internal noise n _q (Sleeman et al. 2006):

$$ {y_{\text{q}}} = {h_{\text{q}}} \otimes x + {n_{\text{q}}}. $$

(1)

A similar equation can be written for the reference seismometer by replacing ‘q’ with ‘r’.

Assuming that both systems are linear and that the noise is completely uncorrelated, the output PSD for the seismometer ‘q’ can be expressed by:

$$ {{\text{P}}_{\text{qq}}} = {H_{\text{q}}}H_{\text q}^{*}{{\text{P}}_{{xx}}} + {{\text{N}}_{\text{qq}}} $$

(2)

where * denotes the complex conjugation, and Pxx = XX ^* is the autopower spectrum of the common input signal (Sleeman et al. 2006). Replacing the index ‘q’ by ‘r’ yields the PSD expression for the reference seismometer. The cross-power spectra P_qr (Proakis and Manolakis 1989) between the sensors ‘q’ and ‘r’ can be written as:

$$ {{\text{P}}_{\text{rq}}} = {H_{\text{r}}}H_{\text{q}}^{*}{{\text{P}}_{{xx}}} $$

(3)

where the noise cross-power spectra N_rq is assumed to be zero. Equation 2 can be rewritten as

$$ {{\text{P}}_{\text{qq}}} - {{\text{N}}_{\text{qq}}} = {H_{\text{q}}}H_{\text{q}}^{*}{{\text{P}}_{{xx}}} $$

(4)

If Eq. 4 is divided by Eq. 3 and then both sides are multiplied by their respective complex conjugated values, the following relationship is obtained:

$$ \frac{{\left( {{{\text{P}}_{\text{qq}}} - {{\text{N}}_{\text{qq}}}} \right)\left( {{\text{P}}_{\text{qq}}^{*} - {\text{N}}_{\text{qq}}^{*}} \right)}}{{{{\text{P}}_{\text{rq}}}{\text{P}}_{\text{rq}}^{*}}} = \frac{{{H_{\text{q}}}H_{\text{q}}^{*}}}{{{H_{\text{r}}}H_{\text{r}}^{*}}} $$

(5)

Using Eq. 4, where the expression for the tested seismometer is divided by the expression for the reference seismometer, we obtain the following relation:

$$ \frac{{\left( {{{\text{P}}_{\text{qq}}} - {{\text{N}}_{\text{qq}}}} \right)}}{{\left( {{{\text{P}}_{\text{rr}}} - {{\text{N}}_{\text{rr}}}} \right)}} = \frac{{{H_{\text{q}}}H_{\text{q}}^{*}}}{{{H_{\text{r}}}H_{\text{r}}^{*}}} $$

(6)

After Eq. 5 is divided by Eq. 6, the ${\text{N}}_{\text{qq}}^{*}$ can be simply expressed and we obtain an equation representing the noise autopower spectrum for the sensor q; this is the self-noise of seismometer under investigation:

$$ {\text{N}}_{\text{qq}}^{*} = {\text{P}}_{\text{qq}}^{*} - \frac{{{{\text{P}}_{\text{rq}}}{\text{P}}_{\text{rq}}^{*}}}{{\left( {{{\text{P}}_{\text{rr}}} - {{\text{N}}_{\text{rr}}}} \right)}} $$

(7)

The advantage of this method becomes evident: there is no need to know the transfer functions of any of the seismometers, and only one reference seismometer is needed. This equation can be applied if the self-noise of the reference seismometer is well known and defined. The self-noise of the reference seismometer can be obtained from the three-sensor test (Sleeman et al. 2006). Equation 7 is also directly correlated with the equations used in this three-sensor test. Let us suppose that the third sensor, marked by the index ‘k’, is used to define the self-noise of the reference seismometer ${{\text{N}}_{\text{rr}}} = {{\text{P}}_{\text{rr}}} - {{\text{P}}_{\text{qr}}}\left( {{{{{{\text{P}}_{\text{rk}}}}} \left/ {{{{\text{P}}_{\text{qk}}}}} \right.}} \right)$ (Sleeman et al. 2006). From this expression the self-noise of the tested seismometer ‘q’ is derived using Eq. 7:

$$ {{\text{N}}_{\text{qq}}}^{*} = {{\text{P}}_{\text{qq}}}^{*} - {{\text{P}}_{\text{qr}}}^{*}\left( {{{{{{\text{P}}_{\text{qk}}}}} \left/ {{{{\text{P}}_{\text{rk}}}}} \right.}} \right). $$

(8)

After the self-noise of the reference seismometer is obtained from the three-sensor test, there is no further need to use two “reference” seismometers in the analysis of the self-noise of the other seismometers in the local seismic network. It is easier to transport and install just one reference seismological system than two at the remote locations, where the seismic stations are usually situated. This approach also reduces the costs and increases the mobility and convenience of the self-noise evaluation procedure.

While the model in Fig. 1 is mathematically simple; in reality, it is difficult to use Eq. 8 to estimate the self-noise of a less noisy seismometer relative to the reference seismometer. In this particular case, Eq. 2 can be rewritten as ${{\text{P}}_{\text{qq}}} = {H_{\text{q}}}H_{\text{q}}^{*}{{\text{P}}_{{xx}}} + {H_{\text{q}}}H_{\text{q}}^{*}{{\text{P}}_{{{x_1}{x_1}}}} + {{\text{N}}_{\text{qq}}}$, where x ₁ is the weak ground-motion signal detected only by the seismometer ‘q’ and the left-hand side of Eq. 8 becomes in this case ${H_{\text{q}}}H_{\text{q}}^{*}{{\text{P}}_{{{x_1}{x_1}}}} + {{\text{N}}_{\text{qq}}}$. The information about the self-noise of the acquisition units that are used in the test needs to be known as well and needs to be lower than the self-noise of the seismometers. For this reason, our technique (Eq. 8) requires a low or at least similar self-noise reference system compared to the system under investigation.

3 Self-noise evaluation using a single reference seismometer without any information about its self-noise

In cases where we do not have any data regarding the self-noise of the reference seismometer and the three-sensor test cannot be performed, the self-noise of the tested seismometer can only be evaluated when the self-noise of the reference seismometer is much lower than the seismic signal and can be neglected. In that case Eq. 7 can be simplified and the estimated self-noise ${\widehat{{\text{N}}}_{{{\text{qq}}}}}$ for the seismometer ‘q’ is given by:

$$ {\widehat{{\text{N}}}_{{{\text{qq}}}}} = {\text{P}}_{{{\text{qq}}}}^{*} - \frac{{{{\text{P}}_{{{\text{rq}}}}}{\text{P}}_{{{\text{rq}}}}^{*}}}{{{{\text{P}}_{{{\text{rr}}}}}}}. $$

(9)

The power spectrum of the self-noise of the reference seismometer is expressed in terms of the cross-power spectra and the autopower spectra of the recordings of the two seismometers and can be easily calculated from the outputs of both seismological systems, y _r and y _q. It is very simple to prove that Eq. 9 is a good approximation of Eq. 7, if P _rr> > N _rr, because the N_rr in the denominator can be neglected. Equation 9 is also a good approximation in the case when the seismic signal is below the self-noise of the tested seismometer (N _qq >> P _xx), because the impact of the seismic signal on the right-hand side of the equation can be neglected. But this equation is also valid in the case when the seismic signal is similar to, or higher than, the self-noise of the tested seismometer N _qq ≤ P _xx when the self-noise of the reference seismometer is below the self-noise of the tested seismometer (N _rr << N _qq), because N _rr << P _xx and the N _rr in the denominator can be neglected, again (under the condition that |P _xx| ≤ |P_rr|). So Eq. 9 represents a good estimate in the case when the self-noise of the seismometer under test n _q is much higher than the self-noise of the reference seismometer n _r. The condition when the self-noise N _rr can be neglected is evaluated using the ratio between the real and the estimated self-noise ${\text{N}}_{{{\text{qq}}}}^{*}/{\widehat{{\text{N}}}_{{{\text{qq}}}}}$,

$$ \frac{{{\text{N}}_{{{\text{qq}}}}^{*}}}{{{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}}} = \frac{{{{\text{P}}_{{{\text{rr}}}}}\left( {\left( {{{\text{P}}_{{{\text{rr}}}}} - {{\text{N}}_{{{\text{rr}}}}}} \right){\text{P}}_{{{\text{qq}}}}^{*} - {{\text{P}}_{{{\text{rq}}}}}{\text{P}}_{{{\text{rq}}}}^{*}} \right)}}{{\left( {{{\text{P}}_{{{\text{rr}}}}} - {{\text{N}}_{{{\text{rr}}}}}} \right)\left( {{{\text{P}}_{{{\text{rr}}}}}{\text{P}}_{{{\text{qq}}}}^{*} - {{\text{P}}_{{{\text{rq}}}}}{\text{P}}_{{{\text{rq}}}}^{*}} \right)}}. $$

(10)

This ratio is a function of the self-noise of the reference seismometer N _rr, which can be now expressed with Eq. 10:

$$ {{\text{N}}_{{{\text{rr}}}}} = \frac{{{{\text{P}}_{{{\text{rr}}}}}{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}\left( {1 - \tfrac{{{\text{N}}_{{{\text{qq}}}}^{*}}}{{{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}}}} \right)}}{{{\text{P}}_{{{\text{qq}}}}^{*} - \tfrac{{{\text{N}}_{{{\text{qq}}}}^{*}}}{{{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}}}{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}}}, $$

(11)

where the expression $\left( {{{\text{P}}_{\text{rr}}}{\text{P}}_{\text{qq}}^{*} - {{\text{P}}_{\text{rq}}}{\text{P}}_{\text{rq}}^{*}} \right)$ is replaced with ${{\text{P}}_{{{\text{rr}}}}}{\widehat{{\text{N}}}_{{{\text{qq}}}}}$. Let us assume that ‘−1dB’ is the allowed error between N _qq and ${\widehat{{\text{N}}}_{{{\text{qq}}}}}$. Then the ratio ${\text{N}}_{{{\text{qq}}}}^{*}/{\widehat{{\text{N}}}_{{{\text{qq}}}}}$is set to be 10^−0.1 and the “−1dB” approximation N _rr(1dB) of the self-noise of the reference seismometer N _rr can be calculated as:

$$ {{\text{N}}_{{{\text{rr(1dB)}}}}} = \frac{{{{\text{P}}_{{{\text{rr}}}}}{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}\left( {1 - {{10}^{{ - 0.1}}}} \right)}}{{{\text{P}}_{{{\text{qq}}}}^{*} - {{10}^{{ - 0.1}}}{{\widehat{{\text{N}}}}_{{{\text{qq}}}}}}}. $$

(12)

Equation 9 becomes a good approximation of the self-noise estimate, if the self-noise of the reference seismometer N _rr is lower than N _rr(1dB).

Manufacturers often give basic measured information about the self-noise for a specific type of seismometer and if N_rr(1dB) is sufficiently higher than the theoretical self-noise of the reference seismometer then Eq. 9 can be used.

If both seismometers are of the same type and the self-noise of the reference seismometer is not known, only an “average” self-noise N_x of the two seismometers with an equal transfer function can be calculated from:

$$ {{\text{N}}_{\text{x}}} = \frac{{{{\text{N}}_{\text{qq}}} + {{\text{N}}_{\text{rr}}}}}{2} = \frac{{{{\text{P}}_{\text{qq}}} + {{\text{P}}_{\text{rr}}}}}{2} - \sqrt {{{{\text{P}}_{\text{qr}}}{{\text{P}}_{\text{qr}}}^{{*}}}}; \;for\;{H_r} \approx {\text{H}}q. $$

(13)

While the average self-noise N _x gives only an approximate value, the equation is useful for the misalignment-error elimination procedure (see Section 4 and Appendix).

4 Errors caused by misalignment

In practice, the physical design of seismometers prevents two seismometers from being perfectly aligned in the same spatial direction. There are two sources that contribute to the misalignment error: small imperfections in the seismometer’s manufacturing, which mean that all three sensors in the seismometer are not orthogonal to each other (Holcomb 2002) and the inaccurate installation of two collocated seismometers. Such misalignment errors prevent the seismic signal from two seismological systems from being purely coherent (Holcomb 1990). Even when performing a test in low-seismic-noise conditions, the secondary microseism has sufficient energy to disturb the self-noise estimation around this frequency. Because of the misalignment error, we can assume that all three sensors of the reference seismometer detect some part of the seismic signal x. If a linear combination of all three outputs of the reference seismometer is used, the misalignment errors can be minimized. The output y _r of the seismometer ‘r’ is rewritten according to Fig. 2 as follows:

$$ {y_{\text{r}}} = {{\text{a}}_1}\left( {{h_{\text{r1}}} \otimes x + {n_{\text{r1}}}} \right) + {{\text{a}}_2}\left( {{h_{\text{r2}}} \otimes x + {n_{\text{r2}}}} \right) + {{\text{a}}_3}\left( {{h_{\text{r3}}} \otimes x + {n_{\text{r3}}}} \right). $$

(14)

Fig. 2

Simple 3D model has similar assumptions to the 1D model depicted in Fig. 1

The output y _r of the reference seismometer is a linear combination of the three sensors in this seismometer and the parameters a₁, a₂ and a₃ represent the transformation matrices. When great care is taken in the co-alignment of the sensors, we can assume that one of the parameters {a_i} has a value close to 1, while the other two have a value close to 0. If the transfer functions of all three components of the reference seismometer are similar, which is often the case for modern broadband seismometers, the differences in the transfer functions can be neglected and the simplified expression h _r1 ≈ h _r2 ≈ h _r3 is valid. Taking this into account, Eq. 14 can be rewritten as:

$$ {y_{\text{r}}} = {{\text{a}}_1}{y_{\text{r1}}} + {{\text{a}}_2}{y_{\text{r2}}} + {{\text{a}}_3}{y_{\text{r3}}} = \sum\limits_{{i = 1}}^3 {{{\text{a}}_i}\left( {{h_{\text{r}}} \otimes x + {n_{{{\text{r}}i}}}} \right)} = {h_{\text{r}}} \otimes x + {n_{\text{r}}}. $$

(15)

The right-hand side of Eq. 15 represents the same output of a seismometer as Eq. 1 expressed for the reference seismometer. The parameters a₁, a₂ and a₃ can be estimated with the help of the self-noise of both seismometers by the procedure presented later in Appendix. When the parameters a ₁, a ₂, and a ₃ are known, the self-noise can be evaluated by using Eqs. 7 or 9.

5 Examples

An estimate of the self-noise will be presented for the CMG-40T seismometer (s/n T4B19, with the bandwidth from 0.033 to 50 Hz) and for the CMG-3ESPC seismometer (s/n T34238, with the bandwidth from 0.083 to 50 Hz)—both manufactured by Güralp Systems Limited (www.guralp.com). In both cases, the STS-2 (s/n 80448) seismometer was used as the reference seismometer. It is important to know that the self-noise is evaluated just for a particular seismometer, uniquely defined by its serial number. The tests were performed in winter 2007/2008 at the Conrad Observatory (www.zamg.ac.at/about/conrad-observatory) of the Central Institute for Meteorology and Geodynamics (ZAMG). A part of the observatory is a 150-m-long tunnel with several piers for the seismometers, which were installed in the tunnel next to a STS-2 seismometer (side by side) with the same orientation. They were placed in a temperature-controlled chamber and connected to a six-channel EarthData PR6 acquisition unit. Because of the test requirements, the digitizer gain was set to be highly sensitive, so that its self-noise was lower than the presumed self-noise of the STS-2 seismometer, verified earlier with a short-circuited input. The input in this procedure was a 12-h finite-length-time seismic-data segment, sampled at 200 samples per second, giving a total of 8,640,000 data points. For the “self-noise” evaluation, Welch’s method for the power spectral density estimation was applied using a Matlab^(C) built-in function with a Hanning window of length 2¹⁶ and with 75% overlapping time-series segments. For both tested seismometers a 3D model was used (see Appendix) and the parameters a ₁, a ₂, and a ₃ for the 3D model were calculated in the frequency interval from 0.2 to 0.5 Hz. An evaluated transformation matrix is also given in Appendix. The self-noise of the STS-2 seismometer (s/n 80448) was evaluated in the frequency band from 1 to 50 Hz using a three-channel correlation analysis (Sleeman et al. 2006) with data from two collocated CMG-3ESPC seismometers. Below 1 Hz it could not be calculated, as described at the end of Section 2 and the theoretical data from the STS-2 noise model was used instead (Hart et al. 2007). This test was performed in the autumn of 2009 at the same location and under similar conditions, only that three (new) CMG-3ESPC seismometers (with serial numbers s/n T35893, s/n T36081 and s/n T36082) were installed together with the same STS-2 (s/n 80448) seismometer, using two six-channel EarthData PR6 acquisition units. Figures 3, 4, 5, and 6 depict the self-noise estimation of the tested seismometers.

Fig. 3

The estimated self-noise N_{CMG40T(3D model)} of the vertical component of a CMG-40T seismometer (s/n T4B19, with bandwidth form 0.033 Hz to 50 Hz) where the reference seismometer was an STS-2 (s/n 80448)

Fig. 4

The same as in Fig. 3, just the estimated self-noise (N_{CMG40T(3D model)}) is for the N-S component of a CMG-40T seismometer (s/n T4B19)

Fig. 5

The estimated self-noise N_{CMG40T(3D model)} for the vertical component of a CMG-3ESPC seismometer (s/n T34238) with bandwidth from 0.083 Hz to 50 Hz

Fig. 6

Estimated self-noises (N_T35893, N_T36081, N_T36082) of the vertical component of CMG-3ESPC seismometers. The self-noise of all seismometers calculated by two reference seismometers (full line; Sleeman et al. 2006) and the self-noise of a particular seismometer calculated by using the one reference seismometer (thin dotted line). For better presentation, the plots of the self-noise PSD estimates are smoothed

5.1 Self-noise of CMG-40T (s/n T4B19) seismometer

This seismometer is designed for installation at medium-noise sites. Because of its relatively high level of self-noise, with regards to the reference seismometer (STS-2; s/n 80448), there is no difference when using Eqs. 7 or 9. Our evaluation shows that the self-noise differs noticeably between the vertical (Fig. 3) and horizontal components (Fig. 4) of the seismometer. Figure 4 depicts only the N–S component, but the result for the E–W component is similar. This difference is probably due to the different design of the vertical sensor in comparison with the horizontal sensors. The 3D model was applied in these evaluations and the evaluated transformation matrix for this case is given in Appendix. For this particular seismometer, the self-noise is below the NLNM for the vertical component, from 0.12 to 0.79 Hz (Fig. 3), and for the horizontal (N–S) component from 0.17 to 0.54 Hz (Fig. 4). The N _rr(1dB) values are also shown in Figs. 3 and 4 and are above the self-noise of the reference seismometer. In conclusion, we can say that the self-noise evaluation using Eq. 9 is a good estimate for this type of seismometer when an STS-2 is used as the reference seismometer.

5.2 Self-noise of the CMG-3ESPC (s/n T34238) seismometer

This seismometer is designed for low-noise sites. The standard bandwidth for this type of seismometer is from 0.0167 to 50 Hz. The tested seismometer has an extended bandwidth (0.0083–50 Hz). The self-noise of the CMG-3ESPC seismometer lies below the NLNM, between 0.033 and 16 Hz, according to the manufacturer’s specification. The 3D model was used and an evaluated transformation matrix for this case is given in Appendix. The calculated self-noise has similar values for all three components, so only the vertical component is depicted in Fig. 5. At low frequencies, it is below the NLNM, starting from 0.046 Hz. At high frequencies, the self-noise of the STS-2 instrument crosses N _rr(1dB) between 2 and 11 Hz, consequently Eq. 7 is used. The self-noise of the CMG3ESPC instrument crosses the NLNM at 8.8 Hz. The particular case, where Eq. 9 was used instead of Eq. 7, is depicted in Fig. 9 of Appendix.

5.3 Comparing the two-sensor test with the three-sensor test

Figure 6 depicts the estimated self-noise of the vertical components of three CMG-3ESPC seismometers (with serial numbers s/n T35893, s/n T36081, and s/n T36082), which were installed together side by side. The inputs in the calculation are 5-h finite-length-time seismic-data segments, sampled at 200 samples/s, giving a total of 3,600,000 data points/segment. The self-noise for each seismometer was calculated first by using two reference seismometers (Sleeman et al. 2006), then using one reference seismometer with known self-noise, by using Eq. 7. For example, the self-noise of the seismometer CMG-3ESPC s/n T35893 was first calculated using two reference seismometers CMG-3ESPC s/n T36081 and s/n T36082. After that, the self-noise of the seismometer CMG-3ESPC s/n T36082 was calculated using two reference seismometers, CMG-3ESPC s/n T35893 and s/n T36081. At the end, the self-noise of the seismometer s/n T35893 was calculated using only one reference seismometer (s/n T36082), including its evaluated self-noise. Again, the 3D model was used in all cases. The differences in the calculated self-noises for the seismometer CMG-3ESPC s/n T35893, using two or one reference seismometer, were negligibly small. For better presentation, the plots of the PSD estimates of the self-noise are smoothed.

6 Discussion and conclusions

Any self-noise evaluation of seismometers should be performed in a stable, quiet, and settled environment, to avoid any influence of non-seismic sources (e.g., acoustic effects, poor anchoring to the ground (Pavlis and Vernon 1994), EM radiation, and electronic noise in a power supply). The self-noise of the acquisition units used in the test should be below the self-noise of the seismometers as well. The 3D model calculations give better results than the 1D model and it is also more promising in an area with higher seismic noise. In cases where the self-noise of a test seismometer is significantly above the self-noise of the reference seismometer, Eq. 9 gives a good result. This is the case with CMG-40T seismometers, where an STS-2 instrument served as a reference seismometer. When a similar self-noise is expected in both seismometers, the self-noise of the reference seismometer needs to be known and Eq. 7 should be used. This is mostly valid for CMG-3SPC seismometers, if an STS-2 instrument serves as the reference seismometer.

Knowing the self-noise of a particular instrument does not guarantee that it will be equal to instruments of the same model. Therefore, it is useful to know the self-noise of each instrument before its installation in a seismic station.

Theoretically, it is desirable that the seismic noise at a particular seismic station is close to the NLNM, and the self-noise of a seismometer and the acquisition unit is so low that the instrumental noise floor has no effect on the seismic noise over the whole of the frequency band. But some form of noise or unwanted signal from seismic equipment, or from the design of seismic stations, affects almost any practical seismic measurement. If a seismic station is tested with a reference seismometer, where the self-noise of this seismometer is well known and is low, all unwanted sources of noise can be found, and if possible, also eliminated. This is also the main purpose of this article, to present a simple algorithm that not only serves as a way to estimate the self-noise, but can also be used at a particular seismic station to eliminate unwanted noise sources and to define some parameters of the installed seismological systems, such as generator constants and instrument orientation misalignment. Accordingly, it is desirable to have a reference seismometer with a well-defined self-noise in each seismic network. This reference seismometer can be referred to as the “secondary standard” of a particular seismic network, and can be used in the testing of other seismometers.

Appendix

We have two three-component seismological systems, each consisting of a broadband seismometer and an analogue-to-digital converter (or an acquisition unit). The first is marked with the index ‘q’, and the second with the index ‘r’. We assume that the transfer functions for both systems are flat inside of their respective bandwidth, noise-independent, and the instrumental noise of the acquisition units is lower than that of the seismometers. Those axes in both seismological systems are not ideally perpendicular to each other (Fig. 7) and also their gains are not the same. The seismometers are not perfectly aligned with each other in the same direction, even if we try to do our best (Holcomb 2002). Because of misalignment errors the signals between the two seismological systems are not purely coherent (Holcomb 1990). To achieve coherency, the data from system ‘r’ need to be transformed into system ‘q’ to detect the same seismic signal. A matrix A represents such a transformation:

$$ {{\mathbf{x}}^q} = {\mathbf{A}}{{\mathbf{x}}^r} \to \left[ {\begin{array}{*{20}{c}} {x_{{1}}^q} \\ {x_{{2}}^{\text{q}}} \\ {x_{{3}}^{\text{q}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} {{a_{{11}}}} & {{a_{{12}}}} & {{a_{{13}}}} \\ {{a_{{21}}}} & {{a_{{22}}}} & {{a_{{23}}}} \\ {{a_{{31}}}} & {{a_{{32}}}} & {{a_{{33}}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}{c}} {x_{{1}}^{\text{r}}} \\ {x_{{2}}^{\text{r}}} \\ {x_{{3}}^{\text{r}}} \\ \end{array} } \right]. $$

(16)

Fig. 7

The sensors of the system ‘q’ lie on the axis of a coordinate system. Sensors in the system ‘r’ are not aligned equal to the system ‘q’

Usually, $\left| {\det ({\mathbf{A}})} \right| \ne 1$: the matrix A includes both rotation and a scaling factor (the ratio of the generator constants) of one seismometer with respect to the other. In the procedure where we use two seismic systems close to each other these matrices are not de facto known. To determine the parameters of the matrix A, the self-noise of the seismometers can be used. In a three-dimensional coordinate system the ‘i’-th sensor of system ‘q’ lies on the axis of the ‘i’-th coordinate system, where i = 1,2,3, (Fig. 7). With the direction ‘i’, the sensor ‘i’ of the seismic system ‘q’ detects the seismic signal ‘x _i’ and the instrumental noise ‘n_i’:

$$ y_{\text{i}}^{\text{q}} = {x_{\text{i}}} + n_{\text{i}}^{\text{q}}. $$

(17)

Similarly, the signal of the system ‘r’ in the direction ‘i’ is a linear combination of all three outputs:

$$ {\text{y}}_{\text{i}}^{\text{r}} = \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}\left( {x_{\text{j}}^{\text{r}} + n_{\text{j}}^{\text{r}}} \right)} = {x_{\text{i}}} + \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}n_{\text{j}}^{\text{r}}}, $$

(18)

where a _i1, a _i2, and a _i3 are the elements of the transformation matrix A for the component ‘i’ and $n_{\text{j}}^{\text{r}}$; j = 1,2,3 is the instrumental noise of the component ‘j’ of the seismic system ‘r’. The notations of Eqs. 17 and 18 in the frequency domain are:

$$ Y_{\text{i}}^{\text{q}} = {X_i} + N_{\text{i}}^{\text{q}}, $$

(19)

$$ Y_{\text{i}}^{\text{r}} = {X_{\text{i}}} + \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}N_{\text{j}}^{\text{r}}}, $$

(20)

where $Y_{\text{i}}^{\text{r}}$, $Y_{\text{i}}^{\text{q}}$, $X_{\text{i}}$, $N_{\text{i}}^{\text{r}}$ and $N_{\text{i}}^{\text{q}}$ represent the Fourier transforms of $y_{\text{i}}^{\text{r}}$, $y_{\text{i}}^{\text{q}}$, $x_{\text{i}}$, $n_{\text{i}}^{\text{r}}$ and $n_{\text{i}}^{\text{q}}$. We assume that the instrumental noise between the outputs of the seismic systems is uncorrelated and the self-noise and the input seismic signal x_i are also uncorrelated. Assuming that the system is linear and the outputs from both seismic systems in the direction ‘i’ can be written using the power spectral density:

$$ {{\text{P}}_{{{{\text{q}}_i}{{\text{q}}_i}}}} = Y_{\text{i}}^{\text{q}}Y_{\text{i}}^{{{\text{q*}}}} = {{\text{P}}_{{{x_i}{x_i}}}} + {{\text{N}}_{{{{\text{q}}_i}{{\text{q}}_i}}}}, $$

(21)

$$ {{\text{P}}_{{{{\text{r}}_i}{{\text{r}}_i}}}} = Y_{\text{i}}^{\text{r}}Y_{\text{i}}^{{{\text{r}}*}} = {{\text{P}}_{{{x_i}{x_i}}}} + \sum\limits_{{{\text{j}} = 1}}^3 {a_{\text{jj}}^2{{\text{N}}_{{{{\text{r}}_j}{{\text{r}}_j}}}}}, $$

(22)

where * denotes the complex conjugation. ${{\text{P}}_{{{x_i}{x_i}}}} = {X_i}X_i^{*}$ is the autopower spectrum (Sleeman et al. 2006) of the seismic input signal (ground motion) in the direction ‘i’ and ${{\text{N}}_{{{{\text{q}}_i}{{\text{q}}_i}}}} = N_{\text{i}}^{\text{q}}N_{\text{i}}^{{{\text{q*}}}}$ and ${{\text{N}}_{{{{\text{r}}_i}{{\text{r}}_i}}}} = N_{\text{i}}^{\text{r}}N_{\text{i}}^{{{\text{r}}*}}$ are the autopower spectra of the instrumental noise. The cross-power spectrum ${{\text{P}}_{{{{\text{r}}_i}{{\text{q}}_i}}}}$is simply:

$$ {{\text{P}}_{{{{\text{r}}_i}{{\text{q}}_i}}}} = {{\text{P}}_{{{x_i}{x_i}}}}. $$

(23)

Using Eqs. 21, 22 and 23 we can apply the “average” instrumental noise power spectra ${\overline {\text{N}}_{\text{ii}}}$ (Eq. 13) in the direction ‘i’ as a function of the frequency ‘v _p ’ and the parameters a _i1, a _i2 and a _i3 as:

$$ \begin{gathered} {\overline {\text{N}}_{{ii}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right) = \frac{1}2\left({{{{\text{P}}_{{{{\text{r}}_i}{{\text{r}}_i}}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right) + {{\text{P}}_{{{{\text{q}}_i}{{\text{q}}_i}}}}\left( {{\nu_p}} \right)}} \right)- \hfill \\ - \sqrt {{{{\text{P}}_{{{{\text{q}}_i}{{\text{r}}_i}}}}({a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}){{\text{P}}_{{{{\text{q}}_i}{{\text{r}}_i}}}}{{\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right)}^{*}}}} . \hfill \\ \end{gathered} $$

(24)

To find the parameters a _i1, a _i2 and a _i3, by which the contribution of the ground motion ${{\text{P}}_{{{x_i}{x_i}}}}$ in the direction ‘i’ from both seismometers at the right-hand side of Eq. 24 are canceled out, is one of our aims. The values a _i1, a _i2 and a _i3 can be estimated by using non-linear least-squares data fitting and the Gauss–Newton method. Let us define the frequency v _p and the interval 2n around this frequency: [p−n, p + n]. The residual vector (Heath 2002) in the direction ‘i’ at this frequency interval is:

$$ {r_i}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_{{p + l}}}} \right) = {\overline {\text{N}}_{\text{ii}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_{{p + l}}}} \right) - S\left( {{\nu_{{p + l}}}} \right),\quad l = - n,...,n. $$

(25)

The function S(v) is a synthetic trace and represents the ideal instrumental noise. This function is usually not known. Instead of this, the synthetic trace can be formulated according to the lowest expected self-noise value. If the frequency interval is short enough, and if the self-noise is the lowest in this frequency band, zero values can be used instead. The initial guess for the initial parameters is set in the direction of the ideal orientation and the alignment of the reference seismometer, so the initial parameters are ${a_{{{1}1}}} = {a_{{{22}}}} = {a_{{{33}}}} = 1$ and 0 otherwise. Using the first approximate solution, a new approximate solution is computed based on local linearization around the current point using the Jacobian matrix of the residual vector. This process is repeated until convergence is achieved. When the residual obtains its minimum, the values of the parameters a _i1, a _i2 and a _i3 represent the optimal solution for the transformation matrix. The parameters are in good agreement with available observations. This approach is a power-based method and, theoretically, produces two possible estimates for each component, because the analysis does not retain the information about the phase (Holcomb 2002). But a close inspection of the evaluated results shows that the vast majority of the evaluated parameters are as expected. The reason is that the orientation of the reference seismometer is mostly known, the vertical component of the tested system is usually set similar to the reference system and the initial parameters are set with regard to the vertical component. When the parameters of the matrix A are determined, the seismic signal of the reference seismological system can be transformed into the seismic signal of the tested seismological system, without any a priori knowledge of the gain constant and of the rotation of the tested seismometer. This procedure can also be performed to define the orientation of the borehole seismometer with regard to the surface seismometer.

Figure 8 depicts the evaluated transformation matrices of a CMG-3ESPC seismometer (s/n T34238) and a STS-2 seismometer (s/n 80448) and the evaluated transformation matrices of a CMG-40T seismometer (s/n T4B19) and a STS-2 seismometer (s/n 80448). The seismometers were installed side by side. The calculated self-noises for both seismometers and for both models are depicted in Figs. 9 and 10, where the self-noise was calculated using Eq. 9 without any information about the reference system’s self-noise. The tests were performed at Conrad Laboratory, Austria. In both cases the input is a 12-h finite-length-time seismic-data segment, sampled at 200 samples per second. For the power spectral density estimation, Welch’s method is used, using a Matlab(C) built-in function, with a Hanning window of length 2¹⁶ and with 75% overlapping time-series segments. For both cases the transformation matrix for the 3D model was calculated in the frequency interval from 0.2 to 0.5 Hz.

Fig. 8

Evaluated transformation matrices used in our article for the 3D model, correlating the tested and the reference seismometer

Fig. 9

The estimated self-noise of the vertical component of a CMG-3ESPC seismometer (s/n T34238), using the 1D model (dotted line, marked N _{(1D model)}) and the 3D model (N _{(3D model)})

Fig. 10

The estimated self-noise of the vertical component of a CMG-40T seismometer (s/n T4B19), using the 1D model (N _{(1D model)}) and using the 3D model (N _{(3D model)})