1 Introduction

The impact of nanotechnology on the field of magnetic materials has triggered active research in this area in last few years. Ferrites are the ceramics comprising of iron oxide along with small proportions of other metals. They are the materials having cubic crystal structure with chemical formula which is MO·Fe2O3, where M is a transition metal ion like iron, manganese, zinc, or nickel. Ferrite nanoparticles are extensively used in various applications in the field magnetics, electronics, and biomedical science due to excellent magnetic, electronic, and optical properties [1,2,3,4]. Crystal chemistry depends on the chemical composition, core structure, distribution of cations, and physical properties of cations and anions. Crystal chemistry has a great impact on magnetic, electrical, and optical properties of ferrite nanoparticle [5,6,7,8].

X-ray diffraction (XRD) is a versatile technique to characterize for nanomaterials. X-ray diffraction pattern is the fingerprint of the periodic atomic arrangements in each material. Many microscopic and spectroscopic techniques such as transmission electron microscopy (TEM), scanning electron microscopy (SEM), Fourier-transform infrared spectroscopy (FTIR), Raman, and UV–Vis are widely used for studying the nature of material but till date, no feasible technique replaces XRD [6]. This technique provides important information regarding the identification of material and provides info such as phase identification, sample purity, crystallite size, lattice parameter, X-ray density, cation distribution, and strain as shown in Fig. 1. It also provides information on crystal structure, cation distribution, preferred crystal orientation, and other structural parameters, such as average crystallite size, strain, and crystal defects [7]. Quantification of preferred orientation in materials can also be achieved. Using XRD pattern, the compositions and crystallinity of the as-prepared materials of the prepared samples can be determined. The various properties and applications of material depend on the crystal structure of sample [8].

Fig. 1
figure 1

Applications of XRD data

Full size image

The properties of ferrite nanoparticles highly depend on experimental conditions during synthesis such as using different precursors, temperature, pressure, pH, time, substitution, or doping by suitable cations because these conditions have great impact on the cationic distribution over tetrahedral and octahedral sites [9,10,11,12]. Doping of foreign ions can improve the various properties of ferrites. Due to the difference in the radii of these foreign ions and ions cations present in ferrites, the lattice gets strained and causes changes in structural and other parameters of the materials. Also, the doping causes an asymmetry in the ferrite structure leading to a decrease in the crystallinity of the material [13].

For the particles having different morphologies, although the positions of peaks remain the same but their relative intensities can change. Peak broadening depends on the widths of the peaks, whereas the relative intensities can be related to the height. For nanoparticles, the peaks broaden as compared to bulk materials but relative intensities would be same. For different orientations of materials, peak broadenings are different [14].

The magnetic properties of ferrites highly depend on the accommodation of metal cations at A and B sites. Therefore, different magnetic nature for different metallic ion distributions such as ferrimagnetic, antiferromagnetic, and paramagnetic has been observed. Using XRD, the cation distribution can be calculated [15]. In spinel ferrites, the distance between cations and angles between ion pairs has great impact on the exchange interaction and thereby on magnetic behavior. Functionalized ferrite nanoparticles or templets are used for many applications as sensors, water purification, and biomedical applications. XRD data could be used to employ the crystal structure and to detect the stability of these samples under desired conditions [16].

X-ray diffraction pattern is the fingerprint of the periodic atomic arrangements in each material. The ASTM (American Society for Testing and Materials) database of XRD patterns enables the phase identification of a large number of crystalline samples. The positions of diffraction peak and their intensities contain important information about the ordered lattice, its dimensions, and the density distribution in the samples [7].

Due to lack of a comprehensive study for all the aspects of XRD for ferrites, the complete information contained in the data could not be used by researchers. This review aims to provide the key features of XRD data to determine the various information regarding crystals and can be helpful for researchers.

In this review, all the aspects of XRD in ferrite have been explored. XRD data could be used to calculate crystallite size, lattice parameter, X-ray density, and strain of the material. It can be used to determine the phases present in the given sample. Rietveld refinement can analyze crystal structure perfectly. The study of Williamson–Hall method could provide crystallite size, strain, and elastic properties of the material. Cationic distribution, bond length, the interionic distances, and bond angles can also be found to analyze various properties of material. Transport properties can be determined by the hopping length.

2 Structure of Ferrites

In the spinel structure of ferrite, tetrahedral (A) sites and octahedral (B) sites are occupied by the cations in a closed-packed oxygen lattice. Spinel ferrite is a face-centered cubic structure with eight formula units in a unit cell which comprises of 8 divalent metal ions, 16 trivalent ions, and 32 oxygen ions. There are 8 metal ions in tetrahedral site and 16 metal ions in octahedral site [17]. Each metal ion on the tetrahedral site is surrounding by four O2− ions and each metal ion on octahedral site is surrounded by six O2− ions. There are 56 atoms in each spinel unit cell [18].

In ferrites, the ions in spinel on tetrahedral (A) site and octahedral (B) sites is arranged as [Mδ2+ Fe1−δ3+]A [M1−δ2+ Fe1+δ3+]BO4 where, δ is the inversion parameter. For normal spinel ferrite, δ = 1, for inverse spinel ferrite, δ = 0, and for mixed spinel ferrite, δ lies between 0 and 1. Spinel in which only divalent ions reside in tetrahedral sites is called normal while compounds with the divalent ions that occupy in the octahedral sites are called inverse [19]. The structure of normal ferrite is shown in Fig. 2.

Fig. 2
figure 2

Inverse spinel structure of ferrite

Full size image

The example of normal spinel ferrite is ZnFe2O4. In the inverse spinel structure, the divalent cations reside in octahedral site while one half of the trivalent ions reside in tetrahedral (A) site and another half of the trivalent cations are in octahedral (B) site. Fe3O4 is an example of inverse spinel ferrite. Spinel intermediate between normal and inverse is known as mixed spinel. The spinel is said to be mixed if it has unequal number of each kind of cations in octahedral and tetrahedral sites. The example of mixed spinel ferrites is MgFe2O4.

3 Study of X-Ray Diffraction (XRD)

3.1 Phase Determination

X-Ray diffraction is mainly used to identify the major and minor phases of an unknown sample. A phase is a crystalline solid with a regular three-dimensional arrangement of the atoms. The diffraction peak positions and their intensities obtained from XRD data are the fingerprint of a specific crystalline phase. These measured peaks are identified by comparing with the entries in reference databases. This is also known as qualitative phase analysis. In ferrite, XRD data shows some extra phases that appear with doping or changing the experimental conditions. With doping, these phases appear because the dopant ions can be incorporated in the crystal lattice to an extent after which extra ions appeared in the form of new phases.

In Bi-doped cobalt ferrite (CBF), up to the Bi doping of 0.05, the pure phase of cobalt ferrite is dominating and when Bi doping level is ≥ 0.10, both cubic and perovskite phase structures are evolved. It is also observed by expanding the peak at (311) where the peak positions are shifted toward the higher angle side. It signifies the distortion in the lattice of pure cubic structure and the formation of a new phase of perovskite beyond the doping of 0.10 [20]. Rietveld refined XRD patterns of Bi-doped cobalt ferrite clearly showed that the refined pattern has exhibited two phases: cubic spinel structure and the perovskite structure. The variation of the spinel and perovskite phases of the with Bi doping is shown in Fig. 3 [20].

Fig. 3
figure 3

XRD pattern of Co1−xBixFe2O4 (x = 0.0, 0.05, 0.10, 0.15, and 0.20). (311) peak positions are shown in inset. The effect of Bi3+doping on spinel (left) and perovskite (right) phases of CBF. Reproduced from ref. 20 under a Creative Commons Attribution 4.0

Full size image

The XRD of PTH (polythiophene) and PTH/Ni0.5Zn0.5Fe2−xCexO4 ferrite composites specifies the incorporation of Ni0.5Zn0.5Fe2−xCexO4 ferrite nanocrystals in the PTH matrix for the formation of composites as shown in Fig. 4a, b. The intensities of the peaks of PTH became weaker after adding ferrite nanocrystal into the polymer matrix which reveals a decrease in the concentration of PTH in the composite. The broadening of peak is attributed to the amorphous nature of PTH, which eliminates the crystalline nature of Ni0.5Zn0.5Fe2−xCexO4 ferrite nanocrystals. The percent crystallinity of samples can be calculated using the following relationship:

$$\% \;Crystallinity =\frac{\sum {A}_{c}}{{A}_{t}}\times 100$$
(1)

where Ac is the area under each crystalline peak and At is the total area under the diffractogram. For fitting of the diffractogram curve, Gaussian functions for each peak were performed. The crystallinity of Ni0.5Zn0.5Fe2−xCexO4 nanoparticles first increases with Ce doping followed by a decrease with increasing Ce concentration [21]. Also, the substitution of Fe3+ ions by Ce3+ ions in the crystal lattice is limited due to different ionic radii of these ions. Therefore, the excessive Ce3+ ions accumulate on the grain boundaries to form the Ce2O3 phase during the sintering process.

Amorphous and crystal nature of the material can be determined using XRD. The behavior of indium-phthalocyanine tethered to magnetite or silica nanoparticles has been shown in Fig. 4c. The XRD pattern of indium phthalocyanine and silica nanoparticles (SiNPs.) showed the broad peak and therefore showed the amorphous nature of these samples whereas sharp peaks of Fe3O4 (MNP), silica-coated magnetic nanoparticles (SiMNP), silica nanoparticles (SiNP-1), and silica-coated magnetic nanoparticles (SiMNP-1) show crystallinity. SiMNP and SiMNP-1 were synthesized using different schemes. The XRD pattern of SiMNP-1 is analogous to that of SiMNPs as shown in Fig. 4c. However, some weak traces of the silica–phthalocyanine peaks appeared in SiMNP-1. Particle sizes calculated from TEM micrographs for the MNPs and SiMNPs are well in agreement with the sizes calculated by XRD. The optical behavior could be depended on this behavior [22].

If no other crystalline phases are detected apart from main phase, the sample is said to be highly crystalline. It has been observed that the peak intensity of composites Fe3O4/SiO2 and Fe3O4/SiO2/PANI (Polyaniline) nanoparticles was reduced because of the coating of SiO2 and PANI layers. Also, the SiO2 and PANI layers have amorphous nature and therefore have broad peak [23].

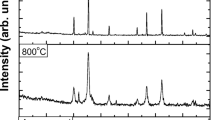
Mn–Ni ferrite forms anti-ferromagnetic α-Fe2O3 phase when annealed for more than 200 °C in air. It has been observed that for a constant sintering temperature, the intensity of anti-ferromagnetic α-Fe2O3 phase depends on the concentration of Mn2+ ions and increases with increasing Mn2+ ion concentration. An increase in α-Fe2O3 phase having antiferromagnetic phase can lead to decrease the value of saturation magnetization [24]. The formation of secondary phases may be due to the changes in the free energy released under reaction during the preparation of samples [25].

3.2 Rietveld Refinement

Hugo M. Rietveld proposed Rietveld refinement method. It is extensively known for its whole-pattern fitting method instead of single-peak analysis. This method minimizes or removes the inaccuracies produced due to particle statistics, orientation, micro absorption, and overlapping of peaks and detects amorphous and trace phases. It is accepted by scientific community as a standard practice to analyze the crystalline materials. Rietveld refinement method is applicable only if the quantified phase is the crystalline phase, and the crystal structure is known [26].

From the Rietveld refinement of powder, XRD data is used to determine the unit cell dimensions, phases in the sample, crystallite sizes, micro-strain in crystal lattice, texture effects, vacancies, etc. From Rietveld analysis, lattice parameters and the actual intensity of a particular phase or plane can be theoretically assessed which gives very accurate interplanar spacing (d), lattice parameters (a, b, c), and other parameter. So, strain present in the sample, crystallinity, calculated intensity, quantitative analysis, etc. can be done. FullProf program was used for the structural refinements. Reliability factors such as weighted profile factor (Rwp), profile factor (Rp), expected R-factor (Rexp), Bragg R-factor (RBragg), and χ2 can be determined using Rietveld refinement. These factors can be used to evaluate the quality of fit. The low values of R-factors and χ2 confirm the correctness of fit [27].

Rietveld refinement of rare earth-doped nickel ferrites is shown in Fig. 5. The lattice parameter and microstrain of the samples were found to increase with doping. The ideal value of oxygen parameter (u) in spinel structure is 0.375 Å. In these ferrites, the values of the u are more than the ideal value which may be due to the expansion of tetrahedral interstices causing the displacement of anions from their original position. Using this value, the other parameters of the crystal could be calculated [28].

Fig. 4
figure 4

(a) XRD pattern of Ni0.5Zn0.5Fe2−xCexO4 ((x = 0.00, 0.02, 0.04, 0.06, and 0.08) ferrite nanocrystals; (b) XRD pattern of PTH and PTH/ Ni0.5Zn0.5Fe2−xCexO4 composites; reproduced from ref. 21 (c) Powder XRD pattern of (a) InPc (1), (b) SiNP, (c) Fe3O4 (MNP), (d) SiMNP, (e) SiNP-1, (f) SiMNP-1; reproduced from ref. 22

Full size image

XRD with Rietveld refinement showed that in the Gd3+ ions substituted Co–Zn ferrite, the diffraction peak of other phases was not present. It confirmed that the Gd3+ ions were incorporated in the interstices of cubic structure and no significant change in the phase of Co–Zn ferrite structure has been observed as shown in Fig. 6 [29].

Fig. 5
figure 5

Undoped, Ho, Gd, Sm, Pr, and La-doped nickel ferrites. The * indicates the peaks due to the secondary phases. (Observed and calculated data are represented by red circles and solid black lines and their difference is shown by the bottom curve). Reproduced from ref. 28 with permission from Elsevier, copyright 2019

Full size image

In Y3+ ions-doped Co–Zn ferrites, the secondary phase of YFeO3 has been observed whose intensity increases with increasing doping concentrations as shown in Fig. 6. The secondary phase was observed as the large radii Y3+ ions can be incorporated in the lattice up to a particular concentration level beyond which extra amount would form the secondary phase [30].

3.3 Scherrer Formula

A perfect crystal should extend infinitely in all directions but in practice, no crystal is perfect because of limitation of finite size. The diffraction peaks broaden due to the deviation from perfect crystallinity. From the analysis of peak width, the crystallite size and lattice strain could be measured. The size of coherently diffracting domains gives the crystallite size. The crystallite size of the particles is not usually the same as the particle size due to the production of polycrystalline aggregates in particles.

X-ray diffraction is a convenient method for determining the mean size of nano crystallites in nano crystalline bulk materials. The broadening of the diffraction peaks indicates the ultra-finite size of ferrite nanoparticles.

In 1918, P. Scherrer observed that, when XRD radiation falls on a random oriented mass of crystals, the diffracted beam become broaden when the particle size is small. He gave an equation known as the Scherrer equation. XRD is sensitive to the crystallite size of the particles. The crystallite size of all the samples was calculated from the XRD data by using Scherrer formula applied to the strongest diffraction peak [31]:

$$\mathrm{Crystallite \;size}=\frac{{0.9}\lambda }{\beta {\mathrm {cos}}\theta }$$
(2)

where β is the full width at half maximum, θ is the angle of diffraction, and λ is the wavelength of X-ray (λ = 1.54 Ǻ). Ferrite doping or substitution of other ion in place of Fe3+ / Fe2+ ion could improve various properties of the material. The dopant ions are able to incorporate in crystal lattice till a particular doping level due to the difference in the ionic radii of dopant and cations. The excess dopant ions appear in the form of secondary phases beyond that level.

In Fe3−xDyxO4 nanoparticles, the crystallite size increases from 13.9 nm for x = 0.00 to 30.8 nm for x = 0.03 and then decreases till 21.4 nm for x = 0.10. The increase in crystallite size could be due to the incorporation of dysprosium in the magnetite up to the doping concentration of 0.03 beyond which it decreases due the formation of secondary phases [32]. Ce-doped Ni0.5Zn0.5Fe2O4 forms a cubic spinel phase system. The incorporation of Ce is limited up to the doping of 0.06 after which extra phase of Ce2O3 starts to appear. The average crystallite sizes using Scherrer formula were found to increase from 29.7 mm to 38.1 nm with Ce doping. The lattice parameter increases with an increase in Ce3+ ion concentration in Ni0.5Zn0.5Fe2−xCexO4 from 8.339 Å for x = 0.00 to 8.363 Å for x = 0.06. After this doping concentration, the lattice parameter was found to decrease due to asymmetry in the spinel structure which was compressed extra phase [21].

3.4 Lattice Constant, X-ray Density, and Porosity

The lattice constant (a) can be calculated by using the following relation at the strongest peak:

$$a=\frac{\lambda }{2\;\mathrm {sin}\;\theta }{({\mathrm h}^{2}+{\mathrm k}^{2}+{\mathrm l}^{2})}^{1/2}$$
(3)

where λ is the wavelength of the X-rays, (hkl) are the planes of diffraction, and θ is the diffraction angle. λ and a are measured in nanometers.

Doping can change the structure of crystal and this variation highly depends on the nature and ionic radii of dopant ions. It could lead to change the lattice parameters. Usually, the doping of bigger ions increases the lattice constants whereas the strain due to change in lattice could decrease this. However, these conditions mainly depend on experimental conditions.

In Mn-substituted cobalt ferrite, lattice parameter (a) increases with increasing Mn content from 8.379 to 8.418 Å. The increase in a could be ionic radius of Mn2+ (0.83°A) and as compared to Co2+ (0.78°A) ions. Mn2+ changes to Mn3+ because of the excess of oxygen that enters due to sintering process [33]. For Mn2+, Co2+, and Cu2+ ions-substituted Ni–Zn ferrite, the lattice constant increased with Mn2+ and Co2+ ion substitution. As the ionic radius of these ions is larger than Ni2+ ions, therefore, the lattice tends to expand resulting to increase the lattice parameter [34].

In Ho3+-doped MnFe2O4 ferrite, with doping, the lattice constant for the MnFe2O4 as well as these of the second phase appearing due to Ho3+ also increased with doping. The increase in both phases revealed that the spinel lattice is not compressed by the intergranular second phase [35]. The radius of rare earth ions is about 1.5 times the radius of Fe3+ ions; therefore, the substitution of Ho3+ swells the lattice by replacing Fe3+ resulting into increase in the distortion in the lattice leading to increase the lattice constant.

The theoretical lattice constant (ath) can be calculated by using the relation:

$${a}_{th}=\frac{8}{3\surd 3}\left[\left({r}_{A}+{R}_{O}\right)+\surd 3\left({r}_{B}+{R}_{O}\right)\right]$$
(4)

where rA and rB are the radius of tetrahedral (A) and octahedral (B) sites and RO is the radius of the oxygen ion (RO = 1.32 Å). The difference between experimental lattice constants may be related to the lattice defects for polycrystalline materials and the presence of large radii Fe2+ ions on A or B sites which are not considered in calculation for ath [35]. Due to this, the experimental value lattice constant is less than the theoretical value.

The density of the nanoparticle is different than the bulk value and difficult to calculate. This density can be found by using the molecular weight and the unit cell volume for nanoparticles. From XRD data, lattice constant (a) can be calculated. Using unit cell volume (a3) and using the molecular mass and Avogadro number, a sample density based on X-ray data can be calculated using the relation:

$${d}_{x}=\frac{8 \;M}{N{a}^{3}}$$
(5)

where dx is the sample density based on X-ray data, M is the formula molecular weight of the samples, N is the Avogadro’s number, and a3 is the volume obtained from lattice parameter.

Bulk density (db) can be calculated for the pellet form of particles that were calculated using the following equations

$${d}_{b}=m/\pi\; {r}^{2}\mathrm h$$
(6)

where m is the mass, r is the radius, and h is the thickness of the pellet, respectively.

The porosity (P) of nanoparticles can be determined using the relation:

$$P\%=\left(1-\frac{{d}_{b}}{{d}_{x}}\right)*100$$

A decreasing trend in density and increasing trend in porosity was observed in Mn-substituted cobalt ferrite. It has been revealed that unsubstituted sample is practically pore-free samples. However, with with Mn substitution, a non-uniformity in the grain size observed resulting to an increase in the porosity of the samples [33]. The porosity was also found to increase with increasing Bi doping in (La0.8Ca0.2)1−xBixFeO3 [36].

3.5 Strain Calculation

A mechanical stress could be produced in the crystal lattice due to incorporation (doping or substitution) of different radii ions in ferrites. Doping can produce a mechanical stress in the crystal lattice due to incorporation of different radii ions in crystal lattice. The diffraction peak would shift in such cases. The strain in the structure can been found using the relation:

$${\varepsilon }_{s}=-\Delta {\theta }_{sp}\mathit{cot}\;{\theta }_{sp}$$
(7)

where \({\theta }_{sp}\) is the diffraction angle for the strongest peak for the doped samples and Δ \({\theta }_{sp}\) represents the difference and the observed value of diffraction angle for the doped sample and the undoped sample.

XRD results of Fe3−xDyxO4 nanoparticles confirmed that the undoped nanoparticles (x = 0) have fcc spinel structure with good crystallinity. However, with doping, an extra phase corresponding to DyFeO3 phase starts appearing as shown in Fig. 7a. The strongest diffraction peak of (311) plane around 35.7° can be used to estimate the strain present in the lattice as shown in Fig. 7.

Fig. 6
figure 6

Rietveld refined X-ray diffraction patterns of (a) Co0.7Zn0.3GdxFe2−xO4 (x = 0.00, 0.05, 0.10) ferrite. Reproduced from ref. 29 under a Creative Commons Attribution 3.0. (b) Co0.25Zn0.75YxFe2−xO4 ferrite. Reproduced from ref. 30 with permission from Elsevier, copyright 2019

Full size image

It was reported that (311) peak of XRD of Dy3+-doped magnetite showed a slight left shift in 2θ values relative to undoped samples. The maximum shift was detected for the doping of 0.03, which indicate the incorporation of Dy3+ in the spinel lattice till that doping. This could produce a mechanical stress in the crystal lattice due to incorporation of large radii Dy3+ ions in magnetite nanopowders [37]. The strain in the lattice can be determined using the relation:

$${\varepsilon }_{s}=-\Delta {\theta }_{(311)}\mathrm{cot}\;{\theta }_{(311)}$$
(8)

From strain calculations, it was observed that strain is maximum for the doping of x = 0.03 after which it decreases due to saturation of Dy3+ in the lattice. At that doping concentration, magnetization of these samples was found to be highest among all samples [32].

3.6 Williamson–Hall (W–H plot) Method

Crystal imperfection, grain boundary junctions, stresses, and stacking faults may cause strain in the lattice [38]. Bragg peaks depend on the crystallite size and lattice strain as these properties change the intensity and peak width leading to shift the 2θ peak positions. Conversely, from the change in 2θ values, i.e., peak broadening, the crystallite size, and strain effects can be determined. Williamson–Hall analysis is an uncomplicated integral breadth method where size-induced and strain-induced broadening is estimated by examining the peak width as a function of 2θ.

Crystallite size can be determined by Scherrer formula because of the dependence of crystallite size on the XRD peak broadening. The drawback of Scherrer formula does not tell anything about the microstructures of the lattice or intrinsic strain. Though, the internal strain also has a significant effect on the broadening of diffraction lines. Williamson–Hall method can be used to calculate intrinsic strain and crystallite size using XRD peak broadening as a function of 2θ [39].

According to Williamson–Hall (W–H) method, physical line broadening of X-ray diffraction peak occurs due to the size and microstrain of the nanocrystals and the total broadening can be split into two parts as

$$\beta ={\beta }_{\text{size}}+{\beta }_{\text{strain}}$$
(9)
$$\beta =K\lambda /D\;{\mathrm{cos}}\theta +\text{ 4}\varepsilon\; {\mathrm {tan}}\theta$$
(10)
$${\beta }\;{\mathrm{cos}}\theta =K\lambda /D+{4}\varepsilon\; {\mathrm{sin}}\theta$$
(11)

A plot is drawn with 4sinθ along the x-axis and β cosθ along the y-axis. After taking the linear fit to the data, the crystalline size was estimated from the y-intercept (Kλ / D), and the strain ε is estimated from the slope of the fit. The strain ε was presumed to be uniform in all crystallographic directions, thus considering that the properties of the particles are independent of the direction along which they are measured, i.e., the isotropic nature of the crystal [40].

The negative slope of Williamson–Hall plots indicate that strain could be very small. The negative slope of the plots also indicates compressive strain produced in smaller grain size samples. This compressive strain may be assumed to be due to change in the number of iron ions in the tetrahedral and octahedral sites with a decrease in the grain size of the samples. The transfer of iron ions from tetrahedral to octahedral sites generates a compressive strain in the nanoparticles due to the small distance between the B site ions as compared to the A site ions.

XRD results of Co1.1Fe1.9−xErxO4 confirmed the formation of the pure spinel cubic lattice for erbium (Er) substitution up to x ≤ 0.10; for x ≥ 0.15, secondary phase of ErFeO3 also begins to form as shown in Fig. 8. Erbium doping induces a strain due to its larger ionic radius. FWHM of the XRD peaks with maximum intensity were used to determine strain and crystallite size using W-D plot Eq. (11). Crystallite size was found to decrease whereas strain and lattice parameter were found to increase with erbium doping [41].

The negative slope for W-D plots indicates the compressive nature of strain. It could be due to the variation of the number of iron ions in the A and B sites. In Ho-doped MnFe2O4, the negative slope was found for all the samples. However, at x = 0.15, the flat nature of nanoparticles is observed which shows that at this doping concentration, the sign of the slope is changing from negative to positive. This indicated the increase in the strain increases at x = 0.15 and thereby represent that the Ho3+ ions (RE ions) have limitation for entering into the Mn–ferrite [35].

It was observed that the crystallite size of Bi-doped La0.8Ca0.2FeO3 calculated using the Williamson–Hall method is greater than that calculated by Scherrer’s formula as shown in Fig. 9 [36]. This could be attributed to the XRD line broadening associated with internal strain being neglected in the Scherrer equation.

Fig. 7
figure 7

XRD pattern of (a) Fe3−xDyxO4 nanoparticles and; (b) its expanded view of (311) peak. Reproduced from ref. 37 with permission from Springer, copyright 2018

Full size image
Fig. 8
figure 8

(a) X-ray diffraction patterns; (b) W-D plots; (c) Induced strain with Er content and induced strain and lattice constant with Er content, of Co1.1Fe1.9−xErxO4. Reproduced from ref. 41 with permission from RSC publication, copyright 2016

Full size image
Fig. 9
figure 9

Variation of the average size for the crystallites of (La0.8Ca0.2)1−xBixFeO3 compounds, calculated using Debye–Scherer and Williamson–Hall methods. Reproduced from ref.36 under a Creative Commons Attribution 3.0

Full size image
Fig. 10
figure 10

The interionic distances and bond angles for effective magnetic interactions for Co0.7Zn0.3GdxFe2−xO4. Reproduced from ref. 29 under a Creative Commons Attribution 3.0

Full size image

3.6.1 Elastic Properties from W–H Plot

The anisotropic nature of strain is detected in real practice even though the uniform deformation stress energy density is considered. According to Hook’s law, within elastic limit, the stress (σ) is linearly proportional to the strain (ε) as the relation σ = Ehkl ε.

where Ehkl is the constant of proportionality known as modulus of elasticity or Young’s modulus.

Here, the lattice deformation stress is assumed to be isotropic and is applicable only for significantly small strain. In this line, the Williamson–Hall equation is changed by substituting the value of ε in Eq. 11; we get

$$\beta \;{\mathrm{cos}}\theta =K\lambda /\text{ D}+\mathrm{4\; sin}\theta \sigma / \mathrm E$$
(12)

Ehkl is Young’s modulus in the direction perpendicular to the set of the crystal lattice plane (hkl) [40]. The uniform stress can be calculated from the slope line plotted between 4sinθ/E and β cosθ, and the crystallite size D, from the intercept.

In Williamson–Hall method, homogenous and isotropic nature of the crystal is considered. However, in nanocrystallite materials, the homogeneity and isotropy of are no longer dependable. Therefore, the strain energy density u is considered. The deformation energy u (energy per unit volume) as a function of strain is given by Hook’s law as u = ε2Ehkl/2. Therefore, equation S can be modified as [42]:

$${\beta }_{\mathrm {hkl}}\mathrm{cos}\theta =\frac{K\lambda }{D}+\left({4sin\theta \left(2u/{E}_{hkl}\right)}^\frac{1}{2}\right)$$
(13)

The uniform deformation energy density (UDEDM) can be determined from the slope of the line plotted between βhkl cosθ and 4sinθ (2/Ehkl)1/2. Ehkl values can be used to calculate the lattice strain of the sample.

3.7 Cation Distribution

The properties of nanocrystalline spinel ferrites are dependent on several factors, such as method used to synthesis, nature, and concentrations of dopant ions and the distribution of metal cations over tetrahedral and octahedral sites. Therefore, it is essential to have the knowledge of cation distribution to determine the physical properties of ferrites in order to develop new materials with enhanced properties.

The X-ray diffraction pattern can be used for cation distribution in the spinel ferrite. The Bertaut method could be used to determine the cation distribution among the sites [35]. The distribution of divalent and trivalent cations among the octahedral and tetrahedral sites can be determined by the ratio of XRD lines, I220/I440, and I422/I400 as these planes are presumed to be sensitive for the cation distribution [34]. The peak intensities due to the (220) and (440) planes are sensitive to cations in the A sites, whereas the peak intensity due to the (400) plane is sensitive on cations in the B sites [7].

In Ho3+-doped MnFe2O4, cation distribution study showed the preference of Ho toward octahedral B-sites; however, Fe3+ ion can occupy both tetrahedral and octahedral sites. It can be concluded from the analysis of cation distribution of RE-doped ferrites that the octahedral B-sites are preferential site for RE ions whereas Fe3+ ions can occupy both tetrahedral and octahedral sites [35]. It has been known that the radius of tetrahedral site is smaller than that of octahedral site in the spinel lattice due to which large radii RE ions prefer octahedral sites. Also, the small amount of RE cations replaced for Fe3+ ions rearrange the cations between the octahedral and tetrahedral sites in order to minimize the free energy of the system.

3.8 Bond Lengths

The oxygen positional parameter (u) is the distance between an oxygen ion and a face of a cube. The oxygen positional parameter “u” can be calculated by using the relation:

$$u=\left[\left({r}_{A}+{R}_{O}\right)\frac{1}{\surd 3a}+\frac{1}{4}\right]$$
(14)

In an ideal value of u, the parameter is 0.375 Å. However, a deviation from this value may be due to the distortion produced in the lattice structure, i.e., lattice constant. The increase in u could be associated with the change of the origin at the tetrahedral sites with the decreasing number of Fe ion at the octahedral sites. If the value of u parameter is less than 0.375 Å, it is assumed that the origin is taken at one of the octahedral sites, not at tetrahedral sites [35].

The bond length among cations in the A-sites (dA−A), B-sites (dB−B), among cations on A-and B-sites (dA−B), among cations on A-sites and oxygen on A − sites (\({d}_{A-{O}_{A}}\)) and cations on B-sites and oxygen on B-sites (\({d}_{B-{O}_{B}}\)) can be determined by the following equations:

$${d}_{A-A}=\frac{a}{4}\surd 3$$
(15)
$${d}_{B-B}=\frac{a}{4}\surd 2$$
(16)
$${d}_{A-B}=\frac{a}{8}\surd 11$$
(17)
$${d}_{A-{O}_{A}}=a\left(u-\frac{1}{4}\right)\surd 3$$
(18)
$${d}_{B-{O}_{B}}=a{\left[{2\left(u-\frac{3}{8}\right)}^{2}+{2\left(\frac{5}{8}-u\right)}^{2}\right]}^{1/2}$$
(19)

The bond length in tetrahedral dA−A and octahedral dB−B sites is known as the hopping length (LA, LB). These are the distance between the magnetic ions in A and B sites, respectively. The bond length also affects the magnetic properties. The increase in bond length indicates less interaction whereas the decrease in bond length is indicative to more interaction. Doping can cause the change of the bond lengths due to the difference in radius of cations and dopants. The bond length changes with doping of Y3+ in cobalt ferrite causing change in interaction [43].

3.9 The Interionic Distances and Bond Angles

In spinel ferrites, the allocation of cations on A and B sites, their stoichiometry, ionic radii, valency, and synthesis method play a major role in determining and explaining various properties of the material. Apart from these, the distance between the ions present on different sites has a vital role in explaining the various behaviors of the material. Spinel ferrites have been investigated intensively in recent years and many routes have been employed to modify the properties of spinel ferrite. Bond lengths have direct relation and bond angles have inverse relations with strength A–B super exchange interaction that is stronger than A–A and B–B interaction as the length of the A–B bond is smaller than that of the A–A and B–B bonds. Highest interaction energy is obtained when the cations are connected by an angle of 180° [44]. The bond angles θ1, θ2, θ3, θ4, and θ5 are associated with exchange interaction as given in Table 1 [29] (Fig. 10).

Table 1 Expressions for determining the cation–cation (Me–Me), cation–anion (Me–O) distances, and the bond angles
Full size table

It has been reported that the doping of Dy in Co–Cu–Zn ferrite at octahedral site give rise to an increase in bond length. The bond angles (θ1, θ2) related with the A–B interaction increased, and that associated with the B–B interaction (θ3, θ4) decreased whereas the angle (θ5) associated with the A–A interaction increased by small amount with doping. The magnetic properties of the system depend on the A–O–B interaction. The variation in bond angles showed that the magnetization in the system strengthened with increasing the doping concentration of Dy ions. Therefore, XRD results may predict the performance of magnetic properties [44]. Similar results were obtained for Gd-doped Co-Zn ferrite nanoparticles. In yttrium-doped cadmium ferrites, the A–B interaction increases whereas the B–B interactions weaken with doping [45].

3.10 Hopping Length

The conduction mechanism in ferrites is described using Verwey and De Boer mechanism according to which the exchange of electrons between the ions of the same elements presents in more than one valence state and randomly is responsible for conduction mechanism. In ferrites, localized charge carriers and all Fe2+ ions present in the octahedral site contribute in the hopping phenomenon. The hopping lengths between the ions at the tetrahedral (LA) and octahedral (LB) sites can be calculated using the formulas:

$${L}_{A}=a\frac{\surd 3}{4}$$
(20)
$${L}_{B}=a\frac{\surd 2}{4}$$
(21)

The following relations are used to determine the hopping lengths (LA and LB) for A and B sub-lattices sites among magnetic ions. The change in hopping length of ions enhances the electrical conduction in spinel ferrites. Hopping length of A site (LA) is larger than hopping length of B site (LB) resulting an enhancement of conduction mechanism. In transition metal–doped nickel ferrites, the hopping length was decreased with increasing dopant concentration in Zn–Cd–Ni ferrite and Cr–Ni ferrite whereas for Mn-doped nickel ferrite, the hopping length was increased slightly [46]. The increase in hopping length indicates that more energy is required for charge carriers to jump from one cationic site to another leading to decrease in conduction mechanism; on the other hand, the decrease in hopping length leads to an increase in conductivity. In Cd2+ ion-doped MgFe2O4, it was observed that hopping lengths increased with doping due to the expansion of unit cell as the Cd2+ ions have large ionic radii as compared to Fe3+ ions [47].

3.11 Elastic Properties

To determine the nature of binding forces in solids, it is necessary to find the elastic constants of solids. Elastic modulus can be calculated from FTIR spectra and X-ray diffraction analysis. The elastic properties are useful in engineering to determine the strength of materials.

The force constants for tetrahedral site and octahedral site are calculated by FTIR data using the relations [48]:

$${k}_{t}=7.62\;X\;{M}_{1}\;X\;{\nu }_{1}^{2}\;X\;{10}^{-7}\;N/m$$
(22)
$${k}_{o}=10.62\;X\;{M}_{2}/2\;X\;{\nu }_{2}^{2}\;X\;{10}^{-7}\;N/m$$
(23)

where M1 and M2 are the molecular weightof cations on A and B sites, respectively, which can be calculated from the cation distribution. ν1 and ν2 are the wavenumbers corresponding to tetrahedral and octahedral sites for magnetite.

Stiffness constant, which determines the hardness of the solid, can be calculated by using the following relation:

$$\mathrm{Stiffness \;constant }\;({C}_{11})=\frac{k}{a}$$
(24)

where k is the average force constant [k = (kt + ko)/2] and a is the lattice constant calculated from XRD data. The longitudinal (Vl), transverse (Vs) velocities, stiffness constants (C11, C12), and various elastic constants can be determined by using the relations [49]:

$$\mathrm{Longitudinal\; velocity}\;{V}_{l}={\left({C}_{11}/\rho \right)}^{1/2}$$
(25)
$$\mathrm{Transverse\; velocity}\;{V}_{S}={V}_{l}/{\left(3\right)}^{1/2}$$
(26)
$${\mathrm{Longitudinal\;modulus}}\;\left(L\right)=\rho \;{\left({V}_{l}\right)}^{2}$$
(27)
$${\mathrm{Rigidity\;modulus}}\;\left(\eta \right)=\rho\; {\left({V}_{S}\right)}^{2}$$
(28)
$$\mathrm{Poisson\; Ratio}\;\left(\sigma \right)=\left(L-2\eta \right)/(2(L-\eta ))$$
(29)
$$\mathrm{Stiffness\; constant }\;({C}_{12})=\sigma {\text{C}}_{11}/\left({1}-\sigma \right)$$
(30)
$${\mathrm{Young^{\prime}s}}\;\mathrm{modulus}\;\left(Y\right)=({C}_{11}+2{C}_{12})({C}_{11}-{C}_{12})/({C}_{11}+{C}_{12})$$
(31)
$$\mathrm{Bulk \;modulus }\;(B)=({C}_{11}+2{C}_{12})/3$$
(32)

The mean velocity of elastic wave can be determined using:

$${V}_{m}={\left[\frac{1}{3}\left(\frac{2}{{V}_{s}^{3}}+\frac{1}{{V}_{l}^{3}}\right)\right]}^{-1/3}$$
(33)

The lattice energy can be determined using mean velocity (Vm) and molecular weight (M) of ferrite samples as shown below:

$$U=-{3}.{1}0{8}\left(M\;{V}_{m}{}^{2}\right)\times \text{ 1}{0}^{-{12}}\;{\mathrm{eV}}$$
(34)

The elastic constants were found to be increased in manganese-doped zinc ferrite nanoparticles. The increase in elastic constant with doping is the indicative of increase in the strength of interatomic binding [50]. Similar results were obtained for Zn-substituted lithium ferrite [51]. Elastic constants have dependance on the rigidity of bonding between atoms present in the lattice. Doping or substitution also varies with the elastic constants as the strength of interatomic bonding highly depends on the distance and the types of cations involved in bond formation.

Elastic properties determined from XRD and FTIR measurements could be different from the direct measurements of these parameters. In (Co/Ni/Cu)-substituted Li–Mn ferrites, the elastic properties obtained from XRD and IR spectroscopy were more than the values obtained from ultrasonic pulse transmission (UPT) technique. This difference may be due to use of different experimental techniques, density, etc. [52]. Whereas, in Zn–Ti-substituted cobalt ferrites, the elastic behavior observed from the ultrasonic pulse transmission method and infra-red spectroscopy is in good agreement with each other [53].

3.12 Future Scope

From this study, it can be revealed that XRD is the ideal technique to elucidate the crystal structure but also, magnetic, electrical, optical, and elastic behavior could be explained by analyzing the XRD data systematically. Apart from the doping and substitution, experimental conditions such as variation in temperature, precursors, pressure, power, pH, and different synthesis route also have a great impact on the XRD of ferrites. Suitable surfactants and templets usually attached for application purposes also affect the XRD of ferrites. These studies could be explored in future.

4 Conclusion

In this review, aspects of X-ray diffraction (XRD) in ferrite have been explored. Ferrite nanoparticles have wide range of application in various fields. XRD data could be used to measure the phases, crystal structure, and related parameters of ferrites. It can also determine the effect of doping and substitution on the crystal structure of the ferrite and the strain on the crystal lattice due to these variations. Magnetic, transport, and elastic properties of ferrites highly depend on cationic distribution, bond length, the interionic distances, bond angles, and hopping length. XRD could calculate these parameters.