1 Introduction

The 2G high-temperature superconductors (HTS) have become a focus of research, not only in the superconducting field but also in electrical applications because of the high critical current density and high irreversibility field [1]. Up to now, superconducting cables such as Roebel are being used for their high current capacity, and other devices such as motors, generators, transformers, and large magnets are designed making use of the high magnetic field achieved by superconducting coils or windings in compact designs[2–4]. However, considering the properties of HTS, it is inevitable to consider the AC loss before manufacturing these devices. Although some devices do not carry alternating current, hysteretic losses also exist because of the change of current, during start up, turn off and other transient operations.

Nowadays, finite element methods (FEMs) have been widely used in simulations and calculations of superconducting tapes and coils. The FEM software can solve the equations which are derived from Maxwell equations based on different state variables. There are three major equations: the A-V formulations based on magnetic vector potential A [5–7], T-O formulations introducing current vector potential T [8, 9], and H formulations solving magnetic field in two- or three-dimensional spaces which were widely used in recent researches [10–13]. It must be pointed out that the advantages of the methods based on H formulations are excellent convergences and easy setups of boundary conditions, when the simulations and calculations are proceeded in a math module that was employed by above-mentioned studies, with partial differential equations.

Based on Faraday’s law, Ampere’s law, and the E-J power law, a set of partial differential equations can be derived which are given by:

$$ \nabla \times E = -\mu_{0} \mu_{r} \frac{\partial H}{\partial t} $$
(1)
$$ \nabla \times H = J $$
(2)
$$ E = E_{0} \left( \frac{J}{J_{c}(B)}\right)^{n} $$
(3)

where E is the induced electric field, H is the magnetic field, and J is the current density. J c is the critical current density which is normally defined with the standard 1×10−4 V/m electric field criterion. E 0 is the value of voltage criterion during measurement, and the n value is defined from DC measurements of the superconductor’s highly nonlinear I–V characteristic and usually ranges from 5 to 130 for a type superconductor [14, 15].

In order to solve for the electromagnetic variables and evaluate the AC loss of HTS, the math module solving PDEs was developed by many researchers, such as Z Hong et al. [10, 11, 16] and Min Zhang et al. [1, 12, 13, 17]. One of the essentials of the way by PDE method is that (1), (2), and (3) should be converted to the input format in the FEM software which is:

$$ D \frac{du}{dt}+\nabla \cdot {\Gamma} = F $$
(4)

where u is the state variable, D, Γ, and F are relevant parameters. In the case of infinite long superconducting wire, based on all of the aforementioned equations, the input equation can be obtained as shown:

$$ \left[\begin{array}{cc} \mu_{0} & 0\\ 0 &\mu_{0}\end{array}\right]\cdot \left[\begin{array}{cc}\frac{dH_{x}}{dt} \\ \frac{dH_{y}}{dt} \end{array}\right] + \nabla \cdot \left[\begin{array}{cc} 0 & E_{z}(J_{z})\\ -E_{z}(J_{z}) & 0 \end{array} \right] = \left[\begin{array}{cc} 0\\ 0 \end{array} \right] $$
(5)

And yet, formula (5) should be changed if the object is coils that should be modeled by 2D-axisymmetric model in cylindrical coordinates, and that is more or less a disadvantage.

Unlike the way by PDE method, Francesco Grilli et al. developed a creative idea to solve the state variables in calculations of AC loss with the magnetic fields module in COMSOL, which had some advantages over the conventional one [18]. That module solves the following equations:

$$ \sigma \frac{\partial A}{\partial t}+\nabla \times H = J_{e} $$
(6)
$$ B=\nabla \times A $$
(7)

here J e stands for an externally imposed current density. In order to obtain the necessary equations, the author made some associations: A→H,σ→μ, 1/μ→ρ, B→J and J e =0. And then, the equations can be converted to the following format used for solutions:

$$ \mu \frac{\partial H}{\partial t}+ \nabla \times E = 0 $$
(8)
$$ J = \nabla \times H $$
(9)

In this paper, a numerical simulation of a 2G HTS coil was modeled in the Magnetic Field Formulation module of COMSOL, in which the physics interface solve Maxwell’s equations formulated using the magnetic field H as the dependent variable, therefore it has no complex mathematical formulation like the PDE module, and no associations with other variables like Magnetic Fields module. Hence, the purpose of this paper is to present a straightforward way to simulate HTS tapes and coils, and later, it can be found that it is easier to simulate complex structures in this module. The distributions of magnetic field, current density, and voltage of the coil were obtained, and then through the results, AC loss could be calculated. So the paper is structured as follows. Section 2 gives the details of the numerical model and verification of its correctness. Section 3 focuses on the simulation and AC loss calculation of a specific 2G HTS coil. The conclusion is presented in Section 4.

2 Numerical Model and Correctness Verification

2.1 Numerical Model

One of the advantages of the Magnetic Field Formulation module is that the format of expressions is consistent in both 2D model and 2D-axisymmetric model. And the primary concern is to determine the material properties. For air, its electrical resistivity is needed, and the value of 1 Ω⋅m is used in the simulation. Although the electrical resistivity of air is much larger than that value, 1 Ω⋅m is extremely greater than that of HTS, and we found that setting like this could increase the computation speed and the solution accuracy is also good. For high-temperature superconducting materials, such as YBCO, we need to know the E-J characteristic and current-field dependence. The former can be input using formula (3) in the module directly, while the later can be expressed by a fitting formulation or experimental data. With regard to other materials, neither magnetic ones nor non-magnetic ones; what we need to do is entering appropriate relative permeability and resistivity. It can be seen that this module is suitable to simulate complex structures.

On the other hand, the applied current of tapes or coils is assigned to superconducting layers using Pointwise constraint. The integration of local J in layers gives the total current of tapes or coils. The Pointwise constraint equals the total current to the predefined applied current. What should be noted is that it is necessary to turn off the automatic divergence constraint in this module which can lead to instability.

All of the above are the main setups in the Magnetic Field Formulation module to simulate HTS. Next step, the correctness of this approach will be verified through the comparison between its results and the results done by others.

2.2 Correctness Verification

The results used for comparison were the AC loss of an infinite long tape with the analytical model proposed by Norris [19] and PDE module by Mark D. Ainslie et al. [20]. The detailed specifications of the superconductor in our analysis are listed in Table 1 [20].

Table 1 Specifications of superconductor
Full size table

Considering the large aspect ratio of superconductor, the thickness of superconductor layer was often increased to obtain faster computation speed in some works. Therefore, 0.2 mm was assumed as the maximum thickness in this analysis, and the thickness was varied from this to 0.002 mm. Definitely, the critical current density must be modified according to the thickness used, because the critical current was assumed to be constant.

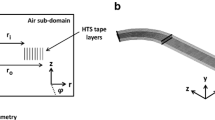
In this validation test, some thicknesses of superconductor layer were modeled: 0.002, 0.003, 0.005, 0.01, 0.02, 0.03, 0.05, 0.1, and 0.2 mm. The amplitudes of the input current I0 had some values: 0.25Ic, 0.5Ic, 0.75Ic, and 0.9Ic. Mapped mesh and Free Triangular mesh were used in the superconductor subdomain and the air subdomain, respectively, which are shown in Fig. 1.

Fig. 1
figure 1

Mesh elements for model

Full size image

The AC loss is calculated with (10):

$$ Q_{sc} = {{\int}_{0}^{T}} {\int}_{s} J \cdot E\, dSdt $$
(10)

And the analytical equation proposed by Norris for calculating the hysteresis loss in hard superconductors is given by (11):

$$\begin{array}{@{}rcl@{}} Q_{N} &=&\frac{\mu_{0}{I_{c}^{2}}}{\pi}[(1-\frac{I_{0}}{I_{c}})ln(1-\frac{I_{0}}{I_{c}})\\ && +(1+\frac{I_{0}}{I_{c}})ln(1+\frac{I_{0}}{I_{c}})-(\frac{I_{0}}{I_{c}})^{2}] \end{array} $$
(11)

The comparison results are presented in Fig. 2. As we can see from our results in Fig. 2, for I0/Ic = 0.25, a marked variation appeared between the numerical result and the analytical result, especially when the thickness was large. And, for I0/Ic values between approximately 0.50 and 0.90, the AC loss calculated by the finite element model was similar to the analytical method. Meanwhile, the deviations between Mark D. Ainslie’s results and ours in which the second-order element was adopted were about 3 %, which might be caused by the number of meshes and was acceptable in numerical calculation.

Fig. 2
figure 2

AC loss of models with different superconductor thicknesses compared with Norris’s analytical model (clockwise from top left: I0/Ic = 0.25, I0/Ic = 0.50, I0/Ic = 0.75, I0/Ic = 0.90)

Full size image

Through the above comparison, we had confirmed that the module of Magnetic Field Formulation was feasible, and had the believable precision to complete the simulation of HTS. Meanwhile, considering the advantages of this module expressed above, in the next analysis, we will calculate the AC loss of a HTS coil using this approach.

3 AC Loss Calculation of Coils

3.1 Coil Model

The coil was simulated with 2D-axisymmetric model and the induced or input current J φ in the superconductor flows in the direction of φ. The sketch of the model is shown in Fig. 3.

Fig. 3
figure 3

The cross section of a coil in 2D-axisymmetric geometry. 𝜃 defines the angle between the tape surface and local magnetic field

Full size image

The coated conductor is a copper-stabilized SuperPower tape of a 4.2 mm width and 90- μm thickness with a YBa2Cu3O7-x superconducting layer of around 1.4 μm, which will be modeled in this paper. The critical current density is 5.366×1010 A/m 2 when the local magnetic field is zero at 77 K [21]. And the value of n in the E-J power law is 31. The pancake coil modeled in this paper had 40 turns, the inner diameter of 10 mm, and the spacing between superconducting layers of 0.2 mm. The input transport current in the coils was I t r = I 0 sin(2π f t), where I 0 = 50 A, and f = 50 Hz.

3.2 Anisotropy of 2G HTS Tapes

Because of the anisotropy of the YBCO tape under an external magnetic field, the current and magnetic field distribution in a coil would greatly influenced by the field created by the rest of the turns. In order to feature the anisotropy of 2G tapes, the Jc-B relationship must be considered. E Pardo et al. [21] obtained a fit formula to describe the relationship of Jc and B in the low magnetic field (below 200 mT). The critical current density as a function of the local magnetic field B with orientation (shown in Fig. 3) fits to the following equation:

$$\begin{array}{@{}rcl@{}} J_{c}(B,\theta) &=& (J_{c,ab}[Bf_{ab}(\theta)]^{m}+J_{c,c}[Bf_{c}(\theta)]^{m}\\ &&+J_{c,i}[Bf_{i}(\theta)]^{m})^{\frac{1}{m}} \end{array} $$
(12)

with

$$ J_{c,ab}[Bf_{ab}(\theta)]=\frac{J_{0p}}{[1+Bf_{ab}(\theta)/B_{0ab}]^{\beta}} $$
(13)
$$ J_{c,c}[Bf_{c}(\theta)]=\frac{J_{0p}}{[1+Bf_{c}(\theta)/B_{0c}]^{\beta}} $$
(14)
$$ J_{c,i}[Bf_{i}(\theta)]=\frac{J_{0i}}{[1+Bf_{i}(\theta)/B_{0i}]^{\alpha}} $$
(15)

and

$$ \left\{\begin{array}{ll} f_{ab}(\theta)=f_{ab0}(\theta) & \theta \in [-90^{o}+\delta_{ab}, 90^{o}+\delta_{ab}]\\ f_{ab}(\theta)=f_{ab\pi}(\theta) & otherwise \end{array}\right. $$
(16)
$$ f_{ab0}(\theta)=\sqrt{\cos^{2}(\theta-\delta_{ab})+u_{ab}^{2}\sin^{2}(\theta-\delta_{ab})} $$
(17)
$$ f_{ab\pi}(\theta)=\sqrt{v^{2}\cos^{2}(\theta-\delta_{ab})+u_{ab}^{2}\sin^{2}(\theta-\delta_{ab})} $$
(18)
$$ f_{c}(\theta)=\sqrt{{u_{c}^{2}}\cos^{2}(\theta-\delta_{c})+\sin^{2}(\theta-\delta_{c})} $$
(19)
$$ f_{i}(\theta)=\sqrt{\cos^{2}(\theta+\delta_{i})+{u_{i}^{2}}\sin^{2}(\theta+\delta_{i})} $$
(20)

The parameters in the (12)–(20) were listed below: m=8, J 0p =4.910×1010 A/m 2, J 0i =3.212×1010 A/m 2, B 0a b = 4.569 mT, B 0c = 2.016 mT, B 0i = 32 mT, β = 0.4764, α = 0.9, δ a b = 1.7 ∘, δ c = −7.2 ∘, δ i = −7.2 ∘, u a b = 8.337, v = 0.6756, u c = 1.794, and u i = 1.7.

From the above equations and parameters, the curves can be obtained, which could intuitively display the relationship between the critical current Ic and the local magnetic field B, including its magnitude and orientation angle. The drawing of the critical current Ic versus the orientation angle in different magnitudes of local magnetic field is shown in Fig. 4.

Fig. 4
figure 4

The relationship of critical current and the orientation angle of local magnetic field when the magnetic field was 50, 100, 150, and 200 mT at 77 K

Full size image

3.3 Results and Discussions

In order to increase the computation speed, we used the mapped meshes, not only in the coil domain but also in the air domain via dividing the air domain into several parts in the simulation. After calculation, the distribution of the normalized current density on each turn of the coil at the time step of 0.001, 0.005, 0.009, and 0.01 s are displayed in Fig. 5.

Fig. 5
figure 5

The normalized current density J/Jc on every layer of the coils (clockwise from top left: t = 0.001, 0.005, 0.009, and 0.01 s, respectively)

Full size image

The distributions and changes of the current density in the coil at different time steps could be clearly observed from the figures. It could be seen that the current penetrated the coil from its upper and lower edges, and the inner turns would be penetrated completely at first with the transport current increasing, because the inner turns sustained larger magnetic field which could be seen in Fig. 6. In our simulation model, the current density had equaled or exceeded the critical current density on the positions of top and bottom of the coils, and that could be simulated because of the usage of E-J power law. However, in the actual employment of HTS devices, that is not allowed.

Fig. 6
figure 6

Magnetic field distribution and flux line plot of the coil

Full size image

The magnetic field and flux line of the same time steps are plotted in Fig. 6. We found that the domains of the inner turns had relatively higher magnetic field and more perpendicular field compared to middle and outer turns. That was in accordance with the results of current penetration as shown in Fig. 5. So in order to protect the inner turns of the coil, it is necessary to redefine the critical current criteria instead of the criteria of 10−4 V/m, as described in [17].

In order to see the voltage variation on each turn, the voltage (μV/m) for each turn in the coil is presented in Fig. 7, when the time step was 0.005 s, which meant the applied current was 50 A.

Fig. 7
figure 7

Simulation results of voltage for each turn when the applied current is 50 A

Full size image

The non-symmetrical distribution of voltage inside the coil is exactly the result of anisotropic current and magnetic field distribution. Although the voltage of each turn was much larger than 100 μV/m because of the large applied current in our model, the voltage variation inside the coil abode by rules that the inner turns had much higher voltage compared to the middle and outer turns. The detailed discussions about the determination of critical current can be seen in the paper written by Min Zhang et al. [17]. In this paper, we just introduced the method based on Magnetic Field Formulation module to simulate the HTS coils, and a profound discussion will be done later.

The hysteretic ac loss in J/cycle in the superconductor layers, Q a c , is calculated by integrating the product of the local electric field and current density [22], as given by (21).

$$ Q_{ac}={{\int}_{0}^{T}} \sum\limits_{n=1}^{N} \int 2\pi r E_{\varphi} \cdot J_{\varphi} \, dsdt $$
(21)

Where T is the period, N is the total turns, r is the radius of turn n, s is the cross-sectional area of turn n, E φ is the local electric field, and J φ is the local critical current density.

We plotted the instantaneous loss in one period to see the loss variation at different time steps, as shown in Fig. 8.

Fig. 8
figure 8

Instantaneous loss of the coil in one period

Full size image

The first half-cycle is generally referred a “transient” and ignored as it has less dissipation because the superconductor is magnetized from its virgin state [23]. From the results of instantaneous loss, it is obvious that the loss during the second half-cycle is larger than that of the first half-cycle. We can integrate only the second half-cycle and double the result due to its hysteretic nature and symmetric waveform [24]. In our model with the input current I t r , the AC loss was 18.6 mW through the integration on the above instantaneous loss. But we should notice that most of the loss was generated by the inner turns according to voltage distribution of the coil, which might lead to local heating. The detailed questions will be discussed when calculating the AC loss of practical HTS devices.

4 Conclusion

In this paper, the finite element model based on Magnetic Field Formulation module is introduced in detail. The brevity of expressions and the consistency between the 2D model and 2D-axisymmetric model make it easy to simulate coils, and henceforth, it can be used for complex constructions. First of all, the validation of this approach was confirmed through the comparison with other authors’ results of the infinite long tape model using analytical equation and PDE method. And then, a coil with 40 turns inputted with current I t r was simulated. The anisotropic distributions of current and magnetic field were plotted at different time steps, which were coincided with others’ studies. And we presented the voltage variation for each turn of the coil when the applied current was 50 A, which showed that the inner turns had much higher voltage compared with the middle and outer turns. At last, the AC loss of our model was calculated. Although the result was only 18.6 mW with the large applied current, we should notice that most of the loss was generated by the inner turns. Therefore, for long-term safe operation of the practical HTS coils, the current and voltage of the inner turns, especially the innermost turn, must be focused specially.