1 Introduction

It has long been known that a repulsive force arises between a magnetic field (generated, for example, by a permanent magnet) and a superconductor [1]. This force is due to the expulsion of the magnetic field from the inside of the superconductor bulk (Meissner effect). After the discovery of high critical temperature superconductors [2], the Meissner repulsive force has become a popular demonstration of superconducting properties [3].

There are several models that can be used to describe the magnetic interaction forces between permanent magnets and superconductors. Most of them are based on the method of the images [4–6]. This method of images has been commonly used in analytical calculations. Due to the complexity of these analytical solutions, only a small number of geometrical configurations can be analyzed. In this context, symmetrical configurations such as cylinders, infinite planes, or spheres are easy to solve.

Recently, a great interest has been shown in a magnetic punctual dipole and a superconducting sphere. Several studies analyze the magnetic interaction energy and lift forces for different relative positions and orientations of a magnetic punctual dipole and a superconducting sphere. Coffey derived analytic solutions by using the method of the images for a radial and horizontal dipole–sphere configuration [7, 8]. In these articles, Coffey concluded that the levitation force for a transverse dipole–sphere system is one half of that for a radial magnetic dipole–sphere system in the Meissner state. However, Lin [9] and Palaniappan [10] independently showed that Coffey’s results for a transverse dipole–sphere configuration were incorrect. More recently, Al-Khateeb et al. [11] (from here referred as AAAA) claimed to have solved the problem of a magnetic dipole–sphere system for arbitrary orientation of the dipole, using the method of the image. However, again Palaniappan showed that these results were also incorrect [12].

In this paper we present some calculations of the interaction forces of a finite permanent magnet–superconducting sphere system using local first-order interaction model. We compare our results with those obtained by Palaniappan and AAAA in order to validate the solution calculated by finite element analysis with respect to analytical solutions. We analyze the effect of the size of a permanent magnet with respect to a magnetic dipole calculation. Moreover, the torque between a superconducting sphere and a magnet in different positions and angular orientations is calculated for the first time. We describe the alignment effect that tends to align a magnet tangentially to the superconducting sphere surface.

2 Magnetomechanical Model of a Superconductor in the Meissner State

A general local model has been used to compute the forces and torques exerted on a finite-size permanent magnet over a superconducting sphere in first approximation. This model [13, 14] has been already used to compute the forces and torques for different superconducting bulk shapes such as full cylinders, hollow cylinders, or a torus [15–17].

The model mentioned above can only be used provided that the applied magnetic field is lower than the first critical field (that we call a complete Meissner state) and assumes \(\frac{\partial D}{\partial t} = 0\) as a quasi-static limit, where D is the electric displacement. It is based on London’s and Maxwell’s equations.

According to this model, the elementary force exerted by an external magnetic field per unit surface on the superconductor may be written in first-order approximation, using the MKS system, as

(1)

where μ 0 is the magnetic permeability of vacuum (or air), \(\vec{n}_{S}\) is the unit vector orthogonal to the superconducting surface, and \(\vec{H}^{\mathrm{ap}}\) is the applied magnetic field generated, in this case, by the permanent magnet only on the surface of the superconductor. The force exerted by the superconductor on the external magnetic field source (in our case a single permanent magnet) is the opposite. Due to its local character, this model can be implemented in a finite element method program. In this case, there has been used a model with tetrahedral finite elements for volumes and triangular elements as surface elements. The mesh size has been optimized to obtain a good agreement between results, error, and computation time [18]. The errors due to numeric approximations are less than the 0.5 % with respect to analytical solutions.

For any shape of superconductor, the torque exerted by the superconductor on the magnet can be written as

(2)

where \(\vec{r}\) is the position vector between the differential surface element and the center of mass of the finite permanent magnet.

The calculation of the torques’ minimum values for different orientation angles (θ) of the magnet provides the equilibrium angles of a magnet over a superconducting sphere. This equilibrium angle, for a certain position of the magnet, is defined as the orientation that makes the magnet not suffer any torque. Usually, two equilibrium angles can be found: a stable equilibrium and an unstable one. It has been experimentally shown that for a superconducting cylinder, with a magnet placed in its axis, the stable equilibrium angle is perpendicular to the axis of revolution of the superconducting cylinder [19].

3 Finite Permanent Magnet–Superconducting Sphere System

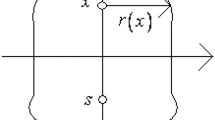
The coordinate system followed for the calculations is shown in Fig. 1. We have followed the nomenclature used by Palaniappan, but in this case the magnet was not a magnetic punctual dipole, rather a 5-mm diameter cylindrical permanent magnet, 5 mm in height. This shape of magnet has been used in all calculations. Its magnetization direction was considered uniform and parallel to its axis of revolution. The material assigned to the permanent magnet was Nd2Fe14B with a volumetric magnetization of M=962 kA/m. The magnetic moment associated then to this cylindrical permanent magnet is \(m = 0.094~\mathrm{A\,m}^{2}\).

Fig. 1
figure 1

Coordinate system of the PM-SC configuration. The dimensions in the figure are scaled

Full size image

The parameter a is the radial distance from the center of mass of the permanent magnet to the center of the sphere. The parameter θ sets the angle between the z-axis and the axis of revolution of the magnet. The radius of the sphere was named as b, and its value has remained constant for all calculations at 20 mm.

4 Results and Discussion

4.1 Force Calculation

The interaction forces between the finite permanent magnet and the superconducting sphere for different values of a and for different angular orientations (θ) have been calculated. In Fig. 2, the force acting on the magnet in the radial direction Z for different combinations of a and θ is shown.

Fig. 2
figure 2

Force Z versus the a position for different orientation angles (θ)

Full size image

A large decrease of the radial force on the PM is observed for values of a lower than 28 mm, but this was not as relevant for higher values of this parameter. On the other hand, the higher the orientation angle (θ), the lower the radial force exerted on the magnet by the superconductor.

Maximum forces can be obtained at θ=0∘ when the magnetization axis of the magnet is radially orientated versus the superconducting sphere. Conversely, minimum forces are obtained at θ=90∘ when the magnet magnetization direction is oriented transversely.

The component of the force on the magnet in the tangential direction X has also been calculated, as shown in Fig. 3.

Fig. 3
figure 3

Force X over the magnet versus the orientation angle for different a positions

Full size image

In this case we observe that the maximum value of the force is always obtained at θ equal to 45∘, becoming null for values of θ equal to 0∘ and 90∘. Again, the lower the value of a, the higher the tangential force exerted on the magnet.

4.2 Torque Calculation

The torque over the magnet in the Y direction has also been calculated (Fig. 4).

Fig. 4
figure 4

Torque on the magnet in the Y direction versus its orientation angle θ for different a positions

Full size image

In Fig. 4, the maximum torque can be observed at θ=45∘ for all a positions. Because the torque on the magnet at both θ=0∘ and θ=90∘ has a value of zero, these orientations of the magnet are considered to be equilibrium angles. Moreover, because of the negative sign of the slope in Fig. 4 for all a values at θ=90∘, this equilibrium angle is considered a stable equilibrium position. That means that a magnet dropped freely over a superconducting sphere would tend to align itself tangentially to the superconducting sphere. Following the same reasoning, θ=0∘ is thereby deemed to be an unstable equilibrium point.

4.3 Comparison of Results

In order to validate our results with respect to those obtained by Palaniappan [12] (7) and AAAA [11] (4) expressions, we have compared both solutions with our results. The magnetic moment of the magnet was considered to be m=0.094 A/m.

In Fig. 5 the results show that for an orientation of θ=0∘, all the solutions are quite similar. However, a very small effect of the finite size of the permanent magnet appears for small values of a. While the magnet is rotated, it can be observed that the deviation between Palaniappan’s and AAAA’s calculations begins to increase. Such deviations have already been predicted by Palaniappan, who pointed out a mistake in AAAA’s paper.

Fig. 5
figure 5

Comparison with punctual magnetic dipole calculations of the Force Z over the magnet versus a position for different orientation angles θ

Full size image

Our results deviate from those of a punctual magnetic dipole when we increase angle θ of the magnet and when we are very close to the superconducting sphere (small a values). Generally, the effect of the finite size of the magnet is to reduce the forces. This effect is higher when the magnet is orientated transversely.

While the distance between the magnet and the superconducting sphere is increased, the effect of the finite size of the magnet on the force exerted on the magnet decreases. Ultimately, for high values of a, the values of forces converge to the same ones obtained by Palaniappan for the punctual magnetic dipole as shown in Fig. 5. This permits to conclude that the first-order approximation of the model used is good enough.

5 Conclusion

This paper details calculations of the magnetic forces and torques that act on a finite-size permanent magnet around a superconducting sphere. It has been shown that force in the radial direction and in the transverse direction decrease as the radial distance from the center of mass of the permanent magnet to the center of the sphere. Also, the forces vary versus the angle of orientation of the magnet.

By calculating the torque, it has been demonstrated that the stable angle of equilibrium of the permanent magnet in relation to the superconducting sphere occurs when the magnetization direction of the magnet is tangential to the sphere. Thus, it has been demonstrated that the torque tends to align the magnet tangentially to the sphere.

A comparison has been undertaken between calculations using the method of the images and using the model presented in this paper. The results obtained by the model are in positive agreement to those considered correct by the method of the images; so we can conclude that the first-order approximation is adequate enough.