1 Introduction

In applications involving airflow through open-cell porous metals, such as in catalytic converters, filters, air-oil separators, breather plugs and heat exchangers, knowing and controlling pressure-drop across such structures is essential. The pressure drop depends both upon the fluid properties and also on the permeability of the porous metal, which is influenced by the porosity, cell size and the morphology of the pores and the pore-network [1, 2].

Fluid flow through porous materials is normally associated with energy being dissipated as a result of the interaction between the two phases. For very slow fluid flow, a viscous-drag energy dissipation mechanism dominates and the pressure-drop–airflow velocity relationship is described by the Hazen–Darcy equation [3, 4];

$$\frac{{\Delta P}}{L} = \frac{\upmu}{K} V$$
(1)

where ΔP is the pressure difference in the flow direction (Pa), L is the sample thickness in the same direction (m), K is the permeability (m2), µ is the fluid dynamic viscosity (Kg m s−1) and V is the Darcian velocity, the volumetric flow rate divided by the cross sectional flow area (m s−1). For flow behaviour obeying this case, the fluid is said to be flowing in the Darcy regime [4, 5].

As the fluid velocity increases, the Hazen–Darcy equation (Eq. 1) fails to describe the pressure-drop behaviour [4]. A quadratic term, referred to as the Forchheimer term or the form drag effect, is added to Eq. 1 in order to capture the effect of the force exerted by any solid surface on the flowing fluid and its resultant effect on the pressure drop. Equation 2 is known as the Hazen–Dupuit–Darcy model or Forchheimer equation:

$$\frac{{ \Delta P}}{L} = \frac{\mu }{K} V + C\rho V^{2}$$
(2)

where ρ is the fluid density (kg m−3) and C is the form drag coefficient (m−1) related to the structure of the permeable medium [5]. For typical fluid velocities and pore-size ranges generally used in engineering flow systems, the Forchheimer equation most accurately describes such unidirectional fluid flow [6].

The empirical Ergun relationship has also been adopted by researchers to describe the pressure-drop across porous materials [7–10] and has a similar form to the Forchheimer equation. It was originally developed for packed columns of spherical particles [11] but has been adapted for porous metals [8] by replacing the particle diameter with the specific surface area. This modified version is presented in Eq. 3 where ε is the porosity, σ is the specific surface area (m2 m−3) and α and β are empirical constants. By comparing Eqs. 3 and  2, the permeability and form drag coefficient can be expressed by Eqs. 4 and 5.

$$\frac{{\Delta P}}{L} = \alpha \frac{{\left( {1 - \varepsilon } \right)^{2} \mu }}{{\varepsilon^{3} \left( {\frac{1}{\sigma }} \right)^{2} }}V + \beta \frac{{\left( {1 - \varepsilon } \right)\rho }}{{\varepsilon^{3 } \left( {\frac{1}{\sigma }} \right)}} V^{2}$$
(3)
$$\frac{1}{K} = \alpha \frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} \left( {\frac{1}{\sigma }} \right)^{2} }}$$
(4)
$$C = \beta \frac{{(1 -\upvarepsilon)}}{{\upvarepsilon^{3} \left( {\frac{1}{\sigma }} \right)}}$$
(5)

When comparing relevant studies in the literature, it is apparent that there are inconsistencies in the values for permeability (K) and form drag coefficient (C) measured for foams with similar porosities and internal structures [3, 12]. This emphasises the need for fuller structural characterisation of the foams and careful assessment of the data from pressure drop measurements. Dukhan and Minjeur [12] investigated the discrepancies in values for both the permeability and form drag coefficient found in the literature. It was found that the testing velocity range varied between researchers and that treating the velocity range as one regime contributed significantly to the discrepancy in the results. The distinction between different regimes with increasing gas velocity, Darcy, Forchheimer and Turbulence, is therefore vital in determining K and C accurately.

The aim of the present work is to measure the pressure drop across porous metal structures as a function of gas velocity and to extend this to velocities that exceed those previously reported in an effort to more clearly identify the different flow regimes and importantly the boundaries of the commonly-studied Forchheimer regime. After determining best practices, these methodologies will be applied to determining the effects of increasing sample density (affected by compression) and of reducing the thickness of the sample on K and C for flow in the Forchheimer regime.

This study will be applied to novel multi-layered porous metal structures for which little or no previous investigations have been reported. Although the research here studies a “simple “material made from a series of diffusion-bonded sheets of the same type, this process offers the possibility for combining sheets with different porosities and pore sizes, giving the ability, once the behaviour is understood, to tailor the laminate structure to achieve bespoke flow conditions for demanding applications. It is expected that these materials will become the focus of many future studies and this investigation seeks to provide a foundation for robust measurement of such materials.

2 Materials and methods

2.1 Specimen characterization

Porous metal samples were provided by Alantum Europe, Munich, Germany. They consisted of multiple 1.6 mm thick foam-sheets of an Inconel 625 alloy, diffusion-bonded together to form a multi-layered porous structure (illustration in Fig. 1). A single sheet has a nominal pore size of 450 µm, which refers to the initial pore diameter of the polyurethane foam used as a substrate to manufacture the metal foam sheets. The density and total porosity of a single sheet are 700 kg m−3 and 91.4 %, respectively. The density and porosity of the multi-layered sample, which is compressed to enhance diffusion bonding, are 970 kg m−3 and 88.0 % respectively.

Fig. 1
figure 1

Schematic drawing of the experimental set-up used in this study

Full size image

The structure of the multi-layered porous metal was investigated using a series of imaging and morphological characterisation techniques. Scanning electron microscopy (SEM) and X-ray micro computed tomography (CT), using a Scanco 40 instrument, were used to provide information on pore size and shape and porosity. Mercury intrusion porosimetry (MIP), using an AutoPoreIV-9500 instrument from Micromeritics was used to calculate the pore size, porosity and, using the method of Hillar et al. [13], to determine the specific surface area. The specific surface area was also measured using the Brunauer–Emmett–Teller (BET) method on a Quantachrome autosorb-1 instrument using krypton gas, rather than nitrogen, owing to its lower saturation pressure [14].

Multi-layered porous samples were also incrementally compressed by uniaxial compaction in the same direction as the testing direction for gas flow. Table 1 shows the thickness reductions and resulting compression factors applied and the densities and porosities for the resulting structures. To investigate and understand the effect of thickness on the pressure-drop, the thickness was reduced by sectioning uncompressed multi-layered porous samples, creating a series of multi-layered structures with thicknesses from roughly 3 to 20 mm.

Table 1 Variation in porous metal characteristics with compression
Full size table

2.2 Pressure drop measurement

The experimental setup was designed and built to accurately measure the pressure drop across metal foam samples over a wide range of compressed air velocities. It consists of a manual control valve, pressure regulator, needle valve, variable area flow meter, and middle assembly (test section) in sequence as shown in Fig. 1. The compressed air is filtered and regulated to a maximum working pressure of 10 bar and maximum air flow rate of 6000 L min−1. Flow rate was measured using a Key Instruments variable area flowmeter with ±2 % full scale accuracy. The flowmeter has a flow rate of 0–1,800 L min−1, which, for the 21.183 mm internal diameter of the stainless steel piping used, corresponds to a velocity range of 0–85 m s−1. Gems pressure transducers with a pressure range of 0–2.5/25 bar, ±0.15 % full scale accuracy and ±1/100 °C thermal error were used to measure upstream and downstream pressures across the middle assembly. In order to restore the flow profile and reduce the turbulence, a flow straightener was installed before the middle (test) assembly.

The middle assembly was designed so it can hold 25 ± 0.2 mm diameter samples with different thicknesses from 2 mm up to 30 mm (in all cases secured in position using a spacer, giving a nominal flow diameter of 21.183 mm). Before placing the sample into the mid-assembly, it was wrapped circumferentially with PTFE tape to avoid any air passing around the sample’s perimeter and the adjacent wall. The mid-assembly is secured by means of two standard Swagelok™ end flanges (part number SS-1610-F16-150). Pressure ports were located on the two end flanges, 25 mm from the sample as shown in Fig. 1. For all tests, the pressure was regulated at 6.5 bar and filtered before going through the sample. The airflow rate was varied using a needle valve covering a wide range of velocities and the output pressure-drop was measured using the two pressure transducers. A stabilization period of 2 min was allowed before starting to record pressure values, where after pressure readings were averaged over a sampling time of 2 min. The signal acquired from the pressure transducers was acquired using Labview software connected to a PC.

When gas is forced to flow through a porous metal, the pressure-drop across the foam length is usually high enough to create compressibility effects leading to gas density change. This change must be taken into consideration [4] as it is likely to happen even at low velocities. Failure to do so may lead to a significant underestimation of the real pressure-drop associated with the foam. To consider these effects, Eq. 6 is used to compute the pressure-drop in the current work in accordance with [4]:

$$\Delta P = \frac{{P_{i}^{2} - P_{o}^{2} }}{{2P_{r} }}$$
(6)

where P i and P o are the absolute pressure values upstream and downstream of the sample holder, respectively. P r is reference pressure, which is taken as atmospheric pressure [4]. Pressure-drop values are then described per unit length by dividing them by the sample thickness, ∆P/L (Pa m−1), and plotted against Darcian airflow velocities, V (m s−1) and a curve of best fit is found. Repeatability testing showed a better than 5 % standard deviation in the results, with an approximate ±1 % error in the pressure-drop measurement.

3 Results and discussion

3.1 Sample characterisation

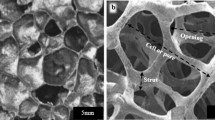
SEM images in Fig. 2 show the interconnected pore structure for the porous metal. The alloying process used to convert the porous metal from Ni to Inconel, results in a rough surface as illustrated in Fig. 2. Thus an increase in specific surface area is likely to be provided by this increased surface roughness, the extent of which depends on the amplitude and the frequency of the asperities on the surface [15]. The cross section of the triangular struts is also shown clearly in Fig. 2b. Although not obvious, the struts are hollow as a result of the burn out of the PU template used to make the porous metal.

Fig. 2
figure 2

SEM images of, a porous metal structure, b strut triangular cross-section

Full size image

SEM and image analysis were used to estimate the size of the pores and the scale of the pore channels within the struts. The mean pore size was estimated to be 190 µm with a standard deviation of 25 µm. The approximate lengths of the sides of the equilateral triangular pore channels within the struts were estimated to be 38 µm. These measurements enabled a cut-off value to be set to enable MIP data to be manipulated to determine the relative contributions of open porosity, that through which the gas will flow, and closed porosity within the struts (but which can be infiltrated during MIP because of sectioning and the very high pressures involved). In addition, MIP was used to estimate the pore size and surface area. These measurements, along with those for the surface area made by BET and open porosity measured by CT (which is unable to resolve the porosity within the struts—so is thus a measure of the interconnected, open porosity) are presented in Table 2. The actual pore size is significantly smaller than the nominal value owing to the thick coating layers applied for the alloy material. Measurements for pore size made by MIP and SEM are, however, in good agreement as are those from CT and MIP for the open porosity. The surface area measurements for the two processes are also fairly similar.

Table 2 Porous metal sample characteristics and property measurements
Full size table

3.2 Verification of the measurement process

The rig capability and robustness of the measurement method were checked and verified against data available in the literature. Because flow behaviour through nickel-based multi-layered (Alantum) samples used in this work has not been reported, a 10 mm thick, 27–33 PPI nickel–chromium sample from Recemat (with an average porosity of 88 %) was tested, enabling close comparison with work by Medraj et al. [9, 16] on the same material.

The experimental data for length-normalized pressure drop versus Darcian velocity (transposed as accurately as possible in Fig. 3 from data in a graph in [16]) are best-fitted over a velocity interval corresponding to the range studied in [9, 16]. A quadratic function, typical of the Darcy–Forchheimer relationship (Eq. 2), describes both the experimental data reported here and that reported in [16] very closely, with >90 % agreement in the drag term and >80 % in the viscous term, giving confidence in the measurement and analysis methods used in this study.

Fig. 3
figure 3

Comparing current study of Recemat 27–33 with Medraj et al. [16]

Full size image

3.3 Pressure-drop for multi-layer porous metal

The pressure-drop for the multi-layered sample was tested over a velocity range of 0–70 m s−1. Figure 4 presents the length-normalized pressure drop versus Darcian velocity relationship. The pressure-drop increases with increasing airflow velocity, as expected, following the typical trends shown in studies by other researchers [4, 9, 12, 16–21] but with a third order polynomial providing a better fit to the data over the entire velocity range. This deviation from the more typical quadratic relationship is a result of the velocities spanning a much wider interval and thus extending beyond the flow regimes normally investigated.

Fig. 4
figure 4

Third order representation of the linear pressure-drop vs. Darcian velocity for multi-layered sample A-45

Full size image

Graphical separation between the Darcy flow regime and other subsequent flow regimes including Forchheimer, post-Forchheimer, turbulent and post-turbulent can be performed using the method used by Boomsma and Poulikakos [18] and adopted in many related works [12, 17, 20, 22, 23]. By dividing Eq. 2 by the Darcian velocity, a plot of ΔP/LV versus V (Fig. 5) will yield a line of constant gradient when the Darcy–Forchheimer relationship is obeyed. A revised version of Fig. 5 is plotted in Fig. 6 (for clarity over the relevant velocity range) and reveals that the Darcy–Forchheimer relationship is only followed for velocities in the range of 4–12 m s−1. The extended airflow velocity range used in this study allows the recognition of various flow regimes beyond the well-documented ones. Figure 6 indicates that beyond the Darcy–Forchheimer transitional point at 12 m s−1, a set of straight line fits to the data can be drawn, implying that subsequent regimes can be of a quadratic, Forchheimer type (but with different K and C values).

Fig. 5
figure 5

Plot of ΔP/LV versus Darcian velocity for a multi-layered sample A-45

Full size image
Fig. 6
figure 6

The plot of ΔP/LV versus Darcian velocity with the flow regimes indicated

Full size image

Transition points between laminar and turbulent behaviour [4, 20] can also be defined by changes in the relationship between the Darcy–Weisbach friction factor (f) and the Reynolds number (Re D ) for flow in the tube. Re D can be calculated using the following equation [23]:

$$Re_{D} = \frac{\rho V D}{\upmu}$$
(7)

where D is the tube inner diameter and Eq. 8 is used to determine the Darcy–Weisbach friction factor [23].

$$f \equiv \frac{{\Delta P}}{{\left( {\frac{{\rho V^{2} }}{2}} \right)}}$$
(8)

In the laminar flow region, the relationship between the friction factor and Reynolds’s number follows a power law. Figure 7 indicates that the transition from laminar to a transitional regime (thereby leaving the Darcy and Forchheimer regimes) occurs at roughly Re D  = 16,000. Deviation from the power law is associated with significant contributions from wall friction. The corresponding airflow velocity at this transition is close to 12 m s−1, which is in close agreement with the Forchheimer-post Forchheimer transition determined in Fig. 6. The high velocities used in this study enable transitions beyond this behaviour to be observed. Figure 7 shows that the beginning of turbulent regime is at about Re D  = 34,000, at a velocity of approximately 23 m s−1.

Fig. 7
figure 7

Differentiation between fluid flow regimes for multi-layered sample A-45

Full size image

In light of these observations, the permeability, K f , and form drag coefficient, C f , as defined by the Forchheimer equation, should only be calculated within the velocity range that is applicable to that regime. In the case of the porous material studied, K f and C f values of 1.43 × 10−9 m2 and 1.89 × 103 m−1 were measured across the relevant velocity range (from 4 to 12 m s−1) as established in Fig. 6. K and C values corresponding to arbitrary velocity ranges, in addition to those of Forchheimer regime, are presented in Table 3. Acceptable fits to the data can be observed in all cases, but the significant differences in K and C (as high as 100 %) highlight the importance of identifying the relevant regime before determining K and C and show how easily inconsistencies between similar studies could arise.

Table 3 Permeability and form drag coefficient for different airflow ranges for the data presented in Fig. 6
Full size table

Comparison with the pressure drop for the Recemat sample measured earlier (which has a similar total porosity but a different pore size) reveals that K and C values for Recemat are 2.33 × 10−9 m2 and 0.54 × 103 m−1, respectively, reducing the magnitude of both terms in Eq. 2. The corresponding pressure drops per unit length, for a gas velocity of 12 m s−1, are approximately 1.8 × 105 and 4.6 × 105 Pa m−1 for the Recemat and the multi-layered samples respectively. This is expected as the specific surface area for the multi-layered sample is roughly twenty-nine times higher than for the Recemat 27–33 (2,800 m2 m−3 [24] ) causing higher energy dissipation and thus a higher pressure-drop [8, 24]. An additional but small contribution to the higher pressure drop may come from misalignment of the different structures at the interfaces between individual layers, an effect postulated in [3, 16] for layers of loosely-stacked porous metals. It should be noted that in the case of the Recemat samples, owing to the different (more open) architecture, the Forchheimer regime is shifted to higher velocities (between 9 and 26 m s−1).

3.3.1 Effect of foam compression on pressure-drop

Figure 8 presents a comparison of the length-normalized pressure-drop versus Darcian airflow velocity for compressed foam samples. Permeability and form drag coefficient were calculated in the Forchheimer regime and are presented in Table 4. The Forchheimer regime was determined at each compression step using the method shown in Fig. 6. It was noticed that for compression below 50 %, there was little change in the Forchheimer velocity range. At the highest compression, this regime shifted to between 2 and 9 m s−1. The large change in the pressure-drop behaviour and shift in the Forchheimer regime in response to compression is a consequence of the foam’s densification, decreasing porosity and increasing tortuosity and internal distortion. Increasing the compression factor from 1.25 to 2.75 causes the value of the form drag coefficient to increase from 5,873.5 to 68,357.5 m−1, which is an increase of 91.4 %. Under the same compression factor, the permeability coefficient decreases from 9.5 × 10−10 to 8.4 × 10−11 m2, almost the same relative reduction.

Fig. 8
figure 8

Pressure drop per unit length versus air flow velocity for multi-layered sample incrementally compressed to 69 % reduction in thickness

Full size image
Table 4 Forchheimer permeability, form drag coefficient and the associated errors
Full size table

The dependence of the permeability and form drag coefficient on porosity can be studied by applying the Ergun relationship (Eq. 5) to the data from the compressed sample using the reciprocal specific surface area as a length scale. The surface area and open porosity were only measured for the uncompressed foam (values given in Table 2). The change in these values with increasing compression was estimated, taking into account the compression factor (given in Table 1).

Figure 9 is a Log–log plot of the reciprocal permeability vs specific surface area term in Eq. 6 and Fig. 10 is the corresponding plot for the form drag coefficient. The plot includes data from the current study in addition to that from Dukhan and Patel [8] in which this relationship was originally deemed suitable.

Fig. 9
figure 9

Log–log of the reciprocal permeability versus specific surface area term (in Eq. 4) for data from this study and [8]

Full size image
Fig. 10
figure 10

Log–log of form drag coefficient versus specific surface area term in Eq. (5) for data from this study and [8]

Full size image

From the best fit lines and the coefficient of determination (R 2) that fit both the data presented in this study and the data from [8], it can be seen that the specific surface area based Ergun equation is able to describe the relationship between both the permeability and the form coefficient and the two important morphological features (porosity and specific surface area) not just for the conventional porous metals tested in [8] but for multi-layered porous materials subjected to compression.

3.3.2 Effect of foam thickness on pressure-drop

Pressure-drop values normalized by the sample thickness are plotted as a function of gas velocity using a third order polynomial fit in Fig. 11. Although not clear at low velocities, the apparent trend, at least at higher velocities, is that rather than the normalised pressure drop data falling on a single line, it increases for thicker samples, following the same trends reported in [3, 16, 22].

Fig. 11
figure 11

Length-normalized pressure-drop versus Darcian velocity for different thicknesses

Full size image

A more focussed analysis of data in the airflow velocity range between 0 and 16 m s−1 ( as illustrated in Fig. 12) shows that a unique relationship between length-normalised pressure drop and velocity is not preserved across the whole airflow velocity range. The trend is, in part, reversed at lower air velocities, with higher normalised pressures being observed for the thinnest samples.

Fig. 12
figure 12

Length-normalized pressure-drop versus Darcian velocity for different thicknesses in a velocity range 0–16 m s−1

Full size image

Figure 13 plots the length-normalized pressure-drop against sample thickness for different air flow velocities. It is clear from this plot that across all the velocities presented the pressure drop per unit thickness increases with decreasing thickness for small sample thicknesses. For air flow velocities below the threshold for the Forchheimer regime, increasing beyond a “critical” thickness, of roughly 8 mm, results in an independence of length-normalized pressure-drop with thickness. This behaviour demonstrates the so-called entrance effect, a result of the flow profile being altered from developed or nearly developed flow to distorted flow as it goes from a large channel (the tube) to multiple smaller channels (the pores) [22]. It should be noted that the rather limited number of data points makes determination of the exact transition and any subtle effects of gas velocity difficult to determine. According to Baril et al. [3], the critical thickness changes dramatically with pore size. For 400 µm diameter pores the critical thickness was about 19 mm (48 pores), whereas for 900 µm pores it was about 50 mm (56 pores), in broad agreement with the observations made in this work (for a transition estimated to be between 37 and 70 pore diameters).

Fig. 13
figure 13

Length-normalized pressure-drop versus sample thickness at different Darcian velocities

Full size image

As the airflow velocity increases into the transitional region (and especially into the turbulent region above 23 m s−1), the length-normalized pressure-drop–thickness relationship becomes more complex with a minimum length-normalized pressure-drop now being observed at the point where previously the critical thickness had been identified. It is thought that in addition to the extent of the entrance effect being a function of gas velocity, increasing with higher velocities [22], exit effects are also important. Once again the importance of the inter-relation between gas velocity and flow behaviour is vital, in this instance it shows that without this is makes normalised pressure drops difficult to compare for samples with different thicknesses, with the potential to cause discrepancies between similar research studies.

4 Conclusions

The pressure drop behaviour of novel, multi-layered nickel-based porous metals has been investigated for airflow velocities in the range of 0–70 m s−1.

The transitions between different flow regimes (Darcy, Forchheimer and Turbulent) were identified using two different approaches, with good agreement, and hence the permeability (K) and form drag coefficient (C) were determined within the Forchheimer regime.

The potential for error in determining the permeability and shape factor through ignorance or incorrect identification of the appropriate flow regime was shown and highlighted as a source of discrepancies in pressure drop measurements between similar studies.

Using best practise, measurements were extended to multi-layered structures that had had their densities changed by successive compression steps and, through appropriate structural characterisation by a number of different and complimentary methods, the dependence of the permeability and form drag coefficient on porosity was well approximated using the specific surface area and an Ergun-based equation.

A complex relationship was observed between length-normalised pressure drop and velocity when testing samples of different thicknesses. In the Darcy and Forchheimer regimes a transition between dependence and independence of length-normalised pressure drop with thickness was established for samples thicker than roughly 8 mm. The complex behaviour in the transition and turbulent regions illustrated additional potential sources of deviation in pressure drop measurements between similar studies.