Introduction

Fractional calculus [1] was introduced in the field of pharmacokinetics (PK) recently, in 2009 [2], but since then a significant number of relevant publications have appeared [3–8]. In other fields, many applications of fractional calculus are developed as extensions of well established mathematical models that are based upon integer order differential equations. Therefore, it is important to understand how to properly fractionalize these classic models. A single ODE is easily fractionalised by changing the derivative on the left-hand-side to a fractional order and this was indeed the first application in PK too [2]. However, in PK and other fields, where compartmental models are used, two or more ODEs are often necessary and it is not as straightforward to fractionalize systems of differential equations, especially when certain properties such as mass balance need to be preserved.

When a compartmental model with two or more compartments is being built, typically an outgoing mass flux is an incoming flux to the next compartment. Thus, an outgoing mass flux that is defined as a rate of fractional order, cannot appear as an incoming flux into another compartment, as a rate of a different fractional order, without violating mass balance [4]. It is therefore impossible to fractionalize multi-compartmental systems simply by changing the order of the derivatives on the left hand side of the ODEs. The latter is possible only in the special case where a common fractional order is considered for all ODEs, such as in an example in [3], or when mass balance is not preserved such as in PK/PD models [6], where there is no mass transfer between the response (PD) and the stimulus (PK). In the general case a different approach for fractionalizing systems of ODEs needs to be applied. Also, since the derived fractional models are unlikely to have analytical solutions, numerical methods to solve them are needed.

In this paper we propose a method to fractionalize multi-compartmental systems and a method to solve numerically such models; we present applications and examples in PK including parameter estimation from the fit of a two-compartment fractional model to PK data. Further, we discuss the implications of the presence of fractional transfer rates by simulations.

Methods

Fractionalizing linear multi-compartmental models

We will first consider a general form of a fractional two-compartment system and then generalize it to a system of an arbitrary number of compartments. A general ordinary linear two-compartment model, shown schematically in Fig. 1, is defined by the following system of linear ODEs,

$$ \begin{aligned} {\frac{{dA_{1} (t)}}{dt}} &= - k_{12} \cdot A_{1} (t) + k_{21} \cdot A_{2} (t) - k_{10} \cdot A_{1} (t) + I_{1} (t)\\ {\frac{{dA_{2} (t)}}{dt}} &= k_{12} \cdot A_{1} (t) - k_{21} \cdot A_{2} (t) - k_{20} \cdot A_{2} (t) + I_{2} (t) \hfill \\ \end{aligned} $$
(1)

where A 1(t) and A 2(t) are the mass or molar amounts of material in the respective compartments and the k ij constants control the mass transfer between the two compartments and elimination from each of them. The notation convention used for the indices of the rate constants is that the first corresponds to the source compartment and the second to the target one, e.g. k 12 corresponds to the transfer from compartment 1 to 2, k 10 corresponds to the elimination from compartment 1, etc. The units of all the k ij rate constants are (1/time). I i (t) are input rates in each compartment which may be zero, constant or time dependent. Initial values for A 1 and A 2 have to be considered also, A 1(0) and A 2(0), respectively.

Fig. 1
figure 1

Schematic representation of a general two-compartment model. The constants k ij control the mass transfer between the two compartments and elimination from each of them. The lightning arrows denote that an initial amount is administered to the particular compartment, as in the case of a bolus injection of a drug

Full size image

In order to fractionalize this system we first integrate the ordinary system, obtaining a system of integral equations and then we fractionalize the integrals. Integrating Eq. 1 results in the following system of integral equations

$$ \begin{aligned} A_{1} (t) - A_{1} (0) &= - k_{12} \int\limits_{0}^{t} {A_{1} (\tau )d\tau } + k_{21} \int\limits_{0}^{t} {A_{2} (\tau )d\tau } - k_{10} \int\limits_{0}^{t} {A_{1} (\tau )d\tau } + \int\limits_{0}^{t} {I_{1} (\tau )d\tau } \\ A_{2} (t) - A_{2} (0) &= k_{12} \int\limits_{0}^{t} {A_{1} (\tau )d\tau } - k_{21} \int\limits_{0}^{t} {A_{2} (\tau )d\tau } - k_{20} \int\limits_{0}^{t} {A_{2} (\tau )d\tau } + \int\limits_{0}^{t} {I_{2} (\tau )d\tau } \hfill \\ \end{aligned} $$
(2)

Having written the system in this integral form we may consider that each of the mass transfer integrals includes a specific kernel: G 12(t,τ), G 21(t,τ), G 10(t,τ), and G 20(t,τ). Hence,

$$ \begin{aligned} A_{1} (t) - A_{1} (0) &= - k_{12} \int_{0}^{t} {G_{12} (t,\tau )A_{1} (\tau )d\tau } + k_{21} \int\limits_{0}^{t} {G_{21} (t,\tau )A_{2} (\tau )d\tau } - k_{10} \int\limits_{0}^{t} {G_{10} (t,\tau )A_{1} (\tau )d\tau } + \int\limits_{0}^{t} {I_{1} (\tau )d\tau } \\ A_{2} (t) - A_{2} (0) &= k_{12} \int\limits_{0}^{t} {G_{12} (t,\tau )A_{1} (\tau )d\tau } - k_{21} \int\limits_{0}^{t} {G_{21} (t,\tau )A_{2} (\tau )d\tau } - k_{20} \int\limits_{0}^{t} {G_{20} (t,\tau )A_{2} (\tau )d\tau } + \int\limits_{0}^{t} {I_{2} (\tau )d\tau } \\ \end{aligned} $$
(3)

In the classic case, each of these kernels is simply G ij (t,τ) = 1, giving Eq. 2. By changing this kernel to an appropriate function in a power-law form, we can convert these integrals to Riemann–Liouville (RL) fractional integrals [1]. The appropriate form of the kernel is the following:

$$ G_{ij} (t,\tau ) = {\frac{{(t - \tau )^{{\alpha_{ij} - 1}} }}{{\Upgamma (\alpha_{ij} )}}} $$
(4)

where 0 < α ij  < 1 is a constant representing the order of the specific process. For α ij  = 1, we have the classic case since G ij (t, τ) = 1. We may consider different values for the orders of different processes, but the order of the corresponding terms of a specific process is kept the same when these appear in different equations, e.g. we can have an order α 12 for the transfer from compartment 1 to 2 and a different order α 21 for the transfer from compartment 2 to 1, but the order for the corresponding terms of the transfer, from compartment 1 to 2, α 12, is the same in both equations. In this way each of the integrals becomes a RL fractional integral since the definition of the latter is:

$$ {}_{0}D_{t}^{{ - \alpha_{ij} }} A_{i} (t) = \int\limits_{0}^{t} {{\frac{{(t - \tau )^{{\alpha_{ij} - 1}} }}{\Upgamma (\alpha )}}} A_{i} (\tau )d\tau $$
(5)

Note that D operator stands for an integral when the order (superscript) is negative and for a derivative when the order is positive. Therefore, the fractionalized version of Eq. 2, can be written as

$$ \begin{aligned} A_{1} (t) - A_{1} (0) &= - k_{12} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{12} }} A_{1} (t) + k_{21} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{21} }} A_{2} (t) - k_{10} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{10} }} A_{1} (t) + \int\limits_{0}^{t} {I_{1} (\tau )d\tau } \\ A_{2} (t) - A_{2} (0) &= k_{12} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{12} }} A_{1} (t) - k_{21} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{21} }} A_{2} (t) - k_{20} \cdot {}_{0}^{{}} D_{t}^{{ - \alpha_{20} }} A_{2} (t) + \int\limits_{o}^{t} {I_{2} (\tau )d\tau } \\ \end{aligned} $$
(6)

Taking the first derivative of Eq. 6 we end up with a system of FDEs with RL derivatives

$$ \begin{aligned} {\frac{{dA_{1} (t)}}{dt}} &= - k_{12} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{12} }} A_{1} (t) + k_{21} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{21} }} A_{2} (t) - k_{10} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{10} }} A_{1} (t) + I_{1} (t) \\ {\frac{{dA_{2} (t)}}{dt}} &= k_{12} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{12} }} A_{1} (t) - k_{21} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{21} }} A_{2} (t) - k_{20} \cdot {}_{0}^{{}} D_{t}^{{1 - \alpha_{20} }} A_{2} (t) + I_{2} (t) \hfill \\ \end{aligned} $$
(7)

It is convenient to rewrite the above system (Eq. 7) with Caputo derivatives [1]. A Caputo derivative of a constant is zero which is not the case for RL derivatives. Also, an FDE with Caputo derivatives accepts the usual type of initial conditions involving the variable itself, as opposed to RL derivatives which involve an initial condition on the derivative of the variable, which is not practical. When the initial value of A 1 or A 2 is zero then the respective RL and Caputo derivatives are the same. This is convenient since a zero initial value is very common in compartmental analysis. When the initial value is not zero, converting to a Caputo derivative is possible, for the particular term with a non-zero initial value. The conversion from a RL to a Caputo derivative of the form that appears in Eq. 7 is done with the following expression:

$$ {}_{0}^{{}} D_{t}^{{1 - \alpha_{ij} }} A_{i} (t) = {}_{0}^{C} D_{t}^{{1 - \alpha_{ij} }} A_{i} (t) + {\frac{{A_{i} (0)t^{{\alpha_{ij} - 1}} }}{{\Upgamma (\alpha_{ij} )}}} $$
(8)

where the C superscript on the left of the D operator denotes a Caputo fractional derivative. Without it the D operator stands for a RL derivative unless the order is negative when it stands for a RL integral. Summarising about initial conditions, we can identify three cases: (i) The initial condition is zero and then the derivative becomes a Caputo by definition. (ii) The initial condition is non-zero but it is involved in a term with an ordinary derivative so it is treated as usual. (iii) The initial condition is non-zero and is involved in a fractional derivative which means that in order to present a Caputo derivative, an additional term, involving the initial value appears, by substituting Eq. 8. Alternatively, we can assume a zero initial value for that variable, and a Dirac delta input to account for the initial quantity for that variable.

So, we derived a general fractional model with two compartments, Eq. 7, where the fractional derivatives can always be written as Caputo derivatives. Note that the units of the k ij rate constants are \( ({\text{time}}^{{ - \alpha_{ij} }} ) \). It is easy to generalize the above approach to a system with an arbitrary number of n compartments as follows.

$$ {\frac{{dA_{i} (t)}}{dt}} = - k_{i0} \cdot {}_{0}^{C} D_{t}^{{1 - \alpha_{i0} }} A_{i} (t) - \sum\limits_{j \ne i}^{n} {k_{ij} \cdot {}_{0}^{C} D_{t}^{{1 - \alpha_{ij} }} A_{i} (t)} + \sum\limits_{j \ne i}^{n} {k_{ji} \cdot {}_{0}^{C} D_{t}^{{1 - \alpha_{ji} }} A_{j} (t)} + I_{i} (t),\quad {\text{for }} i = 1, \ldots ,n $$
(9)

where we have considered Caputo derivatives throughout since, as we explained above, this is feasible. This system of equations (Eq. 9) is too general for most purposes as it allows every compartment to be connected with every other one. Typically the connection matrix would be much sparser than that, with most compartments being connected to just one neighbouring compartment while only a few “hub” compartments would have more than one connection.

The advantage of the described approach of fractionalization is that each transport process is fractionalized separately, rather than fractionalizing each compartment or each equation. Thus, processes of different fractional orders can co-exist since they have consistent orders when the corresponding terms appear in different equations. Also, it is important to note that Eq. 9 do not have problems, such as violation of mass balance or inconsistencies with the units of the rate constants.

A numerical method to solve linear FDEs

The systems of FDEs described in the previous section, in general, cannot be solved analytically, so we are introducing a numerical approach appropriate for the solution of such systems. It is based on rewriting the system in the Laplace domain and then using a numerical inverse Laplace transform (NILT) algorithm to simulate the system’s solution in the time domain. FDEs can be easily written in the Laplace domain since each of the fractional derivatives can be transformed similarly to the ordinary derivatives, as follows, for order α ≤ 1:

$$ L\{ {}_{0}^{C} D_{t}^{\alpha } f(t)\} = s^{\alpha } \hat{f}(s) - s^{\alpha - 1} f(0) $$
(10)

where \( \hat{f}(s) \) is the Laplace transform of f(t) [1]. For α = 1, Eq. 10, collapses to the classic expression for ordinary derivatives, i.e. \( L\{ f^{\prime}(t)\} = s\hat{f}(s) - f(0) \). In the case of FDEs of the form of Eq. 9, where the fractional orders are 1-α ij , Eq. 10 becomes

$$ L\{ {}_{0}^{C} D_{t}^{{1 - a_{ij} }} A_{i} (t)\} = s^{{1 - a_{ij} }} \hat{A}_{i} (s) - s^{{ - a_{ij} }} A_{i} (0) $$
(11)

Although it is always easy to transform an FDE in the Laplace domain and in most cases feasible to rearrange it, solving it explicitly for the system variables, it is more difficult to apply the inverse Laplace transform, such that an analytical solution in the time domain is obtained. However, it is possible to perform that step numerically using a NILT algorithm. In the applications of the present work we are using the MATLAB subroutine “invlap.m” of Hollenbeck which is based on the algorithm by de Hoog et al. [9].

In order to provide evidence that our numerical approach works we apply it to the following simple FDE.

$$ {}_{0}^{C} D_{t}^{1/2} A(t) = - A(t) $$
(12)

with initial value A(0) = 1. Equation 12 has an analytical solution, which is a Mittag–Leffler function of order one half, and can be written as follows [1]

$$ A(t) = E_{1/2} ( - t^{1/2} ) = e^{t} (1 + {\text{erf}}( - \sqrt t )) $$
(13)

Also, Eq. 12 can be written in the Laplace domain, applying Eq. 10, as follows

$$ s^{1/2} \hat{A}(s) - s^{ - 1/2} A(0) = - \hat{A}(s) $$
(14)

which can be rearranged, substituting also the initial value as

$$ \hat{A}(s) = {\frac{1}{s + \sqrt s }} $$
(15)

In the results section we will compare the analytical solution, Eq. 13 to the numerical inversion of Eq. 15 using the NILT algorithm.

Pharmacokinetic models

Based on the generalized approach for the fractionalization of compartmental models, which allows mixing different fractional orders, developed in the previous section, we consider a two - compartment fractional pharmacokinetic model shown schematically in Fig. 2a. Compartment 1 (central) represents general circulation and well perfused tissues while compartment 2 (peripheral) represents deeper tissues. We consider three transfer processes (fluxes): elimination from the central compartment and a mass flux from the central to the peripheral compartment, which are both assumed to follow classic kinetics (order 1), while a flux from the peripheral to the central compartment is assumed to follow slower fractional kinetics accounting for tissue trapping.

Fig. 2
figure 2

Fractional 2-compartment PK models. Elimination from the central compartment and a mass flux from the central to the peripheral compartment, which are both assumed to follow classic kinetics (order 1), while a flux from the peripheral to the central compartment is assumed to follow slower fractional kinetics, accounting for tissue trapping (dashed arrow). a The dose is administered in the central compartment as an IV bolus. b The dose is administered orally, in the gut compartment

Full size image

The system is formulated mathematically as follows:

$$ \begin{aligned} {\frac{{dA_{1} (t)}}{dt}} &= - (k_{12} + k_{10} )A_{1} (t) + k_{21} \cdot {}_{0}^{C} D_{t}^{1 - \alpha } A_{2} (t) \hfill \\ {\frac{{dA_{2} (t)}}{dt}} &= k_{12} A_{1} (t) - k_{21} \cdot {}_{0}^{C} D_{t}^{1 - \alpha } A_{2} (t) \\ \end{aligned} $$
(16)

where a < 1 and initial conditions are A 1(0) = dose, A 2(0) = 0 which account for a bolus dose injection and no initial amount in the peripheral compartment. Note, that we are allowed to use Caputo derivatives here since the fractional derivatives involve only terms with A 2 for which there is no initial amount, which means that Caputo and RL derivatives are identical (Eq. 8).

Applying the Laplace transform, to the above system we obtain:

$$ \begin{aligned} s\hat{A}_{1} (s) - A_{1} (0) &= - (k_{12} + k_{10} )\hat{A}_{1} (s) + k_{21} (s^{1 - \alpha } \hat{A}_{2} (s) - s^{ - \alpha } A_{2} (0)) \\ s\hat{A}_{2} (s) - A_{2} (0) &= k_{12} \hat{A}_{1} (s) - k_{21} (s^{1 - \alpha } \hat{A}_{2} (s) - s^{ - \alpha } A_{2} (0)) \\ \end{aligned} $$
(17)

Solving for \( \hat{A}_{1} (s) \) and \( \hat{A}_{2} (s) \) and substituting the initial conditions, we obtain

$$ \hat{A}_{1} (s) = {\frac{{dose \cdot (s^{\alpha } + k_{21} )}}{{(s + k_{12} + k_{10} )(s^{\alpha } + k_{21} ) - k_{12} \cdot k_{21} }}} $$
(18)
$$ \hat{A}_{2} (s) = {\frac{{dose \cdot s^{\alpha - 1} k_{12} }}{{(s + k_{12} + k_{10} )(s^{\alpha } + k_{21} ) - k_{12} \cdot k_{21} }}} $$
(19)

Using the above expression for \( \hat{A}_{1} (s) \) and \( \hat{A}_{2} (s) \), Eq. 18 and 19, respectively, we can simulate values of A 1(t) and A 2(t) in the time domain by the NILT method. Note that we are primarily interested for A 1(t), since in practice, we only have data from this compartment. The output for A 1(t) from this numerical solution may be combined with the following equation

$$ C_{b} \left( t \right) = A_{ 1} \left( t \right)/V_1 $$
(20)

where C b is the drug concentration in the blood and V 1 is the apparent volume of distribution. Equation 20 can be fitted to pharmacokinetic data in order to estimate parameters V 1, k 10, k 12, k 21 and α.

With our approach it is straightforward to consider compartmental systems of arbitrary structure. One can mix fractional orders and consider different routes of administration. Also, implementing multiple dosing is simple, by superposition of solutions, since the systems are linear.

As a second example we consider a two-compartment model with oral absorption and multiple dosing shown schematically in Fig. 2b, which is a variation the system of Eq. 16. It is basically the same system but with an exponential input to account for the oral absorption. Formally, it is a three-compartment system where the transfer from the gut (first) compartment to the central (second) compartment is unidirectional. The peripheral compartment is denoted as the third compartment in this model. The form of the input function for the ith dose is

$$ I(t) = F \cdot dose_{i} \cdot k_{12} \cdot e^{{ - k_{12} t}} $$
(21)

where k 12 is a first order absorption rate constant and F is the bioavailable fraction of dose. It is derived from the following equation

$$ {\frac{{dA_{1} (t)}}{dt}} = - k_{12} \cdot A_{1} (t) $$
(22)

with A 1(0) = F·dose i . Thus, the fractional two-compartment system with oral absorption can be written as follows:

$$ \begin{aligned} {\frac{{dA_{2} (t)}}{dt}} &= - (k_{23} + k_{20} )A_{2} (t) + k_{32} \cdot {}_{0}^{C} D_{t}^{1 - \alpha } A_{3} (t) + F \cdot dose_{i} \cdot k_{12} \cdot e^{{ - k_{12} t}} \\ {\frac{{dA_{3} (t)}}{dt}} &= k_{23} A_{2} (t) - k_{32} \cdot {}_{0}^{C} D_{t}^{1 - \alpha } A_{3} (t) \\ \end{aligned} $$
(23)

The initial conditions for this system are zero, A 2(0) = A 3(0) = 0. The amount in the central compartment in the Laplace domain is given by the following equation:

$$ \hat{A}_{2} (s) = {\frac{{F \cdot dose_{i} \cdot k_{12} }}{{(s + k_{12} )}}} \cdot {\frac{{(s^{\alpha } + k_{32} )}}{{(s + k_{23} + k_{20} )(s^{\alpha } + k_{32} ) - k_{23} \cdot k_{32} }}} $$
(24)

from which we can simulate values, in the time domain using the NILT algorithm. Assuming that the profile in the central compartment for the ith dose is given by

$$ A^{i} (t) = \left\{ {\begin{array}{ll} 0 & {{\text{for}}\,t < T_{i} } \\ {A_{2} (t + T_{i} ,dose_{i} )} & {{\text{for}}\,t \ge T_{i} } \\ \end{array} } \right. $$
(25)

where T i is the ith dosing time, the total profile A(t) in the central compartment, after superimposing N doses, becomes, simply:

$$ A(t) = \sum\limits_{i = 1}^{N} {A^{i} (t)} $$
(26)

In the same rationale, one may build pharmacokinetic models of any possible structure which also include one or more fractional transfer processes.

As a third example we consider a simple model, a one compartment model with a fractional elimination and a constant rate input. This elementary model has a more abstracted physical meaning than the previous model which allowed a clear separation between fast and deeper tissues, but since it has an analytical solution it allows us to demonstrate important implications of the presence of fractional kinetics, and most importantly accumulation of drug. The system can be described by the following equation

$$ {\frac{{dA_{1} (t)}}{dt}} = k_{01} - k_{10} \cdot {}_{0}^{C} D_{t}^{1 - \alpha } A_{1} (t) $$
(27)

with A 1(0) = 0 and where k 01 is a zero order input rate constant, with units mass/time, k 10 is a rate constant with units time−α and α is a fractional order less than 1.

Equation 27 can be written in the Laplace domain as

$$ s\hat{A}_{1} (s) - A_{1} (0) = k_{01} /s - k_{10} (s^{1 - \alpha } \hat{A}_{1} (s) - s^{ - \alpha } A_{1} (0)) $$
(28)

Since A 1(0) = 0, we can solve Eq. 28 and obtain

$$ \hat{A}_{1} (s) = {\frac{{k_{01} s^{\alpha - 2} }}{{s^{\alpha } + k_{10} }}} $$
(29)

By applying the following inverse Laplace transform formula (Eq. 1.80 in Ref. 1, p 21):

$$ L^{ - 1} \left\{ {{\frac{{s^{\alpha - \beta } }}{{s^{\alpha } + k}}}} \right\} = t^{\beta - 1} E_{\alpha ,\beta } ( - k \cdot t^{\alpha } ) $$
(30)

where E α,β is the Mittag–Leffler function with two parameters, with β = 2 we obtain:

$$ A_{1} (t) = k_{01} \cdot t \cdot E_{\alpha ,2} ( - k_{10} t^{\alpha } ) $$
(31)

Results and discussion

The main result of this work is the approach presented in the methods section that allows us to write fractional compartmental systems of FDEs, mixing different orders without violating mass balance. As already mentioned in the introduction, although it is straightforward to fractionalize a single ODE by simply changing the order of the derivative of the left hand side [2], when one tries to do the same in a system of two or more ODEs then, depending on the scope of the model, a badly defined system may occur which may have units inconsistencies and in the case of compartmental modelling also violates mass balance [4]. This is because in such systems mass flux terms are considered, which are common between equations and account for in- and out- fluxes. These terms that appear in multiple equations cannot correspond to different rate orders for each of them. The problem is pronounced in the inconsistencies of the units but is not limited to the units. Fractionalizing simply by changing the order of the derivative on the left-hand side works only when the order of all the FDEs of the system is common. In [5] this type of system is referred to as “commensurate” and indeed does not suffer from the problems mentioned above but still it is a very special case of limited interest. A PK application of such a “commensurate” system has appeared in [3]. On the other hand when mass balance is not an issue, one may write “non-commensurate” systems which are well defined. Recently, an application of FDEs in PK/PD modelling has appeared [6] where the PK and the PD parts have different orders which cause no problem though, because the PK is a stimulus for the PD response and no mass transfer takes place there.

Our approach instead of fractionalizing by changing the left-hand side derivatives, considers processes of different fractional orders and not compartments of different fractional orders. This allows a specific flux to be of a different order from some other flux, or from some elimination term and all of them are consistent because the corresponding in- and out-fluxes match.

As already mentioned the systems of FDEs described in the methods section cannot, in general, be solved analytically. To address this, numerical methods have to be employed. Our approach is based on rewriting the system in the Laplace domain and then using a NILT algorithm to simulate the system’s solution in the time domain. In order to provide evidence that this approach works we solve a simple FDE, Eq. 12 that has an analytical solution Eq. 13, and compare the numerical solution obtained by the NILT method with the analytical solution.

In Fig. 3 the plots of the solution of Eq. 12 using the NILT algorithm with Eq. 15 and the analytical solution of Eq. 13, can be seen to be overlapping, therefore providing evidence that the approach based on the NILT algorithm works for FDEs. Further on, we provide more examples where the NILT method works well, in more complex models.

Fig. 3
figure 3

Numerical (line) and analytical (circles) solution of Eq. 12 overlap, demonstrating that the solution of FDEs by the NILT approach works well

Full size image

Other numerical methods for solving FDEs also exist. Some rely on appropriate discretization of FDEs and writing the fractional derivatives as fractional finite differences [10, 11]. Alternative methods rely on analytical solutions that exist for special cases of FDEs, such as for FDEs with rational orders [5], taking advantage of the fact that any real number can be approximated by a rational number with an arbitrary accuracy. Note that not all methods are applicable to all types of problems. Our approach is intuitive and relies on the fact that the Laplace transforms of fractional derivatives are simple generalization of the Laplace transforms of ordinary derivatives. Further, several NILT algorithms [12], even applied in PK [13], and different implementations are available in the public domain for a number of platforms including Fortran, MATLAB, C, etc. But, caution must be taken since NILT algorithms have limitations and may be unstable in certain cases, although we haven’t witnessed any of these in the few examples that we have tried ourselves. It is a future task to compare different methods and assess their performance in generality, ease of use, stability and computational speed.

The general form of Eq. 9 allows the formulation of systems of arbitrary structure. As already mentioned the form of Eq. 9 is too general allowing every compartment to be connected to every other. In reality even for models of several compartments the connections would be much sparser with one or two hub compartments rather than a dense network. Also, it is unlikely that in a multi-compartmental system all transfer processes would be fractional and indeed that each process would have its own fractional order. Instead it is more likely that most transfer processes would be of order 1 and only one or very few processes would be fractional. Thus, in the methods section, we described two basic PK models: a two-compartment fractional intravenous single dose model (Eq. 16), shown schematically in Fig. 2a; and a two-compartment fractional oral multiple dose model, (Eq. 23), shown schematically in Fig. 2b. In both models only the transfer from the peripheral to the central compartment is fractional, while all other processes are classical of order 1. The first model, Eq. 16, is fundamental, in the sense that it is the simplest possible fractional model which can be interpreted physiologically depending on the available data. A one-compartment fractional model is simpler [2] but it is an abstracted empirical model which describes an apparent kinetic behavior. On the other hand the basic two-compartment model of Eq. 16, although it cannot be considered as physiological when the available data comes only from the central circulation, still it includes some basic principles. The central compartment corresponds to the blood and the fast distributing tissues, while the peripheral compartment corresponds to deeper tissues where there is trapping of the drug and the return from this compartment back to the central is governed by anomalous diffusion. Clearly one could easily consider extra compartments to account for richer kinetics, e.g. a three-compartment model where the transfer flux of one of the peripheral compartments to the central is fractional and all other transfer fluxes are of order 1. Also, physiological models could be considered if data from specific tissues are available.

In Fig. 4a, b, simulations of the model of Eq. 16 are shown. In the first simulation task, we consider the special case of α = 1 which is the classic 2-compartment model and has a well known analytical solution found in most PK textbooks. By using the NILT method we obtain profiles which overlap with the analytical solution of the classic two-compartment pharmacokinetic model. This is an additional verification to the evidence presented earlier, that the NILT method provides a good approximation to the analytical solutions of differential equations, when these exist. Although in this particular example the solution shown is for a system of ODEs, since α = 1, there is no fundamental reason to expect poorer results with FDEs when α < 1.

Fig. 4
figure 4

a Time profiles for A1 of the system of Eq. 16. The classic case of a = 1 with the NILT method (solid line), analytical solution of α = 1 (circles). Fractional case of a = 0.5 by the NILT method (dashed line). Other parameters take the following values (in arbitrary units): k10 = 1, k12 = 0.8 and k21 = 0.7. b Time profiles for A2 of the system of Eq. 16. c Log–log plot of the fractional case of α = 0.5 for A1, for a longer time scale

Full size image

The next simulation task is to use Eq. 16, for the fractional case of α < 1, more specifically for α = 0.5. Although the solution in this case can be expressed in terms of an infinite series of generalized Wright functions as demonstrated in the book by Kilbas et al. [14], these solutions are hard to implement and apply in practice; therefore, we use only the NILT method in this case. We obtain profiles which exhibit slower, compared to the case of α = 1, non-exponential kinetics, shown in Fig. 4a, b. These non exponential profiles do not have a terminal half-life and the terminal phase resembles a power-law forming a straight line on the log–log scale, Fig. 4c. In Fig. 4a, the fractional profile seems to be initially faster but eventually it becomes slower. Note that although we have used the same parameter values apart from the value of the fractional order, α, parameter k 21 is not comparable between the two cases because it has different units (hours−1 vs hours−0.5) despite the fact that they are arithmetically the same. The slower kinetics arises as a result of the power-law nature of the terminal phase of the fractional case rather than the value of the rate constant. In addition, a power-law is eventually slower than any exponential.

The second model considered in the methods section, Eq. 23, is a variation of that of Eq. 16. It is a two-compartment, oral, multiple dose model. We use this model in order to demonstrate the feasibility of building fractional models with the commonly used features of oral administration and also to demonstrate some of the consequences of the presence of the fractional transfer process in the model. In Fig. 5a the model simulates values for 3 days with the dose being administered every 24 h, for α = 1, the classic case and α = 0.5, the fractional case. In this example the profile corresponding to the fractional case seems to be faster than the classic case. However, like in Fig. 4a, where the fractional profile is initially faster but eventually slower, here too, initially the profile is exponential while the slower, power-law part dominates later. In this example, in Fig. 5a, the power-law kinetics is masked by the next dose, but becomes evident in longer times due to accumulation. In Fig. 5b, c zoom of the profiles around the peak values are shown of the same model, for 2 months, for the classic and the fractional cases, respectively. We can observe that in the classic case (Fig. 5b) the profile reaches quickly a steady state, however, the fractional case, never reaches a steady state and accumulation of drug carries on indefinitely. This fact is one of the most clinically important implications of fractional kinetics. Since the model of Eq. 23 does not have an analytical solution it is difficult to show the accumulation of drug in a way other than plotting a numerical simulation. To demonstrate the infinite accumulation more convincingly, we considered a simpler model, a one-compartment model with a constant input (infusion) and a fractional elimination, Eq. 27. Note that even for that simple model it is necessary to employ our approach of fractionalizing each process separately, since we need to keep the constant rate infusion in classic order. That would have been difficult if one followed the approach of changing the order of the derivative of the left hand side of the ODE, however here it is straightforward. We showed that the solution of this model is Eq. 31. We can also show that the limit of Eq. 31 diverges when t goes to infinity, for α < 1, (see Appendix) which means that unlike the classic case, for α = 1, where Eq. 31 approaches exponentially the steady state k 01/k 10, for α < 1, there is infinite accumulation. In Fig. 6a, a plot of Eq. 31 is shown for α = 1 and α < 1 showing that in the classic case a steady state is approached, as expected, while in the fractional case the amount keeps rising. In Fig. 6b the same profiles are shown for 100 times larger time span, demonstrating the effect of continuous accumulation. Also, in Fig. 6a a solution of Eq. 27 by the NILT method is also shown as an additional example where this numerical method works well. In this case Eq. 29 which is the solution of Eq. 27 in the Laplace domain was inverted numerically back to the time domain, as previously.

Fig. 5
figure 5

Simulation with the system of Eq. 23, 25 and 26 for the classic (α = 1) and the fractional (α = 0.5) case. Other parameter values are: k 20 = 0.2 h−1, k 23 = 0.6 h−1, k 32 = 1 h−1 or h−0.5, k 12 = 2 h−1, doses and amounts in arbitrary units. a The time profile in both cases for 72 h. b Zoom of the peaks of the classic profile for 2 months. c Zoom of the peaks of the fractional profile for 2 months

Full size image
Fig. 6
figure 6

a Plot of Eq. 31 for α = 1 (solid ) and α = 0.5 (dashed ). Circles correspond to the case of α = 0.5 solved by the NILT method. b The same profiles (without the NILT) for 100 times longer time span

Full size image

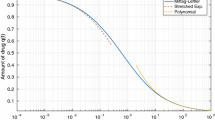
As a final example of the use of the fractional compartmental models we fit the system of Eq. 16 to an amiodarone dataset in order to obtain parameter estimates. Amiodarone is an antiarrhythmic drug known for its anomalous, non-exponential pharmacokinetics, which have important clinical implications due to the accumulation pattern of the drug in long-term administration. Here, we use the fractional two-compartment model of the previous section, to analyze an amiodarone IV dataset which first appeared in [15], and has been analyzed before with a power-law time dependent fractal kinetics [7, 16] as well as a Mittag–Leffler function [2]. For fitting we use the built-in “lsqnonlin” routine of MATLAB. Visual inspection of Fig. 7 reveals that the model provides a good fit to the data for the 60 day period of this study. The non-exponential character of the curve is evident, while the model follows well the data both for long and for short times. Parameter estimates together with the corresponding standard errors are shown in Table 1. The fitted line seems to be similar to the previously used Mittag–Leffler function [2]. This is not surprising since in the current two-compartment model, the slow fractional flux from the peripheral to the central compartment is the limiting step of the entire course. Therefore, it is reasonable that this solution is close to the simple Mittag-Leffler model which basically describes a fractional elimination of the drug from a one-compartment system. Further, it is worth mentioning that the estimated value of α = 0.587 (Table 1) is close to the value 0.56, of the exponent of the power law function, estimated in [16], where a similar idea of the non-exponential back-transport from the deep tissue compartment was employed, although there, a time dependent power-law function was used to account for this rate, and not fractional calculus.

Fig. 7
figure 7

The compartment model of Eq. 16 and 20 (line), fitted to the amiodarone data (circles)

Full size image
Table 1 Parameter estimates with CVs of the model of Eq. 16 and 20 fitted to the amiodarone data (See Fig. 2a for definition of the symbols)
Full size table

Conclusions

FDEs are a useful tool in pharmacokinetics, especially for modelling datasets that have power-law kinetics, accounting for anomalous diffusion and deep tissue trapping. We presented an approach that allows the formulation of multi-compartmental models, mixing different fractional orders, in a consistent manner and we also provided a method for the numerical solution of these systems based on a numerical inverse Laplace transform algorithm. Simulations showed that the presence of a transfer rate of fractional order in the system, produces a non-exponential terminal phase, while a multiple dose system never reaches steady state and drug accumulation carries on indefinitely which has obvious clinical implications.