1 Introduction

Thermography is one of the relatively recent techniques that is being used in non-destructive evaluation for defect characterization and material property evaluation. This method finds applications in a wide range of industries including aerospace, energy, infrastructure, and defense. The process of induction heating consists of development of eddy currents in a conducting material by electromagnetic induction and the consequent generation of heat by Joule heating. The heat diffuses in the material and the temperature on the surface of the specimen changes. Lehtiniemi and Hartikainen [5] discussed about an application of induction heating as a selective heat source for fast thermal nondestructive evaluation. The conductive parts of the sample are heated by a scanning induction coil. Defects such as broken fibers or de-laminations are detected by monitoring the infrared radiations from the sample surface. The functionality of the system was demonstrated by carbon fiber reinforced composites. A proposal for magneto thermal NDT in conducting materials was given by Siakevellas [9]. Here a numerical analysis was done to determine the temperature gradients around a crack tip from which the position and orientation of the surface breaking cracks were determined. Walle and Netzelmann [13] discussed the thermographic crack detection methods in ferritic steel components using induction heating. A theoretical model for the temperature distribution around a crack resulting from a given induction field was set up and the results were compared with experiments. By using an excitation frequency of 100 kHz, they were able to detect perpendicular and slanting surface cracks up to 200 μm. Reigert et al. [8] proposed the method for eddy current lock-in thermography and discussed its potential in the field of non-destructive evaluation. The remote modulated excitation generates thermal waves that interact with the boundaries of the defects therby revealing them. The phase information gives idea about the defect depth. In their paper, Tsopelas and Siakevellas [10, 11] investigated numerically, the effectiveness of an electromagnetic-thermal method for the non-destructive testing of thin conducting plates. They studied the relation of the detection region and detection period to the exciting coil diameter, crack length, crack orientation, and distance of the coil from the surface of the plate. Oswald-Tranta [7] has described the thermo-inductive crack detection in both magnetic and non-magnetic materials. She has presented an analytical and semi analytical methods to calculate the eddy current distribution and temperature distribution for different cases. Another study was carried out by Zenzinger et al. [14] regarding thermographic crack detection by eddy current excitation and described an algorithm to increase the sensitivity of small defects. Vrana et al. [12] used an analytical and finite element model to predict the induced current distribution in plates and discussed a couple of models for crack detection with induction thermography. A 2D finite element study of the simulation induction heating in synchronic thermography was carried out by Louaayou et al. [6]. The defect was localized and its depth was estimated by the phase and modulus of the temperature in synchronic regime. The study was aimed to detect the defect by choosing the electromagnetic and thermal frequencies. Kumar et al. [4] discussed about tone burst eddy-current thermography and compared it with conventional pulsed thermography technique.

Depending on the frequency of excitation, the heating zone can be confined to the surface (surface heating) or to the entire volume of the material (volume heating). For both approaches, the efficiency of material heating and the subsequent retrieval of relevant information for the non-destructive evaluation of materials and components require the use of optimum frequency for induction heating [1]. The heating and the defect detection phenomena using this technique depends on both the thermal and electrical properties of the material [2].

In the current work, it is attempted to determine the defect size from the temperature data. The forward problem of electro-magnetic induction was solved with an axi-symmetric model using finite element method and from the temperature history profiles, an inverse analysis was performed using Genetic Algorithm (GA) to size the defect.

2 Theoretical Background

2.1 Forward Model

The mathematical model for the electromagnetic induction is given by Maxwell’s equations along with the constitutive equations and the Ohm’s law.

Using the definition of potentials,

(1)

the Ampere’s law can be written in the form

$$ \sigma\frac{d\boldsymbol{A}}{dt} + \nabla\times\mu^{-1}\nabla\times \boldsymbol{A} + \sigma\nabla V = \boldsymbol{J} + \varepsilon\frac{d^{2}\boldsymbol{A}}{dt^{2}} $$
(2)

where E is the electric field intensity (V/m), B is the magnetic flux density (T), A is the magnetic vector potential, V is the electric potential, J is the current density (A/m2), ε is the permittivity of the medium (F/m)=ε 0 ε r ,ε r is the relative permittivity, ε 0 is the permittivity of free space=8.854×10−12 F/m, μ is the magnetic permeability (H/m)=μ 0 μ r ,μ r is the relative permeability, μ 0 is the permeability of free space=4π×10−7 H/m, and σ is the electrical conductivity (S/m).

For axially symmetric structures with current passing only in the angular direction, the problem is formulated by considering only the A φ component of the magnetic potential. Since the electric field is present only in the azimuthal direction, the gradient of electric potential can be written as

$$ \nabla V = \frac{ - V_{\mathit{loop}}}{2\pi r} $$
(3)

where V loop is the potential difference for one turn around the z-axis. For time harmonic analysis A=A φ e jωt, (2) takes the form

$$ \bigl(j\omega\sigma -\omega^{2}\varepsilon_{0}\varepsilon_{r}\bigr) A_{\varphi} + \nabla\times\bigl(\mu^{ - 1}\nabla\times A_{\varphi} \bigr) = \sigma\frac{V_{\mathit{loop}}}{2\pi r} + J_{\varphi} $$
(4)

The boundary conditions are magnetic insulation on the domain boundary,

$$ A_{\varphi} =0 $$
(5)

and continuity of magnetic fields on the interior boundaries,

$$ n \times(H_{1} - H_{2}) = 0. $$
(6)

The eddy currents induced in the sample generate heat due to Joule heating. The average value of the heat generated within the plate is taken as

$$ Q = \frac{1}{2}\sigma| E |^{2} $$
(7)

For an axi-symmetric problem, the heat transfer equation is expressed as

$$ \frac{1}{r}\frac{\partial}{\partial r}\biggl(kr\frac{\partial T}{\partial r}\biggr) + \frac{\partial}{\partial z}\biggl(k\frac{\partial T}{\partial z}\biggr) + Q = \rho C_{p}\frac{\partial T}{\partial t} $$
(8)

where ρ is the material density (kg/m3), C p is the specific heat (J/kg K), T is the temperature (K), and k is the thermal conductivity (W/m K).

The boundary conditions used are the prescribed temperature at the domain boundaries,

$$ T=T_{a} \quad\mbox{(Ambient Temperature)} $$
(9)

and the heat flux at the other boundaries

$$ k\frac{\partial T}{\partial n}=h(T_{\infty} -T)+e\sigma\bigl(T_{a}^{4}-T^{4}\bigr) $$
(10)

where h is the convective heat transfer coefficient (W/m2 K), T ∞ is the external temperature (K), e is the emissivity, and σ is the Stefan-Boltzmann constant=5.67×10−8 W/m2 K4.

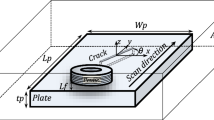
The forward model is solved using COMSOL 3.2 multi physics software. Figure 1 shows the model used for the forward analysis. The specimen was 10 mm thick aluminum plate. The loop potential was calculated from the coil resistance and the current passing through it (during the experiment) and it was approximately equal to 0.25 V. The time of heating was 3 s and the period of observation 10 s, which ensured a detectable temperature rise on the surface of the specimen, no over-heating of the amplifier during the experiments, enough time for the diffusion of heat, and less computation time. The excitation frequency was kept at 1000 Hz which is the optimum frequency for this thickness [1]. The coil was modeled by 4 layers of copper wire of 0.3 mm diameter with each layer consisting of 25 turns as shown in Fig. 1. Both the coil and the specimen were placed in air domain.

Fig. 1
figure 1

Simulation model

Full size image

The material properties and constants used for the simulation studies are listed in Table 1.

Table 1 Material properties and constants used for simulation
Full size table

The boundary conditions used for the electromagnetic induction were

  1. (1)

    Axial symmetry at r=0

  2. (2)

    Magnetic insulation at the air boundaries (A φ =0)

  3. (3)

    Continuity of magnetic fields at the interior boundaries (n×(H 1−H 2)=0)

and those for the heat transfer were,

  1. 1.

    Axial symmetry at r=0.

  2. 2.

    Temperature boundary condition at the air boundaries (T=T a =300 K).

  3. 3.

    Heat flux at the other boundaries

    $$k\frac{\partial T}{\partial n}=h(T_{\infty} -T)+e\sigma\bigl(T_{a}^{4}-T^{4}\bigr) $$

2.2 Inversion Using GA

The temperature rise in a defective sample during the electromagnetic induction is dependent on, apart from the electrical and the thermal properties of the material, the defect size also. From this temperature data, the defect depth (d d ) and defect radius (r d ) are estimated using GA based inversion. The input to the inversion algorithm will be the time-temperature data (T ref (x i ,t j )) which are normally the measured surface temperature at selected locations x i obtained over a short duration of time (t) in j number of steps. Then the inversion process starts by solving the forward problem repeatedly by assuming the defect sizes r d and d d in the given range. The temperature history at the same locations x i are stored as T(x i ,t j ). The GA based search was employed to minimize the difference between the calculated T(x i ,t j ) and the measured T ref (x i ,t j ) using the objective function (fitness function)

$$ f = \sum_{i = 1}^{n} \sum_{j = 0}^{m} \bigl(T_{\mathit{ref}}(x_{i},t_{j}) - T(x_{i},t_{j})\bigr)^{2} $$
(11)

where n is the number of locations and m is the number of time steps, subject to the constraints below:

(12)

The reference temperature data for the inversion were obtained by the forward numerical simulation of a wall thinning defect of 10 mm radius and 1 mm depth in an aluminum plate of 1.7 mm thickness. Six points were selected on the surface of the plate and their temperature history was used for reconstructing the size of the defect. Temperatures were recorded at selected locations between the center of the coil and the inner radius of the coil, since this region is more sensitive to temperature changes. The total observation time of 10 s was divided into 0.1 s time steps. The upper and the lower bounds for the search domain during the GA inversion were selected as given in Table 2.

Table 2 Upper and lower bounds selected for the defect size
Full size table

The GA based inversion method starts with an initial solution set (population) of randomly assumed values of defect size (represented in binary format called chromosomes) within the range specified. Each candidate solution of the population undergoes a set of evolutionary processes like mating, crossover, mutation, etc., to generate offspring. Each step is called a generation. In each generation, the objective function (or fitness function) is evaluated and a few of the candidate solutions with the highest fitness value (or the lowest objective function) are preserved (elitism) while the others are replaced with new offspring. This process continues until the stopping criterion is met. The stopping criterion can be either the specified number of generations or a threshold value of the fitness function. The inversion is performed using the optimization tool box in MATLAB [3].

The evolution process can be summarized as shown in Fig. 2. The GA parameters used in the inversion procedure are given in Table 3.

Fig. 2
figure 2

Flow chart showing the inversion algorithm

Full size image
Table 3 GA parameters used for inversion
Full size table

3 Results and Discussion

3.1 Defect Radius Larger than Coil Inner Radius

In this case, the defect considered is having a radius greater than the coil inner radius (Fig. 1). Simulation studies were conducted for defects of different radii (r d ) and different depths (d d ). A sensitivity analysis was performed to determine the effect of variation of the defect dimensions (radius and depth) on the temperature profile at the point of observation. The inner radius of the coil was fixed at 5 mm and the radii of the defect were taken as 7.5 mm, 10 mm, 12.5 mm, and 15 mm. The thickness of the plate was 1.7 mm. The defect depths were 0.50 mm, 0.75 mm, 1.00 mm, 1.25 mm, and 1.5 mm. For each combination of the defect radius and defect thickness, the temperature profile at the point of observation is calculated and compared with no-defect case. The loop potential was 0.25 V with 900 Hz excitation frequency. Table 4 shows the percentage change in the peak temperature at the point of observation for different defect sizes when compared with no-defect case. As the size of the defect becomes larger, the sensitivity of peak temperature to the changes in the defect size becomes more. The temperature history of a couple of cases described in Table 4 is shown in Fig. 3.

Fig. 3
figure 3

Temperature history of the point of observation when the defect radius is greater than the coil inner radius (Coil radius=5 mm) for different defect depths: (a) defect radius=10 mm, (b) defect radius=15 mm

Full size image
Table 4 Percentage change in the peak temperature at the point of observation for different defect sizes when compared with no-defect case. Inner radius of the coil (r c )=5 mm. Plate thickness=1.7 mm
Full size table

The bounds used for the defect dimensions are given in Table 5.

Table 5 Upper and lower bounds of dimensions of the defect used for inversion
Full size table

The reconstructed values of the defect radius and defect depth are given in Table 6 along with the percentage change when compared with the reference dimensions. In this trial, no noise was introduced in the temperature data. It was possible to reconstruct the defect size with less than 5 % error in 50 generations. The convergence of the error function, for the trial with 50 generations, is given in Fig. 4.

Fig. 4
figure 4

Convergence of the error function during reconstruction of defect size without noise. Number of generations used is 50

Full size image
Table 6 Reconstructed values of defect size for different generations with percentage error, when the defect radius is larger than the coil radius
Full size table

The inversion was repeated by adding a random noise in the range ±0.5∘ to the reference temperature data. The reconstructed values of the defect dimensions after adding the numerical noise is given in Table 7. Even after incorporating a relatively high level of noise, the defects were reconstructed accurately with less than 5 % error.

Table 7 Reconstructed values of defect size for different generations with percentage error after adding a random noise in the range of ±0.5∘ to the reference temperature data
Full size table

3.2 Defect Radius Smaller than Coil Inner Radius

Here, the case of defect radius smaller than the coil inner radius is considered. The model used for the forward analysis is shown in Fig. 5. The coil inner radius was 19 mm and the defects of radii of 7.5 mm, 10 mm, 12.5 mm, and 15 mm were simulated with defect depths of 0.5 mm, 0.75 mm, 1 mm, 1.25 mm, and 1.5 mm in each case.

Fig. 5
figure 5

Model for the sensitivity analysis when the defect radius is smaller than the coil inner radius

Full size image

A sensitivity analysis was performed in this case also to find the influence of the defect size on the peak temperature at the point of observation. The percentage changes in the peak temperature at the point of observation for various defect sizes, when compared with a no-defect case, are given in Table 8. The sensitivity is considerably less than the case when the defect radius is more than the coil radius. This is because, the material above the defect does not involve in the heat generation process. Maximum heat is deposited under the coil, from where it is diffused in to the material. The temperature history of some typical cases is given in Fig. 6.

Fig. 6
figure 6

Temperature history of the point of observation when the defect radius is smaller than the coil inner radius for different defect depths: (a) defect radius=7.5 mm, (b) defect radius=10 mm, (c) defect radius=15 mm. Coil radius=19 mm

Full size image
Table 8 Percentage change in the peak temperature at the point of observation for different defect sizes when compared with no-defect case. Inner radius of the coil (r c )=19 mm. Plate thickness=1.7 mm
Full size table

The defect sizes were reconstructed using the temperature profiles of six points on the surface of the plate. The reference temperature profiles of the same points were obtained by the forward analysis with a defect of radius 10 mm and depth 1 mm. Table 9 shows the reconstructed values of defect sizes for different generations along with the percentage error when compared with the reference defect dimensions. The error in the reconstructed values is fairly high even without adding noise to the temperature data. This is due to the poor sensitivity of the temperature profile to the defect dimensions when the coil inner radius is larger compared to the defect radius. The error may come down with higher number of generations.

Table 9 Reconstructed values of defect size for different generations with percentage error, when the defect radius is smaller than the coil radius
Full size table

4 Summary

A GA based inversion method for the reconstruction of defect size (radius and depth) from the induction heating thermography data is described. Two cases of defect radii, one larger than the coil inner radius and the other smaller than the coil inner radius were considered. It was determined that for the case where the defect radius was larger than the coil radius, it was possible to determine the size of the defect, This has been attributed to the effect of the defect during heating process, since the coil is over the defect edge in this case. A sensitivity analysis was performed in each case to assess the influence of the defect size on the temperature history at the point of observation. The reference temperature history of selected six points with a defect of 10 mm radius and 1 mm depth was used for the inversion. Numerical studies were performed with and without noise. The method demonstrated its ability to reconstruct the defect sizes within 15 % error when the defect radius is larger than the coil inner radius. For the other case where defect radius is less than the coil inner radius, the error in reconstruction was around 20 %.

The smaller size of the coil would improve the sizing of the defects, but at an increased cost of scanning the part. This trade off will have to be considered along with the criticality of the component while deciding on the size of the coil. It is recommended that a coil of size of approximately 20 mm may be employed as a default coil size. The smallest size that is anticipated to be measured reliably will additionally depend on the resolution of the scanning. Regarding the computational time, in a Dell Precision 670 computer with 2 GB ram, 100 generations took around 35 hours to complete the inversion.

This paper is a proof-of-concept demonstration of the inversion of the TBET data for sizing of the defects in metals. The defects used here are isolated defects of the metal loss type (with local wall thinning). More complicated scenarios such as multiple defects, interaction of the adjacent defects etc., will be investigated in the future studies.