Robust Equilibrated Error Estimator for Diffusion Problems: Mixed Finite Elements in Two Dimensions

Abstract

This paper introduces and analyzes an equilibrated a posteriori error estimator for mixed finite element approximations to the diffusion problem in two dimensions. The estimator, which is a generalization of those in Braess and Schöberl (Math Comput 77:651–672, 2008) and Cai and Zhang (SIAM J Numer Anal 50(1):151–170, 2012), is based on the Prager–Synge identity and on a local recovery of a gradient in the curl free subspace of the $H(\text {curl})$-confirming finite element spaces. The resulting estimator admits guaranteed reliability, and its robust local efficiency is proved under the quasi-monotonicity condition of the diffusion coefficient. Numerical experiments are given to confirm the theoretical results.

1 Introduction

Let $\varOmega$ be a bounded, polygonal domain in $\mathfrak {R}^2$. Consider the following diffusion equation

$$\begin{aligned} -\nabla \cdot (A \nabla u) = f \quad \text {in} \quad \varOmega \end{aligned}$$

(1.1)

with boundary conditions

$$\begin{aligned} -A\nabla u \cdot \mathbf{n}= g_N \quad \text {on} \quad \varGamma _N \quad \text {and}\quad u = g_D \quad \text {on}\quad \varGamma _D, \end{aligned}$$

(1.2)

where $\varGamma _D$ and $\varGamma _N$ are Dirichlet and Neumann boundaries, respectively. We assume that $\varGamma _D$ is connected and non-empty, ${\overline{\varGamma }}_D \cup {\overline{\varGamma }}_N = \partial \varOmega$ and $\varGamma _D\cap \varGamma _N =\emptyset$. Let $\mathbf{n}= (n_1,n_2)^t$ be the unit outward vector normal to the boundary, and denote by $\mathbf{t}= (n_2,-n_1)^t$ its corresponding unit tangential vector. We shall use the standard notations and definitions for the Sobolev spaces. Let

$$\begin{aligned} H^1_{g,D}(\varOmega )=\{v\in H^1(\varOmega ):v=g_D \text { on }\varGamma _D \} \quad \text {and}\quad H^1_D(\varOmega )=H^1_{0,D}(\varOmega ). \end{aligned}$$

Then the corresponding variational problem of (1.1)–(1.2) is to find $u \in H^1_{g,D}(\varOmega )$ such that

$$\begin{aligned} a(u,\,v)\equiv (A\nabla u, \nabla v) = (f, v) - (g_N, v )_{\varGamma _N} \quad \forall \; v\in H^1_D(\varOmega ), \end{aligned}$$

(1.3)

where $(\cdot , \cdot )_{\omega }$ is the $L^2$ inner product on the set $\omega$. The subscript $\omega$ is omitted when $\omega =\varOmega$.

Introducing the flux variable

$$\begin{aligned} \varvec{\sigma }= -A\nabla u, \end{aligned}$$

(1.4)

it is easy to see that the flux satisfies the following equilibrium equation and boundary condition

$$\begin{aligned} \nabla \cdot \varvec{\sigma }=f \quad \text {in} \quad \varOmega \quad \text{ and }\quad \varvec{\sigma }\cdot \mathbf{n}= g_{_N} \quad \text {in} \quad \varGamma _{_N}. \end{aligned}$$

Let

$$\begin{aligned} H_{g,N}(\mathrm{div};\varOmega ) =\{\varvec{\tau }\in H(\mathrm{div};\varOmega ) :\varvec{\tau }\cdot \mathbf{n}= g_N \text { on }\varGamma _N \} \text { and } H_{N}(\mathrm{div};\varOmega ) = H_{0,N}(\mathrm{div};\varOmega ) , \end{aligned}$$

where $H(\mathrm{div};\varOmega )$ is the space of all square-integrable vector fields whose divergence is also square-integrable. Then the mixed weak formulation for problem (1.1)–(1.2) is to find $(\varvec{\sigma },\,u)\in H_{g,N}(\mathrm{div};\varOmega )\times L^2(\varOmega )$ such that

$$\begin{aligned} \left\{ \begin{array}{lclll} (A^{-1}\varvec{\sigma },\,\varvec{\tau })-(\nabla \cdot \varvec{\tau },\, u) &{}=&{} - ( \varvec{\tau }\cdot \mathbf{n}, g_D)_{\varGamma _D} \quad &{} \forall \,\, \varvec{\tau }\in H_N(\mathrm{div};\varOmega ),\\ (\nabla \cdot \varvec{\sigma }, \,v) &{}=&{} (f,\,v) &{}\forall \,\, v\in L^2(\varOmega ). \end{array}\right. \end{aligned}$$

(1.5)

For simplicity of presentation, we consider only triangular elements. Let $\mathcal{T}= \{K\}$ be a finite element partition of the domain $\varOmega$ that is regular, and denote by $h_K$ the diameter of the element K. Let $P_k(K)$ be the space of polynomials of degree less than or equal to $k\ge 0$ on element K. Assume that $f|_K \in P_{k}(K)$ for every $K \in \mathcal{T}$, and that A is a symmetric, positive definite piecewise constant matrix.

Denote the $H(\mathrm{div})$-conforming Raviart-Thomas (RT) and Brezzi-Douglas-Marini (BDM) finite element spaces by

$$\begin{aligned} RT_{_\mathcal{T}}&=\{\varvec{\tau }\in H(\mathrm{div}; \varOmega ) :\varvec{\tau }|_K \in P_k(K)^2 +\mathbf{x}P_k(K),\,\, \forall \, K\in \mathcal{T}\}, \\ \text { and } \,\, BDM_{_\mathcal{T}}&=\{\varvec{\tau }\in H(\mathrm{div}; \varOmega ) :\varvec{\tau }|_K \in P_{k+1}(K)^2, \,\,\forall \, K\in \mathcal{T}\}. \end{aligned}$$

Let

$$\begin{aligned} \varSigma _{_\mathcal{T}} = RT_{{_\mathcal{T}}} \, \text{ or } \, BDM_{{_\mathcal{T}}}, \quad \text{ and }\quad V_{_\mathcal{T}} = \{v \in L^2(\varOmega ) : v|_K \in P_k(K), \, \forall \, K\in \mathcal{T}\}. \end{aligned}$$

And for simplicity, we assume $g_N$ is piece-wisely defined polynomials such that it lies in the normal trace space of $\varSigma _{_\mathcal{T}}$. Then the mixed finite element method is to find $(\varvec{\sigma }_{_\mathcal{T}},\,u_{_\mathcal{T}}) \in \left( \varSigma _{_\mathcal{T}}\cap H_{g,N}(\mathrm{div};\varOmega ) \right) \times V_{_\mathcal{T}}$ such that

$$\begin{aligned} \left\{ \begin{array}{lclll} (A^{-1}\varvec{\sigma }_{_\mathcal{T}},\,\varvec{\tau })-(\nabla \cdot \varvec{\tau },\, u_{_\mathcal{T}}) &{}=&{}- ( \varvec{\tau }\cdot \mathbf{n}, g_D)_{\varGamma _D} \quad &{} \forall \,\, \varvec{\tau }\in \varSigma _{_\mathcal{T}} \cap H_{N}(\mathrm{div};\varOmega ) ,\\ (\nabla \cdot \varvec{\sigma }_{_\mathcal{T}},\, v) &{}=&{} (f,\,v)&{}\forall \,\, v\in V_{_\mathcal{T}}. \end{array}\right. \end{aligned}$$

(1.6)

1.1 Equilibrated Error Estimator

For the $H^1$-conforming finite element approximation, various equilibrated a posteriori estimators have been studied recently by many researchers (see [6, 8, 9, 17, 18, 21, 24, 27,28,29,30]). In [15], we presented a systematic study of the equilibrated a posteriori error estimator based on the Prager–Synge identity for the diffusion problem in (1.1)–(1.2) with an emphasis on the interface problem ($A=\alpha (x) \,I$ and $\alpha (x)$ being piecewise constants).

Let $u\in H^1_{g,D}(\varOmega )$ be the solution of (1.1)–(1.2), and denote the equilibrated subset of $H_{g,N}(\mathrm{div};\varOmega )$ by

$$\begin{aligned} \varSigma _N(f,g;\varOmega )=\{\varvec{\tau }\in H_{g,N}(\mathrm{div};\varOmega ) :\nabla \cdot \varvec{\tau }= f\,\,\text{ in }\,\,\varOmega \}. \end{aligned}$$

(1.7)

Then the well-known Prager–Synge identity [6, 8, 15, 26]

$$\begin{aligned} \Vert A^{1/2} \nabla (u - v)\Vert _0^2 + \Vert A^{1/2} \nabla u + A^{-1/2}\varvec{\tau }\Vert _0^2 = \Vert A^{1/2} \nabla v + A^{-1/2}\varvec{\tau }\Vert _0^2 \end{aligned}$$

(1.8)

holds for all $v\in H^1_{g,D}(\varOmega )$ and all $\varvec{\tau }\in \varSigma _N(f,g;\varOmega )$. (1.8) follows easily from the orthogonality of quantities $A^{1/2} \nabla (u - v)$ and $A^{1/2} \nabla u + A^{-1/2}\varvec{\tau }$ with respect to the $L^2$ inner product.

Remark 1.1

For simplicity of presentation, we assume that all data, $f, \, g_{_D}$, and $g_{_N}$, are piecewise polynomials of proper degrees so that Prager–Synge identity (1.8) may be used and that data oscillations do not appear in the error estimator. For non-polynomial data, Prager–Synge identity (1.8) may be modified for constructing estimator with data oscillation terms. For example, when only f is not a polynomial, Prager–Synge identity becomes

$$\begin{aligned} \Vert A^{1/2} \nabla (u - v)\Vert _0^2 + \Vert A^{1/2} \nabla u + A^{-1/2}\varvec{\tau }\Vert _0^2 = \Vert A^{1/2} \nabla v + A^{-1/2}\varvec{\tau }\Vert _0^2 +2(v-u,\,f-Q_kf) \end{aligned}$$

for all $\varvec{\tau }\in \varSigma _{_\mathcal{T}}\cap \varSigma _N(Q_kf, g;\varOmega )$, where $Q_k$ is the local $L^2$ projection onto piecewise $P_k$.

For the conforming finite element approximation $u_{_\mathcal{T}}^c\in H^1_{g,D}(\varOmega )$, (1.8) with $v=u_{_\mathcal{T}}^c$ implies

$$\begin{aligned} \Vert A^{-1/2}\nabla (u-u_{_\mathcal{T}}^c )\Vert _0 \le \xi (\varvec{\tau }) := \Vert A^{1/2}\nabla u_{_\mathcal{T}}^c +A^{-1/2} \varvec{\tau }\Vert _0, \quad \forall \,\, \varvec{\tau }\in \varSigma _N(f,g;\varOmega ). \end{aligned}$$

(1.9)

This indicates that for any $\varvec{\tau }\in \varSigma _N(f,g;\varOmega )$, $\xi (\varvec{\tau })$ is a reliable estimator with the reliability constant being one. Estimators with such guaranteed reliability may be used for error control on pre-asymptotic meshes, that is difficult, but important for reliability of computer simulations of computationally challenging problems. To recover a flux ${\hat{\varvec{\sigma }}}_{_\mathcal{T}}$ in a finite-dimensional subset of $\varSigma _N(f,g;\varOmega )$ from the numerical flux $-A\nabla u_{_\mathcal{T}}^c$, we localized the problem through a partition of unity as in [8] and then solve local minimization problems over vertex patches. Local minimization introduced in [15] is necessary to ensure the robustness of the error estimator with respect to the coefficients of the underlying problem. Efficiency of the resulting local indicator is proved by using the stability bound of the saddle point formulation of the local minimization problem and the efficiency bound of the explicit residual error estimator.

For the mixed finite element approximation $\varvec{\sigma }_{_\mathcal{T}} \in \varSigma _N(f,g;\varOmega )$, (1.4) and (1.8) with $\varvec{\tau }=\varvec{\sigma }_{_\mathcal{T}}$ imply

$$\begin{aligned} \Vert A^{-1/2} (\varvec{\sigma }- \varvec{\sigma }_{_\mathcal{T}}) \Vert _0 \le \Vert A^{1/2} \nabla v + A^{-1/2}\varvec{\sigma }_{_\mathcal{T}} \Vert _0, \quad \forall \,\, v\in H^1_{g,D}(\varOmega ). \end{aligned}$$

(1.10)

This indicates that for a recovered numerical solution ${\hat{u}}_{_\mathcal{T}}$ in a finite-dimensional subset of $H^1_{g,D}(\varOmega )$, $\Vert A^{1/2} \nabla {\hat{u}}_{_\mathcal{T}} + A^{-1/2}\varvec{\sigma }_{_\mathcal{T}} \Vert _0$ is a guaranteed reliable error estimator. Such an idea will be explored in a forthcoming paper. In this paper, we study an error estimator based on a recovery of the gradient in a proper finite element space. To this end, define the curl of a two-dimensional vector field $\varvec{\tau }= (\varvec{\tau }_1,\varvec{\tau }_2)^t$ by

$$\begin{aligned} \nabla \times \varvec{\tau }= \partial _x \varvec{\tau }_2 -\partial _y \varvec{\tau }_1, \end{aligned}$$

and denote by $\nabla ^{\perp }$ the formal adjoint of the curl: $\nabla ^{\perp }v = (\partial _y v, -\partial _x v)^t$.

Let

$$\begin{aligned} H_{g,D}({\text {curl}};\varOmega ) := \{ \varvec{\tau }\in H({\text {curl}}; \varOmega ) : \varvec{\tau }\cdot \mathbf{t}= \nabla g_D \cdot \mathbf{t}\text { on } \varGamma _D \}, \end{aligned}$$

where $H({\text {curl}};\varOmega )$ is the space of all square-integrable vector fields whose curl is also square-integrable. Note that if $\varGamma _D$ is connected, then $\{ \nabla v : v\in H^1_{g,D}(\varOmega ) \}$ is equal to the curl free subset of $H_{g,D}({\text {curl}};\varOmega )$:

$$\begin{aligned} \mathring{H}_{g,D}({\text {curl}};\varOmega ) := \{ \varvec{\tau }\in H_{g,D}({\text {curl}}; \varOmega ): \nabla \times \varvec{\tau }=0 \}, \end{aligned}$$

which, together with (1.10), yields

$$\begin{aligned} \Vert A^{-1/2} (\varvec{\sigma }- \varvec{\sigma }_{_\mathcal{T}}) \Vert \le \Vert A^{1/2}\varvec{\rho }+ A^{-1/2}\varvec{\sigma }_{_\mathcal{T}}\Vert , \quad \forall \,\, \varvec{\rho }\in \mathring{H}_{g,D}({\text {curl}};\varOmega ). \end{aligned}$$

(1.11)

For the rotation matrix $\chi = \left( \begin{array}{cc} 0 &{} 1 \\ -1 &{} 0 \end{array}\right)$, it is easily to see that

$$\begin{aligned} \nabla \times \varvec{\rho }= \nabla \cdot \left( \chi \,\varvec{\rho }\right) \quad \text{ and }\quad \varvec{\rho }\cdot \mathbf{t}= \left( \chi \,\varvec{\rho }\right) \cdot \mathbf{n}, \end{aligned}$$

which, together with (1.11), implies

$$\begin{aligned} \Vert A^{-1/2} (\varvec{\sigma }- \varvec{\sigma }_{_\mathcal{T}}) \Vert \le \Vert A^{1/2}\chi ^{t}\,\varvec{\tau }+ A^{-1/2}\varvec{\sigma }_{_\mathcal{T}}\Vert , \quad \forall \,\, \varvec{\tau }\in \varSigma _D(0, h;\varOmega ) \end{aligned}$$

(1.12)

with $h=\nabla g_{_D}\cdot \mathbf{t}$, where $\varSigma _D(0,h;\varOmega )$ is defined similarly in (1.7), i.e.,

$$\begin{aligned} \varSigma _D(0, h;\varOmega ):= \{\varvec{\tau }\in H(\mathrm{div};\varOmega ) :\nabla \cdot \varvec{\tau }=0 \text{ in } \varOmega , \varvec{\tau }\cdot \mathbf{n}= \nabla g_{_D}\cdot \mathbf{t} \text{ on } \varGamma _D \}. \end{aligned}$$

(1.12) is identical to (1.9) with different data. Hence, the local flux recovery procedure developed in [15] may be applied directly, and robust efficiency of the resulting local indicator may be established in a similar fashion. However, the local flux recovery procedure needs to solve minimization problems over vertex patches with two constraints: the equilibrium equation and the jump condition across interior edges. This is due to the fact that local error flux is computed in [15] which also makes the robust efficiency analysis quite complicated. In this paper, we will simplify the efficiency analysis as well as the local recovery procedure by directly computing the flux instead of the error flux as in [8, 15]. Note that the $H({\text {curl}})$-conforming Nédélec finite element spaces are basically rotations of the $H(\mathrm{div})$-conforming RT or BDM finite element spaces in two dimensions. In this paper, the numerical scheme is presented based on (1.11) by recovering the gradient in the Nédélec finite element spaces. Moreover, under the suitable assumption on the distribution of the diffusion coefficients, the robust efficiency bound is proved by analyzing the stability of the saddle point problem of the local error gradient.

For the conforming finite element approximation to the interface problem, robust error estimators have been studied by Bernardi and Verfürth [4] and Petzoldt [25] for the residual-based estimator, Luce and Wohlmuth [21] for an equilibrated estimator on a dual mesh, and by us [13] for the recovery-based error estimator. Ainsworth in [1, 2] studied robust error estimators for nonconforming and mixed methods, respectively. Robust error estimators for locally conserved methods were studied by Kim [20]. We also studied robust recovery-based estimators for lowest order nonconforming, mixed, and discontinuous Galerkin methods (see [12, 14]) via the $L^2$ recovery. In [11], we proved the robustness of residual a posteriori error estimators for nonconforming and discontinuous Galerkin methods without the assumption on the distribution of coefficients. Equilibrated a posteriori error estimator for the interior penalty discontinuous Galerkin method is studied in [7].

For the Poisson equation, polynomial-degree-robust analysis for the mixed discretizations is discussed in [19]. The two-dimensional case is purely viewed as a rotation of of $H(\mathrm{div})$ case there. The analysis in [19] is also focused on the robustness with respect to the polynomial degree while the robustness thus some explicit construction is used in the proof, while our analysis is more focused on the robustness with respect to the coefficients where explicit construction is non-robust.

In this paper, only two dimensional case is analyzed. The equilibrated construction in the three dimensional case, the conforming mixed problem (2.11) can be constructed identically. The analysis through the broken version will be more complicated, since the trace spaces of the Néélec finite element spaces are nontrivial, see [16]. One possible way of the analysis is given in the Remark 4.11. The three dimensional case is the topic of our on-going research.

The paper is organized as follows. Section 2 describes a localization of the gradient via a partition of unity. The a posteriori error estimator is presented in Sect. 3. Section 4 establishes the local efficiency bound and Sect. 5 provides numerical results for a benchmark test problem.

2 Local Gradient Recovery

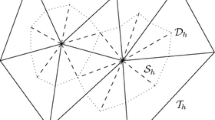
The identity in (1.11) suggests that one should recover an approximated gradient in a finite-dimensional subset of $\mathring{H}_{g,D}({\text {curl}};\varOmega )$ that also minimize the quantity $\Vert A^{1/2}\varvec{\tau }+ A^{-1/2}\varvec{\sigma }_{_\mathcal{T}}\Vert$. This requires solving a global minimization problem. Instead, we adopt the idea of localization through a partition of the unity using the conforming linear finite element basis functions as in [8, 15]. Differing from that of [8, 15], local gradients are computed through local minimization problems with only curl constraint.

To this end, denote the set of vertices of the triangulation $\mathcal{T}$ by

$$\begin{aligned} \mathcal{N}:=\mathcal{N}_{I}\cup \mathcal{N}_{D}\cup \mathcal{N}_{N}, \end{aligned}$$

where $\mathcal{N}_{I}$ is the set of interior vertices, $\mathcal{N}_{D}$ and $\mathcal{N}_{N}$ are the sets of boundary vertices on $\varGamma _D$ and ${\overline{\varGamma }}_N$, respectively. Note that $z\in {\overline{\varGamma }}_N\cap {\overline{\varGamma }}_D$ is in $\mathcal{N}_{N}$ but not $\mathcal{N}_{D}$. Denote by $\phi _{z}(\mathbf{x})$ the standard linear Lagrange basis function associated with the vertex $z\in \mathcal{N}$, then $\{\phi _z(\mathbf{x})\}_{z\in \mathcal{N}}$ forms a partition of the unity in $\varOmega$. Hence, the true gradient, $\varvec{\rho }= \nabla u$, has the following decomposition

$$\begin{aligned} \varvec{\rho }=\displaystyle \sum _{z\in \mathcal{N}} (\phi _{z} \varvec{\rho })=\displaystyle \sum _{z\in \mathcal{N}} \varvec{\rho }_z \quad \text {with}\quad \varvec{\rho }_{z} =\phi _{z} \varvec{\rho }. \end{aligned}$$

(2.1)

For any vertex $z\in \mathcal{N}$, denote by $\omega _z$ the interior of $\hbox {supp }(\phi _z(\mathbf{x}))$, which is the vertex patch, and by $\mathcal{T}_{z} = \{K\in \mathcal{T}: \,\omega _{z}\cap K \ne \emptyset \}$ its triangulation. For any $K\in \mathcal{T}_{z}$, $\nabla \times \varvec{\rho }_z = - \nabla ^{\perp }\phi _{z} \cdot \nabla u$, replacing $\nabla u$ by its numerical approximation $-A^{-1}\varvec{\sigma }_{_\mathcal{T}}$, we have

$$\begin{aligned} \nabla \times \varvec{\rho }_z \quad \text{ is } \text{ approximately } \quad \nabla ^{\perp }\phi _{z} \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}) \quad \text{ on } \, K. \end{aligned}$$

Value of the tangential component of $\varvec{\rho }_z$ on a boundary edge F of the vertex patch $\omega _z$ is determined by either the fact that $\phi _z$ vanishes on F or the Dirichlet boundary condition of the solution u when $F\subset \varGamma _D$ and $\phi _z|_F\not =0$. To precisely describe boundary conditions of $\varvec{\rho }_z$, we first introduce edge notations. To this end, denote the set of edges of the triangulation $\mathcal{T}$ by

$$\begin{aligned} \mathcal{E}:= \mathcal{E}_{I}\cup \mathcal{E}_{D}\cup \mathcal{E}_{N}, \end{aligned}$$

where $\mathcal{E}_{I}$ is the set of interior element edges, $\mathcal{E}_{D}$ and $\mathcal{E}_{N}$ are the sets of boundary edges on $\varGamma _D$ and $\varGamma _N$, respectively. Denote by ${\tilde{\mathcal{E}}}_{z}$ the set of all edges having $z\in \mathcal{N}$ as the common vertex. Denote the set of all edges of $\mathcal{T}_z$ by

$$\begin{aligned} \mathcal{E}_{z} = \{ F \in \mathcal{E}:\, F \cap {\overline{\omega }}_{z} \ne \emptyset \} = \mathcal{E}_{I, z}\cup \mathcal{E}_{b, z}, \end{aligned}$$

where $\mathcal{E}_{I, z}$ and $\mathcal{E}_{b, z}$ are the sets of the respective interior and boundary edges of $\mathcal{T}_z$. Let

$$\begin{aligned} \mathcal{E}_{0,z} = \left\{ \begin{array}{llll} \mathcal{E}_{b,z} &{} \text {if} &{}z\in \mathcal{N}_{I},\\ \{ F\in \mathcal{E}_{b,z}: F\not \in \partial \varOmega \}&{} \text {if} &{}z\in \mathcal{N}_{D}\cup \mathcal{N}_{N}. \end{array} \right. \end{aligned}$$

It is then easy to see that $\varvec{\rho }_z\cdot \mathbf{t}= 0$ on $F\in \mathcal{E}_{0,z}$. For $z\in \mathcal{N}_D\cup \mathcal{N}_N$, we have $\varvec{\rho }_z\cdot \mathbf{t}= \phi _z\nabla g_D \cdot \mathbf{t}_F$ on $\mathcal{E}_{D, z}= \mathcal{E}_{b, z}\cap {\tilde{\mathcal{E}}}_{z} \cap \mathcal{E}_D$.

Thus, on the vertex patch $\omega _z$, we wish to find a ${\hat{\varvec{\rho }}}_{_\mathcal{T},z}$ in a finite dimensional subspace of $H({\text {curl}};\omega _z)$ satisfying the curl constraint on each $K\in \mathcal{T}_z$

$$\begin{aligned} \nabla \times {\hat{\varvec{\rho }}}_{_\mathcal{T},z} = \nabla ^{\perp }\phi _{z} \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}) \end{aligned}$$

and the following boundary conditions

$$\begin{aligned} {\hat{\varvec{\rho }}}_{_\mathcal{T},z}\cdot \mathbf{t}= \phi _z\nabla g_D \cdot \mathbf{t}\,\, \text{ on } F\in \mathcal{E}_{D,z}\,\, \text{ if } z\in \mathcal{N}_D\cup \mathcal{N}_N \quad \text{ and }\quad {\hat{\varvec{\rho }}}_{_\mathcal{T},z} \cdot \mathbf{t}= 0 \,\, \text{ on } F\in \mathcal{E}_{0, z}.\nonumber \\ \end{aligned}$$

(2.2)

Since for $\varvec{\sigma }_{_\mathcal{T}} |_K \in P_{k+1}(K)$, $\nabla ^{\perp }\phi _{z} \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}})|_K \in P_{k+1}(K)$, the local finite element space we used is the Nédélec finite element space of the first type ($\textsf {ND}$) [22, 23]. The $\textsf {ND}$ element on an element K is defined as $\textsf {ND}_k(K) = P_k(K)^2 +(x_2,-x_1)^t P_k(K)$. For an F, an edge of K, the trace space is $\{\varvec{\tau }\cdot \mathbf{t}_F : \varvec{\tau }\in \textsf {ND}_{k}(K)\}=P_{k}(F)$, and $\nabla \times (\textsf {ND}_{k}(K))=P_{k}(K)$, for a $K\in \mathcal{T}$. Thus at least $\textsf {ND}_{k+1}$ is a necessary to handle the $\nabla ^{\perp }\phi _{z} \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}})$ term.

For simplicity, we assume $g_D|_F \in P_{k+2}(F)$ for all $F\in \mathcal{E}_D$. to ensure that $\nabla g_D \cdot \mathbf{t}$ lies in the tangential trace space of the global space of $\textsf {ND}_{k+1}$. Let $\varPi ^{k+1}_F$ be the $L^2$ projection on to $P_{k+1}(F)$, define

$$\begin{aligned} \textsf {ND}_{0,z}= & {} \left\{ \varvec{\tau }\in H(\text {curl};\omega _z) : \begin{array}{llll} \varvec{\tau }|_K \in \textsf {ND}_{k+1}(K)\,\, \forall \, K \in \mathcal{T}_{z} \\ \varvec{\tau }\cdot \mathbf{t}|_F = 0\,\, \forall \, F\in \mathcal{E}_{0, z}, \\ \varvec{\tau }\cdot \mathbf{t}|_F = \varPi ^{k+1}_F(\phi _z \nabla g_D \cdot \mathbf{t}_F) \text{ on } \\ F\in \mathcal{E}_{D,z}, \text{ if } z\in \mathcal{N}_D\cup \mathcal{N}_N \end{array} \right\} ,\\ \text{ and } {{\mathcal {Y}}}_z= & {} \left\{ \varvec{\tau }\in \textsf {ND}_{0,z} : \nabla \times \varvec{\tau }= (\nabla ^{\perp }\phi _{z}) \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}) \right\} . \end{aligned}$$

Here, we also need to check the compatibility condition of ${{\mathcal {Y}}}_z$ to see if it is well defined:

$$\begin{aligned} \int _{\omega _z} \nabla \times \varvec{\tau }dx = \int _{\partial \omega _z} \varvec{\tau }\cdot \mathbf{t}ds \quad \forall \, z\in \mathcal{N}_I\cup \mathcal{N}_D. \end{aligned}$$

This is true since

$$\begin{aligned} (A^{-1}\varvec{\sigma }_{_\mathcal{T}}, \nabla ^{\perp }\phi _z)_{\omega _z} = - (\nabla u, \nabla ^{\perp }\phi _z)_{\omega _z}=(\nabla u\cdot \mathbf{t},\phi _z)_{0,\omega _z} =\sum _{F\in \mathcal{E}_{D,z}}(\nabla g_D \cdot \mathbf{t},\phi _z)_{F}.\nonumber \\ \end{aligned}$$

(2.3)

For $z\in \mathcal{N}_N$, since there will always be some part of the $\omega _z$ without specified boundary condition, the compatibility condition is not a problem.

Since $\varvec{\sigma }_{_\mathcal{T}} \in \varSigma _{_\mathcal{T}}$, so $\phi _z A^{-1}\varvec{\sigma }_{_\mathcal{T}} |_K\in P_{k+2}(K)^2$, it seems natural to choose the following minimization:

$$\begin{aligned} \varvec{\rho }_{{_\mathcal{T}},z} = \arg \min _{\varvec{\tau }\in {{\mathcal {Y}}}_z^{k+2}}\Vert A^{1/2}(\varvec{\tau }+A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z)\Vert _{0,\omega _z} \quad z\in \mathcal{N}\quad \text{ and }\quad \varvec{\rho }_{{_\mathcal{T}}} = \sum _{z\in \mathcal{N}} \varvec{\rho }_{{_\mathcal{T}},z}, \end{aligned}$$

where the space ${{\mathcal {Y}}}_z^{k+2}$ is the space replacing $\textsf {ND}_{k+1}$ to $\textsf {ND}_{k+2}$ in the definition of ${{\mathcal {Y}}}_z$ and removing the projection on the Dirichlet boundary. It is big enough to contain $A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z$. But as discussed in [8, 15] and later in this paper, it is possible to use spaces with one degree lower ${{\mathcal {Y}}}_z$ to recover the local and global gradient.

Let the element interpolation $\varPi _{K}^{nd}$ be the Nédélec interpolation to $\textsf {ND}_{k+1}(K)$. For $\varvec{\tau }\in \{\varvec{\tau }\in L^t(K)^2:\nabla \times \varvec{\tau }\in L^t(K)\}$ for some $t>2$, define

$$\begin{aligned} ( (\varvec{\tau }-\varPi ^{nd}_{K} \varvec{\tau })\cdot \mathbf{t}, p )_{F}= & {} 0, \quad \forall \, p \in P_{k+1}(F), \forall F\in \partial K, k\ge 0, \end{aligned}$$

(2.4)

$$\begin{aligned} (\varvec{\tau }-\varPi ^{nd}_{K}\varvec{\tau }, \nabla ^{\perp }q)_K= & {} 0, \quad \forall \, q \in P_{k+1}(K), k\ge 1, \end{aligned}$$

(2.5)

Define the interpolation on a patch on the whole $\varOmega$ element-wisely by $\varPi ^{nd} \varvec{\tau }|_K := \varPi _{K}^{nd} \varvec{\tau }$.

The corresponding economical minimization problem is:

Local$H({\text {curl}})$conforming minimization problem Find $\varvec{\rho }_{{_\mathcal{T}},z}\in {{\mathcal {Y}}}_z$,

$$\begin{aligned} \varvec{\rho }_{{_\mathcal{T}},z} = \arg \min _{\varvec{\tau }\in {{\mathcal {Y}}}_z} \Vert A^{1/2}(\varvec{\tau }+\varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z))\Vert _{0,\omega _z} \quad z\in \mathcal{N}. \end{aligned}$$

(2.6)

Let

$$\begin{aligned} {\widehat{\textsf {ND}}}_{0,z}&: =&\left\{ \varvec{\tau }\in H(\text {curl};\omega _z) : \begin{array}{llll} \varvec{\tau }|_K \in \textsf {ND}_{k+1}(K)\,\, \forall \, K \in \mathcal{T}_{z} \\ \varvec{\tau }\cdot \mathbf{t}|_F = 0\,\, \forall \, F\in \mathcal{E}_{0, z} \\ \varvec{\tau }\cdot \mathbf{t}|_F = 0 \text{ on } F\in \mathcal{E}_{D,z}, \text{ if } z\in \mathcal{N}_D\cup \mathcal{N}_N \end{array} \right\} , \end{aligned}$$

(2.7)

$$\begin{aligned} P_z:= & {} \{ v \in L^{2}(\omega _{z}):\, v|_{K} \in P_{k}(K)\,\, \forall \, K \in \mathcal{T}_{z}\}, \end{aligned}$$

(2.8)

$$\begin{aligned} {\overline{P}}_z:= & {} \{ v \in L^{2}(\omega _{z}):\, v|_{K} \in P_{k}(K)\,\, \forall \, K \in \mathcal{T}_{z}, (1, v)_{0,\omega _z} = 0 \}. \end{aligned}$$

(2.9)

Let

$$\begin{aligned} Q_z = \left\{ \begin{array}{lll} {\overline{P}}_z &{} z\in \mathcal{N}_I, \\ P_z &{} z\in \mathcal{N}_D\cup \mathcal{N}_N. \end{array}\right. \end{aligned}$$

(2.10)

The constraint minimization problem (2.6) is equivalent to the following saddle point formulation:

Local$H({\text {curl}})$conforming saddle point problem Find $(\varvec{\rho }_{{_\mathcal{T}},z}, w_{z}) \in {\textsf {ND}}_{0,z}\times Q_z$ such that

$$\begin{aligned} \left\{ \begin{array}{llll} (A\varvec{\rho }_{{_\mathcal{T}},z},\,\varvec{\tau })_{\omega ,z} + (\nabla \times \varvec{\tau },\, w_z)_{\omega _z} &{}=&{} -(A\varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}}\phi _z),\,\varvec{\tau })_{\omega _z} &{} \forall \, \varvec{\tau }\in {\widehat{\textsf {ND}}}_{0,z} , \\ (\nabla \times \varvec{\rho }_{{_\mathcal{T}},z},\, v)_{\omega _z} &{}=&{} (\nabla ^{\perp }\phi _{z} \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}), v)_{\omega _z} &{} \forall \; v \in Q_z. \end{array} \right. \qquad \end{aligned}$$

(2.11)

The existence and uniqueness of the above problem can be proved by the standard mixed finite element theory or can be shown by the analysis of its equivalent local broken $H(\text{ curl })$ saddle point problem in Sect. 4. Note that for an interior node, it is corresponding to a pure Neumann problem, thus the zero average condition is needed for the space $Q_z$ to guarantee the uniqueness.

3 A Posteriori Error Estimator

With the local gradient $\varvec{\rho }_{{_\mathcal{T}},z}\in {{\mathcal {Y}}}_z$ computed in the previous section. Let

$$\begin{aligned} \varvec{\rho }_{{_\mathcal{T}},K} = \sum _{z\in \mathcal{N}_{K}} \varvec{\rho }_{{_\mathcal{T}},z} \quad \text {and}\quad \varvec{\rho }_{{_\mathcal{T}}} = \sum _{z\in \mathcal{N}} \varvec{\rho }_{{_\mathcal{T}},z}, \end{aligned}$$

Lemma 3.1

The recovered gradient $\varvec{\rho }_{{_\mathcal{T}}}$ is in $\mathring{H}_{g,D}({\text {curl}};\varOmega )$.

Proof

On each $K \in \mathcal{T}$, by the facts that $\sum _{z\in \mathcal{N}_{K}}\phi _{z}(\mathbf{x}) =1$,

we have

$$\begin{aligned} \nabla \times \varvec{\rho }_{_\mathcal{T}}|_{K} = \sum _{z\in \mathcal{N}_{K}} \left( \nabla \times \varvec{\rho }_{{_\mathcal{T}},z}\right) = \sum _{z\in \mathcal{N}_{K}} \nabla ^{\perp }\phi _z \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}) = \nabla ^{\perp }1 \cdot (A^{-1}\varvec{\sigma }_{_\mathcal{T}}) = 0. \end{aligned}$$

For an interior edge $F\in \mathcal{E}_I$, since all $\varvec{\rho }_{{_\mathcal{T}},z}$ is in $H({\text {curl}}; \omega _z)$ with continuous tangential components, then

$$\begin{aligned}{}[\![ \varvec{\rho }_{_\mathcal{T}}\cdot \mathbf{t}]\!]_{F} =\sum _{z\in \mathcal{N}_F} [\![ \varvec{\rho }_{{_\mathcal{T}},z}\cdot \mathbf{t}]\!]_{F} = 0,\quad \forall F\in \mathcal{E}_I. \end{aligned}$$

For a Dirichlet edge $F\in \mathcal{E}_D$,

$$\begin{aligned} \varvec{\rho }_{_\mathcal{T}}\cdot \mathbf{t}|_F= & {} \sum _{z\in \mathcal{N}_F}\varvec{\rho }_{{_\mathcal{T}},z}\cdot \mathbf{t}|_{F} = \sum _{z\in \mathcal{N}_F} \varPi ^{k+1}_F (\phi _z (\nabla g_D \cdot \mathbf{t}|_F))\\= & {} \varPi ^{k+1}_F(\nabla g_D \cdot \mathbf{t}|_F) =\nabla g_D \cdot \mathbf{t}|_F, \forall F\in \mathcal{E}_D. \end{aligned}$$

The lemma is proved. $\square$

Define the local indicators and the error estimator by

$$\begin{aligned} \eta _{z}= & {} \Vert A^{1/2} (\varvec{\rho }_{{_\mathcal{T}},z} + \varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}}\phi _z))\Vert _{0,\omega _z} ,\quad \forall z\in \mathcal{N}\end{aligned}$$

(3.1)

$$\begin{aligned} \eta _{K}= & {} \Vert A^{1/2} (\varvec{\rho }_{{_\mathcal{T}},K} + A^{-1}\varvec{\sigma }_{_\mathcal{T}})\Vert _{0,K} , \quad \forall K\in \mathcal{T}, \end{aligned}$$

(3.2)

$$\begin{aligned} \text {and}\quad \eta= & {} \Vert A^{1/2} (\varvec{\rho }_{{_\mathcal{T}}} + A^{-1}\varvec{\sigma }_{_\mathcal{T}})\Vert _{0,\varOmega }, \end{aligned}$$

(3.3)

respectively.

Remark 3.2

From (3.1), it is clear that the interpolation $\varPi ^{nd}$ is necessary, otherwise, even in the ideal case that the numerical solution $\varvec{\sigma }_{_\mathcal{T}}$ is exact: $\varvec{\sigma }_{_\mathcal{T}} = \varvec{\sigma }$ and $\nabla u|_K = -A^{-1}\varvec{\sigma }_{_\mathcal{T}}|_K \in P_{k+1}(K)^2$, $\eta _z$ without the interpolation will not be zero since $\varvec{\rho }_{{_\mathcal{T}},z}|_K \in \textsf {ND}_{k+1}(K)$ is not big enough to contain all $A^{-1}\varvec{\sigma }_{_\mathcal{T}}\phi _z|_K \in P_{k+2}(K)^2$. To remove this interpolation, one can choose Nédélec finite element spaces with higher order at the cost of solving a slightly larger problem locally.

Theorem 3.3

(Reliability) The error estimator $\eta$ is reliable with the reliability constant being one; i.e.,

$$\begin{aligned} \Vert A^{1/2}\nabla u + A^{-1/2}\varvec{\sigma }_{_\mathcal{T}} \Vert _{0,\varOmega } \le \eta . \end{aligned}$$

(3.4)

Proof

The conclusion is obvious from (1.10), (1.11) and Lemma 3.1. $\square$

4 Robust Efficiency for the Case $A = \alpha I$

In this section, we establish robust efficiency bounds for the local indicators $\eta _{_K}$ and $\eta _{z}$ for the interface problem $A = \alpha (x) I$ with $\alpha$ being a given scalar, piecewise positive constant function with respect to the triangulation $\mathcal{T}$. For the full tensor case, if we assume that the ratio of the largest and the smallest eigenvalues on each element K is bounded with a constant independent of location x, the generalization is easy.

Similar to the analysis we did in [15], the robust efficiency is analyzed though a stability estimate of the mixed finite element problem of the error gradient in (4.14) which relates the local indicator to the local discrete dual norm of local representation of the error. Then the dual norm is connected with the classical residual type of error indicator whose efficiency is well known.

In order to prove the robustness of the indicators, we show that the stability estimate of (4.14) is independent of jumps of the coefficients $\alpha$. This is done by employing the abstract framework of the saddle-point problem (see, e.g., [5]) and by choosing proper mesh- and $\alpha$-dependent norms. Earlier analysis on the mixed methods using mesh-dependent norms can be found in Babuška, Osborn, and Pitkäranta [3] and Braess and Verfürth [10].

This section is organized as follows: we first introduce local edge notations including jumps and weighted averages in Sect. 4.1. In Sect. 4.2, local element residual and jumps and an identity which plays important role in the efficiency proof are introduced. We reformulate the minimization problem (2.6) and its corresponding saddle point problem (2.11) as a problem of the local error gradient in broken-$H(\text {curl};\omega _z)$ space for easier efficiency analysis in Sect. 4.3. The robust stability of the mixd formulation of the local error gradient is analyzed in Sect. 4.4. Finally in Sect. 4.5 the robust local efficiency is proved by comparison with known residual-type of error estimator.

4.1 Local Edge Notations

In order to define the equivalent broken mixed formulation, we need introduce more notations.

Let

$$\begin{aligned} \mathcal{E}_{N, z}= \mathcal{E}_{b, z}\cap {\tilde{\mathcal{E}}}_{z} \cap \mathcal{E}_N. \end{aligned}$$

Note that when $z\in \mathcal{N}_D$, $\mathcal{E}_{D, z}$ is meaningful. For $z\in \mathcal{N}_N$ and z is an interior point of $\varGamma _N$, only $\mathcal{E}_{N, z}$ is meaningful. While if $z\in \mathcal{N}_N$ and z is an intersection point of $\varGamma _N$ and $\varGamma _D$, both $\mathcal{E}_{D, z}$ and $\mathcal{E}_{N, z}$ appear. In other cases, $\mathcal{E}_{D, z}$ or $\mathcal{E}_{N, z}$ is empty.

Define the edge sets for non-zero jump terms (used for error gradient defined later) and zero tangential component terms as follow, respectively:

$$\begin{aligned} \mathcal{E}_{j,z} = \left\{ \begin{array}{llll} \mathcal{E}_{I,z} &{} \text {if} &{} z\in \mathcal{N}_{I},\\ \mathcal{E}_{I,z} \cup \mathcal{E}_{D, z} &{} \text {if} &{}z\in \mathcal{N}_{D},\\ \mathcal{E}_{I,z} \cup \mathcal{E}_{D, z} &{} \text {if} &{}z\in \mathcal{N}_N \text{ and } z\in {\overline{\varGamma }}_D\cap {\overline{\varGamma }}_N, \end{array} \right. \end{aligned}$$

Note that for $z\in \mathcal{N}_N$, Neumann edges belong to neither sets.

For each $F \in \mathcal{E}$, denote by $h_{F}$ the length of the edge F and by $\mathbf{n}_F$ a unit vector normal to F. Let $K_F^{-}$ and $K_F^{+}$ be the two elements sharing the common edge/face F such that the unit outward normal vector of $K_F^{-}$ coincides with $\mathbf{n}_F$. When $F \in \mathcal{E}_{D}\cup \mathcal{E}_{N}$, $\mathbf{n}_{F}$ is the unit outward vector normal to $\partial \varOmega$ and denote by $K_F^{-}$ the element having the edge F. For a function v defined on $K^{-}_F\cup K^{+}_F$, denote its traces on F by $v|_F^{-}$ and $v|_F^{+}$, respectively. The jump over the edge F is denoted by

$$\begin{aligned}{}[\![ v]\!]_F := \left\{ \begin{array}{rll} v|^{-}_F - v|_F^{+} \quad &{} F\in \mathcal{E}_I,\\ v|^{-}_F \quad &{} F \in \mathcal{E}_{D}\cup \mathcal{E}_{N}. \end{array} \right. \end{aligned}$$

We will follow the above definition of the jump on a general domain $\omega$ with a mesh $\mathcal{T}$ on it. When there is no ambiguity, the subscript or superscript F in the designation of the jump will be dropped.

For $A = \alpha (x) I$ with $\alpha$ being a given scalar, piecewise positive constant function with respect to the triangulation $\mathcal{T}$. For $F = \partial K_F^{+} \cap \partial K_F^{-}\in \mathcal{E}_{I}$, denote by $\alpha ^+_{F}$ and $\alpha ^-_{F}$ the restriction of $\alpha$ on the respective $K_F^{+}$ and $K_F^{-}$.

Define the following weighted averages

$$\begin{aligned} \{v(x)\}_w^F = \left\{ \begin{array}{ll} w_F^- v^-_F + w_F^+v^+_F &{} \, F\in \mathcal{E}_{I},\\ 0 &{} \,F \in \mathcal{E}_{D}\cup \mathcal{E}_{N} \end{array}\right. \end{aligned}$$

(4.1)

and

$$\begin{aligned} \{v(x)\}_F^w = \left\{ \begin{array}{ll} w_F^+ v^-_F+ w_F^- v^+_F &{} \, F\in \mathcal{E}_{I},\\ v^-_F &{} \,F \in \mathcal{E}_{D}\cup \mathcal{E}_{N}, \end{array}\right. \end{aligned}$$

(4.2)

where $w^-_{F}=1-w^+_{F}$ and $w^+_{F}$ is defined by

$$\begin{aligned} w^+_{F} = \left\{ \begin{array}{cl} \displaystyle \frac{\alpha ^-_F }{\alpha ^-_F + \alpha ^+_F} =\displaystyle \frac{1/\alpha ^+_F }{1/\alpha ^-_F + 1/\alpha ^+_F} &{} \, F\in \mathcal{E}_{I} ,\\ 1 &{} \,F \in \mathcal{E}_{D}\cup \mathcal{E}_{N}. \end{array}\right. \end{aligned}$$

(When there is no ambiguity, the subscript or superscript F in the designation of the weighted average will be dropped.) A simple calculation leads to the following identity:

$$\begin{aligned}{}[\![ u v]\!]_F = \{v\}^w_F\, [\![ u]\!]_F + \{u\}_w^F \, [\![ v]\!]_F. \end{aligned}$$

(4.3)

For $F\in \mathcal{E}$ and for $0\le c \le 1$, denote a weighted average of $\alpha$ by

$$\begin{aligned} \alpha _F = \left\{ \begin{array}{lll} c \alpha _{K ^- }+ (1-c)\alpha _{K^+} &{} F\in \mathcal{E}_{I} ,\\ \alpha _{K^-} &{} F\in \mathcal{E}_{D}\cup \mathcal{E}_{N}. \end{array} \right. \end{aligned}$$

Obviously, $\min \{\alpha _{K^-},\alpha _{K^+} \} \le \alpha _F \le \max \{\alpha _{K^-},\alpha _{K^+} \}$ for $F\in \mathcal{E}_{I}$. Denote the arithmetic and the harmonic averages of $\alpha$ on $F \in \mathcal{E}$ by

$$\begin{aligned} \alpha _{F,A}= & {} \left\{ \begin{array}{cl} \displaystyle \frac{\alpha _F^+ + \alpha _F^- }{2} &{}\quad F \in \mathcal{E}_{I},\\ \alpha _F^- &{}\quad F \in \mathcal{E}_{{_D}}\cup \mathcal{E}_{{_N}} \end{array}\right. \quad \text {and}\\ a_{F,H}= & {} \left\{ \begin{array}{cl} \displaystyle \frac{2 \alpha _F^+ \alpha _F^- }{\alpha _F^+ + \alpha _F^-},&{}\quad F \in \mathcal{E}_{I},\\ \alpha _F^- &{}\quad F \in \mathcal{E}_{D}\cup \mathcal{E}_{N}, \end{array}\right. \end{aligned}$$

respectively, which are equivalent to the maximum and the minimum of $\alpha$:

$$\begin{aligned} \displaystyle \frac{1}{2}\max \{\alpha _F^+, \alpha _F^- \}\le \alpha _{F,A} \le \max \{\alpha _F^+, \alpha _F^- \} \text { and } \displaystyle \frac{1}{2}\min \{\alpha _F^+, \alpha _F^- \}\le a_{F,H} \le \min \{\alpha _F^+, \alpha _F^- \} .\nonumber \\ \end{aligned}$$

(4.4)

4.2 Local Element Residuals and Edge Jumps

In this subsection, we introduce some notations on local element residuals and edge jumps and their relations.

Define the element residual

$$\begin{aligned} r_K = \nabla \times (A^{-1}\varvec{\sigma }_{_\mathcal{T}})|_{K}. \end{aligned}$$

and the gradient edge jump

$$\begin{aligned} j_{F} = \left\{ \begin{array}{lll} [\![ A^{-1}\varvec{\sigma }_{_\mathcal{T}}\cdot \mathbf{t}]\!]_F &{} F\in \mathcal{E}_I, \\ (A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla g_D)\cdot \mathbf{t}_F &{} F\in \mathcal{E}_D. \end{array} \right. \end{aligned}$$

Lemma 4.1

For all $z\in \mathcal{N}_I \cup \mathcal{N}_D$, the following identity is true on the local patch $\omega _z$:

$$\begin{aligned} \sum _{K\in \mathcal{T}_z}(r_K,\phi _z)_K - \sum _{F\in \mathcal{E}_{j,z}}(j_F, \phi _z)_F =0. \end{aligned}$$

(4.5)

Proof

For mixed methods, the following error equation holds:

$$\begin{aligned} (A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla u, \varvec{\tau }) =(A^{-1}\varvec{\sigma }_{_\mathcal{T}}-A^{-1}\varvec{\sigma }, \varvec{\tau }) = (\nabla \cdot \varvec{\tau }, u_{_\mathcal{T}}-u), \quad \forall \varvec{\tau }\in \varSigma _{{_\mathcal{T}}}. \end{aligned}$$

For all $z\in \mathcal{N}_I \cup \mathcal{N}_D$, we have $\phi _z\in H_N^1(\varOmega )$ and $\nabla ^{\perp }\phi _z \in RT_0\cup H(\mathrm{div};\varOmega )$. Since $\nabla ^{\perp }\phi _z \cdot \mathbf{n}= \nabla \phi _z\cdot \mathbf{t}$, so $\nabla ^{\perp }\phi _z \cdot \mathbf{n}= 0$ on $\varGamma _N$ if $z\in \mathcal{N}_I \cup \mathcal{N}_D$ (note that $\mathcal{N}_D$ only contains the interior nodes of Dirichlet boundary). Thus $\nabla ^{\perp }\phi _z \in RT_0\cup H_N(\mathrm{div};\varOmega ) \subset \varSigma _{N,k}$, and $\nabla \cdot \nabla ^{\perp }\phi _z =0$, thus

$$\begin{aligned} (A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla u, \nabla ^{\perp }\phi _z) = (\nabla \cdot \nabla ^{\perp }\phi _z, u_{_\mathcal{T}}-u) = 0. \end{aligned}$$

(4.6)

Combined this with the interrogation by parts,

$$\begin{aligned} 0= & {} (A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla u, \nabla ^{\perp }\phi _z) \\= & {} \sum _{K\in \mathcal{T}_z}(\nabla \times (A^{-1}\varvec{\sigma }_{_\mathcal{T}}),\phi _z) -\sum _{K\in \mathcal{T}_z}((A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla u)\cdot \mathbf{t}_K,\phi _z)_{\partial K} \\= & {} \sum _{K\in \mathcal{T}_z}(\nabla \times (A^{-1}\varvec{\sigma }_{_\mathcal{T}}),\phi _z) -\sum _{F\in \mathcal{E}_{I,z}}([\![ (A^{-1}\varvec{\sigma }_{_\mathcal{T}})\cdot \mathbf{t}]\!],\phi _z)_{F} \\&-\sum _{F\in \mathcal{E}_{D,z}}((A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla g_D)\cdot \mathbf{t},\phi _z)_{F}\\= & {} \sum _{K\in \mathcal{T}_z}(r_K,\phi _z)_K - \sum _{F\in \mathcal{E}_{j,z}}(j_F, \phi _z)_F. \end{aligned}$$

This proves the lemma. $\square$

4.3 Local Broken-$H(\text {curl};\omega _z)$ Reformulation

In this subsection, we will rewrite the minimization problem (2.6) and its corresponding saddle point problem (2.11) as a problem in broken-$H(\text {curl};\omega _z)$ space for easier efficiency analysis.

First define the broken $H({\text {curl}})$ finite element space

$$\begin{aligned} \textsf {ND}_{-1,z}= & {} \left\{ \varvec{\tau }\in L^2(\omega _z) : \begin{array}{llll} \varvec{\tau }|_K \in \textsf {ND}_{k+1}(K)\,\, \forall \, K \in \mathcal{T}_{z} \\ \varvec{\tau }\cdot \mathbf{t}|_F = 0\,\, \forall \, F\in \mathcal{E}_{0, z}. \end{array} \right\} . \end{aligned}$$

Replace $\varvec{\varepsilon }_{{_\mathcal{T}},z}:=\varvec{\rho }_{{_\mathcal{T}},z}+\varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z)$ in (2.11), we have $\varvec{\varepsilon }_{{_\mathcal{T}},z}\in \textsf {ND}_{-1,z}$ and

$$\begin{aligned} \nabla \times \varvec{\rho }_{{_\mathcal{T}},z} = \nabla \times \varvec{\varepsilon }_{{_\mathcal{T}},z} - \nabla \times \varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z) \quad \text{ on } K\in \mathcal{T}_z. \end{aligned}$$

By the community property of the Nédélec interpolation operator: $\nabla \times \varPi ^{nd}_{K} = \varPi ^k_{K}\nabla \times$, for any $K\in \mathcal{T}_z$, with $\varPi ^k_{K}$ be the $L^2$ projection on $P_k(K)$ space, then for all $K\in \mathcal{T}_z$,

$$\begin{aligned} \nabla \times \varPi ^{nd}_{K}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z) = \varPi ^k_{K}\nabla \times (A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z) = \varPi ^k_{K}(\nabla \times (A^{-1}\varvec{\sigma }_{_\mathcal{T}}\phi _z) -\nabla ^{\perp }\phi _z\cdot A^{-1}\varvec{\sigma }_{_\mathcal{T}}). \end{aligned}$$

On the other hand,

$$\begin{aligned}&[\![ \varvec{\varepsilon }_{{_\mathcal{T}},z}\cdot \mathbf{t}]\!] = [\![ \varvec{\rho }_{{_\mathcal{T}},z}\cdot \mathbf{t}]\!] + [\![ \varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z)\cdot \mathbf{t}]\!]\\&\quad = \left\{ \begin{array}{llll} \varPi ^{k+1}_F([\![ A^{-1}\varvec{\sigma }_{_\mathcal{T}}\cdot \mathbf{t}]\!]\phi _z) &{} \forall \, F\in \mathcal{E}_{I,z},\\ \varPi ^{k+1}_F((A^{-1}\varvec{\sigma }_{_\mathcal{T}}+\nabla g_D)\cdot \mathbf{t})\phi _z) &{} \forall \, F\in \mathcal{E}_{D,z} \end{array} \right. \end{aligned}$$

Thus

$$\begin{aligned}{}[\![ \varvec{\varepsilon }_{{_\mathcal{T}},z}\cdot \mathbf{t}]\!] =\varPi ^{k+1}_{F}(j_F\phi _z),\quad \forall F \in \mathcal{E}_{j,z}. \end{aligned}$$

On the other hand,

$$\begin{aligned} \nabla \times \varvec{\varepsilon }_{{_\mathcal{T}},z} = \nabla \times \varvec{\rho }_{{_\mathcal{T}},z}+\varPi ^k_{K}(r_K\phi _z) -\nabla ^{\perp }\phi _z\cdot A^{-1}\varvec{\sigma }_{_\mathcal{T}}= \varPi ^k_{K}(r_K\phi _z), \quad \forall K\in \mathcal{T}_z. \end{aligned}$$

So the corresponding local minimization problem for $\varvec{\varepsilon }_{{_\mathcal{T}},z}$ is:

Local broken$H({\text {curl}})$minimization problem Find $\varvec{\varepsilon }_{{_\mathcal{T}},z}\in \mathcal{W}_z$,

$$\begin{aligned} \varvec{\varepsilon }_{{_\mathcal{T}},z} = \arg \min _{\varvec{\tau }\in \mathcal{W}_z} \Vert A^{1/2}\varvec{\tau }\Vert _{0,\omega _z} \quad z\in \mathcal{N}, \end{aligned}$$

(4.7)

with

$$\begin{aligned} \mathcal{W}_{z} = \left\{ \varvec{\tau }\in {\textsf {ND}}_{-1,z} : \begin{array}{ll} \nabla \times \varvec{\tau }= \varPi ^{k}_{K}(r_K\phi _z), \; \forall K\in \mathcal{T}_z; \\ {[}\![{\varvec{\tau }\cdot \mathbf{t}}]\!] = \varPi ^{k+1}_{F}(j_{F}\phi _{z}),\; \forall F\in \mathcal{E}_{j,z}. \end{array} \right\} \end{aligned}$$

From our derivation, we see that the problems (4.7) and (2.6) are equivalent: $\varvec{\varepsilon }_{{_\mathcal{T}},z}=\varvec{\rho }_{{_\mathcal{T}},z}+\varPi ^{nd}(A^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z)$, $\forall K\in \mathcal{T}_z$.

The solvability of the minimization problem (4.7) can be derived from the equivalence of (4.7) and (2.6) and the solvability of (2.6). On the other hand, it can also be derived directly by using the result of the identity (4.5) (in Lemma 4.1 ) as did in [8]. Since essentially the conditions (2.3) and (4.5) are two different forms of the same identity.

Since the rest analysis is only valid for $A=\alpha I$, we only use the notation $\alpha$. In the sprit of [15], the weak formulation of the local broken $H({\text {curl}})$ minimization problem can also be written as:

Local broken$H({\text {curl}})$saddle point problem Find $(\varvec{\varepsilon }_{{_\mathcal{T}},z},w_z, \lambda _z) \in \textsf {ND}_{-1,z}\times Q_{z}\times M_z$, such that

$$\begin{aligned} \left\{ \begin{array}{llll} a_z(\varvec{\varepsilon }_{{_\mathcal{T}},z},\,\varvec{\tau }) + c_z(\varvec{\tau },\, w_z) - d_z(\varvec{\tau },\, \lambda _z) &{}=&{} 0 &{} \forall \, \varvec{\tau }\in \textsf {ND}_{-1,z} , \\ c_z(\varvec{\varepsilon }_{{_\mathcal{T}},z},\, v) &{}=&{} \sum _{K\in \mathcal{T}_z}(r_K\phi _z, v)_{K} &{} \forall \; v \in Q_z,\\ d_z(\varvec{\varepsilon }_{{_\mathcal{T}},z},\, \mu ) &{}=&{} \sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \mu )_{F} &{} \forall \; \mu \in M_z,\\ \end{array} \right. \end{aligned}$$

(4.8)

where

$$\begin{aligned} a_z(\varvec{\tau }, \varvec{\chi })= & {} \sum _{K\in \mathcal{T}_Z}(\alpha \varvec{\tau },\varvec{\chi })_K, \quad \forall \, \varvec{\tau },\varvec{\chi }\in \textsf {ND}_{-1,z}, \end{aligned}$$

(4.9)

$$\begin{aligned} c_z(\varvec{\tau },\, v)= & {} \sum _{K\in \mathcal{T}_z} (\nabla \times \varvec{\tau }, v)_K, \quad (\varvec{\tau },v) \in \textsf {ND}_{-1,z} \times Q_{z}, \end{aligned}$$

(4.10)

$$\begin{aligned} d_z(\varvec{\tau },\, \mu )= & {} \sum _{F\in \mathcal{E}_{j,z}} ([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \mu )_F, \quad (\varvec{\tau },\mu ) \in \textsf {ND}_{-1,z} \times M_{z}, \end{aligned}$$

(4.11)

and the space is $M_z = \{ \mu \in L^{2}(\mathcal{E}_{j,z}): \,v|_{F} \in P_{k+1}(F)\,\, \forall \, F \in \mathcal{E}_{j,z} \}$.

Define

$$\begin{aligned} b_z(\varvec{\tau }, (v,\mu )) : = c_z(\varvec{\tau },\, v) - d_z(\varvec{\tau },\, \mu ) \quad \quad \forall \, (\varvec{\tau },v,\mu ) \in \textsf {ND}_{-1,z} \times Q_{z}\times M_z. \end{aligned}$$

Lemma 4.2

The bilinear form $b_z$ has the following representation:

$$\begin{aligned} b_z(\varvec{\tau }, (v,\mu ))= & {} \sum _{K\in \mathcal{T}_z}(\varvec{\tau },\nabla ^{\perp }v)_K + \sum _{F\in \mathcal{E}_{I,z}}(\{\varvec{\tau }\cdot \mathbf{t}\}^w, [\![ v]\!])_F + \sum _{F\in \mathcal{E}_{I,z}}([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \{v\}_w-\mu )_F \nonumber \\&+ \sum _{F\in \mathcal{E}_{D,z}}(\varvec{\tau }\cdot \mathbf{t}, v-\mu )_F + \sum _{F\in \mathcal{E}_{N,z}}(\varvec{\tau }\cdot \mathbf{t},v)_F \nonumber \\= & {} \sum _{K\in \mathcal{T}_z}(\varvec{\tau },\nabla ^{\perp }v)_K + \sum _{F\in \mathcal{E}_{I,z}}(\{\varvec{\tau }\cdot \mathbf{t}\}^w, [\![ v]\!])_F + \sum _{F\in \mathcal{E}_{j,z}}([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \{v\}_w-\mu )_F \nonumber \\&+ \sum _{F\in \mathcal{E}_{N,z}}(\varvec{\tau }\cdot \mathbf{t},v)_F \quad \quad \forall \, (\varvec{\tau },v,\mu ) \in \textsf {ND}_{-1,z} \times Q_{z}\times M_z. \end{aligned}$$

(4.12)

Proof

By integrations by parts and the jump identity (4.3), we have :

$$\begin{aligned} b_z(\varvec{\tau }, (v,\mu ))= & {} \sum _{K\in \mathcal{T}_z} (\nabla \times \varvec{\tau }, v)_K-\sum _{F\in \mathcal{E}_{j,z}} ([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \mu )_F \\= & {} \sum _{K\in \mathcal{T}_z}(\varvec{\tau },\nabla ^{\perp }v)_K + \sum _{F\in \mathcal{E}_{I,z}}([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \{v\}_w)_F + \sum _{F\in \mathcal{E}_{I,z}}(\{\varvec{\tau }\cdot \mathbf{t}\}^w, [\![ v]\!])_F\\&+\sum _{F\in \mathcal{E}_{b,z}\backslash \mathcal{E}_{0,z}}(\varvec{\tau }\cdot \mathbf{t},v)_F -\sum _{F\in \mathcal{E}_{I,z}}([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \mu )_F - \sum _{F\in \mathcal{E}_{D,z}}(\varvec{\tau }\cdot \mathbf{t},\mu )_F \\= & {} \sum _{K\in \mathcal{T}_z}(\varvec{\tau },\nabla ^{\perp }v)_K + \sum _{F\in \mathcal{E}_{I,z}}(\{\varvec{\tau }\cdot \mathbf{t}\}^w, [\![ v]\!])_F + \sum _{F\in \mathcal{E}_{I,z}}([\![ \varvec{\tau }\cdot \mathbf{t}]\!], \{v\}_w-\mu )_F \\&+ \sum _{F\in \mathcal{E}_{D,z}}(\varvec{\tau }\cdot \mathbf{t}, v-\mu )_F + \sum _{F\in \mathcal{E}_{N,z}}(\varvec{\tau }\cdot \mathbf{t},v)_F, \\&\quad \quad \quad \quad \quad \quad \forall \, (\varvec{\tau },v,\mu ) \in \textsf {ND}_{-1,z} \times Q_{z}\times M_z. \end{aligned}$$

$\square$

Let

$$\begin{aligned} R_z(v,\mu ) = \sum _{K\in \mathcal{T}_z}(r_K\phi _z, v)_{K} -\sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \mu )_{F}, \quad \quad \forall \, (v,\mu ) \in Q_{z}\times M_z. \end{aligned}$$

(4.13)

Thus (4.8) can be rewritten as: find $(\varvec{\varepsilon }_{{_\mathcal{T}},z},w_z, \lambda _z) \in \textsf {ND}_{-1,z}\times Q_{z}\times M_z$, such that

$$\begin{aligned} \left\{ \begin{array}{llll} a_z(\varvec{\varepsilon }_{{_\mathcal{T}},z},\,\varvec{\tau }) + c_z(\varvec{\tau },\, w_z) - d_z(\varvec{\tau },\, \lambda _z) &{}=&{} 0 &{} \forall \, \varvec{\tau }\in \textsf {ND}_{-1,z} , \\ b_z(\varvec{\varepsilon }_{{_\mathcal{T}},z},\, (v,\mu )) &{}=&{} R_z(v,\mu ) &{} \forall \; (v,\mu ) \in Q_{z}\times M_z. \end{array} \right. \end{aligned}$$

(4.14)

From our derivation, we see that the problems (2.11) and (4.14) are equivalent, thus all four problems (4.7), (2.6), (2.11) and (4.14) are equivalent with:

$$\begin{aligned} \varvec{\varepsilon }_{{_\mathcal{T}},z}=\varvec{\rho }_{{_\mathcal{T}},z}+\varPi ^{nd}(\alpha ^{-1}\varvec{\sigma }_{_\mathcal{T}} \phi _z)\quad \forall K\in \mathcal{T}_z. \end{aligned}$$

(4.15)

Thus, we have the equivalence of the local indicators:

$$\begin{aligned} \eta _{z}= & {} \Vert \alpha ^{1/2} (\varvec{\rho }_{{_\mathcal{T}},z} + \varPi ^{nd}(\alpha ^{-1}\varvec{\sigma }_{_\mathcal{T}}\phi _z))\Vert _{0,\omega _z} =\Vert \alpha ^{1/2} \varvec{\varepsilon }_{{_\mathcal{T}},z}\Vert _{0,\omega _z} ,\quad \forall z\in \mathcal{N}. \end{aligned}$$

(4.16)

Remark 4.3

We have four equivalent version of local recoveries discussed. Two ((2.6) (4.7)) are in the forms of minimization problems, while the other two are in the form of saddle point problems. Two ((2.6) and (2.11)) are for the $H({\text {curl}})$-conforming recoveries, and two ((4.7) and (4.14)) are for the broken $H({\text {curl}})$ recoveries. The form (2.11) is recommended for implementations. The broken mixed problem (4.14) is convenient for analysis, we will use this to analyze the robust efficiency of our error estimator.

Remark 4.4

An explicit construction similar to that discussed in [15] can also be done. For the broken $H({\text {curl}})$ minimization problem (4.7), one can first construct a $\varvec{\tau }\in \mathcal{W}_z$ explicitly like that been done in [6, 15, 30], then a correction can be added in the local $H({\text {curl}};\omega _z)$-conforming and curl-free space like we did in [15].

4.4 Stability Estimate of the Local Broken $H({\text {curl}})$ Saddle Point Problem

For $\varvec{\tau }\in \textsf {ND}_{-1,z}$ and $(v,\mu ) \in Q_{z}\times M_z$, define $(\alpha ,\,h)$-dependent norms on $\omega _z$ by

$$\begin{aligned} \Vert \varvec{\tau }\Vert _{\alpha , h, z}^2:= & {} \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0,\omega _z}^2 + \sum _{F\in \mathcal{E}_{j,z}} h_F\alpha _{F,A}\Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F}^2 + \sum _{F\in \mathcal{E}_{N,z}}h_F\alpha _F \Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F}^2, \\ |\!|\!|(v,\mu ) |\!|\!|_{\alpha ,h,z}^2:= & {} \Vert \alpha ^{-1/2} \nabla ^{\perp }_h v\Vert _{0,\omega _z}^2 + \displaystyle \sum _{F\in \mathcal{E}_{I,z}} \displaystyle \frac{1}{h_F\alpha _{F,A}} \Vert [\![ v]\!]\Vert _{0,F}^2 \\&+ \displaystyle \sum _{F\in \mathcal{E}_{I,z}} \displaystyle \frac{1}{h_F\alpha _{F,H}} \Vert \{v\}_w-\mu \Vert _{0,F}^2 + \displaystyle \sum _{F\in \mathcal{E}_{D,z}} \displaystyle \frac{1}{h_F\alpha _F} \Vert v-\mu \Vert _{0,F}^2 \\&+ \displaystyle \sum _{F\in \mathcal{E}_{N,z}} \displaystyle \frac{1}{h_F\alpha _F} \Vert v\Vert _{0,F}^2. \end{aligned}$$

Remark 4.5

Here, $\Vert \varvec{\tau }\Vert _{\alpha , h, z}$ is a weighted h-dependent $L^2$-norm and and $|\!|\!|v |\!|\!|_{\alpha , h, z}$ is a weighted h-dependent discrete $H^1$-norm.

Lemma 4.6

For all $\varvec{\tau }\in \textsf {ND}^{k+1}(K)$ and all $v\in P_{k}(K)$, there exists a positive constant C such that

$$\begin{aligned} \displaystyle \sum _{F\in \mathcal{E}_K} h_F \Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F}^2 \le C \Vert \varvec{\tau }\Vert _{0,K}^2 \quad \text {and}\quad \displaystyle \sum _{F\in \mathcal{E}_K} \displaystyle \frac{1}{h_F} \Vert v\Vert _{0,F}^2 \le C\, h_K^{-1}\Vert v\Vert _{0,K}^2 , \end{aligned}$$

where the constant C depends only on the polynomial degree k and shape parameters of $\mathcal{T}_z$.

Proof

The lemma is a simple consequence of the standard scaling argument and the fact that both $\textsf {ND}^{k+1}(K)$ and $P_{k}(K)$ are finite dimensional spaces. $\square$

Let $K^*_F$ be the element of $\omega _F$ with a larger $\alpha _K$, Lemma 4.6 implies that

$$\begin{aligned} h_F\alpha _{F,A}\Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F}^2 \le \Vert \alpha _{K^*}^{1/2}\varvec{\tau }\Vert _{0,K^*_F}^2. \end{aligned}$$

Thus we have the following norm-equivalence:

$$\begin{aligned} \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0,\omega _z} \le \Vert \varvec{\tau }\Vert _{\alpha ,h,z} \le C \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0,\omega _z} \quad \forall \,\,\varvec{\tau }\in \textsf {ND}_{-1,z}. \end{aligned}$$

(4.17)

Lemma 4.7

The bilinear form $a_z(\cdot ,\cdot )$ is continuous and coercive with respect to the norm $\Vert \cdot ~\!\!\Vert _{\alpha ,h,z}$ in $\varvec{\tau }\in \textsf {ND}_{-1,z}$; i.e., there exists a positive constant $a_c$ independent of $\alpha$ and the mesh size such that for all $\varvec{\chi },\,\, \varvec{\tau }\in \textsf {ND}_{-1,z}$

$$\begin{aligned} a_c \Vert \varvec{\tau }\Vert _{\alpha ,h,z}^2 \le a_z(\varvec{\tau },\varvec{\tau }) \quad \text {and}\quad a_z(\varvec{\chi },\varvec{\tau }) \le \Vert \varvec{\chi }\Vert _{\alpha ,h,z}\Vert \varvec{\tau }\Vert _{\alpha ,h,z}. \end{aligned}$$

Proof

The lemma is a direct consequence of (4.17) and the Cauchy-Schwarz inequality. $\square$

Lemma 4.8

The bilinear form $b_z(\cdot ,\cdot )$ is continuous in $\textsf {ND}_{-1,z} \times (Q_z\times M_z)$; i.e., there exists a positive constant C independent of the mesh size such that

$$\begin{aligned} b_z(\varvec{\tau }, (v,\mu )) \le C \Vert \varvec{\tau }\Vert _{\alpha ,h,z} |\!|\!|(v,\mu ) |\!|\!|_{\alpha ,h,z}. \end{aligned}$$

(4.18)

Proof

It follows from (4.12) and the Cauchy-Schwarz inequality that

$$\begin{aligned} b_z(\varvec{\tau }, (v,\mu ))\le & {} \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0.\omega _z} \Vert \alpha ^{1/2}\nabla ^{\perp }_h v\Vert _{0,\omega _z} \\&+ \sum _{F\in \mathcal{E}_{I,z}} \sqrt{h_F\alpha _{F,A}}\Vert \{\varvec{\tau }\cdot \mathbf{t}\}^w\Vert _{0,F} \displaystyle \frac{1}{\sqrt{h_F\alpha _{F,A}}}\Vert [\![ v]\!]\Vert _{0,F} \\&+ \sum _{F\in \mathcal{E}_{I,z}} \sqrt{h_F\alpha _{F,H}}\Vert [\![ \varvec{\tau }\cdot \mathbf{t}]\!]\Vert _{0,F} \displaystyle \frac{1}{\sqrt{h_F\alpha _{F,H}}}\Vert \{v\}_w-\mu \Vert _{0,F} \\&+ \sum _{F\in \mathcal{E}_{D,z}}\sqrt{h_F\alpha _F}\Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F} \displaystyle \frac{1}{\sqrt{h_F\alpha _{F}}} \Vert v-\mu \Vert _{0,F} \\&+ \sum _{F\in \mathcal{E}_{N,z}}\sqrt{h_F\alpha _F}\Vert \varvec{\tau }\cdot \mathbf{t}\Vert _{0,F} \displaystyle \frac{1}{\sqrt{h_F\alpha _{F}}} \Vert v\Vert _{0,F}. \end{aligned}$$

Denote by $\tau _t^{\pm } = \varvec{\tau }|_{K_F^{\pm }}\cdot \mathbf{t}_F$, then by (4.17) and the definitions of weights, $\alpha _{F,A}$, and $\alpha _{F,H}$, we have

$$\begin{aligned} h_F\alpha _{F,A}\Vert \{\varvec{\tau }\cdot \mathbf{t}\}^w\Vert _{0,F}^2\le & {} Ch_F\displaystyle \frac{\alpha _F^+ + \alpha _F^- }{2} \left( \displaystyle \frac{(\alpha ^-_F)^2 }{(\alpha ^-_F + \alpha ^+_F)^2} \Vert \tau _t^{-}\Vert _{0,F}^2 + \displaystyle \frac{(\alpha ^+_F)^2 }{(\alpha ^-_F + \alpha ^+_F)^2} \Vert \tau _t^{+}\Vert _{0,F}^2 \right) \\\le & {} Ch_F \left( \alpha ^-_F \Vert \tau _t^{-}\Vert _{0,F}^2 + \alpha ^+_F \Vert \tau _t^{+}\Vert _{0,F}^2 \right) \le C \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0,\omega _z}^2, \end{aligned}$$

and

$$\begin{aligned} h_F\alpha _{F,H}\Vert [\![ \varvec{\tau }\cdot \mathbf{t}]\!]\Vert _{0,F}^2\le & {} Ch_F\alpha _{F,H} \left( \Vert \tau _t^{-}\Vert _{0,F}^2 + \Vert \tau _t^{+}\Vert _{0,F}^2 \right) \\\le & {} Ch_F \left( \alpha ^-_F \Vert \tau _t^{-}\Vert _{0,F}^2 + \alpha ^+_F \Vert \tau _t^{+}\Vert _{0,F}^2 \right) \le C \Vert \alpha ^{1/2}\varvec{\tau }\Vert _{0,\omega _z}^2. \end{aligned}$$

This proves the lemma. $\square$

Lemma 4.9

(inf-sup condition) The following inf-sup condition holds with constant $\beta >0$ independent of $\alpha$ and h:

$$\begin{aligned} \sup _{\varvec{\tau }\in \textsf {ND}_{-1,z}} \displaystyle \frac{b_z(\varvec{\tau }, (v,\mu ))}{ \Vert \varvec{\tau }\Vert _{\alpha ,h,z}} \ge \beta |\!|\!|(v,\mu ) |\!|\!|_{\alpha , h,z} \quad \forall \, (v,\mu ) \in Q_z\times M_z. \end{aligned}$$

(4.19)

Proof

Choose a ${\tilde{\varvec{\tau }}} \in \textsf {ND}_{-1,z}$ such that

$$\begin{aligned} \int _K (\alpha {\tilde{\varvec{\tau }}} - \nabla ^{\perp }v)\cdot \nabla ^{\perp }q dx=0 \quad \forall \, q\in P_{k+1}(K) \quad \forall \,\, K\in \mathcal{T}_z \end{aligned}$$

and that

$$\begin{aligned} {\tilde{\varvec{\tau }}} \cdot \mathbf{t}_K |_F =\left\{ \begin{array}{llll} \text {sgn}(K,F)\displaystyle \frac{1}{h_F \alpha _{F,A} } [\![ v]\!] + \displaystyle \frac{1}{2 h_F \alpha _{K}}(\{v\}-\mu ) &{} \,\, F\in \mathcal{E}_K \cap \mathcal{E}_{I,z}, \\ \displaystyle \frac{1}{\alpha _K h_F}(v-\mu ) &{} \,\, F\in \mathcal{E}_K \cap \mathcal{E}_{D,z} , \\ \displaystyle \frac{1}{\alpha _K h_F}v &{} \,\, F\in \mathcal{E}_K \cap \mathcal{E}_{N,z}, \\ 0 &{} \,\, F\in \mathcal{E}_K \cap \mathcal{E}_{0,z}, \end{array}\right. \end{aligned}$$

(4.20)

where $\text {sgn}(K,F)= \mathbf{n}_K \cdot \mathbf{n}_F$. Obviously, (4.20) implies

$$\begin{aligned} \{{\tilde{\varvec{\tau }}} \cdot \mathbf{t}_F \}^w = \displaystyle \frac{1}{h_F \alpha _{F,A}} [\![ v]\!] \quad \text{ and } \quad [\![ {\tilde{\varvec{\tau }}} \cdot \mathbf{t}_F ]\!] = \displaystyle \frac{1}{h_F \alpha _{F,H}} (\{v\}_w - \mu ) \quad \forall \, F\in \mathcal{E}_{I,z}, \end{aligned}$$

which, together with (4.12) and (4.17), gives

$$\begin{aligned} b({\tilde{\varvec{\tau }}},v) = |\!|\!|(v,\mu ) |\!|\!|_{\alpha ,h,z}^2. \end{aligned}$$

(4.21)

For every $K\in \mathcal{T}_z$, by the standard scaling argument and (4.4), there exists a constant $C>0$ independent of $\alpha$ and the mesh size such that

$$\begin{aligned} C\Vert \alpha _K^{1/2}{\tilde{\varvec{\tau }}}\Vert _{0,K}^2\le & {} \Vert \alpha ^{-1/2} \nabla ^{\perp }v\Vert _{0,K}^2 \\&+ \displaystyle \sum _{F\in \mathcal{E}_K \cap \mathcal{E}_{I,z}} \displaystyle \frac{1}{h_F\alpha _{F,A}} \Vert [\![ v]\!]\Vert _{0,F}^2 + \displaystyle \frac{1}{h_F\alpha _{F,H}} \Vert \{v\}_w-\mu \Vert _{0,F}^2 \\&+ \displaystyle \sum _{F\in \mathcal{E}_K\cap \mathcal{E}_{D,z}} \displaystyle \frac{1}{h_F\alpha _F} \Vert v-\mu \Vert _{0,F}^2 +\displaystyle \sum _{F\in \mathcal{E}_K \cap \mathcal{E}_{N,z}} \displaystyle \frac{1}{h_F\alpha _{F}} \Vert v\Vert _{0,F}^2. \end{aligned}$$

Hence, there exists a constant ${\tilde{C}}>0$ independent of $\alpha$ and h such that

$$\begin{aligned} \Vert \varvec{\tau }\Vert _{\alpha ,h,z} \le {\tilde{C}} |\!|\!|(v,\mu ) |\!|\!|_{\alpha ,h,z}. \end{aligned}$$

which, together with (4.21), leads to (4.19) with $\beta = 1/{\tilde{C}}$. This completes the proof of the lemma. $\square$

Theorem 4.10

The unique solution $(\varvec{\varepsilon }_{{_\mathcal{T}},z}, w_{z}, \lambda _z) \in \textsf {ND}_{-1,z}\times Q_{z} \times M_z$ of problem (4.14) satisfies the following bound:

$$\begin{aligned} \eta _z= & {} \Vert \alpha ^{1/2}\varvec{\varepsilon }_{{_\mathcal{T}},z}\Vert _{0,\omega _z} \le \Vert \varvec{\varepsilon }_{{_\mathcal{T}},z}\Vert _{\alpha ,h,z}\le \Vert \varvec{\varepsilon }_{{_\mathcal{T}},z}\Vert _{\alpha ,h,z}+|\!|\!|(w_{z},\lambda _z)|\!|\!|_{\alpha ,h,z}\\\le & {} C(a_c,\beta ) \sup _{(v,\mu ) \in Q_z\times M_z } \displaystyle \frac{R_z(v,\mu )}{ |\!|\!|(v,\mu )|\!|\!|_{\alpha ,h,z}}, \end{aligned}$$

where the constant $C(a_c,\beta )>0$ is independent of the mesh size and jumps.

Proof

The theorem follows from the abstract theory of saddle point problem (see, e.g., [5, 6]) and Lemmas 4.7, and 4.9 . $\square$

Remark 4.11

Another possible way to establish the stability of broken mixed problem (4.14) is that we establish the stability of its equivalent version, the conforming version (2.11) first, which might be easier, then the stability of (4.14) is proved by the equivalence of two problems. This approach is less direct, but might be useful for the three dimensional case, where the trace space of Nédélec finite element space (see e.g. [16]) is much more complicated.

4.5 Robust Local Efficiency Bound

For any $z\in \mathcal{N}$, let

$$\begin{aligned} {\hat{\omega }}_z=\{K\in \omega _z \,:\, \beta _K = \max _{K'\in \omega _z} \beta _{K'}\}. \end{aligned}$$

Assume that the distribution of the coefficients $\alpha _{_K}$ for all $K\in \mathcal{T}$ is locally quasi-monotone [25] which is slightly weaker than Hypothesis 2.7 in [4]. For convenience of readers, we restate it here.

Definition 4.12

Given a vertex $z \in \mathcal{N}$, the distribution of the coefficients $\beta _K$, $K\in \omega _z$, is said to be quasi-monotone with respect to the vertex z if there exists a subset ${\tilde{\omega }}_{K,z,qm}$ of $\omega _z$ such that the union of elements in ${\tilde{\omega }}_{K,z,qm}$ is a Lipschitz domain and that

• if $z\in \mathcal{N}\backslash \mathcal{N}_D$, then $\{K\}\cup {\hat{\omega }}_z \subset {\tilde{\omega }}_{{_K},z,qm}$ and $\beta _K\le \beta _{K'} \; \forall K' \in {\tilde{\omega }}_{K,z,qm}$;

• if $z\in \mathcal{N}_D$, then $K\in {\tilde{\omega }}_{K,z,qm}$, $\partial {\tilde{\omega }}_{K,z,qm}\cap \varGamma _D \ne \emptyset$, and $\beta _K\le \beta _{K'} \; \forall K' \in {\tilde{\omega }}_{K,z,qm}$.

The distribution of the coefficients $\beta _K$, $K\in \mathcal{T}$, is said to be locally quasi-monotone if it is quasi-monotone with respect to every vertex $z\in \mathcal{N}$.

In this paper, we assume the distribution of $1/\alpha _K$ is locally quasi-monotone.

Denote the vertex-based local residual error indicator by

$$\begin{aligned} {\hat{\eta }}_z ^2 = \sum _{K\in \mathcal{T}_z} h_K^2 \alpha _K \Vert r_K\Vert _{0,K}^2 + \sum _{F\in \mathcal{E}_{j,z}} h_F \alpha _{F,A} \Vert j_F\Vert _{0,F}^2. \end{aligned}$$

(4.22)

Its robust local efficiency for the lowest mixed method is proved in [14], whose extensions to higher order mixed methods is trivial. There exists a constant $C>0$ which is independent of $\alpha$ and the mesh size such that

$$\begin{aligned} {\hat{\eta }}_z \le C \Vert \alpha ^{1/2}\nabla u + \alpha ^{-1/2} \varvec{\sigma }_{_\mathcal{T}}\Vert _{0,{\tilde{\omega }}_z}, \end{aligned}$$

(4.23)

where ${\tilde{\omega }}_z = \omega _z \cup \{ K \text { and } \partial \omega _z \text { shares an edge}\}$.

Define the following piecewise $H^1$ function spaces

$$\begin{aligned} V_z = \left\{ \begin{array}{lll} \{ v \in L^2(\omega _z) : v|_K \in H^1(K), \int _{\omega _z} v dx =0 \}, &{} z \in \mathcal{N}_I,\\ \{ v \in L^2(\omega _z) : v|_K \in H^1(K) \}, &{} z \in \mathcal{N}_D \cup \mathcal{N}_N. \end{array} \right. \end{aligned}$$

Obviously, $Q_z\subset V_z$. Let $K^{\prime }$ be the element with the smallest $\alpha _K$ in $\omega _z$, define ${\bar{v}}_z = \int _{K'}v dx/|K'|$.

Theorem 4.13

Under the assumptions that $1/\alpha _K$ is locally quasi-monotone in $\mathcal{T}_z$, for any $v\in V_z$, there exists a constant C independent of the mesh size and $\alpha$ such that

$$\begin{aligned} \sum _{K\in \mathcal{T}_z}h_K^{-2}\Vert \alpha ^{-1/2}(v- {\bar{v}}_z)\Vert _{0,K}^2 \le C \left( \sum _{K\in \mathcal{T}_z} \Vert \alpha ^{-1/2}\nabla ^{\perp }v\Vert _{0,K}^2 + \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{ h_{{_F}}\alpha _{F,A}}\Vert [\![ v]\!] \Vert _{0,F}^2\right) ,\nonumber \\ \end{aligned}$$

(4.24)

when $z\in \mathcal{N}_I \cup \mathcal{N}_D$ and

$$\begin{aligned} \sum _{K\in \mathcal{T}_z}h_K^{-2}\Vert \alpha ^{-1/2}v\Vert _{0,K}^2\le & {} C \left( \sum _{K\in \mathcal{T}_z} \Vert \alpha ^{-1/2}\nabla ^{\perp }v\Vert _{0,K}^2 \right. \nonumber \\&\left. + \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{ h_{F}\alpha _{F,A}}\Vert [\![ v]\!] \Vert _{0,F}^2 + \sum _{F\in \mathcal{E}_{N,z}} \displaystyle \frac{1}{ h_{F}\alpha _{F}}\Vert v \Vert _{0,F}^2 \right) ,\nonumber \\ \end{aligned}$$

(4.25)

when $z\in \mathcal{N}_N$.

Proof

The theorem is can be proved in a similar fashion as Corollary 5.10 of [15]. $\square$

Theorem 4.14

(Efficiency) Under the assumptions that $1/\alpha _K$ is locally quasi-monotone in $\mathcal{T}_z$, the local indicators $\eta _{{z}}$ and $\eta _{_{K}}$ are efficient; i.e., there exists a constant $C>0$ independent of $\alpha$ and the mesh size such that

$$\begin{aligned} \eta _z \le C \Vert \alpha ^{1/2}\nabla u + \alpha ^{-1/2} \varvec{\sigma }_{_\mathcal{T}}\Vert _{0,{\tilde{\omega }}_z} \quad \text {and} \quad \eta _K \le C\sum _{z\in \mathcal{N}_k} \Vert \alpha ^{1/2}\nabla u + \alpha ^{-1/2} \varvec{\sigma }_{_\mathcal{T}}\Vert _{0,{\tilde{\omega }}_z}. \end{aligned}$$

(4.26)

Proof

Squaring both sides of the first inequality in (4.26) and summing up over all $z\in \mathcal{N}_K$ imply the second inequality in (4.26). To prove the validity of the first inequality in (4.26), by Theorem 5.1 and (4.23), it suffices to show that

$$\begin{aligned} \sup _{(v, \mu )\in Q_z\times M_z} \displaystyle \frac{R_z(v,\mu )}{ |\!|\!|(v,\mu )|\!|\!|_{\alpha ,h,z}} \le C\, {\hat{\eta }}_{z} \end{aligned}$$

or, equivalently,

$$\begin{aligned} R_{z}(v,\mu ) \le C\, {\hat{\eta }}_{z}\,|\!|\!|(v,\mu ) |\!|\!|_{\alpha ,h,z} \quad \forall \,\,(v, \mu )\in Q_z\times M_z. \end{aligned}$$

(4.27)

We prove the case $z\in \mathcal{N}_I \cup \mathcal{N}_D$ first. By (4.5), for an arbitrary constant c

$$\begin{aligned} R_{z}(c,c) =0, \quad \forall \, z\in \mathcal{N}_I \cup \mathcal{N}_D, \end{aligned}$$

which implies

$$\begin{aligned} R_z(v,\mu ) = R_{z}(v-c,\mu -c) , \quad \forall \, z\in \mathcal{N}_I \cup \mathcal{N}_D, \quad \forall \; (v, \mu )\in Q_z\times M_z. \end{aligned}$$

(4.28)

Choose $c = {\bar{v}}_z$ be the average of v on $\omega _z$. In fact, for $z\in \mathcal{N}_I, v_z = 0$. It follows from the triangle inequality, the facts that $\Vert r_{K}\phi _z\Vert _{0,K} \le \Vert r_{K}\Vert _{0,K}$ and $\Vert j_{F}\phi _z\Vert _{0,F} \le \Vert j_{F}\Vert _{0,F}$, and the Cauchy-Schwarz inequality that

$$\begin{aligned} R_z(v,\mu )= & {} R_{z}(v-{\bar{v}}_z,\mu -{\bar{v}}_z)= \sum _{K\in \mathcal{T}_z}(r_K\phi _z, v-{\bar{v}}_z)_{K} - \sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \mu -{\bar{v}}_z)_{F} \\= & {} \sum _{K\in \mathcal{T}_z}(r_K\phi _z, v-{\bar{v}}_z)_{K} \\&-\sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \{ v - {\bar{v}}_z\}_w)_{F} +\sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \{ v\}_w-\mu )_{F} \\\le & {} \sum _{K\in \mathcal{T}_z} \Vert r_{K}\phi _z\Vert _{0,K} \Vert v- {\bar{v}}_z\Vert _{0,K} \\&+\sum _{F\in \mathcal{E}_{j,z}} \Vert j_{F}\phi _z\Vert _{0,F} (\Vert \{ v - {\bar{v}}_z\}_w\Vert _{0,F}+\Vert \{ v\}_w-\mu \Vert _{0,F}) \\\le & {} {\hat{\eta }}_{z} \left( \sum _{K\in \mathcal{T}_z} \displaystyle \frac{1}{h_K^2 \alpha _K} \Vert v- {\bar{v}}_z\Vert _{0,K}^2\right. \\&\left. +\sum _{F \in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_Fa_{F,A}} (\Vert \{ v - {\bar{v}}_z\}_w\Vert _{0,F}^2+\Vert \{ v\}_w-\mu \Vert _{0,F}^2) \right) ^{1/2}. \end{aligned}$$

Note that $1/\alpha _{F,A} \le 1/\alpha _{F,H}$ and $1/\alpha _{F,A} \le \min \{1/\alpha _{F,-}, 1/\alpha _{F,+}\}$, thus

$$\begin{aligned} \displaystyle \frac{1}{h_Fa_{F,A}} \Vert \{ v - {\bar{v}}_z\}_w\Vert _{0,F}^2 \le \sum _{K\in \{K_F^-, K_F^+\}} \displaystyle \frac{1}{h_K^2 \alpha _K} \Vert v- {\bar{v}}_z\Vert _{0,K}^2 \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{1}{h_Fa_{F,A}} \Vert \{ v\}_w-\mu \Vert _{0,F}^2 \le \displaystyle \frac{1}{h_Fa_{F,H}} \Vert \{ v\}_w-\mu \Vert _{0,F}^2. \end{aligned}$$

Then, by (4.24), we have

$$\begin{aligned} R_z(v,\mu )\le & {} C{\hat{\eta }}_{z} \left( \Vert \alpha ^{-1/2}\nabla ^{\perp }_h v\Vert _{0,\omega _z}^2 + \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_F \alpha _{F,A}} \Vert [\![ v]\!]\Vert _{0,F}^2 \right. \\&\left. + \displaystyle \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_F\alpha _{F,H}} \Vert \{v\}_w-\mu \Vert _{0,F}^2 \right) ^{1/2} \\= & {} C{\hat{\eta }}_{z}|\!|\!|(v,\mu )|\!|\!|_{\alpha ,h,z} . \end{aligned}$$

This proves the validity of (4.27) and, hence, the theorem for $z\in \mathcal{N}_I \cup \mathcal{N}_D$.

For $z\in \mathcal{N}_N$, it follows from the triangle inequality, the facts that $\Vert r_{K}\phi _z\Vert _{0,K} \le \Vert r_{K}\Vert _{0,K}$ and $\Vert j_{F}\phi _z\Vert _{0,F} \le \Vert j_{F}\Vert _{0,F}$, the Cauchy-Schwarz inequality, and (4.25) that

$$\begin{aligned} R_z(v,\mu )= & {} \sum _{K\in \mathcal{T}_z}(r_K\phi _z, v)_{K} -\sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \{ v\}_w)_{F} +\sum _{F\in \mathcal{E}_{j,z}}(j_F\phi _z, \{ v\}_w-\mu )_{F} \\\le & {} \sum _{K\in \mathcal{T}_z} \Vert r_{K}\phi _z\Vert _{0,K} \Vert v\Vert _{0,K} +\sum _{F\in \mathcal{E}_{j,z}} \Vert j_{F}\phi _z\Vert _{0,F} (\Vert \{ v \}_w\Vert _{0,F}+\Vert \{ v\}_w-\mu \Vert _{0,F}) \\\le & {} {\hat{\eta }}_{z} \left( \sum _{K\in \mathcal{T}_z} \displaystyle \frac{1}{h_K^2 \alpha _K} \Vert v\Vert _{0,K}^2 +\sum _{F \in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_Fa_{F,A}} (\Vert \{ v \}_w\Vert _{0,F}^2+\Vert \{ v\}_w-\mu \Vert _{0,F}^2) \right) ^{1/2}\\\le & {} C{\hat{\eta }}_{z} \left( \Vert \alpha ^{-1/2}\nabla ^{\perp }_h v\Vert _{0,\omega _z}^2 + \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_F \alpha _{F,A}} \Vert [\![ v]\!]\Vert _{0,F}^2 \right. \\&\left. + \displaystyle \sum _{F\in \mathcal{E}_{j,z}} \displaystyle \frac{1}{h_F\alpha _{F,H}} \Vert \{v\}_w-\mu \Vert _{0,F}^2 + \sum _{F\in \mathcal{E}_{N,z}} \displaystyle \frac{1}{ h_{F}\alpha _{F}}\Vert v \Vert _{0,F}^2 \right) ^{1/2} \\= & {} C{\hat{\eta }}_{z}|\!|\!|(v,\mu )|\!|\!|_{\alpha ,h,z} . \end{aligned}$$

This proves the theorem for $z\in \mathcal{N}_N$. $\square$

Fig. 1

Mesh generated by $\eta$

Fig. 2

Error and estimator $\eta$

5 Numerical Experiments

In this section, we report some numerical results for an interface problem with intersecting interfaces used by many authors, e.g., [13, 14, 20], which is considered as a benchmark test problem. For simplicity, we only test the $RT_{_\mathcal{T}}$ case with $k=0$. Other cases behave similarly.

Let $\varOmega =(-1,1)^2$ and

$$\begin{aligned} u(r,\theta )=r^{\gamma }\mu (\theta ) \end{aligned}$$

in the polar coordinates at the origin with $\mu (\theta )$ being a smooth function of $\theta$ [13]. The function $u(r,\theta )$ satisfies the interface equation with $A= \alpha I$, $\varGamma _N=\emptyset$, $f=0$, and

$$\begin{aligned} \alpha (x)=\left\{ \begin{array}{ll} R &{} \quad \text{ in } \, (0,1)^2\cup (-1,0)^2,\\ 1 &{} \quad \text{ in } \,\varOmega \setminus ([0,1]^2\cup [-1, 0]^2). \end{array}\right. \end{aligned}$$

The $\gamma$ depends on the size of the jump. In our test problem, $\gamma =0.1$ is chosen and is corresponding to $R\approx 161.4476387975881$. Note that the solution $u(r,\theta )$ is only in $H^{1+\gamma -\epsilon }(\varOmega )$ for any $\epsilon >0$ and, hence, it is very singular for small $\gamma$ at the origin. This suggests that refinement is centered around the origin.

Mesh generated by $\eta$ is shown in Fig. 1. The refinement is centered at origin. Similar meshes for this test problem generated by other error estimators can be found in [13, 14]. The comparison of the error and the $\eta$ is shown in Fig. 2. The error estimator is a guaranteed bound of the energy error. The effectivity index is close to 1. Moreover, the slope of the log(dof)- log(relative error) for $\eta$ is $-1/2$, which indicates the optimal decay of the error with respect to the number of unknowns.