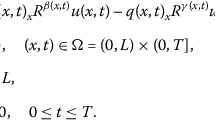A High-Order Compact Finite Difference Scheme for the Fractional Sub-diffusion Equation

Abstract

Based on the weighted and shifted Grünwald operator, a new high-order compact finite difference scheme is derived for the fractional sub-diffusion equation. It is proved that the difference scheme is unconditionally stable and convergent in $L_{\infty }$-norm by the energy method. The convergence order is $O(\tau ^3+h^4)$, where $\tau$ is the temporal step size and $h$ is the spatial step size. Although the unconditional stability and convergence of the difference scheme are obtained for all $\alpha \in (0, \alpha ^{*}],$ where $\alpha ^{*}=0.9569347,$ some numerical experiments show that they are valid for all $\alpha \in (0, 1).$ Finally, some numerical examples are given to confirm the theoretical results.

1 Introduction

During the past several decades, the study of fractional partial differential equations (FPDEs) has attracted many scholars’ attention. The classical integer order derivatives are the local operators, which may not be adequate to describe the underlying phenomena. The fractional integrals and derivatives enjoy the nonlocal properties. They can model anomalous transport phenomena and more accurately describe the evolution of a system in some physical and chemical processes. For more relevant references and books, readers can refer to the works [1–5]. Like traditional partial differential equations, most commonly, the exact solutions of fractional partial differential equations are not available. Even if their solutions can be found, they are usually in the forms of series, which are difficult to evaluate. One can read some relevant works [6–8]. So the numerical investigation of the fractional partial differential equations has been a vital topic in recent years.

For the time-fractional diffusion equations, there have been a lot of numerical works. Langlands and Henry [9] considered an implicit numerical method for solving the fractional diffusion equation and analyzed the accuracy and stability of the scheme. Zhuang et al. [10, 11] integrated the linear and non-linear sub-diffusion equations about the time variable $t,$ then approximated the obtained equivalent equations numerically with the idea of numerical integrals. Sun and Wu [12] first derived the error estimate of the $L_1$ formula to approximate the Caputo derivative and constructed the fully discrete difference scheme for the diffusion-wave equation. Gao and Sun [13] applied the $L_1$ approximation for the time-fractional derivative and developed a compact finite difference scheme for the fractional sub-diffusion equation. The solvability, stability and $L_{\infty }$ convergence are proved by the energy method. Zhang et al. [14] proposed a Crank–Nicolson-type difference scheme for solving the sub-diffusion equation, in which the discrete $H_1$ norm convergence has been proved and the maximum norm error estimate has been obtained. Adopting the Grünwald–Letnikov formula to approximate time-fractional derivative, Yuste [15, 16] proposed the explicit schemes and analyzed these two schemes using the Von Neumann method. Also, Cui [17, 18] proposed a compact difference scheme. In addition, some scholars are devoted to other numerical algorithms, including the finite element method [19], spectral element method [20, 21] and others.

Fractional derivatives are nonlocal and they have the character of history dependence, which implies a high storage requirement. Therefore, developing high-order numerical methods can reduce the requirement and computational complexity. Considerable attentions have been paid to the high-order schemes. Cao and Xu [22] constructed a high-order approximation scheme based on a modified 2-block-by-block method for nonlinear FODEs and proved that the convergence order of the scheme is $3+\alpha$ for $0<\alpha <1$, and 4 for $\alpha >1.$ Gao et al. [23] modified the $L_1$ approximation formula to discretize the Caputo fractional derivative and showed that the order of local truncation error is 3-$\alpha$ for $0<\alpha <1,$ but they did not provide a rigorous theoretical analysis about the stability and convergence of the obtained difference scheme. Li and Ding [24] derived a second-order difference approximation formula based on Lubich’s operator for the Riemann–Liouville fractional derivative, where the strict convergence analysis for the corresponding difference scheme has only been obtained for $\alpha \in [\frac{3}{8},1).$ Recently, by assembling the Grünwald–Letnikov difference operators with different weights and shifts, Deng’ group [25–28] has presented some high-order approximations to discretize the space-fractional derivatives. Following this idea, weighting two shifted Grünwald–Letnikov difference operators and choosing shifts $(p,q)=(0,-1),$ Wang and Vong [29] provided a second-order accuracy formula to approximate the time-fractional derivative and established a compact finite difference scheme for solving the modified anomalous fractional sub-diffusion equation.

Consider the following one-dimensional fractional sub-diffusion equation with non-homogeneous source term on the interval $[a,b]$

$$\begin{aligned}&{}^C_0\mathcal {D}^{\alpha }_tu(x,t)=K_{\alpha }\frac{\partial ^2 u(x,t)}{\partial x^2}+f(x,t),\quad x\in (a,b),~~t\in (0,T], \end{aligned}$$

(1.1)

$$\begin{aligned}&u(x,0)=\psi (x),\quad x\in (a,b), \end{aligned}$$

(1.2)

$$\begin{aligned}&u(a,t)=\beta (t),~~u(b,t)=\gamma (t),\quad t\in [0,T], \end{aligned}$$

(1.3)

where $0<\alpha <1$ and the operator ${}^C_0\mathcal {D}^{\alpha }_{t}$ denotes the Caputo fractional derivative of order $\alpha$ defined by [1]

$$\begin{aligned} {}^C_0\mathcal {D}^{\alpha }_{t}f(t)=\frac{1}{\Gamma (1-\alpha )}\int ^{t}_{0}\frac{f'(\xi )}{(t-\xi )^{\alpha }}d\xi , \end{aligned}$$

$K_{\alpha }$ is the generalized diffusion constant, $\Gamma (\cdot )$ is the gamma function, and $\beta (t),\gamma (t),\psi (x)$ and $f(x,t)$ are the known smooth functions, $\beta (0)=\psi (a),~\gamma (0)=\psi (b)$. Without loss of generality, suppose Eq. (1.1) with zero initial value $u(x,0)=0$, for any $x\in [a,b].$ Otherwise, we take a transform $v(x,t)=u(x,t)-\psi (x)$.

The main goal of this paper is to construct a high-order compact finite difference scheme and establish the corresponding error estimate. The method follows the idea of the weighted and shifted Grünwald–Letnikov difference operators [25, 29]. Choosing shifts $(p,q,r)=(0,-1,-2)$ and utilizing the equivalence of Riemann–Liouville derivative and Caputo derivative under some regularity assumptions, we derive a third-order accuracy formula to approximate Caputo fractional derivative and construct the corresponding compact difference scheme (called the $GL_3$ scheme) for the fractional sub-diffusion equation. The unconditional stability and $L_{\infty }$ convergence are proved by the discrete energy method. The main novelty of this paper is that we obtain a high-order approximation scheme in time by using the same grid points as [29]. This advantage implies that our scheme needs much less storage capacity than the scheme mentioned in [29], since fractional derivatives have memory and hereditary properties.

The outline of this paper is as follows. In Sect. 2, some notations and lemmas are listed. In Sect. 3, the $GL_3$ finite difference scheme is derived for the fractional sub-diffusion equation. The unconditional stability and convergence are rigorously proved in Sect. 4 by the discrete energy method. Some numerical examples are presented in Sect. 5 to support our theoretical results and indicate the efficiency of the difference scheme. Some comments are presented in the concluding section.

2 Some Notations and Lemmas

We commence with some definitions of fractional derivatives and Riemann–Liouville fractional integral.

Definition 2.1

[1–5] The $\alpha (n-1<\alpha <n)$ order fractional derivatives of the function $f(t)$ are defined as

• (1) Riemann–Liouville fractional derivative:

  $$\begin{aligned} {}_{0}\mathcal {D}^{\alpha }_tf(t)=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{dt^n}\int _{0}^t\frac{f(\xi )}{(t-\xi )^{\alpha +1-n}}d\xi , \end{aligned}$$

• (2) Liouville fractional derivative:

  $$\begin{aligned} {}_{-\infty }\mathcal {D}^{\alpha }_tf(t)=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{dt^n}\int _{-\infty }^t\frac{f(\xi )}{(t-\xi )^{\alpha +1-n}}d\xi . \end{aligned}$$

Definition 2.2

[1] The $\alpha \in \mathbb {R}_{+}$ order Riemann–Liouville fractional integral of the function $f(t)$ is defined as

$$\begin{aligned} {}_0\mathcal {D}^{-\alpha }_tf(t)=\frac{1}{\Gamma (\alpha )}\int ^{t}_0\frac{f(\xi )}{(t-\xi )^{1-\alpha }}d\xi . \end{aligned}$$

For the numerical approximation, take two positive integers $M,~N$ and let $h=(b-a)/M,~\tau =T/N$. Define $x_i=a+ih ~(0\le i\le M),~t_n=n\tau ~(0\le n\le N),\Omega _h=\{x_i~|~0\le i\le M\}, \Omega _{\tau }=\{t_n~|~0\le n\le N\}$, then the computational domain $[a,b]\times [0,T]$ is covered by $\Omega _h\times \Omega _{\tau }$. Let $\mathcal {V}=\{u_i^n~|~0\le i\le M,0\le n\le N\}$ be the grid function on the mesh $\Omega _h\times \Omega _{\tau }$. For any grid function $u\in \mathcal {V}$, we introduce the following notations

$$\begin{aligned} \delta _xu^n_{i-\frac{1}{2}}=\frac{1}{h}(u^n_i-u^n_{i-1}),~~ \delta ^2_xu^n_i=\frac{1}{h}(\delta _xu^n_{i+\frac{1}{2}}-\delta _xu^n_{i-\frac{1}{2}}) \end{aligned}$$

and the average operator

$$\begin{aligned} \fancyscript{A}u^n_i={\left\{ \begin{array}{ll}\frac{1}{12}(u^n_{i-1}+10u^n_i+u^n_{i+1})=\left( I+\frac{h^2}{12}\delta ^2_x\right) u^n_i,&{}1\le i\le M-1,\\ u^n_i,&{} i=0~\text {or}~M. \end{array}\right. } \end{aligned}$$

The following four lemmas will be used in the derivation of the difference scheme.

Define

$$\begin{aligned} \fancyscript{C}^{\alpha +m}(\mathbb {R})=\bigg \{f\bigg |\int ^{\infty }_{-\infty }(1+|\omega |)^{\alpha +m}|\hat{f}(\omega )|d\omega <+\infty , \hat{f}~\text {is the Fourier transform of}~ f\bigg \}. \end{aligned}$$

The textbook [30] provided the following result.

Lemma 2.1

If $f\in C^{2+m}(\mathbb {R}),$ then $f\in \fancyscript{C}^{\alpha +m}(\mathbb {R})$ is valid for $\alpha \in (0,1).$

Lemma 2.2

[31] Suppose that $f\in L_1(\mathbb {R})\cap \fancyscript{C}^{\alpha +1}(\mathbb {R})$, and define the shifted Grünwald difference operator by

$$\begin{aligned} A_{\tau ,p}^{(\alpha )}f(t)=\frac{1}{\tau ^{\alpha }}\sum ^{\infty }_{k=0}g^{(\alpha )}_kf(t-(k-p)\tau ), \end{aligned}$$

(2.1)

where $p$ is an integer and $g^{(\alpha )}_k=(-1)^k\left( {\begin{array}{c}\alpha \\ k\end{array}}\right) =\frac{\Gamma (k-\alpha )}{\Gamma (-\alpha )\Gamma (k+1)}$. Then

$$\begin{aligned} A_{\tau ,p}^{(\alpha )}f(t)={}_{-\infty }\mathcal {D}^{\alpha }_tf(t)+O(\tau ) \end{aligned}$$

(2.2)

uniformly for $t\in \mathbb {R}$ as $\tau \rightarrow 0$.

In fact, the sequences $\{g_k^{(\alpha )}\}$ in Eq. (2.1) are the coefficients of the power series of the function $(1-z)^{\alpha }$, i.e,

$$\begin{aligned} (1-z)^{\alpha }=\sum ^{\infty }_{k=0}(-1)^k\left( {\begin{array}{c}\alpha \\ k\end{array}}\right) z^k=\sum ^{\infty }_{k=0}g_k^{(\alpha )}z^k, \end{aligned}$$

for all $-1<z\le 1$, and they can be evaluated recursively

$$\begin{aligned} g^{(\alpha )}_0=1,~~g^{(\alpha )}_k=\left( 1-\frac{\alpha +1}{k}\right) g^{(\alpha )}_{k-1},\quad k=1,2,\ldots \end{aligned}$$

Lemma 2.3

[25] Let $f(t)\in L_1(\mathbb {R}),{}_{-\infty }\mathcal {D}^{\alpha +3}_{t}f(t)$ and its Fourier transform belong to $L_1(\mathbb {R})$. Define the weighted and shifted Grünwald difference operator by

$$\begin{aligned} \mathbb {D}^{\alpha }_{\tau }f(t)=\rho _1A_{\tau ,p}^{(\alpha )}f(t)+\rho _2A_{\tau ,q}^{(\alpha )}f(t)+\rho _3 A_{\tau ,r}^{(\alpha )}f(t), \end{aligned}$$

where

$$\begin{aligned}&\rho _1=\frac{12qr-(6q+6r+1)\alpha +3\alpha ^2}{12(qr-pq-pr+p^2)},~ \rho _2=\frac{12pr-(6p+6r+1)\alpha +3\alpha ^2}{12(pr-pq-qr+q^2)}, \\&\rho _3=\frac{12pq-(6p+6q+1)\alpha +3\alpha ^2}{12(pq-pr-qr+r^2)}, \end{aligned}$$

and $p,q$ and $r$ are all integers. Then we have

$$\begin{aligned} \mathbb {D}^{\alpha }_{\tau }f(t)={}_{-\infty }\mathcal {D}^{\alpha }_{t}f(t)+O(\tau ^3) \end{aligned}$$

uniformly for $t\in \mathbb {R}$ as $\tau \rightarrow 0$.

Remark

From the proof of Lemma 2.3, the condition that $f(t)\in L_1(\mathbb {R}), {}_{-\infty }\mathcal {D}^{\alpha +3}_{t}f(t)$ and its Fourier transform belong to $L_1(\mathbb {R})$ can be replaced by $f\in L_1(\mathbb {R}) \cap \fancyscript{C}^{\alpha +3}(\mathbb {R})$. Furthermore, if $\alpha \in (0,1),$ according to Lemma 2.1, $f\in C^{5}(\mathbb {R})$ satisfies the condition of Lemma 2.3.

Due to the symmetry of $p,q$ and $r$, we can suppose that $p>q>r$. By choosing $(p,q,r)=(0,-1,-2)$, we get

$$\begin{aligned} \rho _1=\frac{24+17\alpha +3\alpha ^2}{24}, \quad \rho _2=-\frac{11\alpha +3\alpha ^2}{12}, \quad \rho _3=\frac{5\alpha +3\alpha ^2}{24}. \end{aligned}$$

If $f(t)\in C[0,T]$, we define

$$\begin{aligned} \tilde{f}(t)={\left\{ \begin{array}{ll} f(t),&{}\text {when}\,\, t\in [0,T],\\ 0,&{}\text {when}\,\, t\in (-\infty ,0), \end{array}\right. } \end{aligned}$$

then $\tilde{f}(t)$ is a function on $\mathbb {R}$.

Now further assume that $f(t)\in C^5[0,T],$ and $d^kf(0)/dt^k=0,~~ k=0,1,\ldots ,5.$ Thus, $\tilde{f}(t)$ satisfies the conditions of Lemma 2.3. According to Lemma 2.3, we have

$$\begin{aligned} {}_0\mathcal {D}^{\alpha }_{t}f(t)&={}_{-\infty }\mathcal {D}^{\alpha }_{t}\tilde{f}(t) \\&=\rho _1A_{\tau ,0}^{(\alpha )}\tilde{f}(t)+\rho _2A_{\tau ,-1}^{(\alpha )}\tilde{f}(t)+\rho _3A_{\tau ,-2}^{(\alpha )}\tilde{f}(t)+O(\tau ^3)\\&=\frac{1}{\tau ^{\alpha }}\bigg [\rho _1\sum _{k=0}^{\infty }g^{(\alpha )}_k\tilde{f}(t-k\tau ) +\rho _2\sum _{k=0}^{\infty }g^{(\alpha )}_k\tilde{f}(t-(k+1)\tau )\nonumber \\&\quad +\rho _3\sum _{k=0}^{\infty }g^{(\alpha )}_k\tilde{f}(t-(k+2)\tau )\bigg ]+O(\tau ^3)\\&=\frac{1}{\tau ^{\alpha }}\bigg [\rho _1\sum _{k=0}^{\big [\frac{t}{\tau }\big ]}g^{(\alpha )}_k\tilde{f}(t-k\tau ) +\rho _2\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-1}g^{(\alpha )}_k\tilde{f}(t-(k+1)\tau )\nonumber \\&\quad +\rho _3\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-2}g^{(\alpha )}_k\tilde{f}(t-(k+2)\tau )\bigg ]+O(\tau ^3)\\&=\frac{1}{\tau ^{\alpha }}\bigg [\rho _1\sum _{k=0}^{\big [\frac{t}{\tau }\big ]}g^{(\alpha )}_kf(t-k\tau ) +\rho _2\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-1}g^{(\alpha )}_kf(t-(k+1)\tau )\nonumber \\&\quad +\rho _3\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-2}g^{(\alpha )}_kf(t-(k+2)\tau )\bigg ]+O(\tau ^3),\quad t\in [t_2,T]. \end{aligned}$$

Noticing the relationship [1, 14] of the Caputo fractional derivative and the Riemann–Liouvile fractional derivative:

$$\begin{aligned} {}_{0}\mathcal {D}^{\alpha }_{t}f(t)= \frac{f(0)t^{-\alpha }}{\Gamma (1-\alpha )}+{}^C_0\mathcal {D}^{\alpha }_{t}f(t), \end{aligned}$$

if $f(0)=0,$ we have

$$\begin{aligned} {}^C_0\mathcal {D}^{\alpha }_{t}f(t)&={}_{0}\mathcal {D}^{\alpha }_{t}f(t)\nonumber \\&= \frac{1}{\tau ^{\alpha }}\bigg [\rho _1\sum _{k=0}^{\big [\frac{t}{\tau }\big ]}g^{(\alpha )}_kf(t-k\tau ) +\rho _2\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-1}g^{(\alpha )}_kf(t-(k+1)\tau )\nonumber \\&\quad \ +\rho _3\sum _{k=0}^{\big [\frac{t}{\tau }\big ]-2}g^{(\alpha )}_kf(t-(k+2)\tau )\bigg ]+O(\tau ^3),\quad t\in [t_2,T]. \end{aligned}$$

(2.3)

Lemma 2.4

If $f(0)=0$, then it holds that ${}_0\mathcal {D}^{-\alpha }_t({}^C_0\mathcal {D}^{\alpha }_tf(t))=f(t)$, for $0<\alpha <1.$

Proof

Let us now consider the Riemann–Liouvile fractional integral of order $q$ of the fractional derivative of order $p$ [1]:

$$\begin{aligned} {}_0\mathcal {D}^{q}_{t}\big ({}_0\mathcal {D}^{p}_{t}f(t)\big )={}_0\mathcal {D}^{p+q}_{t}f(t), \quad -1<q<0<p<1. \end{aligned}$$

(2.4)

Under the condition $f(0)=0,$ we can see that

$$\begin{aligned} {}_0\mathcal {D}^{\alpha }_{t}f(t)={}^C_0\mathcal {D}^{\alpha }_tf(t). \end{aligned}$$

(2.5)

It follows from (2.4) and (2.5) that

$$\begin{aligned} {}_0\mathcal {D}^{-\alpha }_t\big ({}^C_0\mathcal {D}^{\alpha }_tf(t)\big ) ={}_0\mathcal {D}^{-\alpha }_t\big ({}_0\mathcal {D}^{\alpha }_tf(t)\big )=f(t). \end{aligned}$$

$\square$

To obtain the fourth-order accuracy in spatial direction, we need the following lemma.

Lemma 2.5

[32] Denote $\theta (s)=(1-s)^3[5- 3(1 - s)^2].$ If $g(x)\in C^6[a,b],$ $h=(b-a)/M, x_i=a+ih ~(0 \le i\le M),$ it holds that

$$\begin{aligned}&\frac{1}{12}[g^{\prime \prime }(x_{i-1})+10g^{\prime \prime }(x_i)+g^{\prime \prime }(x_{i+1})]=\frac{g(x_{i-1})-2g(x_i)+g(x_{i+1})}{h^2}\\&\quad +\,\frac{h^4}{360}\int _0^1[g^{(6)}(x_i-sh)+g^{(6)}(x_i+sh)]\theta (s)ds, \quad 1\le i\le M-1. \end{aligned}$$

We are now ready to establish our high-order compact scheme in the following section.

3 Derivation of the $GL_3$ Finite Difference Scheme

Let $\mathcal {V}_{\tau }=\{u~|~u=(u^0,u^1,\ldots ,u^{N})\}$ be grid function space on $\Omega _{\tau }$. For any grid function $u\in \mathcal {V}_{\tau }$, for simplicity, we formally define the time weighted and shifted Grünwald-Letnikov difference (TWSGD) operator

$$\begin{aligned} {}_0\mathbb {D}^{\alpha }_{\tau }u^n&=\frac{1}{\tau ^{\alpha }}\bigg [\rho _1\sum _{k=0}^{n}g^{(\alpha )}_ku^{n-k} +\rho _2\sum _{k=0}^{n-1}g^{(\alpha )}_ku^{n-k-1}+\rho _3\sum _{k=0}^{n-2}g^{(\alpha )}_ku^{n-k-2}\bigg ]\nonumber \\&=\frac{1}{\tau ^{\alpha }}\sum _{k=0}^{n}w^{(\alpha )}_ku^{n-k}, \quad n=2,3,\ldots ,N, \end{aligned}$$

(3.1)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} w^{(\alpha )}_{0}=\rho _1g^{(\alpha )}_{0},\\ w^{(\alpha )}_{1}=\rho _1g^{(\alpha )}_{1}+\rho _2g^{(\alpha )}_{0},\\ w^{(\alpha )}_{k}=\rho _1g^{(\alpha )}_{k}+\rho _2g^{(\alpha )}_{k-1}+\rho _3g^{(\alpha )}_{k-2},\quad k\ge 2. \end{array}\right. } \end{aligned}$$

Remark

When applying the TWSGD operator to approximate ${}_0^C\mathcal {D}^{\alpha }_tu(x_i,t_n)$ in Eq. (1.1), it ensures that the truncation error order is 3 on the grid points $t_n=n\tau (n=2,3,\ldots ,N)$ in temporal direction provided that $u(\cdot ,t)\in C^{5}[0,t_n]$ and $\frac{\partial ^k u(\cdot ,t)}{\partial t^k}|_{t=0}=0,~0\le k\le 5$. Nevertheless, we should consider the discretization scheme of Eq. (1.1) at the first time level alone.

Define the grid functions

$$\begin{aligned} U^n_i=u(x_i,t_n),~~f^n_i=f(x_i,t_n),\quad 0\le i\le M,~~0\le n\le N. \end{aligned}$$

Firstly, we derive the compact scheme of the fractional sub-diffusion equation (1.1) from the second level to $N$th level.

Suppose $u(x,t)\in C^{6,5}_{x,t}([a,b]\times [0,T])$ and $\partial ^ku(x,0)/\partial t^k=0$ for $k=0,1,\ldots ,5.$ Considering Eq. (1.1) on the grid point $(x_i,t_n)$, we have

$$\begin{aligned} {}^C_0\mathcal {D}^{\alpha }_tu(x_i,t_n)=K_{\alpha }\frac{\partial ^2 u(x_i,t_n)}{\partial x^2}+f(x_i,t_n),\quad 0\le i\le M,~~2\le n\le N. \end{aligned}$$

(3.2)

For the time discretization, we choose the TWSGD operator ${}_0\mathbb {D}^{\alpha }_{\tau }U^n_i$ to approximate ${}^C_0\mathcal {D}^{\alpha }_tu(x_i,$ $t_n),$ which implies

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_kU^{n-k}_i =K_{\alpha }u_{xx}(x_i,t_n)+f(x_i,t_n)+O(\tau ^3),\quad 0\le i\le M,~~2\le n\le N.\nonumber \\ \end{aligned}$$

(3.3)

For the space discretization, performing the average operator $\fancyscript{A}$ on both sides of Eq. (3.3), we get

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_k\fancyscript{A}U^{n-k}_i \!=\!K_{\alpha }\fancyscript{A}u_{xx}(x_i,t_n)+\fancyscript{A}f(x_i,t_n)+O(\tau ^3),~~1\!\le \! i\!\le \! M-1,~2\!\le \! n\!\le \! N.\nonumber \\ \end{aligned}$$

(3.4)

Using Lemma 2.5, we have

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_k\fancyscript{A}U^{n-k}_i =K_{\alpha }\delta ^2_xU^n_i+\fancyscript{A}f^n_i+R^n_i,\quad 1\le i\le M-1,~~2\le n\le N, \end{aligned}$$

(3.5)

where there exists a positive constant $C_1$ such that

$$\begin{aligned} |R^n_{i}|\le C_1(\tau ^3+h^4),\quad 1\le i\le M-1,~~2\le n\le N. \end{aligned}$$

Next, we derive the compact scheme of the fractional sub-diffusion equation (1.1) at the first time level.

By operating the Riemann–Liouville fractional integral operator ${}_0\mathcal {D}^{-\alpha }_t$ on both sides of Eq. (1.1), we obtain

$$\begin{aligned} {}_0\mathcal {D}^{-\alpha }_t\big [{}^C_0\mathcal {D}^{\alpha }_tu(x,t)\big ]={}_0\mathcal {D}^{-\alpha }_t\bigg [K_{\alpha }\frac{\partial ^2u(x,t)}{\partial x^2}\bigg ] +{}_0\mathcal {D}^{-\alpha }_tf(x,t). \end{aligned}$$

(3.6)

Using Lemma 2.4, we have

$$\begin{aligned} u(x,t)=\frac{K_{\alpha }}{\Gamma (\alpha )}\int ^{t}_{0}\frac{u_{xx}(x,\xi )}{(t-\xi )^{1-\alpha }}d\xi +F(x,t), \end{aligned}$$

(3.7)

where $F(x,t)={}_0\mathcal {D}^{-\alpha }_tf(x,t)$.

Taking $t=t_1$ in Eq.(3.7), we have

$$\begin{aligned} u(x,t_1)=\frac{K_{\alpha }}{\Gamma (\alpha )}\int ^{t_1}_{0}\frac{u_{xx}(x,\xi )}{(t_1-\xi )^{1-\alpha }}d\xi +F(x,t_1). \end{aligned}$$

(3.8)

Using $u_{xx}(x,0), u_{xxt}(x,0)$ and $u_{xx}(x,t_1)$ makes a Hermite interpolation of $u_{xx}(x,\xi )$ on the interval $[0,t_1]$, as follows

$$\begin{aligned} P(x,\xi )= u_{xx}(x,0)+u_{xxt}(x,0)(\xi -0) +\frac{u_{xx}(x,t_1)-u_{xx}(x,0)-\tau u_{xxt}(x,0)}{\tau ^2}(\xi -0)^2, \end{aligned}$$

where

$$\begin{aligned} \tilde{R}(x):=u_{xx}(x,\xi )-P(x,\xi )=\frac{1}{6}u_{xxttt}(x,\eta )\xi ^2(\xi -t_1),\quad \eta \in (0,t_1). \end{aligned}$$

Suppose $u(x,0)=0$ and $u_t(x,0)=0$. We obtain an approximation

$$\begin{aligned} u(x,t_1)&\approx \frac{K_{\alpha }}{\Gamma (\alpha )}\int ^{t_1}_{0}\frac{P(x,\xi )}{(t_1-\xi )^{1-\alpha }}d\xi +F(x,t_1) \nonumber \\&=\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\tau ^{\alpha }u_{xx}(x,t_1)+F(x,t_1),\quad a\le x\le b. \end{aligned}$$

(3.9)

It is easy to check that

$$\begin{aligned}&\big |u(x,t_1)-\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\tau ^{\alpha }u_{xx}(x,t_1)-F(x,t_1)\big | \\&\quad =\frac{K_{\alpha }}{\Gamma (\alpha )}\bigg |\int ^{t_1}_{0}(t_1-\xi )^{\alpha -1} \big [u_{xx}(x,\xi )-P(x,\xi )\big ]d\xi \bigg |\\&\quad \le \frac{K_{\alpha }}{6\Gamma (\alpha )}\int ^{\tau }_{0} (\tau -\xi )^{\alpha -1}\big |u_{xxttt}(x,\eta )\xi ^2(\xi -\tau )\big |d\xi \\&\quad \le \frac{K_{\alpha }C_2\tau ^3}{24\Gamma (\alpha )}\int ^{\tau }_{0} (\tau -\xi )^{\alpha -1}d\xi =\frac{K_{\alpha }C_2\tau ^{3+\alpha }}{24\Gamma (\alpha +1)}, \end{aligned}$$

where

$$\begin{aligned} C_2=\mathop {\max }_{a\le x\le b}\mathop {\max }_{0\le t\le T}|u_{xxttt}(x,t)|. \end{aligned}$$

It follows from (3.9) that

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}u(x_i,t_1) =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}u_{xx}(x_i,t_1)+\frac{1}{\tau ^{\alpha }}F(x_i,t_1)+O(\tau ^{3}),\quad 0\le i\le M. \end{aligned}$$

(3.10)

For the space discretization, performing the average operator $\fancyscript{A}$ on both side of Eq. (3.10), we have

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}\fancyscript{A}u(x_i,t_1) =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\fancyscript{A}u_{xx}(x_i,t_1)+\frac{1}{\tau ^{\alpha }}\fancyscript{A}F(x_i,t_1) +O(\tau ^3),\quad 1\le i\le M-1.\nonumber \\ \end{aligned}$$

(3.11)

Using Lemma 2.5, we obtain

$$\begin{aligned} \frac{1}{\tau ^{\alpha }}\fancyscript{A}U^1_i =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\delta ^2_xU^1_i+\frac{1}{\tau ^{\alpha }}\fancyscript{A}F(x_i,t_1) +R^1_i,\quad 1\le i\le M-1, \end{aligned}$$

(3.12)

where there exists a positive constant $C_3$ such that

$$\begin{aligned} |R^1_i|\le C_3(\tau ^{3}+h^4),\quad 1\le i\le M-1. \end{aligned}$$

(3.13)

Omitting the small terms $R^1_i$ in Eq. (3.12) and $R^n_i$ in Eq. (3.5), replacing $U_i^n$ with its numerical approximation $u^n_i$, and noticing the initial-boundary conditions

$$\begin{aligned}&U_i^0=0 , \quad 1\le i\le M-1, \end{aligned}$$

(3.14)

$$\begin{aligned}&U_0^n=\beta (t_n),\quad U_M^n=\gamma (t_n),\quad 0\le n\le N, \end{aligned}$$

(3.15)

we get the following $GL_3$ difference scheme

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_k\fancyscript{A}u^{n-k}_i =K_{\alpha }\delta ^2_xu^n_i+\fancyscript{A}f^n_i,\quad 1\le i\le M-1,~~2\le n\le N,\end{aligned}$$

(3.16)

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\fancyscript{A}u^{1}_i =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\delta ^2_xu^1_i+\frac{1}{\tau ^{\alpha }}\fancyscript{A}F(x_i,t_1) ,\quad 1\le i\le M-1,\end{aligned}$$

(3.17)

$$\begin{aligned}&u^0_i=0,\quad 1\le i\le M-1,\end{aligned}$$

(3.18)

$$\begin{aligned}&u_0^n=\beta (t_n),~~u_M^n=\gamma (t_n),\quad 0\le n\le N. \end{aligned}$$

(3.19)

For the first time level, Eq. (3.17) is a tridiagonal system of linear algebraic equations and the coefficient matrix is strictly diagonally dominant. Similarly, from the second time level to $N$th time level, Eq. (3.16) is also a tridiagonal system of linear algebraic equations and the coefficient matrix is also strictly diagonally dominant. Therefore, the $GL_3$ difference scheme (3.16)–(3.19) has a unique solution and can be easily solved with Thomas algorithm.

4 The Analysis of Stability and Convergence of the $GL_3$ Difference Scheme

We give some notations and lemmas, which will be used in the analysis of the stability and convergence.

Define $\mathcal {V}_h=\{u~|~u=(u_0,u_1,\ldots ,u_M),~u_0=u_M=0\}$ be grid function space on $\Omega _h$. For any $u,v\in \mathcal {V}_h$, we define the discrete inner products, the corresponding norms and $L_{\infty }$-norm as follows

$$\begin{aligned} (u,v)&=h\sum ^{M-1}_{i=1}u_iv_i,~ \langle u,v \rangle =h\sum _{i=1}^{M}\big (\delta _xu_{i-\frac{1}{2}}\big )\big (\delta _xv_{i-\frac{1}{2}}\big ),\\ \Vert \delta ^2_xu\Vert&=\sqrt{(\delta _x^2u,\delta ^2_xu)},~\Vert \delta _xu\Vert =\sqrt{\langle u,u \rangle }, ~\Vert u\Vert _{\infty }=\mathop {\max }_{0\le i\le M}|u_i|. \end{aligned}$$

Lemma 4.1

[33] Let $u\in \mathcal {V}_h$. Then, it holds that

$$\begin{aligned} \Vert u\Vert _{\infty }\le \frac{\sqrt{b-a}}{2}\Vert \delta _xu\Vert ,\quad \Vert u\Vert \le \frac{b-a}{\sqrt{6}}\Vert \delta _xu\Vert . \end{aligned}$$

Lemma 4.2

[13] Let $v\in \mathcal {V}_h$. Then, it holds that

$$\begin{aligned} \frac{2}{3}\Vert v\Vert ^2 \le (\fancyscript{A}v,v)\le \Vert v\Vert ^2. \end{aligned}$$

Define

$$\begin{aligned} (u,v)_{A}:=(\fancyscript{A}u,v), \quad \text {for}\quad u, v\in \mathcal {V}_h. \end{aligned}$$

Obviously, $(\cdot ,\cdot )_A$ is an inner product. And $\Vert u\Vert _A=\sqrt{(u,u)_A}$ denotes the induced norm.

Lemma 4.3

Let $\{w_k^{(\alpha )}\}^{\infty }_{k=0}$ be defined as in (3.1). If $\alpha \in (0,\alpha ^{*}]$, then for any positive integer $N$ and real vector $(v^0,v^1,\ldots ,v^N)\in R^{N+1}$, it holds that

$$\begin{aligned} \sum ^{N}_{n=0}\left( \sum ^{n}_{k=0}w^{(\alpha )}_{k}v^{n-k}\right) v^n\ge 0, \end{aligned}$$

where $\alpha ^{*}=0.9569347.$

Proof

For simplicity, we denote $w_k=w_k^{(\alpha )}$ without ambiguity. One can easily check that, the validity of Lemma 4.3 is equivalent to proving that the symmetric Toeplitz matrix $W$ is positive semi-definite, where

$$\begin{aligned} W=\left( \begin{array}{ccccc} w_0&{} \frac{w_1}{2} &{}\frac{w_2}{2}&{}\cdots &{} \frac{w_{N}}{2}\\ \frac{w_1}{2} &{}w_0&{} \frac{w_1}{2}&{}\ddots &{} \vdots \\ \frac{w_2}{2}&{} \frac{w_1}{2}&{} \ddots &{}\ddots &{} \frac{w_2}{2}\\ \vdots &{}\ddots &{}\ddots &{} w_0&{} \frac{w_1}{2}\\ \frac{w_{N}}{2}&{}\cdots &{} \frac{w_2}{2}&{}\frac{w_1}{2}&{}w_0\\ \end{array} \right) \!. \end{aligned}$$

Notice that the generating function [25] of $W$ is given by

$$\begin{aligned} f(\alpha ,x)&= w_0+\frac{1}{2}\sum ^{\infty }_{k=1}w_ke^{\mathbf{i}kx}+\frac{1}{2}\sum ^{\infty }_{k=1}w_ke^{-\mathbf{i}kx}\\&=\rho _1g_0^{(\alpha )}+\frac{1}{2}\left( \rho _1g^{(\alpha )}_1+\rho _2g^{(\alpha )}_{0}\right) e^{\mathbf{i}x}+\frac{1}{2} \sum ^{\infty }_{k=2}\left( \rho _1g^{(\alpha )}_{k}+\rho _2g^{(\alpha )}_{k-1}+\rho _3g^{(\alpha )}_{k-2}\right) e^{\mathbf{i}kx}\\&\quad +\frac{1}{2}(\rho _1g^{(\alpha )}_1+\rho _2g^{(\alpha )}_{0})e^{-\mathbf{i}x}+\frac{1}{2} \sum ^{\infty }_{k=2}(\rho _1g^{(\alpha )}_{k}+\rho _2g^{(\alpha )}_{k-1}+\rho _3g^{(\alpha )}_{k-2})e^{-\mathbf{i}kx}\\&=\frac{1}{2}(\rho _1+\rho _2e^{\mathbf{i}x}+\rho _3e^{2\mathbf{i}x})\sum ^{\infty }_{k=0}g^{(\alpha )}_ke^{\mathbf{i}kx} \!+\frac{1}{2}\left( \rho _1\!+\!\rho _2e^{-\mathbf{i}x}\!+\!\rho _3e^{-2\mathbf{i}x}\right) \sum ^{\infty }_{k=0}g^{(\alpha )}_ke^{-\mathbf{i}kx}\\&=\frac{1}{2}\left( \rho _1+\rho _2e^{\mathbf{i}x}+\rho _3e^{2\mathbf{i}x}\right) (1-e^{\mathbf{i}x})^{\alpha } +\frac{1}{2}\left( \rho _1+\rho _2e^{-\mathbf{i}x}+\rho _3e^{-2\mathbf{i}x}\right) (1-e^{-\mathbf{i}x})^{\alpha }\!. \end{aligned}$$

Obviously, $f(\alpha ,x)$ is a real-valued and even function of $x$ on $[-\pi ,\pi ]$, so we just consider its principal value on $[0,\pi ]$ [25]. Applying the formula

$$\begin{aligned} (1-e^{\pm \mathbf{i}x})^{\alpha }=\left( 2\sin \frac{x}{2}\right) ^{\alpha }e^{\pm \mathbf{i}\alpha \left( \frac{x}{2}-\frac{\pi }{2}\right) }, \end{aligned}$$

we obtain

$$\begin{aligned} f(\alpha ,x)&= (2\sin \frac{x}{2})^{\alpha }\bigg [\rho _1\cos \left( \alpha (\frac{x}{2}-\frac{\pi }{2})\right) \bigg .\\&\bigg .+\rho _2\cos \left( x+\alpha \left( \frac{x}{2}-\frac{\pi }{2}\right) \right) +\rho _3\cos \bigg (2x+\alpha (\frac{x}{2}-\frac{\pi }{2})\bigg )\bigg ], \end{aligned}$$

where the generating function $f(\alpha ,x)$ is a transcendental function, which is difficult to analyze the property analytically.

Now, let us analyze the generating function $f(\alpha ,x)$ numerically. Figure 1 shows that $f(\alpha ,x)\le 0$ on a very small domain. To depict the values of $f(\alpha ,x)$ clearly, we draw the contours of the function $f(\alpha ,x)$ and the amplified contours on the partial domain (see Figs. 2, 3). In fact, we need an $\alpha ^{*},$ which satisfies that for all $x\in [0,\pi ],$ $f(\alpha ,x)\ge 0$ when $\alpha \in (0,\alpha ^{*}].$ Based on this, we consider the tangent line parallel to $x$-axis of the curve $f(\alpha ,x)=0$. Solve the simultaneous system

$$\begin{aligned} {\left\{ \begin{array}{ll} f(\alpha ,x)=0,\\ f_x(\alpha ,x)=0. \end{array}\right. } \end{aligned}$$

By Newton iteration method, we get its solution $(\alpha ^{*}, x^{*}) =(0.9569347,0.9529852),$ which is the coordinate of the tangent point. Thus, $f(\alpha ,x)\ge 0$ for $\alpha \in (0,\alpha ^{*}].$ The lemma follows as a result of the Grenander–Szegö Theorem [34]. $\square$

Fig. 1

The generating function $f(\alpha ,x)$

Fig. 2

Contours of the generating function $f(\alpha ,x)$ for $\alpha \in (0,1),\,x\in [0,\pi ]$

Fig. 3

Contours of the generating function $f(\alpha ,x)$ amplified partially for $\alpha \in (0.9,1),\,x\in [0,\pi /2]$

Lemma 4.4

If $\alpha \in (0,1),$ then,

$$\begin{aligned} 10w^{(\alpha )}_0-3\Gamma (\alpha +3)>\frac{1}{3}, \end{aligned}$$

where $w^{(\alpha )}_0=\frac{24+17\alpha +3\alpha ^2}{24}.$

Proof

Noticing a two-side inequality of the Gamma function[35]:

$$\begin{aligned} n^{1-\alpha }<\frac{\Gamma (n+1)}{\Gamma (n+\alpha )}<(n+1)^{1-\alpha },\quad 0<\alpha <1,~~n=1,2,\ldots \end{aligned}$$

Taking $n=3,$ we have

$$\begin{aligned} \frac{3}{2}\cdot 4^{\alpha } <\Gamma (3+\alpha )<2\cdot 3^{\alpha }. \end{aligned}$$

Hence,

$$\begin{aligned} 10w^{(\alpha )}_0-3\Gamma (\alpha +3)=\frac{5(24+17\alpha +3\alpha ^2)}{12}-3\Gamma (\alpha +3)> \frac{5(24+17\alpha +3\alpha ^2)}{12}-6\cdot 3^{\alpha }.\nonumber \\ \end{aligned}$$

(4.1)

Let $g(\alpha )=\frac{5(24+17\alpha +3\alpha ^2)}{12}-6\cdot 3^{\alpha }.$ It is easy to analyze that the function $g(\alpha )$ is monotone increasing for $\alpha \in (0,\alpha _0)$ and monotone decreasing for $\alpha \in (\alpha _0,1),$ where $\alpha _0=0.0957$, acquired by bisection method. Together with $g(0)=4,$ $g(\alpha _0)=4.0241$ and $g(1)=\frac{1}{3},$ one finds that $g(\alpha )\ge g(1)=\frac{1}{3}$ for $\alpha \in (0,1).$ From (4.1), we get

$$\begin{aligned} 10w^{(\alpha )}_0-3\Gamma (\alpha +3)>\frac{1}{3}. \end{aligned}$$

Now we turn to the analysis of the stability and convergence for the $GL_3$ difference scheme. To this end, a Prior estimate will be given to simplify the proof.$\square$

Lemma 4.5

Suppose $\{v_i^n\}$ is the solution of the following difference scheme

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_k\fancyscript{A}v^{n-k}_i =K_{\alpha }\delta ^2_xv^n_i+f^n_i,\quad 1\le i\le M-1,~~2\le n\le N, \end{aligned}$$

(4.2)

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\fancyscript{A}v^{1}_i =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\delta ^2_xv^1_i+f^1_i ,\quad 1\le i\le M-1,\end{aligned}$$

(4.3)

$$\begin{aligned}&v^0_i=\phi _i,\quad 1\le i\le M-1,\end{aligned}$$

(4.4)

$$\begin{aligned}&v_0^n=0,~~v_M^n=0,\quad 0\le n\le N. \end{aligned}$$

(4.5)

then, if $\alpha \in (0,\alpha ^{*}]$, we have

$$\begin{aligned} \tau \sum ^{n}_{m=1}\Vert \delta _xv^m\Vert ^2 \le&\tau \bigg [\frac{80|w^{(\alpha )}_1|^2}{(\Gamma (\alpha +3))^2}+|w^{(\alpha )}_1|^2 +\frac{w^{(\alpha )}_0(b-a)^2}{2K_{\alpha }\tau ^{\alpha }}\bigg ]\Vert \delta _xv^0\Vert ^2+C_4\tau \sum ^{n}_{m=1}\Vert f^m\Vert ^2,\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad 1\le n\le N, \end{aligned}$$

(4.6)

where $C_4=\frac{3(b-a)^2}{8K_{\alpha }^2}+\frac{15(b-a)^2(w_0^{(\alpha )})^2\Gamma (3+\alpha )}{16K_{\alpha }^2(10w_0^{(\alpha )}-3\Gamma (3+\alpha ))}$ and $\Vert f^n\Vert ^2=h\sum ^{M-1}_{i=1}(f^n_i)^2.$

Proof

(I) Multiplying Eq. (4.2) by $h(\frac{1}{K_{\alpha }}\fancyscript{A}v^n_i)$ and summing up for $i$ from 1 to $M-1$, we obtain

$$\begin{aligned} \frac{1}{K_{\alpha }\tau ^{\alpha }}\sum ^{n}_{k=0}w^{(\alpha )}_{k}(\fancyscript{A}v^n,\fancyscript{A}v^{n-k}) -(v^n,\delta ^2_xv^n)_A=\frac{1}{K_{\alpha }}(v^n,f^n)_A,\quad 2\le n\le N. \end{aligned}$$

(4.7)

For the second term on the left hand of (4.7), we have

$$\begin{aligned} -(v^n,\delta ^2_xv^n)_A&=-\left( v^n,\delta ^2_xv^n\right) -\frac{h^2}{12}(\delta ^2_xv^n,\delta ^2_xv^n) \nonumber \\&=\Vert \delta _xv^n\Vert ^2-\frac{h^2}{12}\Vert \delta ^2_xv^n\Vert ^2\ge \frac{2}{3}\Vert \delta _xv^n\Vert ^2. \end{aligned}$$

(4.8)

For the term on the right hand of (4.7), using Lemmas 4.1 and 4.2, it holds that

$$\begin{aligned} \frac{1}{K_{\alpha }}(v^n,f^n)_A&\le \frac{1}{K_{\alpha }}\Vert v^n\Vert _{A}\cdot \Vert f^n\Vert _{A}\nonumber \\&\le \frac{1}{K_{\alpha }}\bigg (\frac{2K_{\alpha }}{(b-a)^2}\Vert v^n\Vert _{A}^2 +\frac{(b-a)^2}{8K_{\alpha }}\Vert f^n\Vert _{A}^2\bigg )\nonumber \\&\le \frac{1}{K_{\alpha }}\bigg (\frac{2K_{\alpha }}{(b-a)^2}\Vert v^n\Vert ^2 +\frac{(b-a)^2}{8K_{\alpha }}\Vert f^n\Vert ^2\bigg )\nonumber \\&\le \frac{1}{3}\Vert \delta _xv^n\Vert ^2+\frac{(b-a)^2}{8K^2_{\alpha }}\Vert f^n\Vert ^2. \end{aligned}$$

(4.9)

Substituting (4.8)-(4.9) into (4.7), we get

$$\begin{aligned} \frac{1}{K_{\alpha }\tau ^{\alpha }}\sum ^{n}_{k=0}w^{(\alpha )}_{k}(\fancyscript{A}v^n,\fancyscript{A}v^{n-k})+\frac{1}{3}\Vert \delta _xv^n\Vert ^2 \le \frac{(b-a)^2}{8K_{\alpha }^2}\Vert f^n\Vert ^2,\quad 2\le n\le N. \end{aligned}$$

(4.10)

Replacing $n$ by $m$ and summing up for $m$ from $2$ to $n$ on both sides of (4.10), we have

$$\begin{aligned} \frac{1}{K_{\alpha }\tau ^{\alpha }}\sum ^{n}_{m=2}\sum ^{m}_{k=0}w^{(\alpha )}_{k}(\fancyscript{A}v^m,\fancyscript{A}v^{m-k})+ \frac{1}{3}\sum ^{n}_{m=2}\Vert \delta _xv^m\Vert ^2 \le \frac{(b-a)^2}{8K_{\alpha }^2}\sum ^{n}_{m=2}\Vert f^m\Vert ^2.\qquad \end{aligned}$$

(4.11)

(II) Multiplying Eq.(4.3) by $\frac{w^{(\alpha )}_0}{K_{\alpha }}h\fancyscript{A}v^1_i$ and summing up for $i$ from 1 to $M-1$, we obtain

$$\begin{aligned} \frac{1}{K_{\alpha }\tau ^{\alpha }}w^{(\alpha )}_0(\fancyscript{A}v^1,\fancyscript{A}v^1) -\frac{2w^{(\alpha )}_0}{\Gamma (\alpha +3)}(v^1,\delta ^2_xv^1)_A =\frac{w^{(\alpha )}_0}{K_{\alpha }}(v^1,f^1)_A. \end{aligned}$$

(4.12)

For the second term on the left hand of (4.12), we have

$$\begin{aligned} -\frac{2w^{(\alpha )}_0}{\Gamma (\alpha +3)}(v^1,\delta ^2_xv^1)_A&=-\frac{2w^{(\alpha )}_0}{\Gamma (\alpha +3)}\left( v^1+\frac{h^2}{12}\delta ^2_xv^1,\delta ^2_xv^1\right) \nonumber \\&=-\frac{2w^{(\alpha )}_0}{\Gamma (\alpha +3)}\left( -\Vert \delta _xv^1\Vert ^2+\frac{h^2}{12}\Vert \delta ^2_xv^1\Vert ^2\right) \nonumber \\&\ge \frac{4w^{(\alpha )}_0}{3\Gamma (\alpha +3)}\Vert \delta _xv^1\Vert ^2. \end{aligned}$$

(4.13)

For the right hand of (4.12), by Lemmas 4.1 and 4.2, we get

$$\begin{aligned} \frac{w^{(\alpha )}_0}{K_{\alpha }}(v^1,f^1)_A&\le \frac{w^{(\alpha )}_0}{K_{\alpha }}\Vert v^1\Vert _A\cdot \Vert f^1\Vert _A \nonumber \\&\le \frac{w^{(\alpha )}_0}{K_{\alpha }}\big (\epsilon \Vert v^1\Vert ^2_A +\frac{1}{4\epsilon }\Vert f^1\Vert ^2_A\big )\nonumber \\&\le \frac{w^{(\alpha )}_0}{K_{\alpha }}\big (\epsilon \Vert v^1\Vert ^2 +\frac{1}{4\epsilon }\Vert f^1\Vert ^2\big )\nonumber \\&=\frac{\epsilon (b-a)^2w^{(\alpha )}_0}{6K_{\alpha }}\Vert \delta _xv^1\Vert ^2 +\frac{w_0^{(\alpha )}}{4\epsilon K_{\alpha }}\Vert f^1\Vert ^2. \end{aligned}$$

(4.14)

Substituting (4.13)–(4.14) into (4.12) and taking $\epsilon =\frac{4K_{\alpha }(10w_0^{(\alpha )}-3\Gamma (3+\alpha ))}{5w^{(\alpha )}_0(b-a)^2\Gamma (3+\alpha )}$, we have

$$\begin{aligned} \frac{1}{K_{\alpha }\tau ^{\alpha }}w^{(\alpha )}_0(\fancyscript{A}v^1,\fancyscript{A}v^1) +\frac{2}{5}\Vert \delta _xv^1\Vert ^2 \le \frac{5(b-a)^2(w_0^{(\alpha )})^2\Gamma (3+\alpha )}{16K_{\alpha }^2(10w_0^{(\alpha )}-3\Gamma (3+\alpha ))}\Vert f^1\Vert ^2, \end{aligned}$$

(4.15)

where one can easily find that $\epsilon >0$ from Lemma 4.4.

Multiplying Eq.(4.3) by $\frac{w^{(\alpha )}_1}{K_{\alpha }}h\fancyscript{A}v^0_i$ and summing up for $i$ from 1 to $M-1$ lead to

$$\begin{aligned} \frac{w^{(\alpha )}_1}{K_{\alpha }\tau ^{\alpha }}(\fancyscript{A}v^0,\fancyscript{A}v^1) -\frac{2w^{(\alpha )}_1}{\Gamma (\alpha +3)}(v^0,\delta ^2_xv^1)_A =\frac{w^{(\alpha )}_1}{K_{\alpha }}(v^0,f^1)_A. \end{aligned}$$

(4.16)

Using the inverse estimate[33], we have

$$\begin{aligned} -\frac{2w^{(\alpha )}_1}{\Gamma (\alpha +3)}(v^0,\delta ^2_xv^1)_A&=-\frac{2w^{(\alpha )}_1}{\Gamma (\alpha +3)}(v^0+\frac{h^2}{12}\delta ^2_xv^0,\delta ^2_xv^1)\nonumber \\&=-\frac{2w^{(\alpha )}_1}{\Gamma (\alpha +3)} \big (-(\delta _xv^0,\delta _xv^1)+\frac{h^2}{12}(\delta ^2_xv^0,\delta ^2_xv^1)\big )\nonumber \\&\ge -\frac{2|w^{(\alpha )}_1|}{\Gamma (\alpha +3)} \big |-(\delta _xv^0,\delta _xv^1)+\frac{h^2}{12}(\delta ^2_xv^0,\delta ^2_xv^1)\big |\nonumber \\&\ge -\frac{2|w^{(\alpha )}_1|}{\Gamma (\alpha +3)} \big (\Vert \delta _xv^0\Vert \cdot \Vert \delta _xv^1\Vert +\frac{h^2}{12}\cdot \frac{2}{h}\Vert \delta _xv^0\Vert \cdot \frac{2}{h}\Vert \delta ^2_xv^1\Vert \big )\nonumber \\&\ge -\frac{8|w^{(\alpha )}_1|}{3\Gamma (\alpha +3)} \Vert \delta _xv^1\Vert \cdot \Vert \delta _xv^0\Vert \nonumber \\&\ge -\frac{1}{15}\Vert \delta _xv^1\Vert ^2-\frac{80|w^{(\alpha )}_1|^2}{3(\Gamma (\alpha +3))^2}\Vert \delta _xv^0\Vert ^2. \end{aligned}$$

(4.17)

According to Lemmas 4.1 and 4.2, the following inequality holds

$$\begin{aligned} \frac{w^{(\alpha )}_1}{K_{\alpha }}(v^0,f^1)_A&\le \frac{|w^{(\alpha )}_1|}{K_{\alpha }}\Vert v^0\Vert _A\cdot \Vert f^1\Vert _A \nonumber \\&\le |w^{(\alpha )}_1|\Vert v^0\Vert \cdot \frac{1}{K_{\alpha }}\Vert f^1\Vert \nonumber \\&\le \frac{2|w^{(\alpha )}_1|^2}{(b-a)^2}\Vert v^0\Vert ^2+\frac{(b-a)^2}{8K^2_{\alpha }}\Vert f^1\Vert ^2\nonumber \\&\le \frac{|w^{(\alpha )}_1|^2}{3}\Vert \delta _xv^0\Vert ^2 +\frac{(b-a)^2}{8K_{\alpha }^2}\Vert f^1\Vert ^2. \end{aligned}$$

(4.18)

Substituting (4.17) and (4.18) into (4.16), we obtain

$$\begin{aligned} \frac{w^{(\alpha )}_1}{K_{\alpha }\tau ^{\alpha }}(\fancyscript{A}v^0,\fancyscript{A}v^1) -\frac{1}{15}\Vert \delta _xv^1\Vert ^2&\le \bigg [\frac{80|w^{(\alpha )}_1|^2}{3(\Gamma (\alpha +3))^2}+\frac{|w^{(\alpha )}_1|^2}{3}\bigg ]\Vert \delta _xv^0\Vert ^2\nonumber \\&+\,\frac{(b-a)^2}{8K_{\alpha }^2}\Vert f^1\Vert ^2. \end{aligned}$$

(4.19)

Adding $\frac{w^{(\alpha )}_0}{K_{\alpha }\tau ^{\alpha }}(\fancyscript{A}v^0,\fancyscript{A}v^0)$ on the both sides of the result of addition of (4.11), (4.15), (4.19) yields

$$\begin{aligned}&\frac{1}{K_{\alpha }\tau ^{\alpha }}\sum ^{n}_{m=0}\sum ^{m}_{k=0}w^{(\alpha )}_{k}(\fancyscript{A}v^m,\fancyscript{A}v^{m-k})+ \frac{1}{3}\sum ^{n}_{m=1}\Vert \delta _xv^m\Vert ^2\nonumber \\&\!\!\quad \le \bigg [\frac{80|w^{(\alpha )}_1|^2}{3(\Gamma (\alpha +3))^2}+\frac{|w^{(\alpha )}_1|^2}{3}\bigg ]\Vert \delta _xv^0\Vert ^2 +\frac{w^{(\alpha )}_0}{K_{\alpha }\tau ^{\alpha }}(\fancyscript{A}v^0,\fancyscript{A}v^0) +\frac{1}{3}C_4\sum ^{n}_{m=1}\Vert f^m\Vert ^2,\nonumber \\&\!\!\quad \le \bigg [\frac{80|w^{(\alpha )}_1|^2}{3(\Gamma (\alpha +3))^2}+\frac{|w^{(\alpha )}_1|^2}{3} +\frac{w^{(\alpha )}_0(b-a)^2}{6K_{\alpha }\tau ^{\alpha }}\bigg ]\Vert \delta _xv^0\Vert ^2 +\frac{1}{3}C_4\sum ^{n}_{m=1}\Vert f^m\Vert ^2,\quad 1\!\le \! n\!\le \! N, \end{aligned}$$

(4.20)

where $C_4=\frac{3(b-a)^2}{8K_{\alpha }^2}+\frac{15(b-a)^2(w_0^{(\alpha )})^2\Gamma (3+\alpha )}{16K_{\alpha }^2(10w_0^{(\alpha )}-3\Gamma (3+\alpha ))}.$ According to Lemma 4.3, we have

$$\begin{aligned} \sum ^{n}_{m=0}\sum ^{m}_{k=0}w^{(\alpha )}_{k}(\fancyscript{A}v^m,\fancyscript{A}v^{m-k})\ge 0. \end{aligned}$$

(4.21)

Combining (4.20) with (4.21), it holds that

$$\begin{aligned} \tau \sum ^{n}_{m=1}\Vert \delta _xv^m\Vert ^2 \le \tau \bigg [\frac{80|w^{(\alpha )}_1|^2}{(\Gamma (\alpha +3))^2}+|w^{(\alpha )}_1|^2 +\frac{w^{(\alpha )}_0(b-a)^2}{2K_{\alpha }\tau ^{\alpha }}\bigg ]\Vert \delta _xv^0\Vert ^2 +C_4\tau \sum ^{n}_{m=1}\Vert f^m\Vert ^2.\nonumber \\ \end{aligned}$$

(4.22)

$\square$

From the above lemma, we can obtain the stability of the difference scheme.

Theorem 4.1

The $GL_3$ difference scheme (3.16)–(3.19) is unconditionally stable to the right hand term and initial value for all $\alpha \in (0,\alpha ^{*}]$.

We now consider the convergence of the difference scheme (3.16)–(3.19).

Theorem 4.2

Assume that $u(x,t)\in C^{6,5}_{x,t}([a,b]\times [0,T])$ is the solution of problem (1.1)–(1.3), and $\{u^n_i|0\le i\le M,0\le n\le N\}$ is the solution of the finite difference scheme (3.16)–(3.19). Suppose

$$\begin{aligned} \frac{\partial ^ku(x,0)}{\partial t^k}=0,\quad k=0,1,\ldots ,5. \end{aligned}$$

(4.23)

Denote

$$\begin{aligned} e^n_i=u(x_i,t_n)-u_i^n,\quad 0\le i\le M,~~0\le n\le N. \end{aligned}$$

Then, when $N\tau \le T,$ it holds

$$\begin{aligned} \tau \sum ^{N}_{m=1}\Vert e^m\Vert _{\infty }\le \frac{b-a}{2}\sqrt{C_4T(C^2_1T+C^2_3)}(\tau ^3+h^4). \end{aligned}$$

Proof

Subtracting (3.16)–(3.19) from (3.5), (3.12), (3.14) and (3.15), respectively, we have the error equations

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\sum _{k=0}^nw^{(\alpha )}_k\fancyscript{A}e^{n-k}_i =K_{\alpha }\delta ^2_xe^n_i+R^n_i,~~~1\le i\le M-1,~2\le n\le N,\end{aligned}$$

(4.24)

$$\begin{aligned}&\frac{1}{\tau ^{\alpha }}\fancyscript{A}e^{1}_i =\frac{2K_{\alpha }}{\Gamma (\alpha +3)}\delta ^2_xe^1_i+R^1_i ,~~1\le i\le M-1,\end{aligned}$$

(4.25)

$$\begin{aligned}&e^0_i=0,~~~1\le i\le M-1,\end{aligned}$$

(4.26)

$$\begin{aligned}&e_0^n=0,~~e_M^n=0,~~~0\le n\le N. \end{aligned}$$

(4.27)

From Lemma 4.5, it holds that

$$\begin{aligned} \tau \sum ^{n}_{m=1}\Vert \delta _xe^m\Vert ^2 \le C_4\tau \sum ^{n}_{m=1}\Vert R^m\Vert ^2\le C_4(C^2_1T+C^2_3)(b-a)(\tau ^3+h^4)^2,\quad 1\le n\le N, \end{aligned}$$

or,

$$\begin{aligned} \frac{4}{b-a}\tau \sum ^{n}_{m=1}\Vert e^m\Vert ^2_{\infty }\le C_4(C^2_1T+C^2_3)(b-a)(\tau ^3+h^4)^2,\quad 1\le n\le N. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \bigg (\tau \sum ^n_{m=1}\Vert e^m\Vert _{\infty }\bigg )^2&\le \bigg (\tau \sum ^n_{m=1}1^2\bigg )\bigg (\tau \sum ^n_{m=1}\Vert e^m\Vert ^2_{\infty }\bigg )\\&\quad \le \frac{1}{4}C_4T(C^2_1T+C^2_3)(b-a)^2(\tau ^3+h^4)^2,\quad 1\le n\le N. \end{aligned}$$

Hence,

$$\begin{aligned} \tau \sum ^n_{m=1}\Vert e^m\Vert _{\infty }\le \frac{b-a}{2}\sqrt{C_4T(C^2_1T+C^2_3)}(\tau ^3+h^4),\quad 1\le n\le N. \end{aligned}$$

$\square$

Remark

The condition (4.23) can be guaranteed by Dimitrov’s work [36]. Furthermore, the condition (4.23) is only sufficient but not necessary. Some examples in Sect. 5 can verify this conclusion. On the other hand, under the condition $\alpha \in (0,\alpha ^{*}]$, the stability and convergence of $GL_3$ difference scheme can be acquired. Though we can not get the same conclusion for $\alpha \in (\alpha ^{*},1)$ by using the present analytical method, many numerical examples show that the stability and convergence of our scheme still hold for $\alpha \in (\alpha ^{*},1)$. We hope that such a problem can be solved in the near future work.

5 Numerical Examples

In this section, we report on some numerical results to show the effectiveness and convergence orders of our difference scheme.

Consider the following problem

$$\begin{aligned} {}^C_0\mathcal {D}^{\alpha }_tu(x,t)&=\frac{\partial ^2u(x,t)}{\partial x^2} +\sin (x)t^{\beta }\bigg [\frac{\Gamma (\beta +1)}{\Gamma (\beta +1-\alpha )}t^{-\alpha }+1\bigg ],~~x\in (0,1) ,~~t\in (0,1],\end{aligned}$$

(5.1)

$$\begin{aligned} u(x,0)&=0,~~x\in (0,1),\end{aligned}$$

(5.2)

$$\begin{aligned} u(0,t)&=0,~~~u(1,t)=\sin (1)t^{\beta },~~t\in [0,1], \end{aligned}$$

(5.3)

where $\beta \in \mathbb {R}_{+}$. The exact solution is $u(x,t)=t^{\beta }\sin (x)$.

Let

$$\begin{aligned} E_{\infty }(h,\tau )=\max _{0\le k\le N}\max _{0\le i\le M}|u(x_i,t_k)-u^k_{i}|, \end{aligned}$$

and assume

$$\begin{aligned} E_{\infty }(h,\tau ) = O(\tau ^p+h^q). \end{aligned}$$

If $\tau$ is small enough, then $E_{\infty }(h,\tau ) \approx O(h^q)$. Consequently, $\frac{E_{\infty }(2h,\tau )}{E_{\infty }(h,\tau )}\approx 2^q$ and hence $q \approx \log _2\left( \frac{E_{\infty }(2h,\tau )}{E_{\infty }(h,\tau )}\right)$ is the convergence order with respect to the spatial step-size. Similarly, we obtain $p \approx \log _2\left( \frac{E_{\infty }(h,2\tau )}{E_{\infty }(h,\tau )}\right)$ for small enough $h$. Denote

$$\begin{aligned} \hbox {Order1}=\log _2\left( \frac{E_{\infty }(h,2\tau )}{E_{\infty }(h,\tau )}\right) ,\quad \hbox {Order2}=\log _2\left( \frac{E_{\infty }(2h,\tau )}{E_{\infty }(h,\tau )}\right) . \end{aligned}$$

We solve problem (5.1)–(5.3) by using $GL_3$ finite difference scheme (3.16)–(3.19). In order to check the convergence order in temporal direction, we apply our scheme on a coarse grid $\tau$ and then on a finer grid of size $\tau /2$ with the same sufficiently small spatial step size $h$. Similarly, in order to check the convergence order in spatial direction, we apply our scheme on a coarse grid $h$ and then on a finer grid of size $h/2$ with the same sufficiently small temporal step size $\tau$.

Firstly, taking $\beta =5$, Table 1 presents the maximum norm errors and the corresponding convergence orders of $GL_3$ finite difference scheme for $\alpha \in (0,1)$ in temporal direction, where the spatial step size $h=\frac{1}{1000}$ is fixed. We observe that our scheme generates the temporal accuracy with the order of $3$. Table 2 shows that our scheme has the accuracy of order $4$ in spatial direction for $\alpha \in (0,1)$, where the temporal step size $\tau =\frac{1}{12000}$ is fixed.

Table 1 The maximum norm errors and convergence orders in temporal direction with $\beta =5$

Table 2 The maximum norm errors and convergence orders in spatial direction with $\beta =5$

In Figs. 4 and 5, we compare the exact solution and the numerical solution with different $\alpha , \alpha =0.25,0.75$ respectively. We can see that the fitting degree is perfect by using the $GL_3$ difference scheme to approximate the problem (5.1)–(5.3) with $\beta =5$, which implies that our scheme is efficient.

Secondly, taking $\beta =3+\alpha , 3, 2.5$ respectively, one can find that the condition (4.23) in convergence Theorem 4.2 is not satisfied longer. Now we would like to test the efficiency of the $GL_3$ finite difference scheme for those cases.

In order to test the convergence order of our scheme in temporal direction, we fix sufficiently small spatial step size $h=\frac{1}{1000}$ and vary the temporal step sizes. Tables 3, 4 and 5 list the numerical results for different parameters. Just as we hope, the third-order convergence of our scheme in temporal direction can still be achieved. The results tell us that maybe the conditions of the above convergence theorem can be relaxed a little. Similarly, in order to test the convergence order of our scheme in spatial direction, we fix sufficiently small temporal step size $\tau =\frac{1}{12000}$ and vary the spatial step sizes. The numerical results show our scheme has the fourth-order accuracy in spatial direction for $\alpha \in (0,1)$. Here, Table 6 just lists the numerical results for $\beta =2.5$.

Fig. 4

Comparison between the exact solution and the numerical solution with $\alpha =0.25$ when $\beta =5$

Fig. 5

Comparison between the exact solution and the numerical solution with $\alpha =0.75$ when $\beta =5$

Table 3 The maximum norm errors and convergence orders in temporal direction with $\beta =3+\alpha$

Table 4 The maximum norm errors and convergence orders in temporal direction with $\beta =3$

Table 5 The maximum norm errors and convergence orders in temporal direction with $\beta =2.5$

Table 6 The maximum norm errors and convergence orders in spatial direction with $\beta =2.5$

Thirdly, taking $\beta =2$, the exact solution does not satisfy $\frac{\partial ^2 u(x,0)}{\partial t^2}=0$ . With sufficiently small spatial step $h=\frac{1}{1000}$, we test the temporal convergence order. From Table 7, we can see that the third-order convergence in temporal direction can only be achieved for $\alpha \in (0,0.5)$, which implies that the condition $\frac{\partial ^k u(x,0)}{\partial t^k}=0$ for $k=0,1,2$ in Theorem 4.2 is a must. Table 8 shows that the fourth-order convergence in spatial direction can still be achieved.

Table 7 The maximum norm errors and convergence orders in temporal direction with $\beta =2$

Table 8 The maximum norm errors and convergence orders in spatial direction with $\beta =2$

Finally, Tables 9 and 10 report the numerical errors and convergence orders in temporal direction for the problems with the exact solutions $u(x,t)=t^{0.2}\sin (x)$ and $u(x,t)=t\sin (x)$, respectively. The third-order convergence of difference scheme in temporal direction can not be achieved for the above two problems. However, the maximum norm errors are sufficiently small, which implies our scheme still has a good fitting degree for those cases.

Table 9 The maximum norm errors and convergence orders in temporal direction with $\beta =0.2$

Table 10 The maximum norm errors and convergence orders in temporal direction with $\beta =1$

6 Conclusion

In this paper, based on the weighted and shifted Grünwald operator in time direction and the compact technique in space direction, a high-order compact difference scheme ($GL_3$ scheme) is derived to solve the fractional sub-diffusion equation. By using the energy method, we proved that our difference scheme is unconditionally stable to the non-homogeneous term and the numerical solution is convergent in the maximum norm. The temporal convergence order and the spatial convergence order of our scheme can reach three and four respectively, provided that some regularities of solution hold. Some numerical examples have been given to show the effectiveness and convergence orders of our scheme.

The Caputo fractional derivative is equivalent to the Riemann–Liouvile fractional derivative with zero initial value for $\alpha \in (0,1)$. By weighting the shifted Grünwald-Letnikov operator linearly, we choose $(p,q,r)=(0,-1,-2)$ to obtain the TWSGD operator, which approximates the Caputo fractional derivative with the third-order accuracy. The absolute values of $p, q$ and $r$ are the numbers of left shifts of the grid point.

For multi-dimensional fractional sub-diffusion equation, alternating direction implicit (ADI) methods become urgent and important due to large amounts of storages and computation complexity. How to construct a third-order convergent ADI difference scheme in time to solve this kind of problems seems to be a difficult task, which will be considered in the future.