1 Introduction

In this article, we are interested in the derivation of an integrated Herschel-Bulkley model for shallow flows, as well as in the design of a numerical algorithm to solve the resulting equations. The goal is to simulate the evolution of thin sheet of viscoplastic materials on inclined planes and, in particular, to be able to compute the evolution from dynamic to stationary states.

Let us recall that for Newtonian fluids the constitutive law expresses the linear relation between the deviatoric part of the stress tensor, σ′, and the rate of strain tensor, D(u), through a constant coefficient, the viscosity μ: σ′=μD(u). This law typically leads to the well-known Navier-Stokes equations. However, many materials of real world applications can not be described by such a linear constitutive law. This leads to more refined relations which take into account these more complicated rheologies—generically referred to as non-Newtonian. Non-Newtonian fluids can exhibit various forms of “non-linearity”: for instance, instead of being constant, the viscosity coefficient can be a function of the rate of shear or can depend on the history of the flow and exhibits signs of hysteresis; another example is the presence of a threshold in the constitutive law (the reader is referred to classical textbooks on rheology for more examples and details, e.g. [7, 25]). One of the causes of non-Newtonian character of the rheology studied in this paper is indeed plasticity (along with another property which is shear-thinning or shear-thickening as we will see in the following).

Viscoplastic materials are characterized by the existence of a yield stress: below a certain critical threshold in the imposed stress, there is no deformation and the material behaves like a rigid solid, but when that yield value is exceeded, the material flows like a fluid. Such flow behavior can be encountered in many practical situations such as food pastes, cosmetics creams, heavy oils, mud and clays, lavas and avalanches. As a consequence, the theory of the fluid mechanics of such materials has applications in a wide variety of fields such as chemical industry, food processing and geophysical fluid dynamics.

Among numerous models used to describe the rheology of viscoplastic materials, Bingham (linear model with plasticity, [6]) and Herschel-Bulkley (power law model with plasticity, [19]) models are probably the most iconic. The Herschel-Bulkley model is expressed as:

(1)

where K is the consistency, τ y is the yield stress and |D(u)| is the second invariant of the rate of strain (we will give complete definitions and notations in the following section). This model can be seen as a generalization of the Bingham model which is retrieved from (1) by taking ℘=1. On the one hand, Bingham model is the simplest model when it comes to describe plasticity. On the other hand, if we take τ y =0 and ℘<1, we end up with the classical power-law (shear-thinning) model. Evidently, if τ y =0 and ℘=1, (1) leads to the classic Navier-Stokes equations.

We will illustrate our developments on a model based on (1) with applications in the field of avalanche of dense material. We note that it is clear, from the literature on the subject (see [1] and references therein), that it is very difficult to postulate a precise constitutive relation for the stress tensor in terms of a deformation measure that correctly describes avalanche behavior encountered in natural environments (landslides, debris flow, snow avalanches, etc). However, in recent years, Herschel-Bulkley model has attracted growing attention both from the experimental and theoretical viewpoints (see for instance [2] and references therein). Indeed, it allows to gain insight into the dynamics of aforementioned natural viscoplastic materials.

As mentioned at the beginning of this introduction, apart from the difficulty associated to the constitutive relation, there is another source of complication associated to the flows we are considering here: we have to deal with free surfaces. Since this article aims at laying foundations for simulations of 3D non-Newtonian free surface flows, we want to work with reduced models. Indeed, even if it is now possible to compute such 3D flows by solving the full equations, it must be noted that the global computational time is still very expensive, especially if one wants to reach long physical times to study the stopping dynamics of the material (such times can be rather long depending on the value of τ y ). The classical idea is thus to rely on reduced models, in such a way important physical features are retained as much as possible, but computational difficulties are significantly smoothed out. In the context of non-Newtonian fluids, there are essentially two families of approaches to deal with this issue: lubrication theory and shallow water models.

On the one hand, in lubrication models, fluid velocity and pressure are determined by the local fluid height and its derivatives. Originally, these methods were derived for gentle slopes and thin flows. Nevertheless, they can be extended to the case of steep slopes, as it was pointed out by Balmforth et al. in [4]. Some other works on this issue, and in the context of the Herschel-Bulkley model, can be found for instance in [2, 3, 24].

On the other hand, for thicker flows, shallow water approaches consist in deriving governing equations by averaging the local mass and momentum equations across the stream depth. Regarding the modeling of Herschel-Bulkley fluids, we can mention the works [20, 22, 26, 28]. In [8], another kind of shallow water model is derived by considering a constant profile for the velocity along the vertical and using a variational formulation of the Navier-Stokes equations for Bingham fluids, by choosing convenient test functions. Compared to previous ones, the advantage of this model lies in its validity for null slopes.

In this paper, we thus extend our previous work [8], dedicated to Bingham model, by considering instead the model (1). This allows us to tackle practical situations, such as the one presented in [2]. More precisely, starting from a 3D incompressible fluid modeled by the Navier-Stokes equations, together with the Herschel-Bulkley constitutive law (1), and with a free surface, we introduce its formulation as a variational inequality and derive a shallow water asymptotic of this system. To solve numerically the obtained model, we need to treat the optimization problem coming from the plastic behavior of the material: this is done with an augmented Lagrangian approach inspired by the seminal work of Glowinski and coworkers (see [11] for a recent review). In the context of shallow water problems, we adopt a finite volume approach to discretize the equations. A careful treatment must be made to design a well-balanced scheme when coupling the finite volume scheme and the augmented Lagrangian method. This idea was first introduced in [8], in the context of a linear viscoplastic law, and is extended here to the case of a power viscoplastic law such as (1). We note that [16] present the numerical simulation of compressible viscoplastic flows by another method coupling augmented Lagrangian, finite volume scheme and flux limiter based techniques for the convective terms encountered in the model. However, the well-balanced aspect was not considered.

The well-balanced properties are related to the stationary solutions of the system. In our case, we seek numerical schemes which preserve exactly two types of stationary solutions. For hyperbolic systems with source terms, a discretization of the source terms compatible with the one of the flux term must be performed. Otherwise, stemming from the numerical diffusion terms, a first order error in space takes place. This error, after time iterations, may yield large errors in wave amplitude and speed. The pioneering work by Roe [27] relates the choice of the approximation of the source term with the property of preserving stationary solutions. Bermúdez and Vázquez-Céndón introduce in [5] an extension of Roe solver, in the context of shallow water equations, which preserves exactly the stationary solution of water at rest. This work originated the so-called “well-balanced” solvers, in the sense that the discrete source terms balance the discrete flux terms when computed on some (or all) of the steady solutions of the continuous system. Different extensions have been done: see for instance Greenberg-Leroux [17], LeVeque [23], Chacón et al. [10].

In the present paper, the difficulty to design a well-balanced scheme comes from the fact that an extra source term depends on the multiplier of the augmented Lagrangian method.

This work is organized as follows: after this introduction we describe the three-dimensional Herschel-Bulkley model from which we derive the integrated model. This derivation is developed in Sect. 3, where we perform the asymptotic analysis of the system. In Sect. 4, a coupled finite volume/augmented Lagrangian method with well-balanced property is proposed to solve the model and illustrated in the one-dimensional-in-space case. Finally, in Sect. 5, we present several numerical tests to validate the various properties of the model and the numerical approximation. First, a simplified model for a duct flow is studied and compared to an analytical solution. Then, we set-up two numerical tests to explore the various regimes of the rheological law: at high and small rate of shear. The latter corresponding to an academic test of avalanche which shows the ability of the method to compute stationary states, i.e. to determine the time and material height profile when the avalanche stops.

2 Variational Formulation of the Herschel-Bulkley Model

In this section, we describe the governing equations for a Herschel-Bulkley fluid confined to a domain \(\mathcal{D}(t) \subset\mathbb{R}^{3}\) with a smooth boundary \(\partial\mathcal{D}(t)\).

Since we deal with an incompressible fluid, we have

$$ \operatorname{div} {\boldsymbol{u}}= 0 \quad\hbox{in }\mathcal{D}(t),$$
(2)

where u is the Eulerian velocity field. We consider the time interval (0,T) with T>0 to solve the evolution problem.

In the following, the space and time coordinates as well as all mechanical fields are non dimensional, so we introduce some notations for the characteristic variables: ρ c , V c , L c , T c , f c , τ c and p c corresponding respectively to density, velocity, length, time, body force, yield stress and pressure.

The conservation of mass is given by

$$ \mathrm{St} \frac{\partial\rho}{\partial t} + {\boldsymbol{u}}\cdot \nabla\rho= 0\quad\hbox{in } \mathcal{D}(t)$$
(3)

where \(\rho=\rho(t,x) \ge\underline{\rho} > 0\) is the mass density distribution and \(\mathrm{St}= L_{c}/(V_{c}T_{c})\) is the Strouhal number.

For incompressible fluids, the stress tensor σ is usually decomposed into an isotropic part \(-p\mathbf{I}\) where \(p=-\operatorname{trace}({\boldsymbol{\sigma}})/3\) represents the pressure field and a remainder called the deviatoric part of the stress tensor \({\boldsymbol{\sigma}}'= {\boldsymbol{\sigma}}+p\mathbf{I}\). Thus, momentum balance law in Eulerian coordinates reads

$$ \rho \biggl(\mathrm{St}\frac{\partial{{\boldsymbol{u}}} }{\partial t} + ({\boldsymbol{u}}\cdot \nabla) {\boldsymbol{u}} \biggr) - \operatorname{div} {\boldsymbol{\sigma }}' + \frac{1}{\mathrm{Fr}^2} \nabla p = \frac{1}{\mathrm{Fr}^2}\rho{{\boldsymbol{f}}} \quad\hbox{in } \mathcal{D}(t),$$
(4)

where f denotes the body forces. The Froude number is \(\mathrm{Fr}^{2}= \rho_{c} V_{c}^{2}/p_{c}\) where the characteristic pressure is chosen as p c =ρ c f c L c .

With the definition of the deviatoric stress, we specify the rheology of the fluid and we get a closed problem together with conservation of mass and momentum (3), (4). We write the constitutive law for a Herschel-Bulkley fluid:

(5)
(6)

where D(u)=(∇ u+∇ T u)/2 is the rate of strain tensor, \(|{\boldsymbol{D}}({\boldsymbol {u}})|=(\sum_{i,j=1}^{3} [({\boldsymbol{\nabla}}{\boldsymbol{u}}+{\boldsymbol{\nabla}}^{T} {\boldsymbol{u}})/2]_{i j}^{2} )^{1/2}\) and 0<℘<1 is the power associated to the Herschel-Bulkley law. For this range of values the effective viscosity decreases with the amount of deformation, leading to the so-called shear-thinning effect. The coefficient \(\eta_{1} \ge\underline{\eta} > 0\) is defined as a function of ℘ and the consistency K through,

$$ \eta_1= 2^{\wp-1} K.$$
(7)

When considering a density-dependent model, the coefficient η 1 depends on the density ρ through a constitutive function, i.e.

$$ \eta_1=\eta_1(\rho).$$
(8)

We now describe the Reynolds and the Bingham numbers, respectively,

$$\mathrm{Re} =\frac{\rho_c V_c L_c}{K ( \frac{V_c}{L_c})^{\wp-1} }, \quad\quad\mathrm{Bi} =\frac{\tau_c L_c^{\wp}}{K V_c^{\wp}},$$

and we also define the quotient \(\mathrm{B} = \mathrm{Bi/Re}\).

For boundary conditions, we assume that \(\partial\mathcal{D}(t)\) is split in two disjoint parts: \(\partial\mathcal{D}(t) = \varGamma_{b}(t)\cup\varGamma_{s}(t)\) where Γ b (t) is the part of the fluid which is on the solid bottom, and Γ s (t) is the free surface region.

We will denote as n the outward unit normal on \(\partial\mathcal{D}(t)\) and we adopt the following notation for the tangential and normal decomposition of any velocity field u and any density of surface forces σn,

$${\boldsymbol{u}}= u_n {\boldsymbol{n}}+ {\boldsymbol{u}}_t,\quad \hbox{with } u_n = {\boldsymbol{u}}\cdot{\boldsymbol{n}}, \quad \quad {\boldsymbol{\sigma}} {\boldsymbol{n}}= \sigma_{n}{\boldsymbol{n}}+ {\boldsymbol{\sigma}}_{t} \quad\hbox{with }\sigma_{n} ={\boldsymbol{\sigma}} {\boldsymbol{n}}\cdot{\boldsymbol{n}}.$$

On Γ b (t), we consider a Navier condition with a friction coefficient α and a no-penetration condition

$$ {\boldsymbol{\sigma}}_t=-\alpha{\boldsymbol{u}}_t,\quad \quad {\boldsymbol{u}}\cdot{\boldsymbol{n}}= 0 \quad\hbox{on }\varGamma_b(t).$$
(9)

As usual for a free surface, we assume a no-stress condition

$$ {\boldsymbol{\sigma}} {\boldsymbol{n}}= 0 \quad \hbox{on }\varGamma_s(t),$$
(10)

and the advection of the fluid by the flow:

$$ \mathrm{St}\frac{\partial1_{\mathcal{D}(t)}}{\partial t} + {\boldsymbol {u}}\cdot\nabla 1_{\mathcal{D}(t)} =0,$$
(11)

where \(1_{\mathcal{D}(t)}\) is the characteristic function of the domain \(\mathcal{D}(t)\).

Finally, we denote initial conditions as:

$$ {\boldsymbol{u}}\vert_{t=0}= {\boldsymbol{u}}^0,\quad\quad\rho\vert_{t=0}=\rho^0.$$
(12)

To tackle this problem, we opt for a variational formulation, originally presented by Duvaut-Lions in [12]. We use a variational principle written in terms of velocities and the mathematical formulation ends up with an implicit variational inequality.

Let us set the following space for the test functions:

$$\mathcal{V}(t) = \bigl\{{\boldsymbol{\Phi}}\in W^{1,1+\wp}\bigl(\mathcal {D}(t)\bigr)^3 / \operatorname{div} {\boldsymbol{\Phi}}= 0 \hbox{ in } \mathcal{D}(t), {\boldsymbol{\Phi}}\cdot {\boldsymbol{n}}= 0 \hbox{ on }\varGamma_b(t) \bigr\}.$$

The variational formulation of (2), (4), (5), (6), (9) and (10) for the velocity field yields

(13)

Note that if we prefer to formulate the problem in terms of velocity and pressure, we may consider the space:

$$\mathcal{W}(t) = \bigl\{{\boldsymbol{\Phi}}\in W^{1,1+\wp}\bigl(\mathcal {D}(t)\bigr)^3 / {\boldsymbol{\Phi}}\cdot{\boldsymbol{n}}= 0\hbox{ on } \varGamma_b(t) \bigr\},$$

to deduce:

$$ \left\{ \everymath{\displaystyle}\begin{array}{l}\forall t\in(0,T),\ {\boldsymbol{u}}(t,\cdot) \in\mathcal{W}(t), p(t,\cdot) \in L^{1+\wp}\bigl( \mathcal{D}(t)\bigr),\ \forall{\boldsymbol {\varPhi}}\in\mathcal{W}(t),\ \forall q \in L^{1+\wp}\bigl(\mathcal{D}(t)\bigr)\\[6pt]\int_{\mathcal{D}(t)} \rho \biggl(\mathrm{St} \frac{\partial{{\boldsymbol{u}}} }{\partial t} + ({\boldsymbol {u}}\cdot\nabla) {\boldsymbol{u}} \biggr) \cdot({\boldsymbol{\Phi}}- {\boldsymbol{u}}) - \frac{1}{\mathrm{Fr}^2} \int_{\mathcal{D}(t)} p( \operatorname{div} {\boldsymbol{\Phi }}- \operatorname{div} {\boldsymbol{u}}) \\[12pt]\quad{} + \frac{1}{\mathrm{Re}}\int_{\mathcal{D}(t)} 2 \eta_1(\rho)\frac{{\boldsymbol{D}}({\boldsymbol{u}})}{|{\boldsymbol{D}}({\boldsymbol {u}})|^{1-\wp}}: \bigl({\boldsymbol{D}}({\boldsymbol{\Phi}})- {\boldsymbol{D}}({\boldsymbol{u}})\bigr) + \tau_y \mathrm{B} \int _{\mathcal{D}(t)} \bigl( \vert{\boldsymbol {D}}({\boldsymbol{\Phi}})\vert - \vert {\boldsymbol{D}}({\boldsymbol{u}})\vert \bigr) \\[12pt]\quad{}+ \int_{\varGamma _b(t)} \alpha{\boldsymbol{u}}_t \cdot ({\boldsymbol{\Phi}}_t-{\boldsymbol{u}}_t) \ge \frac{1}{\mathrm{Fr}^2} \int_{\mathcal{D}(t)} \rho{\boldsymbol{f}}\cdot({\boldsymbol{\Phi }}- {\boldsymbol{u}}),\\[12pt]\int_{\mathcal{D}(t)} q \operatorname{div} {\boldsymbol{u}}=0.\end{array} \right.$$
(14)

To conclude, the problem of the flow of an inhomogeneous Herschel-Bulkley fluid is thus recast as finding the velocity field u and the density ρ verifying (3), (8), (12) and (13), or equivalently, as finding the velocity field u, the pressure p and the density ρ verifying conditions (3), (8), (12) and (14).

3 An Integrated Herschel-Bulkley Model

We now derive an integrated model and further consider an asymptotic regime, with respect to physical constants, to finally obtain a shallow water type model involving a variational inequality.

From now on, we focus on the problem (14) and consider the case of a plane slope.

Let \(\varOmega\subset\mathbb{R}^{2}\) be a fixed bounded domain, so

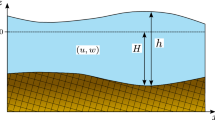
$$\mathcal{D}(t) = \bigl\{ (x,z); x \in\varOmega, 0 < z < h(t,x) \bigr\},$$

where h(t,x) is the thickness of the fluid and x=(x 1,x 2). In this case, free surface and bottom boundaries are defined as

$$\varGamma_s(t)=\bigl\{ (x,z); x \in\varOmega, z = h(t,x) \bigr\},\quad\quad \varGamma_b(t)=\partial\mathcal{D}(t) \setminus \varGamma_s(t).$$

We denote by v=(v 1,v 2) (resp. f x ) the horizontal (in the (Ω×z) frame of reference) component of the velocity field (resp. body forces) and by w (resp. f z ) the vertical one, i.e. u=(v,w) (resp. f=(f x ,f z )).

3.1 Averaged Equations

First of all, we rewrite (11), taking into account our choice of geometry, so it reads

$$ \mathrm{St} \frac{\partial h}{\partial t} +{\boldsymbol{v}}\cdot \nabla_x h - w = 0, \quad\mbox{for } z=h(t,x).$$
(15)

If we choose a test function q=q(x) which depends only on x, we get from (14)

Using the kinematic condition (15) this expression becomes:

$$ \int_\varOmega q \biggl(\mathrm{St} \frac{\partial h}{\partial t}+ \operatorname{div}_x (h\overline{{\boldsymbol{v}}}) \biggr) dx =0,\quad \forall q \in L^{1+\wp}(\varOmega),$$
(16)

where \(\overline{{\boldsymbol{v}}}(t,x):= \frac {1}{h(t,x)}\int_{0}^{h(t,x)} {\boldsymbol{v}}(t,x,z) dz\) is the vertical mean value of the horizontal velocity.

Using the same technique as before one can deduce from (3) that

$$ \int_\varOmega q \biggl(\mathrm{St} \frac{\partial\overline{\rho}h}{\partial t}+ \operatorname{div}_x(h\overline{\rho{\boldsymbol{v}}}) \biggr) dx=0, \quad \forall q \in L^{1+\wp}(\varOmega),$$
(17)

where \(\overline{\rho}(t,x):= \frac{1}{h(t,x)}\int_{0}^{h(t,x)} \rho(t,x,z) dz\) is the vertical mean value of the mass density and \(\overline{\rho{\boldsymbol{v}}}(t,x):=\frac{1}{h(t,x)}\int_{0}^{h(t,x)} \rho(t,x,z){\boldsymbol{v}}(t,x,z)dz\) is the vertical mean value of the mass flux.

From the divergence free condition (2), thanks to the no-penetration assumption we write:

$$ w(t,x,z)= - \int_0^{z}\operatorname{div}_x{\boldsymbol{v}}(t,x,s) ds, \quad \forall (x,z) \in\mathcal{D}(t).$$
(18)

Momentum equation will now be rescaled. We consider the parameter ε≪1 as the aspect ratio between the thickness and the length of the domain, as commonly done in the shallow flow hypothesis. Following the standard scaling technique in this case, we denote:

(19)

We now write the former equations in these new variables. We thus denote by \(\widetilde{\mathcal{D}}\) the domain (rescaled in z) defined by Ω×(0,1).

Equations (16–17) read:

(20)
(21)

where in an analogous way

$$\overline{{\boldsymbol{V}}}(t,x):= \frac {1}{H(t,x)}\int _0^{H(t,x)} {\boldsymbol{V}}(t,x,z) dz$$

and

$$\overline{\rho{\boldsymbol{V}}}(t,x):= \frac{1}{H(t,x)}\int _0^{H(t,x)} \rho(t,x,z){\boldsymbol{V}}(t,x,z) dz$$

are the mean values across the thickness of the fluid.

To write the variational inequality (14) in the rescaled variables, we consider each term separately. For the test functions Φ=(Ψ,εθ) we choose the same scaling. Thus, we decompose the left-hand side of (14) in five terms \(\mathbf{I}_{i}\) for i=1,…,5. They read:

(22)
(23)
(24)
(25)
(26)

where |D(u)|1−℘ appearing in \(\mathbf{I}_{3}\) is defined as:

$$|{\boldsymbol{D}}({\boldsymbol{u}})|^{1-\wp}= \Biggl( |D({\boldsymbol{V}})|^2 + \biggl(\frac{1}{H}\partial_ZW\biggr)^2 + \frac{1}{2} \sum_{i=1}^2\biggl(\varepsilon\partial_{x_i} W + \frac{1}{\varepsilon H}\partial_Z V_i\biggr)^2\Biggr)^{(1-\wp)/2}.$$

Finally, the right-hand side, denoted as \(\mathbf{I}_{6}\), becomes:

$$\mathbf{I}_6 = \int_{\widetilde{\mathcal{D}}} \bigl( \rho H {\boldsymbol {f}}_x\cdot({\boldsymbol{V}}-{\boldsymbol{\Psi}}) +\varepsilon H \rho f_z (W-\theta) \bigr) d X d Z.$$
(27)

3.2 Asymptotic Approximation

In order to derive the shallow water approximation, we just keep terms up to order ε, but we must first specify the asymptotic regime. This is the purpose of present section.

Let us assume an asymptotic regime where dimensionless numbers are such that:

$$\mathrm{St} = \mathrm{Re} = \mathrm{B} = \mathrm{Fr} = {\mathcal{O}}(1),$$

external forces f x and f z verify

$${\boldsymbol{f}}_x= \varepsilon\widetilde{{\boldsymbol{f}}_x}= {\mathcal{O}}(\varepsilon) \quad\mbox{and} \quad f_z ={\mathcal{O}}(1),$$

and the friction coefficient verifies:

$$\beta= \varepsilon\tilde{\beta} = {\mathcal{O}}(\varepsilon).$$

We search for solutions, in the rescaled formulation, under the form:

(28)

where we denote V 0=(V 0,1,V 0,2).

We must write the approximation up to second order. To do so, we first divide the variational inequality by ε and then inject expressions (28) to write the terms of order 1/ε ℘+1, for ℘>0, and the terms of order one.

  • Terms of order 1/ε 1+℘.

From \(\mathbf{I}_{3}\), up to order 1/ε ℘, we obtain:

$$\int_{\widetilde{\mathcal{D}}} \frac{\eta_1(\rho_0)}{H} \partial_Z {\boldsymbol{V}}_0 \cdot\partial_Z ({\boldsymbol{\Psi }}-{\boldsymbol{V}}_0) = 0.$$

Assuming \(\eta_{1} > \underline{\eta} > 0\) in \(\widetilde{\mathcal{D}}\) and using boundary conditions reads:

$$ \partial_Z V_{0,1} = \partial_ZV_{0,2} = 0.$$
(29)

  • Terms of order ε 0.

We write (20)–(21) up to order ε, and get:

(30)
(31)

From the momentum inequality: for all Ψ,

(32)

Thanks to (29), the divergence free condition \(\operatorname{div}({\boldsymbol{V}}_{0},W_{0})=0\) and the boundary conditions, we have \(W_{0} = - Z H{\operatorname{div}_{x}} {\boldsymbol{V}}_{0}\). Regarding the test functions, we choose Ψ independent of Z and we assume the same relation between its components, that is \(\theta = - Z H {\operatorname{div}_{x}} {\boldsymbol{\Psi}}\).

As \(\widetilde{\mathcal{D}}=\varOmega\times(0,1)\), we can also integrate in Z∈(0,1). Thus, if we define the mean values:

we obtain from (32): for all Ψ,

(33)

Variational inequality (33) together with (30) and (31) represent our viscous Shallow Water formulation for a Herschel-Bulkley type fluid.

Remark 1

From (33), if ℘=1, we obtain the 2D viscous Shallow Water formulation of Bingham type presented in [8]. If the yield stress is also neglected, i.e. τ y =0, then we recover the classical 2D viscous Shallow Water equations.

Remark 2

This model is obtained by assuming small slopes for the bottom, and it is still valid for horizontal bottoms. On the contrary, up to our knowledge, integrated Herschel-Bulkley models proposed in the literature are not valid for null slope. Indeed, they are usually obtained by using an asymptotic expansion around a uniform free surface flow involving a sine term of the angle of the slope, and by the way, they can not be used when the slope is null.

4 A Coupled Finite Volume/Augmented Lagrangian Scheme for Herschel-Bulkley

In this section, we describe an approach to solve numerically the model derived in the previous one. The outline of the method is as follows: (i) after discretizing in time, we realize that the problem associated to the variational inequality can be seen as a minimization problem and can be solved with an augmented Lagrangian method, following the ideas of Glowinski and coworkers (see [11] and [14, 15]). (ii) As the global problem is of shallow water-type, we want to use a finite volume method to design the space discretization, since this approach is known to be efficient for this kind of problem. (iii) This finally leads us to build a complete scheme which couples the problem on speed (V) and the one on the height (H) in order to be well-balanced. Let us mention that this outline can be designed both in 1D and 2D. In this paper, we fully describe the scheme in the 1D framework. Being a work of its own, the full description of the 2D version is thus postponed to a future study.

The one-dimensional in space model coming from (30), (31) and (33) is obtained by considering (x,t)∈[0,L]×[0,T], H=H(x,t), \(\overline{\rho_{0}}=\overline {\rho_{0}}(x,t)\), V 0=V 0(x,t). We also suppose that the force does not depend on the vertical variable. The 1D model thus reads:

(34)
(35)
(36)

This model contains several difficulties both from the theoretical and numerical viewpoints; among them are viscoplasticity effects. In this paper, we focus on the design of numerical algorithms which handle the mathematical features of viscoplasticity effects associated to the Herschel-Bulkley law. By the way, in the following, we will consider that the density ρ 0=ρ is constant in time and in space. This implies that (34)–(35) reduce to (34). Moreover, for the sake of readability, we denote V 0 by V. Finally, we will take the gravity for the external forces:

$$f_x = -g \sin\theta, \quad\quad f_z= -g \cos\theta.$$

Then, going back to dimensional variables, the model under consideration will be:

(37)
(38)

where ν 1=η 1/ρ is the viscosity coefficient, τ y is the yield stress, g is the constant of gravity and \(\tilde{\alpha }=\beta/\rho\) is the friction coefficient between the material and the bottom.

4.1 Semi-Discretization in Time and Augmented Lagrangian

We consider the following time discretization for (37)–(38)

(39)
(40)

where Δt is the time step and superscripts with n refer to time iteration at t n=nΔt.

Directly inspired by books [14, 15] on augmented Lagrangian methods, we can rewrite (40) as an optimization problem: V n+1 is the solution of the minimization problem:

$$ \mathcal{J}^n\bigl({\boldsymbol{V}}^{n+1}\bigr) = \min_{{\boldsymbol{V}}\in\mathcal{V}} \mathcal{J}^n ({\boldsymbol{V}}),$$
(41)

where \(\mathcal{J}^{n}({\boldsymbol{V}})=F^{n}(\mathcal{B}({\boldsymbol {V}}))+G^{n}({\boldsymbol{V}},\mathcal{B}({\boldsymbol{V}}))\), with \(\mathcal{V}=H_{0}^{1}([0,L])\), \(\mathcal{H}=L^{2}([0,L])\),

$$\mathcal{B}: \left ( \begin{array}{c}\mathcal{V} \rightarrow \mathcal{H} \\{\boldsymbol{V}} \mapsto \mathcal{B}({\boldsymbol{V}}) = \partial_x {\boldsymbol{V}}\end{array} \right ), \qquad F^n: \left ( \begin{array}{c}\mathcal{H} \rightarrow \mathbb{R} \\\lambda \mapsto F^n(\lambda)=\int_0^L \tau_y\sqrt{2}H^n|\lambda|dx\end{array} \right ),$$

and

As \({\mathcal{J}}^{n}(V)\) is a non-differentiable function, we consider the Lagrangian function

and the augmented Lagrangian function, for a given positive value \(r\in \mathbb{R}\), as:

$$ \mathcal{L}^n_r({\boldsymbol{V}},q,\mu)=\mathcal{L}^n({\boldsymbol {V}},q,\mu)+\frac{r}{2}\int_0^LH^n\bigl(\mathcal{B}({\boldsymbol {V}})-q\bigr)^2 dx.$$
(42)

Then, we search for the saddle point of \(\mathcal{L}^{n}_{r}({\boldsymbol {V}},q,\mu)\) over \(\mathcal{V}\times\mathcal{H}\times\mathcal {H}\). Indeed, if we denote by (V ∗,q ∗,μ ∗) this saddle point, then V ∗ is the solution of the minimization problem (41) (cf. [11, 14, 15]).

We consider the algorithm proposed in [11, 14, 15], based on the Uzawa’s algorithm, to approximate the saddle point of (42). Recall that, during time iterations, if we know everything at time t n, then we need to solve (39)–(40) for unknowns at time t n+1. Consequently, it is worth noting that (39) and (40) are decoupled with respect to the resolution of the saddle point problem, which is the resolution of V n+1. In other words, we can first solve the problem for V n+1 using the augmented Lagrangian algorithm and then solve it for H n+1.

Augmented Lagrangian algorithm

  • Initialization: suppose that V n, H n and μ n are known. For k=0, we set V k=V n and μ k=μ n.

  • Iterate:

    • Find \(q^{k+1} \in{\mathcal{H}}\) solution of

      $${\mathcal{L}}^n_r\bigl({\boldsymbol{V}}^k,q^{k+1},\mu^k\bigr) \leq{\mathcal{L}}^n_r\bigl({\boldsymbol{V}}^k,\underline{q},\mu^k\bigr), \quad\forall \underline{q} \in{\mathcal{H}}.$$

      In other words, \(q^{k+1} \in\mathcal{H}\) is the solution of following minimization problem:

      $$ \min_{\underline{q}\in\mathcal{H}} \biggl(\frac{H^n r}{2}\underline {q}^2+H^n 2^{\frac{\wp+3}{2}}\nu_1\frac{|\underline{q}|^{\wp +1}}{\wp+1}+H^n\tau_y\sqrt{2}|\underline{q}|-H^n\bigl(\mu^{k}+r\mathcal{B}\bigl({\boldsymbol{V}}^k\bigr)\bigr)\underline{q} \biggr).$$
      (43)

      And the solution of this problem is the solution of the following equation (see, e.g., Huilgol & You [21]):

      $$ \bigl(2^{\frac{\wp+3}{2}}\nu_1|q^{k+1}|^{\wp -1}+r\bigr)q^{k+1}=\bigl(\mu^{k}+r \partial_x \bigl({\boldsymbol {V}}^{k}\bigr)\bigr) \biggl(1-\frac{\tau_y\sqrt{2}}{|\mu^{k}+r \partial_x{\boldsymbol{V}}^{k}|} \biggr)_+.$$
      (44)

      The subscript “+” in the last term stands for the positive part (λ +:=max(0,λ)). This is a non-linear problem which is solved numerically with a fixed point-like method (described in Sect. 4.2, (51), and in Appendix A).

    • Find \({\boldsymbol{V}}^{k+1} \in{\mathcal{V}}\) solution of

      $${\mathcal{L}}^n_r\bigl({\boldsymbol{V}}^{k+1},q^{k+1},\mu^k\bigr) \leq{\mathcal{L}}^n_r\bigl({{\boldsymbol{V}}},q^{k+1},\mu^k\bigr), \quad\forall{{\boldsymbol {V}}} \in{\mathcal{V}}.$$

      Thus, V k+1 is the solution of a minimization problem, which can be characterized by differentiating \(\mathcal {L}^{n}_{r}({\boldsymbol{V}},q,\mu)\) with respect to V. From (42), we deduce that V k+1 is the solution of the following linear problem (whose resolution is detailed in Sects. 4.2 and 4.3):

      (45)

    • Update the Lagrange multiplier via

      $$ \mu^{k+1}=\mu^{k} + r \bigl(\partial_x {\boldsymbol{V}}^{k+1} - q^{k+1} \bigr);$$
      (46)

    • Check convergence (see below) and update: V k=V k+1, μ k=μ k+1, k=k+1 and go to the next iteration ….

  • … until convergence is reached:

    $$ \frac{\| \mu^{k+1} - \mu^{k} \|}{\| \mu^{k} \|} \leq \mathit{tol}.$$
    (47)

At convergence, we get the value of V n+1 by setting V n+1=V k+1 (in the numerical tests presented in this paper, we set \(\mathit{tol}=10^{-5}\)). It is shown in [11, 14, 15] that this algorithm converges to the saddle point of (42).

To complete the discretization, it remains to describe the treatment of spatial derivatives, which will be done with a finite volume approach as mentioned previously. To do so, it is worth realizing that the underlying global problem coupling (39) and (40) involves the following system (using a cosmetic change of notation which will be useful in the presentation: H n+1 is denoted as H k+1; again, note that H k+1 is not involved in the augmented Lagrangian algorithm and, so, does not change in this loop):

$$ (P)^{n,k} \quad \left \{ \everymath{\displaystyle}\begin{array}{l}\frac{H^{k+1}-H^n}{\Delta t} + \partial_x \bigl(H^n {\boldsymbol{V}}^n\bigr) = 0 , \\[10pt]H^n \frac{{\boldsymbol{V}}^{k+1}-{\boldsymbol {V}}^n}{\Delta t} + H^n \partial_x \biggl( \frac{({\boldsymbol {V}}^n)^2}{2} + g \cos\theta H^n \biggr) -r \partial_x \bigl(H^n \bigl( \partial_x {\boldsymbol{V}}^{k+1} - q^{k+1} \bigr) \bigr) \\[10pt]\quad= {-}\tilde{\alpha} {\boldsymbol{V}}^{k+1} - g H^n \sin\theta+ \partial_x (H^n \mu^{k}).\end{array}\right .$$
(48)

This problem can be seen as a semi-discretization in time of a parabolic system, which for r=0 degenerates into a hyperbolic system with source terms. Although in terms of time discretization and augmented Lagrangian algorithm the problem is decoupled, we must consider the coupling between mass and momentum equations, in order to obtain a well-balanced solver. It is induced by the source terms involving topography and the Lagrange multiplier. This is well documented for shallow water type systems with source term defined by the topography. In our case, the extra difficulty is to treat the source term defined in terms of the Lagrange multiplier. The good news being that this coupling only needs to be done with all the quantities obtained at the convergence of the augmented Lagrangian algorithm. We describe this in detail in the following sections.

4.2 Finite Volume Method for Spatial Discretization

In this section, we describe the discretization in space of all the terms involved in (44), (45), (46), and (48). It is essentially inspired by finite volume methods for shallow water type systems.

First, the space domain [0,L] is divided in the computing cells I i =[x i−1/2,x i+1/2]. For simplicity, we suppose that these cells have a constant size Δx. Let us define \(x_{i+\frac {1}{2}} = (i+1/2) \Delta x\) and by x i =iΔx, the center of the cell I i . We define W k+1(thanks to the aforementioned cosmetic harmonization of the notation), the following vector of the unknowns of problem (P)n,k,

$$W^{k+1}(x) = \bigl[ H^{k+1}(x), {\boldsymbol{V}}^{k+1}(x)\bigr].$$

We denote by \(W_{i}^{k+1}\) the approximation of the cell average of the exact solution provided by the numerical scheme:

$$W_i^{k+1} \cong\frac{1}{\Delta x}\int_{x_{i-1/2}}^{x_{i+1/2}}W^{k+1}(x) dx.$$
(49)

Furthermore, μ and q are approximated at the center of the dual mesh: \(\mu_{i+1/2}^{k}\) and \(q_{i+1/2}^{k}\) are approximations of μ k(x i+1/2) and q k(x i+1/2), respectively. As mentioned during the presentation of the augmented Lagrangian algorithm, we can suppose that the values \(W_{i}^{k}\), \(W_{i}^{0}=[H^{n},{\boldsymbol{V}}^{n}]\) and \(\mu_{i+1/2}^{k}\) are known for all i. Then, we proceed as follows.

Concerning the discretization of (46), the value of \(\mu^{k+1}_{i+1/2}\) is updated via:

$$ \mu^{k+1}_{i+1/2}=\mu^k_{i+1/2} + r \biggl( \frac{{\boldsymbol {V}}^{k+1}_{i+1}-{\boldsymbol{V}}^{k+1}_i}{\Delta x} -q_{i+1/2}^{k+1} \biggr),$$
(50)

making the most of the staggered position between discrete μ and V.

For the non linear problem (44), we update \(q_{i+1/2}^{k+1}\) as the solution of the following equation, which is solved point-wise at all x i+1/2:

$$ \bigl(2^{\frac{\wp+3}{2}}\nu_1|q_{i+1/2}^{k+1}|^{\wp-1}+r\bigr)q_{i+1/2}^{k+1} = \biggl( \mu_{i+1/2}^{k}+ r \frac{{\boldsymbol {V}}^k_{i+1}-{\boldsymbol{V}}^k_i}{\Delta x} \biggr) \biggl( 1-\frac {\tau_y\sqrt{2}}{\big|\mu_{i+1/2}^{k}+r \frac{{\boldsymbol {V}}^k_{i+1}-{\boldsymbol{V}}^k_i}{\Delta x}\big|} \biggr)_+.$$
(51)

In Appendix A, we prove that this equation has a unique solution and a regula-falsi method to approximate the solution is detailed.

Finally, we consider the two equations (48) of problem (P)n,k. We can rewrite them under the form:

(52)

where

b(x)=xsinθ and \(\underline{I}\) is the vector [0,1]t.

System (52) is then discretized as

(53)

where

$$H^n_{i+1/2}=\frac{H^n_i+H^n_{i+1}}{2}, \quad\quad\overline{\sigma }^{n,k}_{i+1/2}= \left ( \begin{array}{c}b(x_{i+1/2}) \\ H_{i+1/2}^n \mu^{k}_{i+1/2}\end{array} \right ),$$

and \(\phi(W_{i}^{n},W_{i+1}^{n},\{\mu_{j+1/2}^{k}\}_{j=i-1}^{j=i+1})\) is a numerical flux function, approximation of F(W n) at x i+1/2.

In order to complete the numerical scheme, we must precise the definition of ϕ. We consider a family of numerical flux functions which defines a well-balanced finite volume solver. System (52) can be seen as a semi-discretization in time of a parabolic system, which for r=0 degenerates into a hyperbolic system with source terms. Following [10], in order to obtain a well-balanced finite volume method, the numerical flux ϕ, approaching the flux function F(W) at x i+1/2, must depend on the definition of source terms.

Namely, we consider the following class of numerical flux functions:

(54)

where \(Q_{i+1/2}^{n}\) is the numerical viscosity matrix which particularises the numerical solver and \({\mathcal{G}}(\{\mu_{j+1/2}^{k}\}_{j=i-1}^{j=i+1})\) is a term designed to obtain a well-balanced finite volume method.

The numerical viscosity matrix can be defined in terms of the Roe matrix associated to the flux F(W). Let us denote by \({\mathcal{A}}^{n}_{i+1/2}\) the Roe matrix verifying,

$$F\bigl(W_{i+1}^n\bigr)-F\bigl(W_{i}^n\bigr)= {\mathcal{A}}_{i+1/2}^n \bigl(W_{i+1}^n-W_{i}^n\bigr).$$

This matrix can be diagonalized and its eigenvalues are:

$$\lambda_{1,i+1/2}^n= \widetilde{{\boldsymbol{V}}}_{i+1/2}^n-\sqrt{g \cos\theta H_{i+1/2}^n}, \quad\quad \lambda_{2,i+1/2}^n=\widetilde {{\boldsymbol{V}}}_{i+1/2}^n+\sqrt{g \cos\theta H_{i+1/2}^n},$$

where \(\widetilde{{\boldsymbol{V}}}_{i+1/2}^{n} = (\sqrt{H_{i}^{n}}{\boldsymbol{V}}_{i}^{n} + \sqrt{H_{i+1}^{n}} {\boldsymbol {V}}_{i+1}^{n})/(\sqrt{H_{i}^{n}}+ \sqrt{H_{i+1}^{n}})\).

As we consider explicit finite volume solvers, a CFL condition must be considered to compute the time step. We set Δt by imposing the following restriction,

$$ \frac{\Delta t}{\Delta x} \max_i \bigl(|\lambda_{j,i+1/2}^n|,j=1,2\bigr)= \gamma, \quad\mbox{with }\gamma\in(0,1].$$
(55)

Some possible definitions of matrix \(Q_{i+1/2}^{n}\) are:

  1. 1.

    \(Q_{i+1/2}^{n}= abs({\mathcal{A}}_{i+1/2}^{n})\) corresponds to Roe method (where, abs(.) denotes the absolute value (and not the norm) of the matrix).

  2. 2.

    \(Q_{i+1/2}^{n}=\alpha^{n}_{0,i+1/2} \mathbf{I}\) leads to different solvers depending on the value of \(\alpha^{n}_{0,i+1/2}\). The Lax-Friedrichs method is defined by \(\alpha^{n}_{0,i+1/2}=\frac{\Delta x}{\Delta t}\). The modified Lax-Friedrichs method is given by \(\alpha^{n}_{0,i+1/2} = \gamma\frac{\Delta x}{\Delta t}\), where γ is the CFL parameter (see (55)). Rusanov method corresponds to \(\alpha^{n}_{0,i+1/2}= \max(|\lambda_{1,i+1/2}^{n}|,|\lambda_{2,i+1/2}^{n}|)\).

  3. 3.

    Other methods such as HLL, Lax-Wendroff, Force, Gforce and WAF can also be included thanks to alternative form of matrix \(Q_{i+1/2}^{n}\). Actually, all of them can be written as a polynomial evaluation of the Roe matrix, namely

    $$Q^n_{i+1/2}= \sum_{j=0}^{m}\alpha^n_{j,i+1/2} \bigl({\mathcal{A}}^n_{i+1/2}\bigr)^j,$$

    with a suitable value m and definitions of the coefficients \(\{\alpha^{n}_{j,i+1/2} \}_{j=0,\ldots, m}\). Note that in fact Rusanov and Lax-Friedrichs methods correspond to the case m=0. (See [13] and [9] for more details).

The reason to mention all these methods lies in the fact that, in the next section, we will discuss implementation issues associated to the global scheme, depending on the choice of the numerical viscosity matrix.

Finally, we must describe the term \({\mathcal{G}}(\{\mu_{j+1/2}^{k}\}_{j=i-1}^{j=i+1}) \) in order to complete the numerical flux function (54). The definition of \({\mathcal{G}}\) is related to the well-balanced properties of the numerical scheme. We propose the following definition, based on the technique introduced in [10]:

$${\mathcal{G}}\bigl(\bigl\{\mu_{j+1/2}^{k}\bigr \}_{j=i-1}^{j=i+1}\bigr) = \frac{1}{g \cos \theta} \left ( \begin{array}{c}g (b(x_{i+1})-b(x_i))- \Delta\mu^{k}_{i+1/2} \\ 0\end{array} \right ),$$

where \((\Delta\mu^{k}_{i+1/2}/\Delta x)\) is an approximation of ∂ x (μ k) at x i+1/2. Since we know the approximations of μ k at x j+1/2, for all j, there exist several ways to define \(\Delta\mu^{k}_{i+1/2}\) in terms of \(\{\mu_{j+1/2}^{k}\}_{j=i-1}^{j=i+1}\). Furthermore, since we want to approximate solutions with discontinuities, we propose to set it in terms of a slope limiter. For example, we can use a minmod limiter:

where \(\mathrm{sign}\) is the sign function.

4.3 The Coupled Scheme and Its Well-balanced Property

It is then possible to gather all the previous ingredients to describe and discuss the global scheme proposed to solve the evolution problem (37)–(38).

Global numerical scheme for (37)–(38)

  • Initialization at time t=0 for n=0: V n, H n, μ n are given by initial conditions

  • Time loop: For n=0,…,n max

    • Resolution of the problem on V k+1

      \(\{{\boldsymbol{V}}_{i}^{n}\}_{i}\), \(\{ H^{n}_{i} \}_{i} \) and \(\{\mu_{i+1/2}^{n}\}_{i}\) are known;

      Compute quantities which are invariant in the following loop:

      Augmented Lagrangian loop:

        [Step 0]:

      Initialize for k=0: for all i, \({\boldsymbol{V}}_{i}^{k}={\boldsymbol{V}}_{i}^{n}\) and \(\mu^{k}_{i+1/2}=\mu^{n}_{i+1/2}\).

        [Step 1]:

      Update \(\{q_{i+1/2}^{k+1}\}_{i}\) by solving (51).

        [Step 2]:

      Update \(\{{\boldsymbol{V}}^{k+1}_{i}\}_{i}\) by solving the linear system defined by the second component of (53).

        [Step 3]:

      Update \(\{\mu_{i+1/2}^{k+1}\}_{i}\) via (50).

        [Step 4]:

      Set: for all i, \({\boldsymbol {V}}^{k}_{i}={\boldsymbol{V}}^{k+1}_{i}\), \(\mu^{k}_{i+1/2}=\mu^{k+1}_{i+1/2}\) and return to Step 1.

        [Step 5]:

      At convergence, when condition (47) is verified, set \({\boldsymbol{V}}_{i}^{n+1}={\boldsymbol {V}}_{i}^{k+1}\) and \(\mu^{n+1}_{i+1/2}=\mu_{i+1/2}^{k+1}\) ∀i.

    • Resolution of the problem on H k+1

      Compute H n+1=H k+1 with the finite volume method defined by the first component of (53), defined in terms of the most recent Lagrange multiplier \(\{ \mu^{n+1}_{i+1/2} \}_{i}\).

It is worth giving some more details about [Step 2]. Remark that the second component of (53) defines a linear system where the unknowns are \(\{{\boldsymbol{V}}^{k+1}_{i}\}_{i}\). If we denote V k+1 the vector whose ith component is \({\boldsymbol{V}}_{i}^{k+1}\), the aforementioned linear system can be written as:

$$ {\boldsymbol{A}}^n {\boldsymbol{V}}^{k+1}={\boldsymbol{b}}^{n,k},$$
(56)

where A n is a matrix defined in terms of \(\{H^{n}_{i}\}_{i}\); consequently, A n does not change during the augmented Lagrangian loop (in k). As a matter of fact, A n is a tridiagonal matrix, whose line i is defined by the following entries:

On the contrary, the right hand side of the linear system (56) changes for each iteration in k. The ith component of b n,k is decomposed as:

$${\boldsymbol{b}}_{i}^{n,k}={\boldsymbol{b}}_i^{n,(1)}+{\boldsymbol {b}}_i^{n,k,(2)}+{\boldsymbol{b}}_i^{n,k,(3)},$$

where

(57)
(58)
(59)

Note that, a priori, terms \({\boldsymbol {b}}_{i}^{n,k,(2)}\) and \({\boldsymbol{b}}_{i}^{n,k,(3)}\) change during the iterative algorithm in k. Nevertheless, let us remark that, for some numerical schemes, \({\boldsymbol{b}}_{i}^{n,k,(3)}\) does not depend on k. Indeed, this term is given by the second component of \(\phi (W_{i-1}^{n},W_{i}^{n},\{\mu_{j+1/2}^{k}\}_{j=i-2}^{j=i})\), which is defined by (54) in terms of the numerical viscosity matrix \(Q^{n}_{i+1/2}\). Then, if \(Q^{n}_{i+1/2}\) is a diagonal matrix, the second component of the numerical flux function does not depend on \(\{\mu_{j+1/2}^{k}\}_{j=i-2}^{j=i}\). Consequently, for the Rusanov, Lax-Friedrichs and modified Lax-Friedrichs methods, the definition of \({\boldsymbol{b}}_{i}^{n,k,(3)}\) does not change in the augmented Lagrangian algorithm.

In terms of computational cost:

  • \({\boldsymbol{b}}_{i}^{n,(1)}\) is inexpensive to compute and furthermore does not depend on k; it can be computed once for all before the augmented Lagrangian loop;

  • \({\boldsymbol{b}}_{i}^{n,k,(2)}\) depends on k but is not very expensive to compute at each iteration in k;

  • the potentially more expensive component is \({\boldsymbol {b}}_{i}^{n,k,(3)}\), since for methods where \(Q^{n}_{i+1/2}\) is not diagonal (e.g. Roe, HLL or FORCE methods), a flux term must be computed at each iteration in k; the good news is that we can use instead methods where \(Q^{n}_{i+1/2}\) is diagonal, leading to an algorithm where the flux term is computed once for all before the augmented Lagrangian loop.

To sum up, in terms of flux computation at each iteration in time, with a diagonal numerical viscosity matrix, the present method has a cost which is equal to the cost of a classical finite volume method for standard shallow water system (in (H,V) and without a variational inequality on V). Here, the extra computational cost is only induced by the computation of \({\boldsymbol{b}}_{i}^{n,k,(2)}\) at each iteration in k, which is cheaper than the computation of a flux like \({\boldsymbol{b}}_{i}^{n,k,(3)}\).

The numerical tests presented in this paper are done using a Rusanov method. The description of the overall scheme is thus complete.

To close this section, we describe the well-balanced property of the numerical scheme. By substituting V=0 in (38), we can characterize two types of stationary solutions. The first one corresponds to the case of an horizontal free surface (in the global frame of reference), i.e. a stationary solution with a constant free surface:

$$\forall x \in[0,L], \quad b(x) + H(x) \cos\theta= \mathit{cst},$$

where b(x)=xsinθ. The second type of stationary solution is a constant height over an inclined slope. We can see that if

$$ \forall x \in[0,L], \quad \biggl( x- \frac{L}{2} \biggr) \sin \theta\leq\frac{\tau_y \sqrt{2}}{g},$$
(60)

then \(H\equiv \mathit{cst}\) is a stationary solution of the system. We can show:

Proposition 1

Let (H=H(x);V≡0) be a stationary solution of (38), and assume that the proposed numerical scheme uses the following initialization for μ:

$$\forall i, \quad\mu_{i+1/2}= \biggl( H(x_{i+1/2}) - H \biggl(\frac {L}{2} \biggr) \biggr) \cos\theta + \biggl( x_{i+1/2} -\frac {L}{2} \biggr) \sin\theta,$$

then, this scheme exactly preserves both stationary solutions: (i) horizontal free surface and (ii) constant height, verifying (60), over an inclined plane.

The proof of this result is simple to compute but long to write. For purpose of brevity, we omit it.

5 Numerical Tests

5.1 A Simplified Model for a Duct Flow Test

In this section, we consider a simplified case associated to the standard “duct flow” (it is inspired by the Poiseuille flow associated to (Navier-)Stokes between two infinite parallel plates with an Herschel-Bulkley law instead of the classical Newtonian law) for which we know an analytical stationary solution. This model contains all difficulties associated to the numerical approximation of the Herschel-Bulkley model (optimization problem to compute V and non-linear root finding to compute q, as presented previously). Namely, for this simpler case, the model (40) degenerates to:

(61)

where f is a constant force (if ones thinks back on the Poiseuille flow in a duct, f is the pressure gradient in the direction of the flow). In the duct, there is no equation associated to H, which is stationary and constant, H=1; furthermore, we put \(\tilde{\alpha}= 0\) (no friction) and we drop the non-linear term ∂ x (V n)2 since we suppose that we are in a Stokes’ regime.

In the model (61), the time derivative acts as a relaxation term in the sense that (i) there exists a stationary asymptotic solution u (when t→+∞) and that (ii) an initial data V, different from this asymptotic solution, will converge in time to u. The interest of this test is that u is a non-trivial stationary solution: \(u \not\equiv 0\).

This analytical stationary solution is (see [18]):

$$ u(\xi)= \frac{ \wp f^{1/\wp} }{ ( 2^{\frac{3+\wp}{2}}\nu_1 )^{1/\wp} (1+\wp)} \left \{ \everymath{\displaystyle}\begin{array}{l@{\quad}l}{ { \biggl(\frac{L}{2} - \xi_o \biggr)}^{\frac{1}{\wp }+1} }& \mbox{ if } 0 \leq\xi\leq\xi_o, \\[8pt]{ { \biggl(\frac{L}{2} - \xi_o \biggr)}^{\frac{1}{\wp }+1} - (\xi- \xi_o)^{\frac{1}{\wp}+1} } & \mbox{ if } \xi_o < \xi \leq\frac{L}{2}.\end{array}\right .$$
(62)

where \(\xi=|x-\frac{L}{2}|\), \(\xi_{o}=\frac{\sqrt{2} \tau_{y}}{f}\) and the domain is defined for x∈[0,L].

In the following tests, we thus study the evolution of V(t) from the initial data: ∀x∈[0,L],V(t=0,x)=0. Dirichlet boundary conditions are imposed:

$$\forall t \geq0, \quad{\boldsymbol{V}}(t,0) = 0,\quad \quad{\boldsymbol {V}}(t,L) =0.$$

The idea is to check the ability of the numerical method to converge to the stationary solution (62), for various values of the power ℘ of the Herschel-Bulkley model.

We compute the evolution of the solution with the proposed numerical scheme and we consider that we have a numerical stationary solution when the relative error between two iterations in time is smaller than 10−8, that is

$$\frac{\|{\boldsymbol{V}}^{n+1}-{\boldsymbol{V}}^n\|_1}{\|{\boldsymbol{V}}^{n+1}\|_1} < 10^{-8}.$$

We set a domain of length L=1, discretized with 100 points. Moreover, ν 1=0.2 and \(\tau_{y} = 4/\sqrt{2}\). We consider four values of ℘. For ℘=1, 0.75 and 0.5, we impose a force f=25. Whereas for ℘=0.25, we use a force f=12.5.

In Fig. 1, we present the convergence from the initial solution V≡0 to the stationary solution, for ℘=1, 0.75, 0.5 and 0.25 (Figs. 1(a), (b), (c) and (d), respectively). To improve the visibility, for each value of ℘, we use a variable time step \(\overline{\Delta t}\) to plot the evolution of V, as shown in Table 1.

Fig. 1
figure 1

Test 1: Evolution of the computed velocity (dashed lines) to the analytical stationary solution (continuous line). \(\overline {\Delta t}\) gives the time separating each numerical curves

Full size image
Table 1 Time steps \(\overline{\Delta t}\) used to plot V(t), in the convergence study
Full size table

In Tables 2, 3, 4, 5, the absolute errors between the numerical asymptotic solution and the analytical one are presented in norm L 1 and L ∞, as well as the associated order of the method.

Table 2 Test 1. Errors and order of convergence for ℘=1
Full size table
Table 3 Test 1. Errors and order of convergence for ℘=0.75
Full size table
Table 4 Test 1. Errors and order of convergence for ℘=0.5
Full size table
Table 5 Test 1. Errors and order of convergence for ℘=0.25
Full size table

We observe that the method converges to the analytical stationary solution and that the convergence under mesh refinement is of second order in space. We can also observe that the error increases when ℘ diminishes, showing that the problem becomes more numerically difficult to solve when ℘ tends to 0. Indeed, during the simulation, the convergence is obtained with a number of iterations, in the augmented Lagrangian, which increases when ℘→0.

5.2 Test at High Rate of Shear—Exploring the Rheological Law

In this section, we want to present the results of the method applied to a case where the rate of shear is high, in the sense that it is a regime where the Bingham fluid is the more “viscous” (compared to the Herschel-Bulkley fluid). This is a feature induced by the rheological richness of Herschel-Bulkley model.

More precisely, previous feature is linked to the rheological study presented in Appendix B and to which the reader is referred before reading the following of this section.

In the present section, we consider a test where the solution is in a rheological state which is covered by Herschel-Bulkley law when the solutions are moving at high rates of shear. With the present section and the next section, we will show that the method is able to handle the variety of behaviors exhibited by the Herschel-Bulkley constitutive law.

Being concerned with high shear rate, the following test case is in opposition with the ones in the next section where we will focus on the ability of the method to handle stationary states (which is linked to the well-balanced property of the method designed in this paper).

The test case is as follows. Physical parameters are those given in Appendix B. We consider an initial sinusoidal free surface over an horizontal slope (θ=0) as shown in Fig. 2. We put a non zero initial velocity (see also Fig. 2), which will act together with the gravity g=9.81 to move the free surface. Namely (the domain is [0;L] with L=10 and we use a discretization grid in space with 1000 points; discretization in time is adaptive through CFL condition equals to 0.8; furthermore, there is no friction):

Fig. 2
figure 2

Initial conditions for the test with high rate of shear. The four dashed vertical lines indicate the probes’ locations (denoted as Probe 1, 2, 3 and 4, from left to right respectively)

Full size image

This initial velocity is chosen in such a way that, during all the simulation, the rate of shear is in the Zone 3 described in the Appendix B, i.e. in this case |∂ x V|≥0.22. In this test, the final time of the simulation is t=0.3. We can check on Fig. 3 the evolution of ∥∂ x V∥∞ along time. It is worth noting that for t∈[0,0.1] the maximum of the gradient, which is measured by this norm, is located near the boundaries of the domain. Then for t∈[0.1,0.3] the maximum is located at the center of the domain, where the fluid is moving in opposite directions (V is continuous but antisymmetric and changes its sign at x=5: V>0 (resp. V<0) on the left (resp. right) of x=5) inducing a rise of the free surface, as it can be seen on the Probe 1 of Fig. 4. Indeed, we put four probes at x=5,6,7 and 8 (denoted as Probe 1, 2, 3 and 4, respectively) to monitor the evolution of the free surface H at these points.

Fig. 3
figure 3

Time evolution of the maximum of the gradient of V over the domain. This shows that the flow is in the regime of Zone 3, described in Appendix B

Full size image
Fig. 4
figure 4

Time evolution of H at the four probes, for the three fluids. See text and also Fig. 5 to have a clear view of their respective locations on the final H

Full size image

The fact that, in this regime, the fluid with ℘=0.4 is the less “viscous” can be seen in Fig. 5; this fluid has a better ability to move and:

  • goes more down near the boundaries (x∈[0;1] and symmetrically) due to the strong initial velocity that “smashes” the top of the “mountain”, …

  • … induces an expulsion of the fluid to the center, this expulsion creates (i) a kind of “splash ring” around x=2 (and symmetrically around x=8) which goes higher for ℘=0.4, …

  • … as well as (ii) a global motion in the inner zone leading to an increase of the free surface at the center (x∈[2;5] and symmetrically). In a neighborhood of x=5, we clearly see that the free surface with ℘=0.4 is higher than the others.

On the contrary, for the Bingham fluid which is, in this regime, the more “viscous” fluid, we see that the motion is a bit less important than the others. For the third fluid which has the medium “viscosity”, its free surface is perfectly bounded by the two others.

Fig. 5
figure 5

The free surface H at the final time t=0.3, for the three fluids. The dashed vertical lines indicates the probes’ locations (denoted as Probe 1, 2, 3 and 4, from left to right respectively)

Full size image

We add that we performed a mesh refinement study of this test which leads to similar results. This test thus shows the ability of the numerical method to capture the various rheological behaviors of the Herschel-Bulkley model for “high” rates of shear. We will see in the next section that it is also the case for low rate of shear by focusing on the study of the convergence to stationary states of the fluid on an inclined plane (θ≠0).

5.3 Avalanche Test Case—Rheology at Smaller Shear Rate

In this section, we simulate an academic test of avalanche. This will allow us to show the behavior of the numerical method with respect to several aspects: (i) ability to compute stationary states of a viscoplastic flow on an inclined plane and (ii) role of the Herschel-Bulkley parameter ℘ on the evolution of H when the rate of shear is small (in the sense that the flow occurs in Zone 1, described in Appendix B).

To do so, we consider an initial condition such that V(t=0)≡0 and

$$ H(t=0,x)=\left \{ \begin{array}{l@{\quad}l}2.3 & \mbox{if } 6.5\leq x\leq7.5\\1 & \textrm{otherwise}.\end{array} \right .$$
(63)

This rectangular pulse is above a plane slope inclined with an angle of 5 degrees. As it can be seen on Fig. 6, where we also add the location of probe points at x=0.6,6.4,7,9.4. We monitor the evolution of H along time, at these four points, whose locations were chosen to be at the most significant locations for the dynamics of this test, as we will see in what follows.

Fig. 6
figure 6

Initial height (thick rectangular pulse), bottom (thin continuous line) and location of the 4 probes (dashed lines) to monitor the evolution of H along time (cf. Fig. 8)

Full size image

Physical parameters are those given in Appendix B. In this context, upon the influence of slope and gravity, the fluid is able to spread and to flow down the slope but there exists a finite time at which the fluid stops, since the load goes below the yield limit.

We perform numerical simulations of the evolution of the free surface and its convergence to a stationary state, for several values of the exponent ℘. In particular, we take the Bingham case ℘=1 and two values for a “true” Herschel-Bulkley material, namely ℘=0.7 and ℘=0.4. The domain [0;10] is discretized with 8000 points.

The method presented in this paper has been shown to be well-balanced. As a consequence, it is able to compute accurately aforementioned stationary states. To show this, we purposely take a final time of simulation T=20 which is by far greater than the time at which the avalanche stops (approximately 2 for the three fluids considered here). We note that we use a CFL condition of 0.8, associated to the discretization in time.

The stationary heights obtained are shown on Fig. 7. The first obvious thing to note, thanks to the graphical help of the probes’ location (and comparing Figs. 6 and 7), is the motion of the material down the slope: the rectangular pulse is shifted a bit to the left and its height decreases; as a consequence, this flowing material accumulates at the bottom of the slope (see Probe 1), inducing an increase of the height in this zone. The evolution of each height along time, measured at the four probes is shown on Fig. 8: we can clearly see that stationary states are obtained since all the curves are flat after t≈2.

Fig. 7
figure 7

Final heights obtained at the stationary state, for various powers of the Herschel-Bulkley law. Note that, contrary to Fig. 6, the scale is not the same between the abscissa and the ordinate

Full size image
Fig. 8
figure 8

Height for the probe points: x=0.6,6.4,7,9.4

Full size image

We can also describe the behavior of the height evolution with respect to the Herschel-Bulkley power. First, it can be noted that the rate of shear (see Fig. 9) in this test is always less than 0.35 and that the flow regime of this test is essentially (i.e. most of the time of the simulation) the one of Zone 1 described in Appendix B (rate of shear between 0 and 0.11), especially when the height reaches the stationary state (at t≈2). The Bingham fluid ℘=1 is thus supposed to flow better than the two others. This can be seen on the final heights, where the Bingham fluid has a hump shape which is below the others (in the neighborhood of x=7) and its level is higher at the bottom of the slope (in the neighborhood of x=1). Furthermore, we see that the position of the three stationary heights is in accordance with the value of ℘:

  • in the top of the hump, if we denote \(h_{\wp_{i}}\) the height of fluid ℘ i ={1,0.7,0.4}, we have:

    $$h_{1} \leq h_{0.7} \leq h_{0.4},$$

  • whereas, in the bottom of the slope, we have:

    $$h_{1} \geq h_{0.7} \geq h_{0.4},$$

which is in accordance to the fact that in this regime where the stationary states are reached, the rates of shear are close to zero, leading to an increasing “fluency” of the flow when ℘ goes from 0 to 1.

Fig. 9
figure 9

The gradient of V as a function of time, showing that the flow is essentially in the regime of Zone 1 described in Appendix B

Full size image

This can also be seen on the time evolution of H at the probes (see Fig. 8). Note that the height at Probe 4 is totally stationary during all the simulation: actually, in its neighborhood, the velocity is zero during all the simulation, due to the fact that the material remains under the yield limit. On the contrary, at Probe 3, which is at the center of the initial rectangular pulse, we see that the height is constantly decreasing until the stationary state is reached. This is natural: the initial rectangular pulse is flowing down and its shape, remaining quasi-rectangular, is essentially changing by converting the decrease in height in an increase of width. This explains also the behavior of Probe 2 which, at t=0, is just near the initial pulse: due to the increase of the width of the pulse, the height first increases at Probe 2, but when this height corresponds to the top of the rectangular pulse (which is decreasing), Probe 2 exhibits the same behavior as Probe 3 and shows a decrease of the height to a stationary state.

Again, we add that we performed a mesh refinement study of this test which leads to similar results, showing the robustness of the present numerical method.

6 Conclusion

In this work, we derive an integrated Herschel-Bulkley model coming from the full 3D Navier-Stokes Herschel-Bulkley equations with a free surface. An asymptotic expansion leads to a viscous shallow water-type model involving a variational inequality. A nice property of this formulation is that it allows to treat the case of a null slope and is valid up to moderate slopes.

We then design a coupled augmented Lagrangian/finite volume scheme which fully takes into account both the threshold of plasticity and the power law. The overall method is well balanced, in the sense that it exactly preserves two types of stationary solutions. All these characteristics lead to a scheme which is able to compute the evolution to stationary solutions which can arise in these types of flow (thanks to plastic behavior). It is quite a remarkable feature of the present approach since many of the numerical methods presented in the literature use a so called regularization of the constitutive law, skipping the mathematical difficulty induced by plasticity and making them unable to compute stationary states (in these methods the material can not become rigid and is always flowing). The well balanced property is obtained by remarking that the spatial discretization of all the terms involved must induce a coupling between the height and the speed problem. The overall scheme is exact for the two particular cases mentioned in Proposition 1.

Aforementioned properties are finally illustrated numerically. Thanks to the first numerical test associated to the duct case, for which we have an analytical solution, we show that the implemented scheme is of order 2 in space for a nontrivial stationary solution. The second numerical test is designed to compute a flow at high rate of shear, where the Bingham fluid (℘=1) is “more viscous” than “true” Herschel-Bulkley fluids (℘<1). This allows to show the ability of the method to catch the various rheological behaviors of Herschel-Bulkley. As a matter of fact, the third numerical test—an academic test of avalanche—explores small rate of shear where the Bingham fluid is the “less viscous”. In both cases, the numerical results are in accordance with the expected physical evolution. Furthermore, the third test is the typical illustration of the well-balanced property of our scheme, since accurate numerical stationary solutions are exhibited for a long time after the reach of the arrested state of the avalanche.