1 Introduction

The orthorhombic unit cell of Bi(Pb):2212 superconducting systems with a critical temperature TC of 87 K consists of two units of (Bi,Pb)2Sr2CaCu2O8) and 15 layers. This compound should be over-doped with excess oxygen atoms δ in the range of (0.10–0.23). The extra atom of oxygen requires two more electrons which are provided by transforming 2Cu2+ ions into 2Cu3+ions [1]. In particular Bi(Pb):2212 exhibits anisotropy and a small coherence length together with elevated values of Tc, and therefore has a large effect on the superconducting order parameter [2,3,4,5]. Due to the short coherence length and high Tc of such system, the thermal fluctuations of the superconducting order parameter (Cooper pairs) have been previously observed above Tc as excess conductivity [1, 6]. The fluctuations of Cooper pairs begin to be created spontaneously at a temperature twice the mean field temperature Tmfc (T ≥ 2Tmfc ), and normally increase as the temperature approaches Tc.

The analyses of fluctuation-induced conductivity (FIC) reveal that the contribution of excess conductivity is due to Gaussian fluctuations in the mean field region as well as the critical field fluctuations region [7]. Gaussian fluctuations are probably dominant in the temperature region above Tmfc when the fluctuations in the order parameter are small and the interactions between Cooper pairs can be neglected, while the critical fluctuation occurs below the Tmfc when the fluctuation in the order parameter is large and the interactions between Cooper pairs are considered. The variation of excess conductivity ∆σ with the reduced temperature Є helps the researchers to find a lot of superconducting parameters such as the crossover temperature, the dimensional exponent, the interlayer coupling, the coherence length, the Ginzburg–Landau parameter, the Ginzburg number and the anisotropy [8]. However, the dimensional exponents in high Tc materials are found to be zero dimensional (0D), one dimensional (1D), two dimensional (2D) and three dimensional (3D) [9, 10]. It seems that the dimensional crossover takes place between any two different dimensions regions at a crossover temperature To.

The dimensional exponents of pure Bi(Pb):2212 systems are well described by 2D or quasi-2D nature [11,12,13,14,15,16,17]. It may also become 3D depending on the method of synthesis that modifies the state of microscopic disorder and induces spatial fluctuations near Tc. Usually, the crossover can occur either from 3D to 2D or from 1D to 2D in the doped samples [18, 19]. However, the substitution of rare earth elements RE3+ at Ca2+ sites in these systems mutually have different dimensional exponents due to the changes of carrier concentration in the CuO2 planes or excess oxygen in the system. For example, the substitution of Ca by RE in the Bi:2212 system suggests a 2D superconducting order parameter, and a distinct 2D–3D crossover behavior near Tc could be obtained [20,21,22,23,24,25]. These studies, however, do not discuss in detail the effects of La substitution on the above physical parameters, especially the anisotropy, Ginzburg number, critical fields and critical currents.

The lattice vibrations in ceramic cuprates have been considered previously as the subject of numerous studies and applications such as optical Kerr shutters (OKS), switching broad-band amplifiers, detectors and many other switching devices. Now, some evidence for electron–phonon coupling has been reported by infrared spectroscopy. The Fourier-transform infrared (FTIR) spectroscopy has been previously based on interference of radiation between two beams [26, 27]. FTIR records the percentage of transmittance over a wide range of wavelengths like near infrared (frequency range 10000–4000 cm−1), middle infrared (4000–200 cm−1) and far infrared (200–10 cm−1). Therefore, in order to distinguish the different roles between the spin vacancy and the carrier concentration against substitution content such as La in Bi(Pb): 2223 system, FTIR spectra (400–4000 cm−1) are examined at room temperature.

Based on this background, we report here the fluctuation-induced excess conductivity for the same batch of samples. We have restricted our analysis to the mean field regime and crossover behavior, and tried to extract some of the above critical superconducting parameters. Furthermore, dc-magnetization in both zero field cooling (ZFC) and field cooling (FC) at dc magnetic field of 20 Oe are performed with the goal of establishing some evidence for the existence of local moments. The FTIR spectra are taken in the frequency range of 400–4000 cm−1.

2 Experimental

The Bi2O3, PbO, SrO, La2O3, CaCO3 and CuO oxides and carbonates of 4 N purity (Bi,Pb)2Sr2Ca1−xLaxCu2Oy) are thoroughly mixed in the required proportions and calcined at 825 °C in air for 24 h. This exercise is repeated three times with intermediate grinding at each stage. The resulting powder was reground, mixed and pressed into pellets at a force up to 10 tons, and then sintered in air at 840 °C for 36 h and left in the furnace for slow cooling to room temperature by a rate of (5o/min). The phase purity of the samples is examined using X-ray diffraction (XRD) and the electrical resistivity is obtained using the standard four-probe technique in a closed-cycle cryogenic refrigerator within the range of (18–300 K) employing helium gas. In order to determine the onset temperature of diamagnetism Tcm, dc magnetization measurements are carried out by means of a SQUID magnetometer (Quantum Design) in both field cooling (FC) at a field of 20 Oe and zero-field cooling (ZFC) in the temperature range of (10–150) K. More precisely, the samples are first cooled down to 20 K in the absence of the applied field, then the field is switched on and the data are acquired for increasing temperature (ZFC) up to 150 K. After that, the samples are cooled down again and the FC magnetization is acquired in the presence of the field. On the other hand, the FTIR absorption spectra of the samples are carried out in powder form in the range of 400–4000 cm−1 (with a resolution of 4 cm−1 and scanning speed 2 cm−1/s at room temperature) using a spectrum 400-FT-1R/FT-NIR spectrometer. The samples are homogenized in spectroscopic grade of KBr carrier in an agate mortar and pressed into 2 mm pellets. The grinding time is minimized as much possible to avoid the structure deformation, ion exchange and water absorption from atmosphere.

3 Results and Discussion

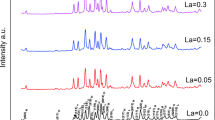
It is evident from the XRD pattern of the samples shown in Fig. 1 that all of the obtained peaks are identified by Bi: 2212 (hkl)H and 2201 (hkl)L as majority and minority phases, and no secondary lines are obtained. This behavior indicated that the pure and La doped samples are single phase and free from any impurity lines as reported elsewhere [28, 29]. The variations of lattice parameters a, b and c listed in Table 1 indicated that the b-parameter is slightly decreased by La up to 0.15 followed by an increase at 0.30, while a small simultaneous expansion along a and c axes is obtained followed by a decrease at 0.30. The average crystallite diameter Dhkl is evaluated by the following Scherrer’s equation [30,31,32]:

$$ D_{hkl} = \frac{k\lambda }{\Delta \theta \cos \theta } $$
(1)

where λ is the X-ray wavelength (λ = 1.5418 Ẳ), ∆θ is the half maximum line width, θ is the Bragg angle and k is constant (k = 0.93 for most of ceramic materials). By using the Lorentz square method, the values of Dhkl listed in Table 1 are 18.76, 22.87, 19.03 and 25.93 nm for pure and La samples, respectively. The dislocation densities, β = 1/D2, and listed in Table 1 are between (0.0029 and 0.0015) for all samples, which indicates that the samples have nearly very few lattice defects and good crystalline quality as obtained by XRD [33].

Fig. 1
figure 1

XRD patterns for pure and La the samples

Full size image
Table 1 Lattice parameters, inter-plane spacing, D, β, TcR, TcM, average TcM, ∆TcM and (TcR− TcM) versus La for pure and La samples
Full size table

The resistivity versus temperature curves for the samples are shown in Fig. 2. The critical temperatures TcR for zero resistivity listed in Table 1 are 94 K for a pure sample and decreased to 85, 63 and 51 K for the La samples, respectively. Figure 3a, b show the magnetic moment as a function of temperature in both zero-field-cooled (ZFC) and field-cooled (FC) for the samples. It is noted that the results for ZFC exhibits a broader drop for the magnetic moment and extended from 20 K up to the diamagnetic onset, possibly due to a strong flux pinning effect, while the FC exhibits a sharp drop close to the onset of diamagnetism and is nearly saturated as the temperature decreases to 20 K, indicating the presence of weak links. It is also noted that the magnetic moment is negative below the onset of diamagnetism for all samples in both FC and ZFC, but its value for FC is higher than that of ZFC. Furthermore, it is shifted to lower values close to zero as La increases up to 0.30. Moreover, the clear difference in the superconducting signal coming from the ZFC curve, with respect to that of the FC curve, can be taken as a proof for the correct ZFC protocol. The values of diamagnetic onset TcM for both cases are determined in terms of the values of the temperature corresponding to the onset of the zero magnetic moment. As listed in Table 1, the average values of TcM for FC and ZFC cases are 91, 79, 73 and 80 K, and the temperature difference between them are 2 K. As compared to the values of TcR, the difference between the values of TcR and TcM are 3, 6, 10 and 29 K, respectively. Although the diamagnetic signal is zero at this temperature, the area of the diamagnetic is higher than zero, indicating the presence of a superconducting state with a considered critical current [34, 35]. This observation suggests that the correct determination of TcM is influenced by the presence of a magnetic background which overcomes the superconducting signal, particularly in the region close to the diamagnetic transition. However, the higher difference between TcR and TcM occurs especially for the La = 0.30 sample may be due some of intrinsic in-homogeneities in the superconductor which reflect two critical temperatures. The first is the local temperature TcL as a result of small clusters, and the other is the percolation threshold temperature TcP due to an infinite cluster and nearly giving a true zero resistance (R = 0). In case of high accuracy of magnetic measurements, it is possible to determine the TcM of the first islands due to pure clusters present essentially and appeared in the sample [36, 37].

Fig. 2
figure 2

Resistivity versus temperature for pure and La samples

Full size image
Fig. 3
figure 3

a The FC magnetic moment versus temperature for pure and La samples. b The ZFC magnetic moment versus temperature for pure and La samples

Full size image

The excess conductivity ∆σ due to thermal fluctuations is defined from the deviation of the measured conductivity σm (T) from the normal conductivity σn (T) as follows:

$$ \Delta \sigma = \left(\frac{1}{{\rho_{m} }} - \frac{1}{{\rho_{n} }}\right) = \sigma_{m} - \sigma_{n} . $$
(2)

where ρm and ρn are the measured and normal resistivity, respectively. ρn is obtained from the measured resistivity ρm at a temperature TB–2 Tmfc by applying the least square method to the Anderson and Zou relation, \( \rho_{n} (T) = A + BT \) [38]. In order to estimate the paraconductivity, Aslamazov and Larkin (AL) deduced the following relation for the fluctuation-induced excess conductivity; ∆σ = AЄ−λ [39]. A is a constant, λ is the order parameter exponent and their values are 2, 0.5, 1 and 1.5 for (0D/SW), 3D, 2D and 1D fluctuations, Є is the reduced temperature given by \( \frac{{T - T_{c}^{mf} }}{{T_{c}^{mf} }} \) [40,41,42].

Tmfc is the mean field temperature above which the interactions between the Cooper pairs can be neglected. We have followed the dρ/dT versus temperature plot to obtain the values of Tmfc from the peaks.

Here, \( A = \frac{{e^{2} }}{{32\hbar \xi_{p} (0)}} \) for 3D, \( A = \frac{{e^{2} }}{16\hbar d} \) for 2D and \( A = \frac{{e^{2} \xi_{c} (0)}}{32\hbar s} \) for 1D, e is the electronic charge, d is the interlayer spacing between any two successive planes, ћ is the reduced Planck constant, ξp(0) is the effective characteristic coherence length at 0 K, ξc(0) is the c-axis 3D coherence length at zero temperature and s is the cross-sectional areas for 1D.

The crossover behavior from 2D to 3D occurs at a temperature T0 given by [43, 44]:

$$ T_{0} = T_{c}^{mf} \exp \left( {\frac{{2\xi_{c} (0)}}{d}} \right)^{2} $$
(3)

where \( \xi_{c} (0) = \left( {\frac{{dJ^{{\frac{1}{2}}} }}{2}} \right) \) [45, 46] and J is the interlayer coupling given by \( J = \ln \left( {\frac{{T_{0} }}{{2T_{c}^{mf} }}} \right) \) [47, 48].

The normal resistivity shown in Fig. 2 is found to be linear as the temperature is reduced from room temperature down to a certain temperature TB, and follows the \( \rho_{n} (T) = A + BT \) formula. TB ≃ 2Tmfc is the temperature below which the Cooper pair formation starts [49]. As the temperature is further reduced below TB, the rate of resistivity change becomes entirely different due to increasing Cooper pair formation. Therefore, the fluctuation-induced conductivity in this region follows the Aslamazov and Larkin (A–L) model to yield the dimensional exponent appropriate to fluctuation-induced conductivity [50].

However, ρn(T) is calculated by using the values of A and B parameters obtained from the fitting shown by straight columns in Fig. 2. One of them drawn at a temperature close to TB and the second drawn at a temperature very close to room temperature. The mean field temperature Tmfc listed in Table 2 is estimated from the peak of dρ/dT against temperature plot as shown in Fig. 4. By using the values of ∆σ and reduced temperatures Є, we have plotted ln∆σ against ln Є for all samples, see Fig. 5. Evidently, above Tmfc , we first observe a power law region which clearly means that the G–L theory breaks down and the short wave fluctuations play a dominant role [17]. Also, the excess conductivity decreases sharply in this temperature region and agrees well with the theoretical prediction. However, three distinct linear parts are obtained from each curve. The first part occurs in the normal field region (NFR), the second occurs in the mean field region (MFR) and the third occurs in the critical field region (CFR). The corresponding temperatures where the slope change occurs are designated as the crossover temperatures To1 and To2, respectively. The values of both Tmfc , To1 and To2 listed in Table 2 are decreased as La increases up to 0.30 as well as TcR behavior. The interlayer coupling J is calculated in terms of Tmfc and To2 values, and after that ξc(0) could be also obtained, in which d = c/2 for BSCCO systems, see Table 1 [18]. It is clear that both of J and ξc(0) are decreased as La increases up to 0.30 as well as the c-parameter.

Table 2 Tc, Tmfc , T01, T02, J, ξc(0) and OPD versus La for Bi(Pb):2223 system
Full size table
Fig. 4
figure 4

dρ/dT versus temperature for the pure and La samples

Full size image
Fig. 5
figure 5

Ln ∆σ against Ln Є for pure and La samples

Full size image

In order to compare the experimental data with the theoretical predictions, these regions are individually linearly fitted, and the values of the dimension exponents λ are well determined. However, the first exponent occurs in the normal field region (NFR) at a temperature range of (0.754 ≥ ln Є ≥ − 0.330) for the La = 0.00, (0.844 ≥ ln Є ≥ − 0.666) for the La = 0.05, (0.1.223 ≥ ln Є ≥ − 1.168) for the La = 0.15 and (1.453 ≥ ln Є ≥ − 0.786) for the La = 0.30. The values of exponents are 0.90 (2D), 0.67(2D), 0.23 (3D) and 0.77 (2D), respectively. The second exponent occurs in the mean field region (MFR) at a temperature range of (−0.349 ≥ ln Є ≥ − 2.693) for the La = 0.00, (−0.693 ≥ ln Є ≥ − 2.996) for the La = 0.05, (−1.235 ≥ ln Є ≥ − 2.428) for the La = 0.15 and (−0.841 ≥ ln Є ≥ − 2.036) for the La = 0.30. The values of exponent are 0.51 (3D), 0.23 (3D), 1.05 (2D) and 0.17 (3D), respectively. The third exponent occurs in the critical field region (CFR) at a temperature range of (−2.906 ≥ ln Є ≥ − 4.564) for the La = 0.00, (−3.088 ≥ ln Є ≥ − 4.187) for the La = 0.05, (−2.715 ≥ ln Є ≥ − 3.814) for the La = 0.15 and (−2.242 ≥ ln Є ≥ − 3.629) for the La = 0.30. The values of the exponents are 0.90 (2D), 0.78 (2D), 0.70 (2D) and 0.35 (3D), respectively. The above behavior indicates that the OPD is generally (2D/3D) in the NFR, (3D/2D) in the MFR and (2D/3D) in the CFR. Although, the OPD is not uniform as La increases up to 0.30, the considered La content shifted the OPD from 2D to 3D in the CFR.

The appearance of 0D in the NFR for the La = 0.30 sample may be due to the short wave length of critical fluctuations in the conductivity region of the microscopic granular superconductor, and it is extremely sensible to the applied magnetic field as seen in the diamagnetic behavior [19, 20, 22, 51, 52]. Our interesting point here is related to the values of exponents of the third region, where the order parameter is shifted from 2D to 3D for the La = 0.00 and 0.15, and from 3D to 2D for the La = 0.05 and 0.30. This may be related to the effective length in the direction perpendicular to the current flow which is found to be more reduced in RE3+ substituted Bi(Pb):2223 system [16]. This is because most of pure BSCCO systems are 2D in behavior in the CFR, and normally the crossover occurs from 3D to 2D due to the effect of substitution or radiation. But at present, the crossover is observed from 3D to 2D and also from 2D to 3D. Actually, the CFR is usually controlled by the critical fluctuations resulting from the small mean free path of the charge carriers produced as the carrier concentration is changed [53,54,55,56]. Our strange point here is that why the crossover is not systematic as compared to the increase in La content, which is clearly difficult for understanding.

The anisotropy parameter could be obtained using the relation [57]:

$$ \gamma = \left[ {\frac{{0.71K_{B} }}{{\sqrt {N_{G} } H_{c}^{2} (0)\xi_{c}^{3} (0)}}} \right]^{{\frac{1}{2}}} = \frac{{\xi_{ab} (0)}}{{\xi_{c} (0)}} $$
(4)

NG is the Ginzburg reduced number given by \( N_{G} = \frac{{T_{02} - T_{cR}^{{}} }}{{T_{cR}^{{}} }} \), ξab(0) is the in-plane coherence length and Hc(0) is the thermodynamic critical field at 0 K given by: \( H_{c} (0) = \frac{{\varphi_{0} }}{{2\sqrt 2 \pi \lambda_{L} (0)\xi_{c}^{{}} (0)}} \), where \( \varphi_{0} \) is the quantum flux given by \( \varphi_{0} = \frac{{h_{{}} }}{2e} = 2.07 \times 10^{ - 15} ({\text{web}}/{\text{m}}^{2} ) \), and λL is the London penetration depth at 0 K which is about 300 nm for Bi(Pb):2223 superconductors [58]. From the values of γ and ξab(0), the effective coherence length, ξp(0) is obtained with the help of the following relation [56]:

$$ \frac{1}{{\xi_{p} (0)}} = \frac{1}{4}\left[ {\frac{1}{{\xi_{c} (0)}} + \left( {\frac{1}{{\xi_{c}^{2} (0)}} + \frac{8}{{\xi_{ab}^{2} (0)}}} \right)^{{\frac{1}{2}}} } \right] $$
(5)

The upper critical fields at 0 K along the c-axis \( H_{c21} (c{\text{ - axis}}) \) and along a–b plane \( H_{c21} (ab{\text{ - plane}}) \), and also the critical current density at 0 K and Jc1(0) are calculated by using the following relations [59, 60]:

$$ \begin{aligned} H_{c21} (c{\text{ - axis}}) = \frac{{\varphi_{s0} }}{{2\pi \xi_{ab}^{2} (0)}} \hfill \\ H_{c21} (ab{\text{ - plane}}) = \frac{{\varphi_{0} }}{{2\pi \xi_{c}^{{}} (0)\xi_{ab}^{{}} (0)}} \hfill \\ H_{c21} (0) = \sqrt {[H_{c21} (ab{\text{ - plane}})]^{2} + [H_{c21} (c{\text{ - axis}})]^{2} } \hfill \\ J_{c1} (0) = \frac{{2\varphi_{0} }}{{\sqrt 6 \pi \lambda_{L}^{2} (0)\xi_{p} (0)}} \hfill \\ \end{aligned} $$
(6)

On the other hand, the lower critical field Hc1(0), upper critical fields Hc2(0) and also the critical current density at 0 K are estimated by the other following relations [61,62,63,64]:

$$ \begin{aligned} H_{c} (0) = \frac{{\varphi_{0} }}{{2\sqrt 2 \pi \lambda_{L} (0)\xi_{c} (0)}};\quad H_{c1} (0) = \frac{{H_{c} (0)\ln \kappa }}{\sqrt 2 \kappa } \hfill \\ H_{c22} (0) = \sqrt 2 \kappa H_{c} (0);\quad J_{c2} (0) = \frac{{4\kappa H_{c1} (0)}}{{3\sqrt 3 \lambda_{L} (0)\ln \kappa }}, \hfill \\ \end{aligned} $$
(7)

where κ is Ginzburg–Landau parameter of the superconducting system given by \( \kappa = \frac{{\lambda_{L} (0)}}{{\xi_{c} (0)}} \). As listed in Tables 3 and 4, the values of ξab(0), ξp(0) and γ are decreased as La increases up to 0.30 as well as both of c-axis, d, J, ξc(0) and TcR. While the values of NG, κ, critical fields and currents are gradually increased. Interestingly, the values of critical fields and currents obtained from Eq. 6 are approximately higher than that obtained by Eq. 7, see Fig. 6a, b. Although the above two equations have been used individually, it is not clear what the main reason is for the difference between them. In light of these observations, one can say that the increase in excess oxygen and hole carries/Cu ions which are introduced by La in the CuO2 planes of the Bi(Pb):2212 may affect the path of current flow in the system and eventually the critical parameters are increased. This leads to electronic or chemical inhomogeneous in the charge reservoir layer (BiO/SrO), and supplies the charge carriers to the CuO2 planes through which the actual super-current is believed to flow [65,66,67].

Table 3 NG, γ, ξab, ξp, Hc-axis(0), Hab-plane(0) and Jc(0) versus La for the samples
Full size table
Table 4 k, Hc(0), Hc1(0), Hc2(0), Jc(0) and Gi versus La for the samples
Full size table
Fig. 6
figure 6

a Critical fields versus La content for the samples. b Critical currents versus La content for the samples

Full size image

The order of thermal fluctuations in a superconductor is given by Ginzburg number Gi as follows [68, 69]:

$$ G_{i} = \left[ {\frac{{\pi \kappa^{2} \xi_{0} (c)K_{B} T_{c} \mu_{0} }}{{2\varphi_{0}^{2} }}} \right]^{2} $$
(8)

where µ0 = 4π × 10−7 A/m. The values of Gi listed in Table 4 are decreased from 8.7 × 10−3 for the pure sample to 7 × 10−3, 3.2 × 10−3 and 2.1 × 10−3 for the La samples. These values are comparable with the reported Gi = (10−3–10−4) for HTSC, and they are several orders of magnitude larger than 10−9 for conventional superconductors [68, 69]. Decreasing the values of Gi supports the decrease in critical temperature and also the crossover behavior from 2D/3D or 3D/2D as La increases.

The FTIR absorption spectra of the samples are shown in Fig. 7 and also the associated wave numbers for the absorption peaks are listed in Table 5. Regarding the pure sample, the presence of a broad absorption peak at 3851.20 cm−1 and a specific peak at 3493.25 cm−1 corresponds to the stretching vibration of the intermolecular hydrogen bond (O–H), indicating the assignment of fundamental stretching of the OH groups [70, 71]. The appearance of the peak band at 1633.36 cm−1 is confirmation of the complex formation of Bi(Pb):2223 phase, in agreement with the result reported elsewhere [72, 73]. There is a weak and broad absorption peak at 1379.14 cm−1, which may appear due to the presence of a small amount of residual carbon. The two successive peaks appearing at 1184.14 cm−1, 1110.95 cm−1 confirms the bond stretching of other metal oxides and carbonates such as SrCO3, CaCO3 and CuO [74, 75]. The observed strong peaks at around 586.45 cm−1, 563.28 cm−1, and 532.67 cm−1 may be attributed to the characteristic (metal oxide) O–M vibrations. However, with La substitution, the wave numbers of a few peaks are shifted from their position such as 3493.25 cm−1, which decreased to 3429.77 cm−1 and 3436.72 cm−1 for the La = 0.05 and 0.15 samples and then increased to 3493.25 cm−1 for the La = 0.30, and vice is versa for the 1379.14 cm−1 band, while the M–O absorption peaks are generally shifted to higher values. Furthermore, the peaks obtained at 1184.14 cm−1 1110.95 cm−1 remain constant for the La = 0.05 and 0.15, but they are increased to 1190.14 cm−1 and 1132.57 cm−1 for the La = 0.30 sample. Although some of the peaks such as OH and residual carbon are recorded, the intensity of the peaks are negligible and may be due to some other unknown impurities of external atmospheric sources unclear for us at present.

Fig. 7
figure 7

The FTIR absorption spectra of pure and La samples

Full size image
Table 5 The FTIR spectra for pure and La samples
Full size table

Anyhow, the FTIR spectra of BSCCO superconductors reflect the contributions of electronic response of the charge carriers and lattice vibrations. The FTIR spectra show different active modes which can be shifted to another wave number by changing either excess oxygen or carrier concentration [26, 76, 77]. The nature of substitutions in BSCCO is considerably simplified by involving the excess oxygen Oδ which makes several predictions that can be easily tested against the observed FTIR spectra [78]. In a marginally stable elastic network, equilibrium conditions require approximate equality of local atomic forces [79, 80]. The highest frequency ωD of an O–O defect pair scales with its reduced mass µD against the reduced mass of the host Cu–O LO mode, µH. Thus, µDω2D  = µHω2H and with M (Cu) = 4 M (O), ωD = 1.26 ωH. The maximum LO neutron peak energy is ~ 75 meV = 600 cm−1 in BSCCO, in agreement with the present data (586.45 cm−1).

However, the fluctuation-induced excess conductivity study for pure and La substituted Bi(Pb):2223 phase is considered by the following points: (i) decreasing the values of Tmfc and To as well as Tc; (ii) appearance of three different exponents; (iii) decreasing the coherence lengths, interlayer coupling, G–L parameter and anisotropy; (v) increasing the Ginzburg number, critical fields and currents. This is due to some effects such as decreasing c-lattice parameter even La3+ ionic size is higher than that of Ca2+ at the same 8-fold co-ordination; increasing the excess oxygen and hole carriers concentration per Cu ion. The consistency of these points gives a fair degree of certainty to the appearance of the fluctuation-induced excess conductivity of La substitution in Bi(Pb):2223 system. As far as we know, analysis of fluctuation-induced conductivity for the La substituted at Ca site in Bi(Pb):2223 may be considered for the first time and also improving the diamagnetic onset temperature for the La = 0.30 sample, which highlight the present work.

4 Conclusion

Excess conductivity, diamagnetic transition and FTIR spectra of pure and La substituted Bi(Pb):2223 superconductors have been investigated. We have shown negative magnetic moments below the diamagnetic transition in both field cooling (FC) and zero-field cooling (ZFC) for all samples, but the values of FC are higher than that of ZFC. Furthermore, the diamagnetic onset temperature (TcM) for the La = 0.30 sample is 80 K, which is about 29 K higher than that obtained from resistivity (TcR= 51 K). On the other hand, the logarithmic plots between ∆σ and Є reveal three different exponents corresponding to two crossover temperatures for all samples. The first exponent occurs in the normal field region (NFR) and its values are 0.90 (2D), 0.67 (2D), 0.23 (3D) and 0.77 (2D). The second exponent occurs in the mean field region (MFR) and its values are 0.51(3D), 0.23 (3D), 1.05 (2D) and 0.17 (3D). The third exponent occurs in the critical field region (CFR) and its values are 0.90 (2D), 0.78 (2D), 0.70 (2D) and 0.35 (3D). Although the substitutions of Ca2+ by La3+ could increase Ginzburg-Landau parameter, critical fields and currents, the interlayer coupling, coherence lengths, anisotropy and Ginzburg number are decreased. Finally, nine successive FTIR absorption peaks due to O–H, Bi(Pb):2223, residual carbon, SrCo, CaCo3 and CuO, and M–O could be obtained. These results are discussed in terms of the balance between hole carriers/Cu ion and excess oxygen which are introduced by La through CuO2 planes of BSCCO superconductors.