Detailed Investigation of Structural, Morphology, Magnetic, Electical and Optical Properties of the Half-Doped PerovsikteNd_0.5Ba_0.5FeO₃

Abstract

The highly crystallized orthoferrite of formula Nd_0.5Ba_0.5FeO₃ (NBFO) was synthesized by the sol-gel method. The phase of our compound and the average particle size were studied using X-ray diffraction (XRD) and scanning electron microscopy (SEM) methods. The X-ray diffraction patterns showed that the NBFO sample crystallize in the cubic structure with Pm-3 m space group. The average crystallite size value determined by Williamson-Hall (W-H), Halder–Wagner (H–W) formula and using the method of Debye-Scherer is in the range of 60 nm, 56 nm and 55 nm, respectively. In the other hand, SEM result shows an overall average particle size of about 251 nm. Obviously, the particle sizes observed by SEM are larger than those calculated by XRD, which indicates that each particle observed by SEM consists of several crystallized grains. Moreover, the antiferromagnetic (AFM)–paramagnetic (PM) phase transition has been confirmed by magnetic measurements at 0.05 T applied field. This AFM–PM transition has been observed for the Neel temperature T_N = 49 K. Frequency and temperature dependencies of capacitance (C−f/T) and conductance (G−f/T) of the sample were investigated in the frequency and temperature ranges of 40 Hz–100 MHz and 220–400 K, respectively. On the other hand, the optical characteristics of this polycrystalline were analyzed by UV–Vis absorption spectroscopy. By investigating the UV absorption and reflectance measurements, we identify the direct optical band gap close to 4.75 eV, which confirms that our sample is a direct gap semiconductor. In addition, the Urbach energy, the optical extinction coefficient and the refractive index were determined from the absorbance and reflectance measurements. We have also shown that the refractive index n follows the Cauchy law in the area where the absorbance is maximized. On the other hand, the dispersion parameters E₀ and E_d of this compound have been calculated based to the Wemple-Didomenico model. Dielectric investigation indicates that the dissipation factor tan δ has a very low value.

1 Introduction

In recent years, perovskite materials of general formula ABO₃ are the most studied [1]. Indeed, these materials have very interesting physical and chemical properties; they show a different electronic behavior from one state to another [2]. In particular, rare earth orthoferrites (RFeO₃) is a class of functional materials, that attract great attention due to their remarkable fascinating physical properties and potential application in the field of ultrafast optomagnetic recording, spin-switching valves, magnetoelectric sensor, spin reorientation-based modulator, magneto-efficiency, etc. [3, 4]. Another characteristic of RFeO₃ is the coexistence of two magnetic subsystems of R³⁺ and R⁴⁺. The competing network of Fe–Fe, R–Fe and R–R interactions causes some interesting phenomena in these materials. For orthoferrite perovskites, the substitution of Ln or Fe sites (where Ln is a rare earth element such as La, Nd and Pr) by other elements that offer multi-valence and defect sites in their structures, leads to the tuning of redox and electromagnetic properties of materials [5]. For NdFeO₃, the magnetic pairs of Fe and Nd form two non-equivalent magnetic sublattices with antiparallel coupling. The electrons in the 3-d and 4-f orbitals of these two sublattices react with spin–lattice coupling, leading to a very unstable magnetic state and, furthermore, to exceptionally large magnetic anisotropy, magnetization change, and spin permutation in weak magnetic fields [6]. For all orthoferrites, the basic magnetic structure of the ferrous subsystem just below T_N is an irreducible representation. The distorted FeO₆ octahedron in Pbnm space group which create asymmetric crystal field on Fe³⁺ ions, give rise to antisymmetric Dzyloshonki–Moriya interaction (DMI) [7]. Owing to DMI Fe³⁺spins is little canted and ReFeO₃ becomes weakly ferromagnetic instead of exact antiferromagnet [8]. In addition, orthoferrites generally possess rectangular magnetic hysteresis cycles from the phase transition regions, these hysteresis mechanisms have been described in previous reports as ErFeO₃ and TmFeO₃ [9]. The ferrites such as the neodymium orthoferrite NdFeO₃ is a soft compound with an orthorhombic deformation derived from a cubic perovskite structure. So generally; iron-based oxides are divided into three categories according to the ABO_3−δ perovskite substitution site. Type-A refers to the substitution of the A site, such as Pr_1−xSr_xFeO₃ [10], Ba_1−xLa_xFeO_3−δ [11], etc. Type-B is the B-site substitution, e.g. LaNi_0.6Fe_0.4O_3−δ [12], BaM_0.05Fe_0.95O_3−δ (M = Ti, Zr and Ce) [13], etc., while type-AB involves substitution of A and B sites, such as NdBaFe_2-xMn_xO_5+δ [14], etc. However, the A and B types, especially the A type, have been analyzed in majority.

Regarding the synthesis protocol, pure RFeO₃ orthoferrites (where R is La or Y), as well as RFeO₃ orthoferrites doped with Ca, Ba, Zn, and Co cations, can be produced by the following two-step approach without any surfactants: (1) hydrolysis of the cations in boiling water and (2) precipitation with suitable agents [15, 16]. Moreover, Neodymium orthoferrite NdFeO₃ have been prepared by many methods, the most common of which are: the high-temperature ceramic fabrication technique [17], the sol–gel method [18], combustion [19], ultrasonics, and co-precipitation techniques that contain octanoic acid as an organic surfactant [20]. Neodymium-based materials are used in application areas and productions such as magnetic dispersions, photoluminescence, and determination of grain size distribution in thin films, magnetic molecules and optical ring cores. PrFeO₃ nanoparticles have been synthesized via various methods including high-temperature ceramic fabrication [20], hydrothermal methods [20] and sol-gel complex methods [21].

In recent times, optical absorption spectroscopy in the energy range of ~ 6 eV to ~ 0.5 eV has been widely used to probe the electronic structure of various transition metal oxides including that of rare earth orthoferrites such as LaFeO₃, PrFeO₃, YFeO₃, etc [20]. In this context studies have been carried out to investigate the effect of doping in NdFeO₃ compound. Indeed, Shahid Husaina et al. [22] found that the energy band gap of NdFeO₃ sample decreases with Zn doping from 3.12 eV to 2.86 eV. On the other hand, Ti doped on LaFeO₃ has been presented to reduce the crystallite size, increases the band gap and creates weak ferromagnetic behavior [23].

On the other hand, this type of materials are considered as potential candidates for optoelectronic devices such as spin-photonic and ultraviolet devices, light-emitting diodes, magneto-optical devices and sun-blind UV photodetectors [24].

Based on previous works [14, 18, 22], it is interesting to study the half doping of Ba on Nd sites for NdFeO₃ compound. In this paper, we have presented the crystal structure, magnetic behavior, particle morphology and optical characteristics of Nd_0.5Ba_0.5FeO₃ (NBFO) powders obtained by the sol gel method.

2 Experimental

The NBFO sample is elaborated by the sol-gel method. A solution that contains a stoichiometric amounts of neodymium nitrate [Nd(NO₃)₃, 6H₂O, 99.9%, Sigma Aldrich], barium nitrate [Ba(NO₃)₂, ≥ 99.0%, Sigma Aldrich] and iron(III) nitrate nonahydrate [Fe(NO₃)₃.9H₂O, 99.9%, Sigma Aldrich], was evaporated at 90 °C. The pH of the solution was maintained at seven by adding ammonia [25]. Controlled amounts of citric acid, which is a complexing agent, and ethylene glycol, which is a polymerization agent, were introduced into the mixed solution [25]. After approximately 4 h, a viscous liquid (gel) can be observed, which was then dried at 250 °C (for 12 h). The resulting powder underwent numerous grinding and sintering cycles, and the desired crystalline phase was well formed at 900 °C. The detailed procedure for the preparation was summarized in the Fig. 1.

Fig. 1

Synthesis steps for NBFO sample using the sol–gel method

In the context of this paper, we employed a diffractometer with a copper anticathode (λ = 1.5406 A°) [25, 26]. The X'Pert High Score and X’Pert diagrams were recorded at room temperature with an angle range of 5° to 100° and a step of 0.02° per 2°. X’Pert High Score and Fullprof software were used to study the XRD results [27]. The microstructure of NBFO was analyzed by scanning electron microscopy (SEM). This allows us to identify grain morphology and size. Magnetic measurements at low temperatures were performed using a BS2 extraction magnetometer. In addition, Infrared spectra were recorded at room temperature with a Perkin Elmer spectrophotometer. Finally, the absorbance and reflectance spectra of the sample are made using a spectrophotometer Schimadzu 3101 PC at room temperature and recorded in the wavelength range [200–2000 nm]. The principle of operation of a spectrophotometer is described as follows: polychromatic light from an appropriate source (xenon lamp for our study) is dispersed by a grating monochromatic. In a double beam instrument, the light is separated into two beams before reaching the sample. One of the beams is used as a reference and passes through air of zero absorbance (or a sample of known reference), the other passes through our sample. The light passing through the sample and the reference is collected by a detector that converts it into an electrical signal (which will then undergo amplification and filtering operations).

3 Results and Discussion

3.1 Crystal Structure Characterization and Particle Morphology

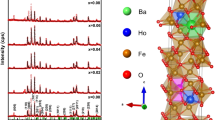
The synthesized NBFO sample was analyzed by XRD to identify the obtained phases and the approximate size of the particles. All peaks corresponding to the phase are indexed in Fig. 2. a. Otherwise, the spectrum shows fine and strong lines, which means that our compound has good crystallinity. As shown, the sample has a pure perovskite (ABO₃) structure with no secondary phase. The desired crystallographic phase of the sample was verified by the Rietveld method as presented in Fig. 2. b. All refection lines were indexed in the cubic structure with a Pm-3 m space group. Similar results are found in other studies [28]. The cubic structure parameters, corresponding refinement parameters such as reliability factors (R_F, R_p, R_B and R_exp) and goodness of fit (χ²) of NBFO sample are listed in Table 1.

Fig. 2

a Room-temperature XRD pattern for the polycrystalline sample NBFO, b XRD pattern and the corresponding Rietveld refinement: experimental data in red, calculated data in black, Bragg positions in green, and difference between them in blue, c The extrapolation function F(θ) by plotting the calculated values a_exp, Inset (c): SEM image for NBFO compound

Table 1 Crystallographic data deduced from the Rietveld refinement of X-ray diffraction data for NBFO sample

The mesh parameter (a_exp) of NBFO compound was determined from X-ray data analysis using the Eq. 1 [29].

$$a_{\exp } =_{2\sin \theta }^{{\lambda \sqrt {h^{2} + k^{2} + l^{2} } }}$$

(1)

where λ is the X-ray wavelength, θ is the diffraction angle, and (h, k and l) are the Miller indices. The values of the mesh parameter a₀ are also determined using the extrapolation function F (θ) by plotting the calculated values a_exp of each diffraction peak against the Nelson–Riley function (N–R) for each reflection using the Eq. 2 [29].

$$F\left( \theta \right) = \frac{1}{2}\left( {\frac{{\cos^{2} \theta }}{\sin \theta } + \frac{{\cos^{2} \theta }}{\theta }} \right)$$

(2)

The mesh parameter values a_exp for our sample are plotted in Fig. 2. c as a function of F (θ). It was found that the true value of the mesh parameter a₀ = 3.927A° is a value almost equal to that determined by the Rietveld method. The unit mesh volume for a cubic system was calculated from the following relationship: V = a_exp³.The mesh parameters a₀, a_R and the volume V are given in Table 1.

The Goldschmidt tolerance factor t allows us to prejudge the found structure of our NBFO compound. The factor t is given by the Eq. 3 [25]:

$$t = \frac{{r_{A} + r_{O} }}{{\sqrt {2(} r_{B} + r_{O} )}}$$

(3)

Among them, r_A, r_B and r_O correspond to the ionic radii associated with cations A, B and oxygen, respectively. For NBFO, we have: 〈r_A〉 = 0.5r_Nd³⁺ + 0.5 r_Ba²⁺and〈r_B〉 = 0.5 r_Fe³⁺. With r_Nd³⁺ = 1.163 A°; r_Ba²⁺ = 1.47 A°; r_Fe³⁺ = 0.67 A°. In this case, the value of t for our NBFO compound is 1.028. This result is consistent with the cubic structure related to the Rietveld refinement.

In the Inset of Fig. 2c we represent the SEM (Secondary electron micrograph) image. This morphological analysis reveals a homogeneous distribution of spherical grains. We can also notice on this image small hollows which are associated with the porosity of the sample. Overall, the sintering temperature affects the distribution of grain size and shape as well as their agglomeration in the synthesized compound. In the present context, the NBFO sample was prepared at a relatively high sintering temperature (250 °C). This indicates that this sintering temperature is favorable for good crystallinity and microstructural homogenization.

The chemical element composition and homogeneity analyzed by EDX microanalysis are shown in Fig. 3. We can note the presence of all the chemical constituents’ elements (Ba, Fe, Nd, O) that were introduced during the treatment; they are all non-volatile at 250 °C. This step allows us to ensure that no precursor has been forgotten. The statistical particle size distribution using Image J software is plotted in the Inset of Fig. 3. Fitting the histogram by applying the Gaussian function provides an average particle size around 251 nm. On other hand, the average grain size (crystallite) for the NBFO sample is given by the most intense diffraction peak (110), using Debye-Scherer formula (Eq. 4) [25]

$$D_{sc} = \frac{k.\lambda }{{\beta \cos (\theta )}}$$

(4)

where, k is a constant k = 0.9, λ is the X-ray wavelength (1.54059 Å), β is the width at half maximum (FWHM), and θ is the Bragg angle of the peak. The average size of crystallites is approximately equal to 55 nm.

Fig. 3

Chemical analysis by EDX, Inset: grains size distribution for NBFO

To examine the stress and crystallite size (D), which is inversely proportional to the peak width in the XRD profile, we performed the Williamson Hall W–H (Fig. 4) and Halder–Wagner H–W (Inset Fig. 4) analysis. The Williamson-Hall (W–H) graph method is given by the Eq. 5. Par versus, Halder-Wagner (H–W) graph is determined using the Eq. 6 [29]:

$$\beta \cos (\theta ) = \frac{K\lambda }{{D_{W - H} }} + 4\varepsilon si(\theta )$$

(5)

$$\left( {\frac{{\beta^{ * } }}{{d^{ * } }}} \right)^{2} = \frac{1}{{D_{H - W} }}\left( {\frac{{\beta^{ * } }}{{d^{ * 2} }}} \right) + \frac{{\varepsilon^{2} }}{4}$$

(6)

Where $\beta^{*} = \frac{\beta cos\left( \theta \right)}{\lambda }$, $d^{*} = \frac{2\sin \left( \theta \right)}{\lambda }$ and ε is the average value of lattice strain [29].

Fig. 4

The Williamson–Hall plot, Inset: Halder–Wagner plot for NBFO compound

A plot between βcosθ on the y-axis and 4sinθ on the x-axis for Williamson–Hall (W–H) method, however for Halder–Wagner (H–W), we have plotted (β^*/d^*)² on the y-axis and (β^*/d^*2) on the x-axis. The average value of crystallite size determined by W–H plot and H–W plot has the order of 60 nm and 56 nm, respectively. The lattice strain ε is found to be 2.42 × 10⁻³ (W–H) and 7.59 × 10⁻³ (H–W). The geometric parameters of crystallite size (D) and strain (ε), estimated from various models such as Scherer, Williamson–Hall (W–H) and Halder-Wagner (H–W) formula are given in Table 1. It is observed that the crystallite size calculated using Williamson-Hall and Halder–Wanger models is higher compared to the crystallite size (D_SC) estimated from Scherer’s formula, due to the elimination of the deformation contribution (ε), which indicates that the line widening in the sample is not only due to the smaller size, but also to the deformation. This is evident from the ratio of the number of atoms on the surface increasing and decreasing within the volume due to the increase in particle size, leading to a reduction in the number of broken bonds for the surface atoms, thus reducing the deformation.

4 Analysis of Magnetic Properties

Figure 5 shows the variation of magnetization M and dM/dT with temperature at a magnetic field of 0.05 T over the temperature range of 0 – 400 K for NBFO sample. Therefore, if the temperature decreases, the branch of M (T) is subject to an abrupt decrease of the magnetization towards 49 K where the maximum of the dM/dT curve is observed. This temperature is defined as the Neel temperature (T_N). Therefore, we can conclude from this variation that our compound presents an antiferromagnetic (AFM)–paramagnetic (PM) transition. It appears on the same figure (Fig. 5) that when the critical temperature is reached, the magnetic moments are completely disordered, and the NBFO becomes paramagnetic. This result is similar to other studies in the literature [30].

Fig. 5

Variation of the magnetization and the plot of dM/dT versus T, Inset: The inverse of the susceptibility variation as a function of temperature at 0.05 T

The variation of the inverse of susceptibility ${\chi }^{-1}$(T) determined from the branch of curves M (T) (from H/M) is shown in the Inset of Fig. 5. It is obvious that ${\chi }^{-1}$(T) increases in a non-linear way for T < T_N, on the other hand, with the increase of temperature until T_N = 49 K, ${\chi }^{-1}$(T) increases in a linear way. This kind of behavior is mainly due to the modification of the spin magnetic moment configuration with the increase of temperature. The susceptibility value of the present sample is higher compared to that found in other works [31]. The measured values of the susceptibility are fitted using the modified Curie–Weiss law (Eq. 7). The linear part of this curve shows the presence of a dominant paramagnetic phase in the sample:

$$\chi = \chi_{p} + \frac{C}{{T - \theta_{CW} }}$$

(7)

where ${\chi }_{p}$ is a temperature independent paramagnetic term that appears in the observed susceptibility.

By a linear fit in the paramagnetic part, it is possible to determine the experimental effective moment (Eq. 8):

$$\mu_{eff}^{\exp } = \sqrt {8C} \mu_{B}$$

(8)

The values of $\mu_{eff}^{\exp }$, $\theta_{CW}$ and C estimated for NBFO by fitting $\chi^{ - 1}$ versus T data above T_N are 3.427 $\mu_{B}$, −577.106 K and 2.337emu K/mol, respectively, as shown in the Inset of Fig. 5 and listed in Table 2. We note that these values are relatively close to those determined for Pb_0.5La_0.5FeO₃ sample [29].

Table 2 Magnetic data determined from the inverse of magnetic susceptibility ${\upchi }^{-1}$ and optical data deduced by characterization based on optical absorbance and reflectance for NBFO compound

5 Temperature and Frequency Dependence of Capacitance and Conductance

The variation of capacitance and conductance under the variation of frequency from 40 Hz to 100 MHz for different temperatures (220–400 K) is shown in Fig. 6 (a, b). In fact, capacitance increases with temperature in the low frequency range presenting a high dispersion with increasing temperature, which due to rapid response to space charge at low frequency in zone I. The linear behavior in zone II on moderate frequency can be explain by the decrease of space charge density. Zero values of capacitance in zone III showing independence with temperature at high frequency that is related to the difference of time response of space charge [32]. At high frequencies, capacitance also exhibits a metallic characteristic. Negative capacitance (NC) values were observed at moderate frequencies, were explained by lowering the device capacitance from its geometrical value to achieve negative values. Moreover, NC according to some studies is caused by a rise in the positive space charge density around the electrodes. Because electrons (free negative charge carriers) travel toward the metal electrodes from the ceramic sample, the positive space charge is most likely near the device outer surface [33]. This could potentially be due to charge carrier blockage at the electrodes and minority carrier injection (This is polarization effect). This behavior of C (f) is the result of the space charge located at the grain boundaries and the resistivity of the device. It is important to note that the trap charges have sufficient energy to empty the traps localized between grain and grain interface in the band gap at higher temperatures.

Fig. 6

Plots of capacitance C (a) and conductance G (b) versus frequency at different temperatures

The conductance frequency dependence, at different temperatures for the studied sample is shown in Fig. 6.b. The conductance G plots show an abnormal behavior with the conventional behavior of superconductor materials. In moderate frequency, we notice an important pic shifted to low frequency range when temperature increases that can be attributed to having a higher grain density located at boundaries [33,34,35].

6 Analysis of Optical Properties

6.1 FTIR Spectroscopy

Figure 7 shows the infrared transmission spectrum at room temperature in the wave number range (400–1100 cm⁻¹). These spectra show active vibrational band that correspond to the functional groups found in the compound studied. The main band appeared at about 568 cm⁻¹; this band represents the antisymmetric stretching vibration in the Fe–O–Fe bond of FeO₆, a regular octahedron. The main band represents the vibrational stretching of Fe–O–Fe bond in the absorption spectra of samples. This band represents the vibrational stretching of Fe–O–Fe bond in the absorption spectra of samples. The aforementioned main band appeared at around 574 cm⁻¹ and 400 cm⁻¹as represented by Li et al. and E.K Abdel-Khalek et al. [36, 37], respectively. While the band around 555 cm⁻¹ corresponds to the stretching vibration of the Fe–O band [38, 39]. The two peaks observed are main characteristics of perovskite oxides [40]. Then, the band detected at 600 cm⁻¹ is due to Nd-O vibration. Finally, the FTIR band at 852 cm⁻¹was attributed to Ba–O vibrations in our NBFO sample [41]. The broad peak at about 3436 cm⁻¹ represents the symmetric and asymmetric stretching vibration of water molecules.

Fig. 7

FTIR spectra of NBFO sample

6.2 Absorption Measurement

The evolution of the absorbance A for NBFO perovskite at room temperature in the range 200–2000 nm is presented in Fig. 8. As shown, this material has a strong optical absorption behavior for λ about 800 nm. The strong absorption found in this range may be related to the electronic transition from the valence band to the conduction band. We can note that the charcoal layers of our sample are used as absorber of the electromagnetic spectrum in the visible and near infrared. Due to their low mass heat capacity (J.kg⁻¹.K⁻¹), these metals are used to make infrared thermal detectors and solar radiation absorbing layers for high temperature photothermal energy conversion.

Fig. 8

UV–visible absorption spectre, Inset the plot of dα/dλ as a function of wavelength at room temperature

The absorption coefficient α can be obtained from Eq. 9, knowing that (e) is the thickness of the sample by applying the Beer-Lambert law [42]:

$$\alpha = \frac{2303.A}{e}$$

(9)

From the Inset of Fig. 8, where we have plotted dα/dλ versus wavelength λ, the band gap E_g is estimated to be 4.71 eV. The optical band gap of our compound was also evaluated using Tauc’s law described by Eq. 10 [43, 44]:

$$(\alpha h\nu )^{1/p} = A_{1} \left( {h\nu \, - \, E_{g} } \right)$$

(10)

where A₁ is a constant named the Tauc pre-factor that accounts for material characteristics, hν is the incident photon energy and p gives information on the nature of the transition: p = 0.5 for the direct transition, but for p = 2, the transition is indirect. The Tauc plot of our NBFO sample for p = 1/2 and p = 2 are presented in Fig. 9.a. The direct and indirect optical band gap are evaluated by an extrapolation of these plots, the E_g value of our compound is found by intersecting the fitted straight line with the (αhv)^1/p axis (y = 0). So, the band gap is found at (4.75 0 eV) for p = 0.5 and (1.96 eV) for p = 2. We conclude from the optical band that our material is a semiconductor. To determine the value of p and consequently to know the type of transition, we used the Eq. 11. For this reason, we have plotted on Fig. 9.b the evolution of ln (αhν) as a function of ln (hν−E_g) keeping as test values for E_g, those which have been obtained previously. We managed to obtain straight lines whose slopes provide the power factor (p). For E_g = 4.75, p is closer to 0.5 which confirms the direct transition character of the studied compound. The energy gap obtained for our studied sample is quite comparable to that of other rare earth RFeO₃ [45]:

$$\ln \left( {\alpha h\nu } \right) \, = \ln A_{1} + p\ln \, ( \, h\nu \, {-}E_{g} )$$

(11)

Fig. 9

a Plot of (αhν)^1/2 and (αhν)² versus hν (E_gd and E_gid are respectively the direct and the indirect band gap) and b Evolution of Ln (αhν) against Ln (hν−Eg)

The absorption coefficient shows some difference below the band gap, which proves that the optical spectrum is subject to sub-band absorption optics. In addition, the Urbach energy, due to the presence of structural deficits or gaps causing localized states that can be extended into the band gap and gives us an idea of the width of the absorption edge. From the theoretical point of view, this absorption band tail mentioned for E_u, is determined by the Urbach–Martienssen model (Eq. 12) [46]:

$$\alpha = \alpha_{0} \exp \left( {\frac{{h_{v} - E_{g} }}{{E_{u} }}} \right)$$

(12)

With ${\alpha }_{0}$ is a constant. By applying Eq. 12, we can determine the Urbach energy E_u through the slope of ln(α) as a function of the energy hν as shown in Fig. 10 and after using a linear fit of the first absorption peak that gives a slope value close to 0.407. The obtained value of Urbach energy $E_{u} = \frac{1}{slope}$ = 2.5 eV, proves the presence of disorder in our prepared sample. Urbach energy was used to determine the localized defect condition. As a result, using the thermal energy k_BT, we may rewrite the Urbach energy formula E_u as follows ${E}_{u}=\frac{{K}_{\beta }T}{\beta (T)}$, with T = 300 K is the absolute temperature, while k_B is the Boltzman's constant. Physically, the steepness parameter β (T) describes the thickening of the absorption edge generated by electron–phonon or excitation–phonon interactions in the band gap. The value of the steepness parameter was found β = 0.0074. In addition, the steepness parameter is related to the strength of the electron–phonon interaction (E_e−ph) as follows E_e−ph = $\frac{2}{3\beta }$. So, the estimated value of the strength of the electron–phonon interaction (E_e−ph) is close to 89.28 eV.

Fig. 10

Evolution of the Urbach energy for the NBFO compound

On the one hand, the calculation of the absorption factor or the extinction coefficient k is made from the Eq. 13 [24]:

$$k = \frac{\alpha .\lambda }{{4\pi }}$$

(13)

Figure 11 shows the variation of the extinction coefficient k as a function of photon energy hν. It is clear that the extinction coefficient k of our ceramic decreases with the increase of (hν). Indeed, the values of k are of the order of 10^–4, these low values justify the transparency of our material. As this compound presents a strong absorption in the UV range. We can deduce from these last results that, the prepared compound can be employed as sensor optoelectronic in this research. On the other hand, the penetration depth δ of incident radiation inside the material is given using the Eq. 14 [24]:

$${{\varvec{\updelta}}} \, = \frac{1}{\alpha }$$

(14)

Fig. 11

Evolution of the penetration depth δ and the optical extinction k versus hν for NBFO compound

In the same Fig. 11, we have presented the variation of δ. As it can be seen as the photon energy increases, a significant reduction in penetration depth is observed in the vicinity of the strong absorption, confirming that the incident light was strongly absorbed. In addition, the latter result can be attributed to the reduction of incident photon energy near the surface, which may affect the number of neighboring Fe³⁺ ions.

6.3 Reflectance Measurement

The refractive index n being the result of complex phenomena of interaction between the incident light and the atoms of our NBFO perovskite can be determined by applying the Eq. 15 [47].

$$n = \frac{(1 + R)}{{(1 - R)}} + \sqrt {\frac{4R}{{(1 - R)^{2} }} + k^{2} }$$

(15)

With k is the extinction coefficient.

Figure 12 shows the variation of the optical refractive coefficient as a function of λ at room temperature. As we observed the refractive character of our compound is weak for wavelengths in the vicinity of 835 nm or in this region the absorption is maximum. In the Inset of Fig. 12, we have presented the evolution of dR/dλ as a function of λ. The band gap energy E_g for this compound has been evaluated from the maximum of the dR/dλ curve (4.8 eV). We note that this value is relatively close to that determined for nanoparticles Nd_0.5La_0.5FeO₃ [44].

Fig. 12

Evolution of the refractive index as a function of λ, Inset: plot of dR/dλ versus (λ) for NBFO compound

To determine the E_g band gap for our NBFO compound, we used the Kubelka–Munk function (Eq. 16) which was determined from the reflectance spectra [42]:

$$F(R) = \frac{K}{S} = \frac{{(1 - R(\lambda ))^{2} }}{2R(\lambda )}$$

(16)

It is important to note that the Kubelka–Munk model is commonly used for semi-trans- parent and opaque materials. Moreover, this model combines the refectance data with the variation of absorption coefcient (α) in function of the wavelength as follows: $\alpha = F\left( R \right)/e$, with e the thickness of our sample. In addition, the plot of (F(R)hν)^1/2 versus hν or (F(R)hν)² versus hν referring to $\left( {F\left( R \right) \, h\nu } \right) \, = B\left( { \, h\nu - E_{g} } \right)^{1/p}$, where E_g is the optical band gap (eV), h the Planck’s constant (J.s), ν the light frequency (Hz) and F(R) the extinction coefcient, which is propor-tional to α. 1/p is a constant accounting for the type of optical transition. Indeed, p = 1/2 indicates direct allowed transition and p = 2 for indirect allowed transition.

In Fig. 13. a, we have plotted the curve (F(R) hν)^1/p as a function of hν for p = 0.5 and p = 2. From this curve, the E_g value of our compound is found by cutting the fitted straight line with the (F(R) hν) ^1/p axis (y = 0). Therefore, we find an optical band gap equal respectively to 4.77 eV for p = 0.5 and 2.43 eV for p = 2. These latter determined gap energy values confirm that our compound belongs to the family of semiconductor materials. The direct gap transition obtained for our sample is quite comparable to that of other rare earth orthoferrites [44]. In Table 3, we have made a comparison of the value and nature of the band gap transition of the compound NBFO with previous reports.Moreover, this value of the band gap and the direct character of the transition are in good agreement with those determined by absorbance measurements. Anand Somvanshi et al., Nd_0.5R_0.5FeO₃ (R = La, Pr, and Sm) [44] show a in her study a direct transition and a bandgap value nearly to the value our sample and the gap energy close 3.5 to 3.8 eV. Many others studies, confirms that these materials are a good semiconductor to optoelectronics compounds [44, 45].

Fig. 13

(a) Band gap analysis of NBFO powder pellet by using (F(R) hν)² plot versus the photon energy (hν) and (b) evolution of Ln (α_DRShν) against Ln (hν−E_g)

Table 3 Comparison of the value and nature of gap band transition with previous reports

In order to evaluate the energy of urbach E_u based on the Eq. 17, we have plotted (hν−E_gd) on the x-axis and ln (α_DRS) on the y-axis in Fig. 14. This energy E_u is determined by the extrapolation of the linear part of the same curve as represented in the inset of the same figure.

$$\alpha DRS = \alpha_{0} \exp \left( {\frac{{h\nu - E_{g} }}{{E_{{U_{DRS} }} }}} \right)$$

(17)

Fig. 14

Evolution of the Urbach energy, Inset: Determination of the E_u value for the NBFO compound

With ${\alpha }_{0}$ is a constant. The value of E_u is in the order of 1.02 eV, this value explains that in our NBFO ceramic the disorder is very low. Besides the steepness parameter β is close to 0.018 and the strength of the electron–phonon interaction value (E_e−ph) is in the order of 37.03 eV (These two characteristics are determined by the same way for E_u determined from absorbance measurements).

The experimental value of E_u determined by the DRS method is lower than the one determined by the tauc method because the DRS method takes into account the ratio of the sum of the molar absorption coefficient k and the diffusion factor S. Figure 15 illustrates the evolution of the extinction coefficient K and the penetration factor δ of NBFO sample, which are obtained from reflectance measurements and calculated by Eq. 18 and Eq. 19, respectively [24]:

$$K_{DRS} = \frac{{\alpha_{DRS} \lambda }}{4\pi }$$

(18)

$$\delta_{DRS} = \frac{1}{{\alpha_{DRS} }}$$

(19)

Fig. 15

Evolution of the penetration depth δ_DRS and the optical extinction K_DRS versus hν

As observed, the experimental data indicate that if the photon energy increases, the K coefficient decreases.We can conclude from these data that our compound has good transparency thanks to the low values of K in the order of 10^–4. On the other hand, these last results are in coherence with that determined by the Tauc model. In the same figure (Fig. 15), the variation of penetration depth proves that our NBFO perovskite absorbs the light well thanks to the values of δ. We base this statement on the possibility or which the intensity of the incident radiation falls to 1/e of its initial incident value. It is clear that the penetration depth is sensitive to the photon energy.

From Table 2, we found that there is a difference between the results obtained from the analysis by absorption or by reflectance. This difference comes from the technique of reflectance spectroscopy that is sensitive to the relative amounts of optical absorbing materials. In this regard, we can say that the best approach to determine E_g is the use of DRS method because it takes into account the amount of powders through. Moreover, it allows determining not only E_g and the main absorption mechanism, but also gives information about the coexisting phenomena [47,48,49,50,51]. In these models, the re-emission function of a mixture of N constituents, F (R), is just the ratio of the sum of their coefficients K and S, each weighted by the mass fraction W_i of constituent i.

Figure 16 shows the variation of optical conductivity σ_opt as function of wavelength λ for our compound. The optical conductivity is given by Eq. 20 [24]:

$$\sigma_{opt} = \frac{\alpha \left( \lambda \right)n\left( \lambda \right)C}{{4\pi k\left( \lambda \right)}}$$

(20)

Fig. 16

Optical conductivity σ_opt as a function of λ

The optical conductivity of NBFO sample decreases slightly for high wavelengths and thus for low photon energies. This last result proves that our material can be used as an optical filter in the visible domain to select specific frequencies and in optoelectronic devices.

Figure 17 a illustrates the results of the experimental refractive index in the spectral range of low absorption, which are adjusted using the formula of Cauchy (Eq. 21) [43, 51]. The best fit result of the experimental data proves that our NBFO sample has a normal dispersion. The parameters values of Cauchy are collected in Table 2.

$$n = n_{0} + \frac{{n_{1} }}{{\lambda^{2} }} + \frac{{n_{2} }}{{\lambda^{4} }}$$

(21)

Fig. 17

(a) The plot of n versus (λ⁻²) (b) Evolution of (n²−1)⁻¹ versus (hν)² and (c) (n²−1)⁻¹ versus (λ)⁻²

We have also performed some optical constants based on the Wemple–DiDomenico model, with a single oscillator, by applying Eq. 22 [48]. Figure 17.b represents the linear fit of the experimental results based on the Wemple–DiDomenico model to determine E₀ (energy of the effective single oscillator) and E_d (dispersion energy which is a measure of the intensity of inter-band optical transitions). E₀ and E_d can be determined from the intercept, (E₀/E_d) and the slope is (−1/E₀E_d). These values are listed in Table 2.

$$n^{2} - 1 = \frac{{E_{0} E_{d} }}{{E_{0}^{2} - hv^{2} }}$$

(22)

In the same model, we can also examine the refractive index to define the average oscillator wavelength λ₀ and the strength of the oscillator length S₀ of our studied sample, which are determined from Eq. 23 [48, 51]. From Fig. 17c, we obtain S₀ and λ₀ values from the linear fit of [n² (λ) − 1]⁻¹ versus λ⁻². The values recorded are given in Table 2.

$$n^{2} - 1 = \frac{{S_{0} \lambda_{0}^{2} }}{{1 - (\frac{{\lambda_{0} }}{\lambda })^{2} }}$$

(23)

In addition, the oscillator energy E₀ and the dispersion energy E_d are actually related to the M_-1 and M_-3 moments through the WDD model which are determined from the expressions $E_{0}^{2} = M_{( - 1)} /M_{( - 3)}$ and $E_{d}^{2} = (M_{( - 1)}^{3} )/M_{( - 3)}$, respectively [49, 50]. The values of the moments of the optical spectra M_-1, M_-3 obtained are gathered in Table 2.

6.4 The Optical Dielectric Costants

The complex dielectric constant [ε (ω) = ε₁ (ω)−iε₂ (ω)] is used to describe the optical properties of our material. The real and imaginary parts of the dielectric constant for this perovskite are also calculated by Eq. 24 and Eq. 25 [48,49,50,51]:

$$\varepsilon_{1} = n(\lambda )^{2} - K(\lambda )^{2}$$

(24)

$$\varepsilon_{2} = 2n\left( \lambda \right)K\left( \lambda \right)$$

(25)

Figure 18.a illustrates the photon energy dependence $\mathrm{h\nu }$of the real ε₁ and imaginary ε₂ part of permittivity. The obtained spectrum shows that the permittivity ε₁ is similar to that of the refractive index due to the smaller values of k (λ). On the other hand, the spectrum of ε₂ depends mainly on the values of k (λ). We noticed that ε₂ < ε₁ which explains that the energy loss of light passing through the compound is low. This last result is confirmed by the loss factor tan δ (also called dissipation factor), which presents the ratio, of the imaginary and real parts of the permittivity. The variation of the loss factor tan δ as a function of photonic energy $\mathrm{h\nu }$ at room temperature is shown in Fig. 18.b. In particular, in the near infrared range, the imaginary part ε₂ of the dielectric permittivity according to the classical theory is written as Eq. 26 [24]. The variation of ε₂ as a function of λ³ is reported on the Inset of Fig. 18 b.

$$\varepsilon_{2} = C_{1} \lambda^{3}$$

(26)

Fig. 18

a Real and imaginary parts of the dielectric constant of versus hν. b represent the energy loss of the light. Inset (b) Imaginary part of the dielectric constant as function of λ³

with C₁ is a constant, C₁ is found to be 3.611 × 10^–14 nm⁻³.

In Table 4, we report a comparison between Tauc, DRS and first derivative methods (dA/dλ and dR/dλ). Indeed, we can note from Table 4 an important difference of the optical band gap value obtained by the three methods. In addition, for the other parameters K, δ and E_u, a big gap of value obtained by Tauc and DRS method. S. Husain et al. [40, 51] estimated the optical factors values and they show that the obtained values by DRS method are nearly to those estimated by the Tauc method.

Table 4 Comparison between Tauc, DRS and first derivative (dA/dλ and dR/dλ) methods

7 Conclusion

The explored orthoferrite NBFO is successfully prepared by the sol gel technique. Studies including microstructural, magnetic and optical properties are successively presented. SEM analysis reveals that the sample has a homogeneous surface with regularly shaped grains. The Rietveld fit of the XRD model confirms the cubic structure of the sample with a Pm-3 m space group. On the other hand, the magnetic results proves the existence of antiferromagnetic–paramagnetic transition of Neel type at T_N = 49 K. Our results show an important dispersion of the C−f/T and G−f/T curves. The C−f/T and G−f/T plots give us much information about space charge transfer in all frequency zones. The optical properties of the NBFO compound are analyzed to determine the value of the direct optical band gap E_g which deduced from the absorption spectrum (Tauc model) and reflectance (DRS) to be 4.77 eV and 4.75 eV, respectively. This result characterizing our NBFO sample as a semi-conductor material. The optical parameters are determined from absorbance and reflectance measurements. The Urbach energies (E_u) as well as the refractive index (n), extinction coefficient (k) and the penetration factor (δ) have been deduced for our compound. The Couchy indices n₀, n₁, n₂ and the dispersion parameters such as E₀, E_d, λ₀, and S₀ are obtained using the Couchy model and Wemple and Di-Domenico model. The real and imaginary parts of the dielectric permittivity are evaluated. A comparison between the three methods used shows a difference between the obtained values.