A symmetry-based splitting strategy for discretizable distance geometry problems

Abstract

Discretizable distance geometry problems consist in a subclass of distance geometry problems where the search space can be discretized and reduced to a tree. Such problems can be tackled by applying a branch-and-prune algorithm, which is able to perform an exhaustive enumeration of the solution set. In this work, we exploit the concept of symmetry in the search tree for isolating subtrees that are explored only one time for improving the algorithm performances. The proposed strategy is based on the idea of dividing an original instance of the problem into sub-instances that can thereafter be solved (almost) independently. We present some computational experiments on a set of artificially generated instances, with exact distances, to validate the theoretical results.

1 Introduction

Given an integer $K>0$ and a simple undirected graph $G = (V,E)$ whose edges are weighted by a function $d: E \longrightarrow {\mathbb {R}_{++}}$, the Distance Geometry Problem (DGP) asks whether there exists a map $x: V \longrightarrow \mathbb {R}^{K}$ such that

$$\begin{aligned} \Vert x(u)-x(v)\Vert =d(\{u,v\}), \quad \forall \{ u,v \} \in E, \end{aligned}$$

where $\Vert .\Vert$ denotes the Euclidean norm.

The edge set E indicates the available distances between pairs of objects, represented by vertices of V, whose values are given by the function d. Hereafter we will use the short notation: $x_v = x(v)$ and $d_{uv} = d(\{u,v\})$. A solution x to the above problem is called a realization. For several interesting applications of DGP we point the reader to [8, 16]. We remark that in this paper we consider the input distances $d_{uv}$ exact (noiseless).

The DGP can be formulated as a global optimization problem [9], where the search space is continuous. However, under particular assumptions, this search space can be discretized so that it assumes the structure of a tree [5]. The discretization assumptions are strongly based on the existence of a vertex order for V which ensures that the first K vertices form a clique and, for every vertex with rank¹ greater than K (in the vertex order), there are at least K adjacent predecessors. In this case, we can find a finite set of possible positions for each vertex which are represented by nodes belonging to a common layer of the search tree [4]. A branch-and-prune (BP) algorithm has been developed for exploring this search tree with the aim of enumerating the entire solution set [7].

In recent years, thanks to the presence of symmetries in this search tree, some important theoretical results were discovered. For example, the number of solutions is almost always a power of two [10]. Additionally, it is possible to construct the entire solution set from a known solution by applying partial reflections corresponding to the symmetries [14].

In this work, we exploit such symmetries for developing a new strategy that, if integrated in the BP algorithm, allows us to speed up the search while keeping the quality of the obtained solutions. The basic idea is to split DGP instances in sub-instances that can be solved (almost) independently.

This paper is organized as follows. Section 2 focuses on different facets of the discretizable DGP: the assumptions that allow the discretization to take place, the definition of the search tree, the tree symmetries and the BP algorithm. Section 3 contains the theory behind the proposed splitting strategy. Some computational experiments are presented in Sect. 4. Section 5 concludes the paper with some directions for future works.

2 The discretization and the importance of symmetries

A 3-dimensional instance of the DGP (DGP$_3$) can be discretized if there exists an order ($\le$) relation between vertices of V satisfying certain assumptions. Let us assume that such an order is total so that each vertex has a unique rank. In order to simplify the notation, we use $v > K$ to mean that the rank of v is greater than K and $v - u$ to mean the difference in the ranks of v and u.

Given a DGP$_3$ instance, if there exists a vertex order such that

• 1. for every pair of vertices $u, v \in V$ with $1\le v-u\le 3$,

  $$\begin{aligned} \{ u,v \} \in E \, \, ({ discretization}), \end{aligned}$$

• 2. strict triangular inequalities

  $$\begin{aligned} d_{v-2,v}<d_{v-2,v-1}+d_{v-1,v} \end{aligned}$$

  hold for all $v \ge 3$     (non-collinearity),

then the instance can be discretized [4].

We refer to a vertex order satisfying these assumptions as discretization order and the class of DGP$_3$ instances that admit a discretization order as the Discretizable Molecular Distance Geometry Problem (DMDGP). This class of problems was, in fact, initially inspired by calculations of 3D protein backbones. However, the DMDGP is actually a general problem that can have other applications [16], not only in structural biology (for this particular application, the reader can make reference to [2]). Although we restrict our discussion to the case $K = 3$, all presented theoretical results can be trivially extended to any dimension $K>0$.

The discretization assumption ensures that the first 3 vertices in the order induce a 3-clique. Moreover, for every $v \in V$, $v>3$, there exist 3 immediate adjacent predecessors of v. This means that all distances between the vertices $v,v-1,v-2,v-3$ are available. Therefore, a set of feasible positions (w.r.t. the considered distances) for the vertex v can be obtained by intersecting 3 spheres centered in the reference vertices, and having as radii $d_{v-3,v}, d_{v-2,v}$ and $d_{v-1,v}$. If this intersection is non-empty, then it consists of 2 points only, with probability 1 [4, 8]; the role of the non-collinearity assumption is to prevent the intersections from containing infinitely many points. Notice that the set of triplets $(d_{v-2,v},d_{v-2,v-1},d_{v-1,v})$ for which the triangular inequality is satisfied as equality has zero Lebesgue measure in the set of all such triplets. We also remark that the strict triangular inequalities can be verified in advance (before exploring the search tree) for a given discretization order.

2.1 The search tree

Given a vertex v and the positions for its 3 immediate preceding vertices $v-3$, $v-2$ and $v-1$, the two DMDGP assumptions ensure that the sphere intersection provides 2 possible positions for v: $x'_v$ and $x''_v$. By recursively iterating this procedure for all vertices of G, in the vertex order associated to G, then a finite search space can be defined. This search space has the structure of a tree, where the entire set of possible positions for a certain vertex v is organized in a common layer. Finding the solution set for a DMDGP instance can be seen as the process of pruning the search tree from all the branches that do not correspond to feasible solutions w.r.t. the distance constraints.

Let us divide the edge set E into two subsets: $E_d$, containing all the edges which are related to the distances required by the discretization assumption, and $E_p = E \smallsetminus E_d$, which contains edges whose related distances can be used for verifying the feasibility of computed vertex positions (we say that distances related to $E_{p}$ correspond to pruning edges, see Sect. 2.3). If $E_p$ is empty, the feasibility of the vertex positions cannot be verified and none of them can be pruned. So, in this case, the solution set (modulo rotations and translations) coincides with the search tree and, in total, $2^{n-3}$ paths can be identified from the root of the tree until the leaf nodes at level n, all of them leading to a feasible solution to the problem.

When $E_p$ is not empty, instead, there are pruning edges that can be used for checking the feasibility of computed vertex positions. In the event a pruning edge is not compatible with one or more computed positions for the current vertex, then it prunes the corresponding branch(es). Naturally, the more edges in $E_p$, the more the branches can potentially be pruned from the search tree.

2.2 Symmetries of the search tree

Since the very first papers on the DMDGP (see, for example, [5]), it was empirically noticed that the number of solutions of DMDGP instances is always an even number. The reason for this was soon attributed to the fact that, on the layer 4 of the search tree, it is not possible to prune because the number of reference vertices is 3, and they are all necessary for the discretization. This symmetry is implied by the absence of pruning edge at layer 4, together with the fact that a pruning edge crossing the layer 4 may only be incident to the reference vertices, whose coordinates are common for the two branches rooted at $x'_4$ and $x''_4$, respectively. As a consequence, for every solution on the branch rooted at $x'_4$ there exists a symmetric one on the branch rooted at $x''_4$.

Since the first computational experiments on the DMDGP, it was noticed as well that the total number of solutions is not only even, but also a power of 2. This remained unexplained for a while, until it was formally shown that DMDGP search trees do not only contain one symmetry (at layer 4, around the plane defined by the first 3 vertex positions), but also several others [10]. Moreover, every symmetry implies the duplication of the number of solutions: every feasible DMDGP instance has, at least, 2 solutions (because the first or trivial symmetry is present at layer 4) and this number doubles for every other non-trivial symmetry that we can identify.

Fig. 1

Situation 1: the pruning edge incident to v shows that $x'_v$ is not feasible

Fig. 2

Situation 2: $x''_v$ is here infeasible, while $x'_v$ is supposed to be feasible

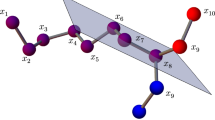
As for the trivial symmetry, the other symmetries appear in the absence of pruning edges. Let us consider the situation depicted in Fig. 1. We suppose that a pruning edge is available for verifying the two possible positions for the current vertex v. The dashed line indicates that the computed position $x'_v$ is not feasible w.r.t. the available pruning edge, while the other position is feasible. In Fig. 2, we have a similar situation, where $x'_v$ is feasible and $x''_v$ is not. It is important to remark that we may also have the situation where both $x'_v$ and $x''_v$ are infeasible. In this case, if our instance is feasible, the infeasibility of both positions comes from the fact that an infeasible position for a previous vertex (on the same branch) was chosen, because no pruning edge was available for its feasibility check (on the previous layers).

In order to explain this concept in more detail, let us consider two other situations shown in Figs. 3 and 4. In both cases, there are no pruning edges that are incident to v and, consequently, it is not possible to verify the feasibility of the vertex positions $x'_v$ and $x''_v$, which have been computed by simply exploiting the reference vertices. But, they differ in one detail.

Fig. 3

Situation 3: no pruning edge is incident to v, and no pruning edge crosses v

Fig. 4

Situation 4: no pruning edge is incident to v, but at least one pruning edge crosses v

In Fig. 3, we suppose that there are no pruning edges that cross over the current vertex v: more formally, we suppose that there is no edge $\{ u,w \} \in E_p$ such that $u + 3 < v$ and $v \le w$. Here, we are in the same situation as for the trivial symmetry, and in fact the two computed positions $x'_v$ and $x''_v$ are both feasible at the current layer, and they give rise to two new subtrees in the search tree, which are symmetric [14].

The situation described in Fig. 4 is different, because it is supposed that there exists a pruning edge crossing over the current vertex v. Therefore, even if both vertex positions $x'_v$ and $x''_v$ are considered as “feasible” at the current layer, and a new branch starting from each of them is initialized, they cannot be both part of a solution to the problem. When the crossing pruning edge will be used for pruning during the search, then we will be able to verify which vertex position is actually correct. We remark that they may even be both infeasible.

This very last situation shown in Fig. 4 is the one that requires more computational resources. The pruning phase of the BP algorithm is not effective at the current layer, but only in subsequent layers. Meanwhile, there may be no other pruning edges that can be exploited for reducing the tree width. In this subtree, therefore, we can experience a combinatorial explosion that can potentially worsen the performances of a tree search. In the strategy that we will propose in Sect. 3, this subtree is explored separately only one time (rather than as many times as the number of nodes at the layer where this subtree is rooted).

The symmetries in the search tree can be identified by verifying for every vertex of the DMDGP graph whether there are pruning edges that cross or pass over the associated layer [13, 14, 17]. This way, a subset of the vertex set V can be defined, as follows:

$$\begin{aligned} S_G = \{ v \in V : \not \exists \{ u,w \} \in E \,\, \text{ such } \text{ that } \,\, u + 3 < v \le w \} , \end{aligned}$$

where all the symmetric layers of the tree are included [14]. We say that $S_G$ is the symmetry set of G; it is trivial if it only contains the rank 4 (as mentioned in Sect. 2, we will refer to the rank of the related vertex). Notice that different instances may have the same $S_{G}$.

Figure 5 shows the search tree related to a DMDGP instance whose symmetry set is $S_G = \{ 4,11,16 \}$ and $E_{p} = \{ \{1,6\} , \{1,10\} , \{2,7\}, \{3,10\}, \{8,14\}, \{10,14\} , \{11,15\},$ $\{13,19\} , \{14,20\}, \{15,20\} \}$.

All the situations described above can be found in this search tree. Let us suppose to explore the search tree in a depth-first manner and from left to right. Since the instance has two non-trivial symmetries, no pruning occurs at layers 11 and 16: all generated positions for vertices 11 and 16 are feasible. At layer 12, for example, there are no pruning edges for verifying the feasibility of the computed vertex positions as well, but $12 \not \in S_G$. So, it is necessary to accept the two generated positions at layer 12 for every triplet of positions for the immediate preceding vertices, but they may be not part of a feasible solution. In Fig. 5, we represent the positions that are firstly accepted and subsequently pruned with light-red dashed circles. At layer 14, because of the pruning edge incident to the current vertex, it can be immediately exploited for verifying the feasibility of the computed positions.

Fig. 5

The search tree related to a DMDGP instance for which $S_G = \{ 4,11,16 \}$

2.3 The BP algorithm

The BP algorithm computes the two possible positions for the current vertex v as the intersection of 3 spheres in $\mathbb {R}^3$ by exploiting the reference vertices that are guaranteed by the discretization assumption. Each position is tested in turn for feasibility, and the algorithm invokes itself, in order to work on the next vertex of the pre-defined vertex order, only in correspondence with the computed positions that result to be feasible. The feasibility check is performed by using the so-called pruning devices. The easiest pruning device to implement, but yet very efficient when there is no uncertainty or errors affecting the data, is the Direct Distance Feasibility (DDF) check, where the pruning edges are verified for the computed vertex positions. Various pruning devices can be developed and added to BP [19].

Algorithm 1 is a sketch of the BP algorithm, where $v \in V$ is the current vertex for which we are looking for a position, $n = |V|$ and d represents the weights associated to the edges.

It can run to termination to find all possible realizations of G, or it can be stopped after the first leaf node at level n is reached, in order to find only one realization of G (which is called BP-one).

To the best of our knowledge, the BP algorithm is currently the only method for the DMDGP that is able to find all incongruent solutions. When compared to continuous search algorithms (e.g. [12]), the performance of the BP algorithm on instances without any uncertainty or errors on the distances is in general impressive from the point of view of both efficiency and reliability [4, 18].

3 Subtree splitting strategy based on symmetries

Our interest in this work is to define an efficient strategy for splitting up DMDGP instances with the aim of identifying subtrees that can be explored one (and only one) time, and that have as few as possible pruning edges which are shared with other subtrees. In previous works [3, 18, 20], the idea of dividing the vertex set of a DMDGP instance was already investigated, and some implementations in parallel computing environments provided some interesting results. The BP algorithm, integrated with our strategy, is rather suitable for sequential executions (see the computational experiments in Sect. 4).

Let $G=(V,E,d)$ be the graph representing a DMDGP instance. Because of DMDGP assumptions are satisfied, there exists a vertex order r on V for which the discretization and the non-collinearity assumptions both hold. Let us denote with $V_i$ a subset of vertices of V that are consecutive in the order r. Let $G[V_i]$ be the subgraph of G induced by $V_i$.

It is immediate to verify that, if we define a set $\{V_{1} , \ldots , V_{k}\}$ of subsets $V_i$ of the vertex set V, then every $G[V_i]$ also represents a DMDGP instance, because the necessary assumptions still hold. However, the union

$$\begin{aligned} \bigcup _{\ell \le k} G[V_\ell ] \end{aligned}$$

may not correspond to the initial graph G. In fact, the pruning edges in $E_p$ for which the two adjacent vertices happen to belong to two different subsets of V cannot be included in any induced subgraph. For this reason, once all the local solutions to all the sub-instances related to the induced subgraphs $G[V_i]$ have been obtained, it is necessary to consider all these extra pruning edges when concatenating the local solutions.

Our idea is to split the vertex set of G by exploiting the information about its symmetries, in a way to have no extra pruning edge to consider when concatenating local solutions. When we split by taking into consideration the tree symmetries, then no pruning edges can cross over the obtained vertex subsets, because this would go against the definition of symmetry (see Sect. 2). When this is not possible, we can leave out a few pruning edges that allow for generating some fictive symmetries in the search tree. Those pruning edges need to be considered thereafter when local solutions are concatenated.

We point out that there exist real applications where the removal of a few pruning edges could give rise to the generation of new symmetries in the tree. One important example is given by protein instances [11]. Proteins are chains of smaller molecules called amino acids (implying the existence of several short-range distances to be used for the discretization) which may be very compact (so that experimental techniques are able to estimate distances between atoms that are far in the chain, to be used as pruning edges). Therefore, short-range distances may be used for generating our subtrees, which would give us an idea of the local geometry of the object, while pruning edges could be exploited for finding the global fold.

In the next section, we will go over the theory of the proposed strategy for splitting DMDGP instances.

3.1 Splitting instances by symmetry

In the following, all statements such as “$\forall p\in P, F(p)$ holds with probability 1”, for some uncountable set P and valid sentence F, actually mean that there is a Lebesgue-measurable $Q\subseteq P$ with Lebesgue measure 1 w.r.t. P such that $\forall p\in Q, F(p)$ holds. In Sect. 2, we have already wrote one of such statements when we stated that the intersection of 3 spheres in the Euclidean space $\mathbb {R}^3$, if not empty, gives 2 points, with probability 1.

We begin our discussion with some basic definitions. Recall $G=(V,E,d)$ represents the DMDGP instance and $G[V_i]$ denotes the subgraph induced by $V_i \subset V$.

Definition 1

A covering of V is a set $\mathcal{C} = \{ V_{1}, \ldots , V_{k} \}$ such that

• (i) $V_{i} \subset V$ is non-empty, for all $i \le k$ and

• (ii) $V = V_{1} \cup V_{2} \cup \ldots \cup V_{k}$ .

The value k (the cardinality of $\mathcal{C}$) can be either fixed, or variable. In the former case, a strong constraint is associated to the covering, so that methods looking for optimal coverings (for some given criteria) need to deal with a strongly constrained search domain. In the latter case, instead, when k is free to take any possible value, the optimization of the given criteria actually leads to the definition of the optimal k [1].

In this study, we restrict our attention to coverings where each $V_i$ consists in consecutive vertices according to a given vertex order.

Once a covering $\mathcal{C}$ for the vertex set V is found, it can be used for defining a covering also for the graph G.

Definition 2

A graph covering of G is the graph $\mathcal{C}_G$ obtained as the union

$$\begin{aligned} G[V_1] \cup G[V_2] \cup \dots \cup G[V_k] , \end{aligned}$$

where $\{ V_{1}, \ldots , V_{k} \}$ is a covering $\mathcal{C}$ of the vertex set V. We say that $x : V \longrightarrow \mathbb {R}^{3}$ is locally feasible for $\mathcal{C}_G$ if the image $x(V_i)$, for every $i \le k$, is a realization for the induced subgraph $G[V_i]$.

By definition, the subgraph of G induced by a set $V_i \subset V$ inherits all the edges $\{ u,v \}$ of G such that $u, v \in V_i$. For this reason, if a particular edge $\{ u,v \} \in E$ is such that u is assigned to a certain $V_i$, while v is assigned to another $V_j$, with $i \ne j$, then no subgraph in $\mathcal{C}_G$ can contain the edge $\{ u,v \}$.

Lemma 1

If $x : V \longrightarrow \mathbb {R}^{3}$ is locally feasible for $\mathcal{C}_G$ and

$$\begin{aligned} E = \bigcup _{i=1}^k E_i , \end{aligned}$$

where $E_i$ is the edge set of $G[V_i]$, then x is also a realization of G.

Proof

If x is locally feasible, then it represents one realization for every subgraph $G[V_i]$. Since there are no pruning edges crossing over two different subgraphs, the concatenation of all these local realizations, one per each subgraph $G[V_i]$, defines a realization for the original G. $\square$

Our interest is in defining a strategy for dividing a DMDGP instance into sub-instances that can be efficiently managed. The main issue to overcome consists in minimizing the number of edges that are not included in the graph covering $\mathcal{C}_G$.

A practical consequence of Lemma 1 is that, when all edges of the original graph G are included in the induced subgraphs, the concatenation of local solutions can be performed without verifying any additional pruning edge. In fact, when this is not the case, some of the solutions obtained by concatenation may actually not be a realization for G. So, we search for coverings of V that induce a graph covering $\mathcal{C}_G$ of the original graph G that minimizes the number of crossing pruning edges.

Let $D = (d_{jk})$ be the distance matrix associated to the DMDGP instance represented by G. We suppose that all available distances are nonzero and that $d_{jk}=0$ indicates that this distance is not available. Recall that $S_G$ is the symmetry set of G.

Proposition 1

If $S_{G}$ is non-trivial, then $i \in S_{G}$, with $i \ne 4$, if and only if $d_{jk} = 0$, for each pair of vertices $j = 1, \ldots , i-4$ and $k = i, \ldots , n$.

Proof

By definition, $i \in S_G$ implies that there are no pruning edges $d_{jk}$ such that $j+3 < i \le k$. We point out that the case $4 \in S_G$ is a trivial case. $\square$

As immediate consequence of Proposition 1, the distance matrix can be divided in blocks comprising smaller distance matrices (indicated by dashed rectangles) and null matrices (indicated by a straight rectangles), such as the ones in Fig. 6. Such a matrix visualization shows the distribution of the distances. It naturally suggests the existence of DMDGP sub-instances that can be solved in an independent manner, because its vertices do not share any additional pruning edge with any other sub-instance. Moreover, if a few pruning edges appear in the upper diagonals, they can be ignored when defining the covering and used thereafter when concatenating local solutions.

Fig. 6

An example of a distance matrix for a DMDGP instance. Off-diagonal “zeroes” indicate missing distances

Here, we define a set which will be the generator of the graph covering $\mathcal{C}_{G}$.

Definition 3

Given the symmetry set $S_{G}$ of a DMDGP instance, with n vertices, the symmetry covering genesis set is

$$\begin{aligned} \mathcal{G}(S_{G}) = \{ (i-3,j-1) \in \mathbb {N}^2 : i \in S_{G} \cup \{n+1\}, j = \min ( h \in S_{G} \cup \{n+1\} : h >i ) \}. \end{aligned}$$

Notice that the set $\mathcal{G}(S_G)$ depends on the symmetry set of G and not directly on G itself: graphs with the same number of vertices and having the same symmetry set share the same symmetry covering genesis set.

We employ the algorithm sketched in Algorithm 2 for generating the set $\mathcal{G}(S_G)$ from a given symmetry set $S_G$.

The algorithm also requires the cardinality of V as an input, and it uses its value at the very beginning, in order to avoid the situation where a sub-instance containing only the last ranked vertex can be created in the case it is a symmetry vertex. In the algorithm, the set of symmetry ranks is named S. At the beginning, the algorithm verifies whether there are consecutive ranks in S (also in this case, this is done to avoid to create sub-instances which contain only one vertex). To do so, the algorithm searches for subsets of consecutive ranks in S and replaces all of them with the rank in the subset that is, as much as possible, placed in a central position between its predecessor and its successor. Notice that, when symmetric vertices are removed from S, more than one symmetry can appear in the same sub-instance, implying an increase on the total number of local solutions (it may not be anymore a pair of symmetric solutions).

This procedure may not be optimal when several consecutive ranks belong to $S_{G}$, but this situation is unlikely to be verified by DMDGP instances concerning real-life applications. Finally, the obtained set S is used for constructing the symmetry genesis set. For every rank in S, the pair $(i-3,j-1)$ is included in $\mathcal{G}(S_G)$. Recalling to the example, originally $S_{G} = \{4 , 11, 16\}$. There is no consecutive ranks and the last vertex is not included also. Thus, the symmetry covering genesis set is given by $\mathcal{G}(S_{G}) = \{(1,10), (8,15) , (13,20) \}$. As we see, it guarantees that all the vertices are covered and that the cardinality of the intersections between pairs of consecutive elements of $\mathcal{G}(S_{G})$ are exactly equal to 3.

Definition 4

The graph covering $\mathcal{C}_S$ of G such that

• (i) $|\mathcal{C}_S| = |\mathcal{G}(S_G)|$ and

• (ii) every $G_i \in \mathcal{C}_S$ is $G[ \{ a_i, a_i + 1, \dots , b_i - 1, b_i \}]$, where $(a_i,b_i) \in \mathcal{G}(S_G)$,

is named symmetry covering of G.

Figure 7 shows a schematic representation of a symmetry covering $\mathcal{C}_S$. It represents the graph covering for the same graph G of the example depicted in Fig. 5. The vertex sets of the induced sub-graphs are marked by the triangles. Notice that in Fig. 7, we represented only the branches and nodes that were effectively explored when applying BP-one to each sub-instance. Only the first solution to each sub-instance is necessary, because other solutions may be obtained by exploiting symmetries and partial reflections as will be explained ahead.

Fig. 7

A schematic representation of symmetry covering. The white nodes represent the symmetry vertices. BP-one is applied to each sub-instance whose effectively explored trees are enclosed by the black triangles

By considering all the remarks above, we can immediately prove the following:

Proposition 2

Any map $x:V \rightarrow \mathbb {R}^3$ that is locally feasible for $\mathcal{C}_S$ is a realization of G.

Proof

Let $E_i$ the edge set of the subgraph $G_i \in \mathcal{C}_S$. Since the vertex set $V_i$ of $G_i$ is, by definition, $\{ a_i, a_i + 1, \dots , b_i - 1, b_i \}$, where $(a_i,b_i) \in \mathcal{G}(S_G)$, then there are no edges connecting vertices in $V_i$ to vertices in $V \smallsetminus V_i$. As a consequence,

$$\begin{aligned} \bigcup _{i=1}^k E_i = E , \end{aligned}$$

where E is the edge set of the original graph G. By Lemma 1, under this hypothesis, if x is locally feasible for $\mathcal{C}_{S}$, then it is a realization of G. $\square$

4 Computational experiments

In this section, we will report some preliminary experiments aimed at validating our discussion in Sect. 3. All experiments were performed on a Macbook Pro, Intel Core i7 2.4 Ghz, 8 Gb RAM, running a Mac OS X 10.10.5 operating system.

We consider instances that have been generated by the procedure below. First, n points in $\mathbb {R}^3$ are randomly generated and all pairwise distances are computed. Then, only the distances required by the discretization assumptions are kept, together with additional pruning edges, selected in a way to guarantee a specific number of symmetry vertices ns. A few more pruning distances are added to the DMDGP instance, which are likely to remove some (or even all) the symmetries. Figure 8 gives a schematic representation of the distribution of the distances in the distance matrix of an instance generated with $n = 5000$ vertices and $ns = 10$ initial symmetries (i.e. symmetries in the tree before the inclusion of the last few pruning distances).

Fig. 8

The schematic representation of the distance distribution in the distance matrix related to one of the instances we consider in the experiments. Notice that after the removal of the top-right (bottom-left) subset of distances, the instance presents 10 symmetry vertices

Given an instance and its symmetry set $S_G$, we construct the symmetry covering genesis set $\mathcal{G}(S_G)$ by applying Algorithm 2. If its cardinality is 0, we look for the pruning edges in G having the largest rank difference, leave them out for the generation of the $S_G$ and reapply Algorithm 2. Once splitting the instance in a certain number of sub-instances, we run the BP-one algorithm (we stop Algorithm 1 as soon as the first solution is found) for each of them. One potential solution to the original DMDGP instance is subsequently obtained by concatenating the local found solutions. Since all symmetry vertices are known, all other potential solutions to the original problem may be generated by partial reflections of the first one [14]. In case Algorithm 2 replaced a set of consecutive symmetries with only one symmetry, as well as in case some pruning edges were removed, multiple solutions can be obtained. Thus, all potential solutions for the original instance need to be verified.

Since the search space of a DMDGP instance has the structure of a binary tree, each solution corresponds to a path from the root to a leaf node. Such path can be encoded in a array of size n with 0 and 1 entries [18]. For each sub-instance, the computed local solutions are stored in this binary array format. The concatenation is performed by simply “attaching” the binary vectors representing local solutions in the order given by the symmetry covering. The final set of coordinates for a realization can be constructed by invoking BP on the path specified by the attached binary array. The mentioned partial reflections (used to construct other solutions from the first one) can be implemented by a suitable flipping of parts of this binary array, according to the symmetry vertices.

In our tables of experiments, we will refer to this overall procedure as sBP. Tables 1 and 2 contain some experiments for randomly generated instances having size n ranging between 1000 and 10,000. For every size and every number of symmetries, we report the computational time $t_{tot}$ (in seconds) for the standard BP (to find one solution) and sBP. For the sBP, we report three different computational times: the classical CPU time for performing an entire execution ($t_{tot}$), but also the time for exploring the largest sub-instance ($t_s$), as well as the time for concatenating the local solutions ($t_c$).

Table 1 Computational experiments on instances having size 1000 and 2000

Table 2 Computational experiments on instances having size 5000 and 10,000

The two tables of experiments show that the BP calls on all sub-instances are very fast (see time $t_s$). This is due to the fact that, whenever some pruning edges were ignored or not, the resulting subtree is symmetric and contains, in general, only two symmetric solutions. As remarked above, however, the number of solutions per sub-instance may increase when some symmetries of the original tree are removed from the genesis set $\mathcal{G}$ (see Algorithm 2): the number of solutions doubles for every removed symmetry.

The time necessary for concatenating the obtained local solutions is instead more expensive, especially when the original instance is split in a larger number of sub-instances (see time $t_c$). Even if we suppose that the number of solutions per sub-instance is always 2, then the concatenation process needs to consider all possible combinations of the local solutions, in the order implied by the genesis set $\mathcal{G}$. The easiest situation that can be verified is the one where no pruning edge was left out during the generation of the sub-instances. In this case, all possible combinations of the local solutions give rise to a realization of the original instance. However, the situation where (even only a few) pruning edges are left out is more realistic, and therefore these pruning edges need to be verified for every possible realization obtained with the concatenations. This justifies a larger computational time $t_c$ wrt the time $t_s$.

Finally, we can see, when comparing the total times for BP and sBP, that the new algorithm is able to outperform the standard BP for all instances. We remark, however, that this performance improvement becomes less and less pronounced with the increase of the number of symmetries.

5 Final remarks

We proposed a new strategy for efficiently splitting a graph G representing a DMDGP instance in a set of subgraphs that we define by exploiting the symmetry properties of G. By doing so, we are able to define a covering of G in subgraphs, whose edge sets are able to cover (almost) entirely the edge set E of G. This property allows us to divide a given DMDGP instance in a certain number of sub-instances that can be solved (almost) independently.

Future work directions include extending this strategy to instances satisfying weaker discretization assumptions, such as the ones introduced in [15]. In such weaker assumptions, the reference vertices (for a certain vertex v) are supposed to precede v in the vertex order, but they are not supposed to be the immediate preceding ones. Moreover, we will explore the possibility to run our approach on parallel and distributed computers [21], for solving instances containing interval distances [6].