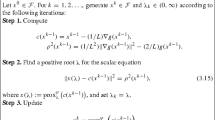Method for solving generalized convex nonsmooth mixed-integer nonlinear programming problems

Abstract

In this paper, we generalize the extended supporting hyperplane algorithm for a convex continuously differentiable mixed-integer nonlinear programming problem to solve a wider class of nonsmooth problems. The generalization is made by using the subgradients of the Clarke subdifferential instead of gradients. Consequently, all the functions in the problems are assumed to be locally Lipschitz continuous. The algorithm is shown to converge to a global minimum of an MINLP problem if the objective function is convex and the constraint functions are $f^{\circ }$-pseudoconvex. With some additional assumptions, the constraint functions may be $f^{\circ }$-quasiconvex.

1 Introduction

The extended supporting hyperplane (ESH) algorithm to solve smooth (continuously differentiable) convex MINLP problems was presented in [9]. It is based on the classical supporting hyperplane method derived in [13]. Numerical comparisons in [9] suggest that the ESH algorithm is efficient and on par with current state-of-art MINLP solvers when solving MINLP problems with smooth convex objective and constraint functions.

Motivated by promising numerical results in [9], we will generalize the ESH algorithm to cover certain classes of nonsmooth convex MINLP problems. By a convex MINLP problem we mean that the objective function is convex and the feasible set is convex when discrete variables are relaxed to continuous ones. We require that the constraint functions are $f^{\circ }$-pseudoconvex. With an additional assumption that the subdifferentials of active constraint functions do not contain zero at points where supporting hyperplanes are computed, the constraint functions may be $f^{\circ }$-quasiconvex. These function classes are modifications of the classical pseudo- and quasi-convexity for a locally Lipschitz continuous function. With these constraint functions the feasible set is convex if the integers are relaxed to continuous variables. The generalization of the ESH algorithm follows similar steps to the generalization of the $\alpha$ECP algorithm in [8]. That is, instead of gradients we will use the subgradients of the Clarke subdifferential.

The generalization implies that the ESH algorithm presented in [9] is suitable for smooth pseudoconvex constraint functions as well. In fact, this was essentially noted in [13], but the term pseudoconvexity was not used.

The ESH and $\alpha$ECP methods share many similarities. In fact, the supporting hyperplanes were seen as an alternative to the cutting planes for the $\alpha$ECP algorithm in [11]. This will essentially lead to the ESH algorithm. Both methods solve a sequence of MILP problems and add linear constraints to the MILP problem. The linear constraints that the ESH method generates are supporting hyperplanes to the feasible set defined by the nonlinear constraints. Thus, a supporting hyperplane usually cuts off more of the infeasible region than a cutting plane. The downsides of ESH are that we have to know an inner point of the integer relaxed feasible set and we have to use a line search procedure.

The ESH algorithm is presented briefly in Sect. 3. In that section, we also prove that it can solve problems with $f^{\circ }$-pseudoconvex constraint functions. Some numerical examples are solved in Sect. 4. Concluding remarks are given in Sect. 5.

2 Preliminaries

In this section, we present some results on nonsmooth analysis and give the definitions of the generalized convexities that we use. First, we define the generalization of the gradient.

Definition 1

[5] Let $f{:}\,\mathbb {R}^n\rightarrow \mathbb {R}$ be locally Lipschitz continuous at ${\varvec{x}}\in \mathbb {R}^n$. The Clarke generalized directional derivative of f at ${\varvec{x}}$ in the direction ${\varvec{d}}\in \mathbb {R}^n$ is defined by

$$\begin{aligned} f^\circ ({\varvec{x}};{\varvec{d}}):=\limsup _{\genfrac{}{}{0.0pt}{}{{\varvec{y}}\rightarrow {\varvec{x}}}{t\downarrow 0}} \frac{f({\varvec{y}}+t{\varvec{d}})-f({\varvec{y}})}{t} \end{aligned}$$

and the Clarke subdifferential of f at ${\varvec{x}}$ by

$$\begin{aligned} \partial f({\varvec{x}}):=\lbrace {\varvec{\xi }}\in \mathbb {R}^n\mid f^\circ ({\varvec{x}};{\varvec{d}})\ge {\varvec{\xi }}^T{\varvec{d}}\ \text {for all}\ {\varvec{d}}\in \mathbb {R}^n\rbrace . \end{aligned}$$

Each element ${\varvec{\xi }}\in \partial f({\varvec{x}})$ is called a subgradient of f at ${\varvec{x}}$.

Some basic properties of the subdifferential are given in the next theorem. The proofs can be found in [5].

Theorem 1

Let $f{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ be locally Lipschitz continuous. Then

• (i) $\partial f({\varvec{x}})$ is a nonempty, convex and compact set.

• (ii) $f^\circ ({\varvec{x}};{\varvec{d}})=\max \,\lbrace {\varvec{\xi }}^T {\varvec{d}}\mid {\varvec{\xi }}\in \partial f({\varvec{x}})\rbrace$ for all ${\varvec{d}}\in \mathbb {R}^n$.

The following definitions present the main function classes we are dealing with.

Definition 2

A function $f{:}\,\mathbb {R}^n\rightarrow \mathbb {R}$ is pseudoconvex, if it is smooth and for all ${\varvec{x}},{\varvec{y}}\in \mathbb {R}^n$

$$\begin{aligned} f({\varvec{y}})< f({\varvec{x}})\quad \text {implies}\quad \nabla f({\varvec{x}})^{T}({\varvec{y}}-{\varvec{x}})< 0. \end{aligned}$$

Definition 3

A function $f{:}\,\mathbb {R}^n\rightarrow \mathbb {R}$ is $f^{\circ }$-pseudoconvex ($f^\circ$-quasiconvex), if it is locally Lipschitz continuous and for all ${\varvec{x}},{\varvec{y}}\in \mathbb {R}^n$

$$\begin{aligned} f({\varvec{y}})<(\le ) f({\varvec{x}})\quad \text {implies}\quad f^\circ ({\varvec{x}};{\varvec{y}}-{\varvec{x}})<(\le ) 0. \end{aligned}$$

Some basic properties of these function classes can be found in e.g. [2]. The following results can be found on the pp. 140–166.

Theorem 2

Let $f{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ be locally Lipschitz continuous.

• (i) If f is convex or pseudoconvex, then it is $f^{\circ }$-pseudoconvex.

• (ii) If f is $f^{\circ }$-pseudoconvex, then it is $f^{\circ }$-quasiconvex.

• (iii) If f is $f^{\circ }$-pseudoconvex, then ${\pmb 0}\in \partial f({\varvec{x}})$ implies that ${\varvec{x}}$ is a global minimizer of f.

• (iv) If f is $f^{\circ }$-quasiconvex, then it is quasiconvex.

• (v) If $f_i,\,i=1,2,\ldots ,m$ are $f^{\circ }$-pseudoconvex ($f^{\circ }$-quasiconvex), then $\max _{i}f_i$ is $f^{\circ }$-pseudoconvex ($f^{\circ }$-quasiconvex).

As can be seen from Theorem 2 (i) $f^{\circ }$-pseudoconvexity is a generalization of the classical pseudoconvexity. By definition, the level sets of a quasiconvex function are convex. Thus, Theorem 2 (ii) and (iv) implies that the level sets of $f^{\circ }$-pseudoconvex or $f^{\circ }$-quasiconvex functions are also convex. The following result is a straightforward consequence of Theorem 2 (ii) and (iii).

Corollary 1

Let $f{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ be an $f^{\circ }$-pseudoconvex function and ${\varvec{x}}\in \mathbb {R}^n$. If there exists ${\varvec{y}}\in \mathbb {R}^n$ such that $f({\varvec{y}})<f({\varvec{x}})$, then f is $f^{\circ }$-quasiconvex and ${\pmb 0}\notin \partial f({\varvec{x}})$.

With a certain assumption, $f^{\circ }$-quasiconvexity implies $f^{\circ }$-pseudoconvexity. For the proof, we need the following lemma, which is also useful in the next section.

Lemma 1

Let $f{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ be an $f^{\circ }$-quasiconvex function, ${\varvec{y}}\in \mathbb {R}^n,\,a > f({\varvec{y}})$ and $A \subset \mathbb {R}^n$. If $a \le f({\varvec{x}})$ and ${\pmb 0}\notin \partial f({\varvec{x}})$ for all ${\varvec{x}}\in A$, then there exists $r > 0$ such that ${\varvec{\xi }}^T({\varvec{y}}-{\varvec{x}}) \le -r \left\| {\varvec{\xi }}\right\| <0$ for all ${\varvec{x}}\in A$ and ${\varvec{\xi }}\in \partial f({\varvec{x}})$.

Proof

Since f is continuous and $f({\varvec{y}})<a$, there exists $r >0$ such that $f({\varvec{z}})<a$ for all ${\varvec{z}}\in \mathbb {R}^n$ such that $\left\| {\varvec{z}}-{\varvec{y}}\right\| \le r$. Let ${\varvec{x}}\in A$ and ${\varvec{\xi }}\in \partial f({\varvec{x}})$ be arbitrary. Since ${\pmb 0}\notin \partial f({\varvec{x}})$ we may define $\hat{{\varvec{y}}} = {\varvec{y}}+\frac{{\varvec{\xi }}}{\left\| {\varvec{\xi }}\right\| } r$. The $f^{\circ }$-quasiconvexity of f and the inequalities $f(\hat{{\varvec{y}}}) < a \le f({\varvec{x}})$ imply

$$\begin{aligned} f^{\circ }({\varvec{x}}; \hat{{\varvec{y}}}-{\varvec{x}}) \le 0. \end{aligned}$$

(1)

By Theorem 1 (ii), inequality (1) implies ${\varvec{\xi }}^{T}(\hat{{\varvec{y}}}-{\varvec{x}}) \le 0$. Thus,

$$\begin{aligned} {\varvec{\xi }}^{T}({\varvec{y}}-{\varvec{x}}) = {\varvec{\xi }}^{T}(\hat{{\varvec{y}}}-\frac{{\varvec{\xi }}}{\left\| {\varvec{\xi }}\right\| } r-{\varvec{x}}) = -r \left\| {\varvec{\xi }}\right\| +{\varvec{\xi }}^{T}(\hat{{\varvec{y}}}-{\varvec{x}})\le -r \left\| {\varvec{\xi }}\right\| . \end{aligned}$$

Since ${\pmb 0}\notin \partial f({\varvec{x}})$ we have $-r \left\| {\varvec{\xi }}\right\| < 0$ proving the lemma. $\square$

Theorem 3

Let $f{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ be an $f^{\circ }$-quasiconvex function. If ${\pmb 0}\in \partial f({\varvec{x}})$ implies that ${\varvec{x}}$ is a global minimum of f, then f is $f^{\circ }$-pseudoconvex.

Proof

Let ${\varvec{x}},{\varvec{y}}\in \mathbb {R}^n$ be points such that $f({\varvec{y}})<f({\varvec{x}})$. By assumption ${\pmb 0}\notin \partial f({\varvec{x}})$. Choosing $a=f({\varvec{x}})$ and $A=\left\{ {\varvec{x}}\right\}$, Lemma 1 implies

$$\begin{aligned} f^{\circ }({\varvec{x}},{\varvec{y}}-{\varvec{x}})=\max _{{\varvec{\xi }}\in \partial f({\varvec{x}})} {\varvec{\xi }}^{T}({\varvec{y}}-{\varvec{x}}) <0. \end{aligned}$$

Thus, f is $f^{\circ }$-pseudoconvex. $\square$

We denote the closed line segment $\left[ {\varvec{x}}, {\varvec{y}}\right] =\left\{ \lambda {\varvec{x}}+(1-\lambda ){\varvec{y}}\mid 0 \le \lambda \le 1 \right\}$ and $\left( {\varvec{x}}, {\varvec{y}}\right)$ by the corresponding open line segment.

3 The ESH algorithm

In this section, we consider the ESH algorithm and its convergence properties. The global convergence is proved for a problem with a linear objective function and $f^{\circ }$-pseudoconvex constraint functions. With an additional assumption, the constraint functions may be $f^{\circ }$-quasiconvex. Note that any nonlinear convex objective function can be transformed to a linear objective function and a convex constraint. We begin by reformulating the ESH algorithm from [9] to deal with nonsmooth functions. After that, we prove the convergence results for an MINLP problem with $f^{\circ }$-pseudoconvex constraint functions.

3.1 Convex constraint functions

The considered problem is

$$\begin{aligned} \min&\quad {\varvec{c}}^{T}{\varvec{x}}\nonumber \\ \mathrm{s.t.}&\quad g_m({\varvec{x}}) \le 0 \quad \forall \, m = 1,\ldots M, \quad (\text {P}) \nonumber \\&\quad {\varvec{x}}\in L \cap Y, \nonumber \end{aligned}$$

where each nonlinear function $g_m{:}\,\mathbb {R}^n \rightarrow \mathbb {R}$ is convex but not necessarily smooth and the compact set $L \subset \mathbb {R}^n$ defines linear constraints. Integer variables are defined by index set $I_{\mathbb {Z}} \subseteq \left\{ 1,2,\ldots ,n\right\}$ and set $Y=\left\{ {\varvec{x}}\mid {\varvec{x}}\in \mathbb {R}^n, {\varvec{x}}_i \in \mathbb {Z}\text { if } i \in I_{\mathbb {Z}} \right\}$. Denote $C_m = \left\{ {\varvec{x}}\mid g_m({\varvec{x}}) \le 0 \right\}$ and $C=\bigcap _{m=1}^{M}C_m$. Thus, the feasible set is $C \cap L \cap Y$. Denoting $F({\varvec{x}}) = \max _{m} \left\{ g_m({\varvec{x}}) \right\}$ we can also write $C=\left\{ {\varvec{x}}\mid F({\varvec{x}}) \le 0 \right\}$. We denote indexes of active constraint functions on the set $\left\{ {\varvec{x}}\mid F({\varvec{x}})=0 \right\}$ by $I_0({\varvec{x}})=\left\{ m \mid g_m({\varvec{x}})=F({\varvec{x}})=0 \right\}$. For the moment, we assume that the Slater constraint qualification holds true. In other words,

$$\begin{aligned} \text {there exists a point } {\varvec{x}}\in L \text { such that } F({\varvec{x}}) <0. \end{aligned}$$

(2)

The algorithm will need a point ${\varvec{x}}_{\text {NLP}}$ such that $F({\varvec{x}}_{\text {NLP}})<0$. This can be obtained by solving the problem

$$\begin{aligned} \min&\quad F({\varvec{x}}) \quad (\text {NLP}) \\ \mathrm{s.t.}&\quad {\varvec{x}}\in L. \end{aligned}$$

Note that the problem (NLP) does not need to be solved to a global minimum. It suffices to find a point ${\varvec{x}}$ such that $F({\varvec{x}})<0$. The idea of the ESH algorithm is to solve a sequence of mixed-integer linear programming problems

$$\begin{aligned} \min&\quad {\varvec{c}}^T {\varvec{x}}\\ \mathrm{s.t.}&\quad l_{j}({\varvec{x}}^{j}) \le 0 \quad j=1,2,\ldots ,k-1 \quad (\text {MILP}_k)\\&\quad {\varvec{x}}\in L \cap Y, \end{aligned}$$

where $l_j({\varvec{x}}^j) \le 0$ is a supporting hyperplane generated at a point ${\varvec{x}}^j$ such that $F({\varvec{x}}^j)=0$. At the first iteration, no such planes exist. Solving $(\text {MILP}_1)$ then gives us a solution point ${\varvec{x}}_{\text {MILP}}^{1}$. If $F({\varvec{x}}_{\text {MILP}}^{1}) \le 0$, we have thus found a feasible point to the original problem (P). It will be a global minimum since it was found through minimization on a set containing the original feasible set.

Suppose then that $F({\varvec{x}}_{\text {MILP}}^{1})>0$. The point ${\varvec{x}}^1$ where the first supporting hyperplane is generated will be found through a line search between points ${\varvec{x}}_{\text {NLP}}$ and ${\varvec{x}}_{\text {MILP}}^{1}$. Since $F({\varvec{x}}_{\text {NLP}})<0<F({\varvec{x}}_{\text {MILP}}^{1})$ and the constraint functions are continuous, a point ${\varvec{x}}^1 \in \left[ {\varvec{x}}_{\text {NLP}}, {\varvec{x}}_{\text {MILP}}^{1} \right]$ such that $F({\varvec{x}}^1)=0$ is guaranteed to exist. Since the constraint functions are convex so is F implying ${\varvec{x}}^1$ will be unique. A new problem $(\text {MILP}_2)$ will be formed by adding to $(\text {MILP}_1)$ the supporting hyperplane $l_1({\varvec{x}}^1)$. More accurately, $l_1({\varvec{x}}^1):={\varvec{\xi }}^T({\varvec{x}}-{\varvec{x}}^1) \le 0$, where ${\varvec{\xi }}\in \partial g_m({\varvec{x}}^1)$ for some $m \in I_0({\varvec{x}}^1)$. The ESH algorithm will continue solving problems $(\text {MILP}_k)$ accordingly until a stopping criterion is satisfied. The algorithm is as follows:

Note that if $\varepsilon _g>0$ then we will make the supporting hyperplanes on points ${\varvec{x}}^k$ such that $F({\varvec{x}}^k)=\frac{\varepsilon _g}{2} \ne 0$. This ploy allows us to deal with problems that do not satisfy the Slater constraint qualification. In the interim, we will consider the theoretical case $\varepsilon _g=0$.

In [9] it was shown that the ESH algorithm will converge to a global minimum if the constraint functions are smooth and convex (and $\varepsilon _g=0$). In the algorithm presented in [9] an LP step was used in order to speed up the algorithm. In this step the $(\text {MILP}_k)$ problem is solved with integer variables relaxed to continuous ones. This allows faster generation of supporting hyperplanes as an LP problem is easier to solve than an MILP problem. The LP step will stop after a certain amount of iteration. After the LP step the algorithm starts solving MILP problems as stated but now there are supporting hyperplanes already in $(\text {MILP}_1)$ giving an initial approximation of the feasible set. The LP step does not affect global convergence although it can result in faster convergence.

3.2 $f^{\circ }$-Pseudoconvex constraint functions

At this point, we are ready to prove that the ESH algorithm can be used successfully for a wider class of problems than those with a smooth and convex objective and constraint functions. We shall first consider the case $\varepsilon _g=0$ in which case we have to require that the Slater constraint qualification holds true. We shall assume that

• (i) $g_m$ is $f^{\circ }$-quasiconvex for all $m=1,2,\ldots ,M$

• (ii) ${\pmb 0}\notin \partial g_m({\varvec{x}})$ if $m \in I_0({\varvec{x}})$.

These conditions are fulfilled for $f^{\circ }$-pseudoconvex constraint functions by Corollary 1 and the Slater constraint qualification (2). Since the level sets of $f^{\circ }$-quasi- and $f^{\circ }$-pseudoconvex functions are convex, we are dealing with a convex MINLP problem. That is, the objective function is convex and the feasible set is a convex set, if the integer variables are relaxed to continuous ones.

The convergence proof proceeds as follows. We will first show that supporting hyperplanes do not cut off any feasible points. However, they will cut off the previous solution points of $(\text {MILP}_k)$ that were not within the set C. In the compact set L, this results in a solution sequence that has an accumulation point. This point will be shown to be feasible in C. Finally, this point proves to be a global minimum of (P).

We begin by proving that supporting hyperplanes, generated for an $f^{\circ }$-pseudoconvex function, will not cut off any feasible point. For differentiable functions a corresponding proof has been given, for example, in [3].

Theorem 4

The supporting hyperplane

$$\begin{aligned} {\varvec{\xi }}^{T}({\varvec{x}}-{\varvec{x}}^k) \le 0, \quad {\varvec{\xi }}\in \partial g_m({\varvec{x}}^k), \quad m \in I_0({\varvec{x}}^k) \end{aligned}$$

(3)

does not cut off feasible points.

Proof

It is sufficient to prove that the hyperplane (3) does not cut off any points in $C_m \supset C$. Let ${\varvec{y}}\in C_m$ be arbitrary. Then $g_m({\varvec{y}}) \le 0 = g_m({\varvec{x}}^k)$ and $f^{\circ }$-quasiconvexity implies $g_{m}^{\circ }({\varvec{x}}^k;{\varvec{y}}-{\varvec{x}}^k) \le 0$. By Theorem 1 (ii),

$$\begin{aligned} {\varvec{\xi }}^{T}({\varvec{y}}-{\varvec{x}}^k) \le \max _{\varvec{\zeta }\in \partial g_m({\varvec{x}}^k)}\varvec{\zeta }^T({\varvec{y}}-{\varvec{x}}^k) = g_{m}^{\circ }({\varvec{x}}^k;{\varvec{y}}-{\varvec{x}}^k) \le 0. \end{aligned}$$

Thus, hyperplane (3) does not cut off ${\varvec{y}}$ proving the theorem. $\square$

The next theorem shows that, if the current solution ${\varvec{x}}_{\text {MILP}}^{k}$ is infeasible, then it will be cut off by the supporting hyperplane generated at point ${\varvec{x}}^k$.

Theorem 5

Let $m \in I_0({\varvec{x}}^k)$ and ${\varvec{\xi }}\in \partial g_m({\varvec{x}}^k)$. If $F({\varvec{x}}_{\text {MILP}}^{k})>0$, then

${\varvec{\xi }}^T({\varvec{x}}_{\text {MILP}}^{k}-{\varvec{x}}^k) >0$.

Proof

We may write ${\varvec{x}}^k=\lambda {\varvec{x}}_{\text {NLP}}+ (1-\lambda ){\varvec{x}}_{\text {MILP}}^{k}$, where $\lambda \in [0,1]$. In point of fact, we have $\lambda \in (0,1)$ since $F({\varvec{x}}_{\text {MILP}}^{k})>0$ and $F({\varvec{x}}_{\text {NLP}})<0=F({\varvec{x}}^k)$. It is then straightforward to show that

$$\begin{aligned} -\frac{\lambda }{1-\lambda }({\varvec{x}}_{\text {NLP}}-{\varvec{x}}^k)={\varvec{x}}_{\text {MILP}}^{k}-{\varvec{x}}^k. \end{aligned}$$

Since $g_m({\varvec{x}}_{\text {NLP}})<g_m({\varvec{x}}^k)$ and ${\pmb 0}\notin \partial g_m({\varvec{x}}^{k})$ (assumption ii) Lemma 1 implies (by choosing $A=\left\{ {\varvec{x}}^{k} \right\}$ and $a=g_m({\varvec{x}}^k)$) that there exists $r>0$ such that

$$\begin{aligned} {\varvec{\xi }}^T({\varvec{x}}_{\text {MILP}}^{k}-{\varvec{x}}^k)=-\frac{\lambda }{1-\lambda }{\varvec{\xi }}^{T}({\varvec{x}}_{\text {NLP}}-{\varvec{x}}^k) \ge -\frac{\lambda }{1-\lambda }(-r \left\| {\varvec{\xi }}\right\| )>0 \end{aligned}$$

proving the theorem. $\square$

With Theorems 4 and 5 we can prove the uniqueness of ${\varvec{x}}^k$.

Corollary 2

If $F({\varvec{x}}_{\text {MILP}}^{k})>0$, then ${\varvec{x}}^k$ is unique.

Proof

Suppose there exist ${\varvec{y}},{\varvec{z}}\in \left( {\varvec{x}}_{\text {NLP}}, {\varvec{x}}_{\text {MILP}}^k \right)$ such that $F({\varvec{y}})=F({\varvec{z}})=0$ and ${\varvec{y}}\ne {\varvec{z}}$. Without loss of generality we may assume that ${\varvec{z}}\in \left( {\varvec{y}},{\varvec{x}}_{\text {MILP}}^{k} \right)$. By Theorem 4, ${\varvec{z}}$ is not cut off by the hyperplane generated at ${\varvec{y}}$. However, the hyperplane will then not cut off either ${\varvec{x}}_{\text {MILP}}^{k}$ contradicting Theorem 5. $\square$

Suppose that at some iteration k we have $F({\varvec{x}}_{\text {MILP}}^{k}) \le 0$. By Theorem 4, the feasible set of $(\text {MILP}_k)$ includes C. Thus, ${\varvec{x}}_{\text {MILP}}^{k}$ is a global minimum of (P). On the other hand, if $F({\varvec{x}}_{\text {MILP}}^{k})>0$ for all k, Theorem 5 implies that the points in sequence $({\varvec{x}}_{\text {MILP}}^{k})$ are distinct. Since $({\varvec{x}}_{\text {MILP}}^{k}) \subset L$ and L is a compact set, the sequence has an accumulation point by the Bolzano–Weierstrass Theorem. Hence, there exists a converging subsequence $({\varvec{x}}_{\text {MILP}}^{k_j}) \subset ({\varvec{x}}_{\text {MILP}}^{k})$.

Next, we will show that the subsequence $({\varvec{x}}_{\text {MILP}}^{k_j})$ converges to a feasible point. To prove this, we need the following lemma.

Lemma 2

Let $({\varvec{x}}_{\text {MILP}}^{k_j})$ be a converging sequence and ${\varvec{\xi }}_j \in \partial g_{m_j} ({\varvec{x}}^{k_j})$, where index $m_j \in I_0({\varvec{x}}^{k_j})$. Then

$$\begin{aligned} \lim _{j \rightarrow \infty } \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})=0. \end{aligned}$$

Proof

Let $\varepsilon >0$ be arbitrary. Choose j such that $\left\| {\varvec{x}}_{\text {MILP}}^{k_{j+1}}-{\varvec{x}}_{\text {MILP}}^{k_j}\right\| < \varepsilon$. Then

$$\begin{aligned}&\left| \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_{j+1}}-{\varvec{x}}^{k_j})- \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| } ({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j}) \right| \nonumber \\&\quad \le \frac{\left\| {\varvec{\xi }}_{j} \right\| }{\left\| {\varvec{\xi }}_{j} \right\| } \left\| {\varvec{x}}_{\text {MILP}}^{k_{j+1}}-{\varvec{x}}_{\text {MILP}}^{k_j} \right\| < \varepsilon . \end{aligned}$$

(4)

Since $F({\varvec{x}}_{\text {MILP}}^{k_j})>0$ Theorem 5 implies $0 < \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }( {\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})$. Then, by the feasibility of ${\varvec{x}}_{\text {MILP}}^{k_{j+1}}$ in problem $(\text {MILP}_{k_{j+1}})$

$$\begin{aligned} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_{j+1}}-{\varvec{x}}^{k_j}) \le 0 < \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }( {\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j}) \end{aligned}$$

for all j. Hence, by inequality (4) we have $\lim _{j \rightarrow \infty } \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})=0$. $\square$

Lemma 2 does not imply, thus far, that subsequence $({\varvec{x}}_{\text {MILP}}^{k_j})$ would converge to a feasible point. It still leaves a possibility that vectors ${\varvec{\xi }}_j$ and ${\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j}$ converge to vectors that are perpendicular to each other. With the help of $f^{\circ }$-quasiconvexity this case will be excluded in the next theorem.

Theorem 6

An accumulation point of the sequence $({\varvec{x}}_{\text {MILP}}^{k})$ is a feasible point.

Proof

By Lemma 2 we may re-index the convergent subsequence in a way that $\frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})-\frac{1}{j} \le 0$ for all $j \in \mathbb {N}$, where ${\varvec{\xi }}_j \in \partial g_{m_j}({\varvec{x}}^{k_j})$ and $m_j \in I_0({\varvec{x}}^{k_j})$. Furthermore,

$$\begin{aligned} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})-\frac{1}{j}\le & {} 0 \\= & {} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}^{k_j}-{\varvec{x}}^{k_j}) \\= & {} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }(\lambda _{k_j} {\varvec{x}}_{\text {NLP}}+(1-\lambda _{k_j}){\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j}). \end{aligned}$$

By rearranging the terms we have

$$\begin{aligned} \lambda _{k_j} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})-\frac{1}{j} \le \lambda _{k_j} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {NLP}}-{\varvec{x}}^{k_j}). \end{aligned}$$

By choosing $a=0$ and $A_m= \left\{ {\varvec{x}}\in L \mid F({\varvec{x}})=0, g_{m}({\varvec{x}})=0 \right\}$ we have ${\varvec{x}}^{k_j} \in A_{m_j}$ and $g_{{m_{j}}}({\varvec{x}}_{\text {NLP}})<a$. Then Lemma 1 implies

$$\begin{aligned} \lambda _{k_j} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {NLP}}-{\varvec{x}}^{k_j}) \le -\lambda _{k_j} \frac{\left\| {\varvec{\xi }}_{j} \right\| }{\left\| {\varvec{\xi }}_{j} \right\| } r_{m_j} = -\lambda _{k_j} r_{m_j}, \end{aligned}$$

for some $r_{m_j} > 0$. Since there are finitely many constraints, $r=\min _{m=1,2,\ldots ,M} \left\{ r_m \right\} >0$ exists and

$$\begin{aligned} -\lambda _{k_j} r_{m_j} \le -\lambda _{k_j} r \, \text { for all } j \in \mathbb {N}. \end{aligned}$$

Thus,

$$\begin{aligned} \lambda _{k_j} \frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j})-\frac{1}{j} \le -\lambda _{k_j} r. \end{aligned}$$

By solving $\lambda _{k_j}$ from this inequality we obtain

$$\begin{aligned} \lambda _{k_j} \le \frac{1}{j \left( r+\frac{{\varvec{\xi }}_{j}^{T}}{\left\| {\varvec{\xi }}_{j} \right\| }({\varvec{x}}_{\text {MILP}}^{k_j}-{\varvec{x}}^{k_j}) \right) } < \frac{1}{j \cdot r}. \end{aligned}$$

Hence, $\lim _{j \rightarrow \infty }\lambda _{k_j} = 0$ implying $F(\hat{{\varvec{x}}})=0$ where $\hat{{\varvec{x}}}= \lim _{j \rightarrow \infty } {\varvec{x}}_{\text {MILP}}^{k_j}$. $\square$

Finally, the convergence result is given.

Theorem 7

An accumulation point of the sequence $({\varvec{x}}_{\text {MILP}}^{k})$ is a global minimum of the problem (P).

Proof

The proof is similar to Lemma 4 in [9]. $\square$

Consider the case where $\varepsilon _g>0$. Then, supporting hyperplanes will be generated at points ${\varvec{x}}^k$ such that $F({\varvec{x}}^k)=\frac{\varepsilon _g}{2}$. This implies that we do not need the Slater constraint qualification to hold true. That is, it suffices that $F({\varvec{x}}_{\text {NLP}}) \le 0$ as was noticed in [9]. In the case of $f^{\circ }$-quasiconvex constraint functions, we have to require that ${\pmb 0}\notin \partial g_m({\varvec{x}})$ if the supporting hyperplane is generated from $g_m$ at ${\varvec{x}}$. Again, an $f^{\circ }$-pseudoconvex constraint function meets this requirement unattended.

Theorem 4 is valid in the case $\varepsilon _g>0$ as well. In the other results, we have to replace 0 by $\frac{\varepsilon _g}{2}$ or $\varepsilon _g$ when appropriate. Then it follows that if we do not find a point ${\varvec{x}}$ such that $F({\varvec{x}}) < \frac{\varepsilon _g}{2}$, the MILP solutions sequence has an accumulation point $\hat{{\varvec{x}}}$ with $F(\hat{{\varvec{x}}})=\frac{\varepsilon _g}{2}$. Thus, we will find a point ${\varvec{x}}$ satisfying $F({\varvec{x}}) \le \varepsilon _g$ after a finite number of iterations. If the objective function is linear, the final solution point ${\varvec{x}}_{\text {MILP}}^k$ will be an $\varepsilon _g$-feasible global minimum. That is, $F({\varvec{x}}_{\text {MILP}}^k)\le \varepsilon _g$ and there exists no feasible point giving a lower objective function value. If a convex objective function is transformed to a linear objective function, there might be a feasible solution giving a lower objective function value than the one found. Nevertheless, this difference is at most $\varepsilon _g$.

3.3 On solving the NLP problem

To be able to solve a problem the ESH algorithm requires a point ${\varvec{x}}_{\text {NLP}}$ satisfying strictly all the nonlinear constraints. As previously mentioned, this can be found by solving $(\text {NLP})$. The compactness of L and the continuity of F guarantees that a solution exists. If functions $g_m$ are $f^{\circ }$-pseudoconvex then so is F by Theorem 2 (v). In this case the nonsmooth problem (NLP) can be solved by e.g. the proximal bundle (PB) algorithm [12]. If the constraint functions are $f^{\circ }$-quasiconvex then F will be $f^{\circ }$-quasiconvex by Theorem 2 (v). The PB algorithm will find a stationary point, which is not guaranteed to solve the problem nor to be a feasible point.

Note that if $\varepsilon _g>0$ the point ${\varvec{x}}_{\text {NLP}}$ need only to satisfy $F({\varvec{x}}_{\text {NLP}}) \le 0$. Then, by relaxing the integer variables of the original problem we can obtain a continuous problem, whose global minimum point can be set to ${\varvec{x}}_{\text {NLP}}$. In the case of $f^{\circ }$-pseudoconvex constraint functions this problem can be solved by, for example, the $\alpha$ECP method. Again, if the constraint functions are $f^{\circ }$-quasiconvex, a stationary point is not guaranteed to be a feasible point. Consider a simple problem

$$\begin{aligned} \begin{array}{lll} &{} \min &{}\quad (x-1)^2 \\ &{} \mathrm{s.t.}&{}\quad (x-1)^3+1 \le 0 \\ &{} &{}\quad -2 \le x \le 2. \end{array} \end{aligned}$$

Here, $x=1$ is a stationary point in the both proposed feasibility problems. However, it is not a feasible point. On our best knowledge there does not exist an algorithm that is guaranteed to find a feasible point if the constraint functions are $f^{\circ }$-quasiconvex. Nevertheless, if each of the $f^{\circ }$-quasiconvex constraints satisfies the condition

$$\begin{aligned} 0 \notin \partial g_m({\varvec{x}}) \quad \text {or} \quad g_m({\varvec{x}}) < 0 \end{aligned}$$

(5)

for all ${\varvec{x}}\in \mathbb {R}^n$, then a stationary point is a feasible point. In addition, the function $\hat{F}({\varvec{x}}):=\max \left\{ 0,F({\varvec{x}})\right\}$ will be $f^{\circ }$-pseudoconvex and the integer relaxed problem can be solved by $\alpha$ECP. Condition (5) is the well-known Cottle constraint qualification.

Recall that a convex objective function f may be transformed to a constraint function $f-\mu$, where the auxiliary variable $\mu$ is the new linear objective function. If the objective function is convex and nonlinear, it sounds reasonable to use the relaxed problem to find ${\varvec{x}}_{\text {NLP}}$. In this case, we can set $\mu _{\text {NLP}}=f({\varvec{x}}_{\text {NLP}})$. If (NLP) is used with constraint function $f-\mu$, the only other constraints that include $\mu$ are user given box constraints. Hence, $\mu _{\text {NLP}}$ would most probably be the given upper bound being somewhat arbitrary. The value of $\mu _{\text {NLP}}$ affects the values of $f-\mu$ in the line search and, thus, also the frequency of computing supporting hyperplanes from $f-\mu$.

4 Numerical considerations and examples

In this section, we solve a few example problems with the ESH and the $\alpha$ECP [8, 14] algorithms. In addition, we will discuss some numerical details, especially, the line search. At first we will motivate why the line search is made to find a point ${\varvec{x}}^k$ that has been shifted $\frac{\varepsilon _g}{2}$ from the set $\left\{ {\varvec{x}}\mid F({\varvec{x}})=0 \right\}$ in the function space. Another possibility is a shift in the variable space.

4.1 On the line search

In the implementation and numerical comparison, we will have $\varepsilon _g >0$. In the Algorithm 3.1, we apply a line search to find a point ${\varvec{x}}^k$ such that $F({\varvec{x}}^{k})=\frac{\varepsilon _g}{2}$. This implies that we do not need the Slater constraint qualification to hold true, but the result will be an $\varepsilon _g$-feasible minimum. When comparing the point ${\varvec{x}}^k$ with the one obtained by the algorithm with $\varepsilon _g=0$ we will make a shift $\frac{\varepsilon _g}{2}$ in the function value space towards ${\varvec{x}}_{\text {MILP}}^{k}$, that is, away from ${\varvec{x}}_{\text {NLP}}$.

Next, we will give an example problem which shows that if $\varepsilon _g=0$ or even if we do similar $\frac{\varepsilon _g}{2}$ shift in the variable space we would need the Slater constraint qualification to hold. More accurately, we will create supporting hyperplanes on points ${\varvec{x}}^k+\varvec{\delta }^k$, where $F({\varvec{x}}^k)=0$ and

$$\begin{aligned} \varvec{\delta }^k= \frac{\varepsilon _g}{2} \frac{{\varvec{x}}_{\text {MILP}}^k-{\varvec{x}}^k}{\left\| {\varvec{x}}_{\text {MILP}}^k-{\varvec{x}}^k \right\| }. \end{aligned}$$

(6)

Consider problem (see Fig. 1)

$$\begin{aligned} \begin{array}{lll} &{} \min &{}\quad -x_1-x_2 \nonumber \\ &{} \mathrm{s.t.}&{}\quad g({\varvec{x}}) \le 0 \quad (\text {P1}) \nonumber \\ &{} &{}\quad -2 \le x_1 \le 2, \, -2 \le x_2 \le 2, \nonumber \end{array} \end{aligned}$$

where $g({\varvec{x}}) = \max \left\{ 0,g_1({\varvec{x}}) \right\}$ and

$$\begin{aligned} g_1({\varvec{x}})= {\left\{ \begin{array}{ll} (x_2-1)^2+x_{1}^2-1, &{}\quad x_2>1 \\ x_{1}^2-1, &{}\quad -1 \le x_2 \le 1 \\ (x_2+1)^2+x_{1}^2-1, &{}\quad x_2 <-1 \\ \end{array}\right. }. \end{aligned}$$

The constraint function g is convex and does not satisfy the Slater constraint qualification.

Fig. 1

The feasible set and a part of the solving process of the given example when $\delta =\frac{1}{2}$. The dashed lines represent the first two hyperplanes

Suppose that we have ${\varvec{x}}_{\text {NLP}}=(1,0)$. Note that (1, 0) is on the boundary. When trying to solve this problem with the ESH algorithm with shifts (6) and $0<\frac{\varepsilon _g}{2}<1$, the first solution will be ${\varvec{x}}_{\text {MILP}}^{1}=(2,2)$. The line search will find ${\varvec{x}}^k={\varvec{x}}_{\text {NLP}}=(1,0)$ and a supporting hyperplane ${\varvec{x}}\le a,\,(a>1)$ will be added to the next MILP problem. More accurately $a=1+\frac{\varepsilon _g}{2\sqrt{5}}$ according to (6), but $a>1$ is the property we are interested in. The next solution will be ${\varvec{x}}_{\text {MILP}}^{2}=(a,2)$. The solution process generates sequence $({\varvec{x}}_{\text {MILP}}^{k})$ that converges to the point (1, 2). However, this point is not even feasible. The ESH algorithm without the shift (6) and $\varepsilon _g=0$ will find ${\varvec{x}}_{\text {MILP}}^{2}=(1,2)$ and become fixed there. This is due to the fact that the supporting hyperplane at ${\varvec{x}}_{\text {NLP}}$ does not cut off (1, 2). However, the Algorithm 3.1 can solve the problem when $\varepsilon _g>0$. In Fig. 2, the first six iterations are shown. The algorithm solves the problem after nine iterations.

Fig. 2

Six iterations of the ESH algorithm when solving (P1) with tolerance $\varepsilon _g=0.001$. Plain numbers indicate points $x_{\text {MILP}}^{k}$ and dotted numbers indicate points $x^k$. The dashed lines represent supporting hyperplanes

In the later examples, we use a line search based on the bisection method. This guarantees that at each iteration of the line search, we have found an interval $\left[ {\varvec{x}}_{L},{\varvec{x}}_{U} \right]$ such that $F({\varvec{x}}_{L}) \le \frac{\varepsilon _g}{2}$ and $\frac{\varepsilon _g}{2} < F({\varvec{x}}_{U}) \le F({\varvec{x}}_{\text {MILP}}^{k})$. We will stop the line search when a point ${\varvec{x}}$ satisfying $\frac{\varepsilon _g}{4} \le F({\varvec{x}}) < \varepsilon _g$ has been found. The supporting hyperplanes will be generated at this point.

In the line search we do not need to calculate all of the constraint functions in each step. If $g_m({\varvec{x}}_{\text {MILP}}^k) < \varepsilon _g$ then, by quasiconvexity [Theorem 2 (iv)], $g_m({\varvec{x}}) < \varepsilon _g$ for all ${\varvec{x}}\in \left[ {\varvec{x}}_{\text {NLP}}, {\varvec{x}}_{\text {MILP}}^k \right]$. Hence, on the line segment $\left[ {\varvec{x}}_{\text {NLP}}, {\varvec{x}}_{\text {MILP}}^k \right]$, it is enough to apply the line search on function

$$\begin{aligned} F_k({\varvec{x}})=\max _{m \in M_k} g_m({\varvec{x}}), \text { where } M_k =\left\{ m \mid g_m({\varvec{x}}_{\text {MILP}}^{k})\ge \varepsilon _g \right\} . \end{aligned}$$

4.2 Theoretical comparison on the $\alpha$ECP and ESH algorithms

Here we present some theoretical differences between the $\alpha$ECP and the ESH algorithms. For details on the $\alpha$ECP algorithm we refer to [8, 14].

The principal difference between the algorithms is the type of cutting plane that they use. The ESH algorithm creates supporting hyperplanes as explained in the previous section and the $\alpha$ECP algorithm creates $\alpha$-cutting planes. For a constraint function $g_m$ the $\alpha$-cutting plane created at point ${\varvec{x}}_{\text {MILP}}^{k}$ reads

$$\begin{aligned} g_{m}({\varvec{x}}_{\text {MILP}}^{k})+\alpha \cdot {\varvec{\xi }}^{T}({\varvec{x}}-{\varvec{x}}_{\text {MILP}}^{k}) \le 0, \end{aligned}$$

where ${\varvec{\xi }}\in \partial g_m({\varvec{x}}_{\text {MILP}}^{k})$ and $\alpha \ge 1$ is sufficiently large. For a convex function $\alpha =1$ is large enough but for an $f^{\circ }$-pseudoconvex function a sufficiently large $\alpha$ value is usually not known. In practice, $\alpha$ is first set to 1 but it is updated until the distance between the $\alpha$-cutting plane and ${\varvec{x}}_{\text {MILP}}^{k}$ is less than the given parameter $\varepsilon _z>0$. Nevertheless, for a given $\varepsilon _z$ it can not be guaranteed that an updated $\alpha$-cutting plane will not cut off feasible points. The supporting hyperplanes does not cut off any points from the feasible set even if the constraint functions are $f^{\circ }$-pseudoconvex. This makes ESH more appealing than $\alpha$ECP to solve problems involving $f^{\circ }$-pseudoconvex functions. With the ESH algorithm the nonlinear functions have to be evaluated also at points where integer variables attain non-integer values due to the line search. This restriction does not apply to $\alpha$ECP.

Presumably, a hyperplane that ESH creates usually cuts off more of the infeasible region than an updated $\alpha$-cutting plane. This could lead to a solving process with a fewer number of MILP problems. If there is more than one constraint function the approximation of the feasible set may be enhanced by adding more than one $\alpha$-cutting plane or supporting hyperplane per iteration. Naturally, creating more linear constraints leads to larger MILP problems. It is a straightforward process to create an $\alpha$-cutting plane for any violating constraint from a solution point ${\varvec{x}}_{\text {MILP}}^{k}$. A supporting hyperplane may be created from a constraint that is active at the point ${\varvec{x}}^k$ at which the line search ends up. The quasiconvexity of the constraint functions implies that there are at least as many violating constraints at ${\varvec{x}}_{\text {MILP}}^{k}$ as there are active constraints at ${\varvec{x}}^k$. In other words, if there are many constraint functions it is possible to make at least as many $\alpha$-cutting planes as supporting hyperplanes per iteration. Thus, the use of more than one cutting plane per iteration benefits $\alpha$ECP more than ESH.

For the ESH algorithm, the cost of solving less MILP problems is an increasing number of function evaluations per iteration due to the line search. This will most probably lead to a greater total number of nonlinear function evaluations. Nevertheless, MILP problems are usually difficult to solve and more time consuming than multiple nonlinear function evaluation. However, this is not always the case. In a chromatographic separation problem [7] some function evaluations require solving partial differential equations and are more time consuming than solving an MILP problem. Another type of time consuming constraint functions are probabilistic constraints which are considered, for example, in [1, 6].

4.3 Example problems

In addition to (P1) we apply the ESH algorithm to another simple example problem and to a facility layout problem [4]. The former of these problems is

$$\begin{aligned} \min&\quad \max \left\{ (x_1-2)^2 , (x_2-4)^2 \right\} \\ \mathrm{s.t.}&\quad \frac{\left| x_1-3 \right| -10x_1}{3x_1+x_2+1}+2 \le 0 \\&\quad (x_1-7)^2-5x_2 \le 0 \quad (\text {P2}) \\&\quad 1\le x_1, \quad x_2 \le 8 \\&\quad x_1 \ge 0, \quad x_2 \in \mathbb {Z}^{+}. \end{aligned}$$

The objective function of (P2) is convex and nonsmooth. The first constraint function is $f^{\circ }$-pseudoconvex and the second constraint function is convex.

The third problem (P3) is the facility layout problem presented in [4, 10]. The formulation of the problem is presented in the “Appendix”. The problem (P3) was solved both by using only one linearization per iteration and by creating linearizations for all violating or active constraint functions.

The number and types of variables together with the types of constraints and objective functions are summarized in Table 1. Transformation of the convex objective function to a constraint function leads to one nonsmooth convex constraint in (P2) and 6 nonsmooth convex constraints in (P3). The use of only one objective function constraint in (P3) would result in a difficult constraint function. Since the objective function is a sum of 12 $l_1$-norms of linear functions, the transformation to only one single constraint would have $2^{12}$ different gradients on its domain of definition. Thus, to make a perfect approximation of the objective function, $2^{12}$ linearizations would be needed. With 6 constraints, each will have only 4 different gradients.

Table 1 Basic information on the example problems

For the problems (P1) and (P2) the inner points are given as $(x_1,x_2)=(1,0)$ and $(x_1,x_2)=(3,4)$, respectively. In the problem (P3) the feasibility problem is the relaxed problem discussed in Sect. 3.3. The feasibility problem was solved by the $\alpha$ECP algorithm.

In all of the problems, nonsmooth functions could be presented as a maximum of two functions. Consequently, a subgradient of a nonsmooth constraint function could be presented as a gradient of an active function. For example, $h(x_1,x_2)=|x_1-x_2|$ is a part of a constraint function in (P3) and its subdifferential is

$$\begin{aligned} \partial h(x_1,x_2) = {\left\{ \begin{array}{ll} (1,-1), &{}\quad x_1 > x_2 \\ \left[ (1,-1),(-1,1) \right] , &{}\quad x_1 = x_2 \\ (-1,1), &{}\quad x_1 < x_2 \end{array}\right. }. \end{aligned}$$

When $x_1=x_2$ we use point $(-1,1)$ as the subgradient.

Parameters for the $\alpha$ECP algorithm were the same as those in problem 2 in [8]. In the ESH algorithm similar parameters were used, that is, $\varepsilon _g= 0.001$. Problems were solved using a 64-bit windows 7 computer with an Intel i3-2100 3.1 GHz processor. The MILP problems were solved by CPLEX. Table 2 summarizes the results.

Table 2 Numerical results

The supposed strength of the ESH algorithm compared with the $\alpha$ECP algorithm is a fewer number of MILP problems due to the tighter underestimates of the nonlinear constraints. From Table 2, we can see that this was true only for problems (P1) and (P2) but not for problems (P3) and (P4). The $\alpha$ECP algorithm managed to solve all the problems in a fewer number of function evaluations, as expected. This holds true even without taking account of the effort needed to solve the feasibility problem to find the inner point. In problem (P3) solving the feasibility problem required 1468 nonlinear function evaluations and 3 s of CPU time. In the example problems, the nonlinear function evaluations were inexpensive. Consequently, the great difference in the number of function evaluations did not convert to a great difference in CPU time.

ESH solved problem (P3) in considerably shorter time. The reason for this is that the MILP problems that the ESH algorithm generated in (P3) were much easier than those generated by $\alpha$ECP. Both algorithms found the best-known solution in all of the problems. The difference between the objective function values in (P2) results from the feasibility tolerance: $\alpha$ECP found a solution that violates the constraints more but the violation is still within the tolerance.

From the last row of Table 2 we see that $\alpha$ECP benefited from using more linearizations per iteration. The number of function evaluations, the number of MILP problems and CPU time were all reduced. Even then $\alpha$ECP could not solve the problem faster than ESH. The size of the last MILP problem was increased as expected. In addition, while ESH also benefited from multiple hyperplanes it was not to the same extent as $\alpha$ECP.

Despite we can solve the nonsmooth formulation of the facility layout problem, a more efficient way to solve it is to use the same formulation as [4] and in MINLP Library2 (http://www.gamsworld.org/minlp/minlplib2/html/) problem fo7. That is, the objective function is transformed to linear constraints and 7 pseudoconvex constraints are replaced by 14 convex constraints. As suggested by the results in Table 2, efficiency is further increased if all possible linearizations are created. In this case, the ESH algorithm solves the problem in 20 s while the $\alpha$ECP algorithm needed 15 s. If the objective function is handled as in (P3) but pseudoconvex constraints are replaced by convex constraints, the solving time for ESH is 170 s and for $\alpha$ECP it is 11s. If the objective function is transformed to linear constraints and the pseudoconvex functions are kept as they are, the solving time for ESH is 190 s and for $\alpha$ECP it is 370 s. Based on these tests, it seems that the difficult MILP problems that $\alpha$ECP created in (P3) are related to the $\alpha$-cutting planes of the pseudoconvex functions.

5 Concluding remarks

In this paper, it was shown that the ESH method can be applied to a problem with nonsmooth locally Lipschitz continuous functions. The only change to the original method is to use Clarke subgradients instead of gradients. For a convex objective function and $f^{\circ }$-pseudoconvex constraint functions the algorithm was shown to converge to a global minimum. This result requires that the Slater constraint qualification holds true. If it does not, we can still solve the problem but the obtained solution might be only $\varepsilon _g$-feasible. If the subdifferentials of the constraint functions do not contain zero at the points where supporting hyperplanes are created, the convergence theorems are also valid for $f^{\circ }$-quasiconvex constraint functions.

Both the ESH and the $\alpha$ECP algorithms solved all the example problems considered to the best known solutions. For the ESH algorithm, the higher number of nonlinear function evaluation was compensated by fewer or easier MILP problems that led to faster solving times in problems (P2) and (P3). However, it is not guaranteed that the ESH algorithm solves a problem with a fewer number of MILP problems as was shown in problem (P3). The superiority of ESH to $\alpha$ECP when solving (P3) was related to the pseudoconvex constraints. If those constraints were replaced by appropriate convex constraints, then the $\alpha$ECP could solve the problem faster.

Generally, if the MILP problems of the original nonsmooth MINLP problem are hard to solve, ESH should do better than $\alpha$ECP. However, if the bottleneck of the solving process is expensive nonlinear function evaluations then $\alpha$ECP has an advantage over ESH.

There is still room for improvement for the ESH algorithm with respect to the problem classes considered in this paper. In addition to using the LP step, we may change the line search of the ESH algorithm and the algorithm that solves the feasibility problem to solve problems more efficiently. Furthermore, by using corresponding types of techniques as in [8, 14] the ESH method to solve problems with an $f^{\circ }$-pseudoconvex objective function will be considered in a forthcoming paper.

Appendix: The facility layout problem: P3

In this problem, 7 departments should be placed in a facility. The width and the height of the facility are $w_F=8.54$ and $h_F=13$, respectively. Parameters for the problem are in Table 3. The decision variables and the indices of the problem are:

• $i=\text {indexes of the departments:}\, 1,2,\ldots ,7$.

• $x_i,y_i=$ coordinates of the center of department i.

• $w_i =$ width of the department i.

• $h_i =$ height of the department i.

• $X_{ij},Y_{ij} =$ auxiliary variables.

The problem reads

$$\begin{aligned} \min&\sum _{i=1}^{6} \left| x_i-x_{i+1} \right| +\left| y_i-y_{i+1} \right| \end{aligned}$$

(7)

$$\begin{aligned} \mathrm{s.t.}&h_iw_i \ge a_i, \quad i=1,2,\ldots ,7 \end{aligned}$$

(8)

$$\begin{aligned}&x_i+\frac{1}{2} w_i \le w_F, \quad i=1,2,\ldots ,7 \end{aligned}$$

(9)

$$\begin{aligned}&-x_i+\frac{1}{2}w_i \le 0, \quad i=1,2,\ldots ,7 \end{aligned}$$

(10)

$$\begin{aligned}&y_i+\frac{1}{2} h_i \le h_F, \quad i=1,2,\ldots ,7 \end{aligned}$$

(11)

$$\begin{aligned}&-y_i+\frac{1}{2}h_i \le 0, \quad i=1,2,\ldots ,7 \end{aligned}$$

(12)

$$\begin{aligned}&\frac{1}{2}(w_i+w_j)-(x_i-x_j) \le w_{F}(X_{ij}+Y_{ij}), \quad 1 \le i< j \le 7 \end{aligned}$$

(13)

$$\begin{aligned}&\frac{1}{2}(w_i+w_j)-(x_j-x_i) \le w_{F}(1+X_{ij}-Y_{ij}), \quad 1 \le i< j \le 7 \end{aligned}$$

(14)

$$\begin{aligned}&\frac{1}{2}(h_i+h_j)-(y_i-y_j) \le h_{F}(1-X_{ij}+Y_{ij}), \quad 1 \le i< j \le 7 \end{aligned}$$

(15)

$$\begin{aligned}&\frac{1}{2}(h_i+h_j)-(y_j-y_i) \le h_{F}(2-X_{ij}-Y_{ij}), \quad 1 \le i< j \le 7 \end{aligned}$$

(16)

$$\begin{aligned}&x_1-x_2 \le 0 \end{aligned}$$

(17)

$$\begin{aligned}&y_1-y_2 \le 0 \end{aligned}$$

(18)

$$\begin{aligned}&w_{i}^{low} \le w_{i} \le w_{i}^{up}, \quad i=1,2,\ldots ,7 \end{aligned}$$

(19)

$$\begin{aligned}&h_{i}^{low} \le h_{i} \le h_{i}^{up}, \quad i=1,2,\ldots ,7 \end{aligned}$$

(20)

$$\begin{aligned}&X_{ij} \in \left\{ 0,1 \right\} , \quad 1 \le i< j \le 7 \end{aligned}$$

(21)

$$\begin{aligned}&Y_{ij} \in \left\{ 0,1 \right\} , \quad 1 \le i< j \le 7 \end{aligned}$$

(22)

Table 3 Parameters of the problem (P3)

The objective is to minimize the distance between consecutive departments. Constraints (7) define the minimum areas of the departments. Constraints (8)–(11) make sure the departments are located inside the facility. Constraints (12)–(15) prevent the overlapping of the departments. Constraints (16)–(17) erase symmetric solutions.