Introduction

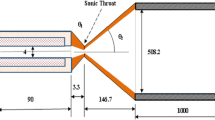
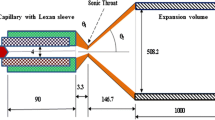
Expansion of aerosol particulates into the vacuum chamber of a fusion reactor following a hard disruption event was previously investigated using a supersonic nozzle on the exit of an electrothermal capillary discharge to allow for the transition between the source and the chamber’s large volume [1]. A schematic of the capillary discharge with the attached expansion is shown in Fig. 1 in which a subsonic to supersonic transition region is inserted between the electrothermal source and the expansion chamber [1].

Fig. 1
figure 1

Supersonic throat transition between the capillary and the expansion regions, θ1 = 2o and θ1 = 60o, dimensions in mm (not to scale) [1]

Full size image

The capillary source simulates hard disruption events by depositing transient radiant high heat flux onto the inner liner of the capillary, which in turn generates particulates from wall evaporation [2, 3]. The particulates form a plasma jet, which moves towards the capillary exit at high speed and high pressure. The capillary serves as a source term simulating surface erosion of the divertor of a tokamak fusion reactor under hard disruption-like conditions [4, 5]. The plasma jet expands into the vacuum vessel, which is simulated herein by the expansion large chamber. The nozzle, converging–diverging, is a method to allow for the computational transition between the capillary exit and the entry of the expansion chamber [1]. The capillary has an inner diameter of 4.0 mm diameter and 12 cm in length with 3.0 cm occupied by the discharge cathode. The discharge time is in the range of 100–200 μs and can be extended to few milliseconds. The produced plasma jet has typical temperature of up to 5 eV, an exit peak pressure of up to 400 MPa and imparts a radiant heat flux up to 60 GW/m2 [3].

In the previous work, it has been shown that the Mach number at the diverging exit drops from 21 to 0.7 after suffering from multiple shocks in the large expansion volume, and that the plasma parameters are almost constant along the axis of the simulated expansion chamber [1]. It was also shown that the Mach number is a function of the ratio \(\left( {A^{'} /A^{*} } \right)\), where \(A^{'}\) is the cross-sectional area along the length of the transition region at any location and \(A^{*}\) is the sonic throat cross-sectional area. Thus, the variation of Mach number along the axis of the transition region, as well as inside the expansion chamber, does not depend on the values of the exit parameters of the capillary source. It has also been observed that two shocks successively take place as soon as the supersonic flow enters into the uniform cross section expansion chamber and brings the flow into sub-sonic steady state. The shock waves result from the sudden restriction in the cross-sectional area through which the plasma flows when the diverging section of the transition region opens into the expansion chamber. The present work introduces a mathematical formalism of a shock pitch length \(Z_{sp}\), which is the spatial separation between successive shocks. It is an intuitively chosen variable, which if measured in an actual capillary discharge, can be used to produce the actual profile of the plasma bulk temperature, density, pressure and velocity.

Discretization Technique and Mathematical Formulation

As previously shown in the previous work, the relation between the cross-sectional area of the sonic throat \(A^{*}\) and inlet cross section to the converging section A, is given by the well-known equation, which was used to establish the relationship between the plasma parameters and the Mach number along the cross-sectional area \(A^{'}\) at any location along the length of the transition region [1, 6, 7]:

$$A^{*} = A\;M_{a} \left[ {\frac{{1 + \left( {\frac{\gamma - 1}{2}} \right)M_{a}^{2} }}{{\left( {\frac{\gamma + 1}{2}} \right)}}} \right]^{{ - \frac{{\left( {\gamma + 1} \right)}}{{2\left( {\gamma - 1} \right)}}}}$$
(1)

where M a is the Mach number at the capillary exit and \(\gamma = C_{p} /C_{v}\) is the specific heat ratio. The plasma parameters at any axial location inside the nozzle are given by the following set of equations [1, 4, 5]:

$$\left. {\begin{array}{*{20}l} {\rho^{'} = \rho \frac{{\left[ {1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a} } \right)^{2} } \right]^{{\frac{1}{\gamma - 1}}} }}{{\left[ {1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a}^{'} } \right)^{2} } \right]^{{\frac{1}{\gamma - 1}}} }} ,} \hfill & {P^{'} = P\frac{{\left[ {1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a} } \right)^{2} } \right]^{{\frac{\gamma }{\gamma - 1}}} }}{{\left[ {1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a}^{'} } \right)^{2} } \right]^{{\frac{\gamma }{\gamma - 1}}} }}} \hfill \\ {T^{'} = T\frac{{1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a} } \right)^{2} }}{{1 + 0.5\left( {\gamma - 1} \right)\left( {M_{a}^{'} } \right)^{2} }} ,} \hfill & {v^{'} = M_{a}^{'} \left( {\frac{{\gamma P^{'} }}{{\rho^{'} }}} \right)^{1/2} } \hfill \\ \end{array} } \right)$$
(2)

The units for the plasma parameters are eV for the temperature, kg/m3 for the density, MPa for the pressure and m/s for the velocity.

To obtain scaling laws for the converging–diverging transition nozzle and beyond, all equations have been discretized in one dimensional space along the axial direction so that one can retrieve the flow parameters at some preferred locations.

In this 1-D approach, it is assumed that there is no radial variation in the parameters and only axial grids are considered. The length of the converging, diverging and the expansion chamber are 0.33, 14.67 and 100 cm, respectively, hence the grid-size is not uniform. Grid-size has been varied in the three separate sections to reflect the changes in the parameters in each section.

In the converging section the successive nodes are separated by a distance of 0.2 mm, whereas in the diverging section the successive nodes are separated by a distance of 5 mm. So essentially there is roughly 16 nodes in the converging section and 29 nodes in the diverging section. In the diverging section more number of nodes has been incorporated because this section deals with the actual supersonic flow. On the other hand, in the 100 cm long expansion chamber, the grid is much coarser as the successive nodes are separated by a distance equal to shock pitch length zsp. For computational purposes it was assumed that zsp = 1 cm, so this region essentially has 100 nodes. This also means that the successive shocks are separated by 1 cm at the entry of the expansion chamber, which is the grid scale length. This assumed length approximately emulates the shape of the parameter profiles, but actual scale lengths can be determined using proper sensing and imaging techniques in different sections of the experimental setup. Nevertheless, in this work the relative dimensions, or in other words the aspect ratios have been chosen realistically, pertinent to disruption events associated with divertor in a practical fusion reactor, e.g. ITER.

In our previous work, a stand-alone routine had been created to simulate the shock [1]. The Mach number, temperature, pressure and density at the diverging exit of the transition region were used there as the input to the shock routine. The routine checks the Mach number and decides whether to use the normal shock or the oblique shock. In case the oblique shock the shock angle is estimated using one of the scaling laws prescribed in that work. In the present formalism, equations were established describing flow parameters only as a function of axial position with respect to the micro-nozzle exit.

For each of the flow parameters, namely plasma bulk velocity (V p ), plasma temperature (T), plasma bulk density (ρ), plasma pressure (P); linear fit was used in the region \(0 \le z \le 0.004\;\text{m}\) (where z is a variable that represents the axial length traversed by the flow); whereas power-law fit was used for the region \(0.004 \le z \le 0.15\;\text{m}\) and this power law fit takes care of the non-linearity in the respective parameter profiles as the flow becomes supersonic.

As the flow enters the expansion chamber of uniform cross section, it suffers from shock. It has been assumed that the changes in respective parameter values due to shock takes place over a small scale length, which in this case is the shock pitch length. This enables the tracking of the abrupt changes in the values of the flow parameters due to the shock in a reasonably gradual manner without changing the major profile features, giving the observer an opportunity to represent the parameter profiles as smooth functions of the axial length inside the expansion chamber in the steady-state subsonic condition.

For all the flow parameters, an easy to implement approach has been used to model the respective profiles inside the expansion chamber. Using the parameter values at the diverging exit and the values obtained right after the first shock, a linear fit equation was established, which predicts the variation of the profile parameters in the region \(0.15 < z \le (0.15 + z_{sp} )\;\text{m}\), where zsp is the shock pitch length. A quadratic fit was used for the region for the region \((0.15 + z_{sp} ) \le z \le (0.15 + 2z_{sp} )\;\text{m}\), using the parameter values at the diverging exit and the values obtained at the end of each of the two shocks. It is to be noted that capillary exit data set corresponding to shot # P 206 has been taken as the standard while formulating these scaling laws [3].

The flow parameters at the micro-nozzle outlet have been defined as P(0) = P e (in MPa), T(0) = T e (in eV), ρ(0) = ρ e (in kg/m3), v p (0) = v pe (in m/s) and Ma(0) = Ma e .

The scaling laws for each zone are as follow:

Scaling laws for the axial length range \(0 \le z \le 0.004 \;{\text{m}}\)

$$\begin{aligned} \left. {\begin{array}{*{20}l} {\begin{array}{*{20}l} {T_{z} = T_{e} \left( {1 - 93.68z} \right)} \hfill \\ {\rho_{z} = \rho_{e} \left( {1 - 37.23z} \right)} \hfill \\ {P_{z} = P_{e} \left( {1 - 120z} \right)} \hfill \\ {Ma_{z} = Ma_{e} \left( {1 + 142.5z} \right)} \hfill \\ {v_{{\text{p,z}}} = v_{pe} (1 + 85.17z)} \hfill \\ \end{array} } \hfill \\ \end{array} } \right\} \hfill \\ \hfill \\ \end{aligned}$$
(3)

Scaling laws for the axial length range \(0.004 < z \le 0.15\;{\text{m}}\)

$$\left. {\begin{array}{*{20}l} {T_{z} = 5.33 \times 10^{ - 4} \, T_{e} \, z^{ - 0.8} } \hfill \\ {\rho_{z} = 0.07 \, \rho_{e} \, z^{ - 0.27} } \hfill \\ {P_{z} = 3.58 \times 10^{ - 5} \, P_{e} \, z^{ - 1.09} } \hfill \\ {Ma_{z} = 45.32 \, z^{0.404} } \hfill \\ {v_{p,z} = 1.91 \, v_{pe} \, z^{0.0024} } \hfill \\ \end{array} } \right\}$$
(4)

Scaling laws for the axial length range \(0.15 < z \le (0.15 + z_{sp} ) \;{\text{m}}\)

$$\left. {\begin{array}{*{20}l} {T_{z} = m_{T} \left( {z - 0.15} \right) + T_{DE} } \hfill \\ {\rho_{z} = m_{\rho } \left( {z - 0.15} \right) + \rho_{DE} } \hfill \\ {P_{z} = m_{P} \left( {z - 0.15} \right) + P_{DE} } \hfill \\ {Ma_{z} = m_{Ma} \left( {z - 0.15} \right) + Ma_{DE} } \hfill \\ {v_{p,z} = m_{v} \left( {z - 0.15} \right) + v_{DE} } \hfill \\ \end{array} } \right\}$$
(5)

where \(m_{X} = (X_{s1} - X_{DE} )/z_{sp}\), \(X_{DE} = X\left( {z = 0.15\;{\text{m}}} \right)\), and \(X \, is \equiv T,\rho ,P,v_{p} , Ma\)

Scaling laws for the range \(\left( {0.15 + z_{sp} } \right) \;{\text{m}} < z \le (0.15 + 2z_{sp} ) \;{\text{m}}\)

$$\left. {\begin{array}{*{20}l} {T_{z} = A_{T} z^{2} + B_{T} z + C_{T} } \hfill \\ {\rho_{z} = A_{\rho } z^{2} + B_{\rho } z + C_{\rho } } \hfill \\ {P_{z} = A_{p} z^{2} + B_{p} z + C_{p} } \hfill \\ {v_{p,z} = A_{v} z^{2} + B_{v} z + C_{v} } \hfill \\ {Ma_{z} = A_{Ma} z + B_{Ma} } \hfill \\ \end{array} } \right\}$$
(6)

where \(A_{X} = \left( {X_{s2} - 2X_{s1} + X_{DE} } \right)/2z_{sp}^{2}\),

$$B_{X} = \left[ {2z_{sp} \left( {X_{s2} - X_{s1} } \right) - 3\left( {X_{s2} - 2X_{s1} + X_{DE} } \right)\left( {0.1 + z_{sp} } \right)} \right]/2z_{sp}^{2}$$
$$C_{X} = X_{DE} - 0.0225 \, A_{X} - 0.15 \, B_{X} \;{\text{and}}\;X \, is \equiv T,\rho ,P,v_{p}$$
$$A_{Ma} = (Ma_{s2} - Ma_{s1} )/z_{sp} ,B_{Ma} = Ma_{s1} - \left( {z_{sp} + 0.15} \right)A_{Ma}$$

Scaling laws for the range \(z > (0.15 + 2z_{sp} ) \;{\text{m}}\)

$$\left. {\begin{array}{*{20}l} {T_{z} = T_{s2} = 0.825 \, T_{e} } \hfill \\ {\rho_{z} = \rho_{s2} = 0.28 \, \rho_{e} } \hfill \\ {P_{z} = P_{s2} = 0.23 \, P_{e} } \hfill \\ {Ma_{z} = Ma_{s2} = 0.7073} \hfill \\ {v_{p,z} = v_{s2} = 1.19 \, v_{Pe} } \hfill \\ \end{array} } \right\}$$
(7)

and \(T_{s1} = 0.23T_{e} ,\rho_{s1} = 0.195\rho_{e} ,P_{s1} = 0.045P_{e} ,v_{s1} = 1.7v_{pe} ,Ma_{s1} = 1.9\)

The parameters \(T_{s1} ,\rho_{s1} ,P_{s1} ,v_{s1} ,Ma_{s1}\) are the plasma temperature, pressure, bulk density, bulk velocity and Mach number, respectively, just after the first shock. The parameters \(T_{s2} ,\rho_{s2} ,P_{s2} ,v_{s2} ,Ma_{s2}\) are the steady state values of plasma temperature, pressure, bulk density, bulk velocity and Mach number, respectively, of sub-sonic flow inside the expansion chamber.

One important aspect, that needs to be addressed while making the scaling formulae, is the continuity in the parameter profiles. The virtual regions created for computational convenience should merge smoothly, without exhibiting any anomaly, abrupt change or discontinuous graphical behavior.

Results and discussion

It was previously mentioned that shot P206, in which Lexan Polycarbonate is the ablating material to form the plasma, has been taken as the standard while formulating the scaling laws, which has peak discharge current of I p(P206)  = 42.81 kA. Four more peak discharge currents were chosen for the calculations based on this discharge current value. They are a factor of 0.5, 0.67, 1.5 and 2.0 of the P206 (I p(P206)  = 42.81 kA), which makes all in comparison with P206. The ETFLOW code [3, 8, 9] was run for all these current values to obtain the respective capillary exit parameters. The capillary exit parameters for each value of the peak discharge current are show in Table 1 as given by the results of the ETFLOW code [3]. The calculated plasma parameters at the source exit are consistent with reported values [10, 11].

Table 1 Capillary exit parameters for the chosen values of discharge current
Full size table

As can be seen from Table 1, the Mach number of the plasma bulk at the exit of the pulsed electrothermal plasma source (PEPS) is almost independent of the magnitude of the peak discharge current. This Mach number at the source exit is the input into the converging–diverging nozzle where the Mach number will be a function of the geometry.

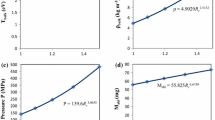
Figure 2 shows the Mach number along the axis with respect to the geometry of the transition region and expansion chamber, and it is the same for all discharge current values. It is changing along the axial direction increasing up to a very high-hypersonic value ~21 at the diverging exit, then after the first shock it comes down to 1.9 and the second shock brings the bulk plasma flow to a steady-state sub-sonic condition of Mach number ~0.707 inside the expansion chamber. The Mach number at the source exit is typical to the calculated values in similar systems and the pattern in the expansion is also similar to that expected in thrusters with diverging nozzles [11]. The pattern and the values of the Mach number into the expansion chamber are also consistent with recent 2-D modeling results and are in good correlation to experiment [12].

Fig. 2
figure 2

Mach number with respect to the geometry of the transition and expansion chamber

Full size image

The plasma bulk density at the source exit increases with the increase in the magnitude of the discharge current [3]. This is also seen in Table 1 where the density increases from 5.8188 to 24.0853 kg/m3 for peak currents of 21.405 to 85.62 kA, respectively. As the flow moves into the converging–diverging nozzle and the Mach number increases, the bulk density drops down as seen in Fig. 3. The newly developed scaling law predicts 0.6837–2.82 kg/m3 at the diverging exit for peak currents of 21.405–85.62 kA, respectively. As the flow suffers from shock and becomes sub-sonic inside the expansion chamber, the bulk density tends to increase. However the steady-state subsonic flow bulk densities are lower in magnitude compared to those estimated at the capillary exit. The scaling law predicts sub-sonic flow bulk densities of 1.6216–6.712 kg/m3 for peak currents of 21.405 to 85.62 kA, respectively.

Fig. 3
figure 3

Plasma density versus the length of the transition and chamber regions

Full size image

Because plasma pressure is directly proportional to the plasma bulk density, the pressure must increase with the increase in the magnitude of the discharge current [2, 3]. The source exit pressure as calculated by ETFLOW ranges from 153.23 to 1060.08 MPa for the tested range of the peak discharge currents. Figure 4 illustrates the plasma pressure along the axial length of the transition region and the expansion chamber. The pressure drops drastically in the converging–diverging nozzle as the Mach number increases. The scaling law predicts 43.3–299.9 kPa at the diverging exit over the tested range of the discharge current. The flow becomes sub-sonic inside the expansion chamber and rises to reach steady-state at 35.25–243.83 MPa for the tested range of the discharge current. This behavior is also consistent with other reported studies [11–13].

Fig. 4
figure 4

Plasma pressure versus the length of the transition and chamber regions

Full size image

The plasma bulk velocity at the source exit as calculated by the ETFLOW code ranges between 5.443 and 6.994 km/s for the tested range of the discharge current, where all the values are consistent with reported values [3, 8–13], and the measured value of 5.333 km/s using a high speed camera on an experimental electrothermal facility [14]. Figure 5 shows the plasma bulk velocity versus the length of the transition and chamber regions. The plasma bulk velocity increases rapidly inside the converging–diverging nozzle and then saturates to almost a steady-state value inside the expansion chamber. The scaling law predicts plasma bulk velocity between 10.36 and 13.31 km/s for the tested range of discharge current at the diverging exit, then drops inside the expansion chamber to 6.48–8.33 km/s for the same range of the discharge current.

Fig. 5
figure 5

Plasma velocity versus the length of the transition and chamber regions

Full size image

The plasma temperature at the source exit, as calculated by the ETFLOW code, ranges between 2.15 and 3.27 eV for the tested range of the discharge current, which is consistent with reported values [3, 8–13], and the measured value via optical emission spectroscopy [14]. Figure 6 shows the plasma temperature along the axis of the transition and chamber regions. Plasma bulk temperature follows a profile that is very similar to that of pressure and bulk density. Plasma temperature rapidly decreases inside the converging–diverging nozzle down to about 0.0053–0.008 eV at the diverging exit for the tested range of discharge current, then rises inside the expansion chamber to 1.78–2.69 eV for the same range of the discharge current and remains almost constant.

Fig. 6
figure 6

Plasma temperature versus the length of the transition and chamber regions

Full size image

Conclusions

The developed scaling laws proposed in this work for fixed dimensions of the converging–diverging nozzle attached to an electrothermal plasma capillary source have shown efficient predictions of the plasma parameters over a tested range of discharge current from 21.405 to 85.62 kA. A change in the geometry and dimensions of the converging–diverging transition region will require adjustment to the power law in the supersonic region and subsequent changes in the scaling of post-shock as well as the steady-state subsonic flow parameters. The predicted plasma parameters and the flow pattern are similar to reported results. Plasma temperature and velocity are consistent with values measured on an electrothermal facility, and within reasonable correlation to published computational values. The plasma parameters suffer from drastic changes in the converging–diverging nozzle with increase in the Mach number and bulk velocity, and decrease in plasma density, pressure and temperature. However, all parameters converge to steady-state values inside of the expansion chamber.