1 Introduction

The analysis of social networks and social media has introduced several interesting problems from an algorithmic point of view. Social networks are usually represented as graphs, where vertices represent the elements of the network, and edges represent a binary relation between the represented elements. There are several relevant properties that can be considered when analyzing a social networks, e.g. degree centrality, closeness centrality, eigenvector centrality. An interesting property is the vertex connectivity of two given vertices, as it is related to the information flow inside a network and vertex connectivity is considered as a measure of the information flow. Furthermore, group cohesiveness and centrality are two other fundamental structural properties that are related to vertex connectivity (Hanneman 2011; Wasserman 1994). A well-known result in graph theory, Menger’s theorem, shows that vertex connectivity is equivalent to the maximum number of disjoint paths between two given vertices.

While social networks analyses usually focus on a single type of relation, the availability of several social networks lead to the problem of integrating the information of several networks into a single network. A model for studying vertex connectivity in a multi-relational social network has been introduced by Wu (2012), where different kinds of relations are considered. In the proposed model, colors are associated with edges of the graph to distinguish different kinds of relations. In order to study vertex connectivity in such an edge-colored graph, Wu (2012) introduced a natural combinatorial problem, called Maximum Colored Disjoint Paths (MaxCDP), that asks for the maximum number of vertex-disjoint paths consisting of edges of the same colors (also called uni-color paths) in the input graph between two terminals. A related combinatorial problem, called Multicolor Path problem, have been considered in Santos et al. (2017), with application in WDM optical networks. Given an edge-colored directed graph, where each edge is associated with a positive weight and a set of colors, Multicolor Path problem asks for one shortest path between a source and a target in the graph, such that edges in the path share a set of at least k colors. The Multicolor Path problem have also been extended to ask for a set of \(p \geqslant 1\) paths (Santos et al. 2017).

The complexity of MaxCDP has been investigated in Wu (2012), Bonizzoni et al. (2013), Gourvès et al. (2012). MaxCDP is polynomial time solvable when the input graph contains exactly one color as it is can be reduced to the maximum flow problem (Wu 2012). When the edges of the input graph are associated with at least two colors, the problem is NP-hard (Wu 2012). Moreover, the problem is even NP-hard when the number of paths is fixed to 2 (and the graph has degree bounded by 4), thus not in the class XP for the parameter number of paths (Gourvès et al. 2012).

The approximation complexity of the problem has also been investigated. On general instance, MaxCDP is not approximable within factor \(O(n^{d})\), where n is the number of vertices of the input graph, for any constant \(0<d<1\) (Bonizzoni et al. 2013). Furthermore, MaxCDP is approximable within factor q, where q is the number of colors of the edges of the input graph, but not approximable within factor \(2 - \epsilon \), for any \(\epsilon > 0\), when q is a fixed constant (Wu 2012).

Since many real networks, and in particular many social networks, have a bounded diameter, Wu introduced a variant of the MaxCDP problem where the length of the paths in the solution are (upper) bounded by an integer \(l \geqslant 1\) (Wu 2012). When \(l \geqslant 4\) MaxCDP is NP-hard, while it is polynomial time solvable for \(l < 4\) (Wu 2012) . The bounded length variant of MaxCDP is fixed-parameter tractable for the combined parameter number of paths in the solution and l (Bonizzoni et al. 2013). Moreover, this variant does not admit a polynomial kernel unless \(NP \subseteq coNP/Poly\), as it follows from the results in (Golovach and Thilikos 2011). Wu (2012) considers also the approximation complexity of the bounded length variant of the problem, showing that is is approximable within factor \((l-1)/2 + \epsilon \) (Wu 2012).

In this paper, we further investigate the complexity of MaxCDP and of a related problem that we introduce, called MaxCDDP. Given an edge-colored graph, MaxCDDP asks for the maximum number of vertex-disjoint and color-disjoint uni-color paths, where two uni-color paths are color-disjoint if they having different colors. We introduce color disjointness of paths as it can be useful how different relations in a network connects two vertices. In this case, we are not interested to have more paths of a single color, but rather to compute the maximum number of color-disjoint paths between two vertices.

In the spirit of a multivariate complexity analysis (Komusiewicz 2012; Fellows et al. 2013), we study how the complexity of MaxCDP and MaxCDDP depends on several parameters. It has already been studied how the complexity of MaxCDP depends on different parameters (number of colors of each edge, degree of the graph, maximum length of a path). We believe that it is interesting to take into account the structure of the input graph when studying the complexity of these two problems for two main reasons. First, real-life networks often exhibit very specific structural property, like “small-world phenomenon” or small degree of separation, and thus information on the structure of the corresponding graphs can be derived. Moreover, studying how the complexity of MaxCDP and MaxCDDP depends on different parameters is also of theoretical interest, since it helps to better understand the complexity of the two problems.

First, we investigate how the complexity of the two problems depends on two graph parameters: distance from disjoint paths (that is the number of vertices one has to remove to make the graph a collection of disjoint paths), and the size of vertex cover of the graph. In Sect. 3 we show that on graphs at distance bounded by a constant from disjoint paths MaxCDP admits a polynomial-time algorithm, whereas MaxCDDP is NP-hard even if the distance to disjoint path has distance two from disjoint paths. This implies the hardness of MaxCDDP even when the treewidth of the input graph is bounded by a constant. Moreover, we show that MaxCDDP admits a polynomial-time algorithm when the input graph, after the removal of the target vertex, is a tree. In Sect. 4 we show that MaxCDP is fixed-parameter tractable when parameterized by the size of the vertex cover of the input graph. Moreover, we show that MaxCDDP admits a parameterized \(\frac{1}{2}\)-approximation algorithm, when parameterized by the size of the vertex cover of the input graph. MaxCDP is fixed-parameter tractable when parameterized by the size of the vertex cover of the input graph. In Sect. 5 we consider the parameterized complexity of the bounded length version of MaxCDDP, for the combined parameter number of vertex and color-disjoint paths of a solution and maximum length of a path, and we extend the FPT algorithm for MaxCDP to MaxCDDP. Finally, we consider the FPT-approximability and we show in Sect. 6 that both problems are not \(\rho \)-approximable in FPT time, for any function \(\rho \).

2 Definitions

In this section we present some definitions that will be useful in the rest of the paper, as well as the formal definition of the two combinatorial problems we are interested in. First, notice that in this paper, we will consider undirected graphs. Given a graph \(G=(V,E)\) and a vertex \(v \in V\), we denote by N(v) the neighborhood of \(v \in V\), that is \(N(v)= \{ u: \{ u,v \} \in E \}\).

Consider a set of colors \(C=\{c_1,\dots , c_q \}\), where \(|C|=q\). A C-edge-colored graph (or simply an edge-colored graph when the set of colors is clear from the context) is defined as \(G=(V,E,f_C)\), where V denotes the set of vertices of G and E denotes the set of edges, and \(f_C: E \rightarrow 2^{C}\) is a function, called coloring, that associates a set of colors in \(C=\{c_1,\dots , c_q \}\) with of each edge in E. In the remaining part of the paper, we denote by n the size of V and by m the size of E.

A path \(\pi \) in a C-edge-colored graph G is said to be colored by \(c_j \in C\) if all the edges of \(\pi \) are colored by \(c_j\). A path \(\pi \) in G is called a uni-color path if there is a color \(c_j \in C\) such that all the edges of \(\pi \) are colored by \(c_j\). Given two vertices \(x,y \in V\), an xy-path is a path between vertices x and y. In the remaining part of the paper, we will mainly consider a C-edge-colored graph G, with two distinct vertices s (the source) and t (the target), and we will consider uni-color paths between s and t, that is uni-color st-paths.

Two paths \(\pi '\) and \(\pi ''\) are internally disjoint (or, simply, disjoint) if they do not share any internal vertex, while a set P of paths is internally disjoint if the paths in P are pairwise internally disjoint. Two uni-color paths \(\pi '\) and \(\pi ''\) are color disjoint if they are disjoint and they have different colors.

Next, we introduce the formal definitions of the problems we deal with.

figure a
figure b

We will consider a variant of the two problems where the length of the paths in the solution is (upper) bounded by an integer \(l \geqslant 1\), that is we are interested only in paths bounded by l. These variants will be denoted by l-MaxCDP and l-MaxCDDP.

We have introduced the optimization definition of MaxCDP and MaxCDDP. In the parameterized definitions of these problems, we are also given an integer \(k>0\) and we look whether there exists at least k (color) disjoint uni-color st-paths.

Moreover, we will consider how the complexity of the problem is influenced by the structure of the graph induced by the set \(V \setminus \{t\}\); we will denote such graph as \(G^{-t}\).

A parameterized problem (I, k) is said fixed-parameter tractable (or in the class FPT) with respect to a parameter k if it can be solved in \(f(k)\cdot |I|^c\) time (in fpt-time), where f is any computable function and c is a constant.

The class XP contains problems solvable in time \(|I|^{f(k)}\), where f is an unrestricted function. We defer the reader to the recent monographs of Downey and Fellows or Cygan et al. for additional information around parameterized complexity (Downey 2013; Cygan et al. 2015).

The natural notion of parameterized approximation was introduced quite recently [see the survey of Marx for an overview (Marx 2008)]. Informally, it aims at giving more time than polynomiality to achieve better approximation ratio. We give the definition of fpt cost \(\rho \)-approximation algorithm, as in Sect. 6 we will rule out the existence of such an algorithm for MaxCDP and MaxCDDP. This is a weaker notion than fpt-approximation, but notice that we will prove negative result (which will thus be stronger).

An NP-optimization problem Q is a tuple \(({{{\mathcal {I}}}}, Sol, val, goal)\), where \({{{\mathcal {I}}}}\) is the set of instances, Sol(I) is the set of feasible solutions for instance I, val(I, S) is the value of a feasible solution S of I, and goal is either max or min.

Definition 1

(fpt cost \(\rho \)-approximation algorithm, Chen et al. 2006) Let Q be an optimization problem and \(\rho :{\mathbb {N}}\rightarrow {\mathbb {R}}\) be a function such that \(\rho (k) \geqslant 1\) for every \(k\geqslant 1\) and \(k \cdot \rho (k)\) is nondecreasing (when goal = min) or \(\frac{k}{\rho (k)}\) is unbounded and nondecreasing (when goal = max). A decision algorithm \({{{\mathcal {A}}}}\) is an fpt cost \(\rho \) -approximation algorithm for Q (when \(\rho \) satisfies the previous conditions) if for every instance I of Q and integer k, with \(Sol(I)\ne \emptyset \), its output satisfies the following conditions:

  1. 1.

    If \(opt(I) > k\) (when goal = min) or \(opt(I) < k\) (when goal = max), then \({{{\mathcal {A}}}}\) rejects (I, k).

  2. 2.

    If \(k\geqslant opt(I) \cdot \rho (opt(I))\) (when goal = min) or \(k\leqslant \frac{opt(I)}{\rho (opt(I))}\) (when goal = max), then \({{{\mathcal {A}}}}\) accepts (I, k).

Moreover the running time of \({{{\mathcal {A}}}}\) on input (I, k) is \(f(k) \cdot |I|^{O(1)}\). If such a decision algorithm \({{{\mathcal {A}}}}\) exists then Q is called fpt cost \(\rho \)-approximable.

3 MaxCDDP and MaxCDP on graphs at bounded distance from disjoint paths

In this section we consider how the complexity of MaxCDP and MaxCDDP on graphs depends on some strong structural properties: distance bounded by a constant from disjoint paths and graph \(G^{-t}\) being a tree. The distance to disjoint paths is the minimum number of vertices to remove to make the graph a set of disjoint paths. The MaxCDP problem on a set of disjoint paths is trivially polynomial time solvable. Thus it is natural to consider the complexity of MaxCDP and MaxCDDP on graphs that are at small distance from this parameter.

First, we consider the MaxCDDP problem and we show that MaxCDDP is in P when the graph induced by the set \(V \setminus \{t\}\) is a tree, while it is NP-hard for graphs at distance two from disjoint paths.

3.1 MaxCDDP on trees

We now show that MaxCDDP is polynomial time solvable when the input graph \(G^{-t}\) is a tree. Notice that MaxCDP when \(G^{-t}\) is a tree is trivially solvable in polynomial time.

Theorem 2

Given an input graph G, MaxCDDP is in P when \(G^{-t}\) is a tree.

Proof

Consider the tree \(G^{-t}\) rooted at s and let \(N(s)= \{v_1, \dots , v_p\}\). Now, define a bipartite graph \(G_B= (V_B, E_B)\) consisting of vertices:

$$\begin{aligned} V_B= \{v_i : \{s,y_i\} \in E \} \cup \{ v'_i : c_i \in C \} \end{aligned}$$

The set \(E_B\) of edges is defined as follows:

$$\begin{aligned} E_B{=} \{ \{ v_i, v'_j\} : \hbox {there exists a uni-color path from} s \hbox {to} t \hbox {colored} c_j \hbox {that passes through} y_i \} \end{aligned}$$

We show that there exists a matching M in \(G_B\) of size h if and only if there exists a solution of MaxCDDP in \(G^{-t}\) consisting of h paths.

Consider a matching M in \(G_B\) consisting of h edges. Construct a set P of h paths in G as follows: if \(\{ v_i, v'_j\} \in M\) then add in P the path colored \(c_j\) from s to t that passes through \(y_i\). First, notice that since the \(G^{-t}\) is a tree, the paths associated with edges of the matching are disjoint, as by construction there exists at most one path that passes through a node \(y_i \in N(s)\). Next, we show that P is a set of color disjoint paths. By construction each edge of M can be incident in at most one vertex \(v'_j\). Then there exists at most one path in P having color \(c_j\), hence P is a set of color disjoint paths.

Consider a set P of h uni-color and color disjoint paths that is a solution of MaxCDDP. We compute a matching M of \(G_B\) as follows: given a path \(\pi \) of P colored \(c_j\) that passes through \(y_i\), add the edge \(\{ v_i, v'_j\}\) to M. Next, we show that M is a matching of M (obviously M consists of h edges). Since the paths in P are color disjoint, the following properties hold: (1) for each \(v_i \in V_B\), there exists at most one edge of M incident in \(v_i\), since \(G^{-t}\) is a tree, hence there exists at most one path that passes through \(y_i\); (2) for each \(v'_j \in V_B\), there exists at most one edge of M incident in \(v'_j\), since the paths in P are color disjoint, hence there exists at most one path in P colored \(c_j\).

Therefore, it follows that an optimal solution P of MaxCDDP can be computed by first finding a maximum matching M of \(G_B\) and then assigning to P those paths whose corresponding edges belong to M. \(\square \)

3.2 Complexity of MaxCDDP on graphs at distance two from disjoint paths

In this section, we show that if the input graph G has distance two from a set of disjoint paths, then MaxCDDP is NP-hard.

We give a reduction from Maximum Independent Set on Cubic graphs (MaxISC). We recall that a graph is cubic when each of its vertices has degree 3. Moreover, we give the definition of the MaxISC problem:

figure c

In this section we give a polynomial reduction from MaxISC to MaxCDDP. We build a graph \(G=(V,E,f_C)\) (input of MaxCDDP) from \(G_I=(V_I,E_I)\), by defining a gadget \(GV_i\) for each vertex \(v_i \in V_I\), and connecting the gadget to vertices s and t.

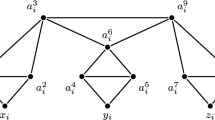
Given \(v_i \in V_I\), define a gadget \(GV_i\) consisting of a set \(V_i\) of 4 vertices (see Fig. 1):

$$\begin{aligned} V_i = \{ v'_i, v'_{i,j}: v_i \in V_I, 1 \leqslant j \leqslant 3 \} \end{aligned}$$

Moreover, define the set C of colors as follows:

$$\begin{aligned} C = \{ c_i : v_i \in V_I \} \cup \{ c_{i,j}: \{ v_i,v_j \} \in E_I \} \end{aligned}$$

We assume that, given a vertex \(v_i\), the vertices adjacent to \(v_i\) (that is the vertices in \(N(v_i)\)) are ordered, i.e. if \(v_j,v_h,v_z \in N(v_i)\) with \(1 \leqslant j \leqslant h \leqslant z\), then \(v_j\) is the first vertex adjacent to \(v_i\), \(v_h\) is the second and \(v_z\) is the third.

We define the edges of G and their colors by means of the following colored paths:

  • a path colored \(c_i\) that consists of s, \(v'_i\), \(v'_{i,1}\), \(v'_{i,2}\), \(v'_{i,3}\), t, with \(1 \leqslant i \leqslant |V_I|\)

  • if, according to the ordering, \(v_j\) is the p-th vertex incident on \(v_i\), \(1 \leqslant p \leqslant 3\), then there exists a path colored \(c_{i,j}\) that passes through s, \(v'_{i,p}\), t

Fig. 1
figure 1

Gadget \(GV_i\) associated with vertex \(v_i \in V_I\). Vertices \(v_j\), \(v_h\), \(v_z\) are three vertices of \(V_I\), with \(N(v_i)=\{ v_j, v_h, v_z \}\) and \(j< h < z\). \(v_j\) is the first vertex adjacent to \(v_i\) in \(G_I\) and thus there exists a path in G colored by \(c_{i,j}\) that passes through s, \(v'_{i,1}\), t; \(v_h\) is the second vertex adjacent to \(v_i\) in \(G_I\) (hence there exists a path in G colored by \(c_{i,h}\) that passes through s, \(v'_{i,2}\), t); \(v_z\) is the third vertex adjacent to \(v_i\) in \(G_I\) (hence there exists a path in G colored by \(c_{i,z}\) that passes through s, \(v'_{i,3}\), t)

Full size image

First, we prove that the graph G has indeed the desired property, that is it has distance two from disjoint paths.

Lemma 3

Given a cubic graph \(G_I\), let G be the corresponding graph input of MaxCDDP. Then G is at distance two from disjoint paths.

Proof

After the removal of s and t, the paths left in the resulting graph are the paths colored by \(c_i\), with \(1 \leqslant i \leqslant |V_I|\), that pass through \(v'_i\), \(v'_{i,1}\), \(v'_{i,2}\), \(v'_{i,3}\). Since these paths are pairwise vertex disjoint, the lemma holds. \(\square \)

Next, we prove the main results of the reduction.

Lemma 4

Let \(G_I\) be a cubic graph and G be the corresponding graph input of MaxCDDP. Given an independent set \(V'_I\) of \(G_I\), we can compute in polynomial time \(|E|+|V'_I|\) disjoint uni-color color paths in G.

Proof

Consider an independent set \(V'_I \subseteq V_I\) of \(G_I\), we define a set \({\mathcal {P}}\) of uni-color disjoint paths as follows:

  • for each \(v_i \in V'_I\), \({\mathcal {P}}\) contains a path \(s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t\) colored by \(c_i\)

  • for each \( \{ v_i,v_j \} \in E_I\), there exists at least one of \(v_i\), \(v_j\) in \(V_I \setminus V'_I\), we pick one of \(v_i\), \(v_j\) in \(V_I \setminus V'_I\), assume w.l.o.g. that \(v_i \in V_I \setminus V'_I\) and that \(v_j\) is the h-th vertex, \(1 \leqslant h \leqslant 3\), adjacent to \(v_i\), then \({\mathcal {P}}\) contains the path \(s, v'_{i,h}, t\) colored by \(c_{i,j}\).

Since \(V'_I\) is an independent set, there exists at most one path colored by \(c_i\) in \({\mathcal {P}}\). Moreover, notice that by construction, for each \( \{ v_i,v_j \} \in E_I\), there exists exactly one path colored by \(c_{i,j}\) in \({\mathcal {P}}\). Thus, in order to prove that \({\mathcal {P}}\) is color disjoint, we have to prove that the paths in \({\mathcal {P}}\) are internally disjoint. Indeed, since \(V'_I\) is an independent set, a path colored by \(c_i\) is the only path that passes though vertices \(s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t\). Furthermore, consider a path \(\pi \) colored by \(c_{i,j}\). Then \(\pi \) passes through vertices s, \(v'_{i,h}\), t, where \(v_i \notin V'_I\), and by construction there is no other path that passes through \(v'_{i,h}\).

\(\square \)

Lemma 5

Let \(G_I\) be a cubic graph and G be the corresponding graph input of MaxCDDP. Given \(|E|+t\) color disjoint uni-color paths in G, we can compute in polynomial time an independent set of size t for \(G_I\).

Proof

Consider a solution \({\mathcal {P}}\) of the instance of MaxCDDP consisting of \(|E|+t\) color disjoint uni-color paths. First, we show that we can assume that \({\mathcal {P}}\) contains, for each color \(c_{i,j}\), a path colored by \(c_{i,j}\). Assume this is not the case. Then, we can replace a path colored by \(c_i\) with a path \(p'\) colored by \(c_{i,j}\) that passes through the vertices of gadget \(VG_i\), without decreasing the number of path in \({\mathcal {P}}\). Indeed, by the property of \(G_I\), there exists only two uni-color paths that passes through vertex \(v'_{i,h}\), with \(1 \leqslant h \leqslant 3\), where \(\{ v_i,v_j \}\) is the h-th edge incident on \(v_i\): a path colored by \(c_i\) that passes through \(s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t\) and a path \(s, v'_{i,h}, t\) colored by \(c_{i,j}\). Hence by replacing a path color \(c_i\) with \(p'\), the set \({\mathcal {P}}\) \(|E|+t\) color disjoint uni-color paths.

Now, starting from \({\mathcal {P}}\), we can compute an independent set \(V'_I\) as follows. If \({\mathcal {P}}\) contains a path \(s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t\) colored by \(c_i\), then \(v_i \in V'_I\). Notice that \(V'_I\) is an independent set, since, if \(v_i\), \(v_j\), with \(\{ v_i,v_j \} \in E\), are both in \(V'_I\), this implies that there is no path colored by \(c_{i,j}\) in \({\mathcal {P}}\), contradicting our assumption. \(\square \)

Hence, we can prove the NP-hardness of MaxCDDP on graphs at distance two from disjoint paths.

Theorem 6

MaxCDDP is NP-hard, even if the graph G has distance two from disjoint paths.

Proof

MaxISC is NP-hard Alimonti and Kann (2000).

Hence Lemmas 3, 4 and 5 imply that MaxCDDP is NP-hard, even if the graph G has distance two from disjoint paths. \(\square \)

The previous result implies that MaxCDDP cannot be solved in \(n^{f(d)}\) time unless P=NP (it is not in the class XP), where d is the distance to disjoint paths of G, but also for “stronger” parameters like pathwidth or treewidth (Komusiewicz 2012).

Corollary 7

MaxCDDP is NP-hard, even if the input graph G has pathwidth and treewidth bounded by 2.

3.3 A polynomial-time algorithm for MaxCDP on graphs at constant distance from disjoint paths

In this section, we show that, contrary to MaxCDDP, MaxCDP is polynomial-time solvable when the input graph G has distance bounded by a constant d from a set \({\mathcal {P}}\) of disjoint paths (that is, it is in the class XP for the parameter distance to disjoint paths).

Next, we present the algorithm. Notice that we assume that a set \(X \subseteq V\) is given, such that after the removal of \(X \cup \{s,t\}\) the resulting graph consists of a set \({\mathcal {P}}\) of disjoint paths.Footnote 1 We assume that X and \({\mathcal {P}}\) are defined so that \(s,t \notin X\) and that no path in \({\mathcal {P}}\) contains s and t. Denote by \(V({\mathcal {P}})\) the set of vertices that belong to a path of \({\mathcal {P}}\), it holds \(V= V({\mathcal {P}}) \cup X \cup \{s,t\}\).

Since G has distance d, where \(d>0\) is constant, from the set of disjoint paths \({\mathcal {P}}\), it follows that \(|X|\leqslant d\). Let \(\mathcal {P'} = \{p_1, \dots , p_b \}\), with \(1 \leqslant i \leqslant b \leqslant d\), such that \(V(\mathcal {P'}) \subseteq V\) is the set of paths of an optimal solution of MaxCDP such that \(p_i\) contains a non-empty subset of X.

The algorithm computes each \(p_i\), with \(1 \leqslant i \leqslant b\), by iterating through subpaths of size at most d in \({\mathcal {P}}\) and a subset of X. More precisely, \(p_i\) is computed as follows. Each path \(p_i\) contains at most \(d+1\) disjoint subpaths that belong to paths in \({\mathcal {P}}\), that are connected through a subset of at most d vertices of X. In time \(O(n^{2(d+1)})\), we compute the at most \(d+1\) disjoint subpaths \(p_x[j_1,j_2]\) of \(P_x \in {\mathcal {P}}\) that belong to \(p_i\); in time \(O(2^d)\) we compute the subset \(X_i \subseteq X\) that belong to each \(p_i\). Let \(V_i=V(p_i) \cup X_i\), that is the set of vertices that belong to \(p_i\) and to subset \(X_i\). Notice that the subsets \(V_i\), with \(1 \leqslant i \leqslant b\), are computed so that they are pairwise disjoint.

The algorithm computes in polynomial time if there exists a uni-color path from s to t that passes through the vertices \(V_i\). If for each i with \(1 \leqslant i \leqslant b\) such a path exists, then the algorithm computes the maximum number of uni-color disjoint paths in the subgraph \(G'\) of G induced by \(V' = V \setminus \bigcup _{i=1}^{b} V_i\). Notice that, since \(V' \cap X = \emptyset \), it follows that, if we remove s and t from \(V'\), \(G'\) consists of a set of disjoint paths \(\{p'_1, \dots , p'_r\}\). The maximum number of uni-color disjoint paths in the subgraph \(G'\) can be computed in polynomial time, as shown in the following lemma.

Lemma 8

Let \(G=(V,E,f_c)\) be an edge colored graph such that \(V^* = V \setminus \{ s,t \}\) induces a set of disjoint paths. Then MaxCDP on G can be solved in polynomial time.

Proof

Let \(P = \{ p'_1, \dots , p'_r \}\) be the set of disjoint paths induced by \(V^*\). Since there is no st-path in G containing a vertex of \(p'_i\) and a vertex of \(p'_j\), with \(i \ne j\), we compute a solution of MaxCDP independently on each path \(p'_i\). Let \({\mathcal {P}}_i\) be the set of uni-color st-paths that contains only vertices of \(p'_i\). For each i with \(1 \leqslant i \leqslant r\), we compute a shortest uni-color st-path p that contains only vertices of \(p'_i\), we add it to \({\mathcal {P}}_i\), and we remove the vertices of p from \(p'_i\). We iterate this procedure, until there exists no st-path that contains only vertices of \(p'_i\).

We claim that \({\mathcal {P}}_i\) is a set of uni-color st-paths of maximum size. Consider a shortest path p added to \({\mathcal {P}}_i\). Let x be the vertex of p adjacent to s and y be the vertex of p adjacent to t. Notice that each vertex in p, except for x and y, is not connected to s or t, otherwise p would not be a shortest path between s and t. Now, assume that there is an optimal solution \({\mathcal {Q}}\) of MaxCDP that does not contain p and that, moreover, contains an st-path that passes through some vertex of p, otherwise we can add p to \({\mathcal {Q}}\) and \({\mathcal {Q}}\) would not be optimal. Then by construction, since P is a set of disjoint paths, \({\mathcal {Q}}\) must contain a path \(p'\) that contains p as a subpath. But then we can replace \(p'\) with p in \({\mathcal {Q}}\), without decreasing the size of the optimal solution. \(\square \)

Now, we give the main result of this section.

Theorem 9

MaxCDP is in XP when the distance to disjoint paths is bounded by a constant.

Proof

Notice that for each i with \(1 \leqslant i \leqslant b \leqslant d\), we compute the set \(V_i\) in time \(O(2^d n^{2(d+1)})\); hence the d disjoint sets \(V_1,\dots , V_b\) are computed in time \(O(2^{d^2} n^{2d(d+1)})\). Since the existence of a uni-color path that passes through the vertices \(V_i\) can be computed in polynomial time and since by Lemma 8 we compute in polynomial time the maximum number of uni-color disjoint paths in the subgraph \(G'\), the theorem holds. \(\square \)

4 FPT algorithms parameterized by vertex cover

In this section we consider the parameterized complexity of MaxCDP and MaxCDDP when parameterized by the size of the vertex cover of the input graph. First, we show that MaxCDP is FPT when parameterized by the size of the vertex cover of the input graph. Then, we show that MaxCDDP can be approximated within factor a \(\frac{1}{2}\) by a parameterized algorithm, when parameterized by the size of the vertex cover of the input graph. We start by describing a simple algorithm for MaxCDP when parameterized by the size of the vertex cover of the input graph.

Theorem 10

MaxCDP is in FPT when parameterized by the size of the vertex cover of the input graph.

Proof

We give a constructive proof, by giving a fixed-parameter tractable algorithm for MaxCDP when parameterized by the size of the vertex cover of the input graph. The algorithm first considers uni-color paths of length three s, v, t, for some \(v \in V\). Uni-color path of length three are greedily added to a solution of MaxCDP. Since any solution of MaxCDP contains at most one uni-color path that passes through vertex v, it follows that there exists an optimal solution of MaxCDP that contains path s, v, t. Hence, the fixed-parameter tractable algorithm adds such path to our solution \({\mathcal {P}}\), and it removes vertex v from G. Let \(G'=(V',E',f'_C)\) be the graph after the removal of vertices.

Let \(V_C\) be a vertex cover of the resulting graph \(G'=(V',E',f_C)\), \(|V_C|=k\) (which can be computed in FPT-time). Since in G there is no uni-color path of length three connecting s and t, the following property holds. Consider a uni-color path p of G, then p either consists of vertices in \(V_C\) or each vertex of \(V' \setminus V_C\) that belongs to p is adjacent in p to vertices of \(V_C \cup \{ s \} \cup \{ t \}\). This is true since \(V_C\) is a vertex cover (and thus \(V' \setminus V_C\) is an independent set in G).

A consequence of this property is that each uni-color path in \(G'=(V',E',f'_C)\) has length at most 2k. Moreover, there can be at most k uni-color paths in a solution of MaxCDP on instance \(G'=(V',E',f'_C)\), since each path must contain a vertex of \(V_C\) and \(|V_C| \leqslant k\). Since both the number of paths and the length of paths are bounded by k and MaxCDP is known to be in FPT w.r.t. the combination of these two parameters (Bonizzoni et al. 2013), the claimed result follows. \(\square \)

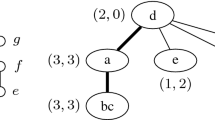
The main difference between MaxCDDP and MaxCDP, when considering as parameter the vertex cover of the input graph, is that in the latter we can safely add a uni-color path s, v, t of length three to a solution, while in the former we are not allowed to do it. Consider for example the uni-color path s, v, t of length three colored by c; if this path belongs to a solution of MaxCDDP, it prevents any other uni-color path \(p'\) that passes through v (colored by some color \(c'\)), but also any path \(p''\) colored by c (that does not pass through v) to be part of the solution. So, by adding the path s, v, t to the solution we are computing, we may get a suboptimal solution, since by removing p and by adding \(p'\) and \(p''\), we possibly compute a larger set of disjoint color uni-color paths (see Fig. 2 for an illustration).

Fig. 2
figure 2

An example where adding first the red (dark gray) path s, v, t avoids the better solution with two paths: s, v, t colored green (light gray) and s, u, t colored red (dark gray)

Full size image

On the other side, we show next that the algorithm described in Theorem 10 returns a solution consisting of at least half of the paths in an optimal solution of MaxCDDP. The existence of an exact parameterized algorithm with respect to the size of the vertex cover of the input graph for MaxCDDP remains however open.

Theorem 11

MaxCDDP admits an approximation fixed-parameter algorithm parameterized by the size of the vertex cover of the input graph of factor \(\frac{1}{2}\).

Proof

As in Theorem 10 we give a constructive proof. We will show that there exists a fixed-parameter algorithm, parameterized by the size of the vertex cover of the input graph, that returns a set \({\mathcal {P}}\) of color disjoint paths of the input graph \(G=(V,E,f_C)\) such that, given an optimal solution OPT of MaxCDDP on instance \(G=(V,E,f_C)\), it holds that \(|{\mathcal {P}}| \geqslant \frac{1}{2}|OPT|\).

As for the algorithm of Theorem 10, the fixed-parameter algorithm first considers uni-color paths of length three s, v, t, for some \(v \in V\). First, the fixed-parameter algorithm defines a set \(APPROX_A\) of color disjoint uni-color paths of length three, by greedily adding uni-color paths of length three to \(APPROX_A\). Define the set of colors

$$\begin{aligned} C'= \{c: \hbox { there exists a path in} APPROX_A \hbox {colored by} c \} \end{aligned}$$

Now, the algorithm constructs an instance of MaxCDDP as follows. First, define the set \(C_H\) of remaining colors: \(C_H=C \setminus C'\). Now, let \(H=(V_H,E_H,f'_C)\) be the subgraph of G obtained from \(G=(V,E,f_C)\) as follows:

Step 1:

Remove the vertices in \(V \setminus \{s,t\}\) that induce paths in \(APPROX_A\) and all the edges having a color in \(C'\).

Step 2:

Remove the vertices that, after Step 1, do not belong to a uni-color path from s to t colored by some \(c \in C_H\).

Similarly to Theorem 10, we compute (in FPT-time) a vertex cover \(V_C\) of H, with \(|V_C|=k\). Our algorithm computes a maximum cardinality set \(APPROX_H\) of color disjoint paths in \(H=(V_H,E_H,f'_C)\) having a color in \(C_H\). We will next show that this is possible in FPT time, where the parameter is \(k=|V_C|\), the size of the vertex cover of H. Notice that there is no uni-color path s, v, t of length 3 in H with color in \(C_H\), otherwise it would have been added to \(APPROX_A\). Let u be a vertex of \(V_H\). Since there is no uni-color path of length three that connects s and t, either \(u \in V_C\) or u is adjacent to at least one vertex of \(V_C\). It follows that each uni-color path in H has length at most 2k. Moreover, there can be at most k color disjoint uni-color paths in a solution of MaxCDDP on instance \(H=(V_H,E_H,f'_C)\), since each path must contain a vertex of \(V_C\) and \(|V_C| = k\). Since both the number of paths and the length of paths are bounded by k and MaxCDDP is shown to be in FPT with respect to the combination of these two parameters (see Sect. 5), we can compute in FPT time, where the parameter is the size of the vertex cover of H, a maximum cardinality set \(APPROX_H\) of color disjoint paths in \(H=(V_H,E_H,f'_C)\).

The algorithm returns the solution \(APPROX=APPROX_A \cup APPROX_H\). Notice that by construction APPROX is a set of color disjoint paths of G. Next, we show that |APPROX| is at least \(\frac{1}{2}|OPT|\), where OPT is an optimal solution of MaxCDDP on instance G.

We partition OPT in two subsets \(OPT_A\) and \(OPT_H\) as follows: let \(OPT_A\) be the set of uni-color paths that either contain a vertex not in \(V_H\) or have a color not in \(C_H\); let \(OPT_H = OPT \setminus OPT_A\). Clearly it holds \(|APPROX_H| \geqslant |OPT_H|\), as each uni-color path in \(OPT_H\) is a uni-color path of H and \(APPROX_H\) is a maximum cardinality set of color disjoint paths in H.

Consider now a uni-color path p of \(OPT_A\). If p is colored by \(c \in C'\), then by construction of \(C'\) there exists a uni-color path, colored by c, in \(APPROX_A\). Hence, assume that p is colored by \(c \notin C'\). Next, we show that p must contain a vertex in \(u \in V \setminus V_H\), such that there exists a uni-color path in \(APPROX_A\) that contains u. Assume that this is not the case. Recall that if p contains a vertex v in \(V \setminus V_H\), then v is removed in the construction of graph H. Hence, in G, there is no path having color in \(C_H\) that passes through v, otherwise it would not have been removed from G in the construction of H, and thus p would have been in \(OPT_H\).

It follows that, for each path in \(APPROX_A\), \(OPT_A\) contains at most two color disjoint uni-color paths. Indeed, consider a path s, v, t in \(OPT_A\), for some \(v \in V \setminus V_H\), colored by c, for some \(c \in C'\). Since \(OPT_A\) is a set of color disjoint paths, \(OPT_A\) contains at most one path colored by c and at most one path that passes through v (recall that \(APPROX_H\) contains only paths of length 3). Thus \(|OPT_A| \leqslant 2 |APPROX_A|\). Since \(|OPT_H| \leqslant |APPROX_H|\), it follows that \(|OPT| \leqslant 2 |APPROX|\). \(\square \)

5 A fixed-parameter algorithm for l-MaxCDDP

In this section, we give a fixed-parameter algorithm for l-MaxCDDP, the length-bounded version of MaxCDDP, parameterized by the number k of uni-color color disjoint st-paths of a solution. Notice that MaxCDDP is W[1]-hard when parameterized by k, as the reduction that prove the W[1]-hardness of MaxCDP parameterized by k consists of paths having distinct colors (Bonizzoni et al. 2013).

Next, we present a parameterized algorithm based on the color coding technique (Alon et al. 1995). The algorithm is inspired by the one for MaxCDP (Bonizzoni et al. 2013). However, in this case we must combine two different labelings, one to label the vertices that belong to a uni-color path, one to label the color associated with a uni-color path of MaxCDDP.

First, we introduce the definition of perfect hash function on which our algorithm is based. A family F of hash functions from a set U (the vertex set in the traditional applications of color coding) to the set \(\{l_1, \ldots , l_k\}\) of labels is k-perfect if, for each subset \(U'\) of U with \(|U'| = k\), there exists a hash function \(f \in F\) such that f assigns a distinct label to each element of \(U'\). Function f is called a labelling function.

Let \(f_v \in F_V\) be a labelling function that assigns to each vertex \(v \in V \setminus \{ s,t \}\) a label \(f_v(v) \in L_v=\{ 1_v, \dots , h_v \}\), where \(h_v=|L_v| \leqslant l k\).

Consider a second labelling function \(f_c \in F_C\) that assigns to each color \(c \in C\) a label \(f_c(v) \in L_c=\{ 1_c, \dots , h_c \}\), where \(h_c=|L_c| \leqslant k\).

By the property of perfect hash functions, we assume that each vertex that belongs to a solution of MaxCDDP is assigned a distinct label by \(f_v\) and that each color d, such that there exists a uni-color path of MaxCDDP colored by d, is associated with distinct label \(f_c\).

A simple path p in G is perfect for a set \(L_v\) of labels assigned to V if and only if for each vertex v of p, with \(v \notin \{s,t\}\), \(f_v(v) \in L_v\), and for each pair of distinct vertices u, v of p, \(f_v(u) \ne f_v(v)\). A set \(\{ p_1, \ldots , p_k \}\) of uni-color paths is perfect for the set \(L_v\) and \(L_c\) of labels if and only if: (1) there exists a partition \(\{ L_{v,1}, \ldots , L_{v,k} \}\) of \(L_v\) such that each \(p_i\) is perfect for \(L_i\); (2) each path \(p_i\), with \(1 \leqslant i \leqslant k\), is colored by \(c \in C\) associated with a distinct label in \(L_c\). We combine two dynamic-programming recurrences to compute, given the labelling functions \(f_v\) and \(f_c\), whether there exists a set of perfect uni-color paths in G.

First, consider the function \(S[L'_v, u, \lambda ]\), with \(L'_v \subseteq L_v\), \(u \in V\) and \(\lambda \in C\). \(S[L'_v, u, \lambda ]=1\) if and only if there exists a path from s to vertex \(u\ne t\), such that the path is perfect for \(L'_v\) and p is colored by \(\lambda \).

We consider a second function \(\Pi [L'_v, M,z] \), with \(L'_v \subseteq L_v\) and \(M \subseteq L_c\), \(0 \leqslant z \leqslant k\). \(\Pi [L'_v, M,z] =1\) if and only if there exist a set of labels \(L'_v \subseteq L_v\) and a set of labels \(M \subseteq L_c\), such that there exists a set of z uni-color paths perfect for \(L'_v\) and M.

\(S[L'_v, u, \lambda ]\) is defined as follows (we recall that \(\uplus \) represents the disjoint union operator). In the base case, when \(u=s\), \(S[L'_v, u, \lambda ] = 1\) if \(L'_v= \emptyset \), otherwise (when \(L'_v \ne \emptyset \)), \(S[L'_v, u, \lambda ] = 0\).

When \(u \ne s\):

$$\begin{aligned} S[L'_v, u, \lambda ] = \max _{w \in N(u)} \big \{ S[L''_v, w, \lambda ] \mid L'_v = L''_v \uplus \{f_v(u)\} \wedge \{w,u\} \hbox { is colored by}\ \lambda \} \end{aligned}$$

Next, we give the recurrence, \(\Pi [L'_v,M,z]\). In the base case, that is when \(z=0\), then \(\Pi [L'_v,M,0]=1\) if \(L'_v = \emptyset \) and \(M = \emptyset \), else \(\Pi [L'_v,M,0]=0\).

Recall that l is the bound on the length of each path, \(L'_v \subseteq L_v\), \(M \subseteq C\) and \(0 \leqslant z \leqslant k\), \(\Pi [L'_v,M,z]\) is defined as follows:

$$\begin{aligned} \Pi [L'_v,M,z] = {\left\{ \begin{array}{ll} \begin{aligned} \!\max \big \{ &{}\Pi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1] \ \wedge \ S[L^*_v, u, \lambda ] \mid \\ &{} L'_v = L''_v \uplus L^*_v \wedge \ |L^*| \leqslant l-1 \ \wedge \ \lambda \in C \wedge f_c(\lambda ) \in M \ \wedge \ \\ &{} \hbox {} \{u, t\}\in E \hbox {is colored by} \lambda \big \} \end{aligned} &{} \end{array}\right. } \end{aligned}$$
(1)

Next, we prove the correctness of the two recurrences. We start by proving the correctness of the recurrence for \(S[L'_v, u, \lambda ]\).

Lemma 12

Given a labelling \(f_v\) of the vertices of G, a color \(\lambda \in C\), a vertex u and a set \(L'_v \subseteq L_v\), there exists a simple path p in G from s to u perfect for \(L'_v\) if and only if \(S[L'_v, u, \lambda ]=1\).

Proof

We prove the lemma by induction on the length of the path p. First, we consider the base case, that is \(u=s\). Since s is not associated with a label in \(L_v\), it holds \(S[L'_v, u, \lambda ]=1\) if and only if \(L'_v= \emptyset \).

Consider now the general case and assume that there exists a path p in G perfect for \(L'_v\) such that p is colored by \(\lambda \). Consider the last vertex u of p, and let w be the vertex adjacent to u in p. By induction hypothesis, it follows that \(S[L''_v, w, \lambda ]=1\), where \(L'_v=L''_v \uplus \{f_v(u) \}\). By the definition of the recurrence, then \(S[L'_v, u, \lambda ]=1\).

Assume that \(S[L'_v, u, \lambda ]=1\). By the definition of the recurrence it holds that \(S[L''_v, w, \lambda ]=1\), where \(L'_v=L''_v \uplus \{f_v(u) \}\) and there is an edge \(\{ u,w \} \in E\) colored by \(\lambda \). By induction hypothesis, since \(S[L''_v, w, \lambda ]=1\), there exists a path \(p'\) from s to w perfect for \(L''_v\) such that \(p'\) is colored by \(\lambda \). Since \(\{ u,w \} \in E\) is colored by \(\lambda \), it follows that there exists a simple path p in G from s to u perfect for \(L'_v\). \(\square \)

Now, we prove the correctness of the recurrence for \(\Pi [L'_v,M,z]\).

Lemma 13

Given a labelling \(f_v\) of the vertices of G and a labelling \(f_c\) of the set C of colors, a set \(L'_v \subseteq L_v\), a set \(M \subseteq L_c\), and integer z with \(0 \leqslant z \leqslant k\), there exists a set \(\{ p_1, \ldots , p_z \}\) of uni-color paths which is perfect for \(L'_v\) and M if and only if \(\Pi [L'_v,M,z]=1\).

Proof

We prove the lemma by induction on the number of uni-color paths. First, we consider the base case, that is \(z=0\). Then there is no uni-color path perfect for \(L'_v = \emptyset \) and \(M= \emptyset \) if and only if \(\Pi [\emptyset ,\emptyset ,0]=1\).

Consider now that there exist z disjoint color uni-color paths. Consider one of such paths, denoted by p, which is colored by \(\lambda \) and whose vertices are associated with set of labels \(L^*_v\) and such that the vertex of p adjacent to t is u, hence \(\{ u,t \} \in E\) is colored by \(\lambda \). Then, by Lemma 12 \(S[L^*_v, u, \lambda ]=1\). Moreover, by induction hypothesis it holds \(\Pi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1\), where \(L'_v = L^*_v \uplus L''_v\) and \(f_c(\lambda ) \in M\). Hence, by the definition of the recurrence for \(\Pi \), it holds \(\Pi [L'_v,M,z]=1\).

Consider the case that \(\Pi [L'_v,M,z]=1\). By the definition of function \(\Pi \), it follows that there exists a color \(\lambda \in C\), with \(f_c(\lambda ) \in M\), and a set of labels \(L^*_v \subseteq L_v\), such that \(\Pi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1 \), where \(L'_v = L''_v \uplus L^*_v \), and \(S[L^*_v, u, \lambda ]=1\). By induction hypothesis, since \(\Pi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1 \), there exists a set \(P'\) of \(z-1\) paths perfect for the sets \(L''_V\) and \(M \setminus \{ f_c(\lambda ) \}\). By Lemma 12 there exists a path \(p'\) from s to u colorful for \(L''_v\) and that has color \(\lambda \). Moreover, since \(\Pi [L'_v,M,z]=1\), \(\{ u,t \} \in E\) is colored by \(\lambda \). By the property of labelling \(f_c\), no path of \(P'\) has label \(f_c(\lambda )\), hence \(P' \cup p\) is perfect for \(L'_v\) and M. \(\square \)

We can now state the main result.

Theorem 14

l-MaxCDDP can be solved in time \(2^{O(l k)}poly(n)\).

Proof

An optimal solution of l-MaxCDDP consisting of k color disjoint paths exists if and only if \(\Pi [L_v,M,k]=1\). The correctness of the recurrence to compute \(\Pi \) follows from Lemma 13. Now, we discuss the time complexity to compute \(\Pi [L'_v,M,z]\) and \(S[L'_v, u, \lambda ]\). First, consider \(S[L'_v, u, \lambda ]\). It consists of \(2^{l k} n q\) entries and each entry can be computed in time O(n), as we consider each vertex \(w \in N(u)\).

Now, consider \(\Pi [L'_v,M,z]\). It consists of \(2^{k(l+1)} k\) entries. In order to compute \(\Pi [L'_v,M,z]\), at most \(2^{kl} k\) entries must be considered, since \(\Pi [L^*_v,M\setminus \{f_c(v)\},z-1]\) is considered, where we have \(2^{kl}\) subsets \(L^*_v \subseteq L'_v\) and k labels \(f_c(v)\). Given two labelling functions \(f_v\) and \(f_c\), the time complexity to compute the entries \(\Pi [L'_v,M,z]\) is \(O(2^{k(2l+1)} k n)\). By the property of color-coding (Alon et al. 1995), a function \(f_v \in F_v\) and a function \(f_v \in F_v \) can be computed in time \(2^{O(l k)}poly(n)\) and \(2^{O(k)}poly(n)\), respectively, hence in time \(2^{O(l k)}poly(n)\) . \(\square \)

6 FPT inapproximation

Since MaxCDP and MaxCDDP are hard to approximate in poly-time and do not admit fixed-parameterized algorithm for parameter number of paths, it is worth to investigate approximation in FPT time, i.e. find approximate solution with additional time. Unfortunately, in this section, we show that both MaxCDP and MaxCDDP do not admit an FPT cost \(\rho \)-approximation, for any function \(\rho \) of the optimum, unless FPT=W[1]. We will show the result by giving a reduction from the Threshold Set problem. Marx showed that the Threshold Set problem does not admit a fpt cost \(\rho \)-approximation, for any function \(\rho \) of the optimum, unless FPT=W[1] (Marx 2013).

First, we introduce the definition of the Threshold Set problem.

figure d

The cost of a solution of Threshold Set is denoted by |T|. Notice that this problem can be seen as a generalization of the Independent Set problem; indeed, for a graph \(G=(V,E)\), we can define \(U = V\), \({\mathcal {S}}= E\) and \(w(S) = 1\) for every set \(S \in {\mathcal {S}}\).

We will reduce Threshold Set to MaxCDP in polynomial time such that there is a “one-to-one” correspondence between the solutions of the two problems, therefore the inapproximability result transfers to MaxCDP, and then to MaxCDDP. The reduction is inspired by the one in Bonizzoni et al. (2013), that shows inapproximability in polynomial time and W[1]-hardness of MaxCDP.

First, we design the reduction for the MaxCDP problem. Notice that we assume that we are given an ordering over the sets in \({\mathcal {S}}\) (i.e. \(S_i< S_j, i<j\)). Consider an instance \((U,{\mathcal {S}},w)\) of Threshold Set, we define a corresponding instance \((G=(V,E,f_C), s, t)\) of MaxCDP. The set V of vertices is defined as follows:

$$\begin{aligned} V = \{s, t\} \cup \{ s_i | i \in [|U|]\} \cup \left\{ S_i^j | i \in \left[ |{\mathcal {S}}|\right] , 1 \leqslant j \leqslant w(S_i) \right\} \end{aligned}$$

The set of colors C is defined as follows: \(C=\{ c_i: i \in U \}\).

Now, we define the set E of edges.

  • for all \(i \in [|U|]\), define an edge \(\{s,s_i \}\) colored by \(c_i\) and an edge \(\{s_i, S_q^j\}\) colored by \(c_i\), for all \(1 \leqslant j \leqslant w(S_q)\), where q is the smallest index of a set \(S_q \in {\mathcal {S}}\) such that \(i \in S_q\),

  • from each \(S_q^j\), define an edge \(\{ S_q^j, S_{q'}^{j'}\}\) colored by \(c_i\), for all \(1 \leqslant j' \leqslant w(S_{q'})\), such that \(i \in S_q\), \(i \in S_{q'}\), \(q' > q\) and, for each \(q<l<q'\), it holds \(i \notin S_l\),

  • from each \(S_q^j\), define an edge \(\{ S_q^j,t \}\) colored by \(c_i\), where \(i \in S_q\) and for each \(q' > q\) with \(S_{q'} \in {\mathcal {S}}\), \(i \notin S_{q'}\).

See Fig. 3 for an example. Now, we prove the main properties of the reduction.

Fig. 3
figure 3

Sample construction of an instance of MaxCDP from an instance of Threshold Set with \({\mathcal {S}}= \{\{1,2,3\}, \{1,4\}, \{2,3,4\} \}, w(S_1) = 2, w(S_2)=1, w(S_3)=2\). A solution for this instance of Threshold Set could be \(T' = \{1,2\}\), and we drawn with dark edges the corresponding disjoint paths for MaxCDP

Full size image

Lemma 15

Given an instance \((U,{\mathcal {S}},w)\) of Threshold Set, let \((G=(V,E,f_C), s, t)\) be the corresponding instance of MaxCDP. Then, given a solution \(T'\) of Threshold Set on instance \((U,{\mathcal {S}},w)\), we can compute in polynomial time a set of \(|T'|\) disjoint uni-color paths in \((G=(V,E,f_C), s, t)\).

Proof

Consider a solution \(T'\) of Threshold Set on instance \((U,{\mathcal {S}},w)\), and define a set P of \(|T'|\) disjoint uni-color paths in \((G=(V,E,f_C), s, t)\) as follows. For each \(i \in T'\), define a uni-color path p colored by \(c_i\) that starts in s, passes through \(s_i\), and for each \(S_q \in {\mathcal {S}}\), if i is the j-th element of \(T'\) in \(S_q\), \(1 \leqslant j \leqslant w(S_q)\), passes through vertex \(S_q^j\). It follows that the path defined are disjoints, as at most one element can be the j-th element of \(T'\) in \(S_q\) and \(|T' \cap S_q| \leqslant w(S_q)\). \(\square \)

Lemma 16

Given an instance \((U,{\mathcal {S}},w)\) of Threshold Set, let \((G=(V,E,f_C), s, t)\) be the corresponding instance of MaxCDP. Then, given a set of q disjoint uni-color paths in \((G=(V,E,f_C), s, t)\), we can compute in polynomial time a solution of size q of Threshold Set on instance \((U,{\mathcal {S}},w)\).

Proof

Consider a set P of disjoint uni-color paths in \((G=(V,E,f_C), s, t)\). First, we claim that each path in P has a distinct color. Indeed, the paths in P must be disjoint and, by construction, for each color \(c_i\) each path must pass trough vertex \(s_i\).

Now, starting from P, we define a solution \(T'\) of of Threshold Set on instance \((U,{\mathcal {S}},w)\). For each path \(p \in P\) colored by \(c_i\), elements \(u_i\) belongs to \(T'\). We show that \(T'\) is a a solution of Threshold Set on instance \((U,{\mathcal {S}},w)\).

Consider a set \(S_i \in {\mathcal {S}}\), then there exists a most \(w(S_i)\) elements in \(T'\). Indeed, notice that, by construction, there exists at most \(w(S_i)\) vertices \(S_i^j\), hence by construction there exist at most \(w(S_i)\) paths in P that passes through vertices of \(S_i^j\), hence at most \(w(S_i)\) elements in \(T'\) belong to \(S_i\). As a consequence \(T'\) is a feasible solution of Threshold Set on instance (U, S, w). By construction, \(|T'|=q\). \(\square \)

Theorem 17

MaxCDP and MaxCDDP cannot be approximated in FPT-time within any function \(\rho \) of the optimum, unless FPT=W[1].

Proof

The theorem holds for MaxCDP since Threshold Set cannot be approximated within any function \(\rho \) of the optimum, unless FPT=W[1] (Marx 2013), and from the properties of the polynomial time reduction proved in Lemmas 15 and 16.

For MaxCDDP, it holds from the fact that in the described reduction all the paths have a distinct color. \(\square \)

7 Conclusion

In this paper, we continued the complexity analysis of MaxCDP and deepen the hardness analysis according to the structure of the input graph. We also introduced a new variant, called MaxCDDP, asking for a solution with vertex and disjoint colors.

In the future, we would like to further deepen the analysis on the the structural complexity of MaxCDP and MaxCDDP. For example is MaxCDP in XP when the parameter if the size of the Feedback Vertex Set of the input graph? Is MaxCDP FPT when the parameter if the distance to disjoint paths of the input graph? Moreover, we have shown that MaxCDDP can be solved within a factor \(\frac{1}{2}\) by a parameterized algorithm, where the parameter is the size of the vertex cover. A natural question is whether MaxCDDP is fixed-parameter tractable when parameterized by the size of the vertex cover.

We would also like to improve the running time of our algorithms and to match them with some lower bounds under widely believed assumptions in order to have a fine-grained complexity analysis of these problems.