1 Introduction

The potential difference between the internal and the external solutions separated by a plasma membrane of living cell is called membrane potential [1,2,3,4]. Membrane theory is the central concept of electrophysiology and the Goldman–Hodgkin–Katz equation (GHK equation) is one of the most successful concepts of membrane theory [5,6,7]. The GHK equation can reproduce the experimentally observed membrane potential quantitatively. The GHK equation is founded on the premise that the transmembrane ion transport across the plasma membrane is responsible for the membrane potential generation and that the membrane permeability to the individual mobile ions governs the membrane potential behavior. Now, I came up with a naive question: What will happen to the potential behavior if the plasma membrane is impermeable to ions? Since there is no such thing as impermeable plasma membrane, we cannot experimentally see it. Although GHK equation is an electrophysiological concept, there are no rational reasons to conclude that it is applicable only to the living cell systems. The GHK equation does not contain any term that is derived only from the characteristics of living cell. Therefore, I fabricated an artificial experimental system as a model of the living cell with “impermeable” membrane and investigated the potential behavior observed in this experimental system.

In this work, I made the measurements of potential across this impermeable membrane separating two KCl solutions and subsequently performed the quantitative analysis using the GHK equation. Without the transmembrane ion transport, the membrane potential generation is unthinkable in principle according to the membrane theory, but I dared to perform the potential calculation using the GHK equation. The computed potential was in quite good agreement with the experimentally measured potential. So, the GHK equation, applicable only to the system employing the permeable membrane, provided us with the right computational potential of the system employing the impermeable membrane. Is that merely an accidental coincidence? How can we settle this issue?

For more than a half-century, Gibert Ling has advocated his electrophysiological concept, which is in conflict with the membrane theory. His theory states that the membrane potential is generated by the adsorption of mobile ions onto the adsorption sites and not by the transmembrane ion transport (hereafter we call this concept Ling’s adsorption theory) [5]. Ling’s adsorption theory has been a long-dismissed electrophysiological concept. However, it appears to be more comprehensive than the membrane theory. I previously reported that Ling’s adsorption theory could reproduce the membrane potential [8]. Why did Ling’s adsorption theory work fine, though we have had the GHK equation for decades? My theoretical analysis reached the conclusion that Ling’s adsorption theory must be the right theory as a mechanism of membrane potential generation. However, the mathematical expression of membrane potential based on the GHK equation happens to coincide with the mathematical expression of membrane potential based on Ling’s adsorption theory, although they are different concepts from each other.

In this paper, I will show step by step how I reached such conclusions, suggesting that reconsideration of long-dismissed Ling’s adsorption theory as a mechanism of membrane potential generation is warranted.

2 Artificial cell model

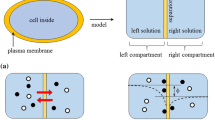
Figure 1a shows the fundamental aspects of a cell considered in the present model. The living cell is regarded as the system consisting of two solutions (internal and external solutions of the cell) separated by a semipermeable membrane (plasma membrane). Based on this view, I derived the cell model illustrated in Fig. 1b. It depicts the system consisting of two electrolytic solutions separated by a membrane.

Fig. 1
figure 1

a Living cell. b Experimental system modeled after the living cell

Full size image

Present membrane theory states that the potential generated in the system depicted in Fig. 1b is governed by the transmembrane ion transport and the potential expected must be represented by the solid line in Fig. 2a. Membrane theory suggests that the membrane potential we can experimentally measure corresponds to ϕm in Fig. 2a, where ϕm is the potential in the left compartment in reference to the potential in the right compartment. On the other hand, Ling’s adsorption theory attributes the membrane potential to the mobile ion adsorption and not to the transmembrane ion transport, as described in the Section 1. Figure 2b is the typical model of Ling’s adsorption theory. In this model, the potential represented by the solid line is expected to be induced owing to the ion adsorption on the membrane surface. When measuring the potential, two electrodes are inserted in the left and right compartments, respectively. Both electrodes are placed at the position infinitely away from the membrane. Therefore, one electrode detects the potential \(\phi _{L}^{\ell }\) and the other electrode detects \({\phi _{L}^{r}}\) (see Fig. 2b). Hence, the actually measured potential ϕL is given by (1):

$$\begin{array}{@{}rcl@{}} \phi_{L} = \phi_{L}^{\ell} - {\phi_{L}^{r}} \end{array} $$
(1)
Fig. 2
figure 2

a Membrane theory model. b Ling’s adsorption theory model. For both models, the solid line represents the trend line of potential expected

Full size image

According to Ling’s adsorption theory, the nonzero potential across the membrane is governed by the quantity of free ions. However, the nonzero potential generation cannot be achieved only by the existence of free ions against our intuition, rather, the ion adsorption is also needed. A free ion is inevitably surrounded by counter ions because of the law of the electroneutrality (this law is often dismissed in the solution chemistry). Therefore, even though the heterogeneous distribution of, say, a cation is realized at a certain moment in the solution phase, it is immediately nullified by the counter anions. From the standpoint of statistical mechanics, the heterogeneous charge distribution of free ions cannot be achieved in reality, no matter how high the free ion concentration is. Therefore, the nonzero potential generation cannot be achieved virtually. However, if a certain quantity of ions is spatially fixed by the adsorption, the ion distribution nearby those fixed ions becomes heterogeneous according to the thermodynamics and statistical mechanics and it results in the nonzero potential.

3 What Ling’s adsorption theory means

According to the membrane theory, the plasma membrane permeability to the individual ions is one of the primary factors governing the membrane potential. Therefore, the relationship between the ion concentration in the left and right compartments is one of the ruling factors of membrane potential behavior. On the other hand, Ling’s adsorption theory suggests that the membrane potential is merely a difference between the potentials which are generated in the left and the right compartment independently of each other. It is explained in detail below.

According to Ling’s adsorption theory, the system can be regarded as the combination of two independent solution systems, as illustrated in Fig. 3a. Namely, there are two independent solution compartments originally as illustrated on the left in Fig. 3b. Then the left compartment is horizontally flipped and combined with the right compartment, resulting in the system in question, as illustrated on the right in Fig. 3b. It is interpreted that we can obtain the potential in the system in question by calculating (1) without actually measuring the potential across the membrane, if we can measure \(\phi _{L}^{\ell }\) and \({\phi _{L}^{r}}\) independently.

Fig. 3
figure 3

Potential generation based on Ling’s adsorption theory

Full size image

4 Experimental verification

In this section, I make a comparison between the GHK equation and Ling’s adsorption theory by performing some experiments.

4.1 GHK equation

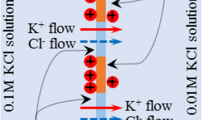
Tamagawa and Morita fabricated an experimental setup illustrated in Fig. 4a [9]. This setup has the same structure as the system shown in Fig. 1b. They used Selemion AMV as a membrane separating two electrolytic solutions. Selemion AMV is an ion exchange membrane manufactured by Asahi Glass Co., Ltd (Tokyo), and it contains the immobile quaternary amine groups (see Fig. 4b), which dissociate into to the immobile cation and mobile anion in the hydrated state. Both Sol-L and Sol-R were KCl solutions, and Sol-R was 0.1 M KCl. They made measurements of potential generated across the Selemion AMV by changing the KCl concentration of Sol-L from 10− 5 M to 3.4 M, where the potential in the right compartment was defined 0V.

Fig. 4
figure 4

a Experimental setup imitating the living cell. Sol-L and Sol-R correspond to the cell inside and outside, respectively, and the separator corresponds to the plasma membrane and the potential detected by the right Ag/AgCl electrode is defined the reference 0V. b Structure of the functional atomic group contained in Selemion AMV

Full size image

ϕ vs. − log10[CR/CL] (ϕ: potential, CL: KCl concentration in the left compartment, CR: KCl concentration in the right compartment) originally reported by Tamagawa and Morita [9] is rearranged into ϕ vs. log10[CL] and shown in Fig. 5 with the symbol ∘, and it forms an almost straight line except for the low concentration region. Since Selemion AMV is an anion exchange membrane, it does not appear to be inappropriate to postulate that its permeability to cation is quite low and that to anion is quite high. In the GHK equation, this postulation can be interpreted as the permeability constants are given by PK = 0 and PCl = 1, respectively, and it leads to the GHK equation given by (2) [3, 10,11,12]. The computed potential obtained by using (2) is represented by the ◇ in Fig. 5, and it is in good agreement with the experimentally obtained potential. The slight disagreement between the experimental and computational potentials can be amended by appropriately adjusting the permeability constants. Postulating PK = 0.004 and PCl = 1, the GHK equation perfectly reproduces the experimental potential behavior as shown in Fig. 5 with the symbol ∙. Such outcomes obtained using the GHK equation are regarded as rigid proofs of the validity of membrane theory. However, the permeability constant does not necessarily represent the actual permeability of membrane to the ion. It sometimes serves as a sort of parameter for achieving the good agreement between the experimental potential and the computational potential based on the GHK equation [13]. Hence, the physical meaning of permeability constant is not necessarily meaningful from the view of electrophysiology.

Fig. 5
figure 5

Potential vs. log10[CL] ∘: Experimentally measured potential across the Selemion AMV, where the standard deviation increases with the decrease of CL, but it is only ±0.008 V (CL = 10− 5 M) at the largest ◇: Potential computed using the GHK equation when PK = 0 and PCl = 1, ∙: Potential computed using the GHK equation when PK = 0.004 and PCl = 1

Full size image
$$\begin{array}{@{}rcl@{}} V &=&-\frac{RT}{F}\ln\frac{P_{K}[K^{+}]_{L}+P_{Cl}[Cl^{-}]_{R}}{P_{K}[K^{+}]_{R}+P_{Cl}[Cl^{-}]_{L}} \\ &\sim& -\frac{RT}{F}\ln\frac{P_{Cl}[Cl^{-}]_{R}}{P_{Cl}[Cl^{-}]_{L}} = -\frac{RT}{F}\ln\frac{[Cl^{-}]_{R}}{[Cl^{-}]_{L}} \end{array} $$
(2)

Next, Tamagawa and Morita performed basically the same experiment using AgCl-coated Ag wire in place of Selemion AMV [9]. AgCl-coated Ag wire is a fine Ag wire of which both ends are coated with AgCl. It was fabricated by the following simple procedure: Both ends of a short and fine Ag wire were immersed in bleach, resulting in the coverage of both ends of it with AgCl. From now on, this wire is referred to as simply AgCl wire. Note that this AgCl wire is not a membrane at all. However, the role of it in our study is equivalent to a membrane such as the Selemion AMV. Namely, both the AgCl wire and Selemion AMV are employed as a separator intervening between two electrolytic solutions. Hence, I sometimes refer to the wire shape separator as a membrane.

The experimental setup is illustrated in Fig. 6, and the experimental result ϕ vs. − log10[CR/CL] originally reported by Tamagawa and Morita [9] is rearranged into ϕ vs. log10[CL] and is shown in Fig. 7 with the symbol ∘. Quite intriguingly, the computational potential obtained by the use of (2) almost perfectly reproduces the experimentally obtained potential behavior, although the AgCl wire is completely impermeable to any ion (no transmembrane ion transport takes place). Postulating PK = 0.00025 and PCl = 1, the computational potential perfectly agrees with the experimentally measured potential, as clearly shown in Fig. 7. Of course, it is inappropriate to use the GHK equation for the experimental system in which no transmembrane ion transport is involved. Nevertheless, I can’t help but to wonder if such a perfect agreement between the experimental and the GHK equation-based computational potentials is merely a coincidence.

Fig. 6
figure 6

Experimental setup for measuring the potential separated by Ag wire, both ends of which are coated with AgCl

Full size image
Fig. 7
figure 7

Potential vs. log10[CL] ∘: Potential across the AgCl wire, where the standard deviation increases with the decrease of CL, but it is only ±0.006 V (CL = 10− 5 M) at the largest. ◇: Potential computed using the GHK equation when PK = 0 and PCl = 1. ∙: Potential computed using the GHK equation when PK = 0.00025 and PCl = 1

Full size image

4.2 Ling’s adsorption theory

Ling’s adsorption theory states that the transmembrane ion transport has nothing to do with the membrane potential generation, and the membrane potential we experimentally measure is merely the potential difference between \(\phi _{L}^{\ell }\) and \({\phi _{L}^{r}}\), which are generated independently of each other, as shown in Fig. 3. \(\phi _{L}^{\ell }\) is governed only by the condition in the left compartment only while \({\phi _{L}^{r}}\) is governed by the condition in the right compartment only.

I performed the following experiment to verify Ling’s adsorption theory. I fabricated an experimental setup illustrated in Fig. 8 and made measurements of the solution potential in reference to the potential of AgCl wire surface (the AgCl wire surface potential is defined 0V). The potential measured is summarized in Table 1.

Fig. 8
figure 8

Measurement of potential of solution in reference to the AgCl wire surface

Full size image
Table 1 Potential in the KCl solution in reference to the AgCl wire surface
Full size table

If Ling’s adsorption theory is valid, the potential across the membrane separating two KCl solutions, which is represented by the symbol ∘ in Fig. 7, can be computationally predicted by using the data in Table 1. For example, the potential is –0.102 V when CL in Fig. 6 is 10− 3 M as in Fig. 7. Using Ling’s adsorption theory, that potential should be calculated by ψC(C = 10− 3M) − ψC(C = 10− 1M) (the definitions of ψC and C are given in Table 1) and it is given by −0.205 V − (−0.092 V) = −0.113 V. It is quite close to the actually measured potential of –0.102 V. In the same manner, I computed the potential using the data in Table 1 to reproduce the potential shown in Fig. 7. The experimentally measured potential and the computed potential are shown in Fig. 9. Both perfectly coincide with each other. Therefore, the potential across the impermeable membrane is reproducible by Ling’s adsorption theory.

Fig. 9
figure 9

Potential generated across the AgCl wire. ∘: Experimental potential data (same data shown in Fig. 7△: Potential computed using the data summarized in Table 1

Full size image

It is more difficult to perform the same experiment using Selemion AMV in place of AgCl wire. Consider the experimental setup illustrated in Fig. 10. The part of the Selemion AMV above the aqueous solution is in the dried state. Since Selemion AMV is a polymeric material, the dried part of the Selemion AMV is insulating. Hence, the solution potential was not measurable. If Selemion AMV is fully submerged into the solution, so as to make the Selemion AMV ionically conductive, the tip of the lead connecting the voltmeter and Selemion AMV is submerged into the solution, and it could cause some undesired side effects on the potential measurement. Therefore, I devised another experiment to verify the validity of Ling’s adsorption theory in the experimental system employing Selemion AMV.

Fig. 10
figure 10

Experimental setup for measuring the solution potential in reference to the Selemion AMV surface potential

Full size image

According to Ling’s adsorption theory, the system illustrated in Fig. 4 is regarded as a combined system of two independent solution systems regardless of the type of membrane employed. The experimental system Tamagawa and Morita employed is regarded as such a system. They measured the potential of CL M KCl solution in the left compartment in reference to the potential of 10− 1 M KCl solution in the right compartment along with changing CL from 10− 5 M to 3.4 M. Although they did not investigate the potential profile of the whole system, I speculate that the potential profile expected could be represented by the solid line in Fig. 11a. Consequently, I conclude that Tamagawa and Morita measured the potential ϕTM defined by (3):

$$\begin{array}{@{}rcl@{}} \phi_{TM}(C_{L}) = \phi(C_{L}) - \phi(10^{-1}) \end{array} $$
(3)
Fig. 11
figure 11

a Experimental setup Tamagawa and Morita employed and b the same setup but only the concentration of right compartment is replaced with 10− 5 M KCl solution

Full size image

I performed the same experiment as Tamagawa-Morita experiment but employed 10− 5 M KCl solution as the KCl solution in the right compartment in place of 10− 1 M KCl solution. The potential profile expected is illustrated in Fig. 11b and the potential measured, ΦTM, is summarized in Table 2. In this experimental system, ΦTM is given by (4), where the definition of Φ(cL) and Φ(10− 5) are given in Fig. 11b:

$$\begin{array}{@{}rcl@{}} {\Phi}_{TM}(c_{L}) = {\Phi}(c_{L}) - {\Phi}(10^{-5}) \end{array} $$
(4)
Table 2 Potential across the Selemion AMV separator when the ion concentration in the right compartment is 10− 5 M
Full size table

Ling’s adsorption theory states that the potential profile in a certain compartment depends only on the condition of that compartment and independent of any condition in the other compartment. Hence, if cL is the same as CL, (5) is derived irrespective of the ion concentration in the right compartment. Therefore, as long as Ling’s adsorption theory is valid, ϕ(CL) can be represented by ΦTM(cL):

$$\begin{array}{@{}rcl@{}} {\Phi}(c_{L}) = \phi(c_{L}) \\ when \ c_{L} = C_{L} \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \phi_{TM}(C_{L}) &=& \phi(C_{L}) - \phi(10^{-1}) = {\Phi}(c_{L}) - {\Phi}(10^{-1}) \\ &=& \left( {\Phi}(c_{L}) - {\Phi}(10^{-5})\right) - \left( {\Phi}(10^{-1}) - {\Phi}(10^{-5})\right) \\ &=& {\Phi}_{TM}(c_{L}) - {\Phi}_{TM}(10^{-1}) \end{array} $$
(6)

Using (6) and the potential data summarized in Table 2, ΦTM(cL) is calculated. The result is shown in Fig. 12. Experimental potential data and the computed potential data are in quite good agreement with each other. Hence, Ling’s adsorption theory is applicable even to a system employing a semipermeable membrane such as the Selemion AMV.

Fig. 12
figure 12

Potential across the Selemion AMV. ∘: Experimental potential data from the Tamagawa-Morita experiment. ◇: Computed potential using the potential data in Table 2

Full size image

Regardless of the membrane permeability of ions, ion adsorption ought to take place as long as the membrane bears the adsorption sites. However, the GHK equation does not take it into consideration. To make matters worse, the GHK equation cannot explain the potential generation across the impermeable membrane, unlike Ling’s adsorption theory and the GHK equation, does not provide any rational reason why the nonzero potential across the impermeable membrane is generated. Therefore, Ling’s adsorption theory is by far a more comprehensive concept than the GHK equation.

5 Similarity of Ling’s adsorption theory to the GHK equation

In this section, I will derive the mathematical expression of potential across the AgCl wire employing Ling’s adsorption theory and discuss the reason why both the GHK equation and Ling’s adsorption theory can reproduce the experimentally measured potential behavior so well.

A coordinate system is set to the system, as shown in Fig. 8 as Fig. 13; x = 0 represents the AgCl wire surface position and x = + ∞ represents the Ag/AgCl electrode position. Vertical direction in this coordinate system represents the potential, ζ. Bear in mind that the potential at the Ag/AgCl electrode, ζ|x= 0, is defined as 0 V, so as to make our discussion simple, while ψC = 0 V is defined at the AgCl wire surface in Fig. 8. Hence, ζ is given by (7):

$$\begin{array}{@{}rcl@{}} \zeta = -\psi_{C} \end{array} $$
(7)
Fig. 13
figure 13

Coordinate system. The dashed line represents the potential profile

Full size image

First, I postulate that the AgCl wire surface bears a hypothetical charge even in the pure water, since ζ is not 0 V, but positive potential even when the bathing solution of the AgCl wire is deionized water (see Table 1). The hypothetical charge on the AgCl wire submerged in the deionized water is denoted by σ0.

I derive the formula of ζ in the C M KCl solution system. The Poisson–Boltzmann equation of this system is given by (8), where ρ, e, 𝜖 and 𝜖0 are charge density in the solution phase, elementary charge, the relative permittivity of water and vacuum permittivity, respectively [14,15,16]. ρ is given by (9). [K+] and [Cl−] in the solution phase are given by (10) and (11), respectively, where Q, k, and T are concentration of K+ and Cl− in the bulk phase, Boltzmann constant, and temperature, respectively, and β ≡ \(\frac {e}{2kT}\). (12) is derived using (8)-(11). Then, (15) is derived by solving (12) under the conditions of (13) and (14).

$$\begin{array}{@{}rcl@{}} \frac{d^{2}\zeta}{dx^{2}} = -\frac{\rho}{\epsilon\epsilon_{0}} \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \rho = e[K^{+}] - e[Cl^{-}] \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} [K^{+}] =Q\exp\left( -\frac{e\zeta}{kT}\right) = Q\exp\left( -2\beta\zeta\right) \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} [Cl^{-}] = Q\exp\left( +\frac{e\zeta}{kT}\right) = Q\exp\left( + 2\beta\zeta\right) \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \frac{d^{2}\zeta}{dx^{2}} = -\frac{Qe}{\epsilon\epsilon_{0}}\left( \exp\left( -2\beta\zeta\right)-\exp\left( + 2\beta\zeta\right)\right) \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} \zeta \rightarrow 0 \ (x \rightarrow +\infty) \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \frac{d\zeta}{dx} \rightarrow 0 \ (x \rightarrow +\infty) \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} \left( \frac{d\zeta}{dx}\right)^{2} = \frac{8QkT}{\epsilon\epsilon_{0}}\sinh^{2}(\beta\zeta) \end{array} $$
(15)

Since \(\frac {d\zeta }{dx}\) should satisfy \(\frac {d\zeta }{dx}\) < 0 (see Fig. 13), (15) can be arranged into (16). Macroscopic electroneutrality should hold in this whole system. Hence, (17) should be satisfied, where σ|x= 0 is the surface charge density of AgCl wire. This equation is solved under the condition (14), resulting in (18):

$$\begin{array}{@{}rcl@{}} \frac{d\zeta}{dx} = -2\sqrt{\frac{2QkT}{\epsilon\epsilon_{0}}}\sinh(\beta\zeta) \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} \sigma|_{x = 0} + {\int}_{0}^{+\infty} \rho dx = 0 \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \left.\sigma\right|_{x = 0} = -\epsilon\epsilon_{0}\left.\frac{d\zeta}{dx}\right|_{x = 0} = 2\sqrt{2\epsilon\epsilon_{0}QkT}\sinh(\beta\zeta|_{x = 0}) \end{array} $$
(18)

Bearing the concept of Langmuir isotherm in mind [9], and noting that Cheng shows that AgCl can adsorb Cl− [17], I hypothesize that Cl− is adsorbed onto the AgCl wire surface. Denoting the adsorption site by “s”, the adsorption reaction is represented by (19). Denoting the association constant by K, (20) is derived. Denoting the total adsorption site density by [s]T, (21) is derived. Using those three equations, (22) is derived.

$$\begin{array}{@{}rcl@{}} s + Cl^{-} \leftrightarrow sCl^{-} \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} K = \frac{[sCl^{-}]}{[s][Cl^{-}]|_{x = 0}} \end{array} $$
(20)
$$\begin{array}{@{}rcl@{}} [s]_{T} = [s] + [sCl^{-}] \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} [sCl^{-}] = \frac{K[s]_{T}[Cl^{-}]|_{x = 0}}{1 + K[Cl^{-}]|_{x = 0}} \end{array} $$
(22)

Assuming that a single adsorption site “s” bears a charge +e, the creation of sCl− by the adsorption of Cl− to s results in the neutralization of +e of s by -e of Cl−. For example, imagine an AgCl wire which has in total seven adsorption sites per unit surface area as illustrated in Fig. 14, so that σ0 = 7e. The adsorption of three Cl−’s on the AgCl wire surface results in the formation of three sCl−, resulting in the neutralization of + 3e out of σ0. Hence, σ|x= 0 = + 4e, which means that four adsorption sites remain unassociated with Cl−. Based on this idea, (23) is derived. (18) and (23) represent the same σ|x= 0. Hence, (24) is derived. The rightmost term of (24) is obtained using (11).

$$\begin{array}{@{}rcl@{}} \sigma|_{x = 0} = \sigma_{0} - e[sCl^{-}] = \sigma_{0} -e\frac{K[s]_{T}[Cl^{-}]|_{x = 0}}{1 + K[Cl^{-}]|_{x = 0}} \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} &&2\sqrt{2\epsilon\epsilon_{0}QkT}\sinh(\beta\zeta|_{x = 0}) = \sigma_{0} -e[sCl^{-}]|_{x = 0} \\ &&= \sigma_{0} -e\frac{K[s]_{T}[Cl^{-}]|_{x = 0}}{1 + K[Cl^{-}]|_{x = 0}} \ = \sigma_{0} -e\frac{K[s]_{T}Q\exp(+ 2\beta\zeta|_{x = 0})}{1 + KQ\exp(+ 2\beta\zeta|_{x = 0})} \end{array} $$
(24)
Fig. 14
figure 14

Surface charge neutralization by the adsorption of mobile anion onto the adsorption site s

Full size image

It is necessary to obtain the K value in order to use (24). For obtaining it, I use (20). So, first, I need to obtain [s], [sCl−] and [Cl−]|x= 0. Those quantities are obtained by the following procedure: ζ|x= 0 is easily obtained by using (7) and the potential data of ψC shown in Table 1. [Cl−]|x= 0 is computed by plugging that potential of ζ|x= 0 into (11), where T = 290 K. σ|x= 0 is given by plugging Q and ζ|x= 0 into (18). Since I earlier postulated that a single surface site s bears a charge +e, (25) establishes. Since I also earlier postulated that Cl− adsorption onto s neutralizes the charge of s, (26) establishes. Substituting σ|x= 0 into (26), [s] is obtained.

$$\begin{array}{@{}rcl@{}} \sigma_{0} = e[s]_{T} \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} [s] = \sigma|_{x = 0} \div e \end{array} $$
(26)

Since [sCl−] is given by (21), we need to obtain [s]T. I calculate it by considering the estimated dimension of s. s represents AgCl, and I assume that its shape is square. Since the length of its edge must be ∼1nm, [s]T is given by 1m2 ÷ 1nm2 = 1.661 × 10− 6 mol⋅m− 2. Substituting this quantity and [s] into (27), [sCl−] can be calculated. So, [s], [sCl−] and [Cl−]|x= 0 are obtained and plugging them into (20), yields Ks. Those quantities are all summarized in Table 3.

$$\begin{array}{@{}rcl@{}} [sCl^{-}] = [s]_{T} - [s] \end{array} $$
(27)
Table 3 Data used for the computation of K, and the computed K values
Full size table

K cannot be calculated when Q = 3.4 M and K becomes a bit larger when Q = 10− 5 M. Except for those two cases, K is almost constant. Hence, the average of the rest of the K values is taken as K value, K = 0.146 M− 1.

The rightmost term of (24) is transformed into the second equation of (28) using (25). Plugging K = 0.146 M− 1, Q and ζ|x= 0 shown in Table 3 into the second equation of (28) results in the almost constant regardless of Q. Thus (28) is represented by AL (≡ const.). Hence, (24) can be approximated into (29). Now, why does (28) become constant? The leftmost equation of (28) represents σ|x= 0 according to (23), and σ|x= 0 is almost constant regardless of Q as in Table 3. Hence, (28) is almost constant. However, the reason why σ|x= 0 is almost constant regardless of Q is not clarified yet. Since exp(βζ|x= 0) > exp(−βζ|x= 0) when Q = 1 M and exp(βζ|x= 0) >> exp(−βζ|x= 0) when Q < 1 M, sinh term in (29) can be roughly approximated as (30). Solving (30) with respect to ζ|x= 0 results in (31).

$$\begin{array}{@{}rcl@{}} \sigma_{0} - e\frac{K[s]_{T}Q\exp(+ 2\beta\zeta|_{x = 0})}{1 + KQ\exp(+ 2\beta\zeta|_{x = 0})} &=& \frac{\sigma_{0}}{1 + KQ\exp(+ 2\beta\zeta|_{x = 0})} \\ &=& const. = A_{L} \end{array} $$
(28)
$$\begin{array}{@{}rcl@{}} 2\sqrt{2\epsilon\epsilon_{0}QkT}\sinh(\beta\zeta|_{x = 0}) \sim A_{L} \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} 2\sqrt{2\epsilon\epsilon_{0}QkT}\frac{\exp(\beta\zeta|_{x = 0})}{2} \sim A_{L} \end{array} $$
(30)
$$\begin{array}{@{}rcl@{}} \zeta|_{x = 0} =\frac{1}{\beta}\ln\frac{A_{L}}{\sqrt{2\epsilon\epsilon_{0}QkT}} \end{array} $$
(31)

Based on Ling’s adsorption theory, the potential generated in Fig. 6 must be represented by the dashed line in Fig. 15b where the actual experimental system is again illustrated in Fig. 15a. The potential represented by Δζ is Fig. 15b corresponds to the potential experimentally measured.

Fig. 15
figure 15

a Actual experimental setup and b model for the mathematical formulation of potential behavior

Full size image

Since the potential in the AgCl wire should be the same everywhere, its potential redefined as 0 V (see Fig. 15b). Δζ is given by (32). ζL|x= 0 and ζR|x= 0 are expressed by (33) and (34), respectively, using (31) where QL and QR represent the ion concentration in the left and right compartments, respectively. The negative sign in front of ζL|x= 0 and ζR|x= 0 of (32) is due to the definition of 0 V position. The potential of the AgCl wire is 0 V in Fig. 15b while the 0 V of ζ is defined as the potential at Ag/AgCl electrode as clearly seen in Fig. 13. Plugging (33) and (34) into (32) results in (35)

$$\begin{array}{@{}rcl@{}} {\Delta}\zeta = (-\zeta_{L}|_{x = 0}) - (-\zeta_{R}|_{x = 0}) \end{array} $$
(32)
$$\begin{array}{@{}rcl@{}} \zeta_{L}|_{x = 0} =\frac{1}{\beta}\ln\frac{A_{L}}{\sqrt{2\epsilon\epsilon_{0}Q_{L}kT}} \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} \zeta_{R}|_{x = 0} =\frac{1}{\beta}\ln\frac{A_{L}}{\sqrt{2\epsilon\epsilon_{0}Q_{R}kT}} \end{array} $$
(34)
$$\begin{array}{@{}rcl@{}} {\Delta}\zeta &=& -\frac{1}{\beta}\ln\frac{A_{L}}{\sqrt{2\epsilon\epsilon_{0}Q_{L}kT}} + \frac{1}{\beta}\ln\frac{A_{L}}{\sqrt{2\epsilon\epsilon_{0}Q_{R}kT}} \\ &=&-\frac{1}{\beta}\ln\left( \frac{\frac{1}{\sqrt{Q_{L}}}}{\frac{1}{\sqrt{Q_{R}}}}\right) =-\frac{kT}{e}\ln\frac{Q_{R}}{Q_{L}} = -\frac{RT}{F}\ln\frac{Q_{R}}{Q_{L}} \end{array} $$
(35)

Equation (35), derived by employing Ling’s adsorption theory, has the same expression of (2) derived by the using the GHK equation. Owing to this theoretical fact and our emphasis that Ling’s adsorption theory is a more comprehensive concept than the GHK equation as earlier described, I suspect that Ling’s adsorption theory is a genuinely correct theory of a membrane potential generation mechanism. However, (35) may not well reflect the characteristics of (24), since (35) is an approximation of (24). Hence, I numerically computed the potential using (36) instead of its approximation given by (35), where the lhs of (36) is the leftmost equation of (24) and the rhs of (36) is the rightmost equation of (24). Plugging QR = 10− 1 M into (36), the potential ζR|x= 0 is numerically calculated. In the same manner, the potential ζL|x= 0 is obtained as a function of QL (= 10− 5 M ∼ 3.4 M). Then the potential Ω, defined by (37), is obtained as a function of QL. The results are shown in Fig. 16. This diagram suggests that (35) is quite a good approximation of (24) derived from the idea of Ling’s adsorption theory and the computed potential reproduce the experimental results well. Thus, Ling’s adsorption theory could be the correct theory as the generation mechanism of membrane potential.

$$\begin{array}{@{}rcl@{}} 2\sqrt{2\epsilon\epsilon_{0}QkT}\sinh(\beta\zeta|_{x = 0}) = \sigma_{0} -e\frac{K[s]_{T}Q\exp(+ 2\beta\zeta|_{x = 0})}{1 + KQ\exp(+ 2\beta\zeta|_{x = 0})} \end{array} $$
(36)
$$\begin{array}{@{}rcl@{}} {\Delta}{\Omega} = (-\zeta_{L}|_{x = 0}) - (-\zeta_{R}|_{x = 0}) \end{array} $$
(37)
Fig. 16
figure 16

Potential vs. log10[CL]. ∘: Potential across the AgCl wire Tamagawa and Morita obtained, which is also shown in Fig. 7 (reference [9]). ∙: Potential computed using (35). Dashed line: Potential computed using (36) and (37)

Full size image

It is quite natural to deny our emphasis, since Ling’s adsorption theory does not necessarily explain everything. For example, the K value cannot be computed when Q = 3.4 M and K value becomes quite high when Q = 10− 5 M, as described earlier. However, the GHK equation cannot explain everything either. Indeed, it is not uncommon that there is disagreement between the experimentally measured membrane potential and the membrane potential predicted by the GHK equation [3, 18]. As described earlier, even though the GHK equation can reproduce the membrane potential behavior, the permeability constant does not necessarily represent the membrane permeability to ions. Other than such a problem, the GHK equation has more problematic facets: It does not take into consideration ion adsorption and does not sufficiently explain the macroscopic electroneutrality [3, 19]. On the other hand, Ling’s adsorption theory is in agreement with the basic physical chemistry-based concepts such as the Boltzmann distribution, the Langmuir isotherm, and macroscopic electroneutrality. So, Ling’s adsorption theory appears to be superior to the GHK equation.

6 Conclusions

Although the membrane theory has been accepted as a firmly established physiological concept, the GHK equation, which has been regarded as the most successful model, does not necessarily provide us with a trustworthy enough membrane potential generation mechanism, and some facets of the membrane theory appear to violate some basic laws of physical chemistry. On the other hand, Ling’s adsorption theory is in harmony with the basic concepts of physical chemistry and can predict the potential behavior well and quantitatively. Although the GHK equation has been employed for decades as a robust tool for predicting and analyzing the membrane potential behavior, the mathematical formula representing the membrane potential derived by use of Ling’s adsorption theory also coincides with the GHK equation. Therefore, the GHK equation may in fact be incomplete and require reinterpretation based on the ion adsorption theory. We cannot rule out the validity of Ling’s adsorption theory as a membrane potential generation mechanism at this moment. These results suggest that a reconsideration of the long-dismissed Ling’s adsorption theory as an alternative theory to the membrane theory is warranted.

After completing the work described in this paper, I focused on more general cell models. Then, I theoretically found that the more general potential formula based on Ling’s adsorption theory is exactly the same as the ordinary expression of GHK equation such as the second equation of (2), and I will report it in the next paper to be submitted shortly.