Academic skills deficits are the primary reason students are referred for special education services (Shapiro, 2004). While reading skills deficits are the most common, (Daly, Chafouleas, & Skinner, 2005), the 2005 National Assessment of Educational Progress (NAEP) findings showed that 64% of 4th-grade students and 70% of 8th-grade students did not demonstrate grade-level competency with mathematics skills (Perie, Grigg, & Dion, 2005). These data would suggest that efficient interventions are needed to prevent and/or remedy math skill deficiencies.

Acquisition influences other stages of skill development

Haring and Eaton (1978) developed a skill mastery hierarchy, in which the first stage in learning a new skill, acquisition, focuses on enhancing response accuracy. Because developing the ability to respond accurately is the first step to skill mastery, procedures designed to enhance accuracy can impact subsequent stages of skill development including fluency, generalization, maintenance, and adaptation. Educators often use manipulatives (e.g., blocks) to teach students strategies that can be used to arrive at accurate answers to basic math facts (Carpenter & Moser, 1982). For example, when learning addition, teachers may provide students with a number line and teach them to add by placing their finger on the number line for the largest numeral in a problem and then counting forward while moving their finger until they say the smaller numeral (Kameenui & Simmons, 1990).

There are several advantages associated with enhancing accuracy when teaching students such strategies and procedures. Teaching students strategies that can be applied across many problems (e.g., using a number line to enhance addition accuracy) may be an efficient instructional procedure for enhancing accuracy across math facts (Stokes & Baer, 1977). Additionally, such procedures may enhance students' conceptual understanding of the target task (i.e., addition) and related concepts (Garnett, 1992; Poncy, Skinner, & O'Mara, 2006). For example, teaching students to add using a counting procedure may enhance their conceptual understanding of addition and related concepts such as greater than, subtraction, and equal intervals.

However, there are also limitations and concerns with using such strategies to enhance accuracy. Many of these procedures require multiple steps, and an error during any step will cause students to arrive at the wrong answer (Pellegrino and Goldman, 1987). When the strategies involve working with physical prompts or manipulatives, (e.g., blocks or number lines), students may become prompt dependent and thus unable to solve the problems unless they have access to prompts (Skinner & Schock, 1995; Stokes & Baer, 1977). Even when the strategies do not require prompts or when they require prompts that are readily accessible (e.g., the students' fingers), students may become strategy dependent, and thus unable to arrive at an accurate response unless they employ the learned strategy. In some instances this may not be a serious concern. However, when these strategies and procedures take a significant amount of time and effort they may hinder the development of subsequent stages of skill mastery (Delazer et al., 2003; Poncy et al., 2006; Skinner, 1998; Skinner, Pappas, & Davis, 2005).

In addition to responding accurately, mastering basic math facts requires the ability to recall the facts quickly and with little effort. Haring and Eaton (1978) refer to this as fluency, while others (e.g., Hasslebring, Goin, & Bransford, 1987) refer to this as automaticity. Developing automaticity with basic mathematics facts is critical for several reasons. Cognitive processing theories indicate that we have a limited cognitive capacity which can make it difficult to consciously attend to multiple tasks simultaneously, unless some of these tasks require little time, cognitive effort, working memory, and/or conscious attention (Deleazer et al., 2003; LaBerge & Samuels, 1974; Pellegrino & Goldman, 1987). Therefore, enhancing automaticity with basic math facts may free up cognitive resources (e.g., attention, working memory) that can be applied to learning more complex tasks (Dahaene, 1997). For example, a student who can respond automatically to basic multiplication facts (e.g., 6×7=42), will have more cognitive resources to allocate toward acquiring new skills (e.g., carrying and place holding) needed to complete more advanced computation problems such as 46×75=3, 450 (Skinner, 1998). Thus, promoting automaticity with basic facts may enhance acquisition of more complex skills when basic fact accuracy is a component step of the more complex skills.

A student who is automatic with basic facts will complete problems at a faster rate and therefore is likely to have more opportunities to respond (i.e., practice trials), which can enhance accuracy, fluency, and maintenance (Ivarie, 1986; Skinner, Bamberg, Smith, & Powell, 1993; Skinner, Belfiore, Mace, Williams, & Johns, 1997; Skinner, Pappas, & Davis, 2005). Providing assigned math tasks that are varied, combined with increased opportunities to respond can be used to promote discrimination, generalization, and adaptation (Skinner, 1998). Because automatic responding requires less effort and often results in higher rates of reinforcement, students who can respond automatically may have less math anxiety and be more likely to choose to do assigned mathematics work than those who can not respond automatically (Billington, Skinner, & Cruchon, 2004; Cates & Rhymer, 2003; Mace, McCurdy, & Quigley, 1990; McCurdy, Skinner, Grantham, Watson, & Hindman, 2001; Skinner, 2002). This is critical because few if any skill development procedures are likely to enhance skills unless students choose to respond (Skinner, Pappas, & Davis, 2005).

Researchers approaching skill development from different theoretical perspectives (e.g., cognitive processing, response effort, reinforcement, choice, opportunities to respond, and math anxiety) have found evidence suggesting that increasing students’ accuracy and speed of accurate responding to basic math facts is crucial for developing and mastering more advanced math skills. Unfortunately, when students are taught and reinforced for using time consuming multi-step strategies for solving basic math facts (e.g., finger counting), they may rely on these strategies that may interfere and even prevent them from learning to solve basic mathematics facts automatically (Carpenter & Moser, 1982; Pellegrino & Goldman, 1987; Poncy et al., 2006; Stokes & Baer, 1977).

Effective strategies for enhancing accuracy and automaticity

Several procedures have been developed that can increase accuracy and automatic responding to basic mathematics facts (Garnett, 1992; McCallum, Skinner, & Hutchins, 2004; Skinner, Turco, Beatty, & Rasavage, 1989). These procedures occasion high rates of active academic responding which can increase both speed of responding and maintenance, provided that the responses are accurate (Skinner, Turco, Beatty, & Rasavage, 1989). To encourage accuracy, many of these procedures use immediate feedback, in order to prevent students from practicing errors and reinforce accurate responding (Skinner & Smith, 1992). Two such interventions are Cover, Copy, and Compare (CCC) and Taped Problems (TP) interventions.

Cover, copy, and compare (CCC)

CCC, originally designed to enhance spelling accuracy (Hanson, 1978 ), was adapted by Skinner et al. (1989) for math facts. In Skinner et al., the CCC procedure involved: (a) giving the student a sheet of target problems, (b) teaching the student to study the problem and answer provided on the left side of the page, (c) cover the problem and answer on the left side of the page, (d) write the problem and answer on the right side of the page, and (e) uncover and evaluate their response. If the problem and answer were written correctly, the student moved to the next problem. If the response was incorrect, students were instructed to re-write the correct response.

Many variations to the CCC procedures described in Skinner et al. (1989) have been shown to enhance mathematics accuracy and fluency across general education and special education students (Skinner, McLaughlin, & Logan, 1997). In some studies students were instructed to overcorrect their errors by writing the correct problem and answer more than one time (e.g., Poncy et al., 2006). In other studies researchers have altered the type of response, using verbal (Skinner et al., 1997) or cognitive responding (Skinner, Bamberg, Smith, & Powell, 1993) as opposed to requiring written responding. CCC may also incorporate performance feedback and reinforcement in order to increase the strength of the intervention (Skinner et al., 1993). CCC can be used with either an individual or group and can target all basic math facts (Poncy et al., 2006; see Skinner et al., 1997).

Taped-problems (TP)

The TP intervention has also been shown to enhance basic fact accuracy and automaticity (McCallum, Skinner, & Hutchins, 2004; McCallum, Skinner, Turner, & Saecker, in press). With TP the student listens to an audio recording of a person reading a series of math fact problems and is instructed to try to write the correct answer before the tape recording provides the answer. If the student incorrectly answers a question, the student is taught to cross out what he wrote and write the correct answer. If the student does not have enough time to write an answer, he is instructed to write the correct answer when it is heard.

The series of problems is repeated several times and time-delay procedures are used to encourage accurate and rapid responding. To prevent initial inaccurate responding and discourage students from applying time consuming strategies (e.g., counting on their fingers for addition) the first sequence provides minimal delay between the reading of the problem and the answer. As the sequence is repeated the interval between the problem and answer being read is increased to promote more independent responding and then decreased to promote automatic responding (McCallum et al., 2004; McCallum et al., in press). Existing research on the taped-problems intervention suggest that it can increase accuracy and fluency when used both at the individual student and group level.

Purpose

Both CCC and TP have been shown to enhance basic math fact fluency with general education students and students with mild learning problems (e.g., McCallum et al., 2004; McCallum et al., in press; Skinner et al., 1997; Skinner et al., 1993). While empirically validating interventions is important, for students with learning skill deficits it is also important to identify which interventions are most effective (Skinner, Belfiore, & Watson, 1995/2002). In the current study we extended research on CCC and TP by comparing the effects of the two interventions on basic math fact accuracy and fluency. The current study extends this research by empirically evaluating the efforts of CCC and TP on math fact accuracy and automaticity in a student functioning at a cognitive level (i.e., IQ score) below that of mild mental retardation.

Method

Student and setting

The participant is a 10-year old female student, we will refer to her as Sandy, attending a public school in the rural mid-western United States. Sandy had a Full Scale IQ of 44, consistent with a diagnosis of moderate mental retardation. She received a majority of her special education services in a pull-out setting working on basic academic and functional skills. The teacher requested services from the school psychologist to increase Sandy's accuracy and fluency in basic addition facts. Previous methods used to increase Sandy's fact accuracy included counting concrete objects (e.g., chips and blocks) and completing worksheets that paired various pictures of objects with math problems. Sandy's teacher indicated that Sandy had difficulty completing basic addition facts accurately using counting strategies, unless she had access to concrete objects, in this case foam blocks. Specifically, she was able to add by manipulating and counting groups of blocks up to 5.

The study was conducted in Sandy's classroom with the special education teacher or school psychologist providing the interventions. Procedures were conducted at a desk with the administrator of the intervention sitting near the student. After completing an intervention session, Sandy was allowed to engage in an activity of her choice for 5-minutes.

Materials

Baseline and intervention assessment data were collected via experimenter-constructed addition probes. Basic addition facts were divided into three mutually exclusive sets containing four problems each: Set A (3+4, 1+4, 2+2, 4+5), Set B (1+5, 2+3, 4+4, and 2+4), and Set C (2+5, 3+3, 3+5, 1+3). Problem sets were matched with each set having answers that combined to sum 25, a single problem with the number 1, and one “doubles” problem (e.g., 2+2). This was done in an attempt to keep the difficulty of the sets as closely aligned as possible.

For each set of problems, six different assessment probes were constructed. Each assessment probe consisted of 24 problems, with six rows of the four problems of the respective set. Problems were arranged so that the same problem was never directly above or below itself and the same problem was never repeated (i.e., the last problem of row one and the first problem of row two). Set A was randomly assigned to the CCC intervention condition, Set B to the TP intervention condition, and Set C a no-treatment control condition.

Each intervention session included a packet consisting of three pages. The first page was the CCC or TP sheet, the second page was a sprint/practice probe containing the problems of the respective condition (i.e., CCC or TP), and the third was an assessment probe to collect data on the dependent variables. The TP sheet, sprint/practice probes for both CCC and TP conditions, and the assessment probes were all taken from six alternate forms containing different combinations of the problems respective to each condition (i.e., CCC, TP, and control). The CCC sheet consisted of a grid containing 20 boxes, 5 boxes across and 4 boxes down, for the student to practice the 4 target problems within the set. The correct problems and answers were placed in the four boxes at the left of the CCC sheet. The remaining boxes contained three circles placed in a column at the right side of each box. Other materials used included a stopwatch, cassettes, and a tape recorder.

Dependent measures and scoring procedures

The dependent measures included the percentage of digits correct (DC) and the number of DC completed per minute on assessment probes. A digit was scored as correct when the appropriate number was written in the proper column (Shinn, 1989). The percentage was calculated by dividing the number of correct digits by the number of digits attempted and multiplying by 100. When Sandy finished the assessment probes before 60 seconds, the number of correct digits was multiplied by 60 and divided by the number of seconds taken to complete the assessment probe. Scores were rounded to the nearest whole number.

Experimental design

The current study combined an adapted alternating treatments design and a multiple-probe design to simultaneously investigate and compare two treatments while implementing a control condition (Skinner & Shapiro, 1989). This design allows for the comparison of two distinct interventions on equivalent sets of instructional items while accounting for history and spillover effects through the use of a continuous control condition (Sindelar, Rosenberg, & Wilson, 1985). The control condition was probed every other day to decrease the student's frequency of inaccurate responding and frustration (Cuvo, 1979). The length of the intervention sessions were not held constant but were recorded to more precisely compare student learning.

Procedures

Baseline data were collected for each of the three probe sets during the first four sessions. On the fifth day, each of the interventions were described and modeled. After Sandy demonstrated the ability to generally describe the procedures of the intervention, she completed it in its entirety. This training sequence was done first for the CCC and subsequently for TP. Following these initial sessions, the CCC and TP interventions were counterbalanced with one intervention being conducted in the morning and the other in the afternoon. Sandy's performance was assessed immediately following each intervention using the assessment probes of the intervention problem set. Every other day her performance on the control problems (Set C) was assessed. The interventions and assessment condition were presented in counterbalanced order across days. The final intervention session was conducted the day before Christmas vacation. To examine Sandy's maintenance of skills, follow up data were collected 14 calendar days later, two days after returning from break.

Baseline

In counterbalanced order, three assessment probes were administered, with each assessment probe consisting of problems types of one of the three sets of problems. Sandy was allowed one minute to complete as many problems as she could during the allotted time.

Cover, copy, compare (CCC) intervention

Each problem on the CCC worksheet required the following steps: (a) Sandy read the printed problem and answer, (b) covered the problem and answer, (c) wrote the problem and answer, (d) checked the accuracy of her response by comparing it to the model, (e) verbalized the correct problem and answer three times and wrote a check mark in one of the three circles on the CCC sheet each time she said the problem and answer. When these steps were completed she moved to the next problem and repeated the above steps. During each CCC session, Sandy performed these steps with each of the four problems in problem set A resulting in 4 correct written responses and 12 verbal responses. If Sandy did not correctly write down the problem and answer accurately, the interventionist pointed to the model, stated the correct problem and answer, and instructed her to correctly record the problem and answer. After the CCC sheet was completed, Sandy completed a sprint/practice sheet. If she wrote down an incorrect response the school psychologist or special education teacher would present her with the correct response and have her write down the correct answer. Sandy worked on this practice page until all of the problems were correctly answered.

Taped problems (TP) intervention

To complete the TP intervention, Sandy was given a practice sheet containing six rows of the four problems of Set B. A tape was made corresponding with the problems on the worksheet. The tape was started and a problem was read with a 4-second delay between the end of a problem being read and the answer to that problem being stated. The 4-second delay was selected by the classroom teacher to allow time for “processing,” a notion that the teacher would later discard. Sandy attempted to write down the correct response before it was identified on the tape. If she incorrectly responded, the teacher or psychologist would pause the tape until she corrected the response. This continued until all 24 problem and answers were presented. After the TP sheet was completed, Sandy completed a sprint/practice sheet using the same procedures as the sprint/practice sheet in the CCC condition.

Administration directions, interscorer agreement, and intervention integrity

The following instructions were read before the first assessment probe was administered each day, “The sheets on your desk are math facts. All the problems are addition facts. When I say ‘Begin’ start answering the problems. Begin with the first problem and work across the page, then go to the next row. If you cannot answer a problem, mark an ‘X’ through it and go to the next one. Are there any questions? Ready, begin.” If a subsequent assessment probe was administered the interventionist said, “Ready, begin.” A stopwatch was used to time each assessment and the student was instructed to stop after 1 min.

The probes were initially scored by the school psychologist. To obtain Interscorer agreement the classroom teacher independently scored 100% of the assessment probes. The teacher was taught, by the school psychologist, how to score computation probes using procedures from Shinn (1989). Interscorer agreement was calculated by dividing the number of agreements on digits correct by the number of possible agreements and multiplying by 100.

The interventionist followed a sequence of 10 steps when implementing each intervention. The self-recording of the interventionist and the accurate completion of each of the problems throughout both the CCC and TP interventions converge to suggest that all steps were correctly completed in the appropriate sequence.

Results

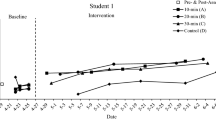
In time series fashion Fig. 1 displays Sandy's data on percent of correct problems for each assessment probe. Immediately after the intervention was implemented Sandy's accurate responding to the single digit addition problem increased to 100% on TP problems and remained at this level throughout the study. Sandy's accuracy on CCC problems immediately increased to 90% and then remained at high levels (89–100%) for the remainder of the study. Because accuracy on the set of control problems remained low (27–44%), these data suggest that both interventions resulted in rapid changes in Sandy's accuracy with little differences in accuracy levels across the two interventions. Follow up data indicate that her accuracy levels were maintained across each probe set with 100% for both TP and CCC sets and 27% for the control set.

Fig. 1
figure 1

Percentage of correct problems

Full size image

In time series fashion Fig. 2 displays Sandy's data on digits correct per minute for each assessment probe. These data show that both CCC and TP resulted in an increasing trend in digits correct per minute. Although TP caused a more immediate and dramatic increase in digits correct per minute, by the end of the treatment Sandy completed more digits correct per minute on the CCC problems. Fig. 2 also shows no increase in digits correct per minute on the set of control problems. Maintenance data on her computational fluency stayed at similar levels as the last few days of intervention with 25 DC/min for TP, 22 DC/min for CCC, and 4 DC/min for the control set.

Fig. 2
figure 2

Digits correct per minute

Full size image

To investigate the efficiency of the two interventions, the time Sandy participated in each intervention was recorded. Sandy spent an average of 6 minutes 36 seconds per day engaged in the CCC intervention and 4 minutes 41 seconds completing the TP intervention. These data suggest that while both interventions were effective in increasing Sandy's percentage and digits correct per minute, TP was the superior intervention as it required less time to complete.

Discussion

The current study extended the research on math fact accuracy and automaticity by showing that both TP and CCC enhanced math performance in a student with low cognitive functioning who often used manipulatives (i.e., blocks) and a counting strategy to arrive at correct answers. Additionally, the current study extends the research on TP, a recently developed intervention, by comparing it to an intervention with a large research base (CCC), demonstrating that TP was as effective as CCC for increasing the student's accuracy and automaticity.

Although both interventions similarly increased Sandy's accuracy and fluency on the targeted math facts, the amount of time spent on each of the interventions was significantly different. Taped problems took approximately 30% less time for Sandy to complete than CCC. Regardless of gains in achievement, the differential evaluation of what intervention is best suited for the student comes down to learning over time (i.e., rate). In essence, knowing the amount of time, in seconds, taken to produce gains in achievement allows researchers and practitioners to precisely determine how much bang we get for our intervention buck (Skinner et al., 1997). If sessions or general estimates of intervention length (e.g., CCC took 7 min), were used, then researchers and practitioners could arrive at different evaluations of which intervention worked the best. For example, a visual analysis of the graphs in the current study would lead one to conclude that both interventions worked similarly. However, when time is taken into account, TP is clearly more efficient than CCC, taking approximately 29% less time. The determination of which intervention worked best for Sandy could differ depending on if time or session was used.

There are several limitations associated with the current study that should be addressed by future researchers. Because of Sandy's low level of cognitive functioning, her apparent dependency on applying strategies while manipulating blocks to arrive at correct answers, and her repeated failure with mathematics skill development, the teacher and researcher designed procedures that were likely to increase her probability of success. Thus, in addition to using two different interventions, we decided to target only four problems under each condition. The results showed that we underestimated Sandy's responsiveness to the interventions. Within one or two session Sandy was able to enhance her accuracy to 100% on the four problems assigned to each treatment. Thus, ceiling effects, caused by the limited pool of items assigned to each treatment hindered our ability to detect differences in acquisition (i.e., accuracy) across the two treatments. Future researchers should use more items or consider using a flow list where unknown items are added after problems are mastered in order to better detect differences across treatments.

A second limitation was the failure to collect treatment acceptability data. Because no interventions will be effective unless the student chooses to engage in assigned work future researchers should assess student preference for interventions. This is particularly important when the interventions are self-managed as students who do not find the intervention acceptable may be unlikely to choose to engage in the self-managed procedures (Skinner & Smith, 1992).

Both CCC and TP contain many different components. Future researchers should conduct component analysis studies to determine which component or combination of components caused the increases in accuracy and fluency. Additionally, researchers should consider how manipulating components (e.g., altering the time delays in the TP intervention) can enhance learning rates.

Perhaps the most obvious limitation with the current study is that only one student participated. Researchers should extend the external validity of the current study by conducting similar experiments across students including general education students, students with mild learning disabilities, and students with behavior disorders. Additionally, researchers should compare the effects of these and other treatments across settings including class-wide application and learning centers.

Because acquisition is the first stage of skill development, how students are taught basic math facts and concepts can influence future skill development. Thus, longitudinal studies designed to compare the effects of different acquisition enhancing procedures on future skill development are needed. Specifically, researchers should consider running across subject experiments comparing the effects of enhancing the acquisition of facts and concepts via counting strategies with strategies designed to enhance automaticity (e.g., CCC and TP) to determine which acquisition procedures and/or sequence of procedures results in the highest levels of future skill and concept development.