Introduction

Since the advent of protein structure determination it has been a long time debate if X-ray crystallography is clearly superior to NMR spectroscopy because X-ray structures are better defined than NMR structures. This is true when focusing to the precision of the coordinates when the available crystals diffract sufficiently well. It is often not realized that the two methods cannot calculate directly the three-dimensional structures of proteins from the experimental data but use iterative search algorithms to find a solution that is consistent with the data. The main differences are in the language of NMR spectroscopy that in general in X-ray crystallography the number and precision of the structural restraints is superior and that the back calculation of NMR spectra from structural models is not as straight forward as the back calculation of diffraction patterns.

However, for proteins in solution the question may be ill-posed since the minimum energy state in the crystal lattice (or better the weighted average of the structural ensemble in the crystal) may not correspond well enough to the average of the structural ensemble in solution. There are a number of examples for that in literature; a typical example is HPr from S. faecalis where we could show that the dominant active center structure in solution (Hahmann et al. 1998) clearly differs from the crystal structure (Jia et al. 1994). In many of these cases, probably more than one conformational state (defined by different local energy minima) exists in solution but only one of them is selected by the crystallization conditions. In addition, software packages used in crystallography tend to suppress alternative conformations even when they are present in the single crystals. A prominent case is the Ras protein complex with Mg2+. GppNHp that exists in solution in two almost equally populated conformational states (Geyer et al. 1996; Spoerner et al. 2001). The published crystal structure (Pai et al. 1990) shows only a single, well-resolved structure but solid-state NMR on the same crystals proves that the two conformational states coexist also in the single crystals (Stumber et al. 2002; Iuga et al. 2004).

Even when only one global energy minimum exists that is identical in crystal and solution, the thermally populated states create a conformational ensemble that in general is different in solid state and solution, since the details of the local energy surface will most probably be different. A full structural description of a protein would require the knowledge of the whole ensemble of structures not only a minimum structure because the properties of the protein may depend on a subset of structures which are similar but not identical to the minimum energy structure.

In crystallography, the B-factor is used to describe the thermally induced conformers as the atoms move from their average positions. In solution, classically relaxation time measurements give information about atomic motions in the local conformational space. Chemical shifts could also provide information on the local conformational equilibrium, since they are strongly structure dependent. Close to a single energy minimum they are usually population averaged since the exchange between neighboring states should be fast on the NMR time scale.

The main problem is that protein chemical shifts cannot be predicted with high accuracy, in spite of the many groups that have worked on this problem over the years. The first attempts to calculate protein chemical shifts started already in 1977 (Perkins et al. 1977). In the mean time, a number of programs are available that are able to predict chemical shifts from a structural data base or calculate chemical shifts from a physical model. Popular examples are SHIFTS (Xu and Case 2001) and SHIFTX (Neal et al. 2003) but also other programs exist such as PROSHIFT (Meiler 2003), PSRI (Wang 2004), SPARTA (Shen and Bax 2007), and 4DSpot (Lehtivarjo et al. 2009).

SHIFTS is a program for predicting 15N, 13Cα, 13Cβ, and 13C′ chemical shifts from protein structures. It was developed based on an additive model of chemical shift contributions, corresponding to various conformational effects found in a database of density functional theory (DFT) calculations on more than 2,000 peptides. Some empirical extensions were used for covering additional regions in the conformation space for different residue types. When experimental shifts are available, an optional refinement process for side-chain orientation can also be carried out, which may help identify problems in either the structure or the shift assignments themselves. SHIFTX can be used to predict all backbone and some of side chain 1H, 13C and 15N protein chemical shifts using only its PDB file as input. SHIFTX uses a unique semi-empirical approach to calculate protein chemical shifts.

In this paper we will focus on the ensemble properties of protein structures and their connections to chemical shifts calculated from these ensembles.

Materials and methods

NMR spectroscopy and structures

The sequential assignments of the NMR signals of the set of proteins (Table 1) were taken from the BMRB data base, the corresponding NMR structures from the PDB-data base. Sequential assignments for wildtype HPr(wt) from S. aureus were taken from Maurer et al. (2004), for the mutant HPr(H15A) from Munte et al. (manuscript in preparation).

Table 1 Test data set of proteins
Full size table

Molecular dynamics calculations

Structure calculations on HPr were performed using the molecular dynamics program CNS v.1.2. (Crystallography and NMR System for crystallographic and NMR structure determination) (Brunger et al. 1998). The restraints (Table 2) were employed in a simulated annealing protocol (Brunger 2007) using extended-strands as starting structures. The high number of experimental restraints required a threefold reduction of the time step (default value 15 fs) for the integration of the equation of motion. In the first stage simulated annealing was performed in the torsional angle space starting at 50,000 K and cooling down in 1,000 temperature steps to 0 K. 3,000 time steps were calculated at each temperature. The second annealing stage was performed with Cartesian dynamics with a starting temperature of 1,000 K and a final temperature of 0 K using 1,000 temperature steps. Again, 3,000 time steps were calculated at each temperature. In the final stage, 2,000 time steps of energy minimization were performed. As force field the default settings were used. The obtained structures were accepted based on the NOE violations. Those structures having more than 5% NOE violations after the final energy minimization were rejected. Once 2,000 structures were calculated using the above simulated annealing protocol, they were refined in explicit water using the TIP3P model (Jorgensen et al. 1983) according to a protocol given by Linge et al. (2003). It consists of three stages, a heating stage from 100 to 500 K, a refinement stage at 500 K, and a cooling stage from 500 to 25 K followed by a short conjugate gradient minimization. The force field OPLSX (Jorgensen and Tirado-Rives 1988) proposed in this protocol was used. After the water refinement the population distribution is fitted with a Gaussian distribution and those structures whose energy is >5σ is removed and refined again with different initial seeds until their energies were <5σ.

Table 2 Number of experimental restraints used for the calculation of the structural sets of wildtype HPr and the mutant HPr(H15A)
Full size table

Programs and structure validation

The program PROCHECK_NMR (Laskowski et al. 1996) was employed to check the stereochemical quality by calculating Ramachandran plots. The program MOLMOL (Koradi et al. 1996) was used to display the structures and to calculate the RMSD-values. The combined chemical shift based error ε (eq. 4–8) were calculated with the chemical shift and atom specific weighting factors published by Schumann et al. (2007).

Theoretical considerations

Structural ensembles and chemical shifts

In solution, a protein is described by a multistate energetic profile, at a given time t it is described by a space ensemble S V = {s 1, s 2,…s N } with N the number of molecules in the solution. In a typical NMR experiment (0.5 mL of a 1 mM solution) N equals to 3.01 × 1020. In addition, for each individual molecule in solution a time ensemble S T is defined as all structural states visited in a time interval Δt. The NMR spectrum obtained in a typical repetitive nD-NMR experiment represents a non-uniform spatial and temporal average of these states. However, the averaging mechanism depends on different NMR properties (e.g., chemical shift and J-coupling), that vary from atom to atom in the same molecule, and may also depend on the path on the energy landscape.

In a time interval Δt the ensemble can be divided in subsets where the exchange between different states is fast on the NMR time-scale for a given atom i. For these subsets S k of N k molecules the chemical shift δ i of an atom i corresponds to the population average 〈δ i (s j )〉 of the shifts δ i (s j ) with

$$ \langle \delta_{i} \rangle = {\frac{1}{{N_{k} }}}\sum\limits_{j = 1}^{{N_{k} }} {\delta_{i} (s_{j} )} $$
(1)

The fast exchange condition can be defined by

$$ {\frac{1}{{\tau (s_{j} ,s_{k} )}}} \gg |\omega_{i} (s_{j} ) - \omega_{i} (s_{k} )| $$
(2)

with τ(s j , s k ) the exchange correlation time for the transition between states j and s k , and ω i (s j ) and ω i (s k ) the resonance frequencies of nucleus i in states s j and s k , respectively. In its simplest form the fast exchange condition must apply for all pairs of states s j and s k .

Since in the repetitive NMR experiment time averaging over the possible M* structural sub states of the total ensemble M where mutual fast exchange conditions exist is also performed, eq. 1 is better written as

$$ \langle \delta_{i}^{*} \rangle = \sum\limits_{j = 1}^{{M^{*} }} {p(s_{j} )\delta_{i} (s_{j} ) = \frac{1}{Z}\sum\limits_{j = 1}^{{M^{*} }} {\delta_{i} (s_{j} )e^{{ - {\frac{{G(s_{j} )}}{RT}}}} } } $$
(3)

Here, δ * i is the chemical shift of atom i in the sub states in mutual fast exchange, p(s j ) the probability to find state s j , Z the state sum over all possible structural states of M*, and G(s j ) the corresponding free enthalpies. Note that the fast exchange condition has not to be fulfilled for all atoms of the macromolecule simultaneously since the selection of structural states enclosed in M* depends on the differences of the resonance frequencies of the states.

For the sake of simplicity we will restrict in the following to an ensemble where for all (or essentially all) structures fast exchange conditions apply (M* = M). Let us denote the experimentally measured chemical shift of atom i as \( \delta_{i}^{e} \), the predicted average chemical shift of the same atom in a structure \( s_{j} \) in the ensemble as \( \delta_{i}^{p} (s_{j} ) \). Then the mean of the predicted chemical shifts \( \delta_{i}^{p} \) of the ensemble of N structures is given by

$$ \langle \delta_{i}^{p} \rangle = \frac{1}{N}\sum\limits_{j = 1}^{N} {\delta_{i}^{p} (s_{j} )} $$
(4)

Using the Hamming distance the error ɛ i in the back calculation for a single atom i can be defined as

$$ \varepsilon_{i} = |\langle \delta_{i}^{p} \rangle - \delta_{i}^{e} | $$
(5)

Alternatively, using the Euclidean distance it would be defined as

$$ \varepsilon_{i} = \frac{1}{N}\sqrt {\sum\limits_{j = 1}^{N} {\left( {\delta_{i}^{p} (s_{j} ) - \delta {}_{i}^{e} } \right)^{2} } } $$
(6)

The mean error ɛ for a subset of n atoms (e.g., all backbone atoms HN, N, Cα, C in the protein or all atoms of a given amino acid) of structural ensemble is defined as

$$ \varepsilon = {\frac{1}{{\sum\nolimits_{i = 1}^{n} {w{}_{i}} }}}\sum\limits_{i = 1}^{n} {w_{i} \varepsilon_{i} } $$
(7)

or alternatively

$$ \varepsilon = \sqrt {{\frac{1}{{\sum\nolimits_{i = 1}^{n} {w_{i}^{2} } }}}\sum\nolimits_{i = 1}^{n} {(w_{i} \varepsilon_{i} )^{2} } } $$
(8)

where w i are weighting factors e.g., the atom and amino acid specific weighting factors as defined by Schumann et al. (2007). The second moment σ 2 of the errors ɛ i of a selection of n atoms is then

$$ \sigma^{2} = \langle w_{i}^{2} \varepsilon_{i}^{2} \rangle - \langle w_{i} \varepsilon_{i} \rangle^{2} = {\frac{1}{{\sum\nolimits_{i = 1}^{n} {w_{i}^{2} } }}}\sum\limits_{i = 1}^{n} {(w_{i} \varepsilon_{i} - \varepsilon )^{2} } $$
(9)

The expectation value of ɛ should go to zero if (1) the experimental data are error free, (2) the experimental ensemble and the ensemble used for the prediction of the chemical shifts are identical and (3) the chemical shift calculation is perfect. In practice, all three conditions are not fulfilled. The experimental data have errors that are caused by assignment errors and the limited precision of chemical shift measurements. The experimental ensemble is not known but has to be replaced by an ensemble obtained from the structure calculation, usually in NMR spectroscopy a restrained molecular dynamics simulation followed by an energy minimization. In general, the number N p of structures is also much smaller than the experimental ensemble with N of the order of 1020. Up to now the classical chemical shift calculations are far from perfect although they are getting better with time.

The error ɛ can then be written as a function of the experimental error in the experimental determination of chemical shifts Δδ e, the differences between the experimental ensemble and the calculated ensemble ΔS and the error of the chemical shift calculation method Δδ s as

$$ \varepsilon (\Updelta \delta^{e} ,\Updelta S,\Updelta \delta^{s} ) = \varepsilon (0,0,0) + {\frac{\partial \varepsilon (0,0,0)}{{\partial \Updelta \delta^{e} }}}\Updelta \delta^{e} + {\frac{\partial \varepsilon (0,0,0)}{\partial \Updelta S}}\Updelta S + {\frac{\partial \varepsilon (0,0,0)}{{\partial \Updelta \delta^{s} }}}\Updelta \delta^{s} $$
(10)

Although the prediction error Δδ s not only depends on the simulation method C used and the atom types T included in calculation but also on specific structural properties of the protein under consideration, for a given method C it can be approximated by a constant Δδ s(C, T) and the corresponding derivative by 1 when enough atoms are involved in the calculation. When we neglect the small experimental error Δδ e and realize that in the above definition ɛ(0, 0, 0) must vanish, this means that eq. 10 simplifies to

$$ \varepsilon = {\frac{\partial \varepsilon (0,0,0)}{\partial \Updelta S}}\Updelta S + \Updelta \delta^{s} (C,T) $$
(11)

At first glance, the error ΔS of the structural ensemble depends on two factors, the correctness of the calculated structures and of the structural ensemble obtained. Even if the two conditions are sufficiently well fulfilled, it is a practical problem to select a minimum number of structures that can represent the experimental structural ensemble from the point of averaged chemical shifts. Therefore, ΔS also is a function of the usually arbitrarily chosen number N of structures that are either ordered according to their energies with the lowest energy assigned to structure s 1 or according to the probability.

Results

Prediction of chemical shifts in a test data set

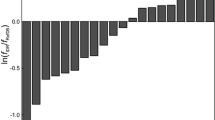
Wang and Jardetzky (2002) prepared a data set of proteins where high resolution structures and heteronuclear chemical shift data were available for the development of a new method of secondary structure prediction. Here, we use a subset of 16 NMR structures for an analysis of the chemical shift predictions (Table 1) where structural bundles are deposited in PDB database. For obtaining an estimate of Δδ s the chemical shifts were calculated with the program SHIFTX and SHIFTS for these structures and compared with the experimental data. The mean ɛ and the second moment σ 2 was calculated using eq. 7 and 9. The deviation of the predicted combined chemical shifts Δδ comb of the backbone atoms from the experimental chemical shifts are shown in Fig. 1. The chemical shifts were calculated from the first structure in the data base (usually the lowest energy structure) and the total ensemble. In general the performance of SHIFTX is slightly better for all structures studied than that of SHIFTS, for the single structure as well as for the ensemble. The weighted mean over all 16 proteins drops from 0.63 to 0.58 ppm for SHIFTX, and from 0.66 to 0.61 ppm for SHIFTS. The non-weighted average for all atoms (Tables 3, 4) drops from 0.66 to 0.61 ppm for SHIFTS and from 0.63 to 0.58 ppm for SHIFTX. The same trend, that SHIFTX gives a more correct prediction than SHIFTS, is observed for the majority of the predicted chemical shifts of groups of atoms (Tables 3, 4). Especially the predicted chemical shifts of the backbone resonances are more precise for SHIFTX.

Fig. 1
figure 1

Precision of chemical shift predictions. The weighted chemical shift deviations ɛ (eq. 7) are plotted for the structures listed in Table 1. The amino acid and atom specific weights used to calculate the combined chemical shifts Δδ comb are defined by Schumann et al. (2007). The chemical shifts were calculated from the lowest energy structure with SHIFTX (white bars) and SHIFTS (dotted white bars) or from the available structural ensemble with SHIFTX (gray bars) and SHIFTS (dotted gray bars). Only those atoms were considered that could be predicted by both methods

Full size image
Table 3 Average performance of chemical shift prediction for specific atoms using SHIFTS
Full size table
Table 4 Average performance of chemical shift prediction for specific atoms using SHIFTX
Full size table

Effect of ensemble size and quality

Ensemble size

In line with the fact that the experimentally observed chemical shifts are ensemble averages, the chemical shift predictions calculated as averages over the structural ensemble, the prediction of the chemical shifts from the ensembles is always more correct. This is clearly seen for the weighted shifts depicted in Fig. 1 where the chemical shift prediction is more accurate for all proteins when ensembles are used. Also for the ensembles the predictions by SHIFTX are again always better than those of SHIFTS. For individual types of atoms the ensemble prediction is always more precise than that obtained from the lowest energy structure independent of the prediction method used (Tables 3, 4). However, when applying the t-test to the data, the improvement is very significant when all atoms or all backbone or all side chain atoms are used (Tables 3, 4) but it is not always significant with p < 0.05, essentially because sometimes the number of events in the data base is too small.

The data base used contains only relatively small structural ensembles, usually of the order of 20 structures. A complete description of a real structural ensemble would most probably require a much larger number of structures. Therefore, we calculated large ensembles of 2,000 structures each for wildtype HPr and a mutant HPr(H15A) from S. aureus (Maurer et al. 2004; Munte et al. to be published). The number of experimental restraints used for the simulated annealing (SA) is given in Table 2. Structures that obviously did not converge and therefore showed large violations of the experimental restraints (see “Materials and methods”) were removed before analysis. The remaining structures were ordered according to their total energies (not including the pseudo energies from experimental restraints) and the weighted cumulative shift difference ɛ(N) (with s 1 the lowest energy structure) was plotted for the backbone atoms as well as for all atoms (more precisely for all atoms with assigned chemical shifts). Figure 2 shows clearly that ε(N) first decreases substantially for the two proteins and shows an asymptotical behavior. The shape of the function is virtually independent on the prediction method used; however, the magnitude of the effect strongly depends on the atoms selected: the lowest values are obtained for the side chain atoms, the highest values for the main chain atoms, and intermediate values for the weighted average of all atoms (constant C in Table 5). The data can rather well be fitted by a lognormal distribution with an additional offset.

Fig. 2
figure 2

Dependence of the chemical shift error ε on the size of the structural ensemble before water refinement. The structures used were obtained by restrained simulated annealing (see “Materials and methods”). The weighted mean error ɛ of the back bone atoms HN, Hα, N, Cα, C (circle), side chain atoms (triangle) and all atoms (square) were plotted as a function of the size N of the ensemble using the Hamming distance (eq. 5). a HPr(wt) type using SHIFTS (black) and HPr(wt) using SHIFTX (gray); b HPr(H15A) using SHIFTS (black), and HPr(H15A) using SHIFTX (gray). The data were fitted with a lognormal distribution \( \varepsilon = {\frac{1}{{N\sigma \sqrt {2\pi } }}} e^{{ - {\frac{{(\ln N)^{2} }}{{2\sigma^{2} }}}}} + C \) and the value of C for back bone atoms (dashed line), side chain atoms (dotted line), and all atoms (solid line) is represented by a straight line

Full size image
Table 5 Minimum ensemble size and error offset
Full size table

Refinement of the obtained structures in explicit water in general leads to an improved quality of the structures and possibly also to a change of ε(N). Therefore, all the 2,000 structures were subjected to a water refinement and ε was recalculated. When the refined structures are given as input the prediction error decreases significantly at the same ensemble size (Fig. 3). However, for large ensembles the asymptotic value differs only slightly by a few percent (Table 5).

Fig. 3
figure 3

Dependence of the chemical shift error ε on the ensemble size after water refinement. The structures used were obtained from the ensemble shown in Fig. 2 by refinement in explicit water (see “Materials and methods”). The weighted mean error ɛ of the back bone atoms HN, Hα, N, Cα, C (circle), side chain atoms (triangle) and all atoms (square) were plotted as a function of the size N of the ensemble using the Hamming distance (eq. 5). a HPr(wt) using SHIFTS (black) and HPr(wt) using SHIFTX (gray); b HPr(H15A) using SHIFTS (black) and HPr(H15A) using SHIFTX (gray). The data were fitted as described in Fig. 2. The value of the parameter C for back bone atoms (dashed line), side chain atoms (dotted line) and all atoms (solid line) is represented by a straight line. c The plot represents expansions of Figs. 2a, b and 3a, b. The mean weighted error ɛ(N) of the backbone atoms are plotted as function of the size of the ensemble. Only the first 50 structures are shown. HPr(wt) before (circle) and after (square) water refinement, HPr(H15A) before (diamond) and after (triangle) water refinement. Solid line shows the corresponding lognormal fit. Only the data calculated with SHIFTX are depicted

Full size image

The largest differences are observed for small ensemble sizes (Fig. 3). Here, water refinement leads to much smaller initial values for the prediction errors. The data can sufficiently well be fitted by the lognormal distribution; however at very small sample sizes a substructure is clearly observable. Without water refinement about 18 structures are necessary for coming close to the asymptotic value, after water refinement only 10 structures are required.

For the structures contained in the experimental data base (Table 1) the same analysis leads to analogous results when we assume that the structures are ordered according to their energies (a fact not known). In general, the ensemble gives better performance of the chemical shift prediction by SHIFTX (Fig. 4) and SHIFTS (data not shown). In most cases a minimum value seems to be reached when about 18 structures are used for the calculations.

Fig. 4
figure 4

Chemical shift error as a function of the ensemble size for the structural data base. The curves shown are fit curves as defined in Fig. 2 of the structures contained in the experimental data base (Table 1). The chemical shift predictions were performed with SHIFTX

Full size image

Energy distributions and their impact on the chemical shift prediction

The ensembles obtained for wildtype HPr and its mutant by simulated annealing followed by refinement in explicit water should not be determined mainly by the experimental pseudo energies but by the physical model itself. Figure 5 shows the energies with and without inclusion of the pseudo energies resulting from the restraint violation. The energies were ordered according to their magnitude for the 2,000 structures. It is obvious that the restraint violations only contribute little to the energy. The probability distributions of the energies are represented in Fig. 5c and d and can be fitted in a good approximation by a Gaussian.

Fig. 5
figure 5

Population of energy states. The structures of wildtype HPr (a) and mutant HPr (b) were ordered according to their total energy (N = 1,…,2000). The total energy (solid line) and the sum of the total energy and the violation energy (dotted line) were plotted as a function of N. c, d The probability of each energy state was plotted as function of total energy (all energies excluding the experimental pseudo energies) and fitted with Gaussian function: c HPr(wt), mean energy 〈E〉 = −3358.5 kcal/mol, σ = 274.0 kcal/mol; and d HPr(H15A), 〈E〉 = −3358.5 kcal/mol, σ = 233.5 kcal/mol. All structures were refined in explicit water, structures which have more than 5% NOE violation were removed before water refinement and structures having energies greater than 3σ were refined again with different random seed

Full size image

The quality of the chemical shift prediction of smaller sets of structures may depend on the total energy of the structures under consideration. This was tested for wildtype and mutant HPr in two different ways: either (1) the total ensemble (ordered according to the total energy) was divided in classes of energies that were multiples of the standard deviation σ starting from the mean value or (2) classes containing the same number of 20 structures (Fig. 6) ordered according to their energies. In the first case, a second order polynomial was required to fit the data; in the second case a first order polynomial was sufficient.

Fig. 6
figure 6

Dependence of the prediction error on the energy of the ensemble. The prediction error ɛ for the backbone atoms is plotted as a function of the total energies E. The probability distribution of the energy E was divided a in classes E n representing multiples of the standard deviation σ that is ɛ(E n ) = 〈ɛ(E)〉 with \( E \in \left( {\langle E\rangle + \left( {n - 1} \right)\sigma ,\langle E\rangle + n\sigma } \right] \) or b in classes E n (n = 0,…) containing 20 structures ordered according increasing values of E − E min. Squares, prediction with SHIFTS; circles, prediction with SHIFTX; black. HPr(wt); gray, HPr(H15A). The data were fitted with a polynomial of first or second order

Full size image

Discussion

Multiconformational ensembles and conformational averaging of chemical shifts

From first principles of thermodynamics it is clear that protein structures in solution form a large ensemble of multiple conformational states. A complete description of a protein would require the knowledge of all coexisting structures; even the knowledge of energetically unfavorable states that are only weakly populated may be important since functional excited states or folding intermediates may be contained in the higher energy part of the energy landscape (Kalbitzer et al. 2009). A complete representation of all states is practically not possible because of the extremely large number of states. Even when one restricts to the ground state ensemble, only the representation of a limited selection of structures is feasible. However, it is not clear, which structures should be selected as being representative for the total ensemble and how many structures must be included for a faithful representation of the ensemble.

Indeed, the definition of a faithful representation of the ensemble depends on the properties of the ensemble that should be represented. In biochemistry, it would often focus on the explanation of functional properties. In the present context, the following general questions are important: (1) Can the quality of the chemical shift prediction be increased by using ensembles of structures in agreement with theory, (2) is the improvement of the prediction by using ensembles independent of the method used, (3) what is the minimum size of the ensemble required for optimum chemical shift prediction, and (4) can the chemical shift prediction be used to define the representative ensemble?

Quality of the chemical shift prediction

For testing and quantifying the quality of the chemical shift prediction we used a set of NMR structures (Table 1) previously designed by Wang and Jardetzky (2002). In general, from the two programs tested here SHIFTX performs somewhat better than SHIFTS, the weighted average error of all atoms of 0.340 ppm calculated with SHIFTX for the lowest energy structure is about 8.2% lower than 0.368 ppm calculated with SHIFTS (Tables 3, 4). The standard deviations of the errors ɛ are for all atom groups rather high (almost as large as the mean itself), indicating that either the structural quality varies much or that the parameterization is not optimal for all conditions found in the structures. From the data itself this cannot be decided but probably variations in the structural quality as well as the computational methods used for the structure calculation may be the dominant factor for these variations. The prediction error varies for the different atom types. For SHIFTX we found mean errors of 0.52, 0.28, 2.53, 1.04, and 1.28 ppm for the HN, Hα, N, Cα, and C atoms, respectively. Similar results were published most recently by Lehtivarjo et al. (2009) for a smaller data base of protein structures with 0.55 and 0.37 ppm for the HN and Hα resonances. Similar results were also published earlier by Arun and Langmead (2004). For the side chain atoms the prediction error is usually much smaller (Tables 3, 4), one factor is the smaller chemical shift variations found here experimentally. However, this cannot be the only reason since the backbone prediction error is also larger than the side chain prediction error when it is calculated with the amino acid type and atom type specific weighting factors (Schumann et al. 2007) that correct for the chemical shift distribution of the atoms under consideration. The chemical shift prediction by SHIFTS and SHIFTX (and by all methods published so far) is still more than one order of magnitude too inaccurate when it should be used for a direct assignment of resonances: here a precision of the order of the typical line width would be required that is about 0.01 ppm for proton and about 0.1 ppm for nitrogen resonances.

Prediction of chemical shifts from the ensemble or the lowest energy structure

In accordance with the fact that chemical shifts represent ensemble averages the use of ensembles generally improves the chemical shift prediction for all structures of the data base (Fig. 1) and for most of the atoms taken into account (Tables 3, 4). The weighted mean error of all atoms decreases by 8.8% when SHIFTX is used and 8.3% when SHIFTS is used. The statistical significance of the observed decrease of the individual prediction errors is not equal for all groups of atoms considered, however atoms and groups of atoms with a large number of observations mostly have p values < 0.05, although exceptions are existing (Tables 3, 4). It also is to be expected that an improvement by averaging over ensembles is largely independent on the prediction method used as it is shown here for SHIFTS and SHIFTX. In fact, for 4Dspot a similar result has been reported recently.

Minimum size of the ensemble required for chemical shift prediction

Usually 10–20 NMR structures are stored in the data base. Our result indicates that this is sufficient as far as the chemical shift prediction is concerned. The extensive simulation of the HPr structures shows that an asymptotic value is reached before water refinement when about 18 structures are averaged (Figs. 4, 5), after water refinement when about 10 structures are averaged (Fig. 4). Under this aspect the traditional way to deposit NMR structures can be considered as sufficient. When during the calculation of the structures those structures are removed that show large violations of the experimental restraints and thus have not converged properly, the error dependence of the chemical shift prediction on the size of the ensemble can be sufficiently well described by a lognormal distribution with a constant offset. Whereas the description with a lognormal distribution is purely empirical, the asymptotic behavior to a constant value can be expected from the chemical shift averaging (eq. 3). However, when the structures with larger pseudo energies (badly converged structure calculations) are included, a continuous increase of the prediction error with the number N can be observed (data not shown).

Dependence of the prediction error on the energy distribution

From a general point of view it is surprising that a very small number of low energy structures can lead to a virtual optimum ensemble when the chemical shift prediction is concerned, although they clearly are not representative for the experimental ensemble but by definition only represent weakly populated states. The obtained energy distributions are shown in Fig. 5c and d for HPr that can be approximated well by a Gaussian. Structures having energy values less than −2σ relative to the mean energy are considered as lowest energy structures, energy values between −σ and +σ are considered as most probable structures and structures above +2σ are considered as high energy structures. When the prediction error is plotted as a function of the deviation from the mean a minimum prediction error is detected close to the most probable ensemble at the mean energy (Fig. 6a) as to be expected from theory. However, the effect is rather small. In the intervals between \( \left[ {\langle E\rangle - \sigma ,\langle E\rangle } \right] \) and \( \left[ {\langle E\rangle ,\langle E\rangle + \sigma } \right] \) the number of calculated structures is much higher than in the other intervals. This may cause a bias on the data evaluation favoring the chemical shift prediction from the larger ensemble of structures. Therefore, the structures were sorted according to their energies and sets of identical size (20 structures) were taken for the chemical shift prediction. Here, a minimum of the error cannot be detected anymore but the prediction error is almost constant and can be well approximated by a straight line with a very small positive slope (Fig. 6b).

Prediction error

The experimentally observed prediction error Δδ S(C, T) (eq. 11) is still rather large for all prediction methods C and for all atoms T considered and is especially large for the backbone atoms. It is much larger than the effects resulting from the ensemble averaging itself, according to the analysis of our structural data basis the ensemble effect ΔS is of the order of 10% of the Δδ S(C, T) (Table 3, 4). Therefore, it is not surprising that we can only observe small effects from the selection of the structural ensemble (Fig. 6). In fact, using the same ensemble size, the quality of the ensemble prediction slightly decreases with the mean energy of the structural set. This bias may be caused by the parameterization procedure and the calculation methods itself that are optimized to obtain the lowest energy NMR structures but not a full structural ensemble in thermal equilibrium. In addition, the parameters of chemical shift predictions are usually optimized with respect to crystal structures that clearly do not represent the solution ensemble measured experimentally and thus may also introduce a bias in the prediction methods towards lowest energy structures and cause a contribution to the prediction error of chemical shifts Δδ S. In a most recent paper, that appeared during the preparation of this manuscript, Lehtivarjo et al. (2009) show that indeed better results can be obtained when MD-ensembles are used for parameterization.

Conclusion

There are a number of good reasons to use an ensemble of structures instead of a single energy minimized structure for chemical shift predictions as well as for functional analyses. The minimum energy structure calculated by restraint molecular dynamics, simulated annealing, and water refinement are actually only representing a subset of structures in the conformation space. The method is not aimed to describe the structural ensemble at a given temperature in thermal equilibrium. However, in the presence of experimental restraints the method creates ensembles that NMR spectroscopists assume to somewhat represent the conformational space at the experimental conditions where the NMR experiments were performed. Experimentally, chemical shift prediction can be improved significantly when a structural ensemble is used. An ensemble size of about 20 structures is sufficient, further increase of the size seems not to lead to better results. The conclusion primarily holds for the two tested, most popular prediction programs SHIFTX and SHIFTS but for theoretical reason most probably also applies for other prediction programs.

The calculation methods used in NMR spectroscopy are aimed to find the lowest energy structure with respect to the experimental restraints, the obtained ensemble is mainly determined by the reduction of the accessible conformational space, not by the MD-potentials. Nevertheless, properties of the true ensemble under the experimental conditions given are reflected in these restraints and lead to calculated ensembles that have some similarities to true thermodynamic ensembles. An interesting question not dealt with in this paper would be, under what conditions a perfect MD simulation of protein in explicit water at a given temperature would provide even better chemical shift predictions or if the inherent prediction error Δδ S not optimized for ensembles would prevent such an effect.