1 Introduction

Zinc oxide (ZnO) is a direct band gap (as per E-k diagram) II–VI semiconductor material with high interest in the research field as a result of its potential use in different technological applications, for example, transparent conducting electrodes, LED (light-emitting diodes) fabrication, UV lasing, gas sensors and chemical sensing, optical solar cells and various photovoltaic devices, catalysis, laser frameworks, biomedical applications, etc. [1,2,3,4,5]. The bulk ZnO displays high band gap energy with value 3.37 eV at room temperature [1,2,3,4,5]. It crystallizes in a hexagonal wurtzite structure with excitonic energy of 60 meV at room temperature [1,2,3,4,5]. It additionally displays many fascinating properties, like magnetic properties, piezoelectricity [6, 7]. ZnO has high chemical and thermal stability and doesn’t effortlessly oxidize in the air. Generally, ZnO is an n-type material (semiconductor), with point local defects and imperfections such as oxygen vacancies (Vo) and zinc interstitials (Zni+) influencing its electrical characteristics [8]. The structural, optical, electrical, dielectric and other various properties of ZnO are influenced by its particle size, morphology, purity and compound synthesis of reactants and the development mechanism [9, 10]. The electrical properties of semiconductor materials are significantly change in the nanoscale compared to their bulk counter. This change in the nanoscale is due to the high surface-to-volume proportion of grains, little size, microstructural changes upgraded commitment from grains and grain limits [11, 12]. In nanoscale quantum confinement of charge transporters, band structure alteration and deformities in grains are a portion of the elements that add to the electrical properties of nanostructured materials [11]. Electrical properties in nanoscale would be altered in a variety of ways, including impedance spectra and dielectric conduct. As a result, it's crucial to look at the electrical transport and overall dielectric performance of ZnO nanosystems. Dielectric characteristics of ZnO nanorods, nanowires, nanoparticles, and their different composites are studied by numerous researchers [13,14,15]. Schmidt et al. studied details about the conductivity of ZnO material with surface modification [16]. Ahmad et al. studied dielectric properties of different sizes ZnO NPs (22–98 nm) with temperature ranging from 80 to 320 K [17]. Different researchers like Baset et al., Mazhdi et al., El-Desoky et al. studied dielectric properties of ZnO NPs [15, 18, 19]. Zulfiqar et al. studied basic dielectric properties of ZnO and Co, Mn co-doped ZnO NPs at a particular temperature [20]. But they have not included details relaxation mechanism and large-scale temperature variation along with high temperature region. Soliman et al. studied optical properties and dielectric response for Polyvinyl Alcohol/ZnO Nanocomposite systems with two different frequencies 100 Hz and 10 kHz [21]. Recently, dielectric properties of different metal doped ZnO NPs and polymer-ZnO NPs composites are studied by different researchers [22,23,24,25,26]. We also previously reported about the temperature dependent some electrical parameters of ZnO NPs [27]. Albeit, different researchers have contemplated the electrical properties of nanoscale ZnO, a total investigation of different dielectric parameters along with relaxation properties in a wide frequency and temperature run for pure ZnO NPs is as yet deficient. The novelty of this study is the exploration of large-scale temperature effects and frequency-dependent dielectric properties, the conductivity study, electric modulus and impedance spectrum analysis along with defect-related relaxation mechanism in details for pure ZnO NPs with an average size 32.5 nm. Also, this study highlights different band structure parameters along with optical and structural properties of such semiconductor nanoparticles.

Here, we focussed on the dielectric properties, electric modulus, conductivity and complex impedance spectroscopy (CIS), AC conductivity with the variation of frequency from 1 o 100 kHz and temperature from 323 to 673 K.

The current study investigates on the optical, structural, electrical and dielectric properties of ZnO nanoparticles, it helps to understand dielectric relaxation properties and electric modulus-based AC conductivity.

2 Experiment

2.1 Materials and growth of ZnO NPs

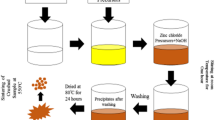
A simple chemical method is used for the fabrication of ZnO NPs, as reported elsewhere [27]. The used chemicals are (i) Zinc nitrate hexahydrate (Zn (NO3)2.6H2O), (ii) sodium hydroxide (NaOH), (iii) ethyl alcohol. Zinc nitrate hexahydrate was purchased from Merck (228737-Sigma-Aldrich) with reagent grade 98% and NaOH was purchased from Merck (S0899-Sigma-Aldrich) with ACS reagent, > 97.0%, pellets. Ethyl alcohol, Pure was purchased from Merck (E7148-Sigma-Aldrich) with assay > 95%. The above chemicals were used in the ZnO nanoparticle fabrication process as supplied (Merck). In this fabrication process, ethyl alcohol was used as a solvent. First 100 mL (0.5 M) Zinc nitrate hexahydrate solution in a flux was stirred through 30 min under constant magnetic stirring. Then, 50 mL (0.5 M) NaOH solution was added dropwise into the Zinc Nitrate Hexahydrate solution.

After a complete mixture of the two solutions, magnetic stirring was continued for twenty-four hours. At the tip of the reaction the white precipitate deposited at very cheap of the flux was collected, filtered, washed many times by de-ionized water and dried at one-thousand-degree temperature for other characterizations. Flowchart of the ZnO NPs growth procedure is shown in Fig. 1.

Fig. 1
figure 1

Flow chart of the ZnO NPs growth procedure

Full size image

2.2 Instrumentation and characterization

Optical UV–Vis spectroscopy of ZnO NPs was measured under absorption mode with wavelength ranges 200–900 nm by using Shimadzu-Pharmaspec-1700 UV–Vis spectrometer. X-ray diffraction of the ZnO NPs power sample was carried using Rigaku X-ray diffractometer system with copper Kα radiation (λ = 1.54A°) over the diffraction angle (2θ) 20° to 80°. Transmission electron microscopy (TEM) and SAED pattern was observed by JEOL JEM-2100F microscope with the operating voltage of 200 kV. Carbon-coated copper grid was used for the TEM sample preparation. A ‘HIOKI 3532–50 LCR Hi Tester’ was used to measure the samples’ dielectric characteristics. A parallel plate capacitor of the ZnO NPs was made by the disc shaped pressed pallet. The ohmic contact was done using silver paste on both sides of the pallet. The capacitance (Cs) and the dissipation factor, D = tan(δ), phase angle (ϕ) and impedance (Z) of the pallet were directly measured in the frequency range 1 kHz to 100 kHz at different temperatures (323–673 K).

3 Results and discussion

3.1 UV–vis spectrum and optical properties

The UV–vis optical spectrum (wavelength, λ = 200–900 nm) of the fabricated ZnO NPs (inset of Fig. 2a), shows a strong excitonic absorption peak at ~ 365 nm. The optical band gap of the ZnO NPs is studied with the accompanying relation (Tauc equation) [28, 29]:

$$\left( {\alpha h\nu } \right)^{2} = c\left( {h\nu - E_{{\text{g}}} } \right)$$

Here, Eg = band gap energy of the ZnO NPs and α is the absorption coefficient. The α value is calculated from UV–Vis optical spectrum [32]. The variation of absorption coefficient (α) as a function of wavelength (λ) is shown in Fig. 2b. The graphical plot of the (αhν)2 versus hν is shown in Fig. 2a, which is used to determine Eg [30]. The value of Eg is found to be ≈ 3.73 eV, which is larger than the bulk ZnO (3.37 eV) [31]. This enhancement in the bandgap energy (∆E ≈ (3.73–3.37) eV = 0.36 eV) compared to bulk ZnO is due to career confinement and formation of discrete energy levels of band in the nanoregion [32]. The dependence of the absorption coefficient with photon energy (hυ) in the lower energy region (1–3.25 eV) can be expressed by the Urbach empirical relation: \(\alpha \, = \,\alpha_{0} \exp \left[ {\frac{h\gamma }{{E_{u} }}} \right]\) [33]. The graphical plot of ln(α) with hγ and its straight line fitting shown in Fig. 2c gives the value of Urbach energy (EU). The average value of EU, calculated from the slope of the straight line is found to be 0.766 eV [34]. Physically, this EU value signifies the crystal disorderness due to the transition from the bulk to nanoregion. The extinction coefficient (K) is calculated from the following formula: K = αλ/4πt, where t = sample thickness. The variation of K with λ is shown in Fig. 2d [35]. Also, the refractive index (n) is studied from the following relation [36, 37]:

$$n = \left( {{1} + {\text{R}}/{1} - {\text{R}}} \right) + \surd \left[ {\left\{ {{\text{4R}}/\left( {{1} - {\text{R}}} \right)^{{2}} } \right\} - K^{{2}} } \right]$$

where R = reflectance. The graphical plot of n with λ is shown in Fig. 3a. Results indicate maximum n value (nmax = 2.75) arises at λ = 900 nm and minimum n value (nmin = 1.71) arises at λ = 200 nm. The plot clearly shows that the normal dispersion (ND) i.e. dn/dλ = − ve occurs with the following wavelength ranges: 336 < λ < 367 nm and 398 < λ < 900 nm, whereas the anomalous dispersion (AD) i.e. dn/dλ =  + ve occurs with two regions: 200 < λ < 336 nm and 367 < λ < 398 nm. The ND and AD regions are marked by dotted lines within Fig. 3a. The excitation is behaving like a light pulse with lower wavelength edge shows ND and higher wavelength edge shows AD. Mostly lower wavelength or UV region is responsible for AD and higher wavelength or visible region is responsible for ND. The dispersion parameters are very important for optical semiconductor material under optical device applications (Fig. 4). Two important parameters, E0 and Ed are determined from the following dispersion relation [38]:

$$\left( {n^{2} - 1} \right)^{ - 1} = \left( {E_{0} /E_{{\text{d}}} } \right) - \left( {1/E_{0} E_{{\text{d}}} } \right) \times \left( {h\upsilon } \right)^{2}$$

where, Ed = dispersion energy and E0 = single oscillator energy. The above refractive index- related dispersion relation is predicated on single oscillator model, called Wemple and DiDomenico (WDD) relation [38, 39]. Variation in (n2–1)−1 vs. (hυ)2 and its linear fitting is shown in Fig. 5d. The calculated values of E0 and Ed are 3.68 and 11.15, respectively. The calculated vale of E0 ≈ 3.68, nearly close to the band gap energy (≈ 3.73 eV). Physically E0 represents the average energy of the oscillator and Ed represent average strength of the inter-band optical transitions. Also, the optical dielectric property is studied to understand the general band structure of ZnO nanomaterial with the help of the following two optical dielectric functions [40, 41]:

$${\text{Real optical dielectric constant (}}\varepsilon^{\prime}_{1} {) } = n^{{2}} - K^{{2}}$$
$${\text{Imaginary optical dielectric constant}}\left( {\varepsilon^{\prime\prime}_{2} } \right)\, = \;{2}nK$$
Fig.2
figure 2

a The variety of (αhν)2 versus photon energy (hν). Inset is the UV–Vis spectrum (λ = 200 to 900 nm); b Variation of Absorption coefficient (α) vs. Wavelength (λ); c Variation of ln(α) vs. photon energy (hν); d Variation of extinction coefficient (K) with wavelength (λ)

Full size image
Fig. 3
figure 3

a Variation of refractive index (n) with wavelength (λ); Plot of (b) Optical dielectric constant (ε1′) vs. λ and c Optical dielectric losses (ε2″) vs. λ of ZnO NPs; d Variation of ε1′ vs λ2 and its linear fitting

Full size image
Fig. 4
figure 4

a The variety of energy loss factor (SELF and VELF) versus photon energy (hν); Plot of b Energy loss factor (SELF and VELF) as a function of optical dielectric constant (ε1′) and c Energy loss factor (SELF and VELF) as a function of Optical dielectric losses (ε2″)

Full size image
Fig. 5
figure 5

a The variety of optical conductivity (σopt) vs. energy (hυ); b Variety of electrical conductivity (σElect.) vs. energy (hυ); c Plot of χc vs λ; d Variation of (n2–1)−1 vs. (hυ)2 and its linear fitting

Full size image

The variation of \(\varepsilon^{\prime}_{1}\) and \(\varepsilon^{\prime\prime}_{2}\) with wavelength is represented in Fig. 3b, c, respectively. The optical dielectric loss associated with \(\varepsilon^{\prime\prime}_{2}\), directly related to the band structure (Eψ(k)c–Eψ(k)v), where ψ(k)c and ψ(k)v are the wavefunction of the conduction band and valence band, respectively [40]. Also, \(\varepsilon^{\prime\prime}_{2}\) is called optical dielectric losses in the material. Optical dielectric response of the semiconductor at lower wavelengths or high-frequency region ɛ∞ is determined with the help of the Spitzer–Fan model. According to this model the relation between \(\varepsilon^{\prime}_{1}\) and λ is given [42, 43]:

$$\varepsilon^{\prime}_{1} = n^{2} - K^{2} = \varepsilon_{\infty } - \left( {e^{2} /4\pi^{2} c^{2} \varepsilon_{0} } \right)\; \times \;\left( {N/m*} \right)\lambda^{2}$$

where, m* = effective mass, N = free carrier concentration, c = speed of light in free space. The graphical plot of \(\varepsilon^{\prime}_{1}\) vs. λ2 and its linear fitted straight line is shown in Fig. 3d, which gives the value of ɛ∞ and N/m*. The calculated value of ɛ∞ and free carrier concentration is found to be 6.5 and 5.55 × 106 per cm3, respectively. This free carrier concentration of ZnO NPs at room temperature is well agreement with the typical semiconductor properties at room temperature.

The energy loss functions are studies from the concept of optical dielectric functions to understand the rate of energy loss inside ZnO NPs. The functions are implemented by the following relations [44]:

$${\text{Volume energy loss }}\left( {{\text{VELF}}} \right) = \;{{\varepsilon^{\prime\prime}_{2} } \mathord{\left/ {\vphantom {{\varepsilon^{\prime\prime}_{2} } {\left( {\varepsilon_{1}^{\prime 2} + \varepsilon_{2}^{\prime \prime 2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\varepsilon_{1}^{\prime 2} + \varepsilon_{2}^{\prime \prime 2} } \right)}}$$
$${\text{Surface energy loss }}\left( {{\text{SELF}}} \right) = {{\varepsilon^{\prime\prime}_{2} } \mathord{\left/ {\vphantom {{\varepsilon^{\prime\prime}_{2} } {\left\{ {\left( {\varepsilon^{\prime}_{1} + 1} \right)^{2} + \varepsilon_{2}^{\prime \prime 2} } \right\} }}} \right. \kern-\nulldelimiterspace} {\left\{ {\left( {\varepsilon^{\prime}_{1} + 1} \right)^{2} + \varepsilon_{2}^{\prime \prime 2} } \right\} }}$$

The variation of VELF and SELF with energy is shown in Fig. 4a. The plot clearly indicates that VELF value is higher than SELF throughout all photon energy, but the variation is similar. A peak arises at the energy 3.38 eV in both of the SELF and VELF graph. Beyond the photon energy 5.38 eV, rate of increase of VELF is much faster than SELF with a significant gap between them. Energy loss factors (VELF and SELF) depend on \(\varepsilon^{\prime}_{1}\) and \(\varepsilon^{\prime\prime}_{2}\). The graphical variations of energy loss factors with \(\varepsilon^{\prime}_{1}\) and \(\varepsilon^{\prime\prime}_{2}\) are shown in Fig. 4b, c, respectively.

The optical conductivity (σOpt.) and electrical conductivity (σelect.), can be determined by the following Eqs. (3) [39, 45, 46]:

$$\sigma_{{{\text{Opt}}}} = {{n\alpha {\text{c}}} \mathord{\left/ {\vphantom {{n\alpha {\text{c}}} {{4}\pi }}} \right. \kern-\nulldelimiterspace} {{4}\pi }}$$
$$\sigma_{{{\text{elect}}}} = \left( {{2}\lambda /\alpha } \right)\sigma_{{{\text{Opt}}}}$$

The variation of the σOpt and σelect. with photon energy (hυ) is presented in in Fig. 5a, b, respectively. The σOpt value gradually increases with an increase in the optical energy up to 3.39 eV, then decreases up to 3.74 eV. Beyond the energy 3.74 eV, it gradually increases up to energy 6.2 eV. The minimum and maximum values of σOpt are 4.35 × 106 s−1 (at energy = 1.38 eV) and 92.25 × 106 s−1 (at energy = 6.2 eV), respectively.

The resultant plot of σelect shows that it gradually decreases from the maximum value 9.15 × 1010esu to the minimum value 1.67 × 1010 esu with a small fluctuation around 3.37 eV. Another important dimensionless parameter is electrical susceptibility (χc), which represents the degree of polarization during the optical dielectric response inside the solid. The dielectric response of the χc can be represent by the following relation [47]:

$$\chi_{c} = \left( {1/4\pi } \right) \times \left[ {n^{2} - K^{2} - \varepsilon_{0} } \right] = \left( {1/4\pi } \right) \times \left[ {\varepsilon^{\prime} - n_{0}^{2} } \right]$$

where n0 is the static refractive index, can be determined from the relation [39]: n0 = [1 + (Ed/E0)]1/2. The value of n0 is found to be 2.01. The variation of χc with wavelength λ is shown in Fig. 5c. The nature of the variation of χc is similar like \(\varepsilon^{\prime}_{1}\) with the maximum value of 2.73 at 404 nm wavelength.

3.2 X-ray diffraction (XRD) study and analysis of different structural parameters

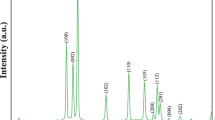
The variation of the X-ray diffraction intensity from the ZnO NPs with the angle of diffraction (2θ) is shown in Fig. 6a. The diffraction pattern shows prominent peaks corresponding to the following crystal planes: (100), (002), (101), (102), (110), (103), (200), (112), (201), (004), and (202). These planes are well matched with the hexagonal crystal phase [48]. The XRD peaks are well matched with the rings appears in SAED pattern (see supplementary S1). The intensities of the different diffraction peaks are different. This intensity variation is due to the anisotropic growth of ZnO NPs along different diffraction direction. The anisotropic growth can be inferred by the clarification of the texture coefficient C(hikili) correlated with the diffraction peaks with Miller indices (hkl). The C(hikili) values are premeditated using the following relation [49, 50, 53]:

$$C(h_{i} k_{i} l_{i} ) = \frac{{I(h_{i} k_{i} l_{i} )}}{{I_{0} (h_{i} k_{i} l_{i} )}}\left[ {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\frac{{I\left( {h_{i} k_{i} l_{i} } \right)}}{{{\text{I}}_{0} \left( {h_{i} k_{i} l_{i} } \right){ }}}} } \right]^{ - 1}$$

Here, I(hikili) and I0(hikili) are the diffraction intensities of the particular (hkl) crystal plane and that from the standard result (JCPDS number 36–1451) of the ZnO semiconductor. The different ‘C(hikili)’ values are tabulated in Table 1. The crystal size of the ZnO NPs (Rhkl) is also calculated from the XRD pattern with the help of the following Scherrer formula (SF) [51]:

Fig. 6
figure 6

a The XRD pattern of the ZnO NPs. b Variation of particle size with different diffraction peaks

Full size image
Table 1 Different structural parameters and texture coefficient of ZnONPs
Full size table
$${R}_{hkl}=\frac{K\lambda }{{\beta }_{1/2}\mathrm{ cos\theta }}$$

The half with (β1/2 or β) corresponding to each diffraction peak is calculated from the Gaussian fitting (Origin Pro 8.5) with the help of the Gaussian equation: \(y = y_{0} + \left( {{A \mathord{\left/ {\vphantom {A {\left( {\beta \times {\text{sqrt}}(PI/2)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\beta \times {\text{sqrt}}(PI/2)} \right)}}} \right) \times \exp \left( { - 2 \times ((x - xc)/\beta )^{2} } \right)\) [52]. The variation of half with (β) corresponding to different diffraction peak is shown in Fig. 7b. The term β signify the broadening of the sample. The exact broadening (/corrected broadening, βcorrected) of the sample for the Gaussian peak is: βcorrected = (β2observed–β2ins)1/2, where βobserved = observed broadening and βins = instrumental broadening [53]. Here, for the crystal size calculation βins is not included, only βobserved = β is included as βobserved >  > βins. The histogram shown in Fig. 6b represents the variation of the calculated crystal size (Rhkl) with diffraction planes. The average crystal size is found to be ~ 30.5 nm. This crystal size of the ZnO NPs from SF is near equal with the HRTEM observed average particle size ~ 31.5 nm (see supplementary S1).

Fig. 7
figure 7

a Variation of the β1/2cosθ vs. 4 sinθ and its linear fitting; b Histogram of β1/2 with different diffraction peaks

Full size image

Different structural parameters of the ZnO NPs are calculated with the help of the following formulas [54]:

$${\text{Unit}}\;{\text{cell}}\;{\text{volume}}\;(V):\; = (\sqrt {3}{/2)(a^{2} c})$$
$${\text{Atomic fraction }}\left( {A_{f} } \right): = \frac{2\pi a}{{3\sqrt {3}{c} }}$$
$${\text{Dislocation density}}\left( \delta \right)\,: = \,1/\left( {R_{hkl} } \right)$$

The lattice constants are a = 3.2267A0 and c = 5.1717A0, respectively, as estimated from (100) and (002) diffraction plans. The unit cell volume is found to be 46.6317(A0)3. The Af and δ are found to be 75.406% and 1.1075 × 10–3 (nm)−2, respectively. All the resultant parameters are tabulated in Table 1.

The ZnO NPs crystal size (D) is also calculated with the help of the Williamson–Hall equation (W–H) [55]:

$$\beta_{1/2} \cos \theta \, = \,\frac{k\lambda }{D} + 4\varepsilon \sin \theta$$

where, ɛ = crystal strain. The slope and intercept of the straight line fitted from the variation of β1/2cosθ vs. 4 sinθ (Fig. 7a) gives ɛ and D, respectively. The resultant plot shows the value of strain (ε) ≈ 0.00152 and average crystal size of ZnO NPs ≈ 35.35 nm. The crystal size obtained from W–H equation is bigger because it included strain. The calculated dislocation density is ≈ 8.003 × 10–4/nm2 from the result of the W–H equation.

3.3 Dielectric measurement and electric modulus

The dielectric properties of the ZnO NPs pallet (circular) of area A (= πr2, r = radius) and thickness d are measured under alternating electric field. The complex dielectric constant (ɛ*) can be expressed in terms of the real part (ɛ') and complex part with the help of the following relation [56]:

$$\varepsilon^{*} (\omega ) = \varepsilon^{\prime}(\omega ) - i\varepsilon^{\prime\prime}(\omega )\quad {\text{were}},\quad i = \sqrt { - 1} ,\quad \omega = 2\pi f,\;\omega \, = \,{\text{angular frequency}}$$

The loss factor (tan δ) can be expressed by the following relation [56]: \(\tan \delta = \frac{{\varepsilon^{\prime\prime}}}{{\varepsilon^{\prime}}}\)

The relative permittivity/dielectric constant (εr) is defined by the formula:

$${\varepsilon }_{r}=\frac{{\varepsilon }_{s}}{{\varepsilon }_{0}}=\frac{{C}_{s}}{{C}_{0}}$$

where, ε0 = Permittivity of a vacuum, C0 = free space capacitance of the parallel plate capacitor \(= \varepsilon_{0} \frac{A}{d}\) εs and Cs are the material permittivity and material capacitor, respectively.The ac conductivity is given by \(\sigma_{{{\text{ac}}}} = \omega \varepsilon_{0} \varepsilon^{\prime\prime}\).

The unwinding of the electric field in the material when the electric dislodging remains constant is referred to as electric modulus (M*(ω)). When the proportional complex permittivity was discussed as an electrical equivalent to the mechanical shear modulus [57], the electric modulus method was born.

When the electric displacement remains constant, the electrical modulus corresponds to the loosening of the electric field in the material. As a result, the modulus refers to true dielectric relaxation [58]. To explain the dielectric response of non-conducting materials, and the modulus was invented.

This concept has been extended to materials with non-zero conductivity in a similar way. When it comes to understanding material relaxation events in complex framework systems, the electric modulus formalism has a few advantages [59].

The \(M^{*} \left( \omega \right)\) is expressed by the following relation:

$$M^{*} \left( \omega \right) = \frac{1}{{\varepsilon ^{*} }} = M^{'} \left( \omega \right) + iM^{''} \left( \omega \right) = M_{\infty } \left[ {1 - \int_{0}^{\infty } {e^{{ - i\omega t}} } \left\{ {\frac{{d\varphi (t)}}{{dt}}} \right\}dt} \right]$$

where, \(\phi (t)\) = a relaxation function, \(\phi (t) = \exp \left[ { - \left( {{\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t {\tau_{M} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\tau_{M} }$}}} \right)^{\beta } } \right]\), \(\beta (0 < \beta < 1)\) = the stretched exponent. The real (M′) and imaginary part (M″) of the electric modulus (M*(ω)) can be expressed by the relation given:

$$\begin{gathered} M^{\prime}\left( \omega \right) = \frac{{\varepsilon^{\prime}\left( \omega \right)}}{{\varepsilon^{\prime}\left( \omega \right)^{2} + \varepsilon^{\prime\prime}\left( \omega \right)^{2} }} \hfill \\ M^{\prime\prime}\left( \omega \right) = \frac{{\varepsilon^{\prime\prime}\left( \omega \right)}}{{\varepsilon^{\prime}\left( \omega \right)^{2} + \varepsilon^{\prime\prime}\left( \omega \right)^{2} }} \hfill \\ \end{gathered}$$

The dielectric properties were calculated using data from the LCR metre. The dielectric properties of ZnO NPs were evaluated in our investigations.

The variation of ε′ and ε″ as a function of frequency under different temperatures (323–673 K) is shown in figure S2 (see supplementary Fig. S2(A), (B)). Two most significant elements of dielectric materials are tan δ and relative dielectric constant (εr). Relative dielectric constant advises how much energy is held in a material, while tan δ tells how much energy is lost.

The relative dielectric constant is for the most part connected with (i) electronic polarization, (ii) atomic polarization and (iii) dipolar polarization impacts of the material, which are under the impact of ac fields. The frequency-dependent dielectric properties and the loss tangent (tan δ) characteristics are illustrated in Figs. 8, 9, respectively. The εr and tanδ both can be believed to diminish at the temperature 623, 648, 673 K with an increase in frequency for ZnO NPs that is practically equivalent to dielectric materials [60]. It is notable that tan δ has two sections: (i) relaxation part (Debye or non-Debye) and (ii) dc conductivity part.

Fig. 8
figure 8

Frequency dependence of dielectric constant of the prepared ZnO NPs

Full size image
Fig. 9
figure 9

Frequency dependence of loss tangent (tanδ) of the ZnO NPs

Full size image

The loss factor is the gauge of how dissipative material is when exposed to an outside electric field. In general, decline in the εr without a peak affirms that the overall relaxation at the temperature 623, 648, 673 K in ZnO NPs is non-Debye type. At lower frequency the spectra show dispersive nature and the trend decrement at higher frequency rely chiefly upon the contribution of space charge polarization [61]. The value of εr maximum arises at T = 598 K and f = 5.1 kHz with value ≈ 345.65. This may be due to the heavy response of the defects and imperfection inside the ZnO nanocrystals during heat-induced dielectric response at that temperature. At that temperature εr increases with increase of frequency up to 5.1 kHz and then gradually decreases with further increase of frequency. The nature of tan δ at that T is also exhibit the same nature. The εr value at the temperature 423, 448, 473, 498, 558, 573 K attain maximum around the frequency 5.01 kHz and then decreases gradually with the increment of frequency. At the peak position for the temperature range 423–573 K the value of εr increases from 55 to 79.2 with the rise of temperature is observed.

The watched pattern of dielectric constant expansion with temperature could be because of the advancement of space charges shaped in the middle of the regions with different conductivities in the ZnO NPs (such as conducting grains and insulating or semi-insulating grain boundaries) during the warmth treatment in the ZnO NPs [17, 62]. Because of oxygen vacancies, interfacial dislocation accumulation, grain boundary effect, and other factors, the εr of ZnO NPs is larger at lower frequencies, while at higher frequencies, the εr decays due to electron aggregation caused by space charge polarization. The higher value of εr may happens duo to large number of dipole moments per unit volume as the number of particles per unit volume is large in the nanoscale and the nanodipoles behaviour of ZnO nanoparticles under the application of electric field [63, 64]. The most extreme peaks show up because of the thermal relaxation of the εr and some disorderness with lattice defects and crystal imperfection in the ZnO nano crystal.

At the temperature range 323–398 K (T = 323, 348, 373, 398 K), the value of the εr attain maximum around the frequency 5.01 kHz and then decreases gradually similarly with the temperature range 423–573 K. The maximum value of εr within this temperature range (323–398 K) at 5.01 kHz is less than T = 423 and 448 K.

The commitment from various sorts of polarization impacts, such as interfacial, atomic, ionic, dipolar, and electronic polarizations, and charge accumulation at the boundary, causes the dielectric constant to expand with a decrease in frequency. However, at higher frequencies, the lack of charge build-up at the interfaces results in an invariant dielectric steady state. Finally, at the higher frequencies, the εr becomes diminishes as the electric dipoles can’t totally follow the applied electric field. Comparative attributes have been seen for the frequency characteristic of loss tangent at the T = 398, 423, 448, 558, 598 K. The loss factor (tanδ) at the temperature 328, 348, 373, 473, 498 K decreases upto ~ 10.1 kHz than increases with rise of frequency. The loss factor esteem increments as the frequency ascend because of charge carriers and arrangement of few defects. Chemically fabricated ZnO Nanocrystals showed largely defect-related properties [65, 66]. Here, the irregular change of the εr and tanδ with the increment of the temperature is mainly due to the heat-induced different response of the defect states, vacancy and interstitial in the chemically fabricated ZnO NPs. An agreeable clarification for the general conduct of the dielectric consistent can be given with the assistance of a basic model of the solid, which is created by Koops [67]. In Koops’ model, it is accepted that there are well-conducting grains inside a strong material (solid/semiconductor/insulator) which have a little dielectric constant, divided by layers of lower conductivity. These layers are profoundly resistive, however contain numerous defects and charged impurity atoms.

The Koops model is also based on the Maxwell–Weigner model [68]. According to Koops’ model, there are well-conducting grains within a strong material (solid/semiconductor/insulator) with a low dielectric constant that are separated by layers of poorer conductivity. These layers are extremely resistant, yet they have a lot of defects and charged impurity atoms in them.

According to Koops’ theory, a material’s dielectric constant is also regulated by grain limits, which have a generally high dielectric constant at lower frequencies.

According to proposal based on Koops’ theory, if there are districts with varying conductivity that give ascent to commitment to a solid's dielectric constant, charge transporters in one region are hampered when they reach a grain limit in another.

A gathering of charges occurs at the interface as a result of the charge carrier's movement, which is responsible for greater dielectric constant estimates at low frequencies or a specific peak frequency in the lower frequency zone.

The large frequency dependence of εr, on the other hand, reveals that the grain limits’ commitment to the dielectric constant becomes insignificant with increasing frequency, and the dielectric reaction of the material governed by the grains at higher frequencies.

As expressed over, an expansion in εr with temperature (423, 448, 473, 498, 558, 573, 598 K) particularly at low frequencies, is clear (Fig. 8). The formation of the dipoles can be attributed to the increase in relative dielectric constant. At somewhat low temperatures, the dipoles frequently fail to align themselves along the bearing of the externally applied field, weakening their commitment to polarization and the dielectric constant (Fig. 8).

When the temperature rises, the bound charge bearers gain enough thermal energy vitality to be able to continue following the adjustment in the outside field without difficulty. As a result, their commitment to polarization improves, resulting in a rise in the dielectric constant at the pinnacle position. The variety of imaginary part of electric modulus M″ versus frequency for the ZnO NPs at different temperatures is shown in Fig. 11. There are humps observations at a particular lower frequency corresponding to a fix temperature. This decompressing top will in general shift toward higher frequencies with expanding temperature.

Figure 10 depicts the change in the real component of the electric modulus M′ with frequency and temperature for ZnO NPs. At low frequencies, M′ values are very low (nearly 0 at T = 623 and 673 K) and grow with increasing frequency, approaching a maximum value at a certain value before decreasing up to a certain frequency (around 5.1 kHz). Then, it again increases with the rise of higher frequencies.

Fig. 10
figure 10

Frequency-dependent real part of complex modulus at different temperatures of ZnO NPs

Full size image

The values of M′ drop with increasing temperature in the low-frequency region, but the M′ bends increases with increasing temperature in the high-frequency region, indicating that the electrode polarization effect in ZnO NPs does not exist [69].

Figure 11 depicts the fluctuation of M″ values with frequency for ZnO NPs at various temperatures. The relaxation process is shown by the peak at higher temperatures. Because of thermally activated charge carriers at high temperatures, the peaks are pushed into higher frequency districts with an increase in temperature as relaxation time decreases [70].

Fig. 11
figure 11

Frequency-dependent imaginary part of complex modulus at different temperatures of ZnO NPs

Full size image

The relaxation time (τ) is calculated with the use of the relation with frequency (f) given: [56]:

$$\omega_{\max } \tau_{M} = 1\;{\text{or}}\;\tau_{M} = \frac{1}{{2\pi f_{\max } }}$$

where fmax is the applied frequency corresponding to the peak maximum and τ = τM is the corresponding relaxation time. The relaxation time (τ) of the ZnO NPs under different temperatures are τ = 8.0585 × 10–5 s at T = 323 K, τ = 7.9379 × 10–5 s at 373 K, τ = 7.8796 × 10–5 s at T = 423 K, τ = 7.8686 × 10−5 s at T = 473 K, τ = 7.8447 × 10–5 s at T = 573 K.The observed \(\tau_{M}\) obeys the Arrhenius law [71]:

$$\tau_{M} = \tau_{0} \exp \left( {{\raise0.7ex\hbox{${E_{A} }$} \!\mathord{\left/ {\vphantom {{E_{A} } {kT}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${kT}$}}} \right)$$

where, \(E_{A}\) = activation energy and \(\tau_{0}\) = pre-exponential factor. The variation of ln(τMax) vs. 1/T is shown in Fig. 12. By linear fitting of ln (\(\tau_{M}\)) with (1/T) (Fig. 12), we find the characteristic pre-exponential relaxation time (\(\tau_{0}\)) of the ZnO NPs. The value determined from the resultant straight line fitting and is found to be τ0 = 7.6595 × 10−5 s [72]. This relaxation mechanism emerges in the ZnO NPs semiconductor because of the oxygen vacancies and static charges.

Fig. 12
figure 12

Variation of ln(τMax) vs. 1/T and its linear fitting

Full size image

3.4 Conductivity

A hopping technique of bound charges is used for a.c. conduction in solid materials, in which charges jump back and forth between all around specified bound states. Electrons experience bouncing between bound states through a burrowing procedure from one site to other. The expansion in frequency supports the hopping process, and a.c. At higher frequencies, conductivity increases.

Despite the fact that a perfect dielectric material does not have any free charge carriers, there can be modest quantity of free charges in them and the deliberate conductivity emerges from the two contributing elements, viz. the a.c. what’s more, d.c. conduction. In the case of wide band gap semiconductor ZnO NPs, there are few number of free charges (above room temperature) than the pure dielectric materials.

The amount of free carrier density of the measured ZnO NPs shows 5.55 × 106 per cm3 as per the optical dielectric analysis from Spitzer–Fan model.

All in all, the deliberate a.c. conductivity is spoken to by the connection:

$$\sigma_{{{\text{a}}.{\text{c}}.}} \left( \omega \right)_{{\text{T}}} \, = \,\sigma_{{{\text{a}}.{\text{c}}}} .\left( \omega \right)\, + \,\sigma_{{{\text{d}}.{\text{c}}}}$$

where σa.c.(ω)T = total frequency-dependent conductivity, σa.c.(ω) = contribution from the a.c. conductivity and ω = signal angular frequency, σd.c. = d.c. conductivity. Figure 13 shows the fluctuation in a.c. conductivity of ZnO NPs with frequency at temperatures ranging from 323 to 673 K. From this (Fig. 13), it will in general be seen that the total conductivity is exceptionally little at 1–2 kHz contrasted with that at higher frequencies. So, the static commitment from the d.c. conductivity is immaterial in the all-out conductivity of the ZnO NPs at all temperatures. The frequency dependence of the a.c. conductivity can be expressed by the following Jonscher’s universal power law [73]:

$$\sigma_{a.c.} \, = \,\sigma_{{{\text{d}}.{\text{c}}{.}}} \, + \,Af^{S}$$
Fig. 13
figure 13

Variation of a.c. conductivity of ZnO NPs with applied frequency at temperatures ranging from 323 to 673 K

Full size image

Since the d.c. conductivity is seen as irrelevant, the equation can be expressed in the structure

$$\sigma _{{a.c.}} = Af^{S} \;{\text{or}}~\;\ln \left( {\sigma _{{a.c.}} } \right) = \log A + s\;\log {\text{ }}f$$

The values of coefficients A and s can be dictated by straight line plotting from ln(σa.c) vs. ln (f) variation. The estimations of s for various temperatures were dictated by plotting ln(σa.c) vs. ln (f), what’s more, by finding the incline of the subsequent straight line. The plots are introduced in Fig. 14. Here, s value gradually decreases with increase of temperature from 323 to 423 K with values from 0.893 to 0.589, and then it again increases up to temperature 573 K with reaches value 0.939. From the temperature range 598 to 673 K the value of s is slightly changes around the average value ~ 0.863. Here the s value depends on temperature throughout the experimental temperature range (323–673 K). Hence, the conduction mechanism is the correlated barrier hopping (CBH), where the conduction happens in the similar barrier. Relaxation mechanisms are for the most part two sorts to be specific (i) quantum–mechanical tunneling (QMT) through the barrier and (ii) classical hopping over the barrier [74, 75]. The QMT conduction of charge carriers through barriers separating localized sites mechanism is not applicable in this ZnO NPs sample because s is depending on temperature in this experiment [76]. Velayutham et al. also observed the CBH in the ZnO NPs sample and they explain the differences between CBH and QMT in semiconducting ZnO nanosystems [77].

Fig. 14
figure 14

Temperature dependence of s for ZnO nanoparticles. Inset is the Variation of ln[σa.c.] with ln[f] of ZnO NPs at temperatures ranging from 323 to 673 K

Full size image

The exploratory information of dc conductivity is dissected utilizing the accompanying equation [78]:

$$\sigma_{{{\text{dc}}\left( T \right)}} \, = \,\sigma_{0} \exp^{{\left( {{{ - E_{A} } \mathord{\left/ {\vphantom {{ - E_{A} } {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}}} \right)}}$$

where σ0 is the pre-exponential factor, EA = activation energy for hopping conduction furthermore, kB is the Boltzmann consistent. The activation energy EA esteems are settled from the slopes of ln(σdc) versus 1/T (Fig. 15). The activation energy (EA) is found to be ≈ 93 meV.

Fig. 15
figure 15

a Variation of ln[σd.c.] with 1/T and its linear fitting f ZnO NPs with temperature ranging from 323 to 673 K

Full size image

3.5 Impedance spectroscopy analysis

Complex impedance spectroscopy (CIS) analysis of the ZnO NPs is studied for impedance analysis. Figure 16a, b shows the frequency characteristics of the real part (Z′) and imaginary part (Z″) of the complex impedance (Z*) spectra of ZnO NPs at different temperatures.

Fig. 16
figure 16

Frequency-dependent (a) real and (b) imaginary part of complex impedance of ZnO NPs at different temperatures

Full size image

The real part (Z′) and imaginary part (Z″) of the complex impedance (Z*) are given by the condition given as follows [79]:

$$Z^{\prime} = \frac{R}{{1 + \left( {\varpi \tau } \right)^{2} }}\;{\text{and}}\;Z^{\prime\prime} = \frac{{\varpi R\tau }}{{1 + \left( {\varpi \tau } \right)^{2} }}$$

It very well may be seen in Fig. 16a that with the increase in frequency, the Z′ decreases gradually for each measurement temperature, which signifies an enhancement in the conductivity. The Z′ is maximum throughout the investigated range of frequency at the temperature 423 K compared to other experimental temperature. With increase the temperature from 473 to 673 K, the Z′ decreases in the low-frequency zone signify the negative temperature coefficient of resistance (NTCR) nature of the ZnO NPs. In the high-frequency region at any temperature, the value of Z′ merges that may occurs because of the arrival of the space charges [80]. The frequency-dependent relaxation mechanism emerges in the ZnO NPs semiconductor because of the oxygen vacancies and static charges.

Figure 16b displays the frequency-dependent Z″ plot, which demonstrates that in the low- frequency region, Z″ steadily declines as temperature rises. With an increase in temperature in the high-frequency range, the pinnacles of Z″ broaden and move to the high-frequency band, where they converge.

The explanation for this pattern might be because of the collection of charge transporters at the grain limit. The variation of resistive segment of impedance (Z′) and the reactive part of impedance (Z″) at various temperatures appeared in Fig. 17. The plot between the Z′ and Z″ help to distinguish the commitments of grain, grain limit, the electrode interface and various components.

Fig. 17
figure 17

Variation of Z″ vs. Z′ of ZnO NPs at selective temperatures(T = 323, 373, 423, 473, 573, 623, 673 K)

Full size image

3.5.1 Nyquist plot

The structure of the compound (ZnO NPs) and electrical properties can be correlated with an electrical equivalent circuit utilizing Nyquist plot. This can be done from complex impedance analysis. The complex impedance can be expressed by the following Cole- Cole equation [81]:

$$Z = \frac{{R_{2} }}{{1 + R_{2} C_{2} \left( {j\varpi } \right)^{{n_{2} }} }} + \frac{{R_{3} }}{{1 + {\text{R}}_{3} C_{3} \left( {j\varpi } \right)^{{n_{3} }} }}$$

where Z = complex impedance, R2 = grain resistance, R3 = grain boundary resistance, C2 = grain resistance, C3 = grain boundary resistance.

The relaxation time distributed function ‘n’ moves from 0 to 1 in this case, and the incentive for ‘n’ should be unity for an unadulterated Debye process. Both grain and grain limits suit the Nyquist plots well with the R-CPE model (appeared in Fig. 18).

Fig. 18
figure 18

Nyquist plot of ZnO NPs at T = 673 K. Inset is the corresponding equivalent circuit

Full size image

The best fitted equivalent circuit at temperature 673 K is obtained by using ZSIMPWIN software. The proposed best fitted equivalent circuit from experimental data at T = 673 K is shown in inset of Fig. 18 and the fitted graph is shown in Fig. 18. Generally, Nyquist plot has two semi-circular arcs, low-frequency side due to contribution of grain boundary and higher frequency from grain. In this experiment, we observe only low-frequency side semicircular arc, so we can conclude that the conduction process mainly attributed by grain boundary in ZnO NPs. The impedance information was fitted to an equivalent circuit that comprises of a mix arrangement of grains and grains limit components. The first comprises a parallel combination of resistance (R2) and fractal capacitance (CPE1), while the second is made out of a parallel combination of resistance (R3), and a constant phase element (CPE2).

The first uses a parallel combination of resistance (R2) and fractal capacitance (CPE1), while the second uses a parallel combination of resistance (R3) and a constant phase element (CPE2).

4 Conclusion

Exciton-related absorption peak (λ = 365 nm) and increase in band gap (∆E ≈ 0.36 eV) was observed in ZnO NPs of average size ≈ 32.5 nm. The estimated free charge carrier density well agreement with typical high bandgap semiconductor. The optical properties showed good optical transparency and mixed type of dispersion nature (normal and anomalous dispersion) of ZnO NPs. The structural phase of the ZnO NPs showed hexagonal crystal phase with atomic fraction ≈ 75.444%. The result of the single oscillator energy well agreed nearly equal with bandgap energy. Relaxation behaviour and prominent defect state-related response were observed in the dielectric studies and electric modulus behaviour in the frequency range of 1–100 kHz under temperature variation from 323 to 673 K. The overall behaviour of the dielectric constants of ZnO NPs wad obeyed Koops model during temperature vitiation. The maximum value of the dielectric constant varies from 50 to 350 with T range from 323 to573 K. The response of the nano-dipoles inside ZnO nanoparticles under the application of electric field was observed. The relaxation time (τ) of the ZnO NPs was varied from 8.0585 × 10–5 s to 7.8447 × 10–5 s with the temperature (T) range 323–573 K. A decrease in the relaxation time was observed in the high temperature range compared to the low temperature range of the experimental investigation. Defects and imperfections inside the ZnO NPs are play important roles during the temperature and frequency-dependent dielectric relaxation mechanisms. The AC conductivity obeys the Jonscher’s universal power law and observed hopping of electron is the correlated barrier hopping. The AC conductivity coefficient value was decreased for the increased of temperature from 323 to 423 K and then it again increased up to temperature 573 K. The activation energy of the ZnO NPs was found to be 92.9 meV. The real part of the complex impedance showed negative temperature coefficient of resistance (NTCR) nature with increase in the temperature from 473 to 673 K in the low-frequency zone. The NTCR behaviour is very encouraging for ZnO NPs-based temperature sensors and current-limiting devices. Microwave semiconductor devices the equivalent circuit for the complex impedance analysis at T = 673 K from Nyquist plots is well fitted with R-CPE model studied from Cole- Cole equation. The conduction process inside the ZnO NPs is mainly attributed to the grain boundary.

The results of this study are likely to be of great interest to the optoelectronic devices, manufacturing of optical devices because of the good refractive index properties and high bandgap semiconductor nature of ZnO NPs along with others optical properties. These dielectric, electrical conductivity and electric modulus results for such a nano-structured materials of high bandgap semiconductor ZnO are an indication that such materials very attractive in fundamental research and for nanocapacitor and other technological applications.