Effect of iron oxide on the electrical conductivity of soda-lime silicate glasses by dielectric spectroscopy

Abstract

A survey of relaxation processes in glasses exhibiting ionic and electronic–ionic conductivity mechanisms is presented. Electrical conductivity and dielectric properties are investigated using complex impedance spectroscopy in a frequency range from 0.1 to 10⁶ Hz and a temperature range from 253 to 423 K. The results reveal that ionic conduction depends on the alkali concentration and ion mobility while electrical conduction is only slightly influenced by alkali ions and a mixed electronic–ionic conduction can occur. The Jonscher’s expression of ac electric conductivity is modified by adding a new term taking into account the displacement current density associated with the dielectric relaxation. The change in the activation energy depends upon the chemical composition indicating a changeover of the predominant conduction mechanism from ionic to polaronic. Quantum mechanical tunneling (QMT) model was suggested to describe the conduction mechanism of alkali-silicate glass G1 where frequency exponent s < 1. However, small polaron tunneling (SPT) model was applied to describe conductivity of semiconductor glass G2 (alkali-silicate glass with iron ions) with s > 1, whose conduction mechanism may be considered in terms of the optical phonon assisted hopping of small polarons between overlapping states. The electrical modulus exhibited relaxation character.

1 Introduction

The studies on electrical properties of transition metal oxides doped glasses have whetted the interest and attracted the attention of numerous researchers for the last several years. The amorphous glasses containing mixed valence transition metal ions (TMI) are appealing systems for several applications such as electrodes or electrolyte in solid state batteries owing to their high capacitance as well as extremely high energy density in addition to its huge memory and photo conducting devices [1,2,3,4]. Besides, these glasses exhibit an interesting application just like cathodes in smart windows and electrochemical cells [5].

Addition of multivalent transition metal ions like iron to conventional alkali silicate glasses like Na₂O–CaO–SiO₂, endows them with such outstanding electrical characteristics as wide band-gap and high dielectric permittivity in view of their larger electrical polarizability. It also grants them semiconducting properties.

Both Fe³⁺ and Fe²⁺ ions are well known paramagnetic ions. Fe²⁺ ions exhibit large magnetic anisotropy owing to their strong spin–orbit originated spin polarization of the 3d Fe orbital, whereas such anisotropy energy of Fe³⁺ ions is small since its orbital angular momentum is zero. The concentration of Fe²⁺ (or Fe³⁺) that has a strong bearing on electrical properties of the glasses depends largely upon the melting temperature, time and other constituents of the glass. Also, Alkali-rich glasses displaying dominant ionic conduction [4] are considered as promising glassy electrolytes for the solid state batteries thanks to their fast ion conductors such as Li⁺, Na⁺, Ag⁺, etc. [6,7,8]. Conversely, oxide glasses containing both alkali and transition metal ions show more variable electrical behavior [9]. It results from anomalies in the conductivity of different orders of magnitude depending on the amount of alkali and transition metal ions (TMI) such as iron.

The main objective of the present study is to investigate the effect of FeO on the conductivity in the Alkali-silicate glass. For this reason, we have measured some electrical properties (dielectric constant, loss, electric modulus, ac conductivity and impedance spectra) of alkali-silicate glass without and with iron ions using complex impedance spectroscopy technique. The analysis of experimental results show a different dielectric behavior related to the chemical composition of glasses, the presence of iron oxide and the frequency range. In particular, a mixed electronic-ionic conduction is observed in soda-lime silicate glass containing iron ions. Such glass exhibits a changeover of conduction mechanism from predominantly ionic to electronic when the TMI coexists with alkali ions in the glass network. The electronic conductivity of the oxide glasses containing transition metal ions is described by the mechanism of small polaron hopping (SPH) between the ions which are present in different valance states [10].

2 Experimental

2.1 Materials

The studied samples stand for tow kinds of glasses [Alkali-silicate glass (G1) and semiconductor glass (G2)] in the form of cylinders (1 mm thick and 10 mm in diameter) obtained from Saint-Gobain company. Their chemical-composition and their physical characteristics (the conductivity σ, the relative dielectric constant ε_r and density ρ provided by Saint Gobain company) are listed in Table 1. The homogeneity of glasses was checked using EPMA analysis after their metallization. Glass G1 is transparent while G2 is black. The black color is mainly due to the presence of ferrous ions [11,12,13].

Table 1 Chemical-composition (in wt%) and Physical characteristics of the studied glasses

Prior to the experiments, the samples were first cleaned ultrasonically in acetone bath for about 15 min and then rinsed with distilled water.

In the present glass system, SiO₂ is the main glass former and other components have been chosen by considering the existing facts in literature. The presence of Na₂O and CaO will generate the mixed alkali effect in the system [14]. According to dynamic structure model, the mismatch of individual ion sites may occur in alkali containing glasses because when a larger ion enters into the smaller site, site relaxation occurs to accommodate the larger ion. There are also possibilities that small interstitial sites, which were previously vacant, become typical ion sites once an ion resides there for a given time. These changes will make a fluctuating percolation pathway for migration of ions for both single and mixed ionically conducting glasses. The ions in mixed alkali glasses generate polarization by reorienting locally and are also responsible for conduction in lower frequencies by separating themselves from immediate neighbourhood [15, 16].

2.2 Experimental methods

Dielectric Spectroscopy experiments were performed in a Novocontrol Broadband Dielectric Spectrometer (BDS), based on an Alpha analyzer and a Quatro temperature controller. Isothermal measurements were carried out in the frequency range between 0.1 Hz and 1 MHz from 253 to 423 K, in 10 K steps, using brass electrodes of 20 mm in diameter and at an oscillation voltage of 1 V. The accuracy of Alpha impedance measurement is 0.01%. The measured dielectric permittivity data were collected and evaluated by WinDETA impedance analysis software.

3 Results and discussion

3.1 Real and imaginary parts of the dielectric complex permittivity

Dielectric storage and dielectric loss are two important properties for determining the suitability of a material for energy storage applications.

Indeed, the dielectric complex permittivity $\upvarepsilon^{*} (\upomega )$ describes the polarizing ability of a material in the presence of an external electric field and is a function of frequency:

$$ \upvarepsilon^{*} (\upomega ) { = }\frac{ 1}{{{\text{i}}\upomega {\text{c}}_{ 0} {\text{ Z}}^{ *} (\upomega )}}{ = }\upvarepsilon^{\prime} (\upomega )- {\text{i }}\upvarepsilon^{\prime\prime} (\upomega ) $$

(1)

where c₀ is the vacuum capacitance of the cell, $\upomega \, = 2\pi f$ is the angular frequency, ${\text{Z}}^{ *} (\upomega )$ is the complex impedance and i is the imaginary unity (${\text{i}}^{2}$ = − 1). $\upvarepsilon^{\prime}(\upomega ) \, = \, \frac{{ - Z^{\prime\prime}}}{{\upomega c_{0} {\mkern 1mu} \left( {Z^{\prime 2} \, + Z^{\prime \prime 2} } \right)}}$ and $\upvarepsilon^{\prime\prime} (\upomega ) { = }\frac{{ - Z^{\prime\prime}}}{{\upomega c_{0} {\mkern 1mu} \left( {Z^{\prime 2} \, + Z^{\prime \prime 2} } \right)}}$ representing respectively the real and imaginary parts of the dielectric permittivity (${\text{Z}}^{*} (\upomega ) = Z^{\prime } (\upomega ) - {\text{i}}Z^{\prime \prime } (\upomega )$ where $Z^{\prime }$ and $Z^{\prime \prime }$ are the real and imaginary parts of the complex impedance). $\upvarepsilon^{\prime}$ is proportional to the capacitance and measures the alignment of dipoles or polarization, whereas $\upvarepsilon^{\prime\prime}$ is the dielectric loss and is proportional to conductance representing the energy required to align the dipoles.

Furthermore, in order to explore ion dynamics in a material, dielectric analysis is desirable by measuring the real and imaginary parts of the complex permittivity.

The frequency dependence (10⁻¹–10⁶ Hz) of the real and imaginary parts of dielectric permittivity [$\upvarepsilon^{\prime} (\upomega )$ and $\upvarepsilon^{\prime\prime} (\upomega )$] for both samples (G1 and G2) at different temperatures (ranging for 253 to 423 K) are presented in Figs. 1a, b and 2a, b respectively. For both glasses (G1 and G2), the value of $\upvarepsilon^{\prime} (\upomega )$ decreases with the increase of frequency and reaches $\upvarepsilon^{\prime}_{\infty } (\upomega )$. However, it increases with increasing temperature for all frequencies. This increase is usually associated with the decrease in bond energies [17].

Fig. 1

Frequency variation of dielectric constant $\upvarepsilon^{\prime}$ for the glasses G1 (a) and G2 (b) at different temperatures ranging from 253 to 423 K with the interval of 10 K. In (a), the inset is the enlarged view of the dielectric constant $\upvarepsilon^{\prime}$ measured at higher frequencies and various temperatures. EP electrode polarization

Fig. 2

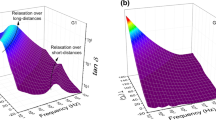
Dielectric loss $\upvarepsilon^{\prime\prime}$ as a function of frequency for G1 (a) and G2 (b) at various temperatures ranging from 253 to 423 K with the interval of 10 K. In (b), the inset is the enlarged view of the dielectric loss $\upvarepsilon^{\prime\prime}$ measured at higher frequencies and low temperatures

The dispersion with temperature is observed to be high in the low frequency region (10⁻¹–10³ Hz). The Na⁺ ions do act as modifier and induce dangling bonds (bonding defects) and non-bridging oxygen’s (NBOs) in the glass network. The structural defects thus produced get accumulated near the electrodes and contribute to the surface charge polarization. As a result, the dielectric constant increases rapidly. The high values of $\upvarepsilon^{\prime} (\upomega )$ in the low-frequency region (0.1–1 Hz) and high temperatures (above 393 K) correspond to an arising phenomenon due to the presence of metallic or blocking electrodes which do not permit the mobile ions to transfer into the external circuit. As a result, mobile ions pile up near the electrodes and endow the materials with a large bulk polarization called electrode polarization (EP).

The increasing temperature brings structural changes in the glass network and reduces the rigidity of the glasses but at the same time the mobility of the ions increases, which enhances the dielectric permittivity [18]. This dielectric permittivity, also measures the ease with which a modifier cations (Na⁺, Ca⁺) can migrate through the glass network. As such silica do not exhibit any dielectric properties, but inclusion of the modifier ions (like Na⁺, Ca⁺ or Al⁺) reduces the network rigidity by creating the non-bridging oxygen (NBOs) in the glass network. These NBOs are responsible for the migration of the ions and polarization in the glass network.

According to Fig. 2a, b, there are two different relaxation regions in both glasses G1 and G2. One is in the low-frequency region (1–10³ Hz), which is associated with the hopping conduction due to the mobile charge carriers (Na⁺) over long distances. The other is in the high-frequency region (10³–10⁶ Hz) and low temperature where the bulk charge carriers (Na⁺) are confined to potential wells and are mobile only over short distances associated with the relaxation polarization process [19].

In fact, in the low-frequency region (1–10³ Hz), the long-range migration of the mobile charge carriers (Na⁺) gives rise to dipoles that behave like localized dipoles in the immobilized state. These localized dipoles respond to the externally applied electric field due to sufficient time which increases the dielectric constant and the bulk capacitance.

Moreover, in this region, the effect of Na₂O on the dielectric behavior with the increasing of temperature of the present samples (G1 and G2) can be clearly seen in terms of maxima shifting of the dielectric loss $\upvarepsilon^{\prime\prime} (\upomega )$ towards higher frequency region and peak broadening. The shifting of maxima towards the higher-frequency region indicates a decrease in the relaxation time due to the increase of temperature, which enhances the ionic conductivity.

When the frequency of the applied field increases (10³–10⁶ Hz), these ions can create bonds with the closest non-bridging oxygens in the volume giving rise to the formation of the Na⁺–O⁻ dipoles, which generates this relaxation phenomenon and disappears when the frequency increases further. This disappearance may be due to the inability of the charge carriers to follow the field that changes direction rapidly and the fast periodic reversal of the electric field preventing the ion diffusion in the direction of the field. Therefore, this relaxation can occur only over short distances and depend on the concentration of the Na₂O (see Fig. 2a, b), which is more important for G1 glass and causes an increase of the concentration of the NBOs in the system and hence the dielectric loss.

In addition to the temperature increase that improves ionic conductivity, the application of the field at higher frequency favors the electron jump between two different sites (Fe²⁺ and Fe³⁺) in the G2 glass which causes also an increase in the contribution of the electronic components to the dispersion of the dielectric loss. Since G2 glass contains both iron and mobile alkaline ions, a mixed ionic-polaronic conductivity [9] can occur. This phenomenon is regarded as a new dielectric relaxation for G2 (see Fig. 2b). In fact, the ionic conductivity is attributed to migration of alkali ions (Na⁺ ions in this case), whereas electronic conduction occurs through polaron hopping between Fe²⁺ and Fe³⁺ ions. Iron ions exist as Fe³⁺ in both tetrahedral and octahedral coordination and as Fe²⁺ in octahedral environment [20]. Owing to the existence of iron ions in different valence states and within a framework of polaronic model, the electron delivered by the impurity atom at the Fe³⁺ site converts this one into a lower valence state Fe²⁺. Subsequently, the trapped electron at this Fe²⁺ site is transferred to the neighboring new Fe³⁺ site by absorbing a photon quantum. Therefore, glass G2 is identified as electron conductors with the polaronic conduction mechanism and electronic conduction takes place by electron hopping from Fe²⁺ to Fe³⁺ ions. This electronic conduction strongly depends on FeO content, redox ratio, Fe²⁺/Fe_tot, and average distance between iron ions [21, 22].

Thus, in the case of G2 glass, the relaxation process at high frequency region and high temperature is governed by the mixed polaronic-ionic conduction phenomena.

3.2 Electric modulus formalism

It is quite likely that sometimes the dipolar effects are strongly influenced (or may be completely masked) by electrode polarization. To avoid such contributions, the electric modulus formalism is much more helpful [23, 24]. The real and imaginary components of electric modulus, ${\text{M}}^{\prime } (\upomega )$ and ${\text{M}}^{\prime \prime } (\upomega )$ using real and imaginary parts of dielectric permittivity are obtained using the following expressions:

$$ {\text{M}}^{ *} { = }\frac{ 1}{{\upvarepsilon^{ *} }}{ = }\frac{ 1}{{\upvarepsilon^{\prime}{\text{ - i}}\upvarepsilon^{\prime\prime}}}{ = }\frac{{\upvarepsilon^{\prime}}}{{\upvarepsilon^{\prime 2} { + }\upvarepsilon^{\prime \prime 2} }}{\text{ + i}}\frac{{\upvarepsilon^{\prime\prime}}}{{\upvarepsilon^{\prime 2} { + }\upvarepsilon^{\prime \prime 2} }}{\text{ = M}}^{\prime } {\text{ + i M}}^{\prime \prime } $$

(2)

where

$$ {\text{M}}^{\prime } (\upomega ){ = }\frac{{\upvarepsilon^{\prime} (\upomega )}}{{\left( {\upvarepsilon^{\prime} (\upomega )} \right)^{ 2} { + }\left( {\upvarepsilon^{\prime\prime} (\upomega )} \right)^{ 2} }}{\text{ and M}}^{\prime \prime } (\upomega ){ = }\frac{{\upvarepsilon^{\prime\prime} (\upomega )}}{{\left( {\upvarepsilon^{\prime} (\upomega )} \right)^{ 2} { + }\left( {\upvarepsilon^{\prime\prime} (\upomega )} \right)^{ 2} }} $$

(3)

The frequency dependence plots of ${\text{M}}^{\prime \prime }$ at different temperatures are presented in Fig. 3a and b for G1 and G2 respectively. These figures show the presence of different relaxation mechanisms which depend upon from temperature and frequency regions.

Fig. 3

Dispersion of electric modulus ${\text{M}}^{\prime \prime }$ with the frequency evaluated in temperature range 253–423 K for glasses G1 (a) and G2 (b)

The small values of ${\text{M}}^{\prime \prime }$ at low frequency (0.1–10 Hz) region and high temperature in both glasses G1 and G2 indicate that the low frequency dielectric constant is mainly due to the electrode effect where the conductivity phenomenon is minimized referring to the electric modulus formalism [25].

At the frequency region (0.1–10³ Hz) where the temperature ranging from 313 to 423 K in G1 (Fig. 3a) and from 283 to 423 K in G2 (Fig. 3b), a clear relaxation processes is observed which is associated to the hopping conduction due to the mobile charge carriers over long distances.

Knowing that the migration of sodium ions is thermally activated [14], this is the reason why the dielectric relaxation starts to appear from 313 K in G1 glass. However, this relaxation can appear even at 283 K in G2 glass. Indeed in G2, an electronic conductivity can take place at low temperature in this glass following the movement of electrons between the Fe²⁺ and Fe³⁺ sites. These charge carriers have the chance during their movements to create dipoles following the interaction with the Na⁺ ions (on the surface).

At the high-frequency region and low temperatures, a relaxation phenomenon is clearly observed in G1, which is associated with the confined charge carriers (ions Na⁺) that are mobile only over short distances. This relaxation disappears as the temperature increases. It can be assumed that at high frequency region, the electric field changes so rapidly that the ions can move only within their potential wells [26]. As a result, mobile ions have been frozen into the glass structure making the glass stiffer in this frequency region. The same phenomenon is observed in G2 glass but with a lower order of magnitude, since Na⁺ ions concentration present in this kind of glass is smaller.

The frequency (f_max) corresponding to maxima of each peak gives the most probable conductivity relaxation time τ (τ ~ 1/f_max) for Na⁺ ions. The Arrhenius plots (logarithm of relaxation time τ versus the reciprocal temperature) are shown in Fig. 4.

Fig. 4

Relaxation time versus the inverse of temperature for G1 and G2 glasses. E_M is the activation energy

The activation energy, E_M, is computed through a fit of the relaxation time data using the following equation:

$$ \tau \,{ = }\,\tau_{ 0} { \exp }\left( {\frac{{{\text{E}}_{\text{M}} }}{{{\text{K}}_{\text{B}} {\text{T}}}}} \right) $$

(4)

where $\tau_{ 0}$, E_M, K_B and T are the pre-exponential factor, the activation energy, the Boltzmann constant and the temperature (Kelvin) respectively. The obtained values of the activation energy E_M from theses curves are given in Fig. 4.

As expected, the activation energy increases with the increase of the alkali cation mass, according to their mobility [27]. In fact, Na⁺ enters the network of the glass as a modifier, which means that Na₂O breaks up Si–O–Si bonds and introduces coordinated defects known as dangling bonds which will increase the disordering in structural network and increase the concentration of non-bridging oxygens (NBOs) [28, 29].

3.3 Electrical conductivity analysis

If one assumes that all the dielectric loss in the temperature range studied is due to conductivity, then conductivity can be expressed as $\upsigma^{\prime}\,{ = }\,\upomega \, \upvarepsilon_{ 0} \, \upvarepsilon^{\prime\prime}$ where $\upsigma^{\prime}$ is the real part of the conductivity and $\upvarepsilon^{\prime\prime}$ is the imaginary part of dielectric constant [30].

The variation of ac conductivity $\upsigma_{\text{ac}} { = }\upsigma^{\prime}$ with frequency (at different temperatures) for both glasses is presented in the Fig. 5a and b. This variation reveals that ac conductivity depends on both frequency and temperature and increases by a few orders of magnitude with frequency and temperature. In the low frequency range, the influence of temperature is more pronounced while the values of conductivity $\upsigma_{\text{ac}} (\upomega )$ display proximity at the high-frequency edge.

Fig. 5

Frequency dependence of conductivity at various temperatures for G1 glass (a) and G2 glass (b)

Several models have been developed in order to describe the variation of the ac conductivity in many disordered solids. Jonscher [31] for example, proposed the following equation for frequency-temperature dependence of the ac conductivity:

$$ \upsigma_{\text{ac}} (\upomega , {\text{T) = }}\upsigma_{\text{dc}} ( {\text{T) + A(T) }}\upomega^{\text{s}} $$

(5)

where $\upsigma_{\text{dc}} ( {\text{T)}}$ is the $\upomega \to 0$ limit value of $\upsigma_{\text{ac}} (\upomega , {\text{T) }}$ corresponding to the dc conductivity values. Generally A and s are parameters depending on temperature [32, 33]. The exponent s represents the degree of interaction between mobile ions with the lattices around them and A determines the strength of polarizability [34]. In this Eq. 5, Jonscher takes into account only the conduction current density.

According to Funke [35], the value of s could have a physical significance. If s < 1 the load carriers adopt a translational movement with a sudden jump, and when s > 1, it means a localized jump of the species (small jump without leaving the neighborhood).

In the intermediate frequency region (1–10³Hz) and at high temperatures (see Fig. 5a, b), the Jonscher law is not able to describe the recorded relaxation (experimental data), which indicates that in the vicinity of the relaxation peaks the power law of Eq. 5 is not applicable.

To highlight the presence of this new dielectric relaxation which appears in the frequency window (1–10³ Hz), the displacement current density must be taken into account in addition to the conduction current density.

In fact, for a sinusoidal electrical fields $\overrightarrow {{{\text{E}}^{ *} }} (\upomega ) = \overrightarrow {{{\text{E}}_{ 0} }} {\text{e}}^{{{\text{i}}\upomega {\text{t}}}}$, the current density in a dielectric material is obtained by the contribution of both the conduction current density $\overrightarrow {{{\text{J}}_{\text{c}}^{ *} }} = \upsigma_{\text{dc}} \overrightarrow {{{\text{E}}^{ *} }}$ and the displacement one $\overrightarrow {{{\text{J}}_{\text{d}}^{ *} }} = \frac{{\partial \overrightarrow {{{\text{D}}^{ *} }} }}{{\partial {\text{t}}}}{\text{ = i}}\upomega \overrightarrow {{{\text{D}}^{ *} }}$. Therefore, the total current density is given by:

$$ \overrightarrow {{{\text{J}}^{ *} }} = \overrightarrow {{{\text{ J}}_{\text{c}}^{ *} }} { + }\overrightarrow {{{\text{J}}_{\text{d}}^{ *} }} = \upsigma_{\text{dc}} \overrightarrow {{{\text{E}}^{ *} }} {\text{ + i}}\upomega \overrightarrow {{{\text{D}}^{ *} }} = \upsigma_{\text{dc}} \overrightarrow {{{\text{E}}^{ *} }} {\text{ + i}}\upomega \upvarepsilon_{ 0} \upvarepsilon^{ *} \overrightarrow {{{\text{E}}^{ *} }} { = (}\upsigma_{\text{dc}} {\text{ + i}}\upomega \upvarepsilon_{ 0} \upvarepsilon^{ *} )\overrightarrow {{{\text{E}}^{ *} }} = \upsigma^{ *} (\upomega )\overrightarrow {{{\text{ E}}^{ *} }} $$

(6)

where $\upsigma^{*} (\upomega )$ is the complex conductivity given by:

$$ \upsigma^{ *} (\upomega ) = \upsigma_{\text{dc}} {\text{ + i}}\upomega \upvarepsilon_{ 0} \upvarepsilon^{ *} (\upomega ) = \upsigma_{\text{dc}} {\text{ + i}}\upomega \upvarepsilon_{ 0} (\upvarepsilon^{\prime}{\text{ - i}}\upvarepsilon^{\prime\prime} ) { = (}\upsigma_{\text{dc}} { + }\upomega \upvarepsilon_{ 0} \upvarepsilon^{\prime\prime} ) {\text{ + i}}\upomega \upvarepsilon_{ 0} \upvarepsilon^{\prime} = \upsigma^{\prime}{\text{ + i}}\upsigma^{\prime\prime} $$

(7)

The real part of the complex conductivity $\upsigma^{\prime} = \upsigma_{\text{dc}} { + }\upomega \upvarepsilon_{ 0} \upvarepsilon^{\prime\prime}$ is associated with electric loss of both ohmic and dielectric origins. Using this new expression of $\upsigma^{\prime}$, the Jonscher universal power low can be then rewritten as:

$$ \upsigma_{\text{ac}} (\upomega ) = \upsigma_{\text{dc}} { + }\upomega \upvarepsilon_{ 0} \,\upvarepsilon^{\prime\prime} (\upomega ) {\text{ + A}}\upomega^{\text{s}} $$

(8)

where $\upvarepsilon^{\prime\prime}(\upomega )$ is the imaginary part of the complex permittivity which can be written as [36]:

$\upvarepsilon^{\prime\prime}(\upomega ) \, = \, \Delta \upvarepsilon \, \frac{\sin \, \theta }{{\left[ {1 + 2(\upomega \tau )^{\alpha } \, \cos \, (\frac{\alpha \pi }{2}) \, + \, (\upomega \tau )^{2\alpha } } \right]^{{\frac{\beta }{2}}} }}$ where $\Delta \upvarepsilon = \, \upvarepsilon_{\text{S}} - \upvarepsilon_{\infty }$ is the relaxation strength of the investigated process, $\tau$ is the relaxation time, ${\alpha }$ and $\beta$(with limits $0 < \, \alpha , \, \alpha \beta \, \le 1$) describe the symmetrical and asymmetrical broadening of the distribution of relaxation times respectively and $\theta \, = \, \beta {\text{ atan }}\left[ {\frac{{(\upomega \tau )^{\alpha } \, \sin \, \left( {\frac{\alpha \pi }{2}} \right) \, }}{{1 + (\upomega \tau )^{\alpha } \, \cos \, \left( {\frac{\alpha \pi }{2}} \right)}}} \right]$.

The obtained conductivity variation (see Fig. 5a, b) is fitted with Eq. 8 for the different temperatures ranging from 383 to 423 K. An example of fitted conductivity at 423 K is presented in Fig. 6 for G1 and G2 glasses.

Fig. 6

Frequency dependence of conductivity at 423 K for G1 glass (a) and G2 glass (b)

According to Fig. 6, three different regions can be distinguished:

• At low frequencies and high temperature, $\upsigma^{\prime}$ shows frequency independent nature (plateau nature), which gives rise to dc conductivity $\upsigma_{\text{dc}}$ arising from the random diffusion of the ionic charge carriers via activated hopping process [37].

• In the intermediate-frequency region (1–10³Hz), a relaxation is associated with the jump conduction where mobile ions can cross the barriers more easily with more thermal energy [38, 39].

• At high frequencies, the power law ${\text{A}}\upomega^{\text{s}}$ is observed and the conductivity increases sharply with the frequency and eventually becomes almost linear at even higher temperatures [31, 40].

3.3.1 Dc electric conductivity

The values of $\upsigma_{\text{dc}}$ are obtained by extrapolating $\upsigma^{\prime}$ to zero frequency using Eq. 8. The temperature dependence of dc electric conductivity $\upsigma_{\text{dc}}$ for G1 and G2 glasses is shown in Fig. 7 as Arrhenius plots of ln $\upsigma_{\text{dc}}$ versus 1000/T. This figure shows that the dc conductivity for both samples G1 and G2 varies as a function of temperature according to the Arrhenius equation:

$$ \upsigma_{\text{dc}} \, = \, \upsigma_{0} \exp \left( {\frac{{ - {\text{E}}_{\text{a}} }}{{{\text{K}}_{\text{B}} {\text{T}}}}} \right) $$

(9)

where $\upsigma_{ 0}$ is the pre-exponential factor, E_a is the activation energy for conduction, K_B Boltzmann constant and T is the temperature in Kelvin. The activation energy is extracted from the slopes of the lines fitting the curves $\upsigma_{\text{dc}}$ against reciprocal temperature 1000/T. The obtained values of E_a are shown in Fig. 7.

Fig. 7

Arrhenius plot of electric dc conductivity for both G1 and G2 glasses

The highest value of the activation energy (E_a) is obtained for the glass sample G1. It shows that the increase of sodium (Na⁺) content in the former G1 not only modifies the network by creating non-bridging oxygens (NBOs) in the structure but also creates ionic sites with different binding energies of the alkali ions.

For G2, it is evident that dc conductivity increases while the activation energy decreases with the addition of iron oxide in the glass composition. These iron ions (Fe²⁺ and Fe³⁺) similar to Na⁺ act as modifiers and create more non-bridging oxygen and dangling bonds inside the glass network. Due to the creation of non-bridging oxygen, the openness of the network results in the weakening of the silicate structure. This is likely to facilitate greater mobility of iron ions, resulting in an increase in conductivity. In Weigel works [41], the structure of a glass with similar compositions shows the clustering of Fe²⁺ and Fe³⁺ ions which favor electron hopping and provide pathways for charge transport. Such behavior is a feature of Small Polaron Hopping (SPH) conduction mechanism in transition metal oxide glasses [10]. According to Sable [42], the increase in dc conductivity is related to the decrease of hopping distance, polaron radius and the increases of density of state at Fermi level when adding an amount of iron. The increase in dc conductivity and decrease in activation energy with addition of FeO concentration is attributed to the decrease in the average distance R between Fe²⁺ and Fe³⁺ ions. The decrease in the average distance between iron ions facilitates electron hopping from the lower valence state to the higher one [43, 44].

Moreover, Na⁺ ions mobility is drastically reduced in the presence of Ca⁺ ions in glass G2 which can be attributed to the formation of dissimilar pairs (Na⁺–Ca²⁺) around NBOs [45].

3.3.2 Ac electric conductivity

The ac conductivity is higher for G2 than for G1. This difference is due to an important contribution of electronic conduction caused by electronic charge transfer between iron species that exist in G2 glass. In order to determine the conduction mechanism of the ac conductivity for both G1 and G2 glasses, the variation of the “s” exponent as a function of temperature is reported in Fig. 8. Though various models have been proposed to explain the behavior of the exponent s in case of amorphous materials [46, 47] and in particular in many glasses [48, 49], two distinct processes have been proposed for the conductivity mechanisms, namely, quantum mechanical tunneling (QMT) through a barrier and classical hopping over a barrier.

Fig. 8

Temperature dependence of the frequency exponent s for G1 and G2 glasses. QMT quantum mechanical tunneling model, SPT small polaron tunneling model

Austin, Mott and Ghosh [50, 51] have suggested (QMT) model for ac conductivity where the exponent s is given by:

$$ {\text{s = }}\frac{{\partial ( {\text{ln }}\upsigma )}}{{\partial ( {\text{ln }}\upomega )}} $$

(10)

In the simple quantum mechanical tunneling (QMT) model [40], the exponent s could be calculated using the expression:

$$ {\text{s = 1}} - \frac{ 4}{{{\text{ln(1/}}\upomega \tau_{ 0} )}} $$

(11)

where τ₀ is the characteristic relaxation time or the reciprocal phonon frequency ν_ph (in order of 10¹³ s⁻¹ [52]).

The QMT model exhibits that 0 < s < 1 and the frequency exponent s is temperature independent but frequency dependent.

Considering typical values of the parameters, τ₀ = 10⁻¹³s and ω = 10⁵ s⁻¹, the calculated value of s from Eq. 11 is found in the order of 0.8, which is in good agreement with the experimental values for the G1 glass as seen from Fig. 8.

For G2 glass, Fig. 8 reveals that the exponent s increases when the temperature increases. This behavior of the ac conductivity is in good agreement with the small polaron tunneling model (SPT). Therefore, the SPT model is the most suitable model to characterize the electrical conduction mechanism in the titled glass G2. Indeed, at high temperature, the conduction mechanism may be considered in terms of the optical phonon assisted hopping of small polarons between overlapping states.

3.4 Impedance analysis

Figure 9a and b represents the complex impedance plots of the imaginary ${\text{Z}}^{\prime \prime }$ versus the real part ${\text{Z}}^{\prime }$ (Nyquist plots) from 373 to 423 K temperature range. The impedance spectra show a semicircular arc with the inclined spur. Good agreement between the experimental data and theoretical values obtained by the best fit using Z-View-software proves that the electrical properties of glass samples are adequately defined with the proposed equivalent circuit (inset in Fig. 9a, b).

Fig. 9

Experimental impedance diagrams of G1 and G2 at different temperatures. The inset represents the corresponding equivalent circuit

For all compositions, the semicircular arcs are depressed, and their centers are situated below the ${\text{Z}}^{\prime}$ axis. This behavior indicates that the electrical response at complex plane impedance presents a non-Debye relaxation [53, 54]. At the beginning, each semicircle is considered to be equal to a circuit composed of two parallel RC elements connected in series [55]. This semicircle is most commonly depressed with its center below the real axis. For this reason, a constant phase element (CPE) is used to replace the capacitor [53]. The total impedance of the equivalent circuit is given by:

$$ {\text{Z}}^{ *} {\text{ = Z' }} - {\text{ i Z'' = }}\left( {\frac{ 1}{{{\text{R}}_{ 1} }}{ + }\frac{ 1}{{{\text{Z}}_{{{\text{CPE}}_{ 1} }} }}} \right)^{ - 1} { + }\left( {\frac{ 1}{{{\text{R}}_{ 2} }}{ + }\frac{ 1}{{{\text{Z}}_{{{\text{CPE}}_{ 2} }} }}} \right)^{ - 1} $$

(12)

${\text{Z}}^{\prime}$ and ${\text{Z}}^{\prime\prime}$ are the real and imaginary components of impedance. The impedance of the CPE is defined via [56]:

$$ {\text{Z}}_{\text{CPE}} = \frac{ 1}{{{\text{A(i}}\upomega )^{\text{p}} }} $$

(13)

where i is the imaginary unit (i² = − 1), $\upomega$ is the angular frequency ($\upomega { = 2}\pi {\text{ f}}$, f the frequency), A being a constant independent of frequency [56] and p is an exponent index which is a measure of arc depressions ranging between zero and unity determining the degree of deviation from an exact semicircle.

In Eq. 13, when the constant p = 1, the CPE behaves as an ideal capacitor with a value A = C, which is the case of a typical Debye behavior. For p = 0, the CPE acts as a pure resistor and takes the value ${\text{R = }}\frac{ 1}{\text{A}}$. The calculation of p parameter is described in details in [57]. The values of equivalent circuit elements are listed in Tables 2 and 3.

Table 2 The best fitting values of equivalent circuit elements in Fig. 9a for G1 glass at different temperatures

Table 3 The best fitting values of equivalent circuit elements in Fig. 9b for G2 glass at different temperatures

R₁ and CPE₁ refer to the resistive and capacitive components of the bulk region at higher frequencies, respectively while R₂ and CPE₂ refer respectively to the resistive and capacitive components of the interfacial impedance at lower frequencies, which determines the electrode polarization [58]. Parameters p₁ and p₂ refer to the exponential index of the bulk region and the interfacial impedance, respectively. Referring to Tables 2 and 3, the values of exponent p₁ and p₂ are less than a unity, indicating the distribution of relaxation times. A better defined semicircular arc at higher frequencies and an inclined spike in the lower frequencies region are detected. With the increase of temperature of measurement, the area under the semicircle is gradually decreased, which indicates the decrease in bulk resistance showing an increase in conductivity. This behavior indicates a thermally activated conduction mechanism. The high frequency arc is representative of the bulk properties and the response at lower frequencies is representative of the electrode polarization caused by the accumulation of Na⁺ at the blocking electrode. The small diameter of the semicircle at a higher frequency represents small bulk resistance, which increases with the decrease of temperature. This behavior indicates increased thermally activated conduction at higher temperatures. The resistance and capacitance of the interfacial impedance is usually larger than the bulk. It can be noted also from Tables 2 and 3 that the bulk capacitance increases by increasing the temperature rapidly for both glasses and decreases with the addition in the iron content. This may be due to the decrease in defect density after the release of free charge carriers. Furthermore, The increase in electrode semiconductor contact capacitance for glass G2 with the increase in temperature may also refer to decrease in the Schottky barrier layer thickness [59].

The bulk conductivity $\upsigma_{\text{dc}}$ of the compound can be evaluated from the impedance data using the relation:

$$ \upsigma_{\text{dc}} = \frac{\text{d}}{{{\text{S R}}_{ 1} }} $$

(14)

where R₁ is the bulk resistance, d is the thickness, and S is the area of the electrode deposited on the sample. R₁ is obtained from the value of low frequency intercept of the semicircle on the real axis (${\text{Z}}^{\prime }$) in the complex impedance plot.

The evolution of $\upsigma_{\text{dc}}$ as a function of temperature in Arrhenius coordinates is given in Fig. 10. The activation energy E_a is extracted from the slopes of the lines fitting the curves $\upsigma_{\text{dc}}$ against reciprocal temperature 1000/T. The obtained values of E_a for both glasses outlined in Fig. 10 are in good agreement with those obtained using Eq. 9 (see Fig. 7).

Fig. 10

Arrhenius plot of electric dc conductivity for both G1 and G2 glasses using Z-view method

4 Conclusion

The present study centering on the electric and dielectric properties in the temperature range 253–423 K and over the frequency range 0.1 Hz–1 MHz for both glasses (G1 Alkali-silicate glass and G2 semiconductor glass containing iron ions) allows us to draw the following conclusions:

• i. For both glasses, $\upvarepsilon^{\prime}$ tends to increase with increasing temperature and decrease with increasing frequency while $\upvarepsilon^{\prime\prime}$ reaches higher values at lower frequencies, and decreases monotonically as both frequency and temperature increase.

• ii. The frequency-dependence plots of ${\text{M}}^{\prime \prime }$ at different temperatures show that there are two different relaxation regions in alkali-silicate glass G1 and three relaxations in semiconductor glass G2. The low-frequency region is associated with the hopping conduction due to the mobile charge carriers over long distances, while the high-frequency region is associated with confined charge carriers that are mobile only over short distances. A mixed electronic–ionic conduction at high frequency region and high temperature is observed in iron containing glass (G2). In this case, electronic conduction occurs by electron hopping between iron ions in different valence states while Na⁺ ion diffusion is responsible for ionic conduction.

• iii. The coexistence of FeO with alkali ions in the glass network (Glass G2) gives rise to an electrical conductivity which causes a changeover of conduction mechanism from predominantly ionic to electronic. Therefore, a mixed electronic–ionic conduction occurs in the case of G2 glass.

• iv. Jonscher’s expression of ac electrical conductivity is modified by adding a new term in Eq. 8 taking into account the displacement current density at the same time with the conduction current density.

• v. Quantum mechanical tunneling (QMT) model was used to describe the conduction mechanism of alkali-silicate glass G1 where the obtained value of exponent is s = 0.8 < 1. The small polaron tunneling (SPT) model was applied to describe conductivity of semiconductor glass G2 with s > 1. In this case, the conduction mechanism may be considered in terms of the optical phonon assisted hopping of small polarons between overlapping states.

• vi. Electrical properties of glass samples are adequately defined with the proposed equivalent circuit using Z-view-software.

• vii. Obtained values of E_a for $\upsigma_{\text{dc}}$ conductivity from both methods [Z-view and modified Jonscher’s expression (Eq. 8)] prove to be in good agreement.