Introduction

Fatigue is a major cause for catastrophic failure in materials. The fatigue behavior of composite and nanocomposite materials is studied by many researchers. For composite materials, three principal approaches are used to predict the fatigue life: residual strength [1], residual stiffness [2, 3], and empirical methodologies [4]. In each category, phenomenological, mechanistic, statistical, and mixed methods are utilized by different authors [5–8].

A set of sudden material property degradation rules, such as stiffness degradation, for various failure modes of a unidirectional ply under a multi-axial state of static and fatigue stress was developed by Shokrieh and Lessard [9] for laminated composite materials. Also, for the quasi-isotropic carbon fiber-reinforced (CFRPs) laminates, sudden material property degradation as damage was investigated by Vavouliotis et al. [10].

For nanocomposite materials, many researchers have focused just on experimental methods and added the optimum weight ratio of nanofillers into epoxy polymers and reported improvements on the fatigue behavior of nanocomposites [11–30].

Dick et al. [11] conducted static and cyclic four-point bending tests on glass short fiber-filled polycarbonate to collect results for the evaluation of a theoretic model on its capability to predict the fatigue life and the residual strength after cyclic loading. Graphene fillers are shown to be remarkably effective in suppressing crack propagation in epoxy polymers. The nano- and microscale dimensions of the graphene nanofillers give rise to unexpected and fascinating mechanical properties, often superior to the matrix including fracture toughness and fatigue crack propagation resistance [12–14].It was shown [15, 16] that the addition of small volume fractions of multi-walled carbon nanotubes (CNTs) to the matrix results in a significant increase in the high-cycle fatigue life and an order of magnitude reduction in the fatigue crack propagation rate for an epoxy system. Carbon nanotubes show potential to significantly enhance the reliability and operating life of structural polymers that are susceptible to fatigue failure. Boeger et al. [17] evaluated the fatigue properties of glass fiber-reinforced epoxy laminates modified with small amounts of nanoparticles [fumed silica SiO2 and multi-wall carbon nanotubes (MWCNT)]. Juwono and Edward [18] studied the fatigue performance and fatigue failure mechanism of clay-epoxy materials under repetitive bending loads. Chen and Wong [19] measured the fatigue life with different displacement ranges under strain control in a tensile mode and implemented a unified model for nylon 6, polypropylene (PP) with 20 wt% CaCO3, and strain fatigue lives were predicted. Gupta and Veeraragavan [20] studied the benefit of Styrene Butadiene Styrene (SBS) polymer-modified bituminous mixes on fatigue performance and evaluated the physical and mechanical properties of polymer-modified and conventional binder mixes. The addition of small amounts of Silica nanoparticles on the fatigue life was evaluated in different types of loadings [21–27]. The cyclic crack growth in both the neat epoxy and the epoxy filled with urea–formaldehyde (UF) microcapsules was investigated by Brown et al. [28]. Toshiharu and Nobumitsu [29] and Zhao et al. [30] used small amounts of Alumina nanoparticles to highlight the mechanisms leading to significant improvements on the fatigue life.

A direct correlation between the stiffness degradation and the electrical resistance change under the cyclic loading has been established, and sudden material property reduction as a damage index of nanocomposites under fatigue loading was investigated by many researchers [31–35]. Alexopoulos et al. [31] used the material property degradation method as a damage control parameter and considered the effect of adding carbon nanotube (CNT) on the glass/epoxy under dynamic fatigue loading conditions. In their research, CNTs have been embedded in glass fiber-reinforced polymers (GFRP) for the structural health monitoring of composite materials. The fatigue behavior and lifetime of Polyimide/silica (Pi/SiO2) hybrid films are investigated by Wang and Zhao [32] to evaluate the fatigue property of this class of hybrid films, where the stress-life cyclic experiments under tension–tension fatigue loading were performed. A semi-empirical model is proposed based on the fatigue modulus concept to predict the fatigue life of this class of hybrid films. An exponential model of fatigue stiffness degradation was suggested by researchers [33, 34] to predict the fatigue life of matrix-dominated polymer composite laminates based on a nonlinear stress/strain response of most polymers or matrix-dominated polymer composites under uniaxial tension fatigue loadings. Guo and Li [35] performed compressive loading on the SiO2/epoxy nanocomposites under different loading rates and revealed that the compressive strength of the composites with silica nanoparticles is higher than that of the pure epoxy at higher strain rates.

A comprehensive survey in the available literature reveals the lack of models to predict the property degradation of nanoparticle-filled fibrous epoxy composites. In this paper, a fatigue model is developed to predict the stiffness reduction of nanoparticle/fibrous polymeric composites.

Modeling strategy

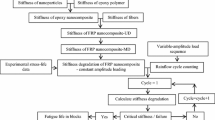
A schematic framework of the modeling strategy is shown in Fig. 1. The model is an integration of two major components: the micromechanical (such as Halpin–Tsai or Nielsen models) and the normalized stiffness degradation approaches. The model is able to predict the final fatigue life of nanoparticle/fibrous polymeric composites under general fatigue loading conditions.

Fig. 1
figure 1

Schematic flowchart of the developed model

Full size image

As shown in Fig. 1, in the first step, the model predicts the equivalent stiffness of nanoparticle/epoxy nanocomposites by means of a micromechanical approach, like Halpin–Tsai or Nielsen models. Then, the normalized stiffness degradation model for polymeric composites under a fatigue loading condition was used to predict the stiffness degradation of polymeric composites. By coupling of the normalized stiffness degradation model for polymeric composites and the micromechanical approach, the normalized stiffness degradation model for polymeric nanocomposites under fatigue loading was developed.

Equivalent stiffness of nanoparticle/epoxy nanocomposites

Halpin–Tsai micromechanics model

The Halpin–Tsai model [36, 37] is a mathematical model for the prediction of elasticity of composite materials, based on the geometry and orientation of the filler and the elastic properties of the filler and matrix. The model is based on the self-consistent field method, although often consider to be empirical.

The Halpin–Tsai model is used to predict the modulus of a nanocomposite material, \( E_{\text{nc}}^{\text{s}} \), containing nanoparticles as a function of the modulus of the matrix, \( E_{\text{m}}^{\text{s}} \), containing no nanoparticles, and of the modulus of the particles, \( E_{\text{P}}^{\text{s}} \) in static loading condition. The predicted modulus of the nanocomposites, \( E_{\text{nc}}^{\text{s}} \), is given by the following equation [38]:

$$ E_{\text{nc}}^{\text{s}} = \frac{{1 + 2\frac{w}{t}\eta V_{\text{f}} }}{{1 - \eta V_{\text{f}} }}E_{\text{m}}^{\text{s}} $$
(1)

where

$$ \eta = {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{{_{\text{m}} }}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{{_{\text{m}} }}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + 2\frac{w}{t}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + 2\frac{w}{t}} \right)}} $$
(2)

and

\( E_{\text{m}}^{\text{s}} \) is the stiffness of the matrix without nanoparticles under static state loading condition, \( E_{\text{P}}^{\text{s}} \) is the stiffness of the nanoparticles under static loading condition, and \( E_{\text{nc}}^{\text{s}} \) is the stiffness of a nanocomposite material under static loading condition. In above equations, w/t is the shape factor and V f is the volume fraction of the particles.

Nielsen micromechanics model

The Nielsen model predicts the Young’s modulus of nanocomposite materials. In this model, the effect of slippage between the nanoparticle and matrix was evaluated by means of a coefficient factor. The Nielsen model is used to predict the modulus of a nanocomposite material containing nanoparticles (\( E_{\text{nc}}^{\text{s}} \)) as a function of the modulus of the polymer containing no nanoparticles (\( E_{\text{m}}^{\text{s}} \)) and of the modulus of the particles (\( E_{\text{P}}^{\text{s}} \)) in static loading condition. The predicted modulus of the epoxy polymer nanocomposites (\( E_{\text{nc}}^{\text{s}} \)) is given by the following equation [38]:

$$ E_{\text{nc}}^{\text{s}} = \frac{{1 + (K_{\text{E}} - 1)\beta \nu_{\text{f}} }}{{1 - \mu \beta \nu_{\text{f}} }}E_{\text{m}}^{\text{s}} $$
(3)

where K E is the generalized Einstein coefficient and β and μ are constants. The constant β is given by:

$$ \beta = {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}} $$
(4)

The value of μ depends on the maximum volume fraction of particles, v max, calculated by the following equation:

$$ \mu = 1 + \frac{{(1 - \nu_{\text{f}} )}}{{\nu_{\max } }}[\nu_{\max } \;\nu_{\text{f}} + (1 - \nu_{\max } )(1 - \nu_{\text{f}} )] $$
(5)

Values of \( \nu_{\max } \) have been published by Nielsen and Landel for a range of particle types [39]. Nielsen and Landel quote a value of ν max = 0.632 for random close-packed, nonagglomerated spheres and this value is used in the present model. The value of K E varies with the degree of adhesion of the epoxy polymer to the particle. For an epoxy polymer with a Poisson’s ratio of 0.5 which contains dispersed spherical particles, (a) K E = 2.5 if there is “no slippage” at the interface (i.e., very good adhesion) or (b) K E = 1.0 if there is “slippage” (i.e., relatively low adhesion). However, the value of K E is reduced when the Poisson’s ratio of the polymer is <0.5.

The earlier studies have also shown that at relatively high values of v f, more than 0.1 of silica nanoparticles, the Nielsen “slip” model gave the best agreement with the measured values. However, Hsieh et al. [38] show that at relatively low values of v f (i.e., at values of v f below than 0.1), the Halpin–Tsai and the Nielsen “no-slip” models show better agreement. Thus, an overall conclusion is that the measured moduli of the different silica nanoparticle-filled epoxy approximately lie between an upper-bound value set by the Halpin–Tsai and the Nielsen “no-slip” models and a lower-bound value set by the Nielsen “slip” model, with the last model being more accurate at relatively higher values of v f [38].

Material properties degradation

In the present work, it is assumed that the major reason for material properties’ reduction of nanoparticle-filled fibrous polymeric composites under fatigue loading conditions is related to the reduction of fibers and matrix properties, while in cyclic load conditions, nanofillers remain unchanged under different states of stress. Due to the crack propagation, material properties of composites are changed by a set of sudden material property degradation rules.

Sudden material property degradation rules

The sudden material property degradation rules for some failure modes of a unidirectional ply under a bi-axial state of stress are available in the literature [40, 41]. A complete set of sudden material property degradation rules for various failure modes of a unidirectional ply under a multi-axial state of static and fatigue stress was developed by Shokrieh and Lessard [9].

Normalized stiffness degradation approach for fibrous polymeric composites under fatigue loading

The residual stiffness of the material is also a function of the state of stress and the number of cycles. Since residual stiffness can be used as a nondestructive measure for damage evaluation, the stiffness degradation models have been developed by many investigators. By means of normalization technique, all different curves for different states of stress can be shown by a single master curve. Shokrieh and Lessard [9] developed a method of normalization and the present study follows the mentioned method to predict the stiffness degradation of nanocomposite materials by means of micromechanics approaches.

A polymeric composite under a constant uniaxial fatigue loading and under static loading, or equivalently at n = 0.25 cycles (quarter of a cycle) in fatigue, is considered. To present the residual stiffness as a function of the number of cycles in a normalized form for polymeric composites in fatigue loading conditions (E f), the following equation is developed [9]:

$$ E^{\text{f}} (n,\sigma ,K) = \left[ {1 - \left( {\frac{\log (n) - \log (0.25)}{{\log (N_{\text{f}} ) - \log (0.25)}}}\right)^{\lambda}} \right]^{{\frac{1}{\gamma }}} \left( {E^{\text{s}} - \frac{\sigma }{{\varepsilon_{\text{f}} }}} \right) + \frac{\sigma }{{\varepsilon_{\text{f}} }} $$
(6)

where, \( E^{\text{f}} (n,\sigma ,K) \) is the residual stiffness for polymeric composites under fatigue loading condition, E s is the static stiffness of polymeric composites, σ is the magnitude of applied maximum stress, ɛ f is the average strain to failure, n is the number of applied cycles, N f is the fatigue life at σ, and γ, λ are experimental curve fitting parameters. By means of the normalization technique [9], all different curves for different states of stress in Fig. (4) collapse to a single curve as shown in Fig. 2.

Fig. 2
figure 2

Normalized stiffness degradation curve [9]

Full size image

There are many models [26, 42–44] to predict the modulus of such modified polymers with nanoparticles in static state condition. In the present study, the Halpin–Tsai and Nielsen models are used as these are considered to be the most applicable for the present systems.

Normalized stiffness degradation model (NSDM) for nanoparticle/fibrous polymeric composites

The Nano-NSDM based on the Halpin–Tsai model

By coupling of the normalized stiffness degradation approach for fibrous polymeric composites under fatigue loading and the Halpin–Tsai micromechanics model, the normalized stiffness degradation model for polymeric nanocomposites under fatigue loading, \( E_{\text{nc}}^{\text{f}} (n,\sigma ,K) \), according to the Eq. 7 was developed.

$$ E_{\text{nc}}^{\text{f}} = \frac{{1 + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}{{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}V_{\text{f}} }}{{1 - {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}V_{\text{f}} }}\left[ {1 - \left( {\frac{\log (n) - \log (0.25)}{{\log (N_{\text{f}} ) - \log (0.25)}}} \right)^{\lambda } } \right]^{{\frac{1}{\gamma }}} \left( {E^{\text{s}} - \frac{\sigma }{{\varepsilon_{\text{f}} }}} \right) + \frac{\sigma }{{\varepsilon_{\text{f}} }} \times \frac{{1 + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}{{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}V_{\text{f}} }}{{1 - {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + {{2w} \mathord{\left/ {\vphantom {{2w} t}} \right. \kern-\nulldelimiterspace} t}} \right)}}V_{\text{f}} }} $$
(7)

The Nano-NSDM based on the Nielsen model

After a combination of the normalized stiffness degradation approach for fibrous polymeric composites under fatigue loading with the Nielsen micromechanics model, the normalized stiffness degradation model polymeric nanocomposites under fatigue loading, \( E_{\text{nc}}^{\text{f}} (n,\sigma ,K) \), according to the Eq. 8 was developed.

$$ \begin{aligned} E_{\text{nc}}^{\text{f}} = & \frac{{1 + (K_{\text{E}} - 1){{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}V_{\text{f}} }}{{1 - \left\{ {1 + \frac{{(1 - \nu_{\text{f}} )}}{{\nu_{\max } }}[\nu_{\max } \;\nu_{\text{f}} + (1 - \nu_{\max } )(1 - \nu_{\text{f}} )]} \right\}{{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}V_{\text{f}} }} \times \\ \left[ {1 - \left( {\frac{\log (n) - \log (0.25)}{{\log (N_{\text{f}} ) - \log (0.25)}}}\right)^{\lambda } } \right]^{{\frac{1}{\gamma }}} \left( {E^{\text{s}} - \frac{\sigma }{{\varepsilon_{\text{f}} }}} \right) + \frac{\sigma }{{\varepsilon_{\text{f}} }} \times \frac{{1 + (K_{\text{E}} - 1){{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}V_{\text{f}} }}{{1 - \left\{ {1 + \frac{{(1 - \nu_{\text{f}} )}}{{\nu_{\max } }}[\nu_{\max } \;\nu_{\text{f}} + (1 - \nu_{\max } )(1 - \nu_{\text{f}} )]} \right\}{{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} - 1} \right)} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{E_{\text{P}}^{\text{s}} }}{{E_{\text{m}}^{\text{s}} }} + (K_{\text{E}} - 1)} \right)}}V_{\text{f}} }} \\ \end{aligned} $$
(8)

Results and model verification

In this research, the silica nanoparticles have been employed to modify the epoxy resin. In general, the dimensions of these particles are in micron ranges. However, with the advance of nanotechnology as well as the processing techniques, various types of particles in nanoscales have recently been developed and then utilized as reinforcement in polymeric composites [27]. Experimental results obtained from tension–tension fatigue tests on a bulk epoxy confirm the reduction of the epoxy laminated composite stiffness, caused by the presence of cracks, which can effectively be compensated by the silica nanoparticles. In their work [27], 185 g/mol of epoxy resin, LY556, bis-phenol A (DGEBA), was supplied by Huntsman, Duxford, UK, and the silica (SiO2) nanoparticles were supplied by Nanoresins, Geesthacht, Germany.

For the spherical silica nanoparticles used in the present work, the aspect ratio is unity, and hence \( w/t \) = 1 will be used. Also, in this case study, ν max = 0.632, \( \nu_{\text{f}} \) = 0.048, so the value of K E is 2.5 and the Nielsen “no-slip” model was implemented. Typical stiffness variation curves obtained at \( \sigma_{ \max } \) = 225 MPa are shown in Fig. 3. In general, all materials exhibit a stiffness reduction with fatigue cycles, as has been previously observed in FRPs [45, 46]. The stiffness reduction was quite steep and very significant in the GRP nanocomposites. By means of neat resin (NR) data of Fig. 3 which was related to the GFRP composites without nanoparticles and by means of the normalized technique, curve fitting parameters λ and γ are obtained and shown in Fig. 4. The other properties of the GRP composites and nano-silica are shown in Tables 1 and 2.

Fig. 3
figure 3

The stiffness variation during fatigue cycling in the GFRP composites at \( \sigma_{ \max } \) = 225 MPa, (i) neat resin (NR), (ii) resin with 9 wt% rubber microparticles (NRR), (iii) resin with 10 wt% silica nanoparticles (NRS), and (iv) resin with a “hybrid” matrix containing both 9 wt% rubber and 10 wt% silica particles (NRRS) [27]

Full size image
Fig. 4
figure 4

Normalized stiffness degradation curve for GFRP composites without nanoparticles, \( \lambda = 3.348,\;\gamma = 0.357 \), \( \varepsilon_{\text{f}} \) = 0.02

Full size image
Table 1 Properties of the GFRP composites [27]
Full size table
Table 2 Properties of the Silica nanoparticles
Full size table

For evaluating the accuracy of the derived equations for the neat resin, according to Fig. 5, the trend for stiffness of neat resin of GFRP composites without nanoparticles versus the number of cycles is depicted, and good agreement with experimental data was obtained. This compatibility shows that obtained curve fitting parameters are suitable for this composite.

Fig. 5
figure 5

Stiffness reduction for neat epoxy resin GFRP composites without nanoparticles, \( \sigma_{\max } \) = 225 MPa

Full size image

Figure 6 shows that the reported stiffness versus the number of cycles for 10 wt% silica-nanoparticle-filled epoxy polymers is in a good agreement with the modified normalized stiffness degradation models. Also, the behavior of the modified Nielsen “no-slip” model is nearer to the result of the experiment compared with the modified Halpin–Tsai model. In Table 3, the results and value of error for each modified model are presented. When the number of cycles was 705 cycles, according to the experimental reported results, \( E_{\text{fib,c}}^{\text{f}} \) was 16.13 GPa. The predicted stiffness by the present model for fibrous polymeric composite material (\( E_{\text{fib,c}}^{\text{f}} \)) was 14.40. Then, the Nano-NSDM based on the Halpin–Tsai model and Nielsen model was used and the stiffness of the fibrous polymeric composite (\( E_{\text{fib,c}}^{\text{f}} \)) with 10 % silica nanoparticles was found equal to 16.59 and 15.90 GPa with 2.84 and 1.43 % error, respectively. Also, a drastic trend of stiffness reduction in the primary level of cycles has been observed.

Fig. 6
figure 6

Stiffness reduction for GRP composites with 10 wt% silica nanoparticles, \( \sigma_{\max } = 225\;{\text{MPa}} \)

Full size image
Table 3 Results and value of error for modified models
Full size table

As the second verification of the model, the results presented in [27] are considered. The fatigue limit, i.e., the maximum applied stress for a life of 106 cycles of the neat epoxy, is about 95 MPa (Please see [27]; Fig. 1). At this state of stress, the N f is 2000226 cycles. By means of the classical lamination theory (CLT), the equivalent stiffness and strain for composites without nanoparticles were obtained. After finding the stiffness of the composites without nanoparticles by applying the normalized stiffness degradation model for polymeric nanocomposites under fatigue loading condition (The Nano-NSDM based on Halpin–Tsai model), the equivalent stiffness of fibrous polymeric nanocomposites (\( E_{\text{fib,c}}^{\text{f}} \)) was obtained equal to 5.54 GPa. Then, at the previous strain, the tensile stress has been achieved equal 111.92 MPa for nanocomposites. This process is demonstrated in Fig. 7 as a schematic flowchart to find the equivalent tensile strength.

Fig. 7
figure 7

Schematic flowchart to generate the equivalent tensile strength

Full size image

For the third verification of the model, the results presented in [21] are considered. It was assumed that the curve fitting parameter in normalized stiffness degradation techniques is valid, as shown in Table 4.

Table 4 Results of neat epoxy and 10 wt% nano-silica-modified GFRP composites, σ = 95 MPa
Full size table

This assumption has a negligible error. By applying the developed model, at 22143 numbers of cycles, the final results are presented in Table 5. The tensile strength for 10 wt% SiO2/LY556 Epoxy nanocomposites calculated by the model is equal to 29.24 MPa (in comparison with 28.8 MPa presented in [21]). Therefore, the accuracy of the developed model is acceptable. The results are expressed in Table 5.

Table 5 Properties of nanoparticle-filled GFRP composites
Full size table

Conclusions

The new model developed in this research is an integration of two major components: the micromechanical and the normalized stiffness degradation approaches. The model is able to predict the final fatigue life of nanoparticle/fibrous polymeric composites under general fatigue loading conditions. In the present work, it is assumed that the major reason for material properties’ reduction of nanoparticle/fibrous polymeric composites under general fatigue loading conditions is related to the reduction of fibers and matrix properties, while in cyclic load conditions, the mechanical properties of nanofillers are assumed to remain unchanged under different states of stresses. Due to the crack propagation, material properties of composites are changed by a set of sudden material property degradation rules.

The stiffness reduction versus the number of cycle was obtained based on the Halpin–Tsai and the Nielsen micromechanical models for a composite reinforced with nanoparticles. In the developed model, called Nano-NSDM, material properties and other required parameters should be obtained by curve fitting techniques.

The developed fatigue model is verified by applying it to different experimental data provided by other researchers. In three steps, verifications have been done and the results obtained by the new fatigue model are in very good agreement with the experimental data for nano-silica/glass fiber epoxy and also nano-silica/epoxy composites under constant cyclic stress amplitude fatigue loading. A maximum of 2.84 % error for the modified Halpin–Tsai approach based on the normalized stiffness degradation model was observed. For the Nielsen model, the maximum error was 1.43 %. The results show that the behavior of the modified Nielsen “no-slip” model in comparison with the modified Halpin–Tsai model is more compatible with experiment results.