Ac conductivity and its scaling behavior in borate and bismuthate glasses

Abstract

In the present work, ac conductivity measurement and its compositional dependence scaling analysis are studied on lithium and sodium based borate and bismuthate glasses in the frequency range from 20 Hz to 1 MHz at different temperatures. The measured conductivity data of these glasses are analyzed using Cole-Cole type impedance response function, Jonscher’s universal power law and Dyre’s random free energy barrier model. To get a consistent stand point on ion dynamics, different microscopic models and theories proposed for the ion conduction mechanism in disordered ionic solids are discussed and compared. Universality features of ac conductivity and its scaling behavior are discussed. The compositional dependence scaling behavior in borate and bismuthate glasses are studied using Jonscher’s power law hopping frequency ω_p and minimum jump frequency γ_min in Dyre’s random free energy barrier model. The scaling results are compared and reported.

Introduction

The dispersion in conductivity has been seen in wide variety of disordered solids like, ion conducting glasses, amorphous semiconductors, ionic and electronic conducting polymers, organic semiconductors, non-stotchiometric or highly defective crystals or doped semi conductors, single crystals, etc. [1–5]. At low frequencies, one observes a constant conductivity while at higher frequencies the conductivity becomes strongly frequency dependent. The generality of this behavior for many widely different classes of materials was pointed out by Jonscher and his co-workers [6]. In all cases, the ac conductivity and permittivity loss above the dielectric loss peak frequency (ω > ω_p) are empirically represented as σ′(ω) ∝ ωⁿ and ε′′(ω) ∝ ωⁿ⁻¹, with 0 < n ≤ 1. There are several diverse viewpoints concerning the conductivity and dielectric dispersion in disordered ionic solids. Many ion–ion interaction theories with different degrees of sophistication, and models have been proposed differing in their approaches to explain the observed ac conductivity [7–9]. These observations are receiving much attention, since they impact strongly on the assessment of new theoretical models on ion dynamics and its relaxation behavior.

In this context, to get a consistent stand point on ion dynamics a brief review on the various microscopic models and theories proposed for the ion conduction mechanism in disordered ionic solids are described in Sect. “Microscopic models and theories on fast ion conductors”. Section “Universality and scaling behavior in disordered ionic solids” is on the universality features of ac conductivity and its scaling behavior. The composition dependence ac conductivity and its scaling behavior in lithium and sodium borate and bismuthate glasses are dealt in Sect. “Ac conductivity in borate and bismuthate glasses”. The summary of the present work is given in Sect. “Conclusion”.

Microscopic models and theories on fast ion conductors

Any intrinsic property that influences ion dynamics in disordered ion conducting solids quite well studied through impedance spectroscopy by electrical relaxation measurements [10]. It is characterized by measurement and analysis of some or all the macroscopic complex quantities such as, impedance (Z*), conductivity (σ*) or admittance (Y*), electric modulus (M*), and permittivity (ε*). The results from complex plane and spectral plots of above complex quantities may often be correlated with material properties such as, mass transport, rates of chemical reaction, corrosion, dielectric properties, defects, microstructure, and the composition influence on the conductance of solids. In the past five decades, impedance spectroscopy is used to investigate the dynamics of bound and/or free ions in the bulk or in the interfacial regions of any kind of solid or liquid material such as ionic, semi-conducting, mixed electronic-ionic and dielectrics. Whatever be the preferred representation, there is no escape from the fact that the measurements which are macroscopic in nature. In the literature, the conductivity representation is a most prominent representation to relate the macroscopic measurement to the microscopic movement of the ions.

The dc part of the conductivity appears to be reasonably understood in terms of activated hopping of ions over energy barriers. This is supported by the Arrhenius temperature dependence exhibited by dc conductivity. A number of successful theoretical efforts, which have been made in predicting the activation energies associated with the dc conductivity. In the early models, viz., Anderson and Stuart microscopic model [11], Ravine and Souquet weak electrolyte theory [12], Minami and his co-worker’s diffusion path model [13] and in Ingram’s cluster by pass model [14], the motion of the ions is coupled with Coulomb interaction and the mechanical dynamics of the host glass matrix.

At one level, in disordered ionic solids, the polarization is inseparable from the eventual conduction process, since, the mobile ions and opposite charged matrix resembles an assembly of dipoles. Consequently, in the past few decades, there are attempts to characterize the ion dynamics through dielectric loss and conductivity [6, 15]. Inevitably, the ac conductivity measurements on variety of disordered ionic solids show universal frequency dependence characterized by

$$ {\sigma }'(\omega )\, = \,\sigma ({\text{o}})\, + \,{\text{A }}\omega ^{n} , $$

(1)

where σ(o) is the zero frequency limit of σ′(ω), ω is the angular frequency, and A is the pre factor which is function of temperature and composition. At low frequencies one observe a constant conductivity, while at higher frequencies the conductivity becomes strongly frequency dependent and increases with frequency. The increase in conductivity usually continues up to phonon frequencies [16]. Many conceptual models have been developed to identify the source of power law dispersion. The power law features are also observed with other non-Debye dielectric response functions such as Cole-Cole, Cole-Davidson, and Havirliak-Negami [17]. The frequency dependence of dielectric dispersion is very well characterized by a broad dielectric-loss peak and constant loss behavior above the dielectric loss peak.

In the literature, explanation for conductivity dispersion is the existence of one or the other kind of inhomogenities in the disordered solids. The inhomogenities may be of a microscopic or a macroscopic nature. However, the emphasis is more on the hopping model, where the inhomogenities are assumed to be on the atomic scale by the distribution of energy barriers. The dc activation energy turns out to be the maximum of a whole range of activation energies needed to account for the frequency dispersion.

In the hopping approach, there are two basic types of theory have been used to describe the universal electrical properties of disordered ionic conductors. In the first approach, the ionic hopping events are independent and have a broad distribution of relaxation times. The distribution of relaxation times are described by William Watts relaxation function [18]

$$ \phi (t)\, = \,\exp [ - (t/\tau )^{\beta} ]. $$

(2)

This is an empirical equation and the corresponding frequency domain response cannot be derived analytically by imaginary Laplace transform of $\phi (t)$. Since, there is no analytical solution, numerical and empirical methods are used [18].

In the second approach, collective effects occur such that each hopping ion has strong interactions (usually of Coulombic type) with surrounding ions. The second approach has received considerable attentions and seems to explain the observed features of σ′(ω) and ε′′(ω).

The universal power law pertains to the second approach. The exponent n seems to characterize the deviation from Debye behavior and can be regarded as a direct measure of the inter-ionic interaction and coupling strength.

In the literature, there are many attempts to justify that the power law, Eq. 1 has the origin of nearest-neighbor Coulomb interactions and site energy variation [19]. Under the second approach, Ngai [20] proposed the coupling model in which the co-operative adjustment of the environment on the migration ions leads to a stretching out of the relaxation process to times much larger than the primitive relaxation time (Debye relaxation time) for a non-interacting jump. Here it is assumed that the dc and ac behavior are coupled together giving rise to stretching exponential relaxation of the type

$$ {\sigma }'(\omega ) = \sigma (0)[1 + (\omega \tau )^{n} ], $$

(3)

there by defining a average relaxation time τ, which is related to a parameter A in Eq. 1 by A = σ(0)τⁿ, where the exponent n is around 0.6. At ωτ = 1, σ′(ω) = 2σ(0), i.e., τ⁻¹ represents the frequency at which σ′(ω) begins to depart substantially from the dc value σ(0). It is argued that the average relaxation time τ, is the Maxwell relaxation time [21], which varies inversely as the dc conductivity. From this it follows that E _σ = E _τ or equivalently

$$ E_{{\text{A}}} \, = \,(1 - n)E_{\sigma } , $$

(4)

where E _A and E _σ are the activation energy for the parameter A and dc conductivity respectively and Eq. 4 is referred as “Ngai relation” [21].

Funke [9] proposed the jump relaxation model, under the second approach. The jump relaxation model brings out the influence of a cage effect potential due to the surrounding ions, with a high probability of return of the jumping ion to its initial position, which contributes only to the ac and not to the dc conductivity. Further, the model explains E _σ = E _τ by the fact that both successful and unsuccessful jumps involve the same potential barrier. This statement seems to be valid only for strong electrolytes, since it is difficult to see how E _τ, can include an energy that determines the increase in number of carriers with increasing temperature.

The diffusion-controlled relaxation (DCR) model of Elliott and Owens [7] incorporates co-operative ionic motions, and has some formal similarities to Funke’s model. In this model, in addition to the Coulombic and strain energy contributions, a contribution from the polarisation relaxation due to the double occupancy effect of diffusion ion is also considered for the activation energy. The DCR model, too, predicts that E _σ = E _τ only for strong electrolyte materials.

The unified site relaxation model proposed by Bunde, Funke, and Ingram [22] combine the essential features of the dynamic structure and jump relaxation models [8, 9]. In this model, the mobile ions hop backward and forward many times, before the coulomb field is relaxed and the target site adjusts itself to the needs of its new occupant.

Another model under the second approach is the random free energy barrier model [RFEBM] proposed by Dyre [23] through hopping conductivity mechanism. In Dyre’s RFEBM, it is assumed that there is distribution of jump frequencies with all the jump distances is assumed to be equal. The ac conductivity derived under RFEBM is given by

$$ {\sigma }'(\omega )\, = \,\frac{{\sigma (o)i\omega \tau }} {{\ln [1 + i\omega \tau ]}}. $$

(5)

The real part of ac conductivity becomes

$$ {\sigma }'(\omega ) = \frac{{\sigma (o)\omega \tau \tan ^{{ - 1}} [\omega \tau ]}} {{\{ [\ln [{\sqrt {1 + \omega ^{2} \tau ^{2} } }]]^{2} + [\tan ^{{ - 1}} [\omega \tau ]]^{2} \} }}, $$

(6)

By Eq. 6 one can observe the dispersion in σ′(ω) through relaxation time τ, which is reciprocal of the minimum jump frequency γ_min for the distribution of energy barriers. In disordered solids, Dyre’s RFEBM explains all the criteria of ac conductivity behavior, predicts the broad dielectric-loss peak with dielectric loss peak frequency ω_p = 4.17/τ [23] and agrees with the BNN relation.

In all these theories, the important point is that the ac relaxation process and dc conductivity are both parts of the same process in an interactive ion jumping. Therefore, in the present work, the ac conductivity and its scaling behavior in borate and bismuthate glasses are studied using Jonscher’s universal power law and RFEBM. However, the universality and scaling behavior in disordered solids are given in the next section.

Universality and scaling behavior in disordered ionic solids

The disordered ionic materials share common features such as: (1) disordered arrangements of the mobile ions within rigid matrix, (2) thermally activated hopping processes of the mobile ions, giving rise to dc conduction, and (3) remarkably similar features in ac conductivity and its scaling behavior. However, in disordered ionic solids, the scaling and its universality feature are seen prominently in the conductivity dispersion [1–4, 24–27]. It is usually possible to scale the temperature and composition dependence of conductivity spectra into a single master curve, which results in a time-temperature superposition principle. The master curve is the representation of conductivity dispersion, where the frequency axis is scaled by arbitrarily determined characteristic frequency ω_c and conductivity axis is scaled by dc conductivity. In recent publications [1, 2, 24–27], the scaling in ac conductivity has been studied using the directly accessible quantities such as the temperature T, the dc conductivity σ(o), the concentration of alkali ions, the dielectric loss strength, Δε = ε_S−ε_∞, the high frequency dielectric constant ε_∞ and the loss peak frequency or hopping frequency ω_p. In the literature, different workers have considered the scaling frequency in different forms as: (a) ω_c = σ(o)T; (b) ω_c = σ(o)T/x; (c) ω_c = ε_o Δε/σ(o); (d) ω_c = ε_o ε′′_max/σ(o) and (e) ω_c = ω_p.

Scaling methods for the analysis of the ac conductivity in ion conducting glasses were first used by Taylor and Isard [28]. Taylor showed that the dielectric loss for the glasses fell on a master curve against the scaled frequency, in accordance with the Debye equation with a distribution of relaxation times. Isard relabeled Taylor scaling by plotting dielectric loss against the log of the product of frequency and resistivity. In 1991, Kahnt [29] compared the master curves of a variety of silicate, borosilicate, and germanate glasses. Further, it has been noticed that there is no difference in shape between different master curves and thus concluded that the shape is independent of the ionic concentration and glassy structures.

Recently, Roling and his co-workers [24] analyzed the scaling properties of the conductivity spectra of sodium borate glasses containing different concentration (x) of sodium oxide at different temperatures. The scaling frequency ω_c = σ(o) T has been used to scale the frequency axis at different temperatures and ω_c = σ(o)T/x for different temperature and compositions. Here x depends on composition, which takes care of the changes in the alkali oxide content. It has been observed that scaling the frequency axis by ω_c = σ(o)T at different temperature collapse the conductivity spectra into a single master curve. However, the superposition of the master curves show deviation with different compositions when it is scaled by ω_c = σ(o)T. This deviation in the master curve is accounted by scaling the frequency axis by ω_c = σ(o)T/x, where x depends upon compositions, which takes care the changes in the cation number density. In spite of this modification, the time-temperature super position of the master curves for different compositions are not exact, but there are small differences in shape between the master curves. Sidebottom [25] attributed the differences in shape of master curves, to the changes in the ion hopping length with changing alkali oxide content of the glasses along with the cation number density. The proposed characteristic frequency is ω_c = ε_o Δε/σ(o), which uses the dielectric relaxation strength, Δε = ε_S–ε_∞ = γ N (qd)²/(3ε_o kT) as a scaling parameter for the frequency axis. Where ε_s is static dielectric constant, ε_∞ is the high frequency dielectric constant, N is the cation number density, γ is the fraction of mobile cations and d is mean distance traversed in a single hop.

Subsequently, Schroder and Dyre [1, 30] established the validity of the Sidebottom’s scaling approach in single and mixed alkali glasses. The results are as follows: (i) the temperature-dependent conductivity spectra of a given glass can be superimposed onto a master curve, if and only if the shape of these spectra does not depend on temperature. (ii) the superposition of the master curves of different glasses are exact, if and only if the master curves of individual glasses are identical in shape and (iii) there are pronounced differences in shape between the conductivity spectra of single and mixed alkali glasses. However, in single alkali glasses, the shapes of the conductivity spectra depend on the alkali oxide content as well as on the nature of the network former.

To fulfill the Sidebottom’s scaling approach to these glasses, Rolling et al. [31] replaced the Δε in the Sidebottom’s scaling by the maximum value of the imaginary part of the dielectric constant ε′′_max(ω), by defining the scaling frequency ω_c = ε_O ε′′_max(ω)/σ(o), where the ε′′_max(ω) was obtained by a Kramers Kronig transformation of ε′(ω). Since, the ε′′_max(ω) is less affected by the electrode polarisation effects than that of the dielectric strength.

In spite of these modifications, there is failure to emphasize the composition dependence of the shape of the conductivity spectra. However, the possible reasons for the changes in the shape of the conductivity spectra of single alkali glasses with increasing alkali content are as follows: (a) the increasing in strength of the Coulombic interactions between the alkali ions on the one hand and the structural changes on the other hand, (b) the shape of the conductivity spectra depends strongly on the local dimensionality of the diffusion pathways, and (c) in alkali oxide glasses, at low alkali concentration, the connectivity of the network increases with the alkali oxide content by the structural units. At the large concentration of alkali oxide, the glass network de-polymerizes due to the formation of the non-bridging oxygen. The cleavage of network linkage will result in the presence of vacant site and this vacancy will introduce the change in the Haven ratio of the diffusion ions.

Further, it is not possible to correlate the scaling frequency with the permittivity change in some alkali oxide glasses and heavy metal oxide glasses, as they do not possess well-defined dielectric loss peaks. Consequently, the exact values of the static dielectric constant could not be obtained from the frequency dependence of dielectric data. Ghosh and Pan [26] used Jonscher’s power law, to the scale the frequency axis and it is given by Eq. 1 as,

$$ {\sigma }'(\omega ) = \sigma (0)[1 + (\omega /\omega _{{\text{p}}} )^{n} ]. $$

(7)

The characteristic frequency is the hopping frequency ω_p is obtained from experimental data by equating frequency at which

$$ {\sigma }'(\omega _{{\text{p}}} ) = 2\sigma (0). $$

(8)

Equations (7) and (8) are constructed by Almond and co-workers [32] and it is still used in the analyses of ac conductivity data and its scaling behavior. Ghosh and Pan [26] justified that the hopping frequency is suitable parameter for scaling, which automatically accounts the Haven ratio change and the dielectric strength implicitly. The hopping frequency is considered as a more appropriate parameter for the scaling of the conductivity spectra for the glasses, where dielectric loss peak maxima or static dielectric constant value cannot be obtained. This appears quite justified as the change in hopping length with composition is manifested in the change in the hopping frequency. Further, the hopping frequency takes into account the correlation effects between successive hops through the Haven ratio.

Ac conductivity in borate and bismuthate glasses

The different compositions of x A₂O + (1−x) B₂O₃ and x A₂O + 1−x Bi₂O₃ (A = Na, Li ) glassy systems were prepared from reagent grade Na₂CO₃, Li₂CO₃, Bi₂O₃, and H₃BO₄ by melt quenching process for x in the range 0.1–0.5 in steps of 0.1 except sodium borate glasses. The preparation, characterization, and ac electrical conductivity measurement on these lithium and sodium borate and bismuthate glasses has been described in detail in our earlier reports [33–35]. In brief, the electrical conductivity was measured using Zentech 3305 component analyzer in the frequency range 20 Hz–1 MHz and in the temperature range from 300 to 500 K for borate systems and 450–600 K for bismuthate systems. Initially, the measured conductivity data were analyzed with electrochemical impedance software Equivalent Circuit Version 3.97 [36] to obtain the bulk dc conductivity. The magnitude of dc conductivity, Cole–Cole type impedance relaxation time τ_cc and exponent α at one particular temperature are given in Tables 1 and 2 for bismuthate and borate systems, respectively. From the temperature-dependent bulk conductivity, the activation energies are obtained from Arrehenius plot. The magnitude of the observed activation energies for the lithium and sodium based borate and bismuthate glasses are shown in Fig. 1 along with some earlier reported values [37–39]. The decrease in activation energy with increases of alkali content reveals that the alkali oxide enters in the host glassy matrix.

Table 1 The magnitude of exponent α, the mean relaxation time τ_cc dc conductivity and activation energy for the x Li₂O + (1−x) Bi₂O₃ system and xNa₂O + (1−x)Bi₂O₃ system

Table 2 The magnitude of exponent α, the mean relaxation time τ_cc, dc conductivity and activation energy for the x Li₂O + (1−x) B₂O₃ system and xNa₂O + (1−x)B₂O₃ system

Fig. 1

Variation of activation energy with alkali ion concentrations for different glassy systems

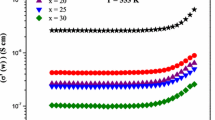
Figure 2 shows the ac conductivity behavior of the sample 0.3 Li₂O + 0.7 B₂O₃ at different temperatures. All the samples exhibit the high frequency dispersion and a frequency independent region at low frequencies. The switch over from the frequency-independent region to frequency-dependent region is the signature of on set of conductivity relaxation, which shifts toward higher frequencies as the temperature increases. The position of the onset frequencies are shown in Fig. 2 by arrow heads at each temperature. Over the fixed frequency window, the conductivity dispersion is described by Jonscher’s UPL as Eq. 1. In Fig. 2, the continuous lines are non-linear least square fit of Eq. 1. For the present glassy systems, the temperature-dependent conductivity scaling behavior has been carried out and some of the results are published [33–35].

Fig. 2

Ac conductivity spectra for 0.3 Li₂O + 0.7 B₂O₃ glassy system at different temperature

The first point of interest is to note that whether the conductivity data at different temperature are merge into a single master curve when the conductivity axis is scaled with respect to σ(o) and the frequency axis with respect to ω_p for a given composition. To verify this, the hopping frequency is computed by using Eq. 1. The experimental data of each conductivity isotherm for all glass compositions are scaled by σ(o) and the corresponding ω_p. In Fig. 3, the temperature-dependent ac conductivity scaling behavior is shown for the lithium borate glassy system for x = 0.3. From Fig. 3, it is observed that the scaling spectra collapse into a single master curve for a narrow range of temperature. In the wide range of temperature, the scaling curves spreads near and above the hopping frequency when the conductivity spectrum is scaled by ω_p. It is true, as the temperature increases, in log-log representation the conductivity dispersion may be found outside the measurement frequency window. Therefore, it is difficult to predict the correct magnitude of n and ω_p using non-linear least square fit. Therefore, in the temperature-dependence scaling spectra, a spread is observed in the high frequency region. The scaling analysis on the other composition indicates that the relaxation mechanism is found to be temperature independent under conductivity formalism only in the narrow range of temperature. The temperature dependence scaling analysis for other samples are reported elsewhere [33–35].

Fig. 3

Temperature dependence scaling spectra for 0.3 Li₂O + 0.7 B₂O₃ glassy system

In literature, the complex electric modulus approach shows a pronounced concentration dependence of the electrical relaxation, whereas such dependence has not been found in analyses of the complex conductivity. The use of electric modulus and conductivity approach to study the composition dependence scaling is still a debate in the literature [2]. Further, the composition dependence of conductivity scaling spectra seems to be applicable with the modification of the scaling frequency as discussed in Sect. “Universality and scaling behavior in disordered ionic solids”. For the composition dependence conducting scaling behavior as described by Sidebottom [24] one need the parameters such as, the static dielectric constant ε_S, the high frequency dielectric constant ε_∞ and/or the dielectric loss maximum ε′′_max. Therefore, the measured conductance and capacitance data of the all the samples are converted into the dielectric domain with proper suppression of dc conductivity for the analysis of dielectric data and to extract the dielectric parameters by numerical fitting procedure. However, in the present glassy systems, the dielectric loss spectra do not possess a well-defined dielectric loss peaks over the measured temperature and frequency range. The real part of permittivity shows anomalous dispersion in the low frequency region due to electrode polarisation and unable to obtain the exact magnitude of static dielectric constant. As a consequence, the value of static dielectric constant and the maximum value of dielectric loss peak cannot be obtained from the numerical fit of the measured data. Therefore, on the closer examination of composition depends scaling behavior, it is found that the loss peak frequency ω_p of Jonscher’s universal power law and the magnitude of minimum jump frequency γ_min = 1/τ in the Dyre’s RFEBM are seems to be more appropriate for composition dependence conductivity scaling studies. Therefore, in the present work ω_p and γ_min are used as scaling frequency for the composition dependence scaling analysis on lithium and sodium based a borate and bismuthate glasses.

The compositions dependence of the scaling spectra (at room temperature for borate systems and at 473 K for bismuthate systems) are shown in Fig. 4a–d with ω_p as scaling frequency. From Fig. 4a–d, it is clear that the scaling spectra for all the composition do not superimpose into a single master curve except sodium borate systems.

Fig. 4

Composition dependence scaling spectra for four glassy systems with ω_p as scaling frequency

This result is not quite surprising with regard to the universality of the scaling behavior of the conductivity spectra. These features are in agreement with the results reported in the literature [24–26, 30, 31]. The exponent n and ω_p may not be suitable factors to study the composition dependence scaling. As an alternate, to get a consistent picture on the composition dependence of ion relaxation mechanism, the composition dependence on scaling behavior is studied using random free energy barrier model. In random free energy barrier model, which is discussed in Sect. “Universality and scaling behavior in disordered ionic solids”, the disorderness is visualized through the jump probability distributions of mobile ions over the random distribution of free energy barriers [23]. Therefore, the effect of number density and mobility of the hopping ions in different samples may reflect the relaxation process through the minimum jump frequency, γ_min = 1/τ. Figure 5a–d show the conductivity spectra for the four samples at different concentration scaled by ω_c = γ_min. It is found that, from Fig. 5a–d the σ′(ω)/σ(ο) vs. (ω/γ_min) curves cannot collapse into a single master curve.

Fig. 5

Composition dependence scaling spectra for four glassy systems with γ_min as scaling frequency

The deviations from the master curve in the composition dependence scaling are accounted by the effect of concentration, mobility of the ion and nearest-neighbor interactions. From Figs. 4 and 5, it is observed that at larger time scales, i.e., at the low frequencies, the effect of the concentration and mobility of the diffusing ions taken care by long range diffusion constant and hence by the dc conductivity. The master curves in Figs. 4 and 5 show a better scaling at low frequencies. However, at shorter time scales, i.e., at higher frequencies, the dynamics of mobile ions coupled with nearest-neighbor interactions between mobile ions and host matrix ions and short range displacement of mobile ions over the local energy barriers. Different compositions have different distribution of local energy barriers and therefore, the dynamics of mobile ions in shorter time scales differ from each other. The composition dependence scaling shows a deviation from the master curve at high frequencies. Hence, the single scaling parameters such as ω_p or γ_min are not sufficient to predict correct picture of ion dynamics over the range of frequencies. An appropriate scaling parameter is needed as a scaling factor for the conductivity and frequency axis. However, the existing scaling behavior is valid only for limited range of composition and temperature under the fixed frequency window.

Conclusion

In the present work, the composition dependence of ac conductivity for various compositions of sodium and lithium borate and bismuthate glasses at different temperatures is studied. Using impedance spectroscopy technique, the data are analyzed based on Cole-Cole type impedance response function. The measured ac data are analyzed using the Jonscher’s universal power law to explain the observed dispersive behavior of the electrical conductivity. Jonscher’s universal power law and Dyre’s RFEBM model are used to explain the observed dispersive behavior of ac conductivity through hopping frequency ω_p and the minimum value of the distribution relaxation times (1/γ_min). The temperature and composition dependence scaling behavior in ac conductivity are satisfactorily explained by scaling the frequency axis by ω_p and γ_min.