A network that uses few active neurones to code visual input predicts the diverse shapes of cortical receptive fields

Abstract

Computational models of primary visual cortex have demonstrated that principles of efficient coding and neuronal sparseness can explain the emergence of neurones with localised oriented receptive fields. Yet, existing models have failed to predict the diverse shapes of receptive fields that occur in nature. The existing models used a particular “soft” form of sparseness that limits average neuronal activity. Here we study models of efficient coding in a broader context by comparing soft and “hard” forms of neuronal sparseness.

As a result of our analyses, we propose a novel network model for visual cortex. The model forms efficient visual representations in which the number of active neurones, rather than mean neuronal activity, is limited. This form of hard sparseness also economises cortical resources like synaptic memory and metabolic energy. Furthermore, our model accurately predicts the distribution of receptive field shapes found in the primary visual cortex of cat and monkey.

1 Introduction

The nature of neuronal representation in primary sensory regions of cortex has been the subject of intense experimental study ever since Hubel and Wiesel showed that neurones in primary visual cortex respond to localised oriented edges. Computational theories of representational learning have provided new ideas about the principles behind the operation of the primary visual cortex, (e.g. Dayan and Abbott, 2003). Specifically, methods for unsupervised learning of neuronal representations have been developed and applied to natural images (Bell and Sejnowski, 1997; Olshausen and Field, 1996). These models have shown that the combination of efficient coding and a sparseness constraint is compatible with physiological measurements in V1: a learning process that optimises the efficiency of coding in sparse neuronal representations yields receptive fields with oriented and localised structure like the ones that have been experimentally observed.

Fig. 1

Empirical distributions of neuronal activities in the different sparse coding models: Diagram (a) shows the results for a model with soft sparseness constraint (Sparsenet with Cauchy sparseness), diagram (b) for a model with hard sparseness constraint (SSC network). The distributions of neuronal activity coefficients are drawn as solid curves, the corresponding distributions of feed-forward projections onto the receptive fields are the dashed curves. The models were trained on $16 \times 16$ image patches and the sparseness parameter in Eq. (7) was set to $\theta=0.22$ for the Sparsenet and $\theta=0.31$ for the SSC network. The width bar in (b) gives the theoretical estimate of the gap size in the distribution of neuronal activity values (see text)

Recently, however, the biological relevance of the early models of efficient coding (Bell and Sejnowski, 1997; Olshausen and Field, 1996) was challenged by work that showed that the receptive fields generated by these models were too stereotyped edge detectors and did not capture the diversity in receptive field structure observed for the primary visual cortex in cat and monkey (Ringach, 2002). Here we investigate the reasons for this discrepancy by reconsidering the particular form of sparseness used in the early models and by exploring alternatives. We propose a new model of sensory coding that uses a different form of sparseness and that can account for the diversity of shapes of biological receptive fields. We explain how our new model relates to signal coding with optimized orthogonal matching pursuit (Rebollo-Neira and Lowe, 2002) and how it might change the current understanding of the computational role of simple cells in primary visual cortex.

1.1 Theories of efficient coding in vision

The biological motivation behind the theory of efficient sensory coding is the assumption of economy in sensory processing (Attneave, 1954; Barlow, 1983; Atick, 1992). If a biological organism is confronted with sensory input of certain properties, it is natural to expect that evolution and learning will adjust the organism to these properties in order to increase the efficiency of sensory processing (Gibson, 1966; Field, 1987). Specifically, it was suggested that efficiency in visual neuronal coding means that neurones become sensitive to independent elements that constitute an image. The receptive fields of neurones should then correspond to the statistically independent structural primitives of natural images. If the number of structural primitives in a patch of a natural image is typically small, this should be reflected in neuronal sparseness, that is, a small number of active neurones.

These general motivations of efficient coding are reflected in individual models of visual coding. Sparsenet (Olshausen and Field, 1996, 1997) is a causal generative model of visual input in which the neuronal representations of images are constrained to be sparse, that is, have a histogram of activity values that is more steeply peaked at zero than a Gaussian distribution. This model is able to learn to construct receptive fields that resemble cortical edge detectors (simple cells) when trained with natural images, but only if sparseness is imposed. A second class of models use independent component analysis of natural visual input (Bell and Sejnowski, 1997) which yields neuronal receptive fields with very similar shapes to those obtained with Sparsenet. Independent component analysis exploits the central limit theorem, which states that when non-Gaussian signals are linearly superimposed, the resulting distribution is more Gaussian than its components. In a linear mixture of signals, independent component analysis determines the individual components whose distributions deviate maximally from Gaussians (Hyvaerinen and Oja, 2000). The degree to which the distributions of individual components deviate from Gaussianity can be measured in different ways. The most commonly used measure of non-Gaussianity determines if a given distribution is more narrowly peaked at zero than a Gaussian distribution. Thus, although the underlying principles appear to be different, both types of coding models rest on a very similar definition of sparseness.

1.2 Different forms of sparseness and their motivations

Neuronal sparseness is defined in different ways in the literature. Both models of efficient sensory coding described above force neuronal activities to smooth distributions that are peakier than Gaussians. This constraint can be viewed as soft sparseness. An alternative form of sparseness often used in the literature is hard sparseness which keeps the proportion of neurones small that are simultaneously active in a network. Hard sparseness, in other words, corresponds to a discontinuous density of neural activities with a Dirac peak at zero. The effects of the two different types of sparseness constraints on the distributions of neuronal activity can be seen in Fig. 1 (solid curves). We refer to sensory representations that are formed using hard sparseness as sparse-set representations because the fraction of active neurones is small. In contrast, soft sparseness confines neural activity levels but not necessarily the fraction of active neurones.

In principle, either soft or hard sparseness can be used to generate efficient sensory representations. However, the two forms of sparseness have different ramifications for other aspects of cortical processing. These include the finite capacity of synaptic memory to make associations (Zetsche, 1990; Földiak, 1995) and restrictions on metabolic energy consumption (Baddeley, 1996; Laughlin and Sejnowski, 2003; Lennie, 2003). Parsimonius use of cortical memory favors hard sparseness. Research on neuronal associative memory has revealed that the memory in Hebbian synapses is best used by neural representations in which only a small fraction of the neural population is active at any instant, e.g. (Willshaw et al., 1969; Gardner-Medwin, 1976; Palm, 1980; Baum et al., 1988; Buhmann and Schulten, 1988; Tsodyks and Feigelman, 1988; Treves, 1991; Palm and Sommer, 1992; Földiak, 1995). Further, we will demonstrate that metabolic energy consumption can be conserved with hard sparse representations.

The agenda in this paper is to compare models of efficient coding that incorporate either hard or soft sparseness in their ability to predict receptive fields recorded in primary visual cortex (Ringach, 2002). We investigate the Sparsenet (Olshausen and Field, 1996) as an example of a model that uses soft sparseness and two different models that enforce hard sparseness. The first is the “sparse-set coding network”, a novel model that explicitly optimises the sparse selection of active neurones to achieve efficient coding. The second model serves as a control; it is a naive combination of Sparsenet with a mechanism for pruning small activity values.

2 Methods

2.1 A generative model of visual input

The idea of efficient coding can be formalised in a causal generative model of visual input. Generative models describe data with complicated probability density (such as visual inputs in natural environments) by estimating a combination of underlying causes. For a particular input x, the most probable instantiation of causes is described by a set of real-valued latent variables b. In general, this type of density estimation is a tractable description of the data if the underlying causes have a simple statistical structure, like for example, to be independent. In linear generative models, the input may be reconstructed by a matrix Ψ: $\hat{x}=\sum_{l=1}^{m}b_{l}\Psi_{l}$. Most models of efficient neuronal coding are based on linear generative models. They interpret the latent variables b as neuronal representations of sensory input and relate the linear map Ψ to neuronal receptive fields.¹

Van Essen and Anderson (1995), have estimated that sensory representations in primary visual cortex are overcomplete; a $14 \times 14 = 196$ array of input fibres is analysed by roughly $100 000$ neurones. The numbers correspond to an overcompleteness of about five hundred which exceeds the size of the models that can be handled in simulations. To enable overcompleteness in principle, we employed overcomplete causal models in which the dimension of the neuronal representation b was larger than the dimension of the input x. Further, we assumed that the neural activities are independent. In other words, the prior distribution of neural activity is factorial: $p(b)= \prod_i p(b_i)$. The joint distribution between inputs and neuronal representations is then given as

$$ p(x,b) = p(x\,|\,b) \prod_i p(b_i)\label{probdist} $$

(1)

where $p(x\,|\,b)$ is the likelihood. Sensory coding can now be defined as the procedure that finds the neuronal representation b that is most probable given a particular sensory input. Mathematically this means that the posterior probability $p(b\,|\,x) = p(x\,|\,b)p(b)/p(x)$ is maximised. For any fixed input, $p(x)$ is fixed and, therefore, the posterior is proportional to the joint distribution in Eq. (1). Thus, a minimisation of the energy function $E(b) = - \log p(x,b)$ describes the coding process. We use a Gaussian likelihood and $p(b_i) \propto \exp[-\theta f(b_i)]$ in Eq. (1), which yields the energy function

$$ E(b)= \frac{1}{2}\sum_{i=1}^{n}\left(x_{i}-\hat{x}_{i}\right)^{2} + \theta \sum_i f(b_i)\label{ofenergy} $$

(2)

As will be explained, the minimisation of the energy function in Eq. (2) with respect to the variables b describes many different methods of visual coding and efficient signal representation. The first term on the right hand side of Eq. (2) is the log likelihood, which is the quadratic error between the reconstruction $\hat{x}$ and the original input x. The second term on the right hand side of Eq. (2) is the log of the factorial prior of the neuronal variables. The learning of receptive fields is described by minimising Eq. (2) with respect to Ψ. It is assumed that the adjustment of the receptive fields Ψ takes place on a slower time scale than the coding process, that is, with neuronal representations b that are optimized for the given stimuli. In the next section, we will insert different functions $f(x)$ that constrain the neuronal representations to different forms of sparseness. The factor θ in the sparseness term governs the balance between reconstruction quality and sparseness. Therefore, we will refer to θ as the sparseness parameter.

2.2 Models of sensory coding

First we introduce different models of sensory coding, that is, different methods to optimise Eq. (2) with respect to the neuronal variables b. The method of optimisation has to be chosen in accordance to the sparseness function $f(x)$. The optimisation of the neuronal variables is assumed to take place on a faster time scale than the adjustments of receptive fields. Therefore, the following coding procedures treat the Ψ variables simply as constants. We will use the following definitions: $c_i := (\Psi x)_i = \left\langle \Psi_i, x\right\rangle$ is the inner product between a receptive field and the image (For inner products we will often use the bracket notation $x^T y =: \left\langle x, y\right\rangle$.) $C := \Psi \Psi^T$ is the matrix of inner products between receptive fields.

2.2.1 Soft-sparseness models

If $f(x)$ in Eq. (2) is chosen to be a smooth differentiable function, the local optimisation process corresponding to the coding of a sensory input can be computed by gradient descent in Eq. (2)

$$ \Delta b_i \propto - \frac{\partial E}{\partial b_i}= c_i - \sum_{j \not = i} C_{ij} b_j - \theta f'(b_i)\label{gradb} $$

(3)

Note that Eq. (3) defines the neuronal update in a network of cortical neurones. The neurones receive the feedforward projection (or thalamic input) c. Further, the neurones are interconnected with synaptic weights that are equal to the inner product of their receptive fields C. Two features in this network bias the neuronal activities towards lower values. First, the mutual connections that introduce competition between neurones with similar receptive fields. Second, the sparseness term. Here we will explore two functions that impose soft sparseness, the Cauchy function $f(x) = \mbox{log}(1+x^2/\sigma^2)$ as used in the original Sparsenet model (Olshausen and Field, 1996) and a hyperbola $f(x) = \sqrt{1+x^2/\sigma^2}$; a soft version of the $L_1$ norm as used in a different model (Chen et al., 1998).

2.2.2 Hard-sparseness models

If $f(x)$ in Eq. (2) is chosen to be the non-differentiable function that counts active neurones: $f(b_i) = ||b||_{L_0} = \sum_i H(|b_i|)$ with $H(x) := 1 {\rm for} x > 0; H(x) := 0 {\rm for } x \leq 0$, gradient descent can no longer be used for the optimisation. Rather, the hard sparseness constraint introduces the combinatorial problem to select the best subset of active neurones. To reveal the optimisation function for selecting active neurones, we rewrite Eq. (2) by expressing the neuronal activities as products $b_i = a_i y_i$ of analogue coefficients $a_i$ and binary usage variables $y_i$ (see Eq. (12) in Appendix A). For any given combination of input c and active neurones y the analogue values that minimise Eq. (2) are given by

$$ a^* = [P^{y}CP^{y}]^{+} c\label{optcoeffs} $$

(4)

where $P^y := \mbox{diag}(y)$ is the projector onto the coefficient subspace spanned by the vector y and $[.]^+$ is the Moore-Penrose pseudoinverse. Inserting the optimal analogue coefficents $a^*$ in Eq. (12) yields the optimization function for selecting active neurones:

$$ E(y) = - \frac{1}{2} \left\langle x, P_{\Psi}^{y} x\right\rangle + \theta ||y||\label{fullmodenergyresid} $$

(5)

where $P_{\Psi}^y := [P^y \Psi]^+ P^y \Psi$ (Eq. 15) is the projector onto the image subspace spanned by the receptive fields of the active neurones $\{\Psi_i: y_i = 1\}$ (for derivation of Eqs. (4) and (5), see Appendix A). Note, that Eq. (5) prefers sets of active neurones whose receptive fields span a subspace that contains as much as possible of the image. Thus, the optimization of Eq. (2) with a hard sparseness constraint dictates to select small sets of active neurones that minimise the residual between input and reconstruction, given by $r^y = x-\hat{x} = (1\!\!1-P_{\Psi}^{y})x$.

In general, the formation of efficient sparse-set codes by minimising Eq. (5) is an NP-complete combinatorial optimisation problem that in practice can only be solved approximately. The literature about adaptive signal representation describes several approximate optimisation strategies of Eq. (5) under the name of matching pursuit. Matching pursuit is a method to optimise the representation of a given signal in a given set of basis functions. The basis functions are the same as the receptive fields Ψ in our model. If Eq. (5) is used to select the single most adequate basis vector for a given input, it becomes $E(i) = - \frac{1}{2} \left\langle x, \Psi_i \right\rangle^2$. This version of Eq. (5) describes the selection of the first basis function in standard matching pursuit (Mallat and Zhang, 1993). In standard matching pursuit the approximation of the signal is refined by iterating the selection process on the residual. However, this iteration minimises Eq. (5) only in cases where the basis functions are orthogonal: Standard matching pursuit does not optimise coding efficiency in the general case because the residual is not orthogonal to the subspace of the basis functions that are already in use.

An extension of matching pursuit to cases of non-orthogonal bases is called optimised orthogonal matching pursuit (Rebollo-Neira and Lowe, 2002). This method calculates a set of biorthogonal basis vectors in each iteration step. The resulting basis set is used to determine the optimal coefficients and for selecting the next basis function. Optimised orthogonal matching pursuit can be reformulated as local minimisation of Eq. (5), that is, a sequential minimisation in which only a single y-variable is changed at a time: The biorthogonal basis vectors are given by the matrix $[P^y \Psi]^+$ which forms the projection operator $P_{\Psi}^y$ in Eq. (5).

In practice, the computation of the biorthogonal basis in each step of optimised orthogonal matching pursuit is computationally much lengthier than standard matching pursuit. This extra computational demand is somewhat ameliorated by calculating each biorthogonal basis recursively from the basis of the previous step. Corresponding to the recursive acceleration in optimised orthogonal matching pursuit, the local minimisation of Eq. (5) can be numerically accelerated by recursive computation of $P_{\Psi}^y$ with the Sherman-Morrison formula.

2.2.3 The sparse-set coding network model

Here we focus on approximate schemes of optimisation of Eq. (5) that are not restricted to greedy, sequential updating and that can be implemented in a neural network. To this end we use Eq. (5) in the form

$$ E(y) = - \frac{1}{2} \left\langle c, [P^{y}CP^{y}]^{+} c\right\rangle + \theta ||y||\label{fullmodenergy} $$

(6)

(Eq. (13) in Appendix A). For the sparse regime, we developed an approximation to Eq. (6) that can be implemented as a Hopfield type network (Hopfield, 1982)

$$ E(y) \simeq - \frac{1}{2} \left\langle y, T y\right\rangle + \theta ||y||\label{energysbn} $$

(7)

with the stimulus dependent interactions $T_{ij} := - c_i C_{ij} c_j + 2 \delta_{ij} c_i^2$ (derivation, see Appendix A). For a given input, the updates for minimising the energy in Eq. (7) can be written as

$$ y_i \leftarrow H\bigg(\frac{T_{ii}}{2} - \sum_{j\not=i} T_{ij} y_j - \theta\bigg) = H(d_i-\theta/c_i)\label{yupdate} $$

(8)

$$ b_i = a_i y_i = d_i H(d_i-\theta/c_i)\label{ssclatentb} $$

(9)

$$ \mbox{with}\;\; d_i = c_i-\sum_{j \not = i} C_{ij} c_j y_j\label{sscd} $$

(10)

Eq. (9) follows from Eq. (17) in Appendix A.

In the following, we refer to the model described by the Eqs. (7)–(10) as the sparse-set coding network or the SSC network. Note that the competition between cells with similar receptive fields in Eq. (10) is mediated by the same set of network connections C as in the Sparsenet. However, the nature of competition is different in the two models. The Sparsenet implements the competition through subtraction of intracortical feedback from feedforward input (Eq. (3)). In the sparse-set coding network, the competition involves nonlinear operations, a threshold function and multiplicative gating.

2.2.4 A control model based on pruning in soft-sparse codes

To assess whether a basis selection involving discrete optimisation (7) pays off in coding efficiency, we compared the sparse-set coding network to a control model. The control model consisted of a combination of Sparsenet with a naive sparse-set coding procedure, without the combinatorial optimization used in the SSC network. Specifically, we pruned neuronal activities smaller than a threshold in the soft sparse representations produced by Sparsenet. In the neurones that remained active after the pruning, the activity levels were readjusted for best reconstruction (using Eq. (4)). We carefully optimised the combination of values for the pruning threshold and for the sparseness parameter θ in Eq. (2).

2.3 Learning of receptive fields

We assume that the learning of receptive fields occurs on a slower time scale than the process of sensory coding. With this assumption, the learning can be formulated as being independent of the dynamics involved in the particular coding model. For all the coding models we have described, the receptive fields Ψ can be learned with gradient descent in the energy function of Eq. (2):

$$ \Delta \Psi_{ij} \propto - \frac{\partial E}{\partial \Psi_{ij}} = \left(x_{i}-\hat{x}_{i}\right)b_{j}\textrm{.}\label{deltarule} $$

(11)

This local “delta” learning rule was applied after the neural representation had been optimised for a given training input. Eq. (11) works equally well for the models with hard sparse coding because once active neurones have been selected according to a given stimulus, the energy is a quadratic (differentiable) function of the receptive fields of the selected neurones. Thus, the learning affects only receptive fields of selected neurones and the synaptic changes can be computed as in Eq. (11), with the gradient descent method. In this study we used batchwise learning, where synaptic changes from several training inputs are accumulated before the receptive fields were updated. After each update step the receptive fields were renormalised.

3 Results

We compared the models of sensory coding with soft and hard sparseness constraints in computer experiments. The number of neurones in each model was three times the dimension of the inputs, that is, the representations were three times overcomplete. All models were trained on patches of natural images that had been “whitened” by reducing low spatial frequency components (Olshausen and Field, 1996). The basis functions were randomly initialised before training. During training, the models were presented with a large number of input patches. Each input was used in the coding and learning procedure as described in the Methods.

First we assessed, after the learning process had converged, how the different types of sparseness constraints affect the distributions of neuronal activity values. The sparseness parameter θ in Eq. (2) was set based on the experiments that will be described in the last paragraph of this Section 3.3.

One can see in Fig. 1 that the feed forward responses of the receptive field filters c (dashed curves) have similar exponentially-tailed distributions in the hard and soft sparse coding model (Ruderman, 1994). The kurtosis values were similar, $K=6.6$ for Sparsenet and $K=5.4$ for the sparse-set coding network. The strong effects of the lateral interactions between the neurones are reflected in distributions of neuronal activity values (solid curves). These distributions look qualitatively different in both models. In the Sparsenet, the lateral interaction leads to a distribution with much higher kurtosis than the feed forward filter response ($K=197.3$) but with similar shape. In the sparse-set coding model, the interaction between the neurones yields a discontinuous distribution of neuronal activities with a delta peak at zero with a kurtosis of $K=287.3$ which is 46% higher than for the Sparsenet distribution. There are gaps in the histogram for small (nonzero) absolute values because for these values the achievable decrease in reconstruction error is outbalanced by the usage penalty. The gap size can be estimated: From Eq. (12) and the fact that the basis functions are normalized, it follows that one neurone whose activity is a can reduce the energy by not more than $a^2 /2$. The energy increase for using an additional neurone is θ. Thus, the gap that one would expect theoretically is $|a| \leq \sqrt{2\theta}$ which is entered in Fig. 1(b) as the width bar. As one can assess, the theoretical estimate corresponds quite well to the gap observed in the empirical distribution.

A typical result of neuronal coding and image reconstruction using the SSC network is shown in Fig. 2. The sparseness parameter θ in Eq. (7) was chosen so that the average number of active neurones per patch was $4.8$ (individual set sizes vary with the input).

Fig. 2

Image coding and reconstruction in the SSC network (trained on $8 \times 8$ patches). The original image (left panel) is tiled into 64 patches of $8 \times 8$ pixels. The middle panel shows the neuronal activities representing the image. Each of the 64 rectangular compartments displays the activities of 192 neurones representing an $8\times8$ patch of the original image. The gray area represents all the inactive neurones, bright and dark dots correspond to the few active neurones. The sparseness parameter in Eq. (7) was set to $\theta=5.6\times 10^{-2}$. The right panel shows the reconstruction based on the sparse representation illustrated in the middle panel

Note in Fig. 2 that although the sensory representation is very sparse, that is, it has very few active neurones (displayed by bright and dark dots in the middle panel), the quality of reconstruction seems remarkably high.

3.1 Coding efficiency versus hard sparseness

We investigated the tradeoff between hard sparseness and quality of reconstruction systematically by varying the sparseness parameter θ in Eq. (7). Because it was time consuming to explore the entire parameter space, we trained the models with smaller patches of natural images ($8 \times 8$ rather than $16\times 16$). Figure 3 shows how the signal-to-noise ratio in the reconstruction increased with increasing size of the active set. Note that for ${\hbox{mean set size}} =1$ the SSC network yields efficient codes that are similar to vector quantisation in which just one most appropriate basis function is selected for a given input patch.

Fig. 3

Reconstruction quality as a function of the number of active neurones. The SSC network used the approximately optimal coefficients (Eq. (17)). The models denoted with ^* used the fully optimised analogue coefficients (Eq. (4)): The model labeled by “SSC^*” employs the neurone selection of the the sparse-set coding network, “Sparsenet^*” and “Sparsenet L1^*” denote the controls where the neurone selection was based on the soft sparse codes of the corresponding coding models

Fig. 4

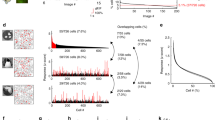
Measurement of metabolic energy consumption of sensory codes ($8 \times 8$ patches). The block diagram (a) depicts how we measured the spike counts required by a particular sparse coding model (see text for explanation.). Diagram (b) compares the required spikes in two sparse coding models, Sparsenet and the SSC network. The y-axis displays the logarithm of the spike counts used to code the visual representations. The x-axis displays the ratio of successful recognitions. Each sparse coding model was tested for three different sizes of the prototype set, the low curve corresponds to 80 patterns, the intermediate curve to 160 patterns and the high curve to 320 patterns

To ask if the discrete optimisation performed in the SSC network is important for quality of reconstruction, we compared the SSC network to a sparse-set coding procedure based on Sparsenet and pruning, see Methods. Notably, for all sparseness levels tested, the reconstruction with the SSC network was significantly better than with the Sparsenet-based control model. Further, one realises from Fig. 3 that the approximative coefficients in the SSC network (Eq. (17)) yielded signal-to-noise values that were almost as high as those generated by a model with fully optimised coefficients (Eq. (4)).

3.2 Metabolic energy consumption

We assessed the amount of metabolic energy that each model would consume if the sensory codes are represented by spike rates. To this end, we measured the number of spikes required to allow an ideal observer to detect one particular input from an ensemble of different visual inputs. To express the neuronal activities, we represented each abstract neurone as two spiking neurones that encoded the positive and negative activity values separately. This introduction of pairs of spiking neurones allowed to represent the visual codes of the abstract coding networks by spike trains. In addition, this duplication of neurones made the model compatible with Dale's law, that is, the observation that biological neurones have either excitatory or inhibitory effects on their targets.

The process of detecting a visual input involved five steps and is visualised in Fig. 4(a). First, ensembles of inputs were formed by a random selection of image patches. Second, the ensembles were used with each model to generate sets of sensory codes that we called prototype sets. Third, one prototype was selected and its coefficients were used as rate parameters in Poisson processes to generate spike trains. Fourth, the resulting spike trains were decoded by a process in which firing rates were estimated from the spike counts in a fixed time interval. Fifth, the code obtained from the rate estimations was assigned to the element in the prototype set with the highest similarity (ideal observer procedure). The similarity between codes was measured by the Cartesian distance. Ultimately, successful detections were defined as cases for which the code resulting from the rate estimations was assigned to the original prototype. The recognition ratio, that is, the ratio of successful detections, naturally increased with the average number of spikes in the spike trains, which, in turn, correlates with the metabolic energy that is spent. Figure 4(b) displays the mean number of spikes per coded image over the ratio of successful identifications. The three curves for each model correspond to prototype sets of 80, 160 and 320 patterns. Evidently, the task was harder for the larger prototype sets. Nonetheless, codes generated by the SSC network consistently required substantially fewer spikes than did soft sparse codes, for all prototype set sizes. Note that Fig. 4(b) shows a clear difference between the two types of coding even with the numbers of required spikes per image displayed on a logarithmic scale. Thus, by this measure, sparse-set codes are metabolically more efficient than soft sparse codes.

3.3 Receptive field structure

To study the shapes of receptive fields that the different models of visual coding produce, we trained with larger patches of natural images ($16\times 16$ pixels) and compared the results to recordings from primary visual cortex in monkey (experimental data courtesy of D. Ringach). To find the best settings of the sparseness parameter θ for the models, we tested a set of values covering different orders of magnitudes. We then choose for each model the value that led to receptive field shapes that matched the biological data the closest. The used values were $\theta = 0.31$ for the SSC network and $\theta = 0.22$ for Sparsenet. A fine tuning of θ within an order of magnitude was prohibitively time consuming for $16 \times 16$ patches. Also, the spot checks that we ran indicated that the results were not very sensitive to such fine tuning.

Figure 5 displays receptive fields of randomly selected cells from the models and from the experimental data (Gabor fits).

Note that the shapes of the experimental receptive fields are diverse. Besides typical edge-detector shaped receptive fields, the upper rows display blob-like and unoriented shapes whereas the lower rows contain structures with many subfields. The SSC network seems to capture the diversity in shapes of the biological receptive fields. The Sparsenet model forms edge-detectors but does not reproduce receptive fields with blob-like shapes or with many subfields.

Fig. 5

Receptive fields from the efficient coding models and from recordings in monkey V1. The models were trained on $16 \times 16$ patches of natural input. Each panel shows 128 randomly selected cells, ordered with respect to shape. Experimental results are shown as Gabor fits (data courtesy of D. Ringach). Scale differences due to distance from the fovea were corrected for

To assess the distributions of receptive field shapes quantitatively, we fitted the receptive fields from the models with Gabor functions and compared them to the fits for the experimental data. Figure 6 shows properties of the Gabor parameters for the entire cell populations, with the exception of those cells from models for which the fitting procedure was unstable, because the fields were centred outside the patch.

Fig. 6

Spatial properties of receptive fields in the models and in monkey V1 (data courtesy of D. Ringach). Red: 146 experimental cells in each graph. Blue: Modelled cells; 302 Sparsenet cells in each left graph, 447 SSC cells in each right graph. (a) and (b) display length and width of the Gabor envelopes measured in periods of the cosine wave (see schematic figure (e) and Appendix C). Circular shapes are located near the origin, slim edge-detectors near the “length” axis and geometries with multiple subfields at large “width” values. (c) and (d) plot the asymmetry of the receptive fields, as measured by the normalised difference between the integrals $h_+$ and $h_-$, see schematic figure (e) and Appendix C. The x-axes of (c) and (d) display the log of the ratio between length and width of the Gabor envelopes

Ringach (2002) reported that Sparsenet was not fully successful in reproducing the natural range in receptive field structure; this finding is confirmed in plot (a). By contrast, the SSC network captures the distribution of the envelopes of the biological receptive fields remarkably well, plot (b).

The asymmetry in the polarity of the receptive fields (definition in appendix C) is plotted over the aspect ratio of the Gabor envelope in figures (c) and (d). Note that the experimental data sample all values of asymmetry and that they form clusters near perfect symmetry (Asym.=0) and full asymmetry (Asym.=1). The SSC network also produces cells at both extrema of the range of asymmetry, although the clustering seems somewhat exaggerated compared to the experimental data. On the other hand, the distribution of fields made by Sparsenet is missing the cluster in the regime of perfect symmetry. Overall, Figs. 5 and 6 suggest that the variety of receptive fields recorded from monkey V1 was more closely reproduced by the SSC than by the Sparsenet model.

4 Discussion

4.1 New model for receptive field formation using hard sparseness

Models in neuroscience can help explain the complexity and diversity of experimental results by simple functional principles. Here we used the approach of computational modelling to explore visual cortical function, with an emphasis on explaining how the shapes of receptive fields emerge in V1. Previous work showed that the computational principle of coding efficiency is able to explain how receptive fields shaped like edge detectors in V1 are formed. However, earlier computational models, the Sparsenet (Olshausen and Field, 1996) and independent component analysis (Bell and Sejnowski, 1997), were unable to capture the distribution of receptive field shapes that had been quantified experimentally (Ringach, 2002). To understand the reason for this gap between theory and biology, we investigated the influence of a central assumption in these earlier models, the choice of soft sparseness in the neural representation.

Thus, we investigated different computational models; Sparsenet (Olshausen and Field, 1996) and two new models (developed in the course of this study) that employed different forms of sparseness. Sparsenet produced soft sparse representations of sensory input and the new models form hard sparse representations. One of the novel models, which we call the sparse-set coding (SSC) network, explicitly optimised coding efficiency. The second model served as a control; it crudely approximated efficient hard sparse representations by pruning small neuronal activity values from the representations formed by Sparsenet.

We trained the models on natural images and compared the resulting receptive fields to biological data. The comparison revealed that the new SSC network had substantial advantages over both the original and modified (control) versions of the Sparsenet model. First, the comparison revealed that soft sparse codes could not be transformed into efficient hard sparse codes just by pruning. In other words, the control model that combined Sparsenet and pruning did a significantly poorer job in reconstructing the stimulus than the sparse-set coding network. Second, the sparse-set coding network had the benefit of conserving metabolic resources (Laughlin and Sejnowski, 2003): the number of spikes required to code sparse-set representations was almost an order of magnitude less than that required for Sparsenet representations. This second feature of sparse-set coding, the economical use of energy, is in line with an earlier result that the optimal tuning curve of a Poissonian neurone is a threshold function rather than a smooth function of a continuous input variable if spike rates are low (Bethge et al., 2003). The parsimonious use of metabolic energy by hard sparse representations is complemented by results of studies of associative memory that have shown that the same type of representation uses also synaptic memory very efficiently (Willshaw et al., 1969; Gardner-Medwin, 1976; Palm, 1980; Buhmann and Schulten, 1988; Tsodyks and Feigelman, 1988; Treves, 1991; Palm and Sommer, 1992; Földiak, 1995; Palm and Sommer, 1995). Third, the sparse-set coding network produced a greater variety of receptive fields than generated by the Sparsenet model; the shapes of receptive fields ranged from those with many oriented subfields to unoriented profiles whereas the Sparsenet produced a somewhat narrow range of edge detectors. In fact, the sparse-set coding network clearly outperformed the Sparsenet in predicting the diverse distribution of receptive field structures observed in recordings from the primary visual cortex of the monkey (Ringach, 2002) and the cat (Jones and Palmer, 1987).² The reason for this difference in the distribution of shapes that the two models produce is that the sparse-set coding network selects many fewer active cells to code any given input than does Sparsenet. Consequently, each receptive field in the sparse-set coding network represents only a small and tightly selected sample of inputs.

4.2 Mathematical methods for hard sparse sensory coding

Generative models. The sparse-set coding network we propose is related to earlier generative models that used hard sparse coding (Hinton et al., 1997; Sallee and Olshausen, 2002). In those models the process of coding sensory input was slow because it involved Gibbs sampling from the posterior. By contrast, the sparse-set coding network forms sensory representations very quickly because the underlying computation is based on an approximation of the (computationally intensive) inference process in causal generative models (Teh et al., 2003).

Basis pursuit. Two of the models that we investigated relate to basis pursuit denoising (Chen et al., 1998), a current method of signal representation. The energy function of basis pursuit is Eq. (2) when an $L_1$-norm sparseness term is used. Because of this sparseness term, the energy function of basis pursuit is not differentiable at zero and, thus, cannot be minimised using gradient descent. The minimisation method in basis pursuit is quadratic programming. One of the models we used for soft sparse coding, Sparsenet with a hyperbolic sparseness constraint, is essentially a gradient-descent approximation of basis pursuit.

Recent theoretical results on basis pursuit indicate that it has a direct connection to hard sparse coding. For certain conditions, it was proven that the representations formed by basis pursuit are the same as solutions of Eq. (12) with the hard sparseness constraint (Donoho and Elad, 2002). Although basis pursuit might provide a fast means of generating hard sparse sensory representations, it is not yet clear if it can be used to model visual cortex. First, it must be determined if the statistics of the visual input meets the prerequisites for basis pursuit to perform sparse-set coding and how the algorithm can be implemented in a neural network.

Matching pursuit. Matching pursuit is a popular algorithm for the step by step refinement of signal representations in the field of adaptive signal processing; when run for a few iterations, it can form sparse-set codes. Thus, matching pursuit has been proposed as a model for visual cortex (Perrinet et al., 2004) (see below). The original form of matching pursuit is fast and guaranteed to converge asymptotically (Mallat and Zhang, 1993). However, as explained in the methods section, codes generated by finite numbers of steps minimise the residual error only for orthogonal basis sets. Thus, sparse overcomplete coding based on standard matching pursuit is not principled by efficient coding in the sense of minimising Eq. (2).

Two extensions of matching pursuit for nonorthogonal basis sets have similarities to our SSC network. First, orthogonal matching pursuit (Pati et al., 1993) uses the same suboptimal basis selection as matching pursuit, but explicitly optimises the coefficients, according to Eq. (4). Second, optimised orthogonal matching pursuit improves on the original method by optimising basis selection in a manner that corresponds to a sequential, greedy minimisation of Eq. (5) (Rebollo-Neira and Lowe, 2002). Thus, our framework for sparse-set coding (Eqs. (5) and (6)) includes optimised variants of matching pursuit as special cases. The sparse-set coding network (Eqs. (7)–(10)) is a new approximate method for computing optimised codes in the sparse regime. It is computationally fast and can be implemented as a neural network without being limited to greedy optimisation.

4.3 Implications for cortical processing

Models of cortical microcircuits. Unlike other causal models of sensory coding using a hard sparseness constraint (Hinton et al., 1997; Sallee and Olshausen, 2002; Rebollo-Neira and Lowe, 2002), ours can be implemented as a neuronal network. Thus, we are able to compare interactions among neuronal elements in our model with interactions among cortical neurones. Causal models of efficient coding, like those we use here, suggest a specific function for interactions between neurones, an “explaining away” between causes. Explaining away means that cells with similar receptive fields compete for inclusion in a given sensory representation. This competition is mediated in the Sparsenet and the sparse-set coding network through the weights C, though the competition takes a different form in each model. That is, each model makes a different prediction about how thalamic and cortical inputs (Peters and Paine, 1994) should be combined. In the Sparsenet, thalamic and cortical inputs superpose linearly (Eq. (3)).³ In the sparse-set coding network, the competition takes a nonlinear, multiplicative form (Eq. (9)). To determine which (if either) scheme is used by the brain will require studies of coding networks closer to biophysical realism, whose predictions can be compared directly to neurophysiology.

Computational purpose of simple cells. We have shown that learning in the sparse-set coding network can predict the diverse shapes of simple cells. The key elements in this network are efficient coding and a hard sparseness constraint. Efficient coding reflects extrinsic conditions imposed by stimuli, whereas hard sparseness reflects intrinsic constraints, such as the metabolic costs and limited resources for memory formation. Together, these elements are sufficient to explain the formation of receptive fields, but to what extent is each necessary to build simple receptive fields? Other models of visual coding suggest that the requirement for efficient coding might not be strict or could be replaced by other computational motives. For example, matching pursuit does not explicitly optimise coding efficiency, yet it generates receptive fields shaped like edge detectors (Sallee, 2002; Perrinet et al., 2004). In addition, other computational motives have been demonstrated to form simple cell-like receptive fields as well. These motives include translation/scaling-invariant coding (Li and Attick, 1994) or slow feature analysis of the spatio-temporal structure of the input (Hurri and Hyvaerinen, 2003). In this study we have quantitatively compared how receptive fields produced by different models of efficient coding match the properties of those found in nature. By extending this approach to models based on other functional principles, it should be possible to identify the prevailing functional principles for visual coding in the broader context.

Discrete processing of visual input. Although it is natural to think that visual perception continues steadily over time, theoretical work has raised the suggestion that visual processing might be executed in discrete epochs (Stroud, 1956). In fact, several psychophysical experiments (VanRullen and Koch, 2003, 2005) provide support for the existence of temporally discrete perceptual processes. With visual input that changes over time, the discrete selection of sparse sets of active neurones in the sparse-set coding network translates into a mode of operation that is discontinuous in time. Thus, a sparse-set coding network could be a first stage for transforming continuously varying visual input into discrete epochs of visual recognition. Our assessment of metabolic efficiency of different coding models did assume a hierarchical scheme of visual processing that involved a form of discrete processing. It consisted of two hierarchical stages. In the first stage a coding model (Sparsenet or SSC network) encoded raw sensory input in terms of functional primitives, the receptive fields that reflect the statistics of the visual input. The second stage contained an ideal observer that compared a given input with discrete elements in the prototype set. In a realistic hierarchical model of cortical sensory processing, the second level should employ learning as well. Rather than selecting the prototypes at random, they should be formed by clustering naturally changing visual input. In addition, the memory and comparison process should be based on computations that can be implemented in cortical networks, for example, associative memory in the superficial cortical layers. Our current research (Rehn and Sommer, 2006) investigates a model of discrete visual recognition that combines the ideas of sparse-set coding with sparse associative memories for temporal sequences (Willwacher, 1982; Sommer and Wennekers, 2005).

Appendices

Appendix A: Derivation of the energy functions for hard-sparseness

Inserting $b_i = a_i y_i, f(x) = ||x||_{L_0}$, and the definitions $c=\Psi x, C = \Psi \Psi^T$ and $P^y = \mbox{diag}(y)$, one can rewrite Eq. (2) (up to the constant $\left\langle x,x\right\rangle\!/2$) as

$$ E(y,a)=\frac{1}{2}\left\langle a,P^{y}CP^{y}a - 2P^{y}c\right\rangle + \theta \,\mbox{Tr}(P^y)\label{energy1} $$

(12)

where $\mbox{Tr}(P^y) = \sum_i y_i = ||y||$. Equation (12) requires interleaved optimisation in both variable sets a and y. For fixed y the optimal analogue coefficients are $a^* = \mbox{argmin}_a ||P^y C P^y a - P^y c||$. The solution can be computed as Eq. (4) using the pseudoinverse. If one inserts Eq. (4) in Eq. (12), the resulting energy function is

$$ E(y) = - \frac{1}{2} \left\langle c, [P^{y}CP^{y}]^{+}c\right\rangle + \theta ||y||\label{fullmodenergydup} $$

(13)

which solely depends on the binary variables since the coefficients are optimised implicitly.

Using the identities for the pseudoinverse: $A^+ = [A^T A]^+ A^T$ and $[A^T]^+ = (A^+)^T$ (see pseudoinverse in Wikipedia), the inner product in Eq. (13) can be written

$$\displaylines{ \left\langle c, [P^{y}CP^{y}]^{+} c\right\rangle = \left\langle x, (P^y \Psi)^T [P^{y}\Psi (P^{y}\Psi)^T]^{+} P^y \Psi x\right\rangle\cr = \left\langle x, [P^y \Psi]^+ P^y \Psi \;x\right\rangle\label{projectors} }$$

(14)

The operator in the inner product on the RHS of Eq. (14) is a projection operator:

$$ [P^y \Psi]^+ P^y \Psi =: P_{\Psi}^y = \left(P_{\Psi}^y\right)^2\label{projector} $$

(15)

which projects into the subspace spanned by the receptive fields of the active units $\{i: y_i=1\}$. Equation (14) and definition 15 yield Eq. (5).

Another way to rewrite Eq. (13) is to insert $P^y C P^y = [P^y (C-1\!\!1) P^y +1\!\!1] P^y =: C^y P^y$. $C^y$ is a full rank matrix if the selected set of basis functions is linearly independent. This is guaranteed in the complete case and very likely to be fulfilled for sparse selections in overcomplete bases. Thus, for sparse y vectors we can replace the pseudoinverse in Eq. (13) by the ordinary inverse and use the power series expansion: $[C^y]^{-1} = 1\!\!1 - P^y (C-1\!\!1) P^y + [P^y (C-1\!\!1) P^y]^2 - \cdots$ Using the expansion up to the first order yields the approximations for Eqs. (5) and (4), respectively

$$ E(y) \simeq \frac{1}{2} \left\langle c, P^y (C-2 \!\cdot\!1\!\!1) P^y c\right\rangle + \theta \,\mbox{Tr}(P^y)\label{recenergyxfo} $$

(16)

$$ a^* \simeq [1\!\!1 - P^y (C-1\!\!1) P^y] c\label{approxcoeffs} $$

(17)

With the definition $T_{ij}:= - c_i C_{ij} c_j + 2 \delta_{ij} c_i^2$, Eq. (7) follows from Eq. (16).

Appendix B: Fitting of receptive fields

In the sparse regime, each basis function can be well fitted with a two-dimensional Gabor function in the image coordinates $u, v$: $h(u',v') = A\; \exp [-( \frac{u'}{\sqrt 2 \sigma_{u'}})^2 - ( \frac{v'}{\sqrt 2 \sigma_{v'}})^2] \cos ( 2 \pi f u' + \Phi )$, where $u'$ and $v'$ are translated and rotated image coordinates, $\sigma_{u'}$ and $\sigma_{v'}$ represent the widths of the Gaussian envelope, and f and Φ are the spatial frequency and phase of the sinoidal grating. Notation in Fig. 6: $\mbox{width}: = \sigma_{u} f$ and $\mbox{length}: = \sigma_{v} f$. To measure asymmetry of a Gabor function we split h along the $v'$ axis into $h_-$ and $h_+$ and use: $\mbox{Asym} := |\int h_+ ds - \int h_- ds |/ \int |h| ds$.