On-printed circuit board emulator with controllability of pinched hysteresis loop for nanoscale $\mathrm{TiO}_2$ thin-film memristor device

Abstract

Since real memristor devices are still not commercially available to most researchers, modeling a memristor is an effective method to explore its properties. In this paper, a flux-controlled memristor emulator circuit that can correctly mimic the memristive behavior of a real nanoscale $\mathrm{TiO}_2$ thin-film memristor device is presented. The mathematical equations for the proposed emulator are explicitly derived, and the design parameters for the circuit in which the emulator works as a passive memristor with positive memductance are discussed. In addition, the proposed emulator can produce various v–i hysteretic behaviors by controlling the nonlinear polynomial cubic function between the flux and charge inside. The results from numerical simulations in PSpice and MATLAB, as well as the measured results from an implemented emulator circuit on a printed circuit board using off-the-shelf electronics components, demonstrate that a controllable emulator can actually be constructed. This study serves as a foundation for understanding and designing different emulators for nanoscale $\mathrm{TiO}_2$ thin-film memristors at the laboratory level.

1 Introduction

The memristor was first postulated by Leon Chua in 1971 as the fourth electrical passive element based on the theory of electrical components from the missing link between charge and flux [1]. Almost four decades later, Williams and his colleagues from Hewlett Packard (HP) Laboratories demonstrated a physical memristor behavior of which approximately matched with the behavior predicted by Chua for the first time [2]. The successful fabrication of a real nanoscale thin-film memristor from HP Labs greatly re-energized the interest of researchers in memristors and their promising future applications, especially during the nanoscale era because of the limitations of CMOS technology. Many works have started to utilize memristor in such diverse areas as nonvolatile random access memory (ReRAM) [3, 4], analog circuits [5, 6], digital circuits [7, 8], relaxation oscillators [9–11], memristor-based chaotic oscillators [12], and neuromorphic synaptic networks [13, 14]. Since the fabrication of nanoscale memristor devices is still a challenging issue owning to technical difficulties involved in nano device fabrication, memristor devices are not expected to be available in the near future. Therefore, a substitute that behaves like a real memristor is urgently needed to allow researchers to study the practical application of memristors. Generally, modeling is a common method that serves as a possible alternative [15–18]. Memristor modeling is mostly used to design and analyze complex phenomena for real solid-state memristor devices; however, memristor models do not provide hands-on experience that is especially beneficial for undergraduate students [19]. To help those engineers and scholars who cannot access memristor fabrication technology but want to study memristor-related research, hardware emulator circuits that can reproduce the physical hysteresis loop of a memristor’s voltage–current relationship are needed.

Fig. 1

a Implemented nanoscale memristor devices from HP Labs, b crossbar architecture—mesh of perpendicular wires with two crossing wires are connected by a memristor as a switch [20]

Fig. 2

Nanoscale thin-film $\mathrm{TiO}_2$ memristor structure: a no bias condition, b forward bias condition, c reverse bias condition, d equivalent model

2 TiO$_2$ thin-film memristor device emulator circuit on a printed circuit board with a v–i hysteresis loop

2.1 Nanoscale $\mathrm{TiO}_2$ thin-film memristor model

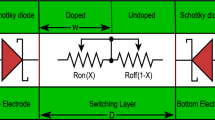
Figure 1 shows the fabricated nanoscale $\mathrm{TiO}_2$ thin-film memristor device that was used as a cross-point switch [5]. The HP memristor is composed of a two-layer thin-film $\mathrm{TiO}_2$ sandwiched between two platinum electrodes. One layer is titanium dioxide ($\mathrm{TiO}_2$), and the other is oxygen-depleted titanium dioxide ($\mathrm{TiO}_{2-x}$, as shown in Fig. 2a). Under a no bias condition (no applied voltage), the boundary between these layers is maintained. If there is a bias condition (Fig. 2b, c for forward bias and reverse bias, respectively), the boundary moves up and down which causes the memristance (memductance) of the memristors to change accordingly.

Before developing an emulator circuit for a nanoscale thin-film memristor devices, a model of the $\mathrm{TiO}_2$ thin-film memristor is presented for future comparison. According to the linear ion drift inside, the memristor can be modeled in a coupled variable-resistor mode as shown in Fig. 2d. The current–voltage relationship can be described by the following equations [2]:

$$\begin{aligned}&v\left( t \right) = \left( {{R_\mathrm{ON}}\frac{{w\left( t \right) }}{D} + {R_\mathrm{OFF}}\left( {1 - \frac{{w\left( t \right) }}{D}} \right) } \right) i\left( t \right) \nonumber \\&M\left( w \right) = {R_\mathrm{ON}}\frac{{w\left( t \right) }}{D} + {R_\mathrm{OFF}}\left( {1 - \frac{{w\left( t \right) }}{D}} \right) \nonumber \\&w\left( t \right) = {\mu _V}\frac{{{R_\mathrm{ON}}}}{D}q\left( t \right) \end{aligned}$$

(1)

Here v(t) and i(t) are the input voltage and input current of the memristor, respectively; $R_\mathrm{ON}$ is the equivalent resistance of the memristor when the entire device is un-doped; $R_\mathrm{OFF}$ is the equivalent resistance of the memristor when the entire device is doped; w(t) is the effective width; D is the total length of the memristor; and $\mu _v$ is the mobility of the dopant. It is important to note that the effective width w is proportional to the charge q overtime just only when the mobility is assumed to be constant. However, since the dimension D of the memristor may change, the particle transport mobility may also vary. This means the hysteresis characteristic of the memristor will change accordingly.

Fig. 3

a Simplified schematic of the proposed controllable flux-controlled emulator circuit for mimicking memristive behavior of $\mathrm{TiO}_2$ thin-film memristor devices, b symbol of controllable emulator, c utilized multiplier AD633 from Analog Devices and its transfer function

Until now, there have been many works that reported on designs for memristor emulators that could mimic the hysteresis behavior of a memristor [21–29]. However, all published works about hardware memristor emulator circuits have a common limitation: the designs were developed for fixed memristive behavior at a specific frequency. Thus, there is no versatile emulator in which the v–i hysteresis characteristic of a real $\mathrm{TiO}_2$ memristor could be mimicked and controlled following the effects from different doping levels as well as different dimensions of real nanoscale thin-film memristors. Furthermore, the mathematical v–i derivations of those designs are not close to the announced thin-film TiO$_{2}$ memristor device from HP Labs, and are difficult to implement at the laboratory level. In this paper, we present an emulator, but we also take into account its controllability for a nanoscale $\mathrm{TiO}_2$ thin-film memristor device. The proposed emulator circuit is very simple and easy to implement on a printed circuit board (PCB) in a laboratory. The measurement results are compared with a real memristor device from HP Labs in order to confirm the work.

2.2 A controllable emulator using a nonlinear polynomial flux-charge function to describe the memristive behavior of a real memristor device

2.2.1 Flux-controlled memristor emulator

In this section, the design procedure for the proposed flux-controlled memristor emulator is derived, and the controllability of the v–i hysteresis characteristics of the emulator circuit is presented in detail. The proposed variable memristor emulator in this paper is a flux-controlled memristor emulator that was originally reported by Muthuswamy based on Zhongs third-order polynomial function of flux-charge [30, 31]. Figure 3a shows the proposed two-terminal flux-controlled memristor emulator which consists of basic off-the-shelf electronics devices including two operational amplifiers, two multipliers, one capacitor and four resistors. Op-amp U1 works as a voltage buffer in order to eliminate the loading effect from the integrator. The integrator, which is composed of op-amp U2, resistor R, and capacitor C, features a transformation from voltage into flux between two terminals of the emulator, while the multipliers U3 and U4 implement a cubic function. In this circuit, the network of $R_{\beta 1}$ and $R_{\beta 2}$ in combination with multiplier U4 increases the gain of the system. Especially, three variable resistors $R_{\alpha }$, $R_{\beta 1}$ and $R_{\beta 2}$ are dedicated to be used as factors to control the memductance (or memristance) profile of the proposed memristor emulator. The symbol of the proposed controllable memristor emulator is illustrated in Fig. 3b.

Generally, the memristor can be characterized by its memductance, which describes the flux-dependence rate change of charge by the following equation:

$$\begin{aligned} W\left( \phi \right) = \frac{{\mathrm{d}q\left( \phi \right) }}{{\mathrm{d}\phi }}\ \end{aligned}$$

(2)

where W is memductance, $\phi$ is the flux, and q is the charge of the memristor. Letting v and i be the voltage across the two terminals of the memristor device, and the current through it, respectively, the v–i relationship of the memristor is defined as:

$$\begin{aligned} i(t) = \frac{{\mathrm{d}q}}{{\mathrm{d}t}} = \frac{{\mathrm{d}q}}{{\mathrm{d}\phi }} \times \frac{{\mathrm{d}\phi }}{{\mathrm{d}t}} = W(\phi (t)) \times v(t) \end{aligned}$$

(3)

In a thin-film memristor, as dimension D of the device shrinks to the nanometer scale, the electric field across the memristor approaches a critical limit (106 V/cm), and it is reasonable to expect a high nonlinearity in the ionic drift diffusion, which later causes the hysteresis characteristic. Therefore, a nonlinear function that represents this phenomenon should be included in the emulator. As mentioned earlier, the proposed memristor in this paper is a flux-controlled memristor described by the memductance function $W(\phi (t))$. The term $q(\phi )$ is chosen with a polynomial cubic function that expresses the relationship between the flux $\phi$ and the charge q in the following form [31]:

$$\begin{aligned} q(\phi ) = \alpha \phi + \beta \xi \phi _{}^3 \end{aligned}$$

(4)

where $\alpha$ and $\beta$ are the coefficients of the cubic function, and $\xi$ is the rescaling factor. It is noted that $\alpha > 0$ and $\beta < 0$ in order to design an emulator for a passive $\mathrm{TiO}_2$-like memristor memductance (or memristance) which is always positive. As defined in Eq. (2) and with the cubic function expressed in Eq. (4), the memductance W is now derived as follows:

$$\begin{aligned} W(\phi ) = \frac{{\mathrm{d}q}}{{\mathrm{d}\phi }} = \alpha + 3\xi \beta \phi _{}^2 \end{aligned}$$

(5)

Substituting the memductance W expressed by Eq. (5) into Eq. (3), the v–i characteristic of the flux-controlled memristor can now be re-written as follows:

$$\begin{aligned} i(t) = ( {\alpha + 3\xi \beta {\phi ^2}} ) \cdot v\left( t \right) \end{aligned}$$

(6)

Before entering the v–i characteristics of the proposed emulator, it is noted that a multiplier AD633 from Analog Devices, which has a transfer function given as $w = xy/10\, +\, z$ is used to implement the emulator (where the factor 10 is an inherent scaling factor in the multiplier). As shown in Fig. 3a, c, the v–i relationship of the proposed memristor emulator can be easily derived as follows:

$$\begin{aligned}&i\left( i \right) = \frac{{v\left( t \right) - {v_{w2}}\left( t \right) }}{{{R_\alpha }}} \nonumber \\&\mathrm{with}: \, {v_{w2}}\left( t \right) = \frac{{v\left( t \right) \cdot {v_{w1}}\left( t \right) }}{{10}} + \frac{{{R_{\beta 2}}}}{{{R_{\beta 1}} + {R_{\beta 2}}}} \cdot {v_{w2}}\left( t \right) \nonumber \\&\mathrm{and}: \, {v_{w1}}\left( t \right) = \frac{{v_x^2\left( t \right) }}{{10}} \end{aligned}$$

(7)

where $v_x$, $v_{w1}$, and $v_{w1}$ are the outputs of integrator U2, multiplier U3, and multiplier U4, respectively. By rearranging Eq. (7), the current–voltage relationship of the circuit can now be expressed in terms of $v_x$ as follows:

$$\begin{aligned} \i \left( i \right) = \left( {\frac{1}{{{R_\alpha }}} - \frac{1}{{100{R_\alpha }}}\,\frac{{{R_{\beta 1}} + {R_{\beta 2}}}}{{{R_{\beta 1}}}} \cdot v_x^2\left( t \right) } \right) \,v\left( t \right) \end{aligned}$$

(8)

In the emulator circuit, the core of implementing the relationship of the charge-flux function uses an integrator which obtains the electric flux across the memristor and then uses this flux to obtain the memristors v–i hysteresis function. For the integrator, the input–output relationship between $v_{x}(t)$ and v(t) can be expressed:

$$\begin{aligned} {v_{x}(t)} = - \frac{1}{{RC}}\int {v(t)\mathrm{d}t}\quad \mathrm{or}\quad \frac{{\mathrm{d}{v_{x}(t)}}}{{\mathrm{d}t}} = - \frac{1}{{RC}}v(t) \end{aligned}$$

(9)

Remember that the relationship between the flux $\phi (t)$ and the voltage v(t) across the memristor device is defined by:

$$\begin{aligned} \frac{{\mathrm{d}\phi }}{{\mathrm{d}t}} = v(t) \end{aligned}$$

(10)

Dividing side to side of Eqs. (9) and (10), the flux $\phi (t)$ can be represented in terms of the output voltage $v_x(t)$ of the integrator as follows:

$$\begin{aligned} {v_x}(t) = - \frac{1}{{RC}}\phi (t) \end{aligned}$$

(11)

Finally, we substitute Eq. (11) into Eq. (8). The voltage–current characteristic of the flux-controlled memristor can be explicitly given in terms of the flux $\phi$ as follows:

$$\begin{aligned} i\left( t \right) = \left( {\frac{{1}}{{{R_\alpha }}} - \frac{1}{{{R^2}{C^2}}} \times \frac{{{R_{\beta 1}} + {R_{\beta 2}}}}{{100 \cdot {R_\alpha } \cdot {R_{\beta 1}}}}{\phi ^2(t)}} \right) \times v\left( t \right) \end{aligned}$$

(12)

Based on the definition for a memristive system as reported by Chua and Kang in [32], it is clear that the circuit is a flux-controlled memristor with a duality as follows: $x = \phi , f(.) = \xi$ with $\xi = 1/R^2C^2; g(.) = W(\phi ) = \alpha + 3\xi \beta \phi ^2$. The flux $\phi$ acts as a state variable in the emulator circuit. It has the same function as compared with the state variable w of the thin-film memristor presented in Eq. (1). As a result, the proposed emulator circuit is expected to mimic the hysteresis behavior of a $\mathrm{TiO}_2$ thin-film memristor.

The fabricated nanoscale $\mathrm{TiO}_2$ memristor device from HP as well as reported devices with memristive behavior are passive elements and do not produce or store energy. They only consume power. Therefore, the proposed emulator can emulate these passive devices only if its memductance (memristance) is nonnegative, that is, $W(\phi )\ge 0)$ [1]. Because the memductance is always positive unless the resistance of the memristor reaches infinity, we can choose $W(\phi ) > 0$. In this study. the proposed emulator can be regarded as a voltage-controlled or flux-controlled emulator as revealed by Eqs. (8) and (12), respectively, in which its memductance W can be written in one of two forms, as follows:

$$\begin{aligned} W(v_x) = \frac{1}{{{R_\alpha }}} - \frac{1}{{100{R_\alpha }}}\,\frac{{{R_{\beta 1}} + {R_{\beta 2}}}}{{{R_{\beta 1}}}} \cdot v_x^2 \end{aligned}$$

(13)

Or:

$$\begin{aligned} W(\phi ) = \frac{{ 1}}{{{R_\alpha }}} - \frac{1}{{{R^2}{C^2}}} \times \frac{{{R_{\beta 1}} + {R_{\beta 2}}}}{{100 \cdot {R_\alpha } \cdot {R_{\beta 1}}}}{\phi ^2} \end{aligned}$$

(14)

Since the flux cannot be directly simulated from the numerical simulation, it is convenient to determine the maximum magnitude of $v_x$ and the corresponding v in voltage-controlled emulator model described by Eq. (13). Obviously, W is a memductance that depends upon the internal state of the device’s $v_x$. As expressed in Eq. (13), because the first term $1/R_\alpha$ is positive and the second term ${-\phi ^2}(R_{\beta 1} + R_{\beta 2})/(100R_{\beta 1}R_{\beta 2})$ is negative, the memductance $W(v_x)$ ($W(\phi )$) of the proposed emulator could be positive and negative, corresponding to both passive and active memristors, respectively. In order to emulate a passive device such as an HP memristor (even though the proposed emulator is an “active emulator” since it needs power supplies to maintain operation), the value of all terms in Eq. (9) must be properly selected. In particular, since $W(\phi )$ is a strongly dependent function of $v_x$ and $\phi$, if $R_\alpha$, $R_{\beta 1}$, $R_{\beta 2}$, R, and C are constants, then $v_x$ must be smaller than the critical limit of $v_{x,\mathrm{max}}$ in order to ensure that the proposed emulator could emulate a passive device such as the HP memristor, where:

$$\begin{aligned} v_{x,\mathrm{max}} = \sqrt{\frac{{100{R_{\beta 1}}}}{{{R_{\beta 1}} + {R_{\beta 2}}}}} \end{aligned}$$

(15)

In addition, within the range of [0, $v_{x,\mathrm{max}}$] in which the emulator works as a passive memristor, the memductance of the proposed emulator is bounded in a range of $[\delta , 1/R_\alpha ], \delta > 0$. In the case where $v_x = 0$ (and flux $\phi = 0$, input voltage $v = 0$), the global memductance W equals $1/R_\alpha$. As input voltage v increases, $v_x$ increases, the memductance W decreases and could be equal to zero when $v_x$ reaches $v_{x,\mathrm{max}}$ as in Eq. (13).

2.2.2 Controllable memristor emulator

In order to mimic the memristive behavior of the memristor device for different nanoscale dimensions, the proposed memristor emulator could also control its behavior accordingly. Comparing Eqs. (6) and (12), and noting that the factor RC is used for the rescaling purposes, the coefficients $\alpha$ and $\beta$ in the cubic polynomial function of the memductance $W(\phi (q))$ are explicitly found:

$$\begin{aligned} \alpha = \frac{{ - 1}}{{{R_\alpha }}};\,\,\beta = \frac{1}{{300}} \times \frac{{{R_{\beta 1}} + {R_{\beta 2}}}}{{{R_\alpha } \cdot {R_{\beta 1}}}};\xi = \frac{1}{{{R^2}{C^2}}} \end{aligned}$$

(16)

As we can see in Eq. (5), the memductance profile of the proposed variable memristor could be controlled according to the value of $\alpha$ and $\beta$ in the cubic-polynomial function $q(\phi )$. By using the memristor emulator depicted in Fig. 3a, the memductance profile of the memristor can be easily controlled by varying $R_{\alpha }$, $R_{\beta 1}$, and $R_{\beta 2}$.

3 Results and discussion

First, the numerical analysis of the dynamics of the proposed controllable memristor represented by Eqs. (8) and (12) is performed in order to verify the potential of the proposed emulator before doing experiments on a PCB. The value of $\alpha$ and $\beta$ in the nonlinear flux-charge function reported in [31] are chosen to identify the model parameters of electronics elements in the emulator in order to observe the v–i hysteresis loop of the variable memristor. In addition, the emulator circuit is controlled by changing the coefficients in the nonlinear cubic polynomial via the adjustable factors $R_{\alpha }$, $R_{\beta 1}$, and $R_{\beta 2}$. As reported in [31], the coefficients of the polynomial flux-charge function of a fixed-memductance memristor are $\alpha = 0.667$E−3 and $\beta = 0.029$E−3. Thus, the values of the circuit elements here were calculated as $R_{\alpha }= 1.5\,\mathrm{k}\Omega$, $R_{\beta 1}= 3\, \mathrm{k}\Omega$ and $R_{\beta 2} = 36\,\mathrm{k}\Omega$. In order to avoid unrealistic values of the voltages that make the analog multipliers and operational amplifiers (for the circuit implementation which will also be presented in Sect. 4) enter saturation, the value of the rescaling factor must be properly chosen. Here we choose the values of $R = 1.5\, \mathrm{k}\Omega$ and $C = 47\,\mathrm{nF}$ for the rescaling factor $\xi$. The model of the proposed controllable emulator was firs simulated in PSpice, and the input sinusoidal voltage source is considered as $v = V_{m}\hbox {sin2 ft}$ where $V_{m}$ is the stimulus amplitude and f is the frequency, respectively, with the assumption that the phase is zero. Typically, the amplitude of the input voltage should be reasonable so that the amplifiers and multipliers of the emulator circuit function properly. This ensures that the memductance $W(v_x)$ (and $W(\phi )$) will be always positive. In this design, the input voltage amplitude should be in a range of 1–4 V and the frequency is in rage of 100 Hz to 2.2 kHz. This is because the memristor emulator frequency band is limited from the bandwidth of the integrator (as is the low voltage filter) with a cutting frequency of 2.2 kHz for the selected values of R and C.

Fig. 4

Numerical simulation results for a flux-controlled memristor: a plot of the input voltage v(t) (blue) and current i(t) (red), b internal state flux $\phi$ (the internal state $\phi$ is calculated as an integral of the input voltage), c v–i hysteresis loop. Simulation condition: @$V_m$ = 2 V. Condition: $f = 500$ Hz (Color figure online)

Fig. 5

v–i hysteresis loop at different stimulus frequencies: 250 Hz, 500 Hz and 1 kHz. Condition @$V_m = 3$ V

Fig. 6

Amplitude limit of the input voltage for a passive memristor-like emulator: a input current versus sinusoidal input voltage at different amplitudes, b corresponding v–i hysteresis loops for those cases in a. The part of the v–i loop in the second and fourth quadrants shows negative memductance. @$V_{in} = 3$ V, 4 V, 5 V; $f = 500$ Hz (b) $f = 20$ kHz with different stimulus amplitudes

Fig. 7

Controllable v–i hysteresis characteristic of the emulator circuit with various flux-charge nonlinear functions: a by $R_\alpha$. b by $R_{\beta 2}$. Insets in v–i plots show single-valued function of flux-charge at different values

The most salient feature of the memristor under sinusoidal excitation is its zero-crossing, frequency-dependent pinched hysteresis loop in the current versus voltage plane [1]. Figure 4a superimposes the applied input voltage v(t) on the proposed circuit for emulation of the memristive behavior (blue line) against the resulting emulator current i(t) (red line) in the time domain. The voltage waveform is sinusoidal and its frequency and magnitude are 500 Hz and 2 V, respectively. It is apparent from this figure that while the current leads the voltage, both curves have the same period, that is the emulator circuit does not store any charge itself but is a totally dissipative circuit element as a real memristor. The variation of the internal state $\phi$ over time is shown in Fig. 4b. At the beginning of each cycle, $\phi$ has the lowest value that means the state variable $\phi$ is in the OFF state. In this state, the emulator circuit acts like a memristor with OFF inductance. After a half cycle, $\phi$ reaches its highest value. This means the state variable $\phi$ is now in the ON state, where the emulator circuit can be considered as ON inductance. At the end of each cycle of the sinusoidal input voltage, the $\phi$ value returns to same value as at the starting point of the sinusoidal function. Figure 4c depicts the symmetric, smooth hysteresis loop of the designed emulator from which it can be seen that the hysteresis loops are pinched at the origin. Additionally, the numerical simulation of the v–i hysteresis loop with different frequencies of sinusoidal excitation are also simulated in order to illustrate the frequency-dependent pinched hysteresis loops of the proposed flux-controlled emulator. Theoretically, as the frequency increases within the mem-frequency band, the lobe area decreases gradually, the current and the voltage become more linearly related, and the hysteresis loop shrinks into a single-value function at an infinite frequency. Figure 5 displays v–i curves in sweep frequency where f is set to 250 Hz, 500 Hz, and 1 kHz, respectively, while the amplitude $V_m = 3$ V is fixed. Basically, these simulation results follow the fundamental fingerprints for identifying memristors as presented in [2] for a thin-film $\mathrm{TiO}_2$ memristor.

Because $i = W(\phi )v$, and the current and voltage have the same symbol of number, the $v{-}i$ curves are only in the first quadrant and the third quadrant for a passive device. With the selected values of the resistor and capacitors, and as presented in Eq. (15) in the previous section, the maximal amplitudes of $v_{x,\mathrm{max}}$ and v are found to be 2.77 and 4.3 V, respectively. Figure 5 verifies the boundary condition of the input voltage amplitude in which the proposed emulator works as a passive memristor device where $f= 500$ Hz is fixed and amplitude $V_m$ is set to 3, 4, and 5 V, respectively, for the input voltage. Although the pinched hysteresis loop occurs regardless of the stimulus amplitude, the v–i loop starts to enter quadrant II and IV as the stimulus amplitude becomes higher than 4.3 V. This means the memductance (and memristance) of the emulator becomes negative (Fig. 6).

As mentioned above, the memristor emulator used a nonlinear function in order to present a high nonlinearity in the ionic drift-diffusion in real thin-film $\mathrm{TiO}_2$ memristor devices. At different dimensions measured in the nanoscale region, the nonlinearity of the ionic-drift diffusion changes, so the memristive behavior also changes accordingly. The versatile controllability of the proposed emulator can be realized by changing one of three resistors, $R_{\alpha }$, $R_{\beta 1}$, or $R_{\beta 2}$ as well as by simultaneously changing more than one resistor. The controllability is realized by changing the coefficients in the cubic flux-change function described in Eq. (2). With the proposed emulator circuit, the coefficient $\alpha$ and $\beta$ can be adjusted by tuning the resistance of $R_{\alpha }$, and the coefficient $\beta$ can independently adjusted by tuning the resistance of $R_{\beta 2}$ as expressed in Eq. (16). Figure 7 shows the different hysteresis loop results for each case. The insets display the changes in the associated nonlinear flux-charge function. These gained simulation results are in agreement about the theoretical analysis about the controllability of the designed emulator circuit presented in Sect. 2.2.2.

Table 1 Part list of the emulator circuit

Fig. 8

Measurement setup of the controllable memristor emulator circuit. Inset at top-left shows a photograph of a memristor emulator prototype implemented on the PCB

Fig. 9

Experimental results for observing the amplitude limit of the input stimulus $V_m$ in which the emulator works as a passive device via v–i in the time domain: a, b $V_m < V_{m,\mathrm{max}}$, c, d $V_m > V_{m,\mathrm{max}}$. Simulation condition: @$f = 500\,\mathrm{Hz}$

4 Experiment results

The emulator circuit in Fig. 3 was also implemented using discrete electronic devices on a prototype PCB for experimental validation and observation of the memristive behavior as well as controllability in the v–i hysteresis loop. AD633 multipliers and HA17741 amplifiers were utilized to implement the memristor proposed in Fig. 3. Three potentiometers were used to control the memristive behavior of the proposed memristor emulator, with two potentiometers of $10\,\mathrm{k}\Omega$ for $R_{\alpha }$ and $R_{\beta 1}$, and one potentiometer of $100\,\mathrm{k}\Omega$ for $R_{\beta 2}$. The details of selected components and their values are presented in Table 1. In order to successfully implement the emulator circuit in the hardware, some critical terms should be observed, as follows:

• 1. It is important that the op-amp device U1 is added and configured as a buffer before the integrator to avoid loading effects This is because the current i(t) of the memristor emulator should follow across $R_{\alpha }$ (assuming that the loading effect from $R_{\beta 1}$ and $R_{\beta 2}$ on the multiplier U4 is small and negligible).

• 2. The value of $R_{\alpha }$ must be higher than 1 $\mathrm{k}\Omega$, as required by the specification of the used multipliers (AD633) in the implementation of the proposed emulator circuit.

• 3. A resistor with a value equal to R is necessary to integrate the capacitor C in parallel to avoid a DC voltage integral drift of the integrator.

Fig. 10

Experimental results for observing the amplitude limit of the input stimulus $V_m$ in which the emulator works as a passive device via v–i in the $x-y$ plane: a, b $V_m < V_{m,\mathrm{max}}$, c, d $V_m > V_{m,\mathrm{max}}@f = 500$ Hz

The measurement setup of the controllable PCB-type memristor emulator was performed using digital (Textronix DPO 4054) and analog oscilloscopes to observe the waveforms of the input voltage and input current of the memristor in the time domain and in the $x-y$ plane, respectively. This is shown in Fig. 8. The response of the emulator was tested first to confirm the magnitude range of the stimulus input signal in which the emulator mimics the v–i hysteresis loop of the passive memristor with $W > 0$. Figure 9 shows the v–i waveforms in the time domain at different amplitudes of the input sinusoidal signal. The associated v–i hysteresis loops for each case are illustrated in Fig. 10. It is noted that the current amplitude of the emulator was doubled in order to reduce the noise from the utilized current probe equipment (Textronix TCP0030). Clearly, as the amplitude increases over the limit of $V_{m,\mathrm{max}}$ (value of which is roughly 4.3 V), the memductance (and memristance) is negative that is, $W < 0$, and closely match the simulation results in Fig. 6.

Finally, the controllability was tested by changing the value of $R_{\alpha }$. In order to reduce the noise from the current probe and the digital oscilloscope, an analog oscilloscope was used to display the plots. In this test, the current i is extracted from the voltage drops on the resistor which is connected in series to the emulator. Figure 11a, c show the current and voltage waveforms at different values of $R_{\alpha } (1.5\,\mathrm{k}\Omega$ and 1.9 $\mathrm{k}\Omega$), while Fig. 11c, d show the corresponding v–i relationship in the $x-y$ plan. As shown in Fig. 11c, d, the memductance profile is controlled by changing the nonlinear flux-charge function via $R_{\alpha }$. It can be seen that the experimental results are in good agreement with those revealed by numerical simulations, as shown in Fig. 7 in Sect. 3. Hence, a controllable memristor emulator is actually constructed.

Fig. 11

v–i characteristic of the memristor under coefficient control (via $R_{\alpha }$): a, c waveform of the input voltage v and input current i in the time domain @ $R_{\alpha } = 1.5\,\mathrm{k}\Omega$ and @ $R_{\alpha }= 1.9\,\mathrm{k}\Omega$, respectively; b, d v–i hysteresis loop of emulator circuit according to a and c, respectively

5 Conclusion

This paper presented a versatile and compact emulator circuit as a replacement for nanoscale thin-film $\mathrm{TiO}_2$ memristors with the capability of controlling its hysteresis characteristic via a nonlinear flux-charge function inside. The values of the design parameters and the amplitude limit of the sinusoidal excitation in which the emulator works as a passive memristor device with positive memductance were also discussed. Based on the results of simulation in PSpice and an experiment on a prototype printed circuit board, it is verified that the proposed emulator can mimic the v–i pinched hysteresis characteristic observed in nanoscale $\mathrm{TiO}_2$ memristor devices. These results serve as a foundation for understanding and designing different emulators, which make it convenient to build a nanoscale thin-film memristor in the “meter scale” at the laboratory level.