1 Introduction

During last 40–50 years, Microstrip antennas have become most burning topic in the field of telecommunications. The reason behind the success is its well known advantages, such as low manufacturing cost, conformability, light weight, low profile, reproducibility, reliability, ease in fabrication and Integration with solid-state devices and its planar structure is quite suitable for vertical integration using multilayer substrates [4]. The use of Microstrip antennas has been boosted by the wireless revolution in the information transfer field [1, 4].

In designing Microstrip antenna, it is very important to determine its resonant frequencies accurately because Microstrip antenna has narrow bandwidths and can only operate effectively in the vicinity of the resonant frequency. So, a model to determine the resonant frequency is helpful in antenna designs.

This antenna is designed for resonance at 2.4 GHz. The material used in design is Glass epoxy of \(\varepsilon _{r}=4.2\) and loss tangent 0.0013.The Initial I-shape antenna is then optimized using PSO program coded in MATLAB. Zealand IE3D version 9.0, Graphmatica and MATLAB are used as simulation, curve fitting and optimization tools.

2 Antenna geometry and design

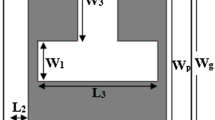
The geometry of the \(I\)-shape Microstrip antenna is shown in Fig. 1. The geometrical parameters are the patch length \(L\), patch width \(W\), height \(H\), slot lengths \(L_{1}, L_{2}\) and the slot width \(W_{2}\). Thus by cutting slots of \(L_{1}\) and \(L_{2}\) * \(W_{2}\) the desired \(I\)- shape of antenna is obtained. The resonant frequency and bandwidth can be optimized by adjusting some of these parameters. For a normal patch antenna its radiation excitation can be equivalent with a simple LC resonant circuit. The Geometrical parameter length and width for a rectangular patch can be calculated using equation (1–4). (At \(f_{r}=2.4\,\hbox { GHz}\), \(\varepsilon _{r}=4.2, H=1.66\,\hbox {mm}\)) [4].

$$\begin{aligned} W&= \left( {\frac{c}{2f_r}}\right) \left( {\frac{\varepsilon _r +1}{2}}\right) ^{-.5}, \end{aligned}$$
(1)
$$\begin{aligned} \varepsilon _{eff}&= \left( {\frac{\varepsilon _r +1}{2}} \right) +\left( {\frac{\varepsilon _r -1}{2}} \right) \left( {1+\frac{12W}{H}}\right) ^{-.5}, \end{aligned}$$
(2)
$$\begin{aligned} \Delta L&= .412H\left( {\frac{\varepsilon _{eff} +.3}{\varepsilon _{eff} -.258}} \right) \left( {\frac{\left( {\frac{W}{H}} \right) +.285}{\left( {\frac{W}{H}} \right) +.8}} \right) , \end{aligned}$$
(3)
$$\begin{aligned} L&= \left( {\frac{c}{2f_r \sqrt{\varepsilon _{eff} }}} \right) -2\Delta L, \end{aligned}$$
(4)

Now, \(L\) and \(W\) are used to calculate the length and width of ground plane by using equation (5–6) [3].

$$\begin{aligned} L_g&= L+6H, \end{aligned}$$
(5)
$$\begin{aligned} W_g&= W+6H. \end{aligned}$$
(6)

Thus an \(I\)-shape antenna is formed by cutting two rectangular slots in the rectangular patch antenna.

Fig. 1
figure 1

Geometry of the I-shaped rectangular patch antenna

Full size image

The radiating patch is fed by a Microstrip line feed along x axis at the bottom of the patch. All parameter of basic I-shape antenna is shown in Table 1.

Table 1 Parameter for I-shape patch antenna
Full size table

3 PSO Algorithm

The particle swarm optimization algorithm was first described in 1995 by Kennedy and Eberhart. The Particle Swarm Optimization algorithm (PSO) searches for the global minimum of the cost-function i.e. minimizes the cost-function of a problem by simulating movement and interaction of particles in a swarm. In PSO, the individuals, called particles, are collected into a swarm and fly through the problem space by following the optima particles. Each individual has a memory, remembering the best position of the search space it has visited. Each individual of the population has an adaptable velocity (position change), according to which it moves in the search space. Thus, its movement is an aggregated acceleration towards its best previously visited position and towards the best individual of a topological neighborhood. The evolution of particles, guided only by the best solution, tends to be regulated by behavior of the neighbors, since we assume that there is no a priori knowledge of the optimization problem, there is equal possibility of choosing any point in the optimization space at the beginning of the optimization. Therefore PSO starts with randomly chosen positions and velocities of particles. Each particle is treated as a point n an N dimensional space which adjusts its “flying” according to its own flying experience as well as the flying experience of other particles. Each particle tries to modify its position using the information of the current positions, the current velocities, the distance between the current position and the personal best position (pbest), the distance between the current position and the global best position (gbest). The manipulation of a particle’s velocity is the key element for the success of PSO. The modification of the particle’s position can be mathematically modeled according the following equation [2].

$$\begin{aligned} V_i\left( {t+1}\right)&= \alpha V_i \left( t\right) +C_1 \delta _1 \left( {X_{pbest}\left( t\right) -X_i \left( t\right) } \right) \nonumber \\&+\,C_2 \delta _2 \left( {X_{gbest}\left( t\right) -X_i \left( t\right) } \right) , \end{aligned}$$
(7)

where \(V_{i}(t):\) is the velocity of the particle in the \(\hbox {i}{\mathrm{th}}\) dimension; \(X_{i}(t):\) is the particle’s coordinate in the \(\hbox {i}{\mathrm{th}}\) dimension; \(t:\) denotes the current iteration; \(\alpha \): is a time-varying weight coefficient, which usually decreases from 0.9 to 0.6 linearly; \(C_{1}\) and \(C_{2}:\) are two random constants usually fixed to be 2.0; \(\delta _{1}\) and \(\delta _{2}\): are two random functions applied independently to provide uniform distributed numbers in the range from 0 to 1.

At the end of iteration the current position of the particle is updated by following equation.

$$\begin{aligned} X_i \left( {t+1} \right) =X_i \left( t \right) +V_i \left( {t+1} \right) . \end{aligned}$$
(8)

The following weighting function is usually utilized in the above equations.

$$\begin{aligned} \alpha =\alpha _{\max } -\left[ {\left( {\alpha _{\max } -\alpha _{\min } } \right) \frac{iter}{\max iter}} \right] , \end{aligned}$$
(9)

where \(\alpha _{\mathrm{max}}\) = initial weight; \(\alpha _{\mathrm{min}}\) = final weight; maxIter = maximum iteration number; iter = current iteration number.

The calculation continues for each of the dimensions in an N-dimensional optimization problem. \(\hbox {X}_{\mathrm{pbest}}\) records the \(\hbox {i}{\mathrm{th}}\) particle’s position which attains its personal best fitness value while \(\hbox {X}_{\mathrm{gbest}}\) records the position which attains its global best fitness value among all.

4 Optimization by PSO

The antenna parameters to be optimize (length, width etc.) forms the position of the particle and a set of such positions is taken initially. Fitness of each position is evaluated based on a cost function, and other parameters of the antenna are provided as input (e.g. substrate dielectric constant, substrate thickness, substrate size etc). Based on the antenna characteristic, the cost function can be single-objective (e.g. only the bandwidth of the antenna or only the resonant frequency) or multi-objective (e.g. bandwidth and resonant frequency of the antenna taken together). Over the 10 parameters stated in Table 1, four parameters \(L_{1}\), \(L_{2}, W_{1}\) and \(W_{2}\) are taken for optimization. The goal of the optimization process was to maximize the Fractional Bandwidth (FBW) by varying these parameters while keeping resonating frequency (\(f_{r}\)) near to 2.4 GHz [1].

4.1 Curve fitting

To generate the relationship equations between variable parameter and \(f_{r}\) or FBW, first, \(L_{1}\) is varied while keeping all other parameter of Table 1 constant. The value of \(L_{1}\) in initial antenna was 10 mm (35.08 mm) to generate data for cost function; \(L_{1}\) is varied from \(-\)4 mm (31.08 mm) to +4 mm (39.08 mm) with an increment of 0.5 mm. So it forms 17 (16+ 1 conventional) different antennas. Similarly \(L_{2}, W_{1}, W_{2}\) is varied in same fashion for the range given in Table 2. And keeping all other parameter fix. Thus a total 65 (\(16\times 4+1\)) antennas are available and for each antenna resonant frequency (\(f_{r}\)) and Fractional Bandwidth (FBW) is calculated [6].

Table 2 Range for variation of parameter
Full size table

Some of these are shown in Table 3.

Table 3 Variable versus \(f_{r}\) and \(FBW\)
Full size table

Applying the values of Table 3 in Graphmatica (curve fitting software), the relationships of \(L_{1}\), \(L_{2}\), \(W_{1}\) and \(W_{2}\) to \(f_{r}\) and FBW is obtained two of them are given below.

$$\begin{aligned} f_{r1}&= -1.6863\times 10^{-6}\times L_1^4 +3.8321\times 10^{-6}\times L_1^3 \nonumber \\&+\, .002\times L_1^2+.0687\times L_1 -.3453 \end{aligned}$$
(10)
$$\begin{aligned} FBW_1&= -2.4337\times {10}^{{-6}}\times L_1^4 -6.9153\times 10^{-5}\times L_1^3 \nonumber \\&+\, .0028\times L_1^2 +.3836\times L_1 +25.8966. \end{aligned}$$
(11)

4.2 Fitness function

The fitness function is generated by using the Root Mean Squared Error (RMSE) based fitness function. The root mean squared error \(E_{i}\) of an individual program-\(i\) is evaluated by the equation

$$\begin{aligned} E_i =\sqrt{\frac{1}{n}\sum _{j=1}^n {\left( {P_{ij} -T_j } \right) ^{2}}} \end{aligned}$$
(12)

where \(P_{ij}\) is the value predicted by the individual program \(i\) for fitness case \(j\) (out of \(n\) fitness cases); and \(T_{j}\) is the target value for fitness case \(j\). For a perfect fit, all \(P_{ij}=T_{j}\) and thus, \(E_{i}=0\). Using the above RMSE based fitness function, our fitness function is

$$\begin{aligned} F\left( x \right) {=}\sqrt{M\left( {f_r {-}f_{rt\arg et} } \right) ^{2}+N\left( {FBW-FBW_{t\arg et} } \right) ^{2}}, \end{aligned}$$
(13)

Here \(M\) and \(N\) are the biasing constant to control the contribution of each term to the overall fitness function and \(f_{rtarget}\), \(FBW_{targetare}\) the desired central frequency and the desired bandwidth. Increasing \(M\) will bias the developed PSO to optimize the Microstrip patch antenna towards the resonating frequency \(f_{r}\), while increasing \(N\) will bias the optimized value towards the Fractional Bandwidth FBW [1].

5 Results and discussions

We wrote a MATLAB program for PSO using the above relationship equations and the RMSE based fitness function and then run it. The value of \(M\) and \(N\) were set to 0.30 and 0.70 to apply more emphasis on bandwidth expansion. After 300 iterations with 100 particles, we obtained the optimized values of the four geometrical parameters \(L_{1}\), \(L_{2}\), \(W_{1}\) and \(W_{2}\). We design and simulate the optimized antenna in IE3D and the results were compared with the conventional antenna as shown in Table 4 and Fig. 2 [5].

Fig. 2
figure 2

Comparative return loss graph of the I-shaped antennas

Full size image
Table 4 Comparison between conventional antenna to PSO optimized antenna
Full size table

6 Conclusion

The design, optimization and practical implementation of a novel antenna has been presented and discussed. This paper discusses the optimizations of Fractional Bandwidth of Microstrip antenna, keeping \(f_{r}\) fix near 2.4 GHz while the flexibility in defining the fitness function allows PSO to address other design requirements. It is observed that as a stochastic global optimizer, PSO is particularly suitable for antenna optimizations which are in general extremely nonlinear [3].

In this work, PSO program is developed using equations obtained by curve fitting. Employing the PSO program, The Fractional Bandwidth of the I-shaped patch antenna is increased by 25 % with resonance at 2.414 GHz.