Stability of native point defects in α-Al₂O₃ under aqueous electrochemical conditions

Abstract

The formation energies of native point defects in crystalline α-Al₂O₃ were investigated by combining first principles-based methods and theoretical models in a grand canonical framework. For defect formation reactions in this framework, the chemical potentials of chemical species and electrons can be constrained by the conditions of aqueous electrochemical systems, where liquid water is thermodynamically stable. Activation relaxation technique (ART) simulations using an empirical interatomic potential were implemented to discover candidates for stable configurations of point defects. Density functional theory (DFT) calculations were then used to confirm the accurate energetics of the candidate defect configurations. The results show that, except Al vacancies, the most stable defect configurations are generated by simply adding/removing atoms at particular high-symmetry sites. We also investigated the stability of these point defects as a function of the chemical potentials of both electron and oxygen. The results reveal that, at the conditions of thermodynamic stability for liquid water in aqueous electrochemical systems, Al vacancies as the most stable point defects in α-Al₂O₃ can be generated in exothermic defect formation reactions with negative formation energies. These thermodynamic tendencies provide critical insights into the nature of passive films formed under aqueous electrochemical conditions, particularly explaining of the formation of amorphous structures of passive alumina.

Graphic abstract

1 Introduction

Passive oxides serve as crucial components for many structural and functional applications. Native oxides that spontaneously form on metals, such as Al₂O₃ and Cr₂O₃, have long been known to passivate the surface and inhibit corrosion under atmospheric and aqueous environments. Charge modulation in the source-drain channel of the field effect transistor is achieved by the fabrication of robust nano-meter-thickness gate dielectrics like Al₂O₃ [1], HfO₂ [2]. Controlling mass and charge transport across the solid electrolyte interface (LiO₂, SiO₂) is paramount to improve the performance of Li ion batteries [3,4,5].

One of the most important factors governing the passivation strength of oxide layers and other functional performances is the atomistic structure, which controls the thermodynamic and kinetic behavior of defect species. Atomistic scale measurements using scanning tunneling microscopy and atomic force microscopy reveal the structure of passive oxides on Cr, Fe, Co, Ni and Co to be crystalline [6,7,8,9,10,11]. Oxides forming on surfaces of Al, Mg and Si are known to be amorphous or nanocrystalline under atmospheric and aqueous environments [12, 13]. The structure and morphology of Al₂O₃ dielectrics used in microelectronic device architectures have been shown to depend on the deposition temperature [14, 15]. It is hence crucial to know the atomistic structures of passive oxides under operational conditions, especially whether these oxides are in amorphous or crystalline states due to electrochemical reactions under aqueous environments.

The above questions are related to the stability of native point defects in the crystalline oxides. This stability can be evaluated by the corresponding defect formation reaction as a function of chemical potentials of the chemical species and electrons in a grand canonical framework, where the chemical potentials are controlled by the reaction environments [16]. An amorphous oxide is preferred from the thermodynamic aspect if it is exothermic for the formation of native point defects in the crystalline oxides. In addition, the native point defects are critical to determine transport and other properties of these oxides. For these reasons, classical and quantum mechanical simulations have previously been used to study the structures of alumina [17,18,19,20]. The corundum structure of alumina (α-Al₂O₃) has been studied using density functional theory (DFT) calculations [19,20,21,22,23,24]. The energetic stability of point defects was analyzed using the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional with a mixing parameter of 0.32 by Choi et al. [21], which produced a bandgap of 9.2 eV close to experimentally reported values [25, 26]. In this study, all point defects, including Al/O interstitials and vacancies, were generated by simply adding or removing atoms at particular high-symmetry lattice sites.

However, several first-principles calculations have suggested that there could be other low-symmetry off-lattice configurations of point defects with higher stability than high-symmetry defects in crystalline α-Al₂O₃. Lei et al. [24] used the Perdew–Burke–Ernzerhof (PBE) functional to construct Al cation and O anion diffusion paths in α-Al₂O₃. It was reported crucially that one of the Al diffusion paths produces an intermediate local minimum, which is energetically more stable than the initial configuration. In the intermediate state, the Al atom rests at the octahedral interstitial site and the initial and final lattice sites are unoccupied. The relative stability of this intermediate state was reported to be more pronounced when the vacancy defect was charged. This split vacancy configuration was earlier reported by Hine et al. [20].

Based on the above studies, it is natural to ask whether there could be other point defect configurations that haven’t been discovered for the corundum structure of alumina. It is also necessary to evaluate the stability of these defects due to chemical and electrochemical reactions under aqueous conditions to understand the corrosion inhibition properties of passive oxides. Thus, we employed a two-step calculation strategy to systematically study the point defects in α-Al₂O₃ (its atomic structure is shown in Fig. 1). First, we applied activation relaxation technique (ART) simulations [27,28,29,30,31] based on a classical interatomic potential to efficiently sample the possible point defect configurations in the potential energy landscape; DFT calculations were then used to obtain the accurate energy of the candidate point defect configurations. The results indeed confirm that, for Al interstitials, oxygen interstitials and oxygen vacancies, the most stable configurations are still generated by simply adding/removing atoms at particular high-symmetry sites. However, for Al vacancies with variable charge states, the most stable configuration is the split vacancy configuration mentioned above.

Fig. 1

An α-Al₂O₃ supercell that contains 120 atoms (48 Al + 72 O). Blue atoms are Al, red atoms are O, and green lines represent interatomic bonds

Based on these results, we also investigated the stability of these point defects as a function of electron chemical potential (Fermi level) and chemical potentials of Al/O in a grand canonical framework as described in Sect. 2.1. In this framework, the chemical potentials of Al/O are constrained by the thermodynamic stability of pure elemental substance (Al crystals or O₂ molecules) and their compound (α-Al₂O₃), and the electron chemical potential is constrained by the bandgap of α-Al₂O₃. In most regions of electron chemical potential, the point defects with the lowest formation energies are those with the large absolute charges, such as Al_i³⁺ interstitial at lower Fermi levels close to the valence band maximum (VBM) and V_Al³⁻ vacancy at higher Fermi levels close to the conduction band minimum (CBM). These results are critical for further studies of point defects in passive oxide films in atmospheric and aqueous environments.

We then address the thermodynamic stability of native defects in crystalline oxides under aqueous electrochemical conditions. These conditions are defined by the macroscopic variables, such as electrode potentials and aqueous pH values, to constrain the chemical potentials of chemical species and electrons so that the liquid water is thermodynamically stable in electrochemical reactions related to water [16, 32]. Details are described in Sects. 2.2 and 2.3. Passive oxide layers are spontaneously formed when a metallic surface comes in contact with aqueous electrolytes. This oxidation reaction creates a sandwich-like metal/oxide/electrolyte system consisting of a metal/oxide interface and an oxide/electrolyte interface. The thermodynamics of defect formation in the oxide depends on the chemical potentials of the chemical species and electronic band alignments at both interfaces. To evaluate oxide stability under aqueous electrochemical conditions, we follow the grand canonical formalism to bridge defect thermodynamics in bulk oxide and aqueous electrochemical systems [16]. The thermodynamics of defect species in both systems (bulk oxide and aqueous electrochemical) was expressed as a function of chemical potentials in global chemical and electron reservoirs. Such an expression allows the integration of the water stability and the oxide stability domains in the $(\mu _{\text{O}},\mu _e)$ parameter space, where $\mu _{\text{O}}$ represents the chemical potential of oxygen and $\mu _e$ represents the electron chemical potential referenced to the vacuum level [32, 33]. This unified representation is useful to identify the nature of predominant crystal defects for any set of externally controllable parameters, such as aqueous pH values and electrode potential ${\text{U}}$. Our results suggest the crystalline α-Al₂O₃ is thermodynamically unstable against the spontaneous formation of the point defects under aqueous electrochemical conditions, so amorphous alumina structures are thermodynamically favorable to be generated at the Al₂O₃/H₂O interface.

2 Theoretical models

2.1 Defect formation energy

The formation of charged point defects in α-Al₂O₃ involves the exchange of elemental species and electrons from the corresponding reservoirs. The reference chemical potentials $\mu _{\text{Al}}^0$ and $\mu _{\text{O}}^0$ are defined by bulk Al metal and isolated O₂ molecule, respectively. Under conditions of thermodynamic equilibrium, the chemical potentials $\mu _{\text{Al}}$ and $\mu _{\text{O}}$ are constrained by the following equation:

$$2\mu _{{{\text{Al}}}} + 3\mu _{{\text{O}}} = \Delta H_{f} \left( {{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} } \right)$$

(1)

where $\Delta H_f$ is the formation enthalpy of Al₂O₃ with the bulk FCC Al ($\mu ^0_{\text{Al}}$) and isolated O₂ molecule ($\mu ^0_{\text{O}}$) as the reference states for pure elements. The formation energy of a defect in α-Al₂O₃ is mathematically computed as

$$\begin{aligned} E^f(D^q)&=E_{\text{tot}}(D^q)-E_{\text{tot}}(\text{Al}_2{\text{O}}_3)\\ {}&-\sum \limits _{\text{i}} n_{\text{i}}\left( \mu _{\text{i}}^0+\mu _{\text{i}}\right) +q\epsilon _F+\Delta ^q \end{aligned}$$

(2)

here $E^f(D^q)$ is the formation energy of a defect D in a charge state q; $E_{\text{tot}}(D^q)$ is the total energy of the defected supercell; $E_{\text{tot}}({\text{Al}}_2{\text{O}}_3)$ is the energy of the pristine supercell; $n_{\text{i}}$ is the change in number of atoms of type ${\text{i}}$ due to defect formation; $\mu _\text {i}^0+\mu _{\text{i}}$ is the energy of elemental species at the reference state (bulk Al metal or isolated O₂ molecule) plus the chemical potential relative to the corresponding reference states; $\epsilon _F$ is the Fermi level relative to the VBM of the oxide; $\Delta ^q$ is a correction term for charged defect interactions in a supercell with periodic boundary conditions [34].

2.2 Chemical potentials in electrochemical systems

The system under investigation comprises 3 phases: (1) a solid metal, (2) a solid metal oxide and (3) liquid H₂O. These phases form the metal/oxide and oxide/water interfaces. It is hence important to evaluate the chemical potentials of oxygen ($\mu _{\text{O}}$), hydrogen ($\mu _{\text{H}}$) and aluminium ($\mu _{\text{Al}}$) as a function of externally controllable parameters. At the metal/oxide interface, the chemical potentials of aluminium $\mu _{\text{Al}}$ and oxygen $\mu _{\text{O}}$ are constrained by Eq. 1 under thermodynamic equilibrium. The reference states for aluminium and oxygen are described by the energies per atom for the bulk Al crystal in FCC lattice and the isolated ${\text{O}}_2$ molecule from DFT calculations.

We now explain the aqueous electrochemical conditions at the oxide/water interface under thermodynamic equilibrium. There are two constraints at the oxide/water interface under thermodynamic equilibrium [16, 32]. The first constraint connects $\mu _{\text{O}}$ and $\mu _{\text{H}}$ to the formation enthalpy of H₂O as the following equation:

$$2\mu _{{\text{H}}} + \mu _{{\text{O}}} = \Delta H_{f} \left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right)$$

(3)

Here the reference of hydrogen chemical potential is the energy per atom of an isolated ${\text{H}}_2$ molecule, and $\Delta H_{f} \left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right) = - \,2.46$ eV is obtained from standard tables [35] but not from DFT calculations. The second constraint is that the formation enthalpies of both ${\text{H}}^+$ and ${\text{OH}}^-$ ions should be positive so that aqueous water is thermodynamically stable. These formation enthalpies can be mathematically expressed as the function of formation enthalpies and hydration energies of certain chemical species, which are available in standard tables based on experimental measurements [35,36,37] (detailed descriptions provided by Todorova et al. [16]).

Another critical parameter in electrochemical systems is the electron chemical potential $\mu _e$. A standard reference for $\mu _e$ is the electron energy level in the vacuum as the solute zero. However, in the electrochemical community, $\mu _e$ is measured relative to the electron chemical potentials of electrons in certain conventional electrodes, such as the standard hydrogen electrode (SHE). Thus, it is necessary to connect the electron chemical potential of electrons from SHE (defined as $\mu _e^{\text{SHE}}$) with respect to the absolute zero energy in vacuum to unify these two references [32]. This connection establishes and combines all theoretical variables: $\mu _{\text{H}}$, $\mu _{\text{O}}$ and $\mu _e$, with the experimental macroscopic variables ${\text{pH}}$ and ${\text{U}}$, where ${\text{U}}$ is the electrode potential with respect to the SHE. By definition, ${\text{pH}}$ is connected to the concentration of ${\text{H}}^+$ ions, as $c({\text{H}}^+)=c_0{\text{exp}}\left( -\frac{\Delta G^0({\text{H}}^+)(\mu _{\text{H}},\mu _e)}{\text {kT}}\right) =10^{-{\text{pH}}}$. Here $\Delta G^0({\text{H}}^+)$ is the formation free energy of proton ${\text{H}}^+$ in aqueous electrolyte and it can also be expressed as the sum of the free energy changes for the ionization of H followed by hydration to form H$^{+}$. These expressions are detailed in reference [16]. SHE conditions are defined when $\mu _{\text{H}}=0$ and ${\text{pH}}=0$. Under these conditions, the value of $\mu _e^{\text{SHE}}$ = -4.73 eV relative to the electron energy level in vacuum [32]. Thus, the measured electrode potential U relative to the SHE can be connected to the electron chemical potential $\mu _e$ relative to the vacuum level as

$${\text{U}} = \left( \mu _e^{\text{SHE}}-\mu _e\right) /e$$

(4)

Here e is the elementary charge. Thus, the electron potential $\mu _e$ relative to the vacuum level is equal to $\mu _e=\mu _e^{\text{SHE}}-e{\text{U}}$. Following this, the variables $\mu _{\text{O}}$ and $\mu _{\text{H}}$ can be expressed in terms of pH and ${\text{U}}$ as:

$$\mu _{{\text{H}}} = \left( {\mu _{e} - \mu _{e}^{{{\text{SHE}}}} } \right) - k_{B} {\text{T}} \cdot \log \left( {10} \right) \cdot {\text{pH}}$$

(5)

$$\mu _{{\text{O}}} = \Delta H_{f} \left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right) - 2\mu _{{\text{H}}}$$

(6)

As mentioned above, the formation enthalpies of both ${\text{H}}^+$ and ${\text{OH}}^-$ ions should be positive so that aqueous water is thermodynamically stable. Thus, the values of $\mu _{\text{H}}$ and $\mu _{\text{O}}$ must lie within specific bounds, which also limit the values of pH and U. Using these limits, the commonly represented H₂O chemical stability is constructed and shown in Fig. 2. Any combination of $({\text{pH,U}})$ is limited by the shaded parallelogram within which H₂O is chemically stable in the liquid phase. The upper end (shaded red) marks the oxygen evolution boundary, where $\mu _{\text{O}}=0$. The lower end (shaded violet) marks the onset of the hydrogen evolution reaction ($\mu _{\text{O}} = \Delta H_{f} \left( {{\text{H}}_{{\text{2}}} {\text{O}}} \right) = - \,2.46$ eV).

Fig. 2

Contour plot showing the dependence of oxygen chemical potential ($\mu _{\text{O}}$) at the oxide/water interface on electrode potential ${\text{U}}$ (relative to SHE) and pH values, obtained from Eqs. 5 and 6

2.3 Electronic band alignment

Fig. 3

Electronic band diagram schematic for the metal-oxide-water system. The horizontal black dashed line marks 0 on the SHE scale. The shaded blue rectangle on the right side represents the $\mu _e$ window for H₂O stability evaluated at pH = 0 obtained from Eqs. 4 and 6

The electronic band alignment in the sandwich-like metal/oxide/electrolyte system of the metallic element ${\text{(M)}}$ and its oxide $\left( {{\text{M}}_{x} {\text{O}}_{y} } \right)$ is determined by the electron chemical potentials inside the metal, oxide and water, respectively. Under open circuit conditions, electron chemical potential in the metal relative to the absolute zero level in vacuum is equal to the negative value of the metallic work function ${\Phi }_{\text{M}}$. The work function of Al, ${\Phi _{\text{Al}}}$, is known to depend on the crystallographic surface from which photoelectrons are emitted [38]. An average value of 4.1 eV was considered for this study [39] ($-{\Phi }_{\text{M}}$ = $-4.1$ eV on the left part of Fig. 3). Similarly, under open circuit conditions, the electron chemical potential in the oxide is equal to the negative value of the oxide work function ${\Phi _{\text{oxide}}}$. For an undoped oxide, $\Phi _{\text{oxide}}$ is close to the middle of the electronic bandgap, centered between the VBM and CBM. The relative position of the VBM with respect to the absolute zero in vacuum must be known to establish equivalence between electron chemical potentials conventionally used in the semiconductor and electrochemistry communities. Using previously published experimental literature, the energy level of the VBM in α-Al₂O₃ is set to $-9.8$ eV from absolute zero [40]. In addition, because standard DFT calculations underestimate the bandgap values, the experimentally reported bandgap [25] of 8.8 eV is used in this paper. Thus, the work function of alumina ${\Phi _{\text{Al}_2{\text{O}}_3}}$ is positioned at 4.4 eV from the VBM (which is in the middle of the experimental 8.8 eV bandgap). This translates to $-5.4$ eV on the absolute $\mu _e$ scale ($-{\Phi }_{\text{oxide}}$ = $-5.4$ eV in the middle part of Fig. 3).

When the electrode potential is applied, the electron chemical potential (Fermi level $\epsilon _F$) changes. Since $\epsilon _F$ in Eq. 2 represents the Fermi level position relative to the VBM in the oxide for most semiconductor studies, the electron chemical potential in the oxide relative to the absolute zero level in vacuum $\mu _e$ is related to $\epsilon _F$ as the following equation:

$$\epsilon _F = \mu _e - \mu _{\text{VBM}}^{\text{oxide}}$$

(7)

Here $\mu _{\text{VBM}}^{\text{oxide}}$ is the relative position of the VBM in the oxide with respect to the absolute zero in vacuum, and $\mu _{\text{VBM}}^{\text{oxide}} = -9.8$ eV for α-Al₂O₃. Combining Eqs. 4 and 7 allows us to transform the definitions of electron chemical potentials ($\epsilon _F$, ${\text{U}}$ and $\mu _e$) in both semiconductor and electrochemical systems [32]. This equivalence enables the representation of point defect thermodynamics (obtained from Eqs. 1 and 2) and water stability (Eqs. 3, 5 and 6 ) on the same scale.

Metal-rich chemical conditions at the metal/oxide interface enforce $\mu _{\text{M}}=0$ and $\mu _{\text{O}} = \frac{{\Delta H_{f} \left( {{\text{M}}_{x} {\text{O}}_{y} } \right)}}{y}$ (Here ${\text{M}}_{x} {\text{O}}_{y}$ is Al₂O₃ in Eq. 1). Similarly, at the oxide/water interface, the electron chemical potential $\mu _e$ in H₂O is equal to $\mu _e^{\text{SHE}}-e{\text{U}}$ according to Eq. 4. Following the discussion in Sect. 2.2, the thermodynamic stability of water restricts the electron chemical potential in H₂O to lie within the shaded blue box in Fig. 3. Oxygen chemical potential $\mu _{\text{O}}$ at the oxide/water interface is computed as a function of ${\text{U}}$ and ${\text{pH}}$ by Eq. 6 as depicted in Fig. 2. The chemical potential of the metallic species is equal to $\frac{{\Delta H_{f} \left( {{\text{M}}_{x} {\text{O}}_{y} } \right) - y\mu _{\text{O}} }}{x}$ according to Eq. 1.

3 Computational methods

The four primary point defects analyzed in this work are the aluminium vacancy (${\text{V}}_{{{\text{Al}}}}^{{q}}$), aluminium interstitial (${\text{Al}}_{i}^{q}$), oxygen vacancy (${\text{V}}_{\text{O}}^{q}$) and oxygen interstitial (${\text{O}}_{i}^{q}$), where q is the electronic charge state of the point defect. First, the potential energy landscape of α-Al₂O₃ was explored by Activation Relaxation Technique (ART) simulations [27,28,29,30,31] in conjunction with a classical force field [41]. Next, DFT calculations were used to compute defect formation energies of the three most stable configurations for each type of point defects identified by ART. Finally, a defect stability map as a function of the oxygen chemical potential and electron chemical potential was constructed using the DFT data. Detailed descriptions of these methods are provided in the following paragraphs.

3.1 Search for stable point defect configurations

The open-source ART nouveau code [27,28,29,30,31] (interfaced with the MD code LAMMPS [42] was used with the Vashishta [41] potential for alumina. The Vashishta interatomic potential [41] is a 3-body fixed charge potential. ART is a method to sample local energy minimum and transition barriers. It is composed of two steps: (1) Changing the configuration of an initial minimum to a local saddle point (the activation step), (2) changing the configuration of the saddle state to obtain a different local minimum (the relaxation step). The following activation parameters were specified within the ART nouveau code: the radial cutoff for local displacements was 2.5 Å; the maximum number of Lanczos steps for activation was 150; the force threshold for the perpendicular hyperplane relaxation during Lanczos steps was 0.1 eV/Å; the maximum atomic displacement was 0.1 Å; the maximum number of iterations before leaving the basin was set to 15; and the force convergence at the saddle point was 0.1 eV/Å. Once at the saddle point, the configuration was displaced away from the initial minimum by a distance equal to 0.1 times the distance between the initial minimum and the saddle locations. A 120-atom supercell (48 Al + 72 O) containing one lattice point defect was allowed to evolve for 9000 ART steps. The 3 lowest energy configurations for each defect were energetically minimized using DFT calculation to evaluate the defect stability accurately.

All DFT calculations were performed using the PBE pseudopotential [43] implemented with the projected augmented-wave (PAW) method [44, 45] in the Vienna Ab initio Simulation Package (VASP) [46]. A 120-atom supercell was constructed with 48 Al and 72 O atoms. A $\Gamma$-centered $3\times 3\times 2$ kpoints mesh and an energy cutoff of 500 eV was used. The $\Delta ^q$ correction for charged defect interactions in a supercell with periodic boundary conditions is computed using the sxdefectalign code [34]. For comparison, we also refer to DFT data from previous studies using HSE06 functionals (120 atoms, 400 eV cutoff, $2\times 2\times 1$ k-point mesh, 32% mixing parameter) by Choi et al. [21].

3.2 Stability of defects under electrochemical conditions

Following the method of Todorova et al. [32, 33], a 2D defect stability map was generated to highlight the defect state with the lowest formation energy as a function of $\mu _e$($\epsilon _F$) and $\mu _{\text{O}}$. From Eq. 2, $E^f(D^q)$ can be evaluated as a function of $\mu _{\text{O}}$ (or equivalently $\mu _{\text{Al}}$) and $\mu _e$. $\mu _{\text{O}}$ is allowed to vary between $\left[ {\frac{{\Delta H_{f}\left( {{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} } \right)}}{3},\,0} \right]$ and $\mu _e$ varies across the bandgap of Al₂O₃. A contour plot is generated by plotting the lowest $E^f(D^q)$ in the $(\mu _{\text{O}},\mu _e)$ parameter space. According to descriptions in Sects. 2.2 and 2.3, the water stability region (Fig. 2), ${\Phi _{\text{Al}}}$ and $\Phi_{\text{Al}_{2} {\text{O}}_{3}}$ are overlaid with the contour plot to predict structural stability under aqueous electrochemical conditions.

4 Results

4.1 Ground-state point defects

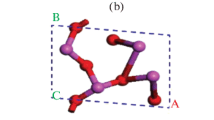
ART simulations reveal the existence of three possible states of the ${\text{V}}_{\text{Al}}$ monovacancy in several configurations (shown by three bands with different colors in Fig. 4a). The configurations with the energy level of the green band in Fig. 4a correspond to ${\text{V}}_{\text{Al}}$ located on a regular Al lattice site. However, the system attains a lower energy configuration (corresponding to the energy level of the orange band in Fig. 4a) by rearrangement of atoms. In this split vacancy state denoted as ${\text{V}}_{\text{Al}\_{\text{s}}}$, an octahedral interstitial site is occupied by an Al atom with 2 on-site Al vacancies as its first-nearest neighbors. DFT calculations confirm the relative stability of the 2 configurations discussed above: the vacancy on a lattice site (${\text{V}}_{{{\text{Al}}}}^{q}$) and the split vacancy configuration (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{q}$). The ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{q}$ point defect has lower energy than ${\text{V}}_{{{\text{Al}}}}^{q}$ for all charge states ($q=0,-1,-2,-3$). The energy difference is equal to 0.05 eV, 0.15 eV, 0.36 eV, 0.73 eV for $q=0,-1,-2,-3$, respectively. These DFT relaxed structures for ${\text{V}}_{{{\text{Al}}}}^{{{\text{3}} - }}$ and ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{{\text{3}} - }}$ are illustrated in Fig. 4b and c, respectively. The stability of the 3rd lowest energy states (corresponding to the energy level of the purple band in Fig. 4a) was also investigated by DFT. These states are found to energetically relax to the configuration shown in Fig. 4b.

Fig. 4

Energetic stability and atomistic structures of the aluminium vacancy

Similar to ${\text{V}}_{{{\text{Al}}}}$, the 3 lowest energy states from ART simulations are considered for Al interstitial ${\text{Al}}_{i}$. In its most stable form, the ${\text{Al}}_{i}$ atom occupies the octahedral interstitial site. DFT calculations replicate these findings. The light grey atom in Fig. 5a is the interstitial Al atom. For the ${\text{Al}}_{i}^{{2 + }}$ and ${\text{Al}}_{i}^{{3 + }}$ defects, the interstitial Al atom is equidistant to 6 O atoms, with the Al-O bond length equal to 1.88 Å and 1.87 Å, respectively. The spatial symmetry surrounding the Al interstitial is broken for defect states with lower charges and Al$_i$ is displaced from the central interstitial position. The same Al-O bond lengths for ${\text{Al}}_{i}^{0}$ and ${\text{Al}}_{i}^{{1 + }}$ vary between 1.86 and 2.71 Å. The DFT calculations also show that other high energy structures obtained from ART results are relaxed to this stable interstitial configuration shown in Fig. 5a.

Fig. 5

Atomistic structures of the aluminium interstitial, oxygen vacancy and oxygen interstitial from DFT calculations

Similar to Al_i, one stable low energy configuration for V_O is found by ART. DFT calculations of the lowest energy configurations from the ART simulations are described as the following. In the perfect crystal, each O atom is bonded to 4 Al atoms to create a tetrahedron with 2 Al–O bond lengths equal to 1.87 Å and the other two equal to 1.99 Å. Removing an oxygen atom alters the positions of the four neighboring Al atoms, thus distorting the original tetrahedron. Such distortion is most severe for ${\text{V}}_{{\text{O}}}^{{2 + }}$, where all four neighboring Al atoms are displaced by a magnitude between 0.17 and 0.28 Å as shown in Fig. 5b. ART simulations also identify two other types of defect configurations with higher energy levels. They correspond to local deviations for one or two Al atoms that are not at the vertices of the tetrahedron surrounding the vacancy, and these structures also relax by DFT calculations to the configuration shown in Fig. 5b.

In contrast to the point defects described previously, ART simulation yields a continuous distribution of ${\text{O}}_{i}$ energies, so a unique energy minimum state cannot be identified. This continuous distribution of energy levels of different defect configurations is most likely due to the nature of the empirical potential used. DFT calculations reveal a charge dependent geometric rearrangement of atoms surrounding the ${\text{O}}_{i}$. For a neutral supercell containing ${\text{O}}_{i}$ shown in Fig. 5c, the green interstitial atom is at a distance of 1.44 Å from the yellow lattice oxygen. This split interstitial arrangement is accommodated inside a distorted octahedron shaded in light green. However, the ${\text{O}}_{i}^{{2 - }}$ defect is stable at the interstitial location (Fig. 5d), which is in between 2 planes of O atoms in the α-Al₂O₃ lattice. DFT relaxations of other randomly selected low energy configurations from ART simulations result in the structures presented in Fig. 5c or d, depending on the charge state of the oxygen interstitial.

4.2 Defect stability as a function of Fermi level

At thermodynamic equilibrium, the chemical potentials of Al and O are bound by Eq. 1. In this equation, the DFT calculated formation enthalpy $\Delta H_f\left( {\text{Al}}_2{\text{O}}_3\right) =-14.99$ eV, and the elemental reference states are bulk FCC Al ($\mu ^0_{\text{Al}}$) and an isolated O₂ molecule ($\mu ^0_{\text{O}}$), respectively. In order to better compare with experimental electrochemical references, we use the experimental value for $\Delta H_f$(Al₂O₃) $=-17.30$ eV [47]. Following the constraint of Eq. 1, $\mu _{\text{O}}\in [-5.76,0]$ eV and $\mu _{\text{Al}}\in [-8.65,0]$ eV. Using Eq. 2, the formation energies of all considered point defects were plotted for the extreme O-rich and Al-rich environments with the variation of electron chemical potential described by $\epsilon _F$ relative to the VBM in the oxide. In the correction scheme followed by Hine et al. [20], the defect formation energy was corrected by $m_{\text{eff}}\Delta E_g$. $m_{\text{eff}}$ is the number of electrons occupying defect states derived from the conduction band and $\Delta E_g$ is the bandgap underestimation. It was shown that $m_{\text{eff}}$ can be approximated by $(\epsilon_{\text{def}}-E_{\text{VBM}})/E_g$, where $\epsilon _{\text{def}}$ is the energy of the defect charge transition relative to the VBM and $E_g$ is the DFT bandgap. We implement this scheme to correct the PBE formation energies. In Eq. 2, $\epsilon _F$ changes from 0 (the energy level of VBM) to the energy level of CBM, so the maximum value of $\epsilon _F$ is the bandgap of the oxide. The PBE calculated bandgap of $\alpha{\text{-Al}}_{2} {\text{O}}_{3}$ = 5.70 eV, close to the previous reported DFT result [48]. However, because standard DFT calculations underestimate the bandgap values, the experimentally reported bandgap [25] of 8.8 eV has been used in the defect formation energy plots shown in Fig. 6.

Fig. 6

Dependence of defect formation energies $E^f$ on Fermi level position and chemical potentials. The left image corresponds to O-rich conditions ($\mu _{\text{O}}=0$, $\mu _{\text{Al}}=\frac{\Delta H_f({\text{Al}}_2{\text{O}}_3)}{2}=-7.5$ eV), and the right image corresponds on Al-rich conditions ($\mu _{\text{Al}}=0$, $\mu _{\text{O}}=\frac{\Delta H_f({\text{Al}}_2{\text{O}}_3)}{3}=-5.0$ eV). The integer numbers with different colors in each image indicate the charge state of the corresponding defect described by the adjacent solid lines

O-rich conditions should favor the formation of Al-depleted defects such as ${\text{V}}_{{{\text{Al}}}}$ (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}$) and O_i. As shown in the left image of Fig. 6, ${\text{V}}_{{{\text{Al}}}}$ (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}$) and O_i with specific charge states can be easily formed in O-rich conditions with the small positive and even negative values of formation energy $E^f$. The neutral aluminium vacancy in the ${\text{V}}_{{{\text{Al}}}}$ configuration has a formation energy $E^f=3.48$ eV, only 0.08 eV larger than $E^f$ of the neutral ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}$. The (${\text{V}}_{{{\text{Al}}}}^{0} |{\text{V}}_{{{\text{Al}}}}^{{1 - }}$) transition occurs at $\epsilon _F$ = 0.44 eV. Both ${\text{V}}_{{{\text{Al}}}}^{{{\text{2}} - }}$ and ${\text{V}}_{{{\text{Al}}}}^{{{\text{3}} - }}$ are also relatively shallow acceptor-type defects, with the $\left( {{\text{V}}_{{{\text{Al}}}}^{{1 - }} \left| {{\text{V}}_{{{\text{Al}}}}^{{2 - }} } \right.} \right)$ transition at $\epsilon _F=1.22$ eV and the $\left( {{\text{V}}_{{{\text{Al}}}}^{{{\text{2}} - }} \left| {{\text{V}}_{{{\text{Al}}}}^{{3 - }} } \right.} \right)$ transition at $\epsilon _F=1.31$ eV. $E^{f}\left( {{\text{V}}_{{{\text{Al}}}}^{{{\text{3}} - }} } \right)$ eventually becomes negative when $\epsilon _F \ge 2.15$ eV. The charge state transitions for (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{0} |\text{V}_{{{\text{Al}}\_{\text{s}}}}^{{1 - }}$) and (${\text{V}}_{{\text{Al}\_\text{s}}}^{{1 - }} |\text{V}_{{\text{Al}\_{\text{s}}}}^{{3 - }}$) occur at 0.38 eV, 0.95 ev, respectively. $E^{f} \left( {\text{V}_{{\text{Al}\_{\text{s}}}}^{{3 - }} } \right)$ eventually becomes negative when $\epsilon _F \ge 1.90$ eV, indicating the formation of ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{{\text{3}} - }}$ is an exothermic reaction under these conditions of $\mu _{\text{O}}$ and $\epsilon _F$. Such negative $E^f$ can induce lattice instabilities due to spontaneous defect formation (details depending on local activation barriers for such reactions). Besides Al-depleted defects, at Fermi levels close to the VBM, the ${\text{V}}_{\text{O}}^{{2 + }}$ is the most probable with the lowest $E^f$. At higher Fermi levels, the ${\text{V}}_{\text{O}}^{0}$ defect has a formation energy higher than $E^f$ of ${\text{V}}_{{{\text{Al}}}}^{0}$ ($V_{{\text{Al}\_{\text{s}}}}^{0}$) and ${\text{O}}_{i}^{0}$ as expected under O-rich conditions, and $E^f$ of ${\text{V}}_{\text{O}}^{0}$ is equal to 7.94 eV. If the additional $(\epsilon _{\text{def}}-E_{\text{VBM}})/E_g$ correction is not included, $E^f({\text{V}}_{\text{O}}^0)=6.77$ eV, in excellent agreement with a reported value of 6.80 eV [22].

Al-rich conditions should favor the formation of O-depleted defects such as ${\text{V}}_{\text{O}}$ and ${\text{Al}}_{i}$. As shown in the right image of Fig. 6, among the neutral defect states, ${\text{V}}_{\text{O}}^{0}$ has the lowest formation energy of $E^f=2.17$ eV as expected. The (${\text{V}}_{\text{O}}^{0} |{\text{V}}_{\text{O}}^{{2 + }}$) transition is located deep at $\epsilon _F=2.83$ eV. It must be noted that the formation energy $E^f$ of ${\text{Al}}_{i}^{0}$ is much greater and comparable to those of ${\text{O}}_{i}^{0}$ and ${\text{V}}_{{{\text{Al}}}}^{0}$. The calculated formation energy of neutral ${\text{V}}_{{{\text{Al}}}}^{0}$ ($E^f=12.18$ eV). Without the additional correction, $E^f=12.04$ eV, consistent with literature reports [22]. In addition, it is found that the defects with the lowest formation energies are those with the largest absolute charge states: at small values of $\epsilon _F$ close to VBM, ${\text{Al}}_{i}^{{3 + }}$ has the negative formation energy, and at larger values of $\epsilon _F$ close to CBM, ${\text{V}}_{{{\text{Al}}}}^{{3 - }}$ (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }}$) has the negative formation energy. Similar to the cases at O-rich conditions, these negative $E^f$ values can also introduce lattice instabilities due to spontaneous defect formation.

4.3 Defect phase diagram

Fig. 7

Defect phase diagram plotting the defect with the lowest formation energy for all allowed values of $(\mu _{\text{O}},\epsilon _F)$. The regions shaded with white horizontal stripes indicate that the lowest defect formation energy is negative. The oxygen chemical potential is limited by the PBE functional determined formation enthalpy of Al₂O₃. The 8.8 eV bandgap was determined by previous experiments [25]. The parallelogram bound by blue lines is the water stability region from Fig. 2. The lowest value of $\mu _{\text{O}}$ at the aqueous interface is limited by $\Delta H_{f} \left( {\text{H}_{2}{\text{O}} } \right) = -2.46$ eV

Equation 2 also allows the construction of a three-dimensional map showing the dependence of defect formation energies $E^f$ on Fermi level position $\epsilon _F$ and oxygen chemical potential $\mu _{\text{O}}$. A planar projection of this 3D map is depicted in Fig. 7. To generate this projected map, only the defect with the lowest formation energy $E^f$ is considered while continuously varying $\epsilon _F$ (bottom, blue axis) and $\mu _{\text{O}}$ (left, black axis). As mentioned in Sect. 2, a combination of Eqs. 4 and 7 allows us to transform the definitions of electron chemical potentials ($\epsilon _F$, $\mu _e$ and $e{\text{U}}$) according to different reference systems. Thus, the $\epsilon _F$ scale can be converted to the electron chemical potential $\mu _e$ (top, red axis) relative to the vacuum level and the electrode potential ${\text{U}}$ relative to the SHE (the top, black axis). Additionally, $\mu _e$ from the Al is defined by the metallic work function ${\Phi _{\text{Al}}}=-4.1$ eV with respect to vacuum [39]. In this paper, the work function of alumina $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ is positioned at 4.4 eV from the VBM (which is in the middle of the experimental 8.8 eV bandgap). This translates to − 5.4 eV on the absolute $\mu _e$ scale. It should also be noted that Fig. 7 can be reconstructed by a change of the variable from $\mu _{\text{O}}$ to $\mu _{\text{Al}}$ using Eq. 1.

The white striped areas indicate regions where the lowest defect formation energy is negative, implying that α-Al₂O₃ is thermodynamically unstable against the formation of native point defects. This is also indicated by the horizontal line at $E^f=0$ in Fig. 6. The stable region (all $E^f\ge 0$) in Fig. 7 is bounded by ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }}$ (the brown region in Fig. 7) and ${\text{V}}_{{\text{O}}}^{{2 + }}$ (the faint red region in Fig. 7) since these defects have the largest absolute charge states. The positively charged ${\text{Al}}_{i}^{{3 + }}$ and ${\text{V}}_{{\text{O}}}^{{2 + }}$ are the most stable defects at Fermi levels near the VBM, where ${\text{Al}}_{i}^{{3 + }}$ and ${\text{V}}_{{\text{O}}}^{{2 + }}$ have smaller and even negative formation energies due to their large positive charge states. When the Fermi level is higher, defects with large negative charge states such as ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }}$ and ${\text{O}}_{i}^{{2 - }}$ should be more stable. The stable region is bound by ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }}$, depicted by the large brown region on the right side of Fig. 7. The O_i point defect never appears on this map.

In addition, two crucial triple intersection points can be identified in the stable region of Fig. 7, due to the proximity of the (${\text{V}}_{\text{O}}^{{2 + }} \left| {\text{V}_{\text{O}}^{0} } \right.$) and the (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{1 - }} \left| {{\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }} } \right.$) transitions. The (${\text{V}}_{\text{O}}^{{2 + }} \left| {{\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{1 - }} } \right.\left| {{\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }} } \right.$) triple point appears at $(\epsilon _F,\mu _{\text{O}})=(0.95,-0.53)$ eV followed by the (${\text{V}}_{\text{O}}^{{2 + }} \left| {{\text{V}}_{\text{O}}^{0} } \right.\left| {{\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }} } \right.$) at $(\epsilon _F,\mu _{\text{O}})=(2.83,-4.28)$ eV. This sequence is observed because the (${\text{V}}_{\text{O}}^{{2 + }} \left| {{\text{V}}_{\text{O}}^{0} } \right.$) transition happens at a larger value of $\epsilon _F$, compared to $\epsilon _F$ of the (${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{1 - }} \left| {{\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }} } \right.$) transition.

Fig. 8

Defect phase diagram plotting the defect with the lowest formation energy for all allowed values of $(\mu _{\text{O}},\epsilon _F)$. The regions shaded with white horizontal stripes indicate that the lowest defect formation energy is negative. The oxygen chemical potential is limited by the HSE06 determined formation enthalpy of Al₂O₃. The defect stability map was constructed using data originally published by Choi. et al. [21]. The 8.8 eV bandgap was determined by previous experiments [25]. The parallelogram bound by yellow lines is the water stability region from Fig. 2. The lowest value of $\mu _{\text{O}}$ at the aqueous interface is limited by $\Delta H_{f} \left( {\text{H}_{2}{\text{O}} } \right)=-2.46$ eV

5 Discussion

5.1 Results with different DFT functionals

For comparison, DFT data computed using hybrid HSE06 functional obtained from previous studies by Choi et al. [21] were also used to construct the defect phase diagram as Fig. 7. The reported values for formation energy of an isolated O₂ molecule and formation enthalpy of the α-Al₂O₃ crystal from HSE06 are $-4.97$ eV and 16.21 eV. The bandgap from HSE06 calculations of α-Al₂O₃ is 9.2 eV. Data from previous studies by Choi et al. [21] are sufficient for the calculations of all defect formation energies in our work, except $E^f$ for the ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}$ split vacancy. The defect phase diagram with the HSE06 data is plotted in Fig. 8. For consistent comparisons, we use $\Delta H_f$(Al₂O₃)$=-17.30$ eV.

In Figs. 7 and 8, the bandgap is always set to be the experimentally reported bandgap [25] of 8.8 eV. The VBM is referenced to $-9.8$ eV from absolute zero, a value obtained by Xu et al. [40]. It is important to note that the length of the bottom $\epsilon _F$ axis in Figs. 7 and 8 depends on the choice of bandgaps obtained from experiments or first principles calculations. Previous experiments have determined the bandgap of α-Al₂O₃ to be 8.8 eV [25] and 9.4 eV [26]. DFT calculations using PBE pseudopotential underestimate crystalline bandgaps. Our calculations show the bandgap of α-Al₂O₃ to be 5.70 eV, while reported HSE calculations [21] with 32% mixing show a bandgap of 9.2 eV. This however only affects the length of the bottom $\epsilon _F$ axis.

The most crucial parameter to evaluate point defect stability is the absolute electron chemical potential $\mu _e$. As mentioned previously in Sect. 4.2, ${\Phi _{\text{Al}}}$ and $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ are located at an electronic potential of − 4.1 eV and − 5.4 eV with respect to absolute zero (also refer to Figs. 7 and 8 as the vertical black dashed lines). However, the exact value of $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ on the scale of $\mu _e$ is bound to vary due to the variation in measured/calculated bandgaps. It can be observed from Fig. 7 that $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ lies mostly in the white striped region (except for highly negative values of $\mu _{\text{O}}$). This indicates that α-Al₂O₃ is thermodynamically unstable when $\mu _{\text{O}}$ lies between 0 and − 4 eV (contrary to the existence of stable bulk α-alumina). This discrepancy is introduced due to artificially scaling the underestimated PBE bandgap to the experimental 8.8 eV bandgap. If $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ (in Fig. 7) were to be placed at 2.85 eV from the VBM (the middle of the PBE bandgap), it would entirely lie within the region where defect formation energies are positive and the α-Al₂O₃ structure is thermodynamically stable. HSE calculations, which reproduce bandgaps closer to the experimental values, provide a more accurate prediction of phase and defect stability. In Fig. 8, $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ lies in the white striped region only for $\mu _{\text{O}}$ between 0 and $-1.63$ eV. For more negative values of $\mu _{\text{O}}$, α-Al₂O₃ is stable since all defect formation energies are positive.

We also report two characteristic differences between the defect stability maps constructed using PBE and HSE06 functionals. First, the defect stability window is shifted towards the VBM for PBE data, as compared to HSE06 data. This is because the charge transition levels for all defects occur at smaller Fermi levels for PBE calculations. As an example, the ${\text{V}}_{{{\text{Al}}}}^{{\text{0}}} \left| {{\text{V}}_{{{\text{Al}}}}^{{1 - }} } \right.$ transition for PBE data occurs at $\epsilon _F=0.44$ eV. The same HSE06 transition occurs at $\approx 1.4$ eV. Hence, the PBE defect formation energy $E^f$ becomes negative at Fermi levels closer to the VBM, shifting the stability window towards the VBM. Second, the oxygen vacancy stability region is much more prominent in Fig. 7 than in Fig. 8. This is due to the ${\text{Al}}_{i}^{0} \left| {{\text{Al}}_{i}^{{1 + }} } \right.$ transition happening at higher Fermi level for HSE06 (8.01 eV), as compared to PBE (6.18 eV). This difference is less severe for ${\text{V}}_{{{\text{Al}}}}^{{\text{0}}} \left| {{\text{V}}_{{{\text{Al}}}}^{{1 - }} } \right.$. Consequently, the aluminium interstitial stability region is more prominent in the HSE06 data (figure 8).

5.2 Stability under different thermodynamic and electrochemical conditions

In the following paragraphs, the stability of the Al/Al₂O₃/air and Al/Al₂O₃/H₂O interface structures under different thermodynamic and electrochemical conditions is discussed. These interface structures were selected to model the 2 most commonly observed environmental conditions for passive Al₂O₃ films. Passive alumina is formed on Al alloys in ambient conditions (temperature = 300 K, pressure = 1 atm). Under these conditions, the oxygen chemical potential on the oxide surface is determined by the chemical potential value of oxygen in the atmosphere. Passive alumina is also formed when Al alloys are exposed to aqueous environments (in natural and controlled laboratory environments). Under aqueous conditions, the chemical potential of oxygen at the surface is determined by the properties of the electrolytic environment, specifically its pH value and applied potential. Thus, we investigate the defect thermodynamics in Al₂O₃ under ambient and aqueous conditions. Unless specifically stated otherwise all further discussions pertain to Fig. 8 that was generated using HSE06 data published by Choi et al. [21].

A key constraint is the chemical potential of electrons (Fermi level) in different materials. For insulators, the Fermi level lies in the middle of the bandgap. Its work function is the energy required to remove an electron from the Fermi level to the vacuum level. Similarly, the metallic work function is the energy required to remove an electron from the Fermi level to the vacuum level. Both of these values are positive. Electron chemical potential is the energy of an electron with respect to the vacuum level. Its sign is negative, with a magnitude equal to the work function. The electron chemical energies on the absolute Fig. 8 has 2 black vertical dashed lines at $\mu _e=-5.4$ eV and $-4.1$ eV on the absolute electron chemical potential scale, corresponding to the negative values of the work functions $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ and ${\Phi _{\text{Al}}}$, respectively, according to descriptions in Sect. 2.3.

The Al/Al₂O$_3$/air structure is discussed first. The two interfaces here are Al/Al₂O₃ and Al₂O₃/air. The Al/Al₂O₃ interface has the Al-rich condition ($\mu _{\text{Al}}=0$, $\mu_{\text{O}}=-5.4$ eV). The electronic chemical potential at this interface is pinned by the negative value of the metallic work function $-{\Phi _{\text{Al}}}$. As a consequence, the band bending will result in $\Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$ moving towards the higher electron chemical potential $-{\Phi _{\text{Al}}}$. As shown in Fig. 8, when $\mu _e=- \Phi _{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }}$, the most stable defect is ${\text{V}}_{\text{O}}^{0}$ at and near the Al-rich condition. However, when $\mu _e=-{\Phi _{\text{Al}}}$, the most stable defect can transform into ${\text{V}}_{{{\text{Al}}}}^{{3 - }}$ near the Al-rich condition. In both cases, the defect formation energy of the most stable defect is still positive, so $\alpha$-Al₂O₃ is thermodynamically stable at the Al/Al₂O₃ interface.

On the other hand, the Al₂O₃/air interface is O rich. The oxygen chemical potential at the Al₂O₃/air interface is a function of temperature (T) and pressure (P). It is equal to half the DFT energy of an isolated O₂ molecule plus a thermodynamic correction $\Delta \mu _{{\text{O}}_2}$ described as the following equations:

$$\mu _{\text{O}} \left( {\text{T},{\text{P}}} \right) = \frac{1}{2}E_{\text{O}_{2}} + \frac{1}{2}\Delta \mu_{\text{O}_{2}} \left( {{\text{T}},{\text{P}}} \right)$$

(8)

$$\Delta \mu_{{\text{O}}_{2}} ({\text{T}},{\text{P}}) = \int\limits_{0}^{\text{T}} {{\text{C}}_{\text{P}} d{\text{T}} - {\text{T}}\int\limits_{0}^{\text{T}} {\frac{{{\text{C}}_{\text{P}} }}{\text{T}}} \,{\text{d}}{\text{T}} + k_{\text{B}} {\text{T}} \times \ln \left( {\frac{\text{P}}{{{\text{P}}_{0} }}} \right)}$$

(9)

Here C$_{\text{P}}$ is the specific heat at constant pressure and P$_0$ = 1 atm. Using data published in the NIST Standard Reference Database Number 69 [49], $\mu_{{\text{O}}_{2}}$ was calculated to be − 0.63 eV at P = 1 atm and T = 300 K. At this value of $\mu_{{\text{O}}_{2}}$, the formation energy of ${\text{V}}_{{{\text{Al}}}}$ is negative. Due to this instability of defect formation, the crystalline structure of α-Al₂O₃ becomes thermodynamically unstable. This ab initio result can explain why native alumina on Al surfaces is known to be nanocrystalline or amorphous. Al₂O₃ can retain its crystal structure closer to the metal interface at the Al-rich condition according to the above discussions. Progressing towards the atmospheric interface introduces large vacancy concentrations that can result in amorphous structures. Here we clarify that zero point energy (ZPE) of the O₂ molecule was not considered in these calculations. Adding the ZPE will increase the value of $\mu_{{\text{O}}_{2}}$, so it would not change the current conclusion. Similar negative point defect formation energies can also be found under the O-rich condition plotted in Fig. 7 based on our DFT calculations using the PBE functional, indicating the conclusion of the amorphous alumina structures at the Al₂O₃/air interface is insensitive to the DFT calculation methods.

The above discussion can also be extended to the Al/Al₂O₃/H₂O interface by overlapping the water stability region previously presented in Fig. 2. In the overlapped yellow dashed parallelogram (in Fig. 8), each yellow dashed contour line represents a certain pH value. ${\text{pH}} = 0$ and pH 14 are explicitly marked, while the middle dashed line is for pH 7. Similar to the previous case of the Al₂O₃/air interface where $\mu _{{\text{O}}}$ was a function of T and P), the value of $\mu _{{\text{O}}}$ at the Al₂O₃/H₂O interface is governed by Eqs. 5 and 6. Any combination of pH and ${\text{U}}$ strictly binds $\mu _{{\text{O}}}$ between 0 and − 2.46 eV (illustrated by the black horizontal dashed lined at $\mu _{\text{O}}=-2.46$ eV corresponding to $\Delta H_{f} \left( {{\text{H}}_{2} {\text{O}}} \right)$). Since the entire parallelogram lies outside the stability region for α-Al₂O₃, the formation of Al vacancy is always an exothermic reaction. Thus, alumina formed in aqueous environments is also expected to be amorphous near the aqueous interface. Similar negative point defect formation energies can also be found in the water stability region plotted in Fig. 7 based on our DFT calculations using the PBE functional, indicating the conclusion of the amorphous alumina structures at the Al₂O₃/H₂O interface is insensitive to the DFT calculation methods.

6 Conclusion

In summary, defect configurations in crystalline $\alpha {\text{-Al}}_{2} {\text{O}}_{3}$ have been systematically explored to study their energetic stability under varying thermodynamic and electrochemical conditions. We applied ART simulations [27,28,29,30,31] based on a classical interatomic potential to efficiently sample the possible point defect configurations in the potential energy landscape; DFT calculations were then used to obtain the accurate energies of the candidate point defect configurations. The results indeed confirm that, for Al interstitials, oxygen interstitials and oxygen vacancies, the most stable configurations are still generated by simply adding/removing atoms at particular high-symmetry sites. However, for Al vacancies with variable charge states, the most stable configuration is the split vacancy configuration.

Based on these results, we also investigated the stability of these point defects as functions of oxygen chemical potential and electron chemical potential, which can be quantified in terms of the Fermi level ($\epsilon _F$), the absolute electron chemical potential ($\mu _e$) and the electrode potential energy (${\text{eU}}$) depending on different reference systems. In most regions of the Fermi level between the VBM and CBM of $\alpha {\text{-Al}}_{2} {\text{O}}_{3}$, the point defects with the lowest formation energies are those with the large absolute charge states, such as ${\text{Al}}_{i}^{{3 + }}$ at lower Fermi levels close to the VBM and ${\text{V}}_{{{\text{Al}}}}^{{3 - }}$ at higher Fermi levels close to the CBM. The stability of these point defects under electrochemical conditions are also investigated. The 2D phase diagram of defect stability in both Figs. 7 and 8 indicate that, under the variations of oxygen chemical potentials and electrode potentials, the most stable point defect in $\alpha {\text{-Al}}_{2} {\text{O}}_{3}$ in the water stability region is Al vacancy ${\text{V}}_{{{\text{Al}}}}^{{3 - }}$ (more accurately, ${\text{V}}_{{{\text{Al}}\_{\text{s}}}}^{{3 - }}$ in the split vacancy configuration), and its defect formation energy is always negative in this water stability region. This result suggests the crystalline $\alpha {\text{-Al}}_{2} {\text{O}}_{3}$ is thermodynamically unstable against the spontaneous formation of the point defects under those electrochemical conditions, so amorphous alumina structures are always generated at the Al$_2$O$_3$/H$_2$O interface. Similar conclusion of amorphous alumina structures can be obtained in the Al$_2$O$_3$/air interface.

All the above discussed DFT calculations and theoretical models provide critical insights into the stability of bulk oxides and surface passive oxides that form in atmospheric and aqueous conditions. Defect phase diagrams like Figs. 7 and 8 can be used to identify the predominant point defect species for given conditions ($\mu _{\text{O}}$, $\mu _e$ or equivalently ${\text{pH}}$, ${\text{U}}$) for other passive oxide layers that form on other metallic surfaces like Cr, Fe, Ni, Zn, Mg, Ti. This information, in conjunction with kinetic activation of relevant defect species, can prove to be useful to model diffusion of ionic species through the passive oxide layer, which are critical for the investigation of localized corrosion according to the Point Defect Model (PDM) [50, 51]. For example, localized passivation breakdown can be studied by modeling electric field dependent mass transport of ionic species in the passive layer, where the local concentrations of ionic species (point defects) under different electrochemical conditions can be calculated based on defect formation energy $E^f$ from the DFT calculations and theoretical models discussed in this study.