1 Introduction

The high thermal stability and safety as well as the high reversibility of olivine LiFePO4 have made it the most promising material for the positive electrode of Li-ion cells, especially for applications in electric vehicles. However, some improvements are still necessary to overcome some of its deficiencies, such as its poor electronic conductivity [1, 2] and low apparent lithium diffusivity [3, 4]. To explain the later one, it should be noted that Li ions can only move inside the structure of lithium iron phosphate (LFP) active material in the [0 1 0] direction (along the b-axis) [5,6,7]. Recently it has been discovered that the diffusion of Li in b-axis of LFP structure happens rapidly [8]. However, inter-unit Li transport limitation and low rate of phase-transformation initiation can be interpreted as the low apparent diffusion in solid phase.

The poor intrinsic ionic and electronic conductivity of this material have been improved by decreasing the size of the LFP powder to the nanoscale and by adding a carbon coating upon the surface of the particles, respectively [2, 4, 9].

Another specific behavior of the LFP active material is its electrochemical lithiation/delithiation reaction, which is occurring through a two-phase process [10]. It is generally accepted that during the intercalation/deintercalation of Li+, lithium iron phosphate undergoes a two-phase mechanism where the existence of both Li-poor LixFePO4 and Li-rich Li1−yFePO4 phases results in a stable voltage plateau at 3.5 V [11]. Nanoscale state of charge mapping has clarified this mechanism. Brunetti et al. [12] used an automatic precession electron diffraction (PED) phase identification tool to illustrate LiFePO4 and FePO4 phase maps at nanometer scale. They concluded that the particles are either fully lithiated or fully delithiated. They also suggest a size effect of the particles in such a way that larger particles are transformed by delithiation before the smaller ones. On the other hand, Chueh et al. [13] observed no correlation between the sequence of delithiation and the particle size when they studied the local state-of charge of individual LFP particles. Weker et al. [14] also reported no correlation between the agglomerate size and the (de) lithiation pathway. In their study, they tracked non-uniform mesoscale transport in LFP agglomerates during cycling and they attributed it to nanoscale pore structures within agglomerates as well as the solid-state lithium diffusion inside the LFP material.

There are different approaches to simulate the complex behavior of LFP including the core–shell [15,16,17,18,19], the phase field [20,21,22], the domino cascade [23], the spinodial decomposition [22, 24], the resistive-reactant (RR) [25,26,27], the variable solid-state diffusivity (VSSD) [28,29,30], the Mosaic models [31], many-particle model [32, 33], and mesoscopic model [34, 35]. There are also different explanations for disagreements among mentioned models [36]: the specific experimental conditions and the dependency of delithiation/lithiation kinetics and phase compositions on the particle size, the morphology and physical properties of the studied LiFePO4 material, to name a few.

Srinivasan and Newman [17] developed a core–shell model initially introduced by Padhi et al. [15]. Intercalation and phase change in LFP were both represented through a shrinking core model consisting of a Li-rich and a Li-poor phases. The diffusion of Li inside the growing shell of one phase (e.g. Li-rich phase of LiFePO4 during discharge) and the mass transfer across the phase boundary to the core of the other phase (e.g. Li-poor phase of FePO4 during discharge) were addressed in their model.

Although the treatment of the two-phase process considered in the core–shell, phase-field, domino cascade and spinodial decomposition models may be appropriate to simulate galvanostatic discharge of the Li-ion cell, it requires important computational resources when simulating cycling working conditions. On the other hand, less demanding models such as VSSD which somehow simulate the influence of the phase change without considering it explicitly [30], are among the best candidates for large-scale applications of secondary batteries such as battery management systems.

Thorat [28] made an effort to find an alternative and easier way to represent the influence of the aforementioned two-phase process. He introduced a model with a concentration-dependent solid-state diffusion coefficient for LFP. However, he had to use a Fickian diffusion approach with a constant solid-state diffusivity to obtain results that are more representative of the battery performance.

Later, in 2012, Farkhondeh and Delacourt [29] improved the approach of Thorat [28] to simulate different commercial LFP electrodes. They introduced a VSSD model while ignoring the porous-electrode effects. To make the model suitable for high C-rates, Farkhondeh et al. [30] merged the VSSD model with the pseudo-2-dimensional (P2D) model of Doyle et al. [37]. They also considered a particle size distribution (PSD) for the active material, taking into consideration four different particle sizes.

Among other approaches to study the nature of phase-change insertion materials, one can find the many-particles and mesoscopic models. These models were developed to support the idea that particles are either fully lithiated or fully delithiated. The “many-particle” model was introduced by Dreyer et al. [32, 33], which assumes that equilibrium potential of LFP material is a non-monotonic function of lithium concentration and lithiation/delithiation of particles occurs randomly. Their model predicted the quasi-static potential hysteresis between charge and discharge in slow galvanostatic operation.

To overcome this limitation of quasi-static operation of the LFP electrode and to introduce a mechanism for mass transfer/phase transition within individual particles, Farkhondeh et al. developed a mesoscopic model [35]. This model was introduced to simulate non-equilibrium lithiation/delithiation and fast solid-state diffusion inside mesoscopic LiFePO4 units. These units are assumed to be small enough so that no intra-unit phase-change happens inside them. Farkhondeh et al. considered homogeneous lithiation/delithiation inside each unit and no intra-unit mass transfer limitations. They also improved the predictability of their previous model [34] by applying the porous electrode theory and by changing the equation for the single-unit equilibrium potential. This potential is a non-monotonic function of composition regular solution model for a binary system containing occupied and vacant Li sites. In their analysis, they concluded that the electrode polarization during each pulse of GITT analysis comes from the Li transport between LiFePO4 units and that the diffusion within the units is not a limiting factor. Ignoring the intra-unit mass transport and assuming a resistance distribution, they captured the loss in potential at intermediate utilization and end-of-discharge capacity.

Nanoscale or mesoscale sophisticated models may be useful to study short time and length scale. However, they are not appropriate in the case of large scale and heavy simulations like the ones involved in the simulation of battery packs or used in battery management system (BMS).

The Mosaic model, proposed by Andersson et al. [31] and selected here to create a simple yet trustable model, is a low-cost approach that projects nanoscale/mesoscale mass transfer (or phase transition) within individual particles into a macroscale model. This model is based on the dependency of particle-radius with the current density. It has been developed to justify the end of discharge capacity of LFP active material and related transport limitations. It implies that the nucleation of reaction sites is favored at higher currents [38]. Therefore, it is allowed to assume that at higher currents, higher number of phase boundaries are created inside a single particle. The experimental analysis of Chueh et al. [13] confirmed this concept, where the rate limiting process was introduced as initiating the phase transformation (nucleating events). Mosaic model has been implemented by others [38,39,40,41,42] to improve the predictability vis-a-vis the capacity of LFP electrode material.

As mentioned earlier, another feature of the LFP electrode is its resistive-reactant behavior. By nature, LFP is an electrically insulating material [43]. Therefore, the use of conducting additives such as carbon is vital to decrease the ohmic drop and to improve the intrinsic electronic conductivity of LFP [44]. Quality and quantity of these conducting additives are at the origin of two different resistances: intraparticle and interparticle, respectively. The former represents the ohmic drop caused by the electrons travelling through non-carbon coated active-particle surface [25]. The later happens when the electrode is composed of poorly connected particles, which causes higher resistivity paths through the conductive matrix [27].

Thomas-Alyea [25] investigated the intraparticle resistivity of LFP by conducting experiments where two electrodes with a different amount of conductive carbon coating are compared. She concluded that the voltage drop in both charge and discharge profiles is due to intraparticle resistivity of LFP rather than the ionic conductivity of electrolyte and the electronic conductivity of the bulk positive electrode. Later, Safari and Delacourt [27] studied the interparticle resistance of LFP active material. They used a different number of current collectors at the anode side as a spacer to modulate the uniaxial pressure. In their experiments, they showed that the increase of the uniaxial pressure improves the connectivity between the active material particles and thus decreases the ohmic drop due to the interparticle resistivity.

In their RR model introduced to simulate LFP, Safari and Delacourt [27] assumed four spherical particle groups with the same particle size but with different electronic connectivities to the conductive matrix. It should be noted that both interparticle and intraparticle resistances of LFP active material cause ohmic drop and consequently make a non-uniform current distribution. RR model has also been applied by others [29, 30] to consider the resistive-reactant feature of LFP.

Although VSSD and RR models seem good approaches to simulate the slow solid-state Li ion transport and the poor electronic conductivity of LFP, they are still not well-suited to investigate the cycling conditions and performing time-consuming studies such as aging and battery pack level simulation. Aiming at introducing a simple model to take into account the resistive reactant feature of LFP, Marcicki [45] combined his simplified Li-ion battery model with a resistance that varies linearly with the depth of discharge (DOD). He used the middle portion of the discharge curve to find a semi-empirical equation for resistive reactant effects. His modeling results show a good agreement when compared to experimental data obtained from a cylindrical graphite/iron phosphate cell for a range of galvanostatic discharge experiments from C/3 to 4.8 C. However, there is also a need to study the resistive reactant effect of LFP in the whole portion of discharge/charge curves of a Li/LFP cell.

In this work, we introduce an improved varying resistance SPM and we apply it to study a Li/LFP cell. When compared to the above mentioned-sophisticated models such as resistive-reactant model, the introduced model is more suitable to rapid and intensive calculations. Thanks to its robust structure and the simplicity of the involved equations, it makes a good candidate for time-consuming studies such as parameter estimation, life prediction and uses in battery management system (BMS). As it is shown in the results, the model is adapted to high current densities. The independent behavior of LFP active material was studied with the assessment of a Li/LFP cell.

We examine the validity of the model for two different Li/LFP cells, a high-capacity and a high-power cells.

In the following sections, the experimental setup is presented. In Sect. 3, the model development and its constitutive equations are explained. Finally, the results are discussed in Sect. 4.

2 Experimental

Experimental studies were performed on a Li (Li/LiFePO4) CR2032 coin cell made of commercially available positive and negative electrode materials. These coin cells were built by assembling the following components (see Fig. 1a): a positive electrode, a negative electrode, a polypropylene separator membrane (Celgard 2400) between both electrode, stainless steel spacers and a spring. Two different kinds of cells were built: a high energy and a high power Li cells. The positive electrode is thicker (100 µm) in the high-energy Li cell than in the high-power Li cell (34 µm).

Fig. 1
figure 1

Schematic of the cell and SEM images of the cross section of the positive electrode and current collector cross section

Full size image

The positive electrode was prepared using 85% LiFePO4/C, 7.5% carbon black (CB) and 7.5% polyvinylidene difluoride (PVDF). The PVDF binder was first dissolved in N-methyl-2-pyrrolidone. The mixture of LiFePO4/C and carbon black was then added to the binder solution after being ball milled for 10 min. The slurry obtained was mixed using a magnetic stirrer for 1 h in order to homogenize the mixture.

The current collector treatment consisted to sandblast the coating side of the aluminum foil (25 µm thick). Prior to the casting, the desired thickness of the Doctor Blade method on the aluminum foil was obtained using several thicknesses of electrical and aluminum tape. The electrical tape layers were first applied to the current collector followed by just one layer of aluminum. The aluminum tape layer was useful to avoid the electrical tape to be attacked by the N-methyl-2-pyrrolidone solvent.

The positive electrode was then cast, applying the slurry on one side of a sandblasted aluminum foil (25 µm thick). The treated electrode dried in an oven at 90 °C under vacuum (25 In Hg) for 6 h. After drying, the positive electrode was calendared in order to reduce the porosity of the coating and finally punched into 2 cm2 disks.

The metallic lithium negative electrode was bought as 2 cm2 disks and prepared simply by slightly scratching the surface that is facing the positive electrode. This treatment ease the access to the bulk of the lithium, more reactive and cleaned. The active material (LiFePO4/C) and the metallic lithium were provided from MTI corporation.

The electrolyte was prepared inside an argon-filled glove box (1 ppm H2O) and consists of 1 M LiPF6 salt in ethylene carbonate (EC), dimethyl carbonate (DMC) and ethyl methyl carbonate (EMC), in a volume fraction of 1/1/1. All battery grade carbonates and Li salt have been bought from Sigma Aldrich.

The particle size distribution (PSD) was determined using a Laser Mastersizer 2000 granulometer from Malvern company. The sample preparation consisted to disperse the powder and analyze it in a liquid medium (water) using ultrasound prior to the analysis. The particle size distribution was inferred from the interaction between a set of particles and an incident radiation. When the laser beam encounters the particles, the light can be absorbed, scattered or transmitted. The result of this interaction generates a diffraction pattern. The diffraction angle is larger as the particles are smaller. The position of the particles and their movement have no effect on the diffraction pattern. The particles are not analyzed individually, but as a whole. It is therefore necessary to use image processing algorithms to convert the signal into particle size information, distribution in size or volume and the number of particles corresponding to each size. The particle size distribution measured by such a method revealed a mean value of 0.35 µm for the particle radius. This value is considered as the radius of particles in 1C discharge rate.

The specific area of the samples was studied using the Brunauer–Emmett–Teller method (BET). In this regard, the specific surface area was determined using a Micrometrics ASAP 2020 instrument. The sample (LiFePO4 powder) preparation consisted of a first rough-drying process in an oven at 100 °C to evaporate water molecules. The dried sample was then placed under vacuum at 100–105 °C for 12 h to evaporate the remaining water prior the analysis, which was performed under nitrogen gas at the temperature of liquid nitrogen. Molecules from the nitrogen gas flow at a given pressure (P) adsorb to the surface of the sample until saturation (P0) is reached. This gas absorption causes a pressure drop measured by a sensor. A signal later converted to the volume of adsorbed gas.

Charge/discharge curves were measured using a MTI cycler BST8-MA, used to analyze the rate performance of the materials at different C-rate considering a cut-off voltage of 2.8–3.6 V. The charge procedure consists of a constant current charge (CCC) up to 3.6 V, followed by a constant voltage charge (CVC) until the current reaches to C/50. On the other side, the discharge procedure consists of a simple constant current discharge (CCD), down to a cut-off voltage of 2.8 V. Once assembled, the cells were exposed to SEI formation which consists of five cycles at low C-rate (C/12) in order to form a stable solid electrolyte interface.

3 Model development

Pseudo-two-dimensional (P2D) model [37, 46,47,48] is well -suited for most simulations of Li-ion batteries because such a model is considering the mass transport and the charge transfer in both solid and electrolyte phases. However, the single particle model (SPM) [49,50,51], used as a simplified version of P2D, is a better candidate for simulating cycling conditions or other time-consuming studies. The current distribution along the thickness of the porous electrode remains uniform in SPM, which is the case of Li-ion batteries with thin and highly conductive electrodes subjected to low current densities [51].

When it comes to fit the end-of-discharge capacity for LFP, SPM and P2D models give poor predictions, both assuming a constant diffusion coefficient in the solid active material (Ds,p) or a constant radius of the active material (Rp). In other words, constant value of Ds,p (or Rp) may result in a good fitting for a specific current density. However, it leads to either under-prediction or over-prediction of utilization when higher or lower current densities are simulated [17]. This is a case where a rate-dependent diffusion coefficient [52, 53] or a rate-dependent radius of particle [38,39,40,41,42] can be implemented to obtain a representative end-of-discharge capacity. The Mosaic model is based on a rate-dependent radius of particle. The radius considered is typically increased when the discharge current goes from a higher to a lower value [39].

Figure 2 schematically compares the results of P2D and SPM with the experimental data for the discharge of the LFP cell (Li/LFP). Potential is depicted as a function of depth of discharge (DOD) in an arbitrary discharge rate higher than 1C. Here, the assumption is that both models are combined with a Mosaic model.

Fig. 2
figure 2

Schematic of the simulated and experimental discharge curves of Li/LFP cell with a thin positive electrode, and b thick positive electrode. OCP is depicted in its plateau condition

Full size image

Figure 2 reveals three important features: (1) the slope in the plateau region, (2) the end-of-discharge capacity, and (3) the increasing polarization as the discharge proceeds, especially at the end of the discharge process. In the case of the thin electrode, both SPM and P2D predict the performance reasonably well, mainly because of the uniform current distribution. However, in the case of the thick electrode, where a non-uniform current distribution exists, only P2D model can represent the slope of the discharge curve and the voltage drop due to the low conductivity of the matrix. For both models, the use of the Mosaic model helps to predict the end-of-discharge capacity. However, both models are unable to follow the increasing polarization at the end of the discharge. This is the place where other models such as the shrinking core, the VSSD or the RR models can be implemented to simulate this specific behavior of the LFP electrode active material. Srinivasan and Newman [17] divided the resistance into two components: (1) contact, matrix and kinetic resistance (R1 in Fig. 2), (2) the diffusion resistance (R2 in Fig. 2). They illustrated promising results in the simulation of LFP positive electrode. Safari and Delacourt [27] and later Farkhondeh and Delacourt [29] attributed the resistance (R1 + R2 in Fig. 2) to the resistive reactant feature of LFP and to the variable solid diffusivity of this active material.

As described later, a model implementing a variable resistance function can produce good results without the necessity of using sophisticated and time-consuming models.

The cell resistance evolution during the charge/discharge process can be interpreted by comparing the flat OCP of LFP in intermediate SOC with the sloped voltage versus capacity curves at higher charge/discharge rates [27]. This resistance sums up the influences the resistive-reactant feature of LFP, including both interparticle and intraparticle resistances.

As the charge/discharge proceeds, electrons and ions have to go through a larger distance inside the low conductive matrix phase [17]. Therefore, the increasing the resistance observed during the end of discharge results from lithiating poorly coated particles (intraparticle resistance) and poorly connected particles to the matrix (interparticle resistance). This behavior represents the resistive-reactant feature of LFP.

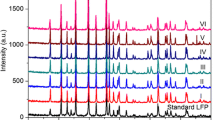
Another explanation for a varying resistance can be interpreted from Fig. 3a where a discharge process is depicted schematically. Here, the potential curve as a function of DOD is compared with the OCP and the corresponding end of discharge capacity is marked on the OCP curve. As it is clear, the end of discharge happens when OCP is still in the plateau region. This conclusion comes from a X-ray diffraction (XRD) analysis of a two identical cells one discharged with C/24 rate and the other with 1C rate up to cut off potential of 2.8 V (Fig. 3b). The XRD pattern demonstrates that two different phases exit in the disassembled LFP electrode when discharged at 1C. In other words, the end of discharge happens before LFP active material reaches the one phase condition. Therefore, the increased overpotential at the end of discharge must come from another resistance, a phenomenon different from the high overpotential found at one phase region of OCP. We thus propose an increasing resistance in order to introduce a simple and applicable model to represent the behavior of the LFP active material at the end of the discharge.

Fig. 3
figure 3

a Schematic of an experimental discharge potential and corresponding OCP, and b XRD analysis of disassembled LFP electrode after discharge process

Full size image

Such a varying resistance can be easily implemented into a SPM to build a rapid and robust model, aimed at performing heavy simulations, for instance to study BMS or aging, applicable to large ranges of C-rate. It should be noted that there is no need for an electrolyte potential drop function [41, 42] because such resistive losses will also be included in the empirical varying resistance.

In SPM, it possible to represent the entire porous electrode (positive/negative) by a single intercalation particle [51] implicitly assuming a uniform current distribution along the thickness of the porous electrode. Fick’s second law in spherical coordinate system represents the mass balance of lithium ions in electrode active material [51]:

$$\,\frac{{\partial {c_{s,j}}}}{{\partial t}}=\frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{D_{s,j}}{r^2}\frac{{\partial {c_{s,j}}}}{{\partial r}}} \right)$$
(1)

with initial conditions as

$$\,{c_{s,j}}\left( {t=0,r} \right)=c_{{s,j}}^{0}$$
(2)

The boundary conditions are zero flux of lithium ions at the center of the spherical particle and \({J_j}\), the molar flux of lithium ions at the surface of particle. These conditions can be expressed respectively as

$$\,{\left. {{D_{s,j}}\frac{{\partial {c_s}}}{{\partial r}}} \right|_{r=0}}=0$$
(3)
$${\left. { - {D_{s,j}}\frac{{\partial {c_s}}}{{\partial r}}} \right|_{r={R_j}}}={J_j}$$
(4)

where j = p, n stands for the positive and negative electrodes respectively, \({D}_{s}\) is the solid phase lithium ion diffusion coefficient, and \({R}_{j}\) is the solid particle radius.

The molar flux of lithium ions in SPM is related to the total currentIpassing through the cell as

$$\,{J_j}=\frac{I}{{F{S_j}}}$$
(5)

where \(F\) is Faraday’s constant and \({S}_{j}\) is the total electroactive surface area of electrode\(j\)

$$\,{S_j}=\frac{{3{\varepsilon _j}{V_j}}}{{{R_j}}}$$
(6)

where \({\epsilon }_{j}\) is the volume fraction of solid phase active material in electrode \(j\) and \({V}_{j}\) is the total volume of that electrode. In the case of Li/LFP cell, the electroactive surface area of the negative electrode, \({S}_{n}\), is equal to the geometrical surface of Li foil,\({A}_{n}\).

The state of charge (SOC) for the positive electrode is defined as

$$SO{C_p}=\frac{{{c_{s,p}}}}{{{c_{{s,p}}^{{\max }}}}}$$
(7)

Guo et al. [51] illustrated that Eq. 1 can be solved with the Eigenfunction Expansion Method (EEM). They indicated that mass balance on lithium ions in an intercalation particle of electrode active material yields the SOC at the surface of particle as [51]:

$$\,SO{C_p}=SO{C_{p,ini}}+{\delta _p}\left[ {3\frac{{{D_{s,p}}}}{{R_{p}^{2}}}t+\frac{1}{5} - \frac{2}{{\lambda _{k}^{2}}}\sum\limits_{{k=1}}^{\infty } {\exp \left( { - \frac{{\lambda _{k}^{2}{D_{s,p}}}}{{R_{p}^{2}}}t} \right)} } \right]$$
(8)

where \({\delta _p}\) is the dimensionless flux of lithium ions at positive electrode:

$$\,{\delta _p}= - \frac{{I\,{R_p}}}{{{S_p}\,F\,{D_{s,p}}\,c_{{s,p}}^{{\max }}}}$$
(9)

and \({\lambda _k}\) is the kth eigenvalue calculated from:

$$\sin {\lambda _k} - {\lambda _k}\cos {\lambda _k}=0$$
(10)

Five lambda are included in this study. Once the SOC in positive electrode is known, the potential of the cell can be found as following [51]:

$${m_p}=\frac{I}{{F{K_p}{S_p}c_{{s,p}}^{{\max }}c_{e}^{{0.5}}{{\left( {1 - SO{C_p}} \right)}^{0.5}}{{\left( {SO{C_p}} \right)}^{0.5}}}}$$
(11)
$${m_n}=\frac{I}{{F{K_n}{S_n}c_{e}^{{0.5}}}}$$
(12)
$${V_{cell}} \approx {U_p}+\frac{{2RT}}{F}\ln \left( {\frac{{\sqrt {m_{p}^{2}+4} +{m_p}}}{2}} \right)+\frac{{2RT}}{F}\ln \left( {\frac{{\sqrt {m_{n}^{2}+4} +{m_n}}}{2}} \right)+I \times {R_{cell}}$$
(13)

In the potential equation (Eq. 13), Rcell is the variable resistance function. Unlike other studies that consider a lumped resistance or a concentration dependent resistance, here a SOC dependent resistance is introduced to calibrate the SPM. More precisely, an exponential resistivity is introduced to account for increasing ohmic losses as the discharge proceeds. The exponential form is there to represent the difference between the potential profile and the OCP curve (Fig. 3a):

$$\,{R_{cell}}={a_1}\exp \,({a_2} \times SO{C_p})+{a_3}$$
(14)

The physical/electrochemical parameters and the unknown variable resistance (Eq. 14) are estimated by virtue of parameter estimation (PE) process [41, 42], which leads to the identification of the following parameters: solid diffusion coefficient (Ds,p), intercalation/deintercalation reaction-rate constant (Kp), volume fraction of active material (εp), unknown coefficients in the cell resistance equation (\({a}_{1}\), \({a}_{2}\), \({a}_{3}\)) and the radius of the particles at each discharge current except 1C. The radius of the particles for the 1C charge/discharge process is assumed to be 0.35 µm, based on the measured particle size distribution. A Genetic Algorithm (GA) is used to minimize the objective function, which is defined as difference between the experimental data for the time-varying cell potential the numerical predictions [41, 42]. The governing equations are numerically solved by using MATLAB.

4 Results and discussion

Two different types of coin cells were custom-built in laboratory to examine the validity of the proposed model for both high-power and high-energy configurations. The thicknesses of the positive electrodes were measured from SEM: the high-power thinner electrode is 34 µm thick while the high-capacity electrode is 100 µm thick. For a discharge rate of 1C, the assumed mean radius of particles is 0.35 µm. This value is measured with a laser diffraction-sizing instrument. However, for other discharge rates, the particle size has been estimated, as it is proposed in the Mosaic model.

The open circuit potential (OCP) for each type of cells was determined from a discharge experiment at low C-rate (C/24). The rate constant (Kn) was assumed from an exchange current density of \({i_n}=F\,{K_n}\,c_{e}^{{0.5}}=1.90\,{\text{mA/c}}{{\text{m}}^{\text{2}}}\), as reported in the literature [26] for a similar technology. Table 1 provides the values of parameters used for LFP and Li.

Table 1 Measured and assumed parameters for the Li/LiFePO4 cell
Full size table

The other parameters are estimated by virtue of the PE process. Table 2 presents the values of the estimated parameters and the ranges used for each of them during the iterative identification process.

Table 2 Estimated parameters for the high-power Li/LFP cell
Full size table

Figures 4 and 5 illustrate good agreements between simulated and experimental potential versus capacity curves obtained in discharge and charge processes, respectively. Even in moderate C-rate, SPM coupled with the use of an exponential resistance function shows promising results.

Fig. 4
figure 4

Simulated (solid lines) and experimental (symbols) discharge curves for high-power cell

Full size image
Fig. 5
figure 5

Simulated (solid lines) and experimental (symbols) charge curves for high-power cell

Full size image

Simulated potential and resistance overpotential curves depicted in Fig. 6 for discharge of high-power cell at 2C rate are used to compare the value derived from resistance equation.

Fig. 6
figure 6

Simulated (solid lines) potential and corresponding resistance overpotential for discharge of high-power cell at 2C rate

Full size image

In parameter estimation studies, it is important to check the risk of over-fitting, which happens when the number of parameters is large. In such a case, the risks are that the inverse method finds parameters that are more representative of the system noise than representing the general trend. One way to examine the over-fitting is to test the model with a new condition differing from those that are used for PE. In this regard, the model is verified by simulating the potential for a discharge rate of 4C (also depicted in Fig. 4). In this case, the estimated parameters are based on lower discharge rates. Obviously, the predictability of the model is still good outside of the conditions used for PE.

The estimated particle radius for both charge and discharge process is depicted in Fig. 7. It is seen that the higher the discharge current is, the smaller gets the apparent particle radius, which is in agreement with the Mosaic model.

Fig. 7
figure 7

Apparent particle radius in each charge/discharge current from the PE and the SPM

Full size image

A changing load test was performed to verify the efficiency of the model. A fully charged cell is discharged at 3C for 8 min, followed by a charge and discharge process each at 2C for 8 min. Finally, a 15 min of charge followed by a 15 min of discharge are applied with 1C rate. Figure 8 shows the good match found between the experimental data and the simulated results.

Fig. 8
figure 8

Simulated (solid lines) and experimental (symbols) potential of high-power Li/LFP cell exposed to a variable load

Full size image

It is generally easier to model cells designed for high-power applications because the electrodes are thinner and the overpotentials are smaller. However, it is necessary to check the accuracy of the model for cells with different applications. Therefore, its validity is examined for thicker positive electrode. Figure 9 illustrates the comparison between the model estimations and experimental measurements for high-energy Li/LFP cell.

Fig. 9
figure 9

Simulated (solid line) and experimental (symbols) discharge curves for high-energy cell

Full size image

Once again, a good agreement is achieved between the simulation results and the experimental measurements, this time with the use of a thicker positive electrode, a design devoted to high-energy applications. The estimated parameters for such a configuration, which are the volume fraction of active material (εp), the unknown coefficients in the cell resistance equation (\({a_1}\), \({a_2}\) and \({a_3}\) in Eq. 14) and the radius of particles in each discharge current (except 1C), are provided in Table 3. The solid diffusion coefficient (Ds,p), and the intercalation/deintercalation reaction-rate constant (Kp) are chosen to be the same as in case of the high-power cell design.

Table 3 Estimated parameters for the high-energy Li/LFP cell
Full size table

Using Eq. 15, the specific error values for each discharge curve are calculated for both high-energy and high-power Li cells and are presented in Table 4.

Table 4 Specific error values of all discharge curves for each cathode material
Full size table
$$\,{e_s}=\left( {\frac{1}{N}} \right){\sum\limits_{{i=1}}^{N} {\left( {V_{{cell,m,i}}^{*} - {V_{cell,i}}\left( {\mathbf{P}} \right)} \right)} ^2}$$
(15)

Although the errors are very low and acceptable, it seems that no correlation exists between the errors and the discharge rates. In other words, the errors do not increase when higher discharge rates are simulated. An interpretation can be that for higher discharge rates, the resistance behaviour of cell gets closer to the exponential form suggested in equation Eq. 14, which would compensate the higher error of SPM simulation at high discharge rates.

5 Conclusion

An empirical variable resistance has been added inside a SPM to represent the increasing overpotential specifically found at the end of the charge/discharge process of a Li/LFP cell. This improved the predictability of the SPM model by taking into account the increasing ohmic resistance from the resistive-reactant feature of LFP. The electrolyte overpotential can also be a part of this increasing resistance, which makes the model well-suited for charge/discharge rates higher than 1C. A well-suited PE method provided the necessary electrochemical parameters of the cell and the constant coefficients of the empirical resistance function. A current-dependent radius (Mosaic model) was considered for the particles to handle the phase transformation in LFP active material identified as the rate limiting process. Model-experiment comparisons indicated promising results for two designs of Li/LFP coin cells, a high-power and a high-capacity configuration.