Application of enhanced cluster validity index function to automatic stock portfolio selection system

Abstract

This paper presents an automatic stock portfolio selection system. In the proposed approach, 53 financial indices are collected for each stock item and are consolidated into six financial ratios [Grey relational grades (GRGs)] using a Grey relational analysis model. The GRGs are processed using a modified form of the PBMF index method (designated as the Huang index function) to determine the optimal number of clusters per GRG. The resulting cluster indices are then processed using rough set theory to identify the stocks within the lower approximate sets. Finally, the GRGs of each stock item in the lower approximate sets are consolidated into a single GRG, indicating the ability of the stock item to maximize the rate of return. It is demonstrated that the proposed stock selection mechanism yields a higher rate of return than several existing portfolio selection systems.

1 Introduction

Predicting the future behavior of the stock market is of great interest to investors, speculators, and industries alike. However, it is extremely difficult to predict future stock prices and construct profitable stock portfolios in today’s volatile markets. Many researchers have attempted to predict stock price movements on a daily, weekly or monthly basis using artificial intelligence (AI) techniques [1–3] or statistical methods [4, 5]. When the problem of stock market prediction is considered, the following three fundamental factors inevitably arise:

• (1) The trading cost increases as the frequency at which the stocks are traded increases. This has a significant impact on the stock prediction problem on a daily basis.

• (2) When the future behavior of the stock market is forecasted, large volumes of external information are required, e.g., probability data (for statistical techniques); membership grade information (for fuzzy set theory techniques [6–8]); available training data (for artificial neural networks (ANNs) [9]), and so on.

• (3) When regression models are adopted to predict stock market trends, the results are not only determined by the financial indices of the stocks involved, but also by external factors such as the financial environment, political changes, changes in company strategy, fluctuations in the demand/supply relationship, and so on. Consequently, the predicted results cannot be guaranteed to be reliable.

In this study, it is argued that the effects of political, economic and other changes are only temporary. Thus, the goal of the study is to analyze the underlying value of each company’s stock from an investor’s perspective, irrespective of the short term impact of external effects. In practice, if the stock value can be predicted rationally and consistently for each company, it is expected that an evaluation process can be constructed as a basis for selecting stocks for investment purposes. In real-world stock market systems, the information associated with each data object may be imprecise and uncertain. Therefore, the task of identifying the relationships between the independent and dependent variables is highly challenging. In this study, the inherent ambiguity of the stock market data is dealt with by applying rough set (RS) theory to process the clustered data in order to identify suitable stocks for investment purposes. However, as described above, to simplify the clustering and stock filtering processes by applying GRA (Grey relational analysis) to datasets, it is first necessary to pre-process the data to identify and consolidate independent variables among the collected information.

Accordingly, the stock selection mechanism proposed in this study comprises two major components, namely (a) data processing and (b) data mining. In the data processing component, a GRA model is used to consolidate the 53 financial indices associated with each stock item into just 6 predetermined financial ratios known as Grey relational grades (GRGs). In the data mining component, the number of clusters per attribute is optimized using a modified form of the PBMF index function, and then RS theory is applied to identify the stocks within the lower approximate sets. These stocks are then processed by a GRA reduction model to establish a single financial indicator for each stock item on which to base the stock selection decision.

Real-world datasets invariably comprise a large number of objects and attributes. Thus, when applying RS theory to classify such datasets, it is desirable to pre-process the dataset to eliminate any conditional attributes which have little or no effect on the classification decision. This simplifies the decision table, and the decision rules can be more easily identified. Among all the available dimension reduction methods (e.g., principle component analysis, independent component analysis and GRA), GRA is particularly attractive since it effectively consolidates attributes.

Grey system theory, proposed by Deng [10] in 1982, is a powerful technique for dealing with systems characterized by poor, incomplete and uncertain information. One of the most fundamental components of Grey system theory is that of GRA [11], in which information from the Grey system is used to quantify the respective effects of the various factors within the system in terms of Grey relational grades (GRGs). In other words, GRA provides the means to weigh the various factors within an uncertain system in accordance with their effects on the system outcome, and therefore, it provides an ideal basis for classification systems. GRA requires a smaller volume of data and can process a large number of factors simultaneously, even when the relationship among these factors is uncertain or complex. As a result, GRA provides an ideal tool to analyze the complex inter-relationships amongst the individual parameters in systems with multiple performance characteristics [12–15], and has therefore been widely applied in a variety of optimization, decision-making and classification problems in the fields of finance, business, economics, design, manufacturing and production [13–22]. In the stock selection mechanism proposed in this study, GRA is initially used to reduce the 53 financial performance indices of each stock item (collected factors) to just 6 core attributes (system parameters) in order to simplify the clustering process whilst retaining the underlying interrelationship between the conditional and decision attributes of the stock system. The GRA model is then reapplied at a later stage of the stock selection process to consolidate the 6 core attributes of each candidate stock item to a single performance indicator, which is then applied to select the stocks for inclusion in the stock portfolio. The data objects in the stock system are then clustered using a fuzzy clustering scheme, and the resulting cluster indices are analyzed using RS theory [16, 23] to identify the stocks within the lower approximate sets. In general, when applying RS theory to categorize real numbers into different classes, it is necessary to eliminate any redundant factors (attributes) and to determine an appropriate number of clusters for each attribute. As described above, the problem of removing the redundant factors is resolved in the proposed stock selection mechanism by using a GRA reduction model.

When any typical clustering problem is considered, two fundamental questions invariably arise: (1) “how many clusters are actually present within the dataset?” and (2) “to what extent do the clustering results reflect the true partitions within the dataset and enable the extraction of reliable decision-making rules? [24]” Traditionally, the problem of evaluating the optimality of the clustering results obtained for a particular dataset is referred to as the cluster validity problem [25]. Many methods have been proposed to assess the performance of fuzzy clustering schemes [26]. Among these methods, early indices, such as the partition coefficient [27, 28] and the classification entropy index [25, 29], are based simply on the membership values of the items within the dataset, and are therefore easily computed. However, recent studies have shown that the performance of clustering schemes can be improved by considering not only the values of the data objects within the dataset, but also the matrix U used to partition the data [16, 30–36]. Existing clustering methods typically cluster the dataset in accordance with the norms of the instances rather than the values of the individual attributes of the instances. However, in most real-world datasets, the instances within the dataset may have multiple attributes, whereby each attribute represents an independent parameter of the corresponding instance. Consequently, the clustering results obtained using traditional methods fail to take sufficient account of the complex interrelationships among the various attributes of the dataset. Therefore, when devising a method to optimize both the clustering results and the classification accuracy, it is necessary to apply some form of classification-defined knowledge to the attribute values of the instances so that the complex interrelationships between the various attributes can be properly taken into account. In the stock selection mechanism proposed in this study, this is achieved using a new index function designated as the Huang cluster validity index function.

The remainder of this paper is organized as follows. Section 2 presents the fundamental principles of GRA theory, the FCM method, RS theory and the conventional PBMF index method. Section 3 describes the integration of these concepts to create the proposed Huang index function. Section 4 compares the performance of the Huang index function with that of the PBMF (FCM-based) clustering function when applied to a hypothetical dataset and a real-world stock market system. Section 5 describes the proposed stock portfolio selection system and evaluates its performance. Finally, Sect. 6 provides some brief concluding remarks.

2 Review of related methodologies

2.1 Grey relational analysis

Basically, a Grey relational analysis (GRA) function is an arithmetic mean, geometric mean or p-norm function applied to specified groupings of conditional attributes. GRA functions provide effective means of resolving multiple-criteria decision-making problems by ranking the potential solutions in terms of their so-called Grey relational grades (GRGs) so that the optimal solution can be easily determined [37]. In the stock portfolio selection system proposed in this study, the GRA method is used to simplify the stock classification and selection processes by consolidating the values of the multiple attributes of each data object into a limited number of attribute values, each representing one particular sub-system of the total stock system.

2.2 Fuzzy C-means (FCM) clustering [38, 39]

The fuzzy C-means (FCM) clustering method, developed by Dunn in 1973 [40] and later refined by Bezdek [27], has many applications, ranging from feature analysis to clustering and classifier design. The FCM clustering method consists of two basic procedures, namely (1) calculating the cluster centroids within the dataset, and (2) determining the cluster memberships of each data object. This two-step procedure is repeated iteratively until the centroids of all the clusters within the dataset converge.

2.3 Index function $I_{\max }$

It is assumed that each object x _i in the dataset has just one conditional attribute, and that this attribute can be partitioned into p groups (i.e., p clusters). As a result, each data object has a total of p membership functions $\mu_{j} (x_{i} )\quad j = 1,2, \ldots p$. In the Huang index function, the data objects are mapped to the p clusters in accordance with the following index function:

$$ I_{\max } (\mu_{j} (x_{i} )) = {\text{Index}}(\max (\mu_{j} (x_{i} ))) = C(x_{i} ) = c,\quad 1 \le c \le p. $$

For example, it is supposed that the conditional attribute is partitioned into 3 clusters and the membership functions of the first object $x_{ 1}$ in each of these 3 clusters are given by $\mu_{ 1} (x_{ 1} ) = 0.35$, $\mu_{ 2} (x_{ 1} ) = 0.63$, and $\mu_{ 3} (x_{ 1} ) = 0.02$, respectively. In this particular example, the index function returns a value of $C(x_{1} ) = I_{\max } (\mu_{j} (x_{1} )) = 2$, and thus, the conditional attribute of the first object is mapped to the second cluster. This approach is easily extended to the case of data objects with multiple attributes. For example, if every object has $m$ conditional attributes and the $l$-th attribute $a_{l}$ can be partitioned into $p_{l}$ clusters, then $C_{{a_{l} }} (x_{i} )$ gives the index of the cluster to which the $l$-th attribute $a_{l}$ of object $x_{i}$ belongs. Here $C_{{a_{l} }} (x_{i} )$ is given by

$$ C_{{a_{l} }} (x_{i} ) = I_{\max } (\mu_{j} (x_{i} (a_{l} ))) = {\text{Index}}(\max (\mu_{j} (x_{i} )))\quad {\text{for}}\quad 1 \le l \le m,1 \le i \le n, $$

where $I_{\max } (\mu_{j} (x_{i} (a_{l} )))$ returns the index of the cluster corresponding to the maximum value among all the membership functions of the $l$-th attribute of $x_{i}$.

2.4 Rough set theory

Rough set (RS) theory was introduced by Pawlak [35] as a means of handling the vagueness and uncertainty inherent in the real-world decision-making process. RS theory is based on the assumption that every object in the universe of discourse is associated with a particular set of information (i.e., attributes). Objects characterized by the same information are regarded as being indiscernible. The indiscernibility relationship among all the objects in the universe of discourse provides the basic mathematical basis for RS theory.

2.4.1 Approximate sets

In RS theory, this indiscernibility of the data objects is handled using approximate sets. It is assumed that the information system $S = (U,A,V_{q} ,f_{q} )$ is represented in the form of a decision table in which $X \subseteq U$ and $R \subseteq A$. The upper and lower approximate sets of $X$ are denoted as $\bar{R} (X)$ and $\underline{R} (X)$, respectively, and are defined as

$$ \begin{gathered} \overline{R} (X) = \{ x \in U|[x]_{p} \cap X \ne \phi \} , \hfill \\ \underline{R} (X) = \{ x \in U|[x]_{p} \subseteq X\} , \hfill \\ \end{gathered} $$

where $[x]_{p}$ denotes the equivalence class determined by $x$ with respect to $P$, i.e., $[x]_{p} = \{ y \in U:(x,y) \in I_{P} \}$. The lower approximate set $\underline{R} (X)$ contains all of the elements ($x$) which have the same rank when evaluated in terms of the $X$-th decision attribute, while the upper approximate set $\overline{R} (X)$ contains the set of all elements ($x$) which may have the same rank when processed in accordance with the $X$-th decision attribute.

Having determined the upper and lower approximate sets, the accuracy of the classification results can be evaluated in accordance with:

$$ \alpha_{c} = {{\left| {\underline{R} (X)} \right|} \mathord{\left/ {\vphantom {{\left| {\underline{R} (X)} \right|} {\left| {\overline{R}(X)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\overline{R}(X)} \right|}}, $$

where $X = \{ x:C_{d} (x) = c,\forall x \in U\}$, and $|\underline{R} (X) |$ and $\left| {\overline{R}(X)} \right|$ are the cardinalities of the lower and upper approximate sets, respectively, when the elements ($x$) are ranked in terms of the $c$-th cluster of the decision attribute $d$.

2.5 PBMF cluster validity index function

The PBMF cluster validity index function [24] ensures the formation of a small number of compact clusters within the dataset and maximizes the separation distance between at least two of these clusters. The PBMF index function is formulated as ${\text{PBMF}}(K) = \left( {\frac{1}{K} \times \frac{{\overline{{E_{1} }} }}{{J_{{m^{\prime } }} }} \times D_{K} } \right)$, where $K$ is the number of clusters, $J_{{m^{\prime}}} = \sum\nolimits_{k = 1}^{K} {\sum\nolimits_{j = 1}^{n} {\mu_{kj}^{{m^{\prime}}} \left\| {x_{j} - z_{k} } \right\|} }$, $\overline{{E_{1} }}$ is constant for a given dataset and is set in such a way as to prevent the second term from vanishing, and $D_{K} = \mathop {\max }\limits_{i,j = 1}^{K} \left\| {z_{i} - z_{j} } \right\|$. In addition, $n$ is the total number of objects in the dataset, $U(X) = [\mu_{kj} ]_{K \times n}$ is a partition matrix, $m^{\prime }$ is the fuzzification parameter and $z_{k}$ is the centroids of the $k$-th cluster. When the PBMF index function is applied to data clustering applications, the objective is to find the value of $K$which maximizes the index value.

3 Huang index function

The performance of RS theory in categorizing real numbers into different classes is critically dependent on the number of clusters used in the clustering process. In other words, an inappropriate choice as to the number of clusters may lead to a significant degradation in the classification performance. Accordingly, in the Huang index function proposed in this study, the FCM clustering scheme, RS theory, and a modified form of the PBMF index function are integrated to optimize both the number of clusters within the dataset and the corresponding classification accuracy. Assuming that $U$ is the domain of discourse and $R$ is the set of equivalences of $U$, the RS classification problem can be formulated as follows:

$$ X \subseteq U\quad {\text{is:}}\quad (\underline{R}_{P} (X),\overline{R}_{P} (X)),BND_{P} (X), $$

where $X$ is the set of elements; $U/I_{P}$ is the quotient set of $U$; $I_{P}$ is the indiscernibility of $R$; $\phi$ is the zero set; $R$ is the attribute set of $X$ and comprises the conditional attribute set ($C$) and the decision attribute set ($D$), $P \subseteq C$; $\underline{R}_{P} (X)$ is the lower approximate set of $X$; $\overline{R}_{P} (X)$ is the upper approximate set of $X$; and $BND_{P} (X)$ is the boundary set of $X$. It should be noted that every element in the domain of discourse $U$ ($X \subseteq U$) has an attribute set ($R$) which describes the particular value of $X$.

As discussed in Sect. 2.3, the Huang index function is applied to cluster the attribute values of the data objects within the dataset, rather than the norms. Thus, in contrast to the conventional PBMF index function, the proposed approach takes better account of the intrinsic interrelationships among various parameters of the information system. In the Huang index function, each attribute (both conditional and decision) is assumed to have an equal number of clusters, and the objective is to map each attribute of element ($X_{i}$) in $U$ to an appropriate cluster among all the clusters associated with the conditional ($C_{1} \sim C_{n}$) or decision ($d$) attributes. The detailed parameters of the Huang index function are presented in the following section.

3.1 Parameters of the Huang index function

The Huang index function proposed in this study has the following form:

$$ H(C,\alpha_{c} ) = \left( {\frac{1}{C} \times \frac{{\overline{{E_{1} }} }}{{F_{C}^{\prime } }} \times D_{C}^{\prime } } \right), $$

where $C$ is the number of clusters assigned to the conditional and decision attributes and $\alpha_{c}$ is the corresponding classification accuracy when evaluated in terms of the $c$-th cluster of the decision attribute $d$. In addition, $F_{C}^{\prime }$ is obtained by accumulating the value of $E_{c}^{\prime }$ for each cluster of the decision attribute (d), where $E_{c}^{\prime }$ is given by $E_{c}^{\prime } = {{\sum\nolimits_{j = 1}^{n} {\overline{\mu }_{cj}^{m\prime } (x_{j} (d))\left\| {x_{j} - z_{c}^{\prime } } \right\|} } \mathord{\left/ {\vphantom {{\sum\nolimits_{j = 1}^{n} {\overline{\mu }_{cj}^{m\prime } (x_{j} (d))\left\| {x_{j} - z_{c}^{\prime } } \right\|} } {\alpha_{c} }}} \right. \kern-\nulldelimiterspace} {\alpha_{c} }}$, in which $\overline{\mu }_{cj} (x_{j} (d))$ is the membership function of data object $x_{j}$ in the c-th cluster of the decision attribute $d$, and $z_{c}^{\prime }$ is the multi-dimensional centroids of the lower approximate sets associated with the $c$-th cluster of the decision attribute d, and is obtained by computing the mean values of the conditional and decision attribute values of each data item within the corresponding sets. Furthermore, $m^{\prime }$ is the fuzzification parameter and $n$ is the total number of data objects in the dataset. Finally, the value of $D_{C}^{\prime }$ is equal to the maximum separation distance among the centroids of all the lower approximate sets associated with the different clusters of the decision attribute, i.e., $D_{C}^{\prime } = \mathop {\max }\limits_{i,j = 1}^{C} \left\| {z_{i}^{\prime } - z_{j}^{\prime } } \right\|$. It should be noted that the value of $D_{C}^{\prime }$ is upper bounded by the maximum separation distance among all possible pairs of data points within the dataset.

Parameter $F_{C}^{\prime }$ in the Huang index function differs from the term $J_{{m^{\prime } }}$ in the PBMF index function (see Sect. 2.5) in that its value depends on $E_{c}^{\prime }$ and therefore, takes classification accuracy into account.

3.2 Tendencies of terms within the Huang index function

As discussed in the previous section, the Huang index function has the form $H(C,\alpha_{c} ) = \left( {\frac{1}{C} \times \frac{{\overline{{E_{1} }} }}{{F_{C}^{\prime } }} \times D_{C}^{\prime } } \right)$. In other words, the index function comprises three terms: ${1 \mathord{\left/ {\vphantom {1 C}} \right. \kern-\nulldelimiterspace} C}$, ${{\overline{{E_{1} }} } \mathord{\left/ {\vphantom {{\overline{{E_{1} }} } {F_{C}^{\prime } }}} \right. \kern-\nulldelimiterspace} {F_{C}^{\prime } }}$ and $D_{C}^{\prime }$. Clearly, the value of the first term decreases as the number of clusters assigned to the conditional and decision attributes, $C$, increases. In other words, the value of the index function falls as the value of $C$ rises. In the second term of the index function, the value of $\overline{{E_{1} }}$ is constant for a given dataset and is equal to $\overline{{E_{1} }}$ in the PBMF index function. As discussed in the previous section, $F_{C}^{\prime }$ represents the sum of all $E_{c}^{\prime }$; each of which includes the classification accuracy $\alpha_{c}$ when evaluated in terms of the $c$-th cluster of the decision attribute $d$. Hence, the Huang index function increases as $E_{c}^{\prime }$ decreases. The third term in the index function, $D_{C}^{\prime }$, measures the maximum separation distance between the centroid of the lower approximate sets associated with the different clusters of the decision attribute, and increases as $C$ increases. Thus, the contribution of $D_{C}^{\prime }$ to the value of the Huang index function increases as the number of decision attribute clusters increases.

3.3 Comparison between the Huang index function and the PBMF index function

Table 1 compares the major components of the Huang index function and the PBMF index function. At a high level, three major differences exist between the two functions, namely (1) the Huang index function clusters the individual attributes of each data object within the dataset, whereas the PBMF index method clusters the data based on the norms of the data objects; (2) the Huang index function is based on $z_{c}^{\prime }$, i.e., the centroid of the lower approximate sets associated with each cluster c of the decision attribute, whereas the PBMF index function is based on $z_{k}$, i.e., the centroid of the k-th cluster obtained when clustering the dataset using the FCM method; and (3) the Huang index function takes explicit account of the classification accuracy when evaluating the optimality of the clustering results, whereas the PBMF index function considers only the optimal number of clusters within the dataset.

Table 1 Detailed definitions of Huang and PBMF indices

3.4 Details of the Huang index function

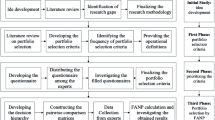
Figure 1 illustrates the basic structure of the Huang index function [41] and summarizes each processing step.

Fig. 1

Basic steps of the Huang index function

4 Performance evaluation of the Huang index method

This section commences by presenting a step-by-step example showing the calculation of the Huang index. The validity of the proposed Huang index method is then evaluated by considering an illustrative example related to electronic stock data extracted from the financial database maintained by the Taiwan Economic Journal (TEJ) [16]. When evaluations are performed, the effectiveness of the proposed index method is measured by comparing the partitioning and classification results with those obtained from the conventional PBMF index (FCM-based) method.

4.1 Step-by-step example showing the calculation of the Huang index value

In the following example, steps 2–6 of the Huang index method are demonstrated for a hypothetical dataset in which each instance has two conditional attributes, i.e., $a_{1}$, $a_{2}$, and one decision attribute, i.e., $d$. The instances in the hypothetical dataset are shown in Table 2.

Table 2 Ten instances in a hypothetical dataset

4.1.1 Step 2: fuzzify attribute values of instances using the FCM method

The continuous data in the hypothetical dataset are clustered using the FCM method. An assumption is made that each conditional attribute can be partitioned into 2 clusters. The membership function values of each attribute of each instance are summarized in Table 3. The centroids of each attribute cluster are shown in Table 4.

Table 3 Membership function values of each attribute of each instance

Table 4 Centroids of each cluster of attributes

4.1.2 Step 3: assign each data object attribute to appropriate conditional or decision attribute cluster

The appropriate conditional and decision attribute clusters are obtained for each instance by applying the index function $I_{\max }$to the membership function values shown in Table 3. The corresponding results are presented in Table 5.

Table 5 Discretization results of data in Table 2

4.1.3 Step 4: identify RS sets and compute the corresponding classification accuracy

The upper and lower approximate sets for each cluster c of the decision attribute d are shown in Table 6. The classification accuracy associated with each cluster of the decision attribute is obtained by computing the cardinality ratio of the corresponding lower approximate sets to the upper approximate sets. The results are shown in Table 7.

Table 6 Lower and upper approximate sets

Table 7 Classification accuracy associated with each cluster of decision attribute $\alpha_{c} = {\left| \underline{R} (X) \right|} / {\left| \overline{R} (X) \right|}$ where $X = \{x : C_d (x) = c, \forall \; x \in U \}$

4.1.4 Step 5: calculate the centroids of the lower approximate sets associated with each cluster of the decision attribute

The multi-dimensional centroids of the lower approximate sets associated with each cluster of the decision attribute d are obtained by calculating the mean attribute values (both conditional and decision) of all of the instances within the corresponding sets. Thus, the centroids of the lower approximate sets associated with the two clusters of decision attribute d are obtained as follows:

$$ \begin{aligned} z_{1}^{\prime } =\, & {\text{mean}}(x|x \in \underline{R} (X), C_{d} (x) = 1)=\, {\text{mean}}(x |x \in \{ x_{ 2} ,x_{ 3} \} ) \\ = \,& (( 1. 6 4 1 1+ 1. 6 9 9 8),( 0. 6 0 9 8+ 0. 7 0 0 1),( 2. 2 5 0 9+ 2. 3 9 9 9)) = ( 1. 6 7 0 5, 0. 6 5 5 0, 2. 3 2 5 4),\quad {\text{and}} \\ z_{2}^{\prime } = \,& {\text{mean}}(x|x \in \underline{R} (X), C_{d} (x) = 2) =\, {\text{mean}}(x |x \in \{ x_{ 8} \} ) = ( 1. 0 1 5 7, 0. 2 2 6 7, 1. 2 4 2 3). \\ \end{aligned} $$

4.1.5 Step 6: determine the value of the cluster validity index

Having determined the classification accuracy and centroids of the lower approximate sets, the optimality of the clustering and classification results is evaluated using the Huang index function $\left( {{\text{i}} . {\text{e}} . , { }H(C,\alpha_{c} ) = \left( {\frac{1}{C} \times \frac{{\overline{{E_{1} }} }}{{F_{C}^{\prime } }} \times D_{C}^{\prime } } \right)} \right).$

The membership functions of the first instance $x_{ 1}$ in the two clusters associated with the decision attribute d are given by $\overline{\mu }_{11} \left( {x_{1} \left( d \right)} \right) = 0. 6 0 7 1$, $\overline{\mu }_{21} \left( {x_{1} \left( d \right)} \right) = 0. 3 9 2 9$, respectively (see Table 3). It should be noted that the first instance $x_{ 1}$ has attribute values of $x_{1} \left( { 1. 0 0 4 4, 0. 9 8 9 6, 1. 9 9 4 1} \right)$ (see Table 2 and the centroid of the lower approximate sets associated with the second cluster of the decision attribute is given by $z_{2}^{\prime } \left( { 1. 0 1 5 7, 0. 2 2 6 7, 1. 2 4 2 3} \right)$(see Table 4). As a result, $(x_{1} (a_{1} )- z_{2}^{\prime } (a_{1} ) )$ = $( 1. 0 0 4 4- 1. 0 1 5 7 )$ = $- 0.0113$, $(x_{1} (a_{2} )- z_{2}^{\prime } (a_{2} ) )$ = $(0. 9 8 9 6- 0. 2 2 6 7 )$ = $0. 7 6 2 9$, $(x_{1} (a_{3} )- z_{2}^{\prime } (a_{3} ) )$ = $( 1. 9 9 4 1- 1. 2 4 2 3 )$ = $0. 7 5 1 8$. Therefore, the vector of $x_{12} = x_{1} - z_{2}^{\prime }$ has the form $\left[ {x_{12} \left( {a_{1} } \right),x_{12} \left( {a_{2} } \right),x_{12} \left( {a_{3} } \right)} \right]$ = $\left[ { - 0.0113,0.7629,0.7518} \right]$, and the corresponding norm is equal to $\left\| {x_{1} - z_{2}^{\prime } } \right\|$ = $\sqrt {x_{12} (a_{1} )^{2} + x_{12} (a_{2} )^{2} + x_{12} (a_{3} )^{2} }$ = $\sqrt {( - 0.0113)^{2} + 0.7629^{2} + 0.7518^{2} }$ = $1. 0 7 1 1$. Let the fuzzification parameter $m^{\prime }$ be specified as 2.0. The effect of instance $x_{1}$ on $z_{2}^{\prime }$, $\left\| {x_{12} } \right\|$, is obtained by multiplying $\left\| {x_{1} - z_{2}^{\prime } } \right\|$ by the square of the corresponding membership function, i.e., $\overline{\mu }_{21}^{2} \left( {x_{1} \left( d \right)} \right) = 0. 3 9 2 9^{2} = 0. 1 5 4 4$. Thus, the value of $\left\| {x_{12} } \right\|$ is 0.1653. The effect of instance $x_{j}$ on $z_{i}^{\prime }$ is shown in Table 8.

Table 8 Values of $\left\| {x_{j} - z_{c}^{\prime } } \right\|\left( { = \overline{\mu }_{{{\text{c}}j}}^{ 2} (x_{j} (d)) \times \left\| {x_{j} - z_{c}^{\prime } } \right\|} \right)$

The value of $E_{2}^{\prime }$ in the Huang index function is computed using the vectors $\left\| {x_{j2} } \right\| = \overline{\mu }_{ 2j}^{ 2} (x_{j} (d)) \times \left\| {x_{j} - z_{2}^{\prime } } \right\|$ and the classification accuracy $\alpha_{2}$ presented in Tables 7 and 8, respectively. Specifically, $E_{2}^{\prime }$ is determined by summing up the products of the norms and the squares of the corresponding membership functions for each of the instances, and then dividing the result by $\alpha_{2}$. Thus, the value of $E_{2}^{\prime }$ is obtained as

$$ \begin{aligned} E_{2}^{\prime } = {{\left( {\sum\nolimits_{{j = 1}}^{{10}} {\overline{\mu } _{{{\text{2}}j}}^{{\text{2}}} (x_{j} (d))\left\| {x_{j} - z_{2}^{\prime } } \right\|} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{{j = 1}}^{{10}} {\overline{\mu } _{{{\text{2}}j}}^{{\text{2}}} (x_{j} (d))\left\| {x_{j} - z_{2}^{\prime } } \right\|} } \right)} {\alpha _{{\text{2}}} }}} \right. \kern-\nulldelimiterspace} {\alpha _{{\text{2}}} }} = & {{\left( {\sum\nolimits_{{j = 1}}^{{10}} {\left\| {x_{{j2}} } \right\|} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{{j = 1}}^{{10}} {\left\| {x_{{j2}} } \right\|} } \right)} {\alpha _{{\text{2}}} }}} \right. \kern-\nulldelimiterspace} {\alpha _{{\text{2}}} }} = {{\left( {\left\| {x_{{12}} } \right\| + \left\| {x_{{22}} } \right\| + \cdots + \left\| {x_{{102}} } \right\|} \right)} \mathord{\left/ {\vphantom {{\left( {\left\| {x_{{12}} } \right\| + \left\| {x_{{22}} } \right\| + \cdots + \left\| {x_{{102}} } \right\|} \right)} {\alpha _{{\text{2}}} }}} \right. \kern-\nulldelimiterspace} {\alpha _{{\text{2}}} }} \\ = & (0.1653 + 0.0001 + \cdots + 0.1640)/0.1250 = 18.1462. \\ \end{aligned} $$

Similarly, the value of $E_{1}^{\prime }$ is obtained as 6.7620. The value of $F_{C}^{\prime }$ is then found to be $F_{C}^{\prime } = \sum\nolimits_{c = 1}^{C} {E_{c}^{\prime } } = 24.9082.$

The factor $\overline{{E_{1} }}$ in the Huang index function is a constant term for a dataset in which the instances belong to only one cluster. Thus, the centroid of the illustrative dataset is given by $z_{1} = {\text{mean}}(x |x \in \{ x_{i} \} ,i = 1,2, \ldots ,10).$ As a result, the centroid $z_{1}$ calculated by the arithmetic mean function ${\text{mean}}(x |x \in \{ x_{i} \} ,i = 1,2, \ldots ,10)$ has attribute values of $\begin{aligned} {\text{mean}}(x |x \in \{ x_{i} \} ,i = & 1,2, \ldots ,10) \\ = & (( 1. 0 0 4 4+ 1. 6 4 1 1+ \cdots \,+\, 1.5732),(0.9896 + 0.6098 + \cdots + 0.4154),(1.9941 + 2.2509 + \ldots + 1.9886)) = z_{1} (1.4665,0.5075,1.9740) \\ \end{aligned}$. Based on the vector of centroid $z_{1}$, it can be shown that $(x_{1} (a_{1} )- z_{1} (a_{1} ) )$ = $( 1. 0 0 4 4- 1. 4 6 6 5 )$ = $- 0.4621$, $(x_{1} (a_{2} )- z_{1} (a_{2} ) )$ = $(0. 9 8 9 6- 0. 5 0 7 5 )$ = $0. 4821$, and $(x_{1} (a_{3} )- z_{1} (a_{3} ) )$ = $( 1. 9 9 4 1- 1. 9 7 4 0 )$ = $0. 0 2 0 1$. Therefore, the vector of $x_{12} = x_{1} - z_{2}^{\prime }$ has the form $\left[ {x_{11} \left( {a_{1} } \right),x_{11} \left( {a_{2} } \right),x_{11} \left( {a_{3} } \right)} \right]$ = $\left[ { - 0.4621,0.4821,0.0201} \right]$, and the corresponding norm is equal to $\left\| {x_{1} - z_{1} } \right\| = \sqrt {x_{11} (a_{1} )^{2} + x_{11} (a_{2} )^{2} + x_{11} (a_{3} )^{2} } = \sqrt {( - 0.4621)^{2} + 0.4821^{2} + 0.0201^{2} } = 0.6681$. Similarly, the norms of $\left\| {x_{ 2} - z_{1} } \right\|,\left\| {x_{ 3} - z_{1} } \right\|, \ldots, \left\| {x_{1 0} - z_{1} } \right\|$, are found to be $0. 3 4 3 1$, $0. 5 2 2 4$,…, $0. 1 4 1 8$, respectively. The value of $\overline{{E_{1} }}$ is then obtained by summing up the norms of $\left\| {x_{\text{j}} - z_{1} } \right\|$ where $j = 1,2, \ldots ,10$, yielding a value of $\overline{{E_{1} }}$ = $4.6403$.

The value of $D^{\prime}_{C}$ in the Huang index function is acquired by calculating the maximum separation distance between the centroids of the lower approximate sets associated with the first and second clusters of the decision attribute. As shown in Table 4, these centroids are given by $z_{1}^{\prime } \left( { 1. 6 7 0 5, 0. 6 5 5 0, 2. 3 2 5 4} \right)$ and $z_{2}^{\prime } \left( { 1. 0 1 5 7, 0. 2 2 6 7, 1. 2 4 2 3} \right)$, respectively. Thus, the vector of $z_{12} = z_{1}^{\prime } - z_{2}^{\prime }$ has the form $\left[ {z_{12} \left( {a_{1} } \right),z_{12} \left( {a_{2} } \right),z_{12} \left( {a_{3} } \right)} \right]$ = $\left[ { 0. 5 6 1 1, - 0. 1543, 0. 4 0 6 9} \right]$, and the corresponding norm is determined to be $\left\| {z_{1}^{\prime } - z_{2}^{\prime } } \right\|$ = $\sqrt {z_{12} (a_{1} )^{2} + z_{12} (a_{2} )^{2} + z_{12} (a_{3} )^{2} } = \sqrt {0.5611^{2} + ( - 0.1543)^{2} + 0.4069^{2} }$ = $1. 3361$.

Finally, the Huang index ($(H(C,\alpha_{c} )) = ( {\frac{1}{C} \times \frac{{E_{1}^{\prime } }}{{F_{C}^{\prime } }} \times F_{C}^{\prime } } )$) is found to have a value of $0. 1 2 4 5$, where $C = 2$,$\overline{{E_{1} }} = 4.6403$, $F_{C} = 2 4. 9 0 8 2$ and $D_{C}^{\prime } = 1. 3361$.

4.2 An illustrative example

In this section, the performance of the Huang index function in partitioning and classifying real-world complex datasets is evaluated using stock data extracted from the TEJ database for the first quarter of 2008. The TEJ database comprises 53 financial indices (attributes) for each stock item (data object). However, for reasons of practicality, the performance evaluations were restricted to just 1 decision attribute and 2 conditional attributes. Having deleted records in which some of the data was incomplete, a total of 327 records were obtained. (See Table 9 for representative values of each index for a selected subset of these 327 records.)

Table 9 Illustrative financial data extracted from TEJ database for first quarter 2008

In this illustrative example, the performance of the Huang index function is compared with that of the PBMF index function for a case in which the clustering process is based on just two conditional attributes (i.e., business profit rate and pre-tax net profit rate) and the single decision attribute (i.e., EPS net income). In this example, the dataset is partitioned into three clusters in the PBMF index function and into three clusters per attribute in the Huang index function. The corresponding clustering results are presented in Figs. 2 and 3, respectively. In this example, Fig. 2 contains all of the data points within the dataset, whereas Fig. 3 includes only those data points belonging to the lower approximate sets associated with each cluster of the decision attribute. (Note: Fig. 3 only shows results for one cluster of the decision attribute, since the other two clusters were both found to have upper approximate sets only.) Figure 2 shows that the partitioning results obtained using the PBMF index function are dominated by the value of the second conditional attribute. In other words, most of the data points within the dataset are assigned to a single cluster. In addition, it can be seen that some of the data points in the first cluster overlap those in the second. Simply put, the PBMF index function yields a poor partitioning and classification performance when applied to real-world information systems characterized by a limited number of attributes. Furthermore, it can be seen in Fig. 3 that the lower approximate sets generated by the Huang index function contain very few data points, yielding very little information for generating reliable decision-making rules when it is applied to complex information systems with a limited number of attributes per cluster.

Fig. 2

Data partitioning results obtained by the PBMF index function when clustering stock market data based on two conditional attributes and one decision attribute

Fig. 3

Data partitioning results obtained by the Huang index function when clustering stock market data based on two conditional attributes and one decision attribute

5 Evaluation of proposed portfolio selection model

In this section, the Huang index function is combined with a GRA dimension reduction model and an RS classification scheme to obtain an automatic stock portfolio selection system. In the proposed system, a specified set of stock items is collected automatically every quarter, and the 53 financial indices associated with each stock item are consolidated into 6 normalized financial ratios using a GRA model. The stock items are then clustered in accordance with their financial ratio values using the Huang index function, and the cluster indices associated with the optimal clustering solution (i.e., the clustering solution which maximizes the value of the Huang cluster validity index) are then processed using an RS classification model in order to identify the stocks within the lower approximate sets. These stock items are then filtered in accordance with Buffet’s general investment principles [42] in order to determine stocks for possible inclusion within the portfolio. Finally, the GRA model is re-applied to consolidate the 6 normalized financial ratios of the filtered stocks into a single GRG, indicating the potential of each stock item to maximize the rate of return on the stock portfolio.

The major concepts of the proposed system are described in Sects. 5.1–5.3. The detailed processing steps within the system are then discussed in Sect. 5.4. Finally, the performance of the proposed system is evaluated in Sect. 5.5.

5.1 GRA dimension reduction mechanism

The GRA model is used to compute the following financial ratios: (1) profitability, (2) rate per share, (3) growth rate, (4) credit capacity, (5) operating capacity, and (6) statutory ratio, where ratio (1) is taken as the decision attribute of the stock system and ratios (2)–(5) are taken as the conditional attributes. (Note: the mapping of the 53 financial indices to the six consolidated ratios is summarized in Table 10).

Table 10 Mapping of 53 financial indices–6 financial ratios

The stock market system is assumed to have the form $S = (U,A,V_{q} ,f_{q} )$, where $U$ is a non-empty finite set of objects (stock items) and $A$ is a finite set of attributes (financial indices) describing these objects. Following the application of the GRA model, a modified information system with the form $S = (U,\hat{A},V_{q} ,f_{q} )$ is obtained, where $\hat{A}$ is a set of six consolidated attributes (financial ratios) describing the same set of objects. The six financial ratios are clustered using the Huang index function, and cluster indices corresponding to the optimal clustering solution are then processed using RS theory to identify the corresponding lower approximate sets. Assuming that $U$ is the domain of discourse and $R$ is the set of equivalences of $U$, the RS problem can be formulated as $X \subseteq U:(\overline{R} (X),\underline{R} (X)),BN_{R} (X)$ (see Sect. 3).

As described above, the GRA model is also used to reduce the six financial ratios of each remaining stock item after the stocks within the lower approximate sets have been filtered using the general investment principles prescribed by Buffet. In this case, the GRA model takes the six consolidated financial ratios (GRGs) of each stock item as inputs. It then outputs a single GRG describing the overall performance of the corresponding stock item. The GRGs are ranked in descending order so that the stock items with a better financial performance are placed above those with a poorer performance, and the ranked sequence is then taken as the input for the final stock selection decision.

5.2 Filtering of stock items in accordance with basic investment principles

To simplify the workload of the GRA model in reducing the six GRGs of each stock item to a single performance indicator, the stocks within the lower approximate sets are filtered in accordance with a set of decision-making attributes, which are defined in accordance with the general investment principles specified by Buffett and formalized by Hagstrom [42]. Buffett argued that reducing costs is essential for enterprises seeking to hone their competitive ability and rival their competitors in terms of price, while high profit margins and a high inventory turnover are both reliable indicators of the financial well-being of a company. Buffet further asserted that only companies with all three attributes can be certain of survival and possess the means to earn profit for their shareholders. Accordingly, in the present study, the stock items within the lower approximate sets identified by the RS classification model are filtered in accordance with the following thresholds: (1) return on asset (after tax) > 0, (2) return on equity > 0, (3) gross profit ratio > 0, (4) equity growth rate > 0, and (5) constant EPS > 0.

5.3 Data extraction

In this study, the feasibility of the proposed stock selection mechanism was evaluated using electronic stock data extracted from the TEJ database over the period extending from the first quarter of 2003–6/1/2009. In general, financial statements for a particular accounting period are subject to a certain delay before publication. For example, annual reports are published after 4 months, half-yearly reports after 2 months, and first and third quarterly reports (without notarization) after a minimum of 1 month. The submission deadlines for the financial statements maintained in the TEJ database are as follows:

(1) Annual report: the submission deadline laid down by the Security Superintendence Commission is 4 months after the closing balance day. However, companies listed in previous years (TSE and OTC) can delay filing until 5/31.

(2) Half-yearly report: the submission deadline laid down by the Security Superintendence Commission is 2 months after the closing balance day. However, companies listed in previous years (TSE and OTC) can delay filing until 9/21.

(3) First-quarter report: the submission deadline laid down by the Security Superintendence Commission is 1 month after the closing balance day. However, companies listed in previous years (TSE and OTC) can delay filing until 5/31.

(4) Third-quarter report: the submission deadline laid down by the Security Superintendence Commission is 1 month after the closing balance day. However, companies listed in previous years (TSE and OTC) can delay filing until 11/15.

Since financial data relating to the last quarter of every year is not available until May 31st of the following year, the data cannot be used by the proposed stock selection system to select suitable investment stocks in the first quarter. As a result, the stock selection system can only be executed three times in every 12 months period, namely 5/31–09/22, 9/22–11/15 and 11/15–05/31 of the following year.

5.4 Detailed processing steps in the Huang index function-based stock selection system

The detailed processing steps in the proposed stock selection system are illustrated in Fig. 4, and summarized below.

Fig. 4

Proposed stock selection system flow chart

5.4.1 Step 1: data collection and attribute determination

In each quarter, the 53 attributes of each specified stock item within the TEJ database are collected automatically, and the user is given the opportunity to modify the choice of financial ratios used for attribute reduction in the initial GRA process, to select a new GRA model for attribute reduction purposes, and to modify the decision-making attributes used to filter the stocks in the lower approximate set prior to their further consolidation using the GRA model.

5.4.2 Step 2: data pre-processing

Having collected the relevant financial data for each quarterly period, a basic pre-processing operation is performed to improve the efficiency of the GRA attribute reduction process. Specifically, the data records containing missing fields (i.e., missing financial indices) are deleted, and the box plots method [43] is applied to resolve the data outlier problem by establishing an inter-quartile range so that any data points falling outside this range are automatically assigned a default value depending on the interval within which they fall.

5.4.3 Step 3: information consolidation using the GRA model

When stock records remain after the pre-processing operation completes, the GRA model normalizes the values of each of the 53 financial indices and then computes the six corresponding financial ratios in accordance with the mapping given in Table 10.

5.4.4 Step 4: information clustering using the Huang index method

The values of the six financial ratios obtained in Step 3 (i.e., five conditional attributes $C_{1} \sim C_{5}$ and one decision attribute $D_{1}$) are processed using the Huang index method in order to identify the optimal number of clusters per attribute (conditional and decision) and the corresponding set of cluster indices.

5.4.5 Step 5: selection and filtering of feasible stocks

The optimal set of cluster indices generated by the Huang index method is processed using RS theory to identify the stock items within the lower approximate sets. These stock items are then filtered in accordance with the general investment guidelines proposed by Buffett in order to identify a set of stocks for possible inclusion within an investment portfolio.

5.4.6 Step 6: fund allocation

The six financial ratios of each stock item remaining after the filtering operation are consolidated to a single GRG (i.e., an overall performance indicator) by the GRA model. The GRGs of all the surviving stock items are then arranged in descending order, and the first five stock items are chosen for investment purposes.

5.4.7 Step 7: check the validity of the modeling

The rate of return on the stock portfolio constructed at the end of quarter k is compared at the end of quarter k + 1, with the average rate of return implied by the variation in the Taiwan Stock Exchange Capitalization Weighted Stock Index (TAIEX) over the equivalent financial period. If the rate of return is acceptable, a decision is made as to whether or not the model should be run for a further quarter using the existing GRA model. However, if the rate of return is deemed unacceptable, the suitability of the GRA model is reviewed and a new GRA model is adopted if appropriate.

5.5 Performance evaluation of the Huang index function-based stock selection system

In [16], an automatic stock market forecasting and portfolio selection mechanism is constructed by integrating a moving average autoregressive exogenous (ARX) prediction model with a GM (1, N) attribute reduction model and RS theory. Meanwhile, in [44], financial data was collected automatically and input to a GM (1, 1) prediction model in order to forecast the future trends of the collected data. The forecast data was then reduced using a GM (1, N) model, classified using a k-means clustering algorithm, and processed by an RS classification module to select suitable investment stocks. Finally, a minimum variance at risk (MVAR) scheme comprising 5 GRA models and a Markowitz mean–variance (MV) model was employed to identify an efficient frontier, which achieved the optimal tradeoff between the minimum risk and the maximum rate of return. The MVAR–MRR model was used to evaluate the expected risk at the point of the maximum expected return rate for the five frontier curves generated by the five GRA models. The stock allocation with the lowest risk value was then selected as being the optimal solution.

In this section, the validity and effectiveness of the proposed stock selection mechanism is initially evaluated by comparing the rate of return on the investment portfolios selected in the 17 investment periods between 2003 and 2009 with the rate of return on the equivalent investment portfolios constructed using a system in which the Huang index function is replaced by a fuzzy-based clustering scheme, with the number of clusters per GRG specified simply as N = 3. The rate of return obtained using the two stock selection schemes is then compared with: (1) the predicted average rate of return implied by the variation in the TAIEX index over the equivalent investment periods; (2) the average rate of return achieved by the portfolio selection method proposed in [16]; and (3) the average rate of return achieved by the MVAR-MRR portfolio selection method proposed in [44].

The corresponding results are presented in Table 11. It can be seen that the accumulated rate of return achieved using the proposed Huang index function-based mechanism (116.90%) is higher than that achieved using the pre-determined clustering based scheme (103.21%). The accumulated rate of return obtained through the proposed method is also higher than that implied by the variation in the TAIEX index (44.90%). Additionally, in the period 2004–2006, the accumulated rate of return achieved using the Huang index function-based mechanism (107.93%) was higher than that achieved using the GM(1,N) attribute reduction based scheme [16] (82.45%) or the MVAR-MRR method [44] (86.22%). Meanwhile, the rates of return achieved in 2004–2006 using the Huang index function-based mechanism are 33.36, 27.27 and 47.30, respectively. In contrast, the rates of return achieved using the GM (1, N) attribute reduction-based scheme are 17.57, 25.90 and 38.98, respectively, while those achieved using the MVAR-MRR method-based scheme are 19.59, 20.84 and 45.79, respectively. In other words, the rates of return achieved using the proposed stock selection scheme are higher than those obtained using the GM (1, N) attribute reduction scheme or the MVAR-MRR method-based scheme. Thus, the overall viability and effectiveness of the proposed stock selection system is confirmed.

Table 11 Rates of return of TAIEX, GM (1, N)-based reduction attributes method, MVAR-MRR method, pre-determined cluster-based stock selection scheme, and the Huang-based stock selection scheme

6 Conclusions

This study has presented an automatic stock portfolio selection system based on a Grey relational analysis (GRA) model, a modified form of the PBMF index method (designated as the Huang index method), and rough set (RS) theory. In the proposed approach, 53 financial indices were collected automatically for each stock item every quarter and a GRA model was used to consolidate these indices into six predetermined financial ratios [Grey relational grades (GRGs)]. The GRGs were then processed using the Huang index function in order to determine the optimal number of clusters per GRG and the corresponding values of the cluster indices for each stock item. The cluster indices were then processed using an RS classification model in order to identify the stock items within the lower approximate sets of the stock system. These items were filtered in accordance with established investment principles and the six GRGs of each surviving stock item were then consolidated into a single GRG, indicating the performance of the corresponding stock item in terms of its ability to maximize the likely rate of return. Finally, the top five stock items were chosen for investment purposes. The general validity of the Huang index function has been confirmed by comparing the clustering results obtained for a real-world database containing stock market information with the corresponding results obtained using the conventional PBMF index (FCM-based) method. Finally, the real-world feasibility of the proposed stock portfolio selection system has been demonstrated by comparing the rate of return on the selected portfolio with that obtained by three alternative stock selection schemes. The results presented in this study support the following major conclusions:

(1) In the PBMF index function, the optimality of the clustering results is evaluated in accordance with (a) the distance between each data object and the cluster centroids, and (b) the maximum separation distance between the cluster centroids. In contrast, in the Huang index function, the optimality of the clustering results is evaluated in terms of (a) the distance between the data objects and the centroids of the lower approximate sets associated with each cluster of the decision attribute, (b) the maximum distance between the centroids of the lower approximate sets associated with the different clusters of the decision attribute, and (c) the classification accuracy of the clustering results (i.e., the cardinality ratio of the lower approximate sets to the upper approximate sets for each cluster of the decision attribute). In other words, in contrast to the conventional PBMF index function, which simply determines the optimal clustering of the data within the dataset given a specified number of clusters, the Huang index function determines the optimal number of attribute clusters within the dataset, which maximizes the separation distance between the attribute values and simultaneously optimizes the classification accuracy.

(2) The PBMF index function clusters the norms of the data objects within the dataset, whereas the Huang index function clusters the attribute values. As a result, the Huang index method takes better account of the intrinsic interrelationships among the various conditional and decision attributes, and prevents the clustering results from being dominated by any attribute(s) with a higher order of magnitude.

(3) In the case of a more complex dataset, e.g., a dataset in which the attributes have relatively homogeneous values, the PBMF index function clusters all of the data points within the dataset, but yields a relatively poor partitioning performance. In contrast, the Huang index function achieves a better partitioning performance, but only classifies a limited subset of the data points. In other words, the Huang index function is only able to extract a limited amount of useful and correct information from the dataset, and is therefore of limited use in defining accurate and reliable decision-making rules.

(4) The stock portfolio selection system based on the Huang index function yields a higher rate of return than a system in which the clustering process is based on a pre-determined number of clusters per attribute. In addition, the rate of return on the selected stock portfolio is considerably higher than that predicted by the overall variation in the TAIEX index over the equivalent investment period. Finally, the rate of return on the selected stock portfolio is superior to that obtained by the GM(1,N) attribute reduction-based scheme in [16] or the MVAR-MRR based scheme in [44].

In fact, the goal of this study is to achieve a possible tendency through our stock portfolio selection system. Incidentally, since the prices in the stock market sometimes fluctuate dramatically, we chose not to measure stock prices over the short term, instead investigating their performance over the long term. In summary, the results presented in this study demonstrate that the Huang index function is an effective tool for optimizing both the number of attribute clusters and the classification accuracy when applied to the partitioning and classification of complex, real-world datasets. As a result, the Huang index function provides an ideal basis for such applications as automatic portfolio selection mechanisms (demonstrated in this study), landslide detection, daily electrical peak load forecasting, and so on.