1 Introduction

Although complementary metal-oxide semiconductors (CMOS) have been scaling down in feature size, the increased density of chip integration is posing new challenges. The significant factors are leakage power consumption and tunneling effect [1,2,3]. Against this issue, several new computing paradigms based on novel computing devices are emerging. Quantum-dot cellular automata (QCA) [4] is one of these emerging nanotechnologies. Due to its small feature size, ultra-low power consumption, and high operational frequency, QCA has great potential for next-generation computing [5, 6].

With the development of QCA circuit design systems, the interconnections between electronic devices, i.e., wire-crossings is a problem that should not be underestimated [7]. Wire-crossings in QCA circuits are receiving increasing attention from the literature [8] because it consumes additional resources and increases the complexity of the QCA circuit. Moreover, a large number of wire-crossings can lead to complex manufacturing problems [9]. This is because wire-crossings in QCA cannot be solved by multiple routing layers and vias as in traditional CMOS. Current automatic layout routing techniques for QCA are still mainly limited to single-layer physical layout implementations [10]. Hence, the design of QCA circuits has gradually shifted from the previous focusing on how to implement functions to how to reduce and further eliminate wire-crossing structures. Minimal the number of wire-crossings could improve circuit design. As a result, the number of wire-crossings has become a significant parameter in the QCA circuit evaluation system.

The main contributions of this paper are as follows.

  1. 1.

    We propose logic expressions of 13 standard three-input Boolean functions based on majority-of-five (MAJ5) primitive (Method A) and its combinations with XOR-of-three (XOR3) logical operation (Method B).

  2. 2.

    The QCA layouts of these 13 functions are presented with reduced number of wire-crossings. Comparing with previously published designs [11], our method achieves 30.69% and 48.35% reduction in QCA area by Method A and B, respectively.

  3. 3.

    The proposed QCA layouts are used as building blocks for large scale circuit design. As one example, the area of Peres reversible gate is reduced by 70.0%.

The remainder of the paper is organized as follows. Section 2 introduces the background of QCA and logic operations. Section 3 presents relevant research work. Section 4 shows the redesigned diagrams of the 13 standard three-input Boolean functions with MAJ5 and XOR3. Afterwards, we perform experiment result obtained by our method as well as case studies in Section 5. We conclude the paper in Section 6.

2 Background

In this section, the backgrounds of QCA and logic primitives are briefly introduced.

2.1 QCA

There are several different implementations types of QCA: metal-island QCA, semiconductor-based QCA, atomic-based QCA, molecular QCA, and magnetic QCA [12]. Metal-island QCA cells [13] are based on aluminum islands coupled by aluminum-oxide tunnel junctions and capacitors, fabricated on an oxidized silicon wafer. Here electrons can tunnel between dots using tunnel junctions. The two connecting pairs of islands are coupled to each other using capacitors. Semiconductor-based QCA [14] can operate at significantly higher temperatures than metal-dot devices. in which four GaAs/AlGaAs semiconductor quantum dots are placed at four different corners. Each cell is also capacitively coupled. Atomic-based QCA [15] is prospective for highly complex and room temperature operational QCA circuitry with atomic silicon quantum dots (ASiQDs). Moleculer QCA [16] is capable of self-assembling to form larger circuits and operating at room temperature. Molecular QCA offers very high device densities, low power dissipation, and ways to directly integrate sensors with QCA logic and memory elements. Magnetic QCA [17] is a nanomagnetic particle which switching times are slower. However, nanoscale magnets offer the advantages of large energy differences between states, tolerance to the effects of radiation, and the demonstrated room-temperature operation. Hence, Magnetic QCA has the potential integration with other magnetic systems such as magnetic random access memory (MRAM), make this a potentially useful technology in spite of its relatively low speed compared with conventional electronic devices. Consequently, numerous experiments on QCA physical realization have been made in the past few years including [18,19,20].

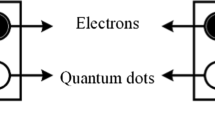
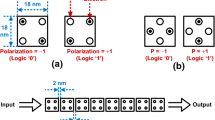
Every type of QCA mentioned before except magnetic QCA all mimic the same behavioral model of a square cell with a length of 18 nm, containing quantum dots at the four corners and two free electrons among the dots [21], which is shown in Fig. 1(a). The four quantum dots are occupied by a tunneling barrier and arranged in a 2 × 2 fashion. The two free electrons in the cell can tunnel between these dots. As the signals pass, the electrons will always be at diagonal positions as a result of Coulomb force repulsion. Therefore, there are two types of energy polarization exist, i.e., P = + 1 and P = − 1. Consequently, logic 1 and 0 can be represented by the polarization of the cell, respectively. Multiple cells are used to form the logic gates and transmission lines. Note that QCA circuits work differently from conventional CMOS circuits. It uses a four-phase clock to control the distribution of electrons, i.e., the transmission of signals, which can be seen in Fig. 2. The four phases are switch, hold, release, and relax. Moreover, QCA’s information transmission is current-free, which results in ultra-low-power consumption [22].

Fig. 1
figure 1

Schematics of QCA basis, (a) QCA cell, (b) majority-of-three (MAJ3), and (c) Inverter

Full size image
Fig. 2
figure 2

Schematic of four-phase clock

Full size image

The three most typical primitive of QCA are transmission line, majority-of-three logic gate (MAJ3) (Fig. 1(b)), and inverter (INV) (Fig. 1(c)) [21]. The Boolean logic expression for the MAJ3 is denoted as

$$ \mathbb{M}_{3}(A, B, C) = AB + AC + BC. $$
(1)

When any one of the three inputs is set to logic 0 or 1, the AND and OR logic gates can be obtained, respectively. For example: \(\mathbb {M}_{3}(A, B, 0) = AB \) and \( \mathbb {M}_{3}(A, B, 1) = A + B \).

With the development of QCA, more and more basic devices based on explicit interactions between QCA cells have been designed, such as majority-of-five (MAJ5), XOR-of-three (XOR3), etc. The introduction of these new devices allows for improvements in both the QCA implementation area and delay.

2.2 QCA Wire-Crossing

2.2.1 Coplanar

Coplanar crossing refers to the transfer of two crossing singles in the same plane in QCA. By rotating cell as shown in Fig. 3(a). The horizontal transmission line is standard cells and the vertical transmission line is the rotated cells. Because the four quantum dots of the rotating cell and standard cell are in different positions, the influence of Coulomb interaction between different transmission lines in the other direction is not enough to change the polarization value. Thus, the signal coplanar cross-transmission is realized. Although rotating coplanar crossing structure does not bring extra redundancy, the stability of rotating cells is weaker than it could have been in a normal wire [23]. One can refer to [24] for more information on the comparison of various coplanar wire-crossing properties.

Fig. 3
figure 3

Schematics of three types of wire-crossings, (a) traditional coplanar, (b) robust coplanar, (c) multilayer, and (d) crossing two wires by using three XORs in [26]

Full size image

2.2.2 Robust Coplanar

Robust coplanar wire-crossing is based on clock region. The behavior of cells in the non-adjacent clock region is mutually independent, that is to say, cells separated by 180∘ phase difference, e.g., Clock phase 0 and Clock phase 2, are independent of each other in the process of information transmission [25]. As shown in Fig. 3(b), the cells at the intersection of horizontal and vertical transmission lines are separated by half a clock cycle. Hence the signal transmission will not cause interference. This is a pretty good way to solve the crossing problem. However, sometimes to match the clock difference, the robust coplanar crossing structure will increase the area and delay of the circuit.

2.2.3 Multilayer

It is very straightforward to understand the multilayer crossing, in which one transmission line crosses over the top of the other. Hence, the lines are not on the same plane. The implementation of multilayer crossing requires at least three layers. As shown in Fig. 3(c), it is designed as a crossing bridge where the signals of two transmission lines do not interfere with each other in the process of transmission. Thus, the cross-transmission of signals is implemented. But this technique brings more complexity to the layout implementation and the difficulty of the implementation will increase as well.

2.2.4 Crossing Elimination by Using Three XORs

In addition to addressing the wire-crossings on the level of physical layout, we can also handle wire-crossings on the logical level. As proposed method in [26], one wire-crossing can be resolved by using three XOR gates. However, it should be noted that each XOR consists of four majority gates proposed in [26]. This structure can reduce all wire-crossings to zero at the cost of introducing three additional XOR gates, which is quite costly.

2.3 Majority-of-Five

Efficient MAJ5 logic gates based on explicit interactions between QCA cells are emerging. Meanwhile, researchers have shown that designs based on MAJ5 are efficient in terms of the area and delay. Many different kinds of QCA MAJ5 gate structures were proposed [27,28,29,30,31,32]. Figure 4(a) gives the schematic diagram of an MAJ5, which will be used in the designs of this paper. An MAJ5 is a Boolean logic gate whose output is true only when it has three or more inputs of logic 1. The logic expression of an MAJ5 can be expressed as:

$$ \begin{array}{@{}rcl@{}} \mathbb{M}_{5}(A, B, C, D, E) &=& ABC + ABD + ABE + ACD \\ && + ACE + ADE + BCD \\ && + BCE + BDE + CDE. \end{array} $$
(2)

MAJ5 can be expressed in terms of MAJ3, which resulted in an expression (3) of optimal depth using exact synthesis [33].

$$ \mathbb{M}_{5}(A, B, C, D, E) = \mathbb{M}_{3}(A, \mathbb{M}_{3}(B, C, D), \mathbb{M}_{3}(\mathbb{M}_{3}(A, B, C), D, E)). $$
(3)

When any two of MAJ5 inputs are set to logic 0 or 1, a three-input AND gate and a three-input OR gate can be implemented, respectively, which can be seen in (4):

$$ \begin{array}{@{}rcl@{}} \mathbb{M}_{5}(A, B, C, 1, 1) &=& A+B+C, \\ \mathbb{M}_{5}(A, B, C, 0, 0) &=& ABC. \end{array} $$
(4)

Moreover, MAJ5 can also be reduced to MAJ3 when either one of the following two conditions is met [34]:

  1. 1.

    There exists two pairs of duplicated inputs.

  2. 2.

    Any two inputs are set to 0 and 1 respectively.

The expressions can be seen in (5)

$$ \mathbb{M}_{5}(A, A, B, B, C) = \mathbb{M}_{5}(A, B, C, 0, 1) = \mathbb{M}_{3}(A, B, C). $$
(5)

Due to symmetries, more identities can be obtained as follows:

$$ \begin{array}{@{}rcl@{}} \mathbb{M}_{5}(A, A, B, B, C) &=& \mathbb{M}_{5}(A, A, B, C, C) \\ &=& \mathbb{M}_{5}(A, B, B, C, C) \\ &=& \mathbb{M}_{5}(A, B, C, 0, 1). \end{array} $$
(6)
Fig. 4
figure 4

Schematic diagrams of majority-of-five and XOR-of-three used in this paper, (a) majority-of-five in [27] and (b) XOR-of-three in [36]

Full size image

2.4 XOR-of-Three

Exclusively-OR (XOR) logic gates have a wide range of applications in digital logic circuits, especially in arithmetic logic circuits. Thus, the introduction of XOR can help to further optimize the circuit area and latency [35]. XOR can also be designed by the explicit interactions between QCA cells. A stable and reliable infrastructure with low energy consumption can be obtained [36,37,38,39]. Figure 4(b) shows the schematic diagram of XOR3 adopted in this paper. Extended from XOR2, the Boolean function of a XOR3 can be expressed as:

$$ \mathbb{X}_{3}(A, B, C) = A \oplus B \oplus C. $$
(7)

When any one of the inputs is set to logic 0 or 1, the XOR and exclusively-NOR (XNOR) can be obtained, respectively. For example:

$$ \begin{array}{@{}rcl@{}} \mathbb{X}_{3}(A, B, 0) &=& A \oplus B,\\ \mathbb{X}_{3}(A, B, 1) &=& A \odot B. \end{array} $$
(8)

3 Related Work

There are considerable researches on QCA wire-crossings optimization. The most typical way is operated by logic restructuring, in which nodes are duplicated or swapped to generate a functional-equivalent circuit with fewer wire-crossings [40,41,42]. The logic restructuring method leads to a tradeoff between wire-crossings and the area. The methods for the automatic placement and routing have been introduced in [43]. There are mainly three steps: intermediate function generation, feedback function generation, and inputs rearrangement for solving wire-crossing issues. However, this methodology is limited to three variables propagating to single output functions. As for maintaining a set of small-scale functions of optimized wire-crossings, the methods based on a universal logic gate or standard functions are presented [8, 11, 44, 45]. Although the universal logic gate method reduces wire-crossings, cell count, and operating clock cycles, it does not lead to high efficiency in circuit designs. In [8], 4-variable logic functions are investigated and simplified with the K-Map as sum of product (SOP) form. The heuristic K-Map includes minterms selecting, inputs reordering, inputs postponement, and universal logic gate using. Afterward, it attempts to replace remaining wire-crossings with three XOR gates, as mentioned in Section 2.2.4. In [11], it provides some novel diagrams for the implementation of standard three-input Boolean functions with the aim of reducing the number of wire-crossings, using five-input majorities and robust coplanar wire-crossing [25]. Then, a new technique is used to merge multiplexers when Boolean functions with more than three inputs are implemented. In this paper, we optimized this approach and proposed a better design.

4 Standard Three-Input Boolean Functions

Logical diagrams are presented in this section for 13 standard three-input Boolean functions introduced in [46] (Table 1). First, MAJ5 is applied as an implementation primitive, which is shown in the “Method A” column in Table 2. A combination of MAJ5 with XOR3 is then applied to the designs as shown in the “Method B” column in Table 2. Moreover, the QCA layouts for all of the 13 standard functions proposed in this paper are illustrated in “Appendix A” (Method A) and “Appendix B” (Method B).

Table 1 13 standard three-input Boolean functions proposed in [46]
Full size table
Table 2 Schematics of simplified 13 standard three-input Boolean functions given in [46]
Full size table

4.1 Cubes of Three-Input Boolean Functions

A Boolean function of n variables can be represented by an n-dimensional binary hyper-cube. In this paper, n= 3 is taken to represent the three-input Boolean functions, the cube of which is shown in Fig. 5. For a total of \( 2^{2^{3}}=256\) distinct Boolean functions, they can be classified into 13 standard three-input Boolean functions. The trivial cases of constants 0 and 1 are not considered. The “Original Diagram” column in Table 1 shows the logic expressions and diagrams proposed in [46]. The functions are labeled using index i ∈ [1,13].

Fig. 5
figure 5

The cube of the three-input Boolean functions

Full size image

The concept of the standard Boolean function is similar to the Negation-Permutation-Negation (NPN) equivalence classes [47]. The NPN-equivalence classes is defined as follows: two functions f(x1,...,xn) and g(x1,...,xn) are NPN-equivalent if there exists an inversion of the inputs \((x_{i} \rightarrow \overline {x_{i}})\) (N), a permutation of the inputs \((x_{i}x_{j} \rightarrow x_{j}x_{i})\) (P), or an inversion of the output \((f \rightarrow \overline {f})\) (N) so that f and g can be made Boolean equivalent. By grouping similar functions into NPN equivalence classes, the representations are compact since n-input Boolean functions can be classified into 14 and 222 classes, for n = {3,4} respectively.

4.2 Proposed Majority-of-Five Representations of the Standard Functions

We first present the proposed logic expression using MAJ5 primitives. The logic diagrams are shown in the “Method A (using MAJ5)” column in Table 2.

  • Functions 2 and 9 There is nothing that has changed since these functions were already represented by one MAJ3 gate [11, 46].

  • Functions 1, 5, and 8 The diagrams proposed in [11] improved the original diagrams in [46]. Especially for functions 1 and 5, the logic depth was optimized by introducing MAJ5. We also adopt these designs proposed in [11].

  • Functions 3, 6, and 12 These functions can be efficiently implemented using MAJ5, which is shown in the “Method A (using MAJ5)” column. The robust coplanar wire-crossings in the previous designs [11] are eliminated, which leads to the reduction of the QCA implementation area and the enhancement of the module stability. Especially, function 3 not only eliminates the robust coplanar wire-crossing but also removes the traditional coplanar wire-crossing which is implemented by rotating cells. Functions 3 and 12 are designed by combining one MAJ3 and one MAJ5. In contrast, function 6 is implemented by two MAJ5s.

  • Function 10 This function designed by [11] was already with no wire-crossing and a small QCA implementation area. We proposed a structure consisting of one MAJ5 and one MAJ3 in this paper.

  • Functions 4, 7, 11, and 13 The long wire robust wire-crossings in the previous designs [11] in these four functions are removed. The structure of too-long wire in designs is not so freely be routed and connected to other circuits. Although each of these four proposed designs still has one robust wire-crossing at the primitive inputs which increases the stability while bringing an additional 0.5 cycles, the QCA implementation area is more compact.

4.3 Proposed Hybrid Representation of Standard Functions

The functions are further studied by using hybrid representation based on MAJ5 and XOR3. The logic diagrams are shown in the “Method B (using XOR3)” column in Table 2.

  • Functions 1, 2, 5, 7, 8, and 9 These functions are left unchanged because they are already well-designed shown in the previous discussions.

  • Functions 12 and 13 Function 13 can be represented by one XOR3 while function 12 is an XNOR. As mentioned earlier in Section 2.4, it can be obtained by setting any of the primitive inputs of XOR3 to logic 1. Hence, the two functions can be implemented by one single QCA logic gate, which not only simplifies the circuit area but also eliminates all types of wire-crossings.

  • Functions 3, 4, and 11 These functions can be implemented in another efficient way by introducing XOR3. All types of the coplanar wire-crossings are eliminated compared to the previous designs [11]. Especially for functions 4 and 11, the hybrid designs remove the wire-crossings that could not be eliminated by introducing MAJ5 alone.

  • Function 6 The hybrid representation also eliminates the wire-crossing for function 6. Although the number of logic gates and levels are the same, the hybrid designs leads to better area.

  • Function 10 The hybrid design also has no wire-crossings. One can select appropriate implementations proposed by [11] or ours in real designs.

4.4 An Example of Using Proposed Diagrams

We use the reversible Peres logic gate [48] as an example to demonstrate the proposed wire-crossing optimization. The schematic and the logic expressions of Peres logic gate over Boolean variables A, B, and C are shown in Fig. 6, in which P, Q, and R are outputs. For a circuit module, the inputs and outputs are often fixed. In this case, we have simplified the inputs layout to highlight the idea of using 13 standard three-input Boolean functions for substitution in order to clarify the usage. However, it is important to note that the inputs layout can also have a significant impact on reducing wire-crossings, which is not explored in this paper. One can refer to [43] for further information. The gate designed with diagrams proposed in [11] is shown in Fig. 7(a). Meanwhile, the gate designed using MAJ5 is shown in Fig. 7(b). The internal modules of output Q and output R are replaced with the standard functions 11 and 12 designed by MAJ5. It can be seen that the robust wire-crossings existing in the previous circuit have been reduced by using XOR3, which is shown in Fig. 7(c). The use of XOR3 allows for a more efficient reduction of wire-crossings and circuit area.

Fig. 6
figure 6

Schematic of Peres reversible gate

Full size image
Fig. 7
figure 7

Schematics of Peres reversible gate using different diagrams, (a) diagrams proposed in [11], (b) diagrams using MAJ5, and (c) diagrams using XOR3

Full size image

5 Experimental Results

5.1 Logic Diagrams Comparison

The comparison of different diagrams implementing 13 standard three-input Boolean functions are presented in Table 3. All the QCA layouts and simulations are implemented by QCADesigner 2.0.3 [49]. The simulation engine parameters of the QCADesigner namely bistable approximation and coherence vector are presented in Table 4. The number of samples is recommended to be set to N = 2000 × 2n, where n is the total number of inputs in the design. We compared the proposed diagrams with the state-of-the-art designs introduced in [11]. The information of the latency (clock), complexity (number of cells), and area are listed. The latency is represented by the QCA clocks, while area is the smallest rectangular containing all QCA cells given by the QCADesigner 2.0.3. It can be seen that all designs are no more than two layers, almost the same or even better than the diagrams presented in [11]. Although we use robust wire-crossings in the primitive inputs which leads to an additional 0.5 cycle delay for the designs, the stability and scalability of the designs are guaranteed. With Method A (using MAJ5), we can achieve an average size of 30.69% reduction. Furthermore, the size is improved to 48.35% after introducing the XOR3 (Method B). In terms of the number of wire-crossings in Method B, only function 7 has one robust wire-crossing in the primitive inputs. All the coplanar and robust wire-crossings used in [11] are eliminated.

Table 3 Comparison of different diagrams implementing 13 standard three-input Boolean functions
Full size table
Table 4 Simulation engine parameters of QCADesigner
Full size table

5.2 Case Studies

We use Peres reversible gate and the MCNC benchmark circuit c17 as study cases to illustrate the advantages of the proposed diagrams. Figure 8 shows the QCA layout of the Peres reversible gate using three different design approaches. The QCA simulation results for all three designs with inputs A, B, and C are shown in Fig. 9. It is important to note that, the first meaningful P, Q, and R signals waveforms are obtained after 1.25 clock cycles.

Fig. 8
figure 8

QCA layout of the Peres reversible gate using three different design approaches, (a) using diagrams proposed in [11], (b) Method A, and (c) Method B

Full size image
Fig. 9
figure 9

QCA simulation result of the Peres

Full size image

Table 5 shows the comparison results of different diagrams (proposed in [11], using MAJ5, and using XOR3) implementing Peres gate when realized in QCA. It should be noted that for the sake of visualising the advantages of our design we have only counted the area and the number of crossed lines in the red dotted box in Fig. 8. By comparing, Fig. 8(c) is the best design, i.e., using XOR3, which occupies an area of 0.06 μm2 and 0.75 clock cycles with no wire-crossings.

Table 5 Comparison of different diagrams implementing Peres gate
Full size table

As for c17, the QCA layout and simulation results are shown in Figs. 10 and 11, respectively. Our design occupies an area of 0.14 μm2 and 1 clock cycle with only one robust wire-crossings. Table 6 shows the comparison results of c17 between the XMG presented in [50] and method proposed in this paper. The comparison result indicates that our method can achieve 42.86%, 88.89%, and 46.15% reduction in latency, the number of wire-crossings, and area, respectively.

Fig. 10
figure 10

QCA layout of the c17 using proposed diagrams

Full size image
Fig. 11
figure 11

QCA simulation result of the c17

Full size image
Table 6 Comparison of c17 between the XMG presented in [50] and ours
Full size table

6 Conclusions

Wire-crossing is a very important issue in QCA, which imposes significant complexity, area dissipation, noise sensitivity, and signal weakness. Aiming at reducing the number of wire-crossings, the majority-of-five gate and the exclusively-OR gate are introduced to address this issue. The diagrams and logic expressions of the simplified 13 standard three-input Boolean functions are proposed, which results in fewer wire-crossings. The experimental results show that we get improvement in size by 30.69% and 48.35% when introducing MAJ5 and XOR3, respectively.