The Mth Coherent State

Abstract

In this article, we propose a new kind of quantum states based on acting the number operator M times ${\hat{n}}^M$ on the coherent state. We term this state the Mth coherent state, based on the value of the power M. We find that it is strongly similar to the coherent state as the analysis of the photonic statistical distributions and the overlap with the coherent state illustrate. Also, we find that it asymptotically reaches the minimum uncertainty and has a localized behavior in the Husimi function. However, in contrast to coherent state, the Mth coherent state has strong nonclassical features such as antibunching and squeezing for a relatively long range. Other parameters and measurements are discussed and studied. Finally, we highlight the similarity between the higher orders of the near coherent states and the Mth coherent states in order to potentially generate our proposed state.

1 Introduction

Nonclassical states are important in many areas of quantum information and quantum optics. A state is said to be nonclassical if its Glauber-Sudarshan P function [1, 2] is negative or more singular than the Dirac delta function. It appears that there are some features, if the state has, it would be directly classified nonclassical. Some of these are, squeezing, antibunching and negative regions in the Wigner function. Different degrees of these features are found in, for example, different types of squeezed states [3,4,5], Schrodinger cat states [6, 7] and Fock states [8]. The nonclassicality is a milestone in many applications including measurement accuracy [9], teleportation [10, 11], quantum computing [12] and lasers [13].

It is known that the Glauber-Klauder-Sudarshan coherent state [14,15,16] is the closest quantum mechanical state to classical fields. It is defined to be the eigenstate of the annihilation operator $\hat{a}\mid \alpha \left\rangle =\alpha \mid \alpha \right\rangle$, where $\hat{a}$ is the annihilation operator, α is the coherent parameter, and |α〉 is the coherent state (CS). This state is also represented as the application of the displacement operator $\hat{D}\left(\alpha \right)={e}^{\alpha {\hat{a}}^{\dagger }-{\alpha}^{\ast}\hat{a}}$ on the vacuum state, $\mid \alpha \left\rangle =\hat{D}\left(\alpha \right)\mid 0\right\rangle$. Based on its classical properties and the relative ease to be generated, it has been widely applied in different areas of quantum mechanics and quantum optics [17,18,19].

The subject of combining the two opposite aspects, the classical and nonclassical properties is widely investigated [20,21,22,23]. Combining the two aspects with high efficiency is a great opportunity to test and deeply study the quantum nature of light and other particles. Furthermore, the states which have the two natures act as intermediate states between the two contradictory behaviors which allow us to study the quantum-to-classical transition to better observe the wave-like, particle-like, and the smooth development from spontaneous to the stimulated light emission [24].

There exist many approaches to reach this goal, for example, superposing two classical states such as different kinds of Schrodinger cat states [6, 7] and categories of nonlinear coherent states [25,26,27,28]. One of the possibilities is to create states that are almost like CS but at the same time nonclassical. The photon added (subtracted) coherent state PACS (PSCS) is an example of these states [29], where it is defined as ${S}_1{\hat{a}}^{\dagger M}\mid \alpha \Big\rangle$(${S}_2{\hat{a}}^M\mid \alpha \Big\rangle$), where S₁ (S₂) is the normalization factor. It adds (subtracts) a quanta to (from) the CS, and they have been experimentally realized [24] and applied [30]. Another example is the different types of truncated CSs, where a cutoff in the summation of the CS is placed [31,32,33]. Many of these states have been experimentally demonstrated for different purposes [34, 35].

However, most of the previous states/approaches are either classically well-pronounced but nonclassically negligible or vice verse, and almost never both of the two natures are extreme. Also, most of them are expected to be more likely close to either CS, as the truncated CSs, or nonclassicality, as the PACS and PSCS. For this purpose, we propose another state which we call the Mth coherent state (Mth stands for the order M, so if for example M = 2 we call it the second coherent state¹). This extension is the application of the number operator M times ${\hat{n}}^M$ on the coherent state as

$$ \mid M\left(\alpha \right)\left\rangle ={N}_M{\hat{n}}^M\mid \alpha \right\rangle, $$

(1)

where |M(α)〉 is the Mth CS, and N_M is the normalization factor. In opposite to most other states, the Mth CS is not clear whether it is close to CS, or if it has a nonclassicality. However from its definition, we expect that the Mth CS is close to CS since we just applied the number operator which has less distortion than, for example, the creation or annihilation operator.

From another side we are motivated to study this state because it is not only a direct extension to CSs but also comes naturally from our previous proposed state; the near coherent state [36, 37]. The near CS is a special kind of a superposition of two CSs that is the two superposed CSs are nearly identical. We found that although the near CS is a superposition of two CSs, its properties are quite different from all the superposed CSs [38]. In fact, for some correct choice of parameters, the state becomes exactly the first CS, M = 1, |1(α)〉, and we found that it is more close to CSs than any comparable states. However, this similarity does not negate its nonclassical features, where it has a fairly strong squeezing and antibunching. Therefore, we expect that the Mth CS will share many similarities with the CS to a level is hard to distinguish between them, and it will have pronounced nonclassical features.

Consequently, this paper is organized as follows: In the first section, the main properties of the Mth CS are introduced. Next section talks about the similarities between the Mth CS and the regular CS. The statistical distributions, overlap with the CS, minimum uncertainties and Husimi function are covered in Section 3. After that, the nonclassical features of the $\mathcal{Q}$ Mandel parameter, squeezing and displaced states are presented in Section 4. Lastly, discussion and a conclusion are in Section 5.

2 Mth Coherent State

The Mth coherent state (Mth CS) is defined as

$$ \mid M\left(\alpha \right)\left\rangle ={N}_M{\hat{n}}^M\mid \alpha \right\rangle ={N}_M{e}^{-{\left|\alpha \right|}^2/2}\sum \limits_{n=0}^{\infty}\frac{n^M{\alpha}^n}{\sqrt{n!}}\mid n\Big\rangle, $$

(2)

where N_M is the normalization factor. If M equals 0, the CS |0(α)〉 = |α〉 is obtained. The normalization factor appears to be

$$ {N}_M=\frac{1}{\sqrt{B_{2M}\left({\left|\alpha \right|}^2\right)}}, $$

(3)

where B_n(x) is the Bell polynomial which is defined as ${B}_M(x)={e}^{-x}{\sum}_{n=0}^{\infty}\frac{x^n{n}^M}{n!}$. The first few polynomials are B₀(x) = 1, B₁(x) = x, B₂(x) = x² + x, B₃(x) = x³ + 3x² + x [39, 40]. From the definition, as mentioned before, the only difference between the Mth CS and the regular CS is the factor n^M. Statistically, this factor is what let it equal a photon state when α → 0, ${\lim}_{\alpha \to 0}\mid M\left(\alpha \right)\left\rangle =\mid 1\right\rangle$, for all M > 0. The average number of photons is given as

$$ {\left\langle \hat{n}\right\rangle}_M=\frac{e^{-{\left|\alpha \right|}^2}}{B_{2M}\left({\left|\alpha \right|}^2\right)}\sum \limits_{n=0}^{\infty}\frac{n^{2M+1}{\left|\alpha \right|}^{2n}}{n!}=\frac{B_{2M+1}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}. $$

(4)

The first three averages are ${\left\langle \hat{n}\right\rangle}_0={\left|\alpha \right|}^2$, ${\left\langle \hat{n}\right\rangle}_1=\frac{1+3{\left|\alpha \right|}^2+{\left|\alpha \right|}^4}{1+{\left|\alpha \right|}^2}$, ${\left\langle \hat{n}\right\rangle}_2=\frac{1+15{\left|\alpha \right|}^2+25{\left|\alpha \right|}^4+10{\left|\alpha \right|}^6+{\left|\alpha \right|}^8}{1+7{\left|\alpha \right|}^2+6{\left|\alpha \right|}^4+{\left|\alpha \right|}^6}$. In all these expressions we notice that at the limit |α|→∞, the ${\left\langle \hat{n}\right\rangle}_M\approx {\left|\alpha \right|}^2$, which is the same as the CS. Also, the opposite limit when |α|→ 0, ${\left\langle \hat{n}\right\rangle}_M$ exactly 1, except for the coherent state of M = 0, at which it becomes a vacuum state.

3 Similarity to Coherent State

3.1 The Statistical Distributions

The photon distribution is of interest for many purposes and is given as

$$ {P}_n^M\left(\alpha \right)=\mid \Big\langle n{\left|M\left(\alpha \right)\Big\rangle \right|}^2=\frac{n^{2M}{\left|\alpha \right|}^{2n}{e}^{-{\left|\alpha \right|}^2}}{B_{2M}\left({\left|\alpha \right|}^2\right)n!}. $$

(5)

The distribution is plotted for different values of M in the left of Fig. 1. We can see that the shapes of all distributions are very similar to the Poissonian distribution. They are approximately Poisson distributions but with a constant shift proportional to M or as

$$ {P}_n^M\left(\alpha \right)\approx \frac{{\left|\alpha \right|}^{2\left(n+2M\right)}{e}^{-{\left|\alpha \right|}^2}}{\left(n+2M\right)!}\approx {P}_{n+2M}^0\left(\alpha \right),\kern3.00em \mathrm{for}\kern1em \alpha \gg 1. $$

(6)

This approximated shift suggests that all Mth CSs are close to CSs. It is of interest to substitute an appropriate α for each |M(α)〉 to a value which makes all the distributions centred at one position. To do so, let us differentiate (5) with respect to n and then equates it to zero. This will yield the position of the peaks, and it gives

$$ {\alpha}_P^M=\exp \left[\frac{1}{2}\psi \left({n}_P+1\right)-\frac{M}{n_P}\right]{e}^{\mathrm{i}\uptheta}, $$

(7)

where ψ(x) = Γ^′(x)/Γ(x) is the digamma function (the logarithmic derivative of the gamma function [41]), and θ is the phase of α. This representation replaces the parameter α to be n_P. We term this replacement the peak representation (peak rep.). Now, if we substitute the value of α in the distribution of (5) to be ${\alpha}_P^M$, then all the distributions will be centered at n_P. The plot of the distributions ${P}_n^M\left({\alpha}_P^M\right)$ for a value of n_P is shown in the right of Fig. 1. We can see that all the photonic distributions have similar shapes to CS and obviously they are sub-Poissonian distributions as well.

Fig. 1

The photon distribution of different Mth CSs. In the left: The value of α is fixed to 4 in all states (alpha rep.). In the right: The same distribution is plotted in the peak rep. for the value n_P = 15.4974. This value is the peak value of the coherent state at |α| = 4

Now, we have two representations to display our measurements, the regular alpha (α) rep. and the peak rep. As Fig. 1 shows, the main advantage of using alpha rep. is to approximately conserve the shape of the CS distribution. On the other hand, the peak rep. provides another advantage which is approximately conserving the average number of photons of (4). In fact, we found that for large values of n_P, the average ${\left\langle \hat{n}\right\rangle}_M$ is approximately given as ≈ n_P + 1/2 for all M values. The average number of photons against n_P in the peak rep. is shown in Fig. 2. As we can see from the figure, the asymptotic behavior of all the curves is independent of M at large n_P.

Fig. 2

The average number photons using the peak rep. against the peak value n_P

Next, the quantum phase distribution of the Pegg-Barnett formulation which has the following expression

$$ \mathcal{P}\left(\varphi \right)=\frac{1}{2\pi}\mid \Big\langle r{\left|\varphi \Big\rangle \right|}^2, $$

(8)

where |φ〉 is the phase state which is defined as

$$ \mid \varphi \left\rangle =\sum \limits_{n=0}^{\infty }{e}^{in\varphi}\mid n\right\rangle, $$

(9)

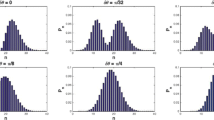
and the state |r〉 is any arbitrary state. This distribution represents the quantum phase nature of the interested state |r〉. If the state is any Fock state, the phase dist. is completely random, and if the state is the CS, then some localized behavior is observed, and the localization is increased as α is increased. The distribution for our state |M(α)〉 is found to be

$$ \mathcal{P}\left(\varphi \right)=\frac{1}{2\pi}\frac{e^{-{\left|\alpha \right|}^2}}{B_{2M}\left({\left|\alpha \right|}^2\right)}{\left|\sum \limits_{n=0}^{\infty}\frac{n^M{\alpha}^n{e}^{in\varphi}}{\sqrt{n!}}\right|}^2. $$

(10)

In Fig. 3, we plotted this phase distribution using the peak and alpha representations. In the figure, we can see that the most localized state of all Mth CS is the CS and then M = 1,2,... We also observe that in the peak rep. if we increase n_P, the localized behavior increases as well and will eventually be identical to the localization of the CS. On the other hand, α rep. is approximately preserving the shape of the distributions as Fig. 3 shows.

Fig. 3

The phase distribution of the Mth CS for different M values. In the left: the peak rep. with n_P = 10. In the right: alpha rep. with $\alpha =\sqrt{10}$

3.2 The Overlap

The overlap between two different states can be measured using their inner product. The inner product reveals how clo0se the states to each other. The overlap between any Mth CS and any CS is found to be

$$ {F}_M\left({\alpha}_0,{\alpha}_M\right)=\mid \Big\langle {\alpha}_0{\left|M\left({\alpha}_M\right)\Big\rangle \right|}^2={e}^{-{\left|{\alpha}_0-{\alpha}_M\right|}^2}\frac{B_M\left({\alpha}_0{\alpha}_M^{\ast}\right){B}_M\left({\alpha}_0^{\ast }{\alpha}_M\right)}{B_{2M}\left({\left|{\alpha}_M\right|}^2\right)}. $$

(11)

When both α₀ and α_M are equal, this is simplified to

$$ {F}_M\left(\alpha, \alpha \right)=\frac{B_M{\left({\left|\alpha \right|}^2\right)}^2}{B_{2M}\left({\left|\alpha \right|}^2\right)}. $$

(12)

In the left of Fig. 4, we plotted the overlap for the states when α is the same value for all M, (12). For large α values, we can see that all the Mth CS will eventually overlap to near %100 with the CSs. For comparison, let us study the overlap when the two parameters of Mth CS, α_M and CS, α₀ are not the same. The best option to obtain high overlapping is to let both of them in their peak rep. values, ${F}_M\left({\alpha}_P^0,{\alpha}_P^M\right)$. The overlap is shown in the right of Fig. 4. We can see that, as the left figure, all the Mth CSs will eventually reach unity when n_P →∞. However, the required number of photons to reach the same amount of overlapping is smaller in ${F}_M\left({\alpha}_P^0,{\alpha}_P^M\right)$. To appreciate the enormous differences between the two ranges take for example M = 1, let F₁(α, α) be equal 0.99. Using (12), α is found to be α = 9.94987 which has average number of photons ≈ 101. However applying ${F}_1\Big({\alpha}_P^0,{\alpha}_P^1$), the required value of n_P to reach the same overlap is n_P = 7.1595 which corresponds to ${\left\langle \hat{n}\right\rangle}_1\approx 9.54952$. This means that the similarities between the Mth CS and the CS are higher when their parameters are substituted by the peak values.

Fig. 4

The overlap between the CSs and the Mth CSs. In the left: the overlap when both the CS and the Mth CS have the same value of α. In the right: the overlap when the two states in their peak rep. ${\alpha}_P^M$

In the next, we will only use the peak rep. to illustrate any physical measurement because of its strong overlap with the CSs and its direct indication of the average number of photons.

3.3 The Minimum Uncertainties

One of the main important features of the CS is that it satisfies the minimum uncertainty value of the Heisenberg relation which is $\left\langle {\left(\Delta \hat{X}\right)}^2\right\rangle \left\langle {\left(\Delta \hat{Y}\right)}^2\right\rangle \ge 1/16$, where

$$ \hat{X}=\frac{\hat{a}+{\hat{a}}^{\dagger }}{2},\kern4.00em \hat{Y}=\frac{\hat{a}-{\hat{a}}^{\dagger }}{2i}. $$

(13)

This definition is a direct extension of the Heisenberg relation of position and momentum. We here seek to know whether the Mth CS will be close to the minimum uncertainty value, which is 1/16, or not. The uncertainties of both $\hat{X}$ and $\hat{Y}$ of the Mth CS are

$$ {\left\langle {\left(\Delta \hat{X}\right)}^2\right\rangle}_M={\left\langle {\hat{X}}^2\right\rangle}_M-{\left\langle \hat{X}\right\rangle}_M^2,\kern4.00em {\left\langle {\left(\Delta \hat{Y}\right)}^2\right\rangle}_M={\left\langle {\hat{Y}}^2\right\rangle}_M-{\left\langle \hat{Y}\right\rangle}_M^2. $$

(14)

The $\hat{X}$ and $\hat{Y}$ averages are

$$ {\left\langle \hat{X}\right\rangle}_M=\frac{{\left\langle \hat{a}\right\rangle}_M+{\left\langle {\hat{a}}^{\dagger}\right\rangle}_M}{2},\kern5.00em {\left\langle \hat{Y}\right\rangle}_M=\frac{{\left\langle \hat{a}\right\rangle}_M-{\left\langle {\hat{a}}^{\dagger}\right\rangle}_M}{2i}. $$

(15)

The averages of their squares are

$$ {\left\langle {\hat{X}}^2\right\rangle}_M=\frac{{\left\langle {\hat{a}}^2\right\rangle}_M+{\left\langle {\hat{a}}^{\dagger 2}\right\rangle}_M+2{\left\langle \hat{n}\right\rangle}_M+1}{4},\kern1.50em {\left\langle {\hat{Y}}^2\right\rangle}_M=\frac{-{\left\langle {\hat{a}}^2\right\rangle}_M-{\left\langle {\hat{a}}^{\dagger 2}\right\rangle}_M+2{\left\langle \hat{n}\right\rangle}_M+1}{4}. $$

(16)

Consequently, in general, we have to calculate the averages ${\left\langle {\hat{a}}^f\right\rangle}_M$ and ${\left\langle {\hat{a}}^{\dagger f}\right\rangle}_M$, where f is a positive integer, in order to find the uncertainties. These averages are found to be

$$ {\left\langle \hat{a}\right\rangle}_M=\alpha \sum \limits_{k=0}^M\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)},\kern2.00em {\left\langle {\hat{a}}^{\dagger}\right\rangle}_M={\alpha}^{\ast}\sum \limits_{k=0}^M\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}. $$

(17)

$$ {\left\langle {\hat{a}}^2\right\rangle}_M={\alpha}^2\sum \limits_{k=0}^M{2}^{M-k}\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\kern-.2em \frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)},\kern1.50em {\left\langle {\hat{a}}^{\dagger 2}\right\rangle}_M={\alpha}^{\ast 2}\sum \limits_{k=0}^M{2}^{M-k}\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\kern-.2em \frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}. $$

(18)

and

$$ {\left\langle {\hat{a}}^f\right\rangle}_M={\alpha}^f\sum \limits_{k=0}^M{f}^{M-k}\left(\kern-.2em \genfrac{}{}{0.0pt}{}{M}{k}\kern-.2em \right)\kern-.2em \frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)},\kern1.50em {\left\langle {\hat{a}}^{\dagger f}\right\rangle}_M={\alpha}^{\ast f}\sum \limits_{k=0}^M{f}^{M-k}\left(\kern-.2em \genfrac{}{}{0.0pt}{}{M}{k}\kern-.2em \right)\kern-.2em \frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}. $$

(19)

Substituting these relations into (15) yields

$$ {\left\langle \hat{X}\right\rangle}_M=\left(\kern-.2em \frac{\alpha +{\alpha}^{\ast }}{2}\kern-.2em \right)\kern-.2em \sum \limits_{k=0}^M\kern-.2em \left(\kern-.2em \genfrac{}{}{0.0pt}{}{M}{k}\kern-.2em \right)\kern-.2em \frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)},\kern1.50em {\left\langle \hat{Y}\right\rangle}_M=\left(\frac{\alpha -{\alpha}^{\ast }}{2i}\right)\sum \limits_{k=0}^M\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}, $$

(20)

and for (16), they become

$$ {\left\langle {\hat{X}}^2\right\rangle}_M=\left(\frac{\alpha +{\alpha}^{\ast }}{4}\right)\sum \limits_{k=0}^M{2}^{M-k}\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}+\frac{B_{2M+1}\left({\left|\alpha \right|}^2\right)}{2{B}_{2M}\left({\left|\alpha \right|}^2\right)}+\frac{1}{4}, $$

(21)

and

$$ {\left\langle {\hat{Y}}^2\right\rangle}_M=-\left(\frac{\alpha +{\alpha}^{\ast }}{4}\right)\sum \limits_{k=0}^M{2}^{M-k}\left(\genfrac{}{}{0.0pt}{}{M}{k}\right)\frac{B_{M+k}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}+\frac{B_{2M+1}\left({\left|\alpha \right|}^2\right)}{2{B}_{2M}\left({\left|\alpha \right|}^2\right)}+\frac{1}{4}, $$

(22)

where ${\left\langle \hat{n}\right\rangle}_M$ is taken from (4). The above relations are exactly sufficient to calculate the uncertainties of (14) and their multiplications.

The multiplication of the two uncertainties ${\left\langle {\left(\Delta \hat{X}\right)}^2\right\rangle}_M{\left\langle {\left(\Delta \hat{Y}\right)}^2\right\rangle}_M$ is illustrated in Fig. 5 for different M values of the Mth CS. First, as expected, all Mth CS for M > 0 start from 9/16 which is the uncertainty of one photon and agrees with (4). We also note that asymptotically all Mth CS eventually reach the minimum value which is 1/16 as n_P is increased. The small values of M approach 1/16 faster than the higher values. In general, the analytic behavior of the multiplication is complicated as M is increased. For small M values, M < 6, all states start to drop down in some behavior but never exceeding 9/16. However, when M > 5, the multiplication starts to be larger than 9/16 in some regions.

Fig. 5

The uncertainty multiplication of the Mth CS for different M values. The left figure is for θ = 0, while the right figure is for θ = π/4

We also note that ${\left\langle {\left(\Delta \hat{X}\right)}^2\right\rangle}_M{\left\langle {\left(\Delta \hat{Y}\right)}^2\right\rangle}_M$ is highly dependent on the phase of the coherent parameter θ. When it equals 0 or π/2, where they have exactly the same expression, the multiplication behavior is the fastest to reach 1/16 as shown in Fig. 5. However, when θ = π/4 as the same figure shows, the behavior is the slowest to reach 1/16. Therefore, the Mth CS is closer to the minimum uncertainty when the phase equals 0 or π/2.

3.4 Husimi Function

The Husimi function is defined as [43]

$$ Q\left(\alpha \right)=\frac{\left\langle \alpha |\hat{\rho}|\alpha \right\rangle }{\pi }, $$

(23)

where $\hat{\rho}$ is the density matrix of the state. The Q function gives the projection of the state with the most classical state, the CS, thus provides an indication of the distribution of the state in the phase space. The Q(α) for the Mth CS |M(β)〉 yields to be

$$ Q\left(\alpha \right)=\frac{e^{-{\left|\alpha -\beta \right|}^2}}{\pi}\frac{B_M\left(\alpha {\beta}^{\ast}\right){B}_M\left(\beta {\alpha}^{\ast}\right)}{B_{2M}\left({\left|\beta \right|}^2\right)}. $$

(24)

The distribution is plotted in Fig. 6. We can see that all the plotted values have high localized behavior, which agrees with the minimum uncertainties calculations. The localization is decreased as the M value is increased, and the shapes start to deform in the direction of the substituted phase of ${\alpha}_P^M$, in the figure is π/2.

Fig. 6

The Husimi function when $\beta ={\beta}_P^M$ for n_P = 20, and the phase is fixed for all M and equals π/2

4 The Nonclassical Features

4.1 The $\mathcal{Q}$ Mandel Parameter

The $\mathcal{Q}$ Mandel parameter is defined by [42]

$$ \mathcal{Q}=\frac{\left\langle {\hat{n}}^2\right\rangle -{\left\langle \hat{n}\right\rangle}^2}{\left\langle \hat{n}\right\rangle }-1=\frac{\left\langle {\left(\Delta \hat{n}\right)}^2\right\rangle -\left\langle \hat{n}\right\rangle }{\left\langle \hat{n}\right\rangle }. $$

(25)

This function expresses the question whether the interested state has a super or sub Poissonian distribution. If it appears sub-Poissonian, it means that the state is antibunched, consequently is nonclassical. The antibunching refers to the photons being more likely separated than the Poisson distribution in a phenomenon has not a classical counterpart. If $\mathcal{Q}$ is negative (positive) the state is antibunched (bunched), and if $\mathcal{Q}$ equals zero (-1), the state is a coherent (Fock) state.

For the Mth CS, the average of the square number operator ${\hat{n}}^2$ is given as

$$ {\left\langle {\hat{n}}^2\right\rangle}_M=\frac{B_{2M+2}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}, $$

(26)

and its uncertainty is

$$ {\left\langle {\left(\Delta \hat{n}\right)}^2\right\rangle}_M={\left\langle {\hat{n}}^2\right\rangle}_M-{\left\langle \hat{n}\right\rangle}_M^2=\frac{B_{2M+2}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}-{\left(\frac{B_{2M+1}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}\right)}^2 $$

(27)

Therefore, the $\mathcal{Q}$ Mandel parameter is

$$ {\mathcal{Q}}_M=\frac{B_{2M+2}\left({\left|\alpha \right|}^2\right)}{B_{2M+1}\left({\left|\alpha \right|}^2\right)}-\frac{B_{2M+1}\left({\left|\alpha \right|}^2\right)}{B_{2M}\left({\left|\alpha \right|}^2\right)}-1 $$

(28)

The $\mathcal{Q}$ Mandel parameter is represented graphically in Fig. 7 in the peak rep. We can see that all Mth CSs have negative values for the whole range of α or n_P, which means that all Mth CSs are strictly speaking antibunched and consequently nonclassical. Comparing this figure with Fig. 4 or Fig. 5 indicates that the nonclassical behavior is extreme, meanwhile the state is also extremely close to CS. For example, for the 10th CS at n_P = 40, the $\mathcal{Q}$ equals ≈− 0.334 while the overlap of (11) gives ≈ 0.98 and the minimum uncertainty of θ = 0 equals ≈ 0.06299. It means that the state is extremely close to CS and significantly antibunched. We also see from the figure that the antibunching is increased as the M value is increased.

Fig. 7

The $\mathcal{Q}$ Mandel parameter of the Mth CS for different M values in the peak rep

4.2 The Squeezing

A state is considered to be squeezed if one of the uncertainty quadratures (position or momentum) is less than the minimum value. As we saw in Section 3.3, the minimum uncertainties of the observables $\hat{X}$ and $\hat{Y}$ satisfies $\left\langle {\left(\Delta \hat{X}\right)}^2\right\rangle \left\langle {\left(\Delta \hat{Y}\right)}^2\right\rangle \ge 1/16$, so if one the two quantities is less than 1/16 then the state is squeezed. The squeezing can be studied using the linear squeezing parameter [44, 45]

$$ {S}_{\phi }={e}^{-2 i\phi}\left\langle {\hat{a}}^2\right\rangle +{e}^{2 i\phi}\left\langle {\hat{a}}^{\dagger 2}\right\rangle +2\left\langle {\hat{a}}^{\dagger}\hat{a}\right\rangle -{\left({e}^{- i\phi}\left\langle \hat{a}\right\rangle +{e}^{i\phi}\left\langle {\hat{a}}^{\dagger}\right\rangle \right)}^2, $$

(29)

where ϕ is the phase of squeezing. This parameter S_ϕ measures the amount of the linear squeezing in the state, and it determines the direction of the squeezing. For a state, if S_ϕ is negative, then that state is squeezed. For our state, S_ϕ yields to be

$$ {S}_{\phi}^M\left(\alpha \right)={e}^{-2 i\phi}{\left\langle {\hat{a}}^2\right\rangle}_M+{e}^{2 i\phi}{\left\langle {\hat{a}}^{\dagger 2}\right\rangle}_M+2{\left\langle \hat{n}\right\rangle}_M-{\left({e}^{- i\phi}{\left\langle \hat{a}\right\rangle}_M+{e}^{i\phi}{\left\langle {\hat{a}}^{\dagger}\right\rangle}_M\right)}^2, $$

(30)

where the expressions of the averages can be taken from (17–19).

In Fig. 8, S_ϕ is plotted when the difference between the phase of the coherent parameter θ and ϕ is zero, θ − ϕ = 0. We can see that after a small shift, which is increased as M is increased, the state starts to be squeezed, and its absolute maximum value is also increased as M is increased. For relatively large values of n_P, we can see that S_ϕ is significant while the overlap with the CS for these values is extremely close to unity. For example, for the 20th CS in n_P = 80, S_θ ≈− 0.331 while the overlap with the CS equals 0.98.

Fig. 8

The squeezing parameter in the peak rep. of the Mth CSs for different M values when θ − ϕ = 0

The maximum squeezing occurs when θ equals ϕ, which indicates that the squeezing maxima are in the direction of the actual phase of the state. The absolute negative value of the squeezing is decreased as the phase differences θ − ϕ is increased until it reaches π/2, at which there is not any squeezing.

4.3 The Displaced State

Other nonclassical features such as negative Wigner function or P-representation can be derived using the previous relations. However, it is better if we can observe the similarities between the Mth CS and CS with the nonclassical features in more direct relation. We found such a relation, that is all the Mth CSs can be written as the displacement operator acting on some initial state

$$ \mid M\left(\alpha \right)\left\rangle =\hat{D}\left(\alpha \right)\mid {I}_M\left(\alpha \right)\right\rangle =\hat{D}\left(\alpha \right)\sum \limits_{s=0}^M{\beta}_s^M\left(\alpha \right)\mid s\Big\rangle, $$

(31)

where $\hat{D}\left(\alpha \right)$ is the displacement operator which generates the coherent state out of the vacuum. ${\beta}_s^M\left(\alpha \right)$ are the polynomials of the |s〉 state of a given M. The initial state |I_M(α)〉 is normalized and is expressed as ${\sum}_{s=0}^M{\beta}_s^M\left(\alpha \right)\mid s\Big\rangle$. The format of (31) explains that the Mth CS is displacing |I_M(α)〉 which has a finite number of terms to a position α. That is if we determine the initial state, we can directly study how the Mth CS is similar to CS. Here we provide the first three |I_M(α)〉

$$ \mid {I}_0\left(\alpha \right)\left\rangle =\mid 0\right\rangle, $$

(32)

$$ \mid {I}_1\left(\alpha \right)\Big\rangle =\frac{\alpha \mid 1\left\rangle +{\left|\alpha \right|}^2\mid 0\right\rangle }{\sqrt{B_2\left({\left|\alpha \right|}^2\right)}}, $$

(33)

$$ \mid {I}_2\left(\alpha \right)\Big\rangle =\frac{\sqrt{2}{\alpha}^2\mid 2\left\rangle +\alpha \left(1+2{\left|\alpha \right|}^2\right)\mid 1\right\rangle +{\left|\alpha \right|}^2\left(1+{\left|\alpha \right|}^2\right)\mid 0\Big\rangle }{\sqrt{B_4\left({\left|\alpha \right|}^2\right)}}, $$

(34)

$$ \mid {I}_3\left(\alpha \right)\Big\rangle =\frac{\sqrt{6}{\alpha}^3\mid 3\left\rangle +3\sqrt{2}{\alpha}^2\left(1+{\left|\alpha \right|}^2\right)\mid 2\right\rangle +\alpha \left(1+6{\left|\alpha \right|}^2+3{\left|\alpha \right|}^4\right)\mid 1\left\rangle +{\left|\alpha \right|}^2\left(1+3{\left|\alpha \right|}^2+{\left|\alpha \right|}^4\right)\mid 0\right\rangle }{\sqrt{B_6\left({\left|\alpha \right|}^2\right)}}, $$

(35)

where they are derived using the relations of [36, 46] and (2) and some lengthy algebraic derivations.

First, as expected, when α equals 0 the only survival state is |1〉. Thus, the Wigner function in small values of α is negative, since for |1〉 is negative. For large α, the asymptotic behavior indicates that the survival state is the vacuum state, since ${\beta}_0^M$ always has the same power of α as $\sqrt{B_{2M}\left({\left|\alpha \right|}^2\right)}$. Consequently, the Mth CS will eventually be the CS when α →∞. However, reaching the vacuum at large α comes with superpositions from different terms leads to strong nonclassical features. Lastly, we realized that the phase of each term is multiplied by e^isθ which also contributes to generate the nonclassical features.

5 Discussion and Conclusion

We found throughout this study that the Mth CS has many similarities with the CS to a level that one might assume the Mth CS is either classical or at least has negligible nonclassical properties. However unexpectedly, it appears that it has a strong antibunching and strong squeezing at the regions where the overlap with the CS is extremely close to unity. On top of that, the nonclassical actions, as Figs. 7 and 8 show, weakly decay as M grows. This way of quickly resembling the CS while having nonclassicality suggests many potential applications. If the requirement is to keep almost the statistical features such as the photon distribution, the phase distribution, and the minimum uncertainties similar to the classical CS but with extreme nonclassical features, then, the Mth CS is an excellent potential candidate in all these experiments. Also, it can be applied to investigate the quantum world by comparing it with the pure classical CS, which allows us to improve studying the quantum-to-classical transition.

Now, let us discuss the possibility to produce the Mth CS. Generating the Mth CS for any arbitrary M value might be challenging. However, for some particular M values, it might be easier. For example, a schematic to generate the first CS |1(α)〉 is already proposed using the near CS [36]. The definition of the near CS is

$$ \mid \alpha, \Delta \uptheta \Big\rangle =\underset{\mid \Delta \alpha \mid \to 0}{\lim }{C}_{\alpha}\left[|\alpha +\Delta \alpha \Big\rangle -|\alpha \Big\rangle \right]=\underset{\mid \Delta \alpha \mid \to 0}{\lim }{C}_{\alpha}\left[|\alpha +|\Delta \alpha |{e}^{i\Delta \uptheta}\Big\rangle -|\alpha \Big\rangle \right], $$

(36)

where Δα is termed the source, Δθ is the source’s phase and C_α is the normalization factor. We found that when the phase difference between the coherent parameter and the source phase is θ −Δθ = π/2, the resultant state is

$$ \mid \alpha, \pi /2+\theta \left\rangle =i\frac{e^{-{\left|\alpha \right|}^2/2}}{\mid \alpha \mid \sqrt{1+{\left|\alpha \right|}^2}}\sum \limits_{n=0}^{\infty}\frac{n{\alpha}^n}{\sqrt{n!}}\mid n\right\rangle =i\mid 1\left(\alpha \right)\Big\rangle . $$

(37)

Thus, the near CS |α, π/2 + θ〉 resembles the first CS.

Repeating the near superposition technique again but to near coherent state

$$ \mid \alpha, \Delta {\theta}_1,\Delta {\theta}_2\Big\rangle =\underset{\mid \Delta \alpha \mid \to 0}{\lim }{C}_{\alpha 2}\left[|\alpha +\Delta \alpha, \Delta {\theta}_1\Big\rangle -|\alpha, \Delta {\theta}_1\Big\rangle \right], $$

(38)

where Δα = |Δα|${e}^{i\Delta {\theta}_2}$ and C_α2 is the normalization factor. Now from our separate work not reported here, we found that the resultant state when the above state at Δθ₁ = Δθ₂ = π/2 + θ, is the second CS with an overall constant phase. We also conjecture that if we repeat this process over and over, we can generate all the Mth CSs.

The strong relationship between the higher types of the near CSs and the Mth CSs reforms the question of generating the Mth CS to generating these types of near states. If we generate these types, the Mth CSs will be directly featured. The scheme that we proposed in [36] to generate (36) might be generalized to generate all higher types. Or other methods be used to realize the Mth CSs for any M.

In conclusion, the Mth CS appears to be very close to the regular CS as we saw, for example, in the photonic distribution, the minimum uncertainty, and the phase distribution. These coincidences are more spelled out when the coherent parameter is large enough. In contrast to CS, the Mth CS is nonclassical as we saw that it is antibunched and squeezed. We would like to emphasize that this work is still in its cradle stage and more studies are needed to better observe the practical usage and the practical demonstration.