1 Introduction

Owing to their special features, coherent states of harmonic oscillator [1,2,3,4] have become a benchmark in many research fields [5]. It is well known that, despite being the quantum mechanical by construction, their behavior is classical-like in many ways. This striking feature of these states is useful to establish the classical-quantum correspondence of the underlying physical system. Inspired by their usefulness and abundant applications, the notion of coherent states was extended to general systems beyond harmonic oscillator. In literature, a lot of generalization techniques have been introduced [6,7,8,9,10,11,12,13,14,15,16,17,18] and their various properties have been explored [11,12,13,14,15,16,17,18]. However, it has been observed in many cases that the generalized coherent states may exhibit some properties which do not have classical analogues, named as non-classical properties. Such coherent states with non-classical properties are of great importance, for instance, in quantum optical sciences [5], quantum information processing [19,20,21] and quantum computation [22]. In particular their ability to get entangled in various optical systems arose them as to become a key resource in many modern technologies, such as, quantum teleportation [23, 24], quantum meterology [25] and implementation of various quantum gates [22, 26].

The photon-added coherent states |α, m〉 (also known as excited coherent states), initially introduced by Agarwal and Tara [27, 28], provide a very important class of non-classical states. These states, |α, m〉, are obtained by repeated actions (m times) of bosonic creation operator \( {\widehat{a}}^{\dagger } \) on the standard coherent states |α〉 as

$$ \mid \alpha, m\Big\rangle =\frac{{\left({\widehat{a}}^{\dagger}\right)}^m\mid \alpha \Big\rangle }{\left\langle \alpha |{\widehat{a}}^m{\widehat{a}}^{\dagger m}|\alpha \right\rangle }, $$
(1)

and can be expressed explicitly as

$$ \mid \alpha, m\left\rangle =\frac{e^{-\frac{{\left|\alpha \right|}^2}{2}}}{\sqrt{{\mathcal{L}}_m\left(-{\left|\alpha \right|}^2\right)m!}}\sum \limits_{n=0}^{\infty}\frac{\alpha^n\sqrt{\left(n+m\right)!}}{n!}\mid n+m\right\rangle, $$
(2)

where \( {\mathcal{L}}_m(.) \) denotes the m th order Laguerre polynomial with m as non-negative integer. It has been shown that these states are non-classical in nature [27, 28] and are equivalent to nonlinear coherent states [29]. Due to their potential applications in different areas, photon-added and photon-subtracted coherent states associated with various general systems have been constructed and analyzed [30,31,32,33,34,35]. Most recently, photon-added coherent states for noncommutative q-photons [36], shape invariant systems [37] and for spin coherent states [38], have been constructed and analyzed.

In this paper, we construct the photon-added coherent states associated with the su(1, 1) Lie algebra. Associated to SU(1, 1) Lie group, there are two main types of coherent states, namely, Barut-Girardello coherent states [6] and Perelomov coherent states [7]. It has been observed that in many situations, these types of coherent states may exhibit non-classical features. In this work, we use the Holstein-Primakoff (HP) realization of su(1, 1) Lie algebra in which the corresponding generators are expressed as a function of standard bosonic operators [39, 40]. This particular realization of su(1, 1) Lie algebra and associated coherent states have attracted a lot of attention due to their applications, especially in the field of quantum optics [41,42,43] and quantum information [44]. In particular, these coherent states can be used to model the intensity dependent nonlinear fields in quantum optics [42]. Here in this paper, we construct the photon-added Barut-Girardello coherent states and the photon-added Perelomov coherent states in the context of HP realization of su(1, 1) Lie algebra. We discuss their basic properties, such as, normalization, orthogonality condition and resolution of identity operator. Our main focus is to analyze the non-classical properties of our constructed coherent states. In this regard, we first analyze their photon detection probability distribution, by computing Mandel Q-parameter, and then explore their quadrature squeezing.

The paper is organized as follow. In Section 2, we present a brief review on the HP realization of su(1, 1) Lie algebra and corresponding Barut-Girardello and Perelomov coherent states. The construction of photon-added SU(1, 1) coherent states and their properties have been discussed in Section 3. In Section 4, we discuss the non-classical properties of the constructed photon-added states and present the corresponding computational results. Finally we conclude our work in Section 5.

2 The HP Realization of S U(1, 1) and Associated Coherent States

We commence this section by collecting some well known facts concerning su(1, 1) Lie algebra, its Holstein-Primakoff (HP) realization and associated coherent states. The su(1, 1) Lie algebra is defined by three generators \( {\widehat{K}}_{+} \), \( {\widehat{K}}_{-} \) (collectively represented by \( {\widehat{K}}_{\pm } \)) and \( {\widehat{K}}_0 \) obeying the following commutation relations

$$ \left[{\widehat{K}}_0,{\widehat{K}}_{\pm}\right]=\pm {\widehat{K}}_{\pm },\kern3.00em \left[{\widehat{K}}_{-},{\widehat{K}}_{+}\right]=2{\widehat{K}}_0. $$
(3)

These generators obey the hermiticity properties, defined as \( {\left({\widehat{K}}_{-}\right)}^{\dagger }={\widehat{K}}_{+} \), \( {\left({\widehat{K}}_{+}\right)}^{\dagger }={\widehat{K}}_{-} \) and \( {\left({\widehat{K}}_0\right)}^{\dagger }={\widehat{K}}_0 \). Moreover, in the HP realization of the su(1, 1) Lie algebra [39, 40], the generators given in (3) are expressed in terms of standard bosonic ladder operators (\( \widehat{a},{\widehat{a}}^{\dagger } \)) as

$$ {\displaystyle \begin{array}{rcl}{\widehat{K}}_0& =& \widehat{n}+k,\\ {}{\widehat{K}}_{-}& =& \left(\sqrt{2k+\widehat{n}}\right)\kern1em \widehat{a},\\ {}{\widehat{K}}_{+}& =& {\widehat{a}}^{\dagger}\left(\sqrt{2k+\widehat{n}}\right),\end{array}} $$
(4)

where \( \widehat{n}={\widehat{a}}^{\dagger}\widehat{a} \) is the standard bosonic number operator. Here the parameter k is the so-called Bargmann index which is related to the eigenvalues of the su(1, 1) Casimir operator, \( C={\widehat{K}}_{+}{\widehat{K}}_{-}-{\widehat{K}}_0\left({\widehat{K}}_0-1\right) \), and takes on the values as k = 1/2, 1, 3/2,.... for the positive discrete series related to the relevant representations [39, 40].

It is well known that there exist four irreducible representations for the su(1, 1) Lie algebra. The corresponding bases {|n, k〉}, with n = 0, 1, 2,.., should satisfy the eigenvalue equation \( {\widehat{K}}_0\mid n,k\left\rangle =\left(n+k\right)\mid n,k\right\rangle \) along with the following rules

$$ {\displaystyle \begin{array}{rcl}{\widehat{K}}_{-}\mid n,k\Big\rangle & =& \sqrt{(n)\left(n+2k-1\right)}\kern1em \mid n+k-1,k\Big\rangle, \\ {}{\widehat{K}}_{+}\mid n,k\Big\rangle & =& \sqrt{\left(n+1\right)\left(n+2k\right)}\kern1em \mid n+k+1,k\Big\rangle .\end{array}} $$
(5)

However, it is evident from (4) that the bases corresponding to the HP realization are independent of the Bargmann index k, i.e., |n, k〉⇔|n〉. This simply means that the relevant bases span the entire infinite dimensional Hilbert space of the number states |n〉 with n = 0, 1, 2,...

As mentioned before, there are two main types of coherent states associated with the su(1, 1) Lie algebra to be considered within the positive discrete series. The first one is the so-called Barut-Girardello coherent states [6] which are defined as the eigenstates of the lowering operator \( \widehat{K_{-}} \), i.e.,

$$ {\widehat{K}}_{-}\mid z,k\left\rangle =z\mid z,k\right\rangle, $$
(6)

where z is a complex coherent state parameter. The states |z, k〉 can be expressed explicitly in terms of number states as

$$ \mid z,k\left\rangle =\frac{1}{\sqrt{{\mathcal{N}}_{bg}\left({\left|z\right|}^2\right)}}\sum \limits_{n=0}^{\infty}\sqrt{\frac{\Gamma (2k)}{n!\Gamma \left(2k+n\right)}}\kern1em {z}^n\mid n\right\rangle, $$
(7)

where \( {\mathcal{N}}_{bg}\left({\left|z\right|}^2\right)={\kern1em }_0{F}_1\left(2k;{\left|z\right|}^2\right) \) is the normalization constant satisfying the condition 〈z, k|z, k〉 = 1 and 0F1(a;b) represents the hypergeometric function.

The second type, introduced by Perelomov in 1972 [7] and often called the SU(1, 1) Perelomov coherent states, is obtained by the action of a unitary displacement operator on the ground state. Here the displacement operator is defined using elements of the corresponding SU(1, 1) group. As a result the explicit form of the Perelomov coherent states [7] can be expressed as

$$ \mid \xi, k\left\rangle =\frac{1}{\sqrt{{\mathcal{N}}_p\left({\left|\xi \right|}^2\right)}}\sum \limits_{n=0}^{\infty}\sqrt{\frac{\Gamma \left(2k+n\right)}{n!\Gamma (2k)}}\kern1em {\xi}^n\mid n\right\rangle, $$
(8)

where ξ is the coherent state parameter and the normalization constant is of the form \( {\mathcal{N}}_p\left({\left|\xi \right|}^2\right)={\kern.1em }_1{F}_0\left(2k;{\left|\xi \right|}^2\right) \).

3 Photon-Added S U(1, 1) Coherent States

Having equipped with su(1, 1) Lie algebra, its HP realization and associated coherent states, we are in a position to construct two types of SU(1, 1) photon-added coherent states, namely, photon-added Barut-Girardello coherent states and photon-added Perelomov coherent states. In both cases, we would require to repeatedly apply the raising operator \( \widehat{K_{+}} \), defined in (4), on the Fock states |n〉, that is,

$$ {\left({\widehat{K}}_{+}\right)}^m\mid n\left\rangle =\sqrt{\frac{\left(n+m\right)!\Gamma \left(2k+n+m\right)}{n!\Gamma \left(2k+n\right)}}\mid n+m\right\rangle, $$
(9)

where we have recursively used (5) to obtain (9). Moreover, we will show that our constructed photon-added Barut-Girardello coherent states and photon-added Perelomov coherent states satisfy the Klauder’s minimal set of conditions, that is, normalization, non-orthogonality and the resolution of unity.

3.1 Photon-Added Barut-Girardello Coherent States

The Photon-added Barut-Girardello coherent states (PABGCSs) can be obtained by (m-times) repeated action of the raising operator \( {\widehat{K}}_{+} \), defined in (4), on the Barut-Girardello coherent states |z, k〉, defined in (7), i.e.,

$$ \mid z,k,m\left\rangle ={\left({\widehat{K}}_{+}\right)}^m\mid z,k\right\rangle . $$
(10)

By making use of (7) and (9) in above (10), the PABGCSs can be expressed as

$$ \mid z,k,m\left\rangle ={\mathcal{N}}_{z,k,m}\left({\left|z\right|}^2\right)\sum \limits_{n=0}^{\infty}\frac{z^n\sqrt{\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}}{n!\kern1em \Gamma \left(2k+n\right)}\mid n+m\right\rangle, $$
(11)

where \( {\mathcal{N}}_{z,k,m}\left({\left|z\right|}^2\right)=\frac{{\mathcal{N}}_{z,k,m}^1\left({\left|z\right|}^2\right)}{\sqrt{{\mathcal{N}}_{bg}\left({\left|z\right|}^2\right)}} \) is the normalization constant and \( {\mathcal{N}}_{z,k,m}^1\left({\left|z\right|}^2\right) \) takes the form as

$$ {\mathcal{N}}_{z,k,m}^1\left({\left|z\right|}^2\right)={\left[\frac{1}{{\mathcal{N}}_{bg}\left({\left|z\right|}^2\right)}\sum \limits_{n=0}^{\infty}\frac{{\left|z\right|}^{2n}\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}\right]}^{\frac{-1}{2}}. $$
(12)

In order to check the orthogonality condition for the PABGCSs, we calculate the inner product 〈z′, k, m|z, k, m〉 using (11), which is given as

$$ \left\langle z,k,m|{z}^{\prime },k,m\right\rangle ={\mathcal{N}}_{z,k,m}\left({\left|z\right|}^2\right){\mathcal{N}}_{z^{\prime },k,m}\left({\left|{z}^{\prime}\right|}^2\right)\sum \limits_{n=0}^{\infty}\frac{{\left({z}^{\prime }{z}^{\ast}\right)}^n\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}. $$
(13)

It is obvious from (13) that the overlap does not vanish, i.e., 〈z′, k, m|z, k, m〉≠ 0, which implies that PABGCSs are non-orthognal. Before discussing the resolution of unity, it is important to note from (11) that the PABGCS is a superposition of Fock states starting from m, where m is the number of photon-addition. Thus in this case, for m > 0 the identity operator does not appear on the full Hilbert space rather on the subspace of the Hilbert space spanned by the bases \( {\left\{|n\Big\rangle \right\}}_{n=m}^{\infty } \), which is written as

$$ I=\sum \limits_{n=m}^{\infty}\mid n\left\rangle \left\langle n|=\sum \limits_{n=0}^{\infty }|n+m\right\rangle \right\langle n+m\mid . $$
(14)

For resolution of identity, defined in (14), we consider a positive definite weight function w(|z|2) such that

$$ \int \mid z,k,m\left\rangle \right\langle z,k,m\mid w\left({\left|z\right|}^2\right){d}^2z=I. $$
(15)

Substituting the value of PABGCS from (11) in above (15), we get the expression

$$ \pi \sum \limits_{n=0}^{\infty}\mid n+m\left\rangle \right\langle n+m\mid \left[\frac{\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}{\int}_0^{\infty }{\mathcal{N}}_{z,k,m}^2(u)w(u){u}^n du\right]=I. $$
(16)

Here new variables z = reiθ, |z|2 = r2 = u (leading to \( {d}^2z=\frac{1}{2} dud\theta \)) have been introduced and the identity \( {\int}_0^{2\pi }{e}^{i\left(n-m\right)\theta}\mathrm{d}\uptheta =2\pi {\delta}_{nm} \) has been used to obtain the (16). It is obvious from (16) that its left hand side is an identity (by virtue of (14)) provided there exists a weight function w(u) such that

$$ {\int}_0^{\infty}\tilde{w}(u){u}^n du=\frac{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}{\left(n+m\right)!\Gamma \left(2k+n+m\right)\Gamma (2k)}, $$
(17)

where \( \tilde{w}(u)=\uppi \mathrm{w}(u){\mathcal{N}}_{z,k,m}^2(u) \). Our next aim is to obtain such weight function, which can be determined by using inverse Mellin transform. It is well known that the Mellin transform of the Meijers G-function [45] is given as:

$$ {\int}_0^{\infty }{G}_{p,q}^{r,t}\left(\begin{array}{c}{a}_1,...{a}_t,{a}_{t+1},...{a}_p\\ {}{b}_1,...{b}_r,{b}_{r+1},...{b}_q\end{array}|\beta u\right){u}^{s-1} du=\frac{\uppi_{j=1}^r\Gamma \left({b}_j+s\right){\uppi}_{j=1}^t\Gamma \left(1-{a}_j-s\right)}{\uppi_{j=r+1}^q\Gamma \left(1-{b}_j-s\right){\uppi}_{j=t+1}^p\Gamma \left({a}_j+s\right)}{\left(\beta \right)}^{-s}.\kern1.00em $$
(18)

Comparison of (17) and (18) with n = s − 1 and β = 1, provides us with the required weight function w(|z|2) for the PABGCSs, given as

$$ w\left({\left|z\right|}^2\right)\kern0.5em =\kern0.5em \frac{{\mathcal{N}}_{z,k,m}^{-2}\left({\left|z\right|}^2\right)}{\pi \left(2k-1\right)!}{G}_{2,4}^{4,0}\left(\begin{array}{c}m,2k+m-1\\ {}0,0,2k-1,2k-1\end{array}\parallel {\left|z\right|}^2\right), $$
(19)

which satisfies the integral (15).

3.2 Photon-Added Perelomov Coherent States

In order to construct the photon-added Perelomov coherent states (PAPCSs), we repeatedly operate the raising operator, \( {\widehat{K}}_{+} \), on the Perelomov coherent states |ξ, k〉, defined in (8), which provides us with

$$ \mid \xi, k,m\left\rangle ={\left({K}_{+}\right)}^m\mid \xi, k\right\rangle . $$
(20)

By using (8) and (9) in above (20), the PAPCSs can be expressed as

$$ \mid \xi, k,m\left\rangle ={\mathcal{N}}_{\xi, k,m}\left({\left|\xi \right|}^2\right)\sum \limits_{n=0}^{\infty}\frac{\xi^n}{n!}\sqrt{\frac{\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{\Gamma (2k)}}\mid n+m\right\rangle, $$
(21)

where \( {\mathcal{N}}_{\xi, k,m}\left({\left|\xi \right|}^2\right)=\frac{{\mathcal{N}}_{\xi, k,m}^1\left({\left|\xi \right|}^2\right)}{\sqrt{{\mathcal{N}}_p\left({\left|\xi \right|}^2\right)}} \) is the normalization constant and \( {\mathcal{N}}_{\xi, k,m}^1\left({\left|\xi \right|}^2\right) \) is given as

$$ {\mathcal{N}}_{\xi, k,m}^1\left({\left|\xi \right|}^2\right)={\left[\frac{1}{{\mathcal{N}}_p\left({\left|\xi \right|}^2\right)}\sum \limits_{n=0}^{\infty}\frac{{\left|\xi \right|}^{2n}\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left(n!\right)}^2\kern1em \Gamma (2k)}\right]}^{\frac{-1}{2}}. $$
(22)

Similar to the case of PABGCSs, it is straightforward to compute the overlap

$$ \left\langle \xi, k,m|{\xi}^{\prime },k,m\right\rangle ={\mathcal{N}}_{\xi, k,m}\left({\left|\xi \right|}^2\right){\mathcal{N}}_{\xi^{\prime },k,m}\left({\left|{\xi}^{\prime}\right|}^2\right)\sum \limits_{n=0}^{\infty}\frac{{\left({\xi}^{\ast }{\xi}^{\prime}\right)}^n\kern1em \left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left(n!\right)}^2\Gamma (2k)}, $$
(23)

which indicates that the PAPCSs are non-orthogonal. Moreover, analogous to the (14), the completeness relation for PAPCSs can be written as

$$ \int w\left({\left|\xi \right|}^2\right)\mid \xi, k,m\left\rangle \left\langle \xi, k,m|{d}^2\xi =I=\sum \limits_{n=0}^{\infty }|n+m\right\rangle \right\langle n+m\mid . $$
(24)

which again appears on the subspace of the Hilbert space spanned by the bases \( {\left\{|n\Big\rangle \right\}}_{n=m}^{\infty } \). Following the same procedure, as done in the case of PABGCSs, the weight function for the PAPCSs comes out to be

$$ w\left({\left|\xi \right|}^2\right)\kern0.5em =\kern0.5em \frac{\left(2k-1\right)!}{\pi {\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)}{G}_{2,2}^{2,0}\left({\left.\begin{array}{c}m,m+2k-1\\ {}0,0\end{array}\Big\Vert \xi \right|}^2\right), $$
(25)

which satisfies the integral given in (24).

4 Non-Classical Properties

In this section, we first present a commonly accepted criteria to investigate the non-classical behavior of a given coherent state. In this regard, sub-Poisson photon counting statistics, anti-bunching correlation, quadrature and amplitude squeezing, negativity of the Wigner function and Glauber-Sudarshan P-function are frequently used indicators of non-classicality. However, our analysis regarding non-classicality relies on exhibiting the sub-Poisson photon counting statistics and quadrature squeezing.

4.1 Non-Classicality Criteria

Now we introduce the non-classicality indicators that will be used to investigate the non-classical features of the photon-added SU(1, 1) coherent states, namely, photon-added Barut-Girardello coherent states and photon-added Perelomov coherent states, introduced previously in section (3). Here we present a general formalism that will be used to compute analytic relations and corresponding numerical results for specific cases of our constructed PABGCSs and PAPCSs in very next two subsections.

  • The detection probability of counting n photons from a given coherent state |β〉 is calculated as Pn = |〈n|β〉|2. The inherent probability distribution can be characterized by means of so-called Mandel’s Q-parameter [46], which is a good measure to decide whether it is Poissonian (Glauber’s coherent states), sub-Poissonian (non-classical states) or super-Poissonian (classical states). This parameter is defined as

    $$ Q=\frac{{\left(\Delta n\right)}^2}{\left\langle n\right\rangle }-1, $$
    (26)

    where 〈n〉 is the mean and (Δn)2 = 〈n2〉−〈n〉2 is the variance of the corresponding distribution. The nature of photon counting distribution of a coherent state is Poissonian if Q = 0, sub-Poissonian if Q < 0 and super-Poissonian if Q > 0.

  • The non-classical nature of a given coherent state can also be analyzed by means of quantum fluctuations of field quadrature operators. These operators are defined as

    $$ {x}_1=\frac{\widehat{a}+{\widehat{a}}^{\dagger }}{\sqrt{2}},\kern4.00em {x}_2=\frac{\widehat{a}-{\widehat{a}}^{\dagger }}{\sqrt{2}i}, $$
    (27)

    which satisfy the commutation relation [x1, x2] = i and in turn the following uncertainty relation

    $$ {\left(\Delta {x}_1\right)}^2{\left(\Delta {x}_2\right)}^2\ge \frac{1}{4}, $$
    (28)

    where \( {\left(\Delta {x}_j\right)}^2=\left\langle {x}_j^2\right\rangle -{\left\langle {x}_j\right\rangle}^2,j=1,2 \), are the uncertainties in respective quadratures. The quantum fluctuations of the quadrature operators, xj, can be inferred by the squeezing parameters, defined as

    $$ {S}_{x_j}=2{\left(\Delta {x}_j\right)}^2-1. $$
    (29)

    These squeezing parameters can be re-written more explicitly as

    $$ {\displaystyle \begin{array}{rcl}{S}_{x_1}& =& 2\left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle +\left\langle {\widehat{a}}^2\right\rangle +\left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle -2\left\langle \widehat{a}\right\rangle \left\langle {\widehat{a}}^{\dagger}\right\rangle -{\left\langle \widehat{a}\right\rangle}^2-{\left\langle {\widehat{a}}^{\dagger}\right\rangle}^2,\\ {}{S}_{x_2}& =& 2\left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle -\left\langle {\widehat{a}}^2\right\rangle -\left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle -2\left\langle \widehat{a}\right\rangle \left\langle {\widehat{a}}^{\dagger}\right\rangle +{\left\langle \widehat{a}\right\rangle}^2+{\left\langle {\widehat{a}}^{\dagger}\right\rangle}^2.\end{array}} $$
    (30)

    A state is squeezed in either of the field quadratures xj, j = 1, 2, if it satisfies the inequality \( -1\le {S}_{x_j}<0 \).

4.2 Non-Classical Properties of PABGCSs

In order to proceed for the non-classical properties of photon-added Barut-Girardello coherent states, we first explore how the detection probability of counting n photons depends on the parameters involved in PABGCSs, such as, the coherent state parameter z, the Bargmann index k and the photon-addition number m. In this case the photon counting probability distribution is given as

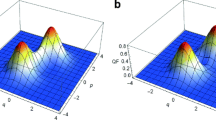
$$ {P}_n={\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\frac{{\left|z\right|}^{2n}\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}. $$
(31)

We numerically compute the probability distribution, Pn, as function of n, z, k and m. The corresponding results are displayed in Figs. 1 and 2 in the form of 3-dimensional (3D) plots.

Fig. 1
figure 1

The photon counting probability distribution Pn of PABGCSs versus photon detection number n and coherent state parameter z with fixed Bargmann index k = 0.5. The values of photon-addition number m are chosen such that: am = 0, bm = 2, cm = 5 and dm = 10

Full size image
Fig. 2
figure 2

The photon counting probability distribution Pn of PABGCSs versus photon detection number n and Bargmann index k with fixed value of z = 6. The values of photon-addition number m are chosen such that: am = 0, bm = 2, cm = 5 and dm = 10

Full size image

Though the 3D plots in Figs. 1 and 2 reflect useful information to understand how the detection probability changes by changing the values of various PABGCS parameters, however, by this it is difficult to decide whether the underlying distribution is Poissonian, sub-Poissonian or super-Poissonian. In this regard we compute the Mandel Q-parameter, defined in (26), which requires to compute the mean and variance of the corresponding distribution. For PABGCSs the first and second moments of probability distribution are, respectively, given as

$$ \left\langle {n}_{bg}\right\rangle ={\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\frac{{\left|z\right|}^{2n}\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}\left(n+m\right), $$
(32)
$$ \left\langle {n}_{bg}^2\right\rangle ={\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\frac{{\left|z\right|}^{2n}\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}{\left(n+m\right)}^2. $$
(33)

By using (32) and (33) in (26), we compute numerically the Mandel Q-parameter for the PABGCSs as a function of z for different values of added-photons m and Bargmann index k. The results are shown by the plots depicted in Fig. 3. It is obvious from these plots that the Q < 0 for all chosen values of m and k which leads us to conclude that the PABGCSs exhibit the sub-Poissonian statistics (narrower than Poisson distribution) and hence non-classical in nature. Moreover, it can be seen from Fig. 3 that the negativity of the Mandel Q-parameter increases as m increases which implies that sub-Poissonian nature of the PABGCSs increases as the number of added-photons increases. As discussed earlier, since the sub-Poissonian distribution is an indicator of non-classicality, therefore, on the basis of our results we conclude that non-classical nature of the PABGCSs increases as the number of added-photons increases.

Fig. 3
figure 3

The Mandel Q-parameter for PABGCSs versus z for two different values of Bargmann index such that: ak = 0.5, bk = 4.5

Full size image

In addition, we examine quadrature squeezing for the PABGCSs through squeezing parameters, \( {S}_{x_j} \), defined in (30). For this we require the following relations

$$ {\displaystyle \begin{array}{rcl}\left\langle {\widehat{a}}^{\dagger}\right\rangle & =& {\left\langle \widehat{a}\right\rangle}^{\ast }={z}^{\ast}\kern1em {\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\sum \limits_n\frac{\left(n+m+1\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)\sqrt{2k+n+m}}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2\left(n+1\right)\left(2k+n\right)}{\left|z\right|}^{2n},\\ {}\left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle & =& {\left\langle {\widehat{a}}^2\right\rangle}^{\ast }={\left({z}^2\right)}^{\ast}\kern1em {\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\sum \limits_n\frac{\left(n+m+2\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)\sqrt{{\left(2k+n+m\right)}_2}}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2{\left(n+1\right)}_2{\left(2k+n\right)}_2}{\left|z\right|}^{2n},\\ {}\left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle & =& \left\langle {n}_{bg}\right\rangle ={\mathcal{N}}_{z,k,m}^2\left({\left|z\right|}^2\right)\sum \limits_n\frac{\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)\kern1em \Gamma (2k)}{{\left[n!\kern1em \Gamma \left(2k+n\right)\right]}^2}{\left|z\right|}^{2n}\kern1em \left(n+m\right).\end{array}} $$
(34)

Using these values of \( \left\langle {\widehat{a}}^{\dagger}\right\rangle \), \( \left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle \) and \( \left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle \) from (34) in (30), we compute the squeezing parameters \( {S}_{x_j}\kern.1em \left(j=1,2\right) \) numerically, as a function of z for different values of photon-addition number m and Bargmann index k. The corresponding results are displayed in Fig. 4. It is clear from the plots (a) and (c) of Fig. 4, that for a wide range of z, the squeezing parameter \( {S}_{x_1} \) takes values such as \( -1<{S}_{x_1}<0 \). This indicates the quadrature squeezing of PABGCSs and in turn their non-classical behavior. Moreover, it can be seen from the magnified images, in the inset plots of Fig. 4, that the negativity of \( {S}_{x_1} \) increases by increasing m, which implies the enhancement of non-classicality by increasing photon-addition number.

Fig. 4
figure 4

The quadrature squeezing parameters \( {S}_{x_1} \) and \( {S}_{x_2} \) of PABGCSs versus z for two different values of Bargmann index k such that: k = 0.5 in (a) and (b); k = 4.5 in (c) and (d)

Full size image

4.3 Non-Classical Properties of PAPCSs

Following the same procedure, as opted for PABGCSs in previous subsection, we now investigate the non-classical features of photon-added Perelomov coherent states (PAPCSs). In this case the photon counting probability distribution comes out to be

$$ {P}_n={\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\frac{{\left|\xi \right|}^{2n}\kern1em \left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left(n!\right)}^2\Gamma (2k)}. $$
(35)

We compute Pn as a function of coherent state parameter ξ, Bargmann index k and photon-addition number m. The corresponding results are shown by means of 3D plots given in Figs. 5 and 6.

Fig. 5
figure 5

The photon counting probability distribution Pn of PAPCSs versus n and k with fixed value of ξ = 0.6. The values of photon-addition number m are chosen such that: am = 0, bm = 2, cm = 5 and dm = 10

Full size image
Fig. 6
figure 6

The photon counting probability distribution Pn of PAPCSs versus n and ξ with fixed Bargmann index k = 1.5. The values of photon-addition number m are chosen such that: am = 0, bm = 2, cm = 5 and dm = 10

Full size image

For the present case, the mean and the second moment of probability distribution are, respectively, given as

$$ \left\langle {n}_p\right\rangle ={\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\frac{{\left|\xi \right|}^{2n}\kern1em \left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left(n!\right)}^2\Gamma (2k)}\left(n+m\right), $$
(36)
$$ \left\langle {n}_p^2\right\rangle ={\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\frac{{\left|\xi \right|}^{2n}\kern1em \left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left(n!\right)}^2\Gamma (2k)}{\left(n+m\right)}^2. $$
(37)

By making use of (36) and (37) in (26), the Mandel Q-parameter is computed as a function of ξ and the results for different values of photon-addition number m and Bargmann index k are shown in Fig. 7. It is clear from this Fig. 7, that the PAPCSs exhibit sub-Poisson distribution (Q < 0) at lower values of coherent state parameter ξ and then get transition to the super-Poisson distribution (Q > 0) at higher values of ξ. Moreover, Fig. 7 shows that, at lower values of coherent state parameter ξ, the negativity of the Q-parameter increases by increasing m. Hence, for a chosen set of parameters, the non-classicality of the PAPCSs increases by increasing photon-addition number m.

Fig. 7
figure 7

The Mandel Q-parameter for PAPCSs versus ξ for two different values of Bargmann index such that: ak = 0.5, bk = 4.5

Full size image

For the PAPCSs the squeezing parameters \( {S}_{x_j},\kern1em j=1,2 \), defined in (30), can be calculated by using the following relations

$$ {\displaystyle \begin{array}{rcl}\left\langle {\widehat{a}}^{\dagger}\right\rangle & =& {\left\langle \widehat{a}\right\rangle}^{\ast }={\xi}^{\ast}\kern1em {\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\sum \limits_n\frac{\left(n+m+1\right)!\kern1em \Gamma \left(2k+n+m\right)\sqrt{2k+n+m}}{{\left[n!\right]}^2\kern1em \left(n+1\right)\Gamma (2k)}{\left|\xi \right|}^{2n},\\ {}\left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle & =& {\left\langle {\widehat{a}}^2\right\rangle}^{\ast }={\left({\xi}^2\right)}^{\ast}\kern1em {\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\sum \limits_n\frac{\left(n+m+2\right)!\kern1em \Gamma \left(2k+n+m\right)\sqrt{{\left(2k+n+m\right)}_2}}{{\left[n!\right]}^2{\left(n+1\right)}_2\kern1em \Gamma (2k)}{\left|\xi \right|}^{2n},\\ {}\left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle & =& \left\langle {n}_p\right\rangle ={\mathcal{N}}_{\xi, k,m}^2\left({\left|\xi \right|}^2\right)\sum \limits_n\frac{\left(n+m\right)!\kern1em \Gamma \left(2k+n+m\right)}{{\left[n!\right]}^2\kern1em \Gamma (2k)}{\left|\xi \right|}^{2n}\kern1em \left(n+m\right).\end{array}} $$
(38)

By using these values of \( \left\langle {\widehat{a}}^{\dagger}\right\rangle \), \( \left\langle {\left({\widehat{a}}^{\dagger}\right)}^2\right\rangle \) and \( \left\langle {\widehat{a}}^{\dagger}\widehat{a}\right\rangle \) from (38) in (30), we compute the squeezing parameters, \( {S}_{x_j} \), as a function of ξ for different values of photon-addition number m and Bargmann index k. The corresponding results are shown in Fig. 8. From these plots, it can be seen that PAPCSs are squeezed either in the x1 quadrature or in x2 quadrature, which indicates their non-classical nature. Analogous to the previous case of PABGCSs, from the magnified images in the inset plots of Fig. 8, again we observe the enhancement of non-classicality by increasing the photon-addition number m.

Fig. 8
figure 8

The quadrature squeezing parameters \( {S}_{x_1} \) and \( {S}_{x_2} \) of PAPCSs versus ξ for two different values of Bargmann index k such that: k = 0.5 in (a) and (b); k = 4.5 in (c) and (d)

Full size image

5 Concluding Remarks

Using the Holstein-Primakoff realization of su(1, 1) Lie algebra, we have constructed photon-added Barut-Girardello coherent states and photon-added Perelomov coherent states. We discussed their basic properties, such as, normalization, orthogonality condition and resolution of identity operator. Our main focus has been to analyze the non-classical properties of our constructed coherent states. In this regard, we first have computed the photon detection probability distribution as a function of various parameters involved and characterized the underlying distribution by numerically computing the Mandel Q-parameter. Then, we have explored the quadrature squeezing properties by numerically computing the quadrature squeezing parameters.

Our numerical results have shown that photon-added Barut-Girardello coherent states exhibit sub-Poisson distribution for all values of coherent state parameter, z, and Bargmann index k. On the other hand, the photon-added Perelomov coherent states exhibit sub-Poisson distribution at lower values of coherent state parameter ξ and then get transition to the super-Poisson distribution at higher values of ξ.However, it has been observed that both types of the constructed photon-added coherent states exhibit squeezing in either of the quadratures, for a chosen set of parameters. These results led us to conclude that our constructed photon-added coherent states are non-classical in nature. Moreover, it has been observed that their non-classical behavior is enhanced as the number of added-photons increases. Due to their non-classical nature these states can be considered as a good candidate for performing various tasks in advanced areas of science and technology, such as, quantum information, quantum computation and quantum meterology.

Finally, we would like to comment that our analytical expressions as well as our numerical results reduce to the ones corresponding to standard Barut-Girardello and Perelomov coherent states, for photon-addition number m = 0. For instance, our numerical results concerning Q-parameter for m = 0, shown in Figs. 3 and 7, are in complete agreement with those appeared previously in literature [44].