Quantum Properties of the Superposition of Two Nearly Identical Coherent States

Abstract

In this paper, we examine the properties of the state obtained when two nearly identical coherent states are superimposed. We found that this state exhibits many nonclassical properties such as sub-Poissonian statistics, squeezing and a partially negative Wigner function. These and other properties indicate that such states, here termed near coherent states, are significantly closer to coherent states more than the generalized Schrördinger cat states. We finally provide an experimental procedure for generating the near coherent states.

1 Introduction

Numerous quantum states have been advanced and examined in quantum optics in order to examine and quantify nonclassical effects such as the negativity of the Wigner function, squeezing, anti-bunching and entanglement [1,2,3,4,5,6]. One quantum state of particular interest is the Schrördinger cat state (SCS) which consists of a superposition of two Glauber coherent states [7], $|\alpha \rangle$, with a $\phi$ phase difference, $|\psi _{S} \rangle = N(|\alpha \rangle + e^{i \phi } |- \alpha \rangle )$ [8,9,10,11], where N is the normalization constant. Such states are particularly relevant to quantum information and computing [12, 13] and have been realized with both optical and atomic states [14, 15].

SCSs have been extended by many authors, for example by employing two different values of the coherent parameter but with a fixed phase for each parameter [16], and two identical magnitude coherent states that are $\pi /2$, $\pi$ or $3 \pi /2$ out of phase [17,18,19,20]. In each case, nonclassical properties such as the squeezing, anti-bunching, and negative Wigner function were found.

The most general expression for the superposition of two arbitrary coherent states, however, was introduced by Hari Prakash and Pankaj Kumarb in 2003 [21, 22], namely

$$ |\psi \rangle= Z_1 |\alpha \rangle + Z_2 |\beta \rangle, $$

(1)

where $Z_{1}$, $Z_{2}$, $\alpha$ and $\beta$ can take any complex value. The normalization condition requires that

$$ \langle \psi | \psi \rangle= |Z_1|^2+|Z_2|^2 + 2 Re \left[ Z_1^{*} Z_2 e^{-\frac{1}{2}(|\alpha|^2+ |\beta|^2)+ \alpha^{*} \beta} \right] = 1. $$

(2)

These authors examined the linear squeezing of the above state and found that the minimum possible value of the uncertainties of the quadrature operators leading to maximum squeezing is 0.11077. This value occurs for an infinite number of parameter sets that satisfy $\alpha -\beta =i 1.59912$ and $Z_{1}/Z_{2}=e^{\alpha ^{*} \beta -\alpha \beta ^{*}}$ [23]. These and many other studies confirm that compared to generalized Schrördinger cat states the superposition of two coherent states is clearly nonclassical. The experimental realization of such states is presented in [9, 12, 13, 24,25,26,27] and numerous applications have been proposed. Additionally, superpositions of states other than coherent states have also been studied [28,29,30].

Despite the many previous extensions and generalizations of SCSs, one superposition has not been examined to the best of our knowledge, namely the superposition of two almost identical coherent states

$$ |\alpha, {\Delta} \theta \rangle= \lim_{|{\Delta} \alpha| \to 0} C_{\alpha} (|\alpha +{\Delta} \alpha \rangle - | \alpha \rangle ), $$

(3)

where $C_{\alpha }$ is a normalization constant, Δα = |Δα|e^iΔ𝜃 is here termed the source of the state and ${\Delta } \theta$ is the phase of the source. While such a state would appear to vanish, the presence of the large normalization constant insures that this state approaches the quantum mechanical analogue of the derivative of a coherent state. We accordingly here term this state the near coherent state.

On the other hand, it is not immediately apparent from the definition of (3) if the near coherent state exhibits nonclassical properties. In fact, however, the analysis of this paper demonstrates that the near state exhibits marked nonclassical properties that differ from those of the SCSs and presumably from other similar quantum states. Below we investigate the quantum properties of such a superposition. We first express these states as a modal superposition, and then examine their mathematical, statistical, and nonclassical properties. After proposing a technique for generating these states we conclude by suggesting some potential applications.

2 The Near Coherent States

We can define the near coherent state mathematically in several different ways. One definition is

$$ |\alpha, {\Delta} \theta \rangle= \lim_{|{\Delta} \alpha| \to 0} C_{\alpha} (|\alpha +{\Delta} \alpha \rangle - | \alpha \rangle )= \lim_{|{\Delta} \alpha| \to 0} C_{\alpha} (|\tilde{\alpha} \rangle- | \tilde{\alpha}- {\Delta} \alpha \rangle)= \lim_{|{\Delta} \alpha \to 0} C_{\alpha}(|\bar{\alpha}+{\Delta} \alpha/2 \rangle- |\bar{\alpha}- {\Delta} \alpha/2 \rangle), $$

(4)

where $\tilde {\alpha }= \alpha + {\Delta } \alpha$ and $\bar {\alpha }=\alpha + {\Delta } \alpha /2$. These formulas are equivalent even if $\tilde {\alpha }$ and $\bar {\alpha }$ are not functions of Δα. Note that in the limit

$$ |\psi \rangle= \lim_{\phi \to 0} N (|\alpha \rangle- |\alpha e^{i \phi} \rangle ). $$

(5)

for which the source phase ${\Delta } \theta$ equals $\theta -\pi /2$, since for small $\phi$, αe^iϕ ≈ α −|α|ϕe^{i(𝜃−π/2)} we recover the second expression of (4) with Δ𝜃 = 𝜃 − π/2, where $\theta$ is the phase of $\alpha =|\alpha | e^{i \theta }$.

The normalization constant $C_{\alpha }$ is obtained from 〈α,Δ𝜃|α,Δ𝜃〉 = 1 and therefore

$$ C_{\alpha}= \frac{ 1}{\sqrt{2- \langle \alpha+{\Delta} \alpha | \alpha \rangle- \langle \alpha | \alpha+{\Delta} \alpha \rangle}}. $$

(6)

Accordingly, the inner product of two general coherent states $| \alpha \rangle$ and $|\beta \rangle$ is given by

$$ \langle \beta | \alpha \rangle +c.c. = e^{- \frac{ 1}{2}|\alpha|^2-\frac{1}{2}|\beta|^2} \left( e^{\beta^{*}\alpha}+ e^{\beta \alpha^{*}} \right). $$

(7)

Using this relation, we find the inner product of 〈α + Δα|α〉 and its complex conjugate as

$$ \langle \alpha+ {\Delta} \alpha | \alpha \rangle+c.c.= 2 e^{-\frac{|{\Delta} \alpha|^2}{2}} \cos(|{\Delta} \alpha| |\alpha| \sin({\Delta} \theta -\theta)). $$

(8)

This expression can be expanded around $|{\Delta } \alpha | \approx 0$ to give

$$ \langle \alpha+ {\Delta} \alpha | \alpha \rangle+c.c. \approx 2- \left[ 1+ |\alpha|^2 \sin({\Delta} \theta-\theta)^2\right] |{\Delta} \alpha|^2 +\cdots. $$

(9)

Then, $C_{\alpha }$ is given as

$$ C_{\alpha}= \frac{1}{|{\Delta} \alpha| \sqrt{1+ |\alpha|^2 \sin({\Delta} \theta-\theta)^2}}. $$

(10)

which diverges in the $|{\Delta } \alpha | \to 0$ limit. Accordingly, the state |α + Δα〉−|α〉 must first be determined after which the limit is taken.

The near coherent state can then be expressed as

$$ |\alpha, {\Delta} \theta \rangle = \frac{1}{\sqrt{1+ |\alpha|^2 \sin({\Delta} \theta-\theta)^2}} \lim_{|{\Delta} \alpha| \to 0} \frac{ |\alpha +{\Delta} \alpha \rangle - |\alpha \rangle} {|{\Delta} \alpha|} . $$

(11)

Substituting $| \alpha \rangle$ as $|\alpha \rangle = e^{-|\alpha |^{2}/2} {\sum }_{n = 0}^{\infty } \alpha ^{n}/\sqrt {n!} |n \rangle$ into (11) yields

$$ | \alpha,{\Delta} \theta \rangle = \frac{1}{\sqrt{1+ |\alpha|^2 \sin({\Delta} \theta-\theta)^2}} \lim_{|{\Delta} \alpha| \to 0} \sum\limits_{n = 0}^{\infty} \frac{1}{\sqrt{n !} |{\Delta} \alpha|} \left[ e^{-\frac{1}{2}|\alpha+{\Delta} \alpha|^2} (\alpha+{\Delta} \alpha)^n -e^{-\frac{1}{2} |\alpha|^2} \alpha^n \right] |n \rangle. $$

(12)

The expression inside the bracket inside the summation can be further written

$$ e^{-\frac{1}{2} |\alpha|^2} \left[ e^{- \frac{1}{2} |{\Delta} \alpha|^2- |\alpha| |{\Delta} \alpha| \cos({\Delta} \theta - \theta)} \left( |\alpha| e^{i \theta} + |{\Delta} \alpha| e^{i {\Delta} \theta} \right)^n- |\alpha|^n e^{i n \theta} \right]. $$

(13)

Expanding the above expression around $| {\Delta } \alpha | \approx 0$ then gives

$$ e^{-\frac{1}{2} |\alpha|^2} \alpha^n \left[ \frac{e^{i({\Delta} \theta - \theta)} n} {|\alpha|}- |\alpha| \cos({\Delta} \theta- \theta) \right] |{\Delta} \alpha| +\cdots. $$

(14)

Substituting this expression back into (12), the source amplitude $| {\Delta } \alpha |$ cancels between the denominator and numerator resulting in

$$ | \alpha, {\Delta} \theta \rangle =e^{-\frac{1}{2}|\alpha|^2} \sum\limits_{n = 0}^{\infty} \frac{\alpha^n \left[ \frac{e^{i({\Delta} \theta - \theta)} n} {|\alpha|}- |\alpha| \cos({\Delta} \theta- \theta) \right]} {\sqrt{ n !} \sqrt{1+ |\alpha|^2 \sin({\Delta} \theta-\theta)^2}} | n \rangle. $$

(15)

This expression can be further simplified as follows

$$ \frac{ \partial | \alpha \rangle} {\partial | \alpha|}= e^{- \frac{1}{2} |\alpha|^2} \sum\limits_{n = 0}^{\infty} \frac{\alpha^n}{\sqrt{n!}} \left[ \frac{ n}{ |\alpha|} - |\alpha| \right] | n \rangle = \frac{e^{- \frac{1}{2} |\alpha|^2}} {|\alpha|} \sum\limits_{n = 0}^{\infty} \frac{ n \alpha^n}{\sqrt{n!}} \, |n \rangle - |\alpha| | \alpha \rangle, $$

(16)

or equivalently

$$ e^{- \frac{1}{2} |\alpha|^2} \sum\limits_{n = 0}^{\infty} \frac{ n \alpha^n}{\sqrt{n!}} \, |n \rangle = |\alpha| \frac{ \partial | \alpha \rangle} {\partial | \alpha|}+ |\alpha|^2 | \alpha \rangle, $$

(17)

where $\frac { \partial \alpha \rangle }{\partial |\alpha |}$ is referred to as the derivative state. The near coherent state is then finally

$$ | \alpha, {\Delta} \theta \rangle = \frac{e^{i\delta \theta}\frac{\partial | \alpha \rangle} {\partial |\alpha|}+ i |\alpha| \sin\left( \delta \theta\right) |\alpha \rangle} {\sqrt{1+ |\alpha|^2 \sin(\delta \theta)^2}}, $$

(18)

where δ𝜃 = Δ𝜃 − 𝜃 is the phase difference.

This constitutes the complete expression for the near coherent state. Evidently the near coherent state exists and adopts the form of a superposition of a coherent state and a derivative state. Also, the structure of the near coherent state depends on the phase differences δ𝜃, which in the $\delta \theta = 0$ limit when the source and $\alpha$ possess the same phase, simplifies to $|\alpha , {\Delta } \theta \rangle =\frac {\partial | \alpha \rangle } {\partial |\alpha |}$. If instead δ𝜃 = ±π/2, the state becomes $|\alpha , {\Delta } \theta \rangle =\pm i(\frac {\partial |\alpha | \rangle }{\partial |\alpha }+|\alpha | |\alpha \rangle )/\sqrt {1+|\alpha |^{2}}$. Lastly for $\alpha = 0$, the near coherent state coincides with $| 1\rangle$.

3 Generalizations of the Near Coherent State

Before examining the properties of near coherent states, we provide a general formulation for constructing a near state starting from any state. Consider a single mode state $| r \rangle$ parametrized by a complex parameter r such as for example a qubit state $| r\rangle = (r |0 \rangle + |1 \rangle )/\sqrt {|r|^{2}+ 1}$. The near state corresponding to $| r \rangle$ is defined as

$$ |r,{\Delta} \theta \rangle= \lim_{|{\Delta} r| \to 0} C_r(|r +{\Delta} r \rangle -|r \rangle)= \lim_{|{\Delta} r| \to 0} C_r(|r +|{\Delta} r|e^{i {\Delta} \theta} \rangle -|r \rangle). $$

(19)

with the normalization constant

$$ C_r= \frac{ 1}{\sqrt{2- \langle r+{\Delta} r | r \rangle- \langle r | r+{\Delta} r \rangle}}. $$

(20)

Expanding the inner product $\langle r | r +{\Delta } r \rangle$ around $|{\Delta } r| \approx 0$, gives

$$ \langle r | r +{\Delta} r \rangle \approx 1+ g_1(r) \, |{\Delta} r|-\frac{g_2(r)}{2} |{\Delta} r|^2+ \cdots, $$

(21)

where $g_{1}(r)$ and $g_{2}(r)$ are expansion functions. Combining this expression with its conjugate

$$ \langle r+{\Delta} r | r \rangle +c.c. \approx 2 + 2 \, \text{Re}(g_1(r)) | {\Delta} r|- \text{Re}(g_2(r)) |{\Delta} r|^2+ \cdots $$

(22)

Substituting (22) into the normalization constant $C_{r}$ then yields

$$ C_r=\lim_{|{\Delta} r |\to 0} \frac{ 1}{\sqrt{- 2 \, \text{Re}(g_1(r)) | {\Delta} r|+\text{Re}(g_2(r)) |{\Delta} r|^2}}. $$

(23)

Since the expansion of $|r +{\Delta } r \rangle - | r \rangle$ in (19) around $|{\Delta } r| \approx 0$ is of the order of |Δr|, the expression of $\text {Re}(g_{1}(r))$ in (23) must be zero to obtain a finite near state. Therefore, if expanding (22) for a given state yields a nonzero value of $Re(g_{1}(r))$, this state cannot construct a near state. Thus $\text {Re}(g_{1}(r))= 0$ is the necessary condition for constructing a nonvanishing near state. Assuming that $| r \rangle$ satisfies this condition, the normalization constant $C_{r}$ then becomes

$$ C_r= \sqrt{ \frac{ 1}{\text{Re}(g_2(r))}} \, \, \frac{1}{|{\Delta} r|}. $$

(24)

Substituting this expression back into the near state $|r,{\Delta } \theta \rangle$ yields

$$ |r,{\Delta} \theta \rangle = \sqrt{ \frac{ 1}{\text{Re}(g_2(r))}} \lim_{|{\Delta} r| \to 0}\frac{ |r+{\Delta} r \rangle -| r \rangle} {|{\Delta} r|}. $$

(25)

After expanding the state $| r+{\Delta } r \rangle$ around $| {\Delta } r| \approx 0$,

$$ |r+{\Delta} r \rangle \approx |r \rangle+ \left( \frac{ \partial | r+{\Delta} r \rangle}{\partial |{\Delta} r|} \right) |_{|{\Delta} r|= 0}|{\Delta} r|+{\cdots} . $$

(26)

which leads to, after combining with the near state expression (25)

$$ |r,{\Delta} \theta \rangle =\sqrt{ \frac{1}{\text{Re}(g_2(r))}} \left( \frac{ \partial | r+{\Delta} r \rangle}{\partial |{\Delta} r|} \right) |_{|{\Delta} r|= 0} . $$

(27)

This final expression describes a near state dependent on a single parameter. Note that (27) depends on two quantities, the state $| r+{\Delta } r\rangle$ and $g_{2}(r)$ which originated in the expansion of the inner product $\langle r| r+{\Delta } r \rangle$. If we assume that both r and ${\Delta } r$ are real, (27) or (25) simplify to

$$ | r,{\Delta} \theta \rangle = \sqrt{ \frac{ 1}{\text{Re}(g_2(r))}} \left( \frac{d | r \rangle}{d r} \right), $$

(28)

which corresponds to a derivative state with respect to the real parameter r.

We next investigate whether near states can be obtained classically. Clearly if two classical waves are superimposed according to

$$ S_1=\lim_{|{\Delta} y| \to 0}\,[ H(y+|{\Delta} y| e^{i {\Delta} \theta})-H(y)], $$

(29)

in which $H(y)$ is any vector field dependent on a variable y which could be, for example, the amplitude, frequency, wave vector of a wave yields S₁ = 0.

On the other hand combining two classical distributions according to

$$ S_2=\lim_{{\Delta} s \to 0} C_s [ P(s+{\Delta} s e^{i {\Delta} \theta})-P(s)], $$

(30)

where $P(s)$ is any non-normalized distribution function, and s, Δs both are real parameters ¹ which characterizes the distribution. For example, $P(s)$ can be a Gaussian distribution, $P(s)=e^{-x^{2}/2s^{2}}$ while s could represent the mean or the standard deviation. Further, x is a real quantity independent of the distribution and $C_{s}$ a normalization constant, which after imposing the normalization condition $\int S_{2} dx= 1$, can be written

$$ C_s=\frac{1}{\int [ P(s+{\Delta} s e^{i {\Delta} \theta})- P(s) ] dx}. $$

(31)

Expanding $P(s+{\Delta } s e^{i {\Delta } \theta })$ around ${\Delta } s \approx 0$, yields

$$ P(s+{\Delta} s e^{i {\Delta} \theta}) \approx P(s)+ e^{i {\Delta} \theta} \frac{\partial P(s)}{\partial s} {\Delta} s+ \frac{1}{2} e^{2 i {\Delta} \theta} \frac{\partial^2 P(s)}{\partial s^2} {\Delta} s^2+ \cdots. $$

(32)

Then, the superposition of (29) becomes

$$ S_2=\lim_{{\Delta} s \to 0} \frac{e^{i {\Delta} \theta} \frac{\partial P(s)}{\partial s} {\Delta} s+ \frac{1}{2} e^{2 i {\Delta} \theta} \frac{\partial^2 P(s)}{\partial s^2} {\Delta} s^2}{ \int \left[ e^{i {\Delta} \theta} \frac{\partial P(s)}{\partial s} {\Delta} s+ \frac{1}{2} e^{2 i {\Delta} \theta} \frac{\partial^2 P(s)}{\partial s^2} {\Delta} s^2 \right] dx}. $$

(33)

If $\frac {\partial P(s)}{\partial s}$ exists, $S_{2}$ becomes

$$ S_2=\frac{ \frac{\partial P(s)}{\partial s}} { \int \frac{\partial P(s)}{\partial s} dx}. $$

(34)

Hence the near distribution of (29) exists and is finite. However the source phase is no longer present in $S_{2}$, so that the resultant distribution is not a function of ${\Delta } \theta$. On the other hand, in (22) or (9) the source’s phase did not factor out as in (32), suggesting that this is a purely quantum mechanical effect. Thus while near states can be formed from classical distributions, these unlike quantum near states are independent of the source phase.

4 Identities and Mathematical Properties

In this section, we derive several mathematical properties of the near coherent state. First, we construct the generator of a state $\hat {A_{\alpha }}$. Observe that if a photon is added to a coherent state by applying the operator $\hat {a}^{\dagger }$, the resulting state is [31]

$$ \hat{a}^{\dagger} |\alpha \rangle =\left( \frac{ \partial} {\partial \alpha}+ \frac{ \alpha^{*}}{2} \right) |\alpha \rangle= \frac{e^{-\frac{1}{2} |\alpha|^2}}{\alpha} \sum\limits_{n = 0}^{\infty} \frac{\alpha^n n}{\sqrt{n!}} \, | n \rangle. $$

(35)

where the derivative is taken with respect to $\alpha$ rather than $|\alpha |$ as in the near coherent state. The relationship between the two derivatives is

$$ \frac{ \partial |\alpha \rangle}{\partial \alpha}= \frac{|\alpha|}{\alpha} \frac{ \partial |\alpha \rangle}{\partial |\alpha|}+ \frac{ |\alpha|^2}{2 \alpha} |\alpha \rangle. $$

(36)

By applying (17), the derivative in (16) simplifies to

$$ \frac{ \partial |\alpha \rangle} {\partial |\alpha|}=\left( \frac{ \alpha}{|\alpha|} \hat{a}^{\dagger} - |\alpha| \right) | \alpha \rangle =\left( \frac{ \alpha}{|\alpha|} \hat{a}^{\dagger} - \frac{|\alpha|}{\alpha} \hat{a} \right) | \alpha \rangle $$

(37)

from which (18) can be rewritten as

$$ |\alpha, {\Delta} \theta \rangle = \left[\frac{e^{i \delta \theta} \frac{\alpha}{ |\alpha|} \hat{a}^{\dagger}-[1-i \sin(\delta \theta)] \frac{|\alpha|}{\alpha} \hat{a}} {\sqrt{1+ |\alpha|^2 \sin(\delta \theta)^2}} \right] |\alpha \rangle = \hat{A_{\alpha}} |\alpha \rangle. $$

(38)

The operator inside the bracket above is the generator $\hat {A_{\alpha }}$. When $\delta \theta = 0$, this becomes

$$ \hat{A_{\alpha}}=\left( e^{i \theta} \hat{a}^{\dagger}- e^{-i \theta} \hat{a} \right), $$

(39)

where again $\theta$ is the complex phase of $\alpha$. Here $\hat {A_{\alpha }}$ is skew-Hermitian and commutes with its Hermitian conjugate and is further nonunitary, implying that a near coherent state cannot be generated from the vacuum state. The commutation relation of $\hat {A_{\alpha }}$ is then

$$ [\hat{A_{\alpha}}, \hat{A_{\alpha}}^{\dagger}]=\frac{ \sin(\delta \theta)^2} {1+ |\alpha|^2 \sin(\delta \theta)^2} [\hat{a}, \hat{a}^{\dagger}]. $$

(40)

The near state can however be related to other known states, such as for example the Agarwal state or the photon-added coherent state, [32] by applying the creation operator according to

$$ a^{\dagger} |\alpha \rangle =\sqrt{1+|\alpha|^2} \, | \alpha , 1\rangle, $$

(41)

where $| \alpha , 1 \rangle$ is the Agarwal state.

Next, acting with the annihilation operator on the derivative of (37) gives

$$ \hat{a} \left( \frac{\partial |\alpha \rangle}{\partial |\alpha|} \right) = \alpha \frac{\partial |\alpha \rangle} {\partial |\alpha |} + \frac{ \alpha}{|\alpha|} |\alpha \rangle. $$

(42)

while applying the annihilation operator to $|\alpha , {\Delta } \theta \rangle$ yields

$$ \hat{a} |\alpha, {\Delta} \theta \rangle = \alpha |\alpha, {\Delta} \theta \rangle +\frac{ e^{i \delta \theta} \alpha} {|\alpha| \sqrt{1+ |\alpha|^2 \sin(\delta \theta)^2}} |\alpha \rangle. $$

(43)

which yields the initial state plus the coherent state. Note that if $\delta \theta$ equals zero, this identity simplifies to

$$ \hat{a} |\alpha, {\Delta} \theta \rangle = \alpha |\alpha, {\Delta} \theta \rangle + \frac{ \alpha}{|\alpha|} |\alpha \rangle. $$

(44)

Also, we can derive

$$ \hat{a}^2 |\alpha, {\Delta} \theta \rangle = \alpha^2 |\alpha, {\Delta} \theta \rangle+ \frac{2 e^{i \delta \theta} \alpha^2}{|\alpha| \sqrt{1+|\alpha|^2 \sin(\delta \theta)^2}} |\alpha \rangle $$

(45)

Next we can find the eigenequation of the near coherent state from (43) and (45) namely

$$ \hat{\mathcal{A}_{\alpha}} |\alpha, {\Delta} \theta \rangle \equiv \left( 2 \hat{a}-\frac{\hat{a}^2}{\alpha} \right) |\alpha, {\Delta} \theta \rangle = \alpha |\alpha, {\Delta} \theta \rangle $$

(46)

in which $\hat {\mathcal {A}_{\alpha }}$ is $\left (2 \hat {a}-\frac {\hat {a}^{2}}{\alpha } \right )$. The near coherent state is not the only possible eigenfunction of this operator as the coherent state $| \alpha \rangle$ itself also constitutes an eigenstate. This eigenequation is closely related to the SCS equation

$$ \hat{a}^2 |\psi_S \rangle = \alpha^2 |\psi_S \rangle, $$

(47)

where $|\psi _{S} \rangle =N(|\alpha \rangle + e^{i \phi } |- \alpha \rangle )$. Hence the operator $\hat {\mathcal {A}_{\alpha }}$ is a combination of the coherent state and SCS operators. Further $\hat {\mathcal {A}_{\alpha }}$ in fact constitutes a special case of the C.Brif operator [33].

To calculate the inner products, (7, 35, 37) can be applied to the coherent state together with the derivative state $\langle \alpha | \left (\frac { \partial |\beta \rangle } {\partial |\beta |} \right )$ to yield

$$ \langle \alpha | \left( \frac{ \partial |\beta \rangle} {\partial |\beta|} \right) = e^{-\frac{1}{2} |\alpha|^2- \frac{1}{2} |\beta|^2+\beta \alpha^{*}} \left[ \frac{ \beta \alpha^{*}}{|\beta|}- |\beta| \right]. $$

(48)

Note that if the derivative is taken with respect to $\alpha$ instead of $\beta$, this inner product becomes zero, implying $\langle \alpha | (\partial |\alpha \rangle /\partial |\alpha |)= 0$. From (48) and (18), the inner product of the near coherent state is then

$$ \langle \alpha |\beta, {\Delta} \theta \rangle = \frac{e^{-\frac{1}{2} |\alpha|^2- \frac{1}{2} |\beta|^2+\beta \alpha^{*}}} {\sqrt{1+ |\beta|^2 \sin(\delta \theta)^2}} \left[ e^{i \delta \theta} \left( \frac{ \beta \alpha^{*}}{|\beta|}-|\beta| \right)+i |\beta| \sin(\delta \theta) \right]. $$

(49)

If both states are instead with respect to $\alpha$,

$$ \langle \alpha |\alpha, {\Delta} \theta \rangle = \frac{ i |\alpha| \sin(\delta \theta)}{ \sqrt{1+ |\alpha|^2 \sin(\delta \theta)^2}} $$

(50)

The inner product of two derivative states is found to be

$$ \left( \frac{ \partial \langle \alpha |}{\partial |\alpha|} \right) \left( \frac{ \partial | \beta \rangle} {\partial |\beta|} \right)= e^{-\frac{1}{2} |\alpha|^2- \frac{1}{2} |\beta|^2+\beta \alpha^{*}} \left[ \frac{ \alpha^{*} \beta}{|\alpha| |\beta|}+ \frac{ \alpha^{*2} \beta^2}{|\alpha ||\beta|}-\frac{|\beta| \alpha^{*} \beta}{|\alpha|}- \frac{|\alpha| \alpha^{*} \beta}{|\beta|}+|\alpha||\beta| \right]. $$

(51)

which can also be employed to calculate the inner product of near coherent states. Observe that this yields unity when $\beta =\alpha$, indicating that the derivative state above is properly normalized.

5 Statistical Properties

Examining next the statistical properties of the near coherent state, the photon probability distribution, is obtained by multiplying (15) with $\langle n |$ and squaring, which yields

$$ P_n=|\langle n |\alpha, {\Delta} \theta \rangle |^2 = \frac{ e^{-|\alpha|^2} |\alpha|^{2 n} \left[ \frac{n^2}{|\alpha|^2}+ \cos(\delta \theta)^2 (|\alpha|^2-2n) \right]}{n! \left( 1+ |\alpha|^2 \sin(\delta \theta )^2 \right)}. $$

(52)

Thus even when $\alpha = 0$ one photon is still present. The photon distribution is illustrated in Fig. 1. When $\delta \theta = 0$, the probability equals zero at n = |α|², indicating the presence of a strong quantum interference. Also for $\delta \theta = 0$ as |α| becomes larger the two peaks of Fig. 1 become identical. Similarly when δ𝜃 = π/2, only one peak is present that is is similar in shape to the Poisson distribution of the coherent state.

Fig. 1

The photon probability distribution of the near coherent state for different values of the phase differences δ𝜃 for |α| = 4

The average number of photons of the near coherent state, $\langle \hat {n} \rangle$, is evaluated from (43),

$$ \langle \hat{n} \rangle = |\alpha|^2+ \frac{1 + 2 |\alpha|^2 \sin(\delta \theta)^2}{1+|\alpha|^2 \sin(\delta \theta)^2}= |\alpha|^2+ M, $$

(53)

where M is defined as

$$ M= \frac{1 + 2 |\alpha|^2 \sin(\delta \theta)^2}{1+|\alpha|^2 \sin(\delta \theta)^2}. $$

(54)

The maximum and minimum value of (53), $2+|\alpha |^{2}$ is attained for $\delta \theta =\pi /2$, $|\alpha |^{2} \gg 1$, and $|\alpha |^{2}+ 1$, $\delta \theta = 0$, respectively. Further, after applying the identity (45), we obtain for the square number operator

$$ \langle \hat{n}^2 \rangle = \langle \hat{a}^{\dagger} \hat{a} \hat{a}^{\dagger} \hat{a} \rangle = |\alpha|^4 + 5 |\alpha|^2+ \frac{1 + 2 |\alpha|^2 \sin(\delta \theta)^2}{1+|\alpha|^2 \sin(\delta \theta)^2}= |\alpha|^4 + 5 |\alpha|^2+M. $$

(55)

So the photon number fluctuation

$$ \langle {\Delta} \hat{n} \rangle= \sqrt{ \langle \hat{n}^2 \rangle -\langle \hat{n} \rangle^2}= \sqrt{|\alpha|^2 (5-2 M)+M(1-M)}=\sqrt{\langle \hat{n} \rangle (5-2M)+M(M-4)}, $$

(56)

with a maximum of $\sqrt {3} \, |\alpha |$ for $\delta \theta = 0$, and a minimum at $\delta \theta = \pi /2$.

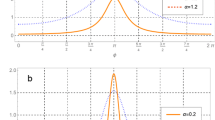
Next, we calculate the quantum phase distribution $\mathcal {P}(\varphi )$ of the near coherent state in the Pegg-Barnett formulation [34, 35], namely

$$ \mathcal{P}(\varphi)= \frac{1}{2\pi} | \langle \varphi| r \rangle |^2, $$

(57)

where the state $|\varphi \rangle$ is defined as

$$ | \varphi \rangle = \sum\limits_{n = 0}^{\infty} e^{i n \varphi} |n \rangle. $$

(58)

Employing (15) then yields

$$ \mathcal{P}(\varphi)=\frac{1}{2 \pi} |\langle \varphi |\alpha, {\Delta} \theta \rangle|^2= \frac{e^{-|\alpha|^2}}{2 \pi [1+|\alpha|^2\sin(\delta \theta)^2]} \left| \sum\limits_{n = 0}^{\infty} \frac{e^{-i (n \varphi-\theta)}|\alpha|^n}{\sqrt{n!}} \left( \frac{n e^{i \delta \theta}}{|\alpha|} -|\alpha| \cos(\delta \theta) \right) \right|^2 $$

(59)

which approaches the single peaked phase distribution of the coherent state as $\delta \theta \rightarrow \pi /2$. In contrast, when $\delta \theta \rightarrow 0$, the distribution exhibits two peaks as Fig. 2 shows.

Fig. 2

The quantum phase distribution $\mathcal {P}(\varphi )$ of the near coherent state for different values of the phase differences δ𝜃 for |α| = 2

6 Nonclassical Properties

6.1 Squeezing Properties

The nonclasicality of the near state also manifests itself through squeezing. The quadrature operators $\hat {X}$ and $\hat {Y}$ are defined as

$$ \hat{X}= \frac{\hat{a}+ \hat{a}^{\dagger}}{2}, \quad \quad \quad \quad \quad \hat{Y}= \frac{\hat{a}-\hat{a}^{\dagger}}{2i}. $$

(60)

These are directly related to the position ($\hat {q}$) and momentum ($\hat {p}$) operators. If one of the uncertainties of these operators is less than $1/4$, then the state is squeezed. To evaluate the expectation values of the quadrature operators for the near coherent state certain mathematical relations derived from (43, 45, 50) are useful, namely

$$\langle \hat{a} \rangle = \alpha \left( 1-i K^{2} \sin(\delta \theta) e^{i \delta \theta} \right), $$

$$\langle \hat{a}^{2} \rangle =\alpha^{2}\left( 1-2i K^{2} \sin(\delta \theta) e^{i \delta \theta}\right), $$

$$ \langle \hat{a} \hat{a}^{\dagger} \rangle = 1+ |\alpha|^2+ K^2(1 + 2 |\alpha|^2 \sin(\delta \theta)^2 )= 1+\langle \hat{n} \rangle, $$

(61)

where K is $1/\sqrt {1+|\alpha |^{2} \sin (\delta \theta )^{2}}$. Note that K is always bounded between 0 and 1. The expectation value of the operators $\hat {X}$ and $\hat {Y}$ are accordingly given by

$$ \langle \hat{X} \rangle =\frac{ \alpha+ \alpha^{*}}{2} + |\alpha| K^2 \sin(\delta \theta) \sin({\Delta} \theta), $$

(62)

$$ \langle\hat{Y} \rangle = \frac{\alpha -\alpha^{*}}{2i} - |\alpha| K^2 \sin(\delta \theta)\cos({\Delta} \theta). $$

(63)

with $\delta \theta ={\Delta } \theta - \theta$. Therefore, both the phase difference $\delta \theta$ and the source phase ${\Delta } \theta$ must be determined. Note that when ${\Delta } \theta =\delta \theta$, the above expressions yield the coherent state results, for which the second term equals zero.

Next, the expectation value for the square of $\hat {X}$ and $\hat {Y}$ operators are

$$ \langle \hat{X}^2 \rangle =\frac{1}{4}+\frac{\alpha^2+\alpha^{*2}}{4}+\frac{|\alpha|^2}{2}+ \frac{K^2}{2} \left[ 1 + 2 |\alpha|^2 S_1 \right], $$

(64)

with $S_{1}=\sin (\delta \theta ) [ \sin (\delta \theta )+ \sin (2{\Delta } \theta -\delta \theta )]$,

$$ \langle \hat{Y}^2 \rangle =\frac{1}{4}-\frac{\alpha^2+\alpha^{*2}}{4}+\frac{|\alpha|^2}{2}+ \frac{K^2}{2} \left[ 1 + 2 |\alpha|^2 S_2 \right], $$

(65)

and $S_{2}=\sin (\delta \theta ) [ \sin (\delta \theta )- \sin (2{\Delta } \theta -\delta \theta )]$. The fluctuations of these operators are then

$$ \langle ({\Delta} \hat{X} )^2\rangle = \frac{1}{4}+K^2 \left[ \frac{1}{2}- |\alpha|^2 K^2 \sin(\delta \theta)^2 \sin({\Delta} \theta)^2 \right], $$

(66)

$$ \langle({\Delta} \hat{Y})^2 \rangle = \frac{1}{4}+K^2 \left[ \frac{1}{2}- |\alpha|^2 K^2 \sin(\delta \theta)^2 \cos({\Delta} \theta)^2 \right]. $$

(67)

From these relations, in general, a state is squeezed if one of the following conditions is satisfied

$$ \frac{1}{2} < |\alpha|^2 K^2 \sin(\delta \theta)^2 \sin({\Delta} \theta)^2, \quad \quad \quad \frac{1}{2} < |\alpha|^2 K^2 \sin(\delta \theta)^2 \cos({\Delta} \theta)^2. $$

(68)

When $\delta \theta = 0$, (66, 67) yield $3/4$, which corresponds to the minimum fluctuation of one photon. In Fig. 3 we display the fluctuations of $\hat {X}$ operator for $\delta \theta$ and ${\Delta } \theta$ phase differences. The figure indicates the presence of squeezing for certain values of ${\Delta } \theta$. The maximum squeezing occurs when $\delta \theta =\pi /2$ and Δ𝜃 = π/2 [0] for the $\hat {X}$ [$\hat {Y}$] operator, and when $|\alpha |=\sqrt {3}$ for which (66) [(67)] yield $3/16$, and (67) [(66)] yield 6/16. In contrast for a phase difference $\delta \theta = 0$ squeezing is not present.

Fig. 3

The fluctuation of $\hat {X}$ operator of the near coherent state for different Δ𝜃 and δ𝜃. Each plot displays curves, from top to bottom, δ𝜃 = 0, π/8, π/4, π/2 where the straight line in both figures is the δ𝜃 = 0 result

The product of (66) and (67) always satisfies the upper and lower bounds

$$ \frac{1}{16} \le \langle ({\Delta} \hat{X})^2 \rangle \langle ({\Delta} \hat{Y})^2 \rangle \le \frac{9}{16} $$

(69)

For example, if both $\delta \theta$ and ${\Delta } \theta$ are $\pi /2$, this product is

$$ \langle ({\Delta} \hat{X})^2 \rangle \langle ({\Delta} \hat{Y})^2 \rangle = \frac{1}{16} \frac{(3+|\alpha|^2)(3+|\alpha|^4)}{ (1+|\alpha|^2)^3}. $$

(70)

which equals $9/16$ for $|\alpha |= 0$ and increases to $1/16$ for |α|≫ 1. The product of (69) is bounded by the fluctuations of the vacuum and a photon unlike the SCS for which fluctuations are unbounded as $\alpha$ increases. This feature is similar to coherent states in which these fluctuations always possess minimum uncertainty values.

6.2 Q Mandel Parameter

The Mandel parameter Q defined by [36]

$$ Q=\frac{ \langle \hat{n}^2 \rangle- \langle \hat{n}\rangle^2}{\langle \hat{n} \rangle}-1. $$

(71)

If $Q>0$ the field exhibits super-Poissonian statistics while for $Q<0$ the field is sub-Poissonian. Further, the field is described by a coherent state if $Q = 0$, and for a number state if $Q=-1$. Sub-Poissonian statistics imply anti-bunching and thus the existence of nonclassical features.

By substituting (53, 56) into the formula for the Mandel Q-parameter (71), we find

$$ Q=\frac{ 2|\alpha|^2(2-M)-M^2}{|\alpha|^2+M} $$

(72)

which is plotted in Fig. 4 against $|\alpha |^{2}$ for different values of $\delta \theta$. The Q parameter indicates that the phase differences between π/4 < δ𝜃 < 3π/4 are uniformly negative implying anti-bunching while phases less than $\delta \theta <\pi /4$ are associated with bunching at large $|\alpha |$. In all cases when $\alpha$ is near zero the field is anti-bunched. The maximum anti-bunching for a given $|\alpha |$ occurs when δ𝜃 = π/2. The anti-bunching of the near coherent state again confirms its nonclassicality.

Fig. 4

The Mandel Q-parameter of the near coherent state for different values of δ𝜃

6.3 Wigner Function

The Wigner distribution $W(\alpha )$ is a distribution over phase space that provides information on whether a state can be described classically. A state with a Wigner function that is negative at any point must be nonclassical, hence the function is often termed a quasi-probability distribution. The Wigner function is defined as

$$ W(\alpha)= \frac{1}{\pi^2} \int d^2 \gamma \, \, Tr \left[ \hat{\rho} \hat{D}(\gamma) \right] e^{-(\gamma \alpha^{*}- \gamma^{*} \alpha)}, $$

(73)

where $\hat {\rho }$ is the density operator of the state, and $\hat {D}(\gamma )$ is the displacement operator, and the integration is taken over the entire physically accessible region. Calculating the Wigner function for a near coherent state with density matrix $\hat {\rho }=|\beta , {\Delta } \theta \rangle \langle \beta , {\Delta } \theta |$ gives

$$\begin{array}{@{}rcl@{}} W(\alpha) & =& -\frac{K^2}{\pi}e^{-2|\alpha-\beta|^2}\left[ 2-8 |\alpha|^2-|\beta|^2(5 + 3 \cos(2 \delta \theta))+(\alpha^{*} \beta+\alpha \beta^{*})(6 + 2 \cos(2 \delta \theta))\right.\\ & &\left. \quad \quad \quad \quad \quad \quad \quad \quad \quad +\, \, \, \, \, 2i (\alpha^{*} \beta-\alpha \beta^{*}) \sin(2 \delta \theta)\right]. \end{array} $$

(74)

which is plotted in Fig. 5 with $\alpha =\alpha _{r}+i \alpha _{i}$ for different values of $\delta \theta$. While the Wigner function appears to always possess negative regions for $\beta < 1$, as β increases the negative regions become smaller in extent except when $\delta \theta = 0$, for which the Wigner function always possesses large negative values as it reduces to

$$ W(\alpha)= \frac{2}{\pi} (4|\alpha-\beta|^2-1)e^{-2|\alpha-\beta|^2}. $$

(75)

This behavior again results from the nonclassical nature of the near coherent state. Also, the Wigner function is local and semi-invariant for a given $\delta \theta$. The shape of the Wigner function will be almost invariant as $\beta$ is increased in (74) while keeping $\delta \theta$ fixed. This feature is similar to coherent state where its shape is exactly invariant for all amplitudes. In contrast, the Wigner functions of SCSs are centered around both $\pm \alpha$, so that as $\alpha$ increases $W(\alpha )$ becomes less localized [8,9,10].

Fig. 5

The Wigner function W(α) of the near coherent state for different phase differences δ𝜃 and β = 2 + i

To summarize, the nonclassical properties of the near coherent state are most pronounced for either $\delta \theta = 0$ or δ𝜃 = π/2. Squeezing and anti-bunching are maximized for δ𝜃 = π/2, while the Wigner function is most negative when δ𝜃 = 0. Indeed, at δ𝜃 = 0, the near coherent state becomes a pure derivative state as (18) demonstrates while when $\delta \theta =\pi /2$, the superposition between the derivative state and the coherent state is maximized.

7 Production

Generating a near coherent states requires a nonunitary procedure as evident from (38). This also is true for SCTs which have nonunitary operators. Here we propose an extension to the Gerry’s method for creating SCTs [37] depicted in Fig. 6. The Mach-Zehnder interferometer in this figure possesses two modes b and c, with one photon in mode b and zero photons in c. Two coherent states $|\alpha \rangle$ and $|\beta \rangle$ are incident as indicated. The interferometer is coupled to a nonlinear medium through the cross-Kerr interaction with mode a where the unitary operator of the nonlinear medium is $\hat {U}_{Kerr}= e^{-i t \chi \hat {a}^{\dagger } \hat {a} \hat {b}^{\dagger } \hat {b}}$. The coefficient $\chi$ is related to the third order nonlinear susceptibility $\chi ^{(3)}$, and t is the interaction time inside the medium and we additionally assume below that χt can be varied.

Fig. 6

A procedure for generating the near coherent states

Next the phase deviation generated by the phase shifter is denoted by $\varphi$ and the corresponding unitary operator is $\hat {U}_{shift}=e^{i \varphi \hat {c}^{\dagger } \hat {c}}$ and $50/50$ splitters are employed in the two sides BS_1,2 with unitary operators $\hat {U}_{BS}= e^{i \frac {\pi }{4}(\hat {c}^{\dagger } \hat {b}+ \hat {c} \hat {b}^{\dagger })}$ while the final 50/50 beam splitter is represented by the unitary operator $U_{BS_{3}}=e^{i \frac {\pi }{4} (\hat {a}^{\dagger } \hat {d}+ \hat {a} \hat {d}^{\dagger })}$. With these conventions, an input state |α〉 _a |1〉 _b |0〉 _c becomes after the first beam splitter (BS₁),

$$ |\alpha\rangle_a |1 \rangle_b |0 \rangle_c \to \frac{1}{\sqrt{2}} |\alpha\rangle_a (|1 \rangle_b |0 \rangle_c+ i |0 \rangle_b |1 \rangle_c). $$

(76)

while after the phase shifter $\varphi$ and the cross-Kerr interaction, the state is transformed to

$$ \frac{1}{\sqrt{2}} |\alpha \rangle_a (|1 \rangle_b |0 \rangle_c+ i |0 \rangle_b |1 \rangle_c) \to \frac{1}{\sqrt{2}}(|\alpha e^{-i \chi t} \rangle_a |1 \rangle_b |0 \rangle_c+ i e^{i \varphi} |\alpha \rangle_a |0 \rangle_b |1 \rangle_c). $$

(77)

The third beam splitter (BS₃), which acts on mode a, yields

$$ \to \frac{1}{\sqrt{2}} \left( \left| \frac{\beta+\alpha e^{-i \chi t}}{\sqrt{2}} \right\rangle_{a} |1 \rangle_b |0 \rangle_c+ i e^{i \varphi} \left|\frac{\beta+\alpha}{\sqrt{2}} \right\rangle_{a} |0 \rangle_b |1 \rangle_c \right). $$

(78)

and finally the second beam splitter (BS₂) generates

$$ | 1 \rangle_b |0 \rangle_c \to \frac{1}{\sqrt{2}} (|1 \rangle_b |0 \rangle_c+ i |0 \rangle_b |1 \rangle_c), \quad \quad \quad \quad | 0 \rangle_b |1 \rangle_c \to \frac{1}{\sqrt{2}} (|0 \rangle_b |1 \rangle_c+ i |1 \rangle_b |0 \rangle_c). $$

(79)

After setting $\varphi = 0$ and rearranging terms, we obtain

$$ |\psi(\chi t) \rangle= \frac{1}{2} \left\{ |1 \rangle_b |0 \rangle_c \left[ | \gamma +{\Delta} \gamma\rangle_a- |\gamma \rangle_a \right]+ i |0 \rangle_b |1 \rangle_c \left[ | \gamma+{\Delta} \gamma \rangle_a+ |\gamma\rangle_a \right] \right\}, $$

(80)

Here $\gamma \equiv (\alpha +\beta )/\sqrt {2}$ and ${\Delta } \gamma \equiv \alpha (e^{-i \chi t}-1)/\sqrt {2}$.

If an event is registered in $D_{1}$, the state projected on mode a is $|\gamma + {\Delta } \gamma \rangle -|\gamma \rangle$, while if $D_{2}$ detects an event, the projected state is $i |\gamma +{\Delta } \gamma \rangle +|\gamma \rangle$. If $\chi t \rightarrow 2\pi$, ${\Delta } \gamma$ becomes $\approx \frac {|\alpha |}{\sqrt {2}}(\chi t-2\pi )e^{i(\theta + 3 \pi /2)}$, which approaches zero as $\chi t \to 2\pi$ and can therefore function as the source of a near coherent state with ${\Delta } \theta _{effective}= \theta + 3\pi /2$. This method can also be applied with $\chi t \to 0$, if the interaction time is suitably small.

After performing the normalization, the projected state in a when a $D_{1}$ event is recorded is a near coherent state with

$$ |\gamma, {\Delta} \theta_{effective} \rangle= \lim_{|{\Delta} \gamma| \to 0} C_{\gamma} (|\gamma+{\Delta} \gamma \rangle- |\gamma \rangle). $$

(81)

To insure that the near coherent state is obtained, χt must be close to but not exactly $2\pi$. If β and $\alpha$ possesses the same amplitude but a different phases, we can write $\alpha = |\alpha | e^{i \theta } ,\beta =|\alpha | e^{i s}$. Then, the amplitude of the near coherent state is $|\gamma |=|\alpha | \sqrt {\frac {1+\cos (\theta -s)}{2}}$, and its phase is $\theta _{effective}=\frac {\theta +s}{2}$ so that the phase difference is

$$ \delta \theta_{effective}={\Delta} \theta_{effective}-\theta_{effective}= \frac{\theta-s}{2}+\frac{3 \pi}{2}. $$

(82)

The value $\delta \theta _{effective}$ can possess any value in the range $0-2\pi$, so, at least in principle, by adjusting the phases of the input coherent states $|\alpha \rangle$ and $|\beta \rangle$, a near coherent state can be produced with any phase difference and amplitude.

8 Conclusion

We have investigated a particular superposition of two coherent states which is characterized by a new parameter, the source phase. The properties of this state, which can be expressed as a superposition of a coherent state and a derivative state, each weighted with a separate function of the phase difference, differ from those of the standard SCSs. In particular, its properties are closer to coherent state while it is nonclassical such that, for example, when $\delta \theta = \pi /2$, the photon probability distribution adopts a quasi-Poissonian distribution and the fluctuation of the quadrature operators approaches the minimum possible value, $1/16$, as $\alpha$ is increased.

A summary of the additional physical properties of the coherent, near coherent and SCS states in Table 1 further establishes the nonclassicallity of the near coherent state as well as its similarity to standard coherent states. Further since the properties of the state can be controlled through the source phase profile, it can be employed to study different aspects of quantum interferences. Its nonclassical properties could also potentially be employed in standard fashion to enable various quantum optics and quantum information applications.

Table 1 Comparison of various physical properties of the coherent state $|\alpha \rangle$, the SCS, as defined in (47) with its properties taken from [8,9,10], and the near coherent state $|\alpha , {\Delta } \theta \rangle$