1 Introduction

Quantum coherence [1] (QC) in semiconductor quantum dots (QDs) offers critical steps toward many technological applications, ranging from manipulation of qubits in quantum logic gates to quantum devices [2] and nano-switches [3]. Numerous coherent properties (CP) common to ideal quantum systems such as electron spin, quantum entanglement, electron photon interaction have already been demonstrated in various types of QDs. Recent reports have also shown that CP in QD qubit is very similar to that in atomic systems qubit [4] or quantum spin qubit [5].

One of the most prominent issues facing investigation of QC in QDs qubit is the effects of the temperature and electric field on the coherence time [6–9]. In fact, except for very low temperatures, the time scale of QC is very short, reaching several hundreds of femtoseconds at room and higher temperatures. Our objective in this paper is to show that the coherence time of nanoparticle QD systems can remain sharp and distinct even when the coherence time of the QDs is of the same order of magnitude of those at room temperature and higher temperatures. We investigate the qubit’s properties of the QDs using the variational method of Pekar type, and study the temperature effect and coherence phenomenon of qubit. For example, Sun et al. [10] studied the effects of magnetic field on the coherence time of a PQD qubit. Xiao and Wang [11] obtained the effect of temperature on the coherence time of a PQD qubit. Recently, considering QDs of different types of potentials (the cylindrical potential, the hyperbolic potential, parabolic potential, etc.) and various semiconductor materials (GaAs, SiC, RbCl, etc.)[12–19], many investigators studied the qubit properties and the quantum coherence effect. Among different QDs, the RbCl parabolic potential QD is a hot point in the low dimensional semiconductor systems. QDs with parabolic potential is an effective theoretical model for describing real dots, and has been demonstrated by some experimental works [20–22]. On the base of the RbCl parabolic potential QD, the quantum coherence time of its qubit in different temperature regions is becoming more and more important. However, the temperature effect of electric field on the coherence time of a RbCl PQD qubit have not been investigated so far by employing VMPT FGRQST. .

In this article, based on the VMPTFGRQST, we calculate the temperature effect on the coherence time of RbCl PQD qubit when electrons are in a superposition state, and discuss the effects of the temperature and electric field on the coherence time of a RbCl PQD qubit. The coherence time temperature effect in RbCl PQD under external electric field is an important subject in quantum computation and quantum information processing.

2 Theoretical Model and Calculations

We consider an electron in the RbCl PQD subjected to an electric field along the ρ x -direction. The electrons are confined much stronger in one direction (taken as the Z- growth direction) than in the other two directions [23, 24]. Therefore, we will focus on the condition of the electron and LO phonon moving only on the X-Y plane. The Hamiltonian of an electron-phonon interaction system reads as follows [25]:

$$ H=-\frac{\hslash^{2}\nabla_{\rho }^{2} }{2m}+\sum\limits_{\mathbf{q}} {\hslash \omega_{LO} } a_{\mathbf{q}}^{+} a_{\mathbf{q}} +\frac{1}{2}m{\omega_{0}^{2}} \rho^{2}+\sum\limits_{\mathbf{q}} {[V_{q} a_{\mathbf{q}} \exp \left( {i\mathbf{q}\cdot \mathbf{r}} \right)+h\cdot c]} -e^{\ast }F\rho_{x}, $$
(1)

where the significances of the physical quantities in (1) are the same with Ref.[25].

Following the VMPT [26–28], the system’s trial GFES wavefunctions of the electron-phonon interaction system takes the form [29, 30]

$$\begin{array}{@{}rcl@{}} \left|\varphi_{0}{(\lambda_{0})}\right\rangle=\left|0\right\rangle\left|\xi(z)\right\rangle\left|0_{ph}\right\rangle, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \left|\varphi_{1}{(\lambda_{1})}\right\rangle=\left|1\right\rangle\left|\xi(z)\right\rangle\left|0_{ph}\right\rangle, \end{array} $$
(3)

where λ 0 and λ 1 are the variational parameters, and |ξ(z)〉 expresses the wavefunction of an electron in the z- growth direction, since the electrons are much more strongly confined in z- growth direction than in other two directions and considered to be confined in an infinitesimally narrow layer, therefore does 〈ξ(z)|ξ(z)〉 = δ(z). The electron’s GFES energies have the following forms:

$$ E_{0} \left( {\lambda_{0} } \right)=\frac{\hslash^{2}{\lambda_{0}^{2}} }{2m}+\frac{\hslash^{2}}{2{\lambda_{0}^{2}} m{l_{0}^{4}} }-\frac{1}{2}\left( {2\pi } \right)^{1/2}\alpha \hslash \omega_{LO} r_{0} \lambda_{0} -\frac{e^{\ast }F\sqrt \pi }{2\lambda_{0}}, $$
(4)

and

$$ E_{1} \left( {\lambda_{1} } \right)=\frac{\hslash^{2}{\lambda_{1}^{2}} }{2m}+\frac{\hslash^{2}}{m{\lambda_{1}^{2}} {l_{0}^{4}} }-\frac{11}{32}\alpha \hslash \omega_{LO} \left( {2\pi } \right)^{1/2}r_{0} \lambda_{1} -\frac{3\sqrt \pi e^{\ast }F}{4\lambda_{1} }, $$
(5)

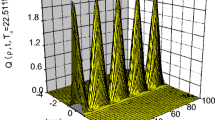
where \(l_{0} =\left (\hslash /{m\omega _{0}} \right )^{1/2}, r_{0} =\left (\hslash /2m\omega _{LO}\right )^{1/2}, l_{0}, r_{0} \) is the ECL and the PR, respectively. A single qubit can be realized in this two-level quantum system. The electron’s superposition state can be calculated using

$$ \left| \psi_{01}\right\rangle=\frac{1}{\sqrt{2}}(\left|0\right\rangle+\left|1\right\rangle), $$
(6)

Under the dipole approximation, based on the Fermi Golden Rule [31], the spontaneous emission rate can be described as

$$ \tau^{-1}=\frac{e^{2}{\Delta} E}{3\pi \varepsilon_{0} \hslash^{2}m^{2}C^{3}}\sqrt {\frac{\varepsilon }{\varepsilon_{0} }} \left| {\left\langle 0 \right|\rho\left| 1\right\rangle } \right|^{2}=\frac{e^{2}{\Delta} E}{3\pi \varepsilon_{0} \hslash^{2}m^{2}C^{3}}\sqrt {\frac{\varepsilon }{\varepsilon_{0} }} \frac{16{\lambda_{0}^{2}} {\lambda_{1}^{4}} }{\left( {{\lambda_{0}^{2}} +{\lambda_{1}^{2}} } \right)^{4}}, $$
(7)

where ΔE = E 1−E 0 depicts the energy separation between the GFES and C is the speed of light in vacuum. ε(ε 0) denotes the material (vacuum) dielectric constant and τ is the coherence time.

3 Temperature Effect

At finite temperature, the properties of the polaron are statistical averages of various states. According to the quantum statistics theory, the statistical average number of the bulk LO phonons is obtained as

$$ \overline N =\left[ {\exp \left( {\frac{\hslash \omega_{LO} }{K_{B} T}} \right)-1} \right]^{-1}, $$
(8)

where K B and T are the Boltzmann constant and the temperature of the system, respectively. The optical phonons’ mean number in superposition state around the electron as follows

$$ N=\frac{1}{4}\left( {2\pi } \right)^{1/2}\alpha r_{0} \lambda_{0} +\frac{11}{64}\left( {2\pi } \right)^{1/2}\alpha r_{0} \lambda_{1}, $$
(9)

through (8) and (9) self-consistently calculation, we can obtain the relationship of λ 0 and λ 1 with the temperature T. From (7) we can see that the coherence time is dependent on the variational parameters λ 0 and λ 1, so it is connected with the temperature T.

4 Numerical Results and Discussion

We take the effective mass of RbCl to be 0.432m 0, and the electron-phonon coupling constant to be α = 3.81 and the energy of bulk LO phonon is \(\hslash \omega _{LO} =21.45meV\) [32].

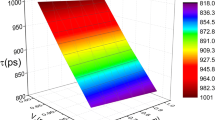
Figure 1 indicates the coherence time τ changing with the temperature T and the electric field F when electrons are in the superposition state of \(\left ({1/{\sqrt {2}}}\right )\left ({\left |0\right \rangle +\left |1\right \rangle }\right )\) for l 0 = 1.0 nm and r 0 = 2.0 nm. The solid and dotted lines correspond to the cases of the electric field F = 0.5, F = 1.0, F = 1.5 and F = 2.0×104 V/cm, respectively. Figure 2 displays the coherence time τ varying the temperature T and the ECL l 0 when electrons are in the superposition state for F = 1.0×104 V/cm and r 0 = 2.0 nm. The solid and dotted lines correspond to cases of the ECL l 0 = 0.5, l 0 = 0.8, l 0 = 1.1 and l 0 = 1.4 nm, respectively. From the two figures, one finds that the coherence time decreases with increasing temperature. The reason is that the increase of temperature results in the increase of the speeds of the electron and the phonon and then the electron will interact with more phonons. The contribution from the electrons interacting with more phonons, which destructs the superposition state, is relatively strong. And the contribution from the increased electron velocity that makes more electrons to be located on the superposition state is relatively weak. Therefore, the coherence time decreases with increasing temperature, which is in good agreement with the results of Makhlin et al. [33], Wang et al. [34] and Xiao et al. [11], whereas this result is the opposite to the case of asymmetric QD qubit [35]. It also can be seen that the coherence time is an increasing function of the ECL, whereas it is a decreasing one of the electric field. Because the increase in the ground state with increasing ECL is smaller than that in the first excited state. Hence, the energy spacing between the GFES will decreases with increasing ECL, and the coherence time increases. The reason of the coherence time decreases with increasing electric field is that the influence of the electric field in the PQD is stronger in the ground-state than that in the first-excited state with increasing electric field. For this reason, the energy space between the GFES increases with increasing electric field and then the coherence time decreases.

Fig. 1
figure 1

The coherence time τ as a function of the temperature T and electric field F for RbCl crystal

Full size image
Fig. 2
figure 2

The coherence time τ as a function of the temperature T and effective confinement length l 0 for RbCl crystal

Full size image

The magnitude of the coherence time obtained in the present paper is in the range of 0–100 microseconds, which is in agreement with that obtained in Refs. [36, 37], which were obtained individually by experiments and the effective mass envelope function theory. Here one can see that by changing the electric field, the temperature and the ECL one can adjust the coherence time.

5 Conclusions

The relations of the coherence time of a RbCl PQD qubit on the temperature, the electric field and the ECL are studied by using the VMPTFGRQST. Numerical results show that the coherence time is a decreasing function of the temperature and the electric field, whereas it is an increasing one of the ECL. By changing temperature, the electric field and the ECL one can adjust the coherence time. Our calculated results should be useful for designing the solid-state implementation of quantum computing.