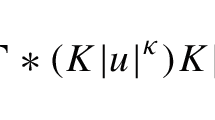Abstract
In this paper we consider solutions of the Dirac equation at ultra high energies. The study provides new insights including features overlooked thus far and also new ramifications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is known that at very high energies, we encounter negative energies. This is because the set of positive energy solutions of the Dirac or Klein-Gordon equations is not a complete set [1]. At usual energies we could apply the well known Foldy-Wothuysen transformation to recover a description in terms of positive energies alone or more precisely a description free of operators which mix negative energy and positive energy components of the wave function. This description also leads in the non-relativistic limit to the two component Pauli equation [2]. The situation is rather different at very high energies as we see below.
2 Solutions at Ultra High Energies
At very high energies the Cini-Toushek transformation of the Dirac equation leads to [3]
where
More conventionally we have
where σ k are the Pauli matrices and I is the 2×2 unit matrix.
We will also require the transformation of the γ 5 operator, which is, given by,
In the transformation (1) γ 5 goes over to Γ 5 given by
In the above \(\vec{n}\) is the unit vector in the direction of the momentum vector. We can see from (6) that
whenever m is negligible compared to \(E:0 (\frac{m}{E} ) \ll 1\).
Returning to the Dirac equation we have:
It may be mentioned that two component spinors belonging to the representation [3],
of the Lorentz group are solutions of the Dirac equation (8). But these are no longer invariant under reflections [4]. It is to preserve this invariance that we have to consider the 4×4 representation
Under reflections, the two spinors transform into each other thus maintaining the overall invariance [3].
A similar much less known analysis was carried out by Sudarshan [5] and co-workers who considered separately the usual Dirac regime denoted by D and the high energy regime denoted by E. They defined projection operators
and
They then obtained the following relations for the coordinates x,y,z marked by subscripts +,− denoting the positive energy and negative energy solutions:
The remarkable result of (11) which was overlooked, was the fact that the coordinates no longer define a commutative spacetime.
3 Noncommutative Spacetime
Indeed Newton and Wigner [6, 7] showed that the correct physical coordinate operator is given by
where E is a projection operator is given by
and the gamma denote the usual Dirac matrices.
To appreciate the significance of (12), we first consider the case of spin zero.
Then (12) goes over to
The first term on the right side of (13) denotes the usual position operator, but the second term represents an imaginary part, which has an ∼1/μ, the Compton wavelength, exactly as in the case of the Dirac electron. Herein can be seen the origin of the Compton scale.
Returning to Dirac’s treatment of the electron [8], the position coordinate is given by
H being the Hamiltonian operator and α’s the non-commuting Dirac matrices, given by (2).
In fact we have the explicit coordinate given by
with α k =γ 0 γ k ,k=1,2,3.
We can see that the oscillatory or Zitterbewegung term is in fact the last term in the above equation, which contains the noncommuting matrices \(\vec{\alpha}\). So a commutator of the coordinates will contain terms of the form [α k ,α j ]L 2 where L is the Compton scale.
It may also be mentioned that Zitterbewegung has been studied in detail by David Hestenes [9]. All this is symptomatic to the fact that we are dealing with a many particle theory, necessitating for example Dirac’s Hole Theory or Quantum Field Theory.
The first term on the right hand side is the usual (Hermitian) position. The second term of \(\vec{x}\) is the small oscillatory term of the order of the Compton wavelength (as in (15)), arising out of Zitterbewegung effects which averages out to zero. In other words the extension l or the Compton scale reappears.
The first term on the right hand side is the usual (Hermitian) position. The second term of \(\vec{x}\) is the small oscillatory term of the order of the Compton wavelength, arising out of zitterbewegung effects which averages out to zero over the Compton scale. In other words to extension l or the Compton scale reappears.
On the other hand, if we were to work with the (non Hermitian) position operator in (14), then we can easily verify that the following non commutative geometry holds,
where α ıj ∼0 (1). The l 2 in (16) arises from the fact that the imaginary or non Hermitian part of (14) is an effect at the Compton scale l. In any case the non commutativity of the coordinates reappear.
While a relation like (16) has been in use recently, in non commutative models including the author’s own, and as will be noted below, was an independent starting point due to the work of Snyder, we would like to stress that it has been overlooked that the origin of this non commutativity lies in the original Dirac coordinates ((14) or (15)).
It may also be mentioned that the Dirac equation with the noncommutative coordinates still has Lorentz symmetry [10]. Indeed Hartland Snyder who first studied the Dirac equation with a minimum spacetime extension also derived Lorentz invariant equations.
Finally the above many body aspect can be viewed as follows: The Dirac particle can be considered as a part of a poly particle in Clifford’s space [11].
The relation (14) shows that
In (17), the first term is the usual momentum. The second term is the extra “momentum” (and therefore energy) \(\vec{p}\) due to the relations (16).
In fact we can easily verify from (17) that
where \(\hat{x}\) has been defined in (14).
Indeed in recent years this has lead to the so called Snyder-Sidharth dispersion relation [12], wherein the energy takes on a small correction term viz.,
4 Further Developments
The Feshbach and Villars interpretation throws further light [1]. Given
the Klein-Gordon equation can be written as
[13]. We note that (20) represent two coupled equations for the two component objects ϕ and χ. If however, e=0=m in (20), these get uncoupled, giving the Klein-Gordon (and Dirac) equations for ϕ and χ separately, representing “uncoupled” neutrinos and antineutrinos. On the other hand, a non-zero mass implies mixing of positive and negative solutions and vice-versa.
More generally this leads to the following scenario: For one observer we have,
and for another higher energy observer we have
This is what may be called the mathematical bound state given after Eq. (8).
The above scenario would be valid for a single observer if a particle velocity got a sudden large boost. All this is true of any Dirac particle. This shows that there is a transmutation between particles and antiparticles as indeed has been observed, for example for the B-meson (cf. Ref. [14]).
We can see the above from another point of view. Our starting point is the solution of the Dirac equation [2] given by
where the current vector is given by
As can be seen from (24), there is the time independent group velocity given by the first term within parenthesis. Additionally there is a sum of two cross products of positive and negative energy solutions. This cross product as can be seen oscillates very rapidly with the frequency \(\frac{2 p_{0}c}{\hbar}\). It is this rapid oscillation that is the Zitterbewegung which needs to be eliminated. For a localized wave packet there are two regions: an inner region of the order of the Compton scale within which the packet is packed and on the region outside. It is in this region, which we may call the outer region that our usual concepts of spacetime appear. Within this region however as can be seen from (24) we have a mixture of eigen states of positive energy and negative energy that is we have a situation where time oscillates between positive and negative values rapidly. Indeed Wigner and Salecker showed that there can be no physical or definite time within the Compton scale and that time as we know it is a phenomenon outside this scale.
The Compton scale gives rise to the Zero Point Field which in the author’s work models dark energy [15]. The positive and negative eigen values which arise from (24) for the \(\frac{d}{dt}\) or energy operator inside the Compton wavelength clearly define a non differentiable time rapidly oscillating (cf. also Ref. [16]).
Another way of looking at this is, following Sudarshan and co-workers, we write the wave function as
where the right side represents positive and negative energy solutions. As we saw, Sudarshan then got [5] a noncommutative geometry, which unfortunately was overlooked.
The above clearly shows that the energy or d/dt operator does not have a fixed eigen value but rather due to the Zitterbewegung rapidly oscillates with eigen value +E and −E represents in the Feshbach-Villars representation a rapid flip flop between particles and antiparticles, or as all this happens in the Compton Scale, it could be interpreted as in recent times, as a particle being surrounded by a cloud of extremely short lived particles and antiparticles. This as we know leads to renormalization techniques.
We could think of the above in terms of the Wiener process. In this case the probability density is given by
whose expectation is zero:
The variance however is given by
It turns out as can be seen from (27) that the time t in this formulation appears as a standard deviation. This was argued several years ago by the author, directly from a Random Walk process [17]. Thus time appears with a slightly different character. With N events which can be likened to N random tosses or steps, the fundamental interval between events being given by τ, we have the time elapsed T given by
One could see that this Wiener process in the Zitterbewegung region, that is the Compton scale clearly leads to a break of symmetry as argued for the Kaon and the B-meson [18]. This could be characterized as a new interaction defined by the covariant derivative which by Ito’s lemma can be written as
where the subscript t refers to the instant of time in question. Equation (28) though stochastic, resembles an electromagnetic (gauge) interaction as σ, the standard deviation is a scalar. On the other hand this arises from the Zero Point Field. This interaction in the model can be looked upon as causing the flip between particles and antiparticles and vice versa.
We also note that the zero point energy encountered above comes from the normal modes of oscillators and is ≈ω/2. As is known [2] such a fluctuating electromagnetic field would persist even when there are no external fields. Even though the average strength is zero, there is the residual mean square value for this field and that is the Zero Point Field whose effect can be seen for instance in the well known Lambshift of energy levels.
We can even show that classical physics with the addition of Zero Point Field leads to the Quantum Mechanical commutation relations, that is Quantum Theory itself [12, 19].
It is also known that it is the Zero Point Field which leads to other Quantum effects like the anomalous g=2 factor. Furthermore, as can be seen from (13) and (14), this field also gives rise to noncommutative spacetime.
We may note that it is fluctuations that underpin the universe. In the author’s 1997 model [20, 21] it was this Zero Point Field, later called Dark Energy that caused the slightly accelerated expansion of the universe which was subsequently confirmed in 1998 by the observations of Perlmutter, Schmidt and Riess [22].
We also note that once we introduce the non differentiable time as above, then rather than the Schrodinger formulation that is usually obtained, we can directly get the Klein-Gordon relativistic case. This has been described in detail [12]. But briefly the origin of this is a treatment of discrete states like the two state system which now leads to
whence the Klein-Gordon equation follows.
5 Matter, Antimatter, Asymmetry
This has been one of the unsolved puzzles because it is widely believed that at the time of the Big Bang particles and antiparticles were created in equal numbers. Yet matter dominates in the universe overwhelmingly. The above considerations throw light on this. This can be seen from equations (21) and (22). In the initial epoch the negative energy solution or antiparticle (22) would dominate but with the rapid cooling of the temperature (21) would begin to dominate. As noted this would imply a flip flop from antiparticles to particles. It has already been pointed out by the author [23] that this process could be designated in terms of a new super spin: Thus one state would be a super spin up and the other would be a super spin down. This has been observed for B-mesons as noted above.
The other aspect is that as argued by the author [24], there is an inherent slight asymmetry between particle solutions and antiparticle solutions. For a slightly different treatment (cf. Ref. [25]). Indeed in recent years there have been indications, particularly from the MINOS experiment of Fermi Lab that indeed neutrinos and antineutrinos not only have slightly different behaviour, but also masses.
References
Freshbach, H., Villars, F.: Rev. Mod. Phys. 30(1), 24–45 (1958)
Bjorken, J.D., Drell, S.D.: Relativistic Quantum Mechanics p. 39. McGraw-Hill, New York (1964)
Schweber, S.S.: An Introduction to Relativistic Quantum Field Theory. Harper & Row, New York (1961)
Heine, V.: Group Theory in Quantum Mechanics p. 364. Pergamon Press, Oxford (1960)
Sudarshan, E.C.G., Bose, S.K., Gambu, A.: Phys. Rev. 113(6) (1959)
Newton, T.D., Wigner, E.P.: Rev. Mod. Phys. 21(3), 400–405 (1949)
Sidharth, B.G.: Found. Phys. Lett. 15(5), 501ff (2002)
Dirac, P.A.M.: The Principles of Quantum Mechanics p. 4ff, 253ff. Clarendon, Oxford (1958)
Hestenes, D.: http://modelingnts.la.asu.edu
Kupriyanov, V.G.: arXiv:1308.1350
Castro, C.: J. Phys. A, Math. Theor. 43, 365201 (2010)
Sidharth, B.G.: Thermodynamic Universe. World Scientific, Singapore (2008)
Sidharth, B.G.: Int. J. Mod. Phys. E 14(6), 927ff (2005)
Sidharth, B.G.: arXiv:1107.4459
Sidharth, B.G.: Chaotic Universe: from the Planck to the Hubble Scale. Nova Science, New York (2001)
Ichinose, T.: Physica 124A, 419 (1984)
Sidharth, B.G.: Chaos Solitons Fractals 12(1), 173–178 (2000)
Sidharth, B.G.: Curr. Sci. 25 (2013)
Sachidanandam, S.: Phys. Lett. A 97(8), 323–324 (1983)
Sidharth, B.G.: Int. J. Mod. Phys. A 13(15), 2599ff (1998)
Sidharth, B.G.: In: Piran, T. (ed.) Proc. of the Eighth Marcell Grossmann Meeting on General Relativity, pp. 476–479. World Scientific, Singapore (1999)
Perlmutter, S., et al.: Nature 391(1), 51–59 (1998)
Sidharth, B.G.: Int. J. Mod. Phys. E 20(10), 2177–2188 (2011)
Sidharth, B.G.: Electron. J. Theor. Phys. 7(24) (2010)
Sidharth, B.G., Glinka, L.A.: On Neutrino and Anti-Neutrino Solutions in Modified Relativity in GPBC-01-01-2013 (2013)
Acknowledgement
I am grateful to the referee for insightful comments which have been incorporated in the text.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sidharth, B.G. High Energy Dirac Solutions: Issues and Ramifications. Int J Theor Phys 53, 1561–1568 (2014). https://doi.org/10.1007/s10773-013-1954-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-013-1954-z