1 Introduction

Quantum entanglement is one of the fascinating features of quantum mechanics, and it is also an very important resource in geometric quantum computing [1–3], quantum teleportation [4], quantum cryptography [5] and quantum state sharing [6, 7]. After Hillery et al. [8] demonstrated that a three-particle GHZ state can be used for quantum information splitting (QIS), QIS have been investigated extensively [9–12]. As one of possible candidates for engineering quantum entanglement, the cavity quantum electrodynamics (QED) system has made many applications in quantum information processing including QIS. In cavity QED systems, QIS of an arbitrary two-atom state can be realized by using cluster state [13], genuine five-atom entangled state [14].

It is well known that the W state has some interesting entanglement-properties [15]. For example, it retains bipartite entanglement when any one of the three qubits is traced out and thus it is much more robust than the GHZ states, as demonstrated in the experiment [16]. We believe that such a state is more favorable to realize the QIS of an arbitrary two-atom state in cavity QED, and which is robust against decoherence.

In this work, we propose a scheme to realize QIS of an arbitrary two-atom state by using three sets of W-class states in cavity QED. Here, we consider that the atoms interact with a thermal cavity with the assistance of the strong classical driving field, so our scheme is not sensitive to both the cavity decay and the thermal field [17, 18].

2 Generation of the W-Class State

We first consider three identical two-level atoms simultaneously interacting with a single-mode cavity field. In the interaction picture and the rotating-wave approximation, the interaction Hamiltonian (we set ħ=1) can be written as [19]

$$ H_{I} = g\sum_{j = 1}^{3} \bigl[ \bigl( e^{ - i\delta t}a^{\dag }\sigma_{j}^{ - } + e^{i\delta t}a\sigma_{j}^{ + } \bigr) \bigr] , $$
(1)

where \(\sigma_{j}^{ + } = | 1_{j} \rangle\langle0_{j} |\), \(\sigma _{j}^{ - } = | 0_{j} \rangle\langle1_{j} |\) with |0 j 〉 and |1 j 〉 being the ground and excited states of the j-th atom, a and a † are in turn the annihilation and creation operator of the cavity-field mode. g represents the atom-cavity-field coupling strength, and δ is the detuning between the transition |1〉 j →|0〉 j and cavity frequency ω. In the case δ≫g the upper levels can be adiabatically eliminated, there is no energy exchange between the atoms transition frequency ω 0 and the cavity frequency ω. Thus the effective Hamiltonian can be given by [20]

$$ H_{e} = \lambda\Biggl( \sum_{j = 1}^{3} | 1_{j} \rangle \langle1_{j} | + \sum _{i,j = 1}^{3} \sigma_{i}^{ - } \sigma_{j}^{ + } \Biggr) \quad i \ne j, $$
(2)

where λ=g 2/δ. Assume that the atoms 1, 2, and 3 are initially in the states |001〉123 then the state evolution of the atom system can be represented by

$$ |\psi\rangle_{123} = \frac{e^{ - i3\lambda t} + 2}{3}|001 \rangle_{123} + \frac{e^{ - i3\lambda t} - 1}{3} \bigl( |010 \rangle_{123} + |100 \rangle_{123} \bigr). $$
(3)

We choose λt=[π−cos−1(1/8)]/3 and perform the single-atom rotation |1〉3→e −iθ|1〉3, where

$$ \theta= - \tan^{ - 1}\frac{\sin ( 3\lambda t )}{1 + \cos ( 3\lambda t )} - \tan^{ - 1}\frac{\sin ( 3\lambda t )}{2 + \cos ( 3\lambda t )}. $$
(4)

Then we can obtain the W-class state [21]

$$ |W \rangle_{123} = \frac{1}{2} \bigl( | 100 \rangle_{123} + |010 \rangle_{123} + \sqrt{2} |001 \rangle_{123} \bigr), $$
(5)

where we have discarded the common phase factor. Then, performing the transformation |0〉→i|0〉 on atom 1, we can obtain the W-class state [21]

$$ | W \rangle_{123} = \frac{1}{2}\bigl( | 100 \rangle_{123} + i| 010 \rangle_{123} + i\sqrt{2} | 001 \rangle_{123} \bigr). $$
(6)

Next, we implement QIS by using the above W-state as quantum channel.

3 QIS of an Arbitrary Two-Atom State in Cavity QED

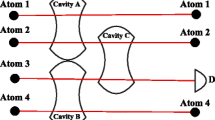
Our scheme can be described as follows. Suppose there are three legitimate parties, say, Alice, Charlie and Bob. Alice is the sender of quantum information. Charlie and Bob are two agents. We suppose Alice has an arbitrary two-atom state, which can be described as follows

$$ | \psi\rangle_{AB} = \alpha| 00 \rangle_{AB} + \beta| 01 \rangle _{AB} + \gamma| 10 \rangle_{AB} + \theta| 11 \rangle_{AB}, $$
(7)

where |α|2+|β|2+|γ|2+|θ|2=1. The quantum channel between Alice and her two agents consists of three sets of W-class states. For splitting an arbitrary two-atom state, Alice first shares two-W-class states |W〉123, |W〉456 with Charlie, then Charlie and Bob share another W-class state |W〉789, where

$$ | W \rangle_{123} = | W \rangle_{456} = | W \rangle_{789} = \frac{1}{2}\bigl( | 100 \rangle+ i| 010 \rangle+ i\sqrt{2} | 001 \rangle\bigr). $$
(8)

The atoms A, B, 1, 2, 4 and 5 belong to Alice, the atoms 3, 7 and 8 belong to Charlie, and the atoms 6 and 9 belong to Bob, respectively.

At the beginning, the combined state of the quantum system composed of the eight atoms A, B, 1, 2, 3, 4, 5 and 6 can be written in the following form of direct product

(9)

with ±1 and ±2 correspond to the three-atom joint measurements on her atoms (A,1,2) and (B,4,5) in the basis of {|η ±〉,|ξ ±〉}, respectively, and they mean multiplication of ± signs. Here |η ±〉 and |ξ ±〉 are a set of orthogonal states in the W-state category given by

(10)
(11)

Then, the more important problem is how to differentiate the four measurement bases. That is to say, whether can it realize the QIS protocol or not? Next, let us introduce an experimentally feasible scheme for distinguishing the four measurement bases in detail.

Firstly Alice performs the transformations |1〉1→e iπ/4|1〉1 and |1〉2→e iπ/4|1〉2, Eqs. (10) and (11) become

(12)
(13)

After that, the atoms 1 and 2 are simultaneously sent through a single-mode cavity and driven by a classical field. The Hamiltonian in the rotating-wave approximation can be written as [22]

(14)

where \(\sigma_{z,j} = \frac{1}{2}\ ( | 1_{j} \rangle\langle1_{j} | - | 0_{j} \rangle\langle0_{j} | )\ ( j = 1,2 )\), g is the atom-cavity coupling strength, Ω is the Rabi frequency, and ω is the frequency of the classical field. Here we consider the case of ω 0=ω. In the large detuning δ≫g/2, and strong driving field 2Ω≫δ,g limit, and there is no energy exchange between the atoms and the cavity. Then in the rotating-wave approximation, the effective Hamiltonian can be described as follows [22]

(15)

with λ=g 2/2δ. The Hamiltonian is independent of the cavity field state, allowing it to be in a thermal state. Then the evolution operator of the system is given by

$$ U( t ) = e^{ - iH_{O}t}e^{ - iH_{e}t}, $$
(16)

with \(H_{0} = \sum_{j = 1,2} \varOmega( \sigma_{j}^{ + } + \sigma _{j}^{ - } )\). Suppose that the two atoms are initially in one of four product states |0〉1|0〉2, |0〉1|1〉2,|1〉1|0〉2 and |1〉1|1〉2. When the two atoms are sent into the single-mode cavity, and λt 1=π/4 and Ωt 1=π, the four product states will become the following states, respectively,

Then Eqs. (12) and (13) would become

(17)
(18)

In succession, Alice sends the atoms A and 1 simultaneously through another single-mode cavity and driven by a classical field. According to Eq. (15), and we choose λt 2=π/4 and Ωt 2=π, Eqs. (17) and (18) finally become

where we have discarded the overall phase factor. Hence the joint measurement can be achieved by detecting atoms A and 1 separately. Alice does the same things on the atoms (B,4,5).

To achieve the purpose of QIS in cavity QED, Alice then measures her atoms A, B, 1 and 4, separately, and informs her measured result to Bob through a classical channel. And she has 16 kinds of possibly measured results with equal probability 1/16. There are also 16 kinds of corresponding collapse states after the measurement by Alice. For instance, if Alice’s measurement outcome is |0101〉 A1B4, then the state of atoms 3 and 6 collapses to

$$ | \varphi\rangle_{36} = \bigl( \alpha| 00 \rangle+ \beta| 01 \rangle+ \gamma| 10 \rangle+ \theta| 11 \rangle\bigr)_{36}. $$
(19)

In this case, the state of the subsystem with the atoms 3, 6, 7, 8 and 9 can be written as

(20)

Then Charlie does the same things on the atoms (3, 7, 8) undergo the same evolutions, according to Eq. (15), the state (20) becomes

(21)

Charlie can measure her atoms 3 and 7, separately, and then he sends the result of his measurement to Bob. If the result is |01〉37, i|10〉37, |11〉37 or i|00〉37, Bob needs to apply the local unitary operation I 9⊗I 6, Z 9⊗I 6, X 9⊗I 6 or Y 9⊗I 6 on his own atoms 6 and 9. And the I, X, Y, Z are four unitary operations, i.e.,

After doing those operations, Bob can successfully reconstruct the original two-atom state |ψ〉 AB .

4 Discussions and Conclusions

For the Rydberg atoms with principal quantum numbers 49, 50, 51, the radiative time is T r =3×10−2 s and the coupling constant is g=2π×24 kHz. Based on the coupling constant g, the required atom-cavity-field interaction time is on the order of T=10−4 s, so that the whole time to discriminate the multipartite measurement is lesser than 10−3 s, which is much shorter than the radiative time [23]. In our scheme, it is necessary to control three atoms interact simultaneously with the thermal cavity field and the strong classical field, which is a large challenge for the experiment. Fortunately, the infidelity is insensitive to the temporal fluctuation of the atoms and thus can be neglected as pointed out by the refs. [24–28]. In addition the two-atom entangled state with such an atom–cavity field interaction has been experimentally realized [23]. Thus, our scheme can be easily realized with present cavity QED techniques.

In conclusion, In this paper we have demonstrated that three sets of W-class states can be used as the quantum channel to realize the deterministic QIS of an arbitrary two-atom state in Cavity QED. The scheme does not involve Bell-state measurement and is not sensitive to both the cavity decay and the thermal field and based on current cavity QED technology. We hope that such a two-atom QIS scheme can be realized experimentally with photons. Work along QIS of an arbitrary N-atom by using W-class states as the quantum channel in cavity QED is under way.