1 Introduction

The observed late-time accelerated expansion of the universe can be explained by either introducing some unknown matter, which is called dark energy (for reviews see [1, 2]) in the framework of general relativity or by modification of general relativity.

The simplest type of modified gravity models is well known as f(R) gravity where the linear scalar curvature term of the Einstein-Hilbert action is replaced by a general function, f(R), of the scalar curvature (see [3–8] for reviews).

There are also other modified gravity models which are the generalization of f(R) gravity and among them, the modified Gauss-Bonnet (GB) gravity i.e. f(G) gravity, is more interesting [9, 10]. The GB combination, G, is a topological invariant in four dimensions and so in order to play some role in the field equations, it is required that either GB combination couples to a scalar field or the Lagrangian density be a arbitrary function of G.

Furthermore, the modified f(G) gravity has the possibility to describe the inflationary era, a transition from a deceleration phase to an acceleration phase, crossing the phantom divide line and passing the solar system tests for a reasonable defined function f [11, 12]. Also, the f(G) gravity might be less constrained by local gravity constraints compared to the f(R) models [13]. Hence, modified f(G) gravity represents a quite interesting gravitational alternative to dark energy (for recent review see [14]).

Recently, different functional forms for f(G) have been suggested in the literature. For example, Ref. [15] has proposed viable models of f(G) gravity to account for the late-time cosmic acceleration. These models have been further analyzed in the context of finite-time future singularities in Ref. [16]. In the other hand, De Felice and Tsujikawa have presented other forms of f(G) gravity in which a cosmic acceleration is followed by the matter era [13]. They have constructed their models by imposing the conditions which are required to ensure the stability of a late-time de-Sitter solution as well as the existence of standard radiation/matter dominated eras in f(G) theory. These models also have the possibility to realize phantom divide crossing before reaching the present universe and we will consider these forms of f(G) in the present work.

Moreover, solar system constraints on viable f(G) models proposed in [13] have been discussed in [17] and additional constraints on modified gravity models may also come by imposing the energy conditions [18–20].

Moreover, the energy conditions are essential for studying the singularity theorems as well as the theorems of black hole thermodynamics. For example the Hawking-Penrose singularity theorems invoke the weak and strong energy conditions, whereas the proof of the second law of black hole thermodynamics needs the null energy condition [21, 22]. Various forms of energy conditions namely, strong, weak, dominant and null energy conditions are obtained using Raychaudhuri equation along with attractiveness property of gravity [21–23]. Energy conditions have been widely studied in the literature. Phantom field potential [24], expansion history of the universe [25–30] and evolution of the deceleration parameter [31, 32] have been investigated using classical energy conditions of general relativity. Energy conditions in the context of f(R) gravity have been derived in [33] and following the formalism developed in [33], several authors have studied some cosmological issues in modified f(R) gravity (see for example [34–36]).

In a recent paper [37], the general energy conditions for modified Gauss-Bonnet gravity or f(G) gravity have been derived and viability of specific realistic forms of f(G) proposed in [15] have been analyzed by imposing the weak energy condition.

In this paper using estimated values of the Hubble, deceleration, jerk and snap parameters, we examine the bounds from f(G)-energy conditions on parameters of the models proposed in [13]. We show that these models can satisfy weak and strong energy conditions inequalities in a region which is essential to ensure the stability of a late-time de-Sitter solution as well as the existence of standard radiation/matter dominated epochs.

An outline of this paper is as follows: in the next section we briefly review the f(G) gravity, equations of motion and energy conditions in this context. In Sect. 3 we examine energy conditions for specific f(G) models. Sect. 4 is devoted to our conclusions.

2 Energy Conditions in f(G) Modified Gravity

We start with the action that defines modified Gauss-Bonnet gravity as follows,

$$ S=\frac{1}{2\kappa^2}\int d^4x\sqrt{-g} \bigl[R+f(G)\bigr]+\mathcal{S}_m.$$
(1)

where g is the trace of the metric tensor g μν , R is the Ricci scalar and \(\mathcal{S}_{m}\) is the action of the matter that is minimally coupled to the metric. G is the Gauss-Bonnet invariant which is given by,

$$ G\equiv R^2-4R_{\mu\nu}R^{\mu\nu}+R_{\mu\nu\alpha\beta}R^{\mu\nu\alpha\beta}.$$
(2)

Variation of the action (1) with respect to the metric g μν leads to,

(3)

where T μν is the energy momentum tensor of the ordinary matter and prime stands for derivative with respect to the G.

For a flat Friedmann-Robertson-Walker (FRW) metric with scale factor a(t),

(4)

and assuming matter as a perfect fluid, the (0,0) component and trace of the (i,i) components of (3) have the following simple forms respectively,

(5)
(6)

where ρ and p are the energy density and pressure, respectively. The overdot denotes a time derivative. The Gauss-Bonnet invariant in FRW background (4) is given by,

(7)

In order to write the field equations as those in general relativity, one can define the effective energy density and pressure,

$$ \rho_{\mathrm{eff}}=\frac{3}{\kappa^{2}}H^{2}, \quad\quad p_{\mathrm{eff}}=-\frac{1}{\kappa^{2}} \bigl(2\dot{H}+3H^{2} \bigr),$$
(8)

so, the ρ eff and p eff have the following forms, respectively,

(9)
(10)

where, we have used (7).

The energy conditions originate from the Raychaudhury equation together with the attractiveness of the gravity [23]. The Raychaudhury equation in the case of a congruence of null geodesics defined by the vector field k μ is given by,

$$ \frac{d\theta}{d\tau}=-\frac{1}{2}\theta^{2}-\sigma_{\mu\nu}\sigma^{\mu\nu}+\omega_{\mu\nu}\omega^{\mu\nu}-R_{\mu\nu}k^{\mu}k^{\nu},$$
(11)

where R μν is the Ricci tensor, θ is the expansion parameter, σ μν and ω μν are the shear and the rotation associate to the congruence respectively.

For any hypersurface of orthogonal congruences (ω μν =0), the condition of attractiveness of gravity (\(\frac{d\theta}{d\tau}<0\)) yields to R μν k μ k ν≥0 (σ μν σ μν≥0).

This condition in the context of general relativity expresses by T μν k μ k ν≥0.

The Raychaudhury equation satisfies for any geometrical theory of gravitation. In the other hand the theory of kind (1) has an Einstein-Hilbert term and evaluating R μν k μ k ν is straightforward. So, using the effective gravitation field equations, the energy conditions in the case of our model are given by,

(12)
(13)
(14)
(15)

where the notation NEC, WEC, SEC and DEC stand for the null, weak, strong and dominant energy conditions, respectively.

It is shown in [37] that energy conditions can be used to place constraints on the parameter of the specific form of f(G). These constraints can be stated in terms of the deceleration (q), jerk (j) and snap (s) parameters defined as,

$$ q=-\frac{1}{H^2}\frac{\ddot{a}}{a}, \qquad j=\frac{1}{H^3}\frac{\dddot{a}}{a}, \quad \mathrm{and} \quad s=\frac{1}{H^4}\frac{\ddddot{a}}{a}.$$
(16)

In terms of the above parameters, time derivatives of the Hubble parameter, \(H=\frac{\dot{a}}{a}\), can be expressed as,

(17)
(18)
(19)

The Gauss-Bonnet invariant, G, is also given by

$$ G=-24H^4 q.$$
(20)

If one shows the present values of the quantities in (15) by the subscript 0, then (11)–(14) can be written as,

(21)
(22)
(23)
(24)

respectively. These forms of energy conditions are suitable to impose bounds on the parameters of a given f(G) model by using the estimated values of the q, j and s.

3 Constraints on Specific f(G) Models

To examine how the energy conditions can constrain the parameters of a given f(G) model, we consider two specific type of models proposed in [13]. These models have been constructed by imposing three conditions: (1) the stability of de-Sitter point (exist in the context of f(G) gravity) that can be used for cosmic acceleration and demands the condition \(0<H_{1}^{6}\frac{d^{2}f}{dG^{2}}|_{H_{1}}\), where H 1 is the Hubble parameter at the dS point, (2) the condition required for the existence of standard radiation and matter eras \(\frac{d^{2}f}{dG^{2}}>0\) for G≤G 1, where G 1 is the Gauss-Bonnet term at the dS point and (3) the regularity of f(G) and its derivatives with respect to G. The following models can satisfy the above conditions:

(25)
(26)

where λ and α are constants and G ∗ is of order \(H_{0}^{4}\).

An important feature of these models is that, they can provide a late-time cosmic acceleration. In addition, the models f 1 and f 2 can be consistent with solar system constraints and given rise to power-law correction to the Schwarzschild metric [17]. As mentioned in [13] the difference between the above models is that f 1 has a logarithmic correction that mildly increases with the growth of G.

In what follows we investigate WEC and SEC for two f(G) gravity models (25) and (26) and obtain bounds on the parameters of them. For simplicity we only examine the vacuum case for which p=ρ=0, although this is not a physically interesting case, as the universe contains matter and radiation. However, this is easily corrected, since one can always add a positive energy density or pressure from matter and/or radiation to any model satisfying the WEC and SEC, and it will still satisfy the WEC and SEC. Thus, f(G) gravity with matter will also satisfy the WEC and SEC if the vacuum model does [37].

3.1 f 1(G)

In the first part we take the model given in (24). According to (21) the weak energy conditions for this model and in the absence of ordinary matter is expressed by the following two equations,

(27)
(28)

The new constraint in order to be fulfilled SEC is also as,

(29)

Indeed the above relation is ρ eff+3p eff≥0.

3.2 f 2(G)

In the second part we consider f 2(G) i.e. (26) and obtain the WEC as follows,

(30)
(31)

In addition, the extra relation for SEC is given by,

(32)

Now, let us study these conditions. The inequalities for WEC and SEC fulfillment conditions (27)–(32) can be written in terms of model parameters α and λ as,

(33)
(34)

where \(\mathcal{A}_{i}\)s, are the coefficients of λ in (27), (29), (30) and (32) which are functions of G ∗ and \(\mathcal{B}_{i}\)s, are the constant coefficients of αλ in these equations. \(\mathcal{C}_{i}\)s are the coefficients of λ in (27) and (30) and they are also functions of G ∗. One can realize that weak and strong energy condition depend on the model parameters α, λ and G ∗.

We need to analyze (32) and (33). By obtaining the root of \(\mathcal{A}_{i}(G_{\ast})=0\), as G ∗1 and \(\mathcal{C}_{i}(G_{\ast})=0\), as G ∗2, we can specify the behavior of them. In Table 1 the G ∗1 and G ∗2 are presented for f 1(G) and f 2(G) models. Note that we have used the following estimated values of deceleration, jerk and snap parameters [38, 39]: q 0=−0.81±0.14, \(j_{0}=2.16^{+0.81}_{-0.75}\), and \(s_{0}=-0.22^{+0.21}_{-0.19}\).

Table 1 G ∗1 and G ∗2 in WEC and SEC inequalities for f 1(G) and f 2(G)
Full size table

As it is clear from Table 1, G ∗1<G ∗2 and we mention that \(\mathcal{A}_{i}\)s are positive for G ∗<G ∗1 and negative for G ∗>G ∗1. Also \(\mathcal{C}_{i}\)s are positive for G ∗>G ∗2 and negative for G ∗<G ∗2. \(\mathcal{B}_{i}\)s are positive for WEC and negative for SEC.

By utilizing the above explanations, we can summarize the constraints on parameters of the models required for weak and strong energy conditions fulfillment in Table 2. One can see that for λ≥0 and λ≤0 the WEC and SEC can be satisfied.

Table 2 Three regions of WEC and SEC fulfillment
Full size table

It is shown [13] that the stability of a late-time de-Sitter solution as well as the existence of standard radiation/matter dominated epochs require the condition \(\frac{d^{2}f}{dG^{2}}>0\) and this condition needs a positive λ. So, in order to have \(\frac{d^{2}f}{dG^{2}}>0\) together with weak and strong energy conditions fulfillment, we should be in the G ∗>G ∗2 region.

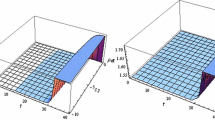
We have plotted WEC and SEC for three regions of Table 2 for the models given by (23) and (24), in Figs. 1–8. The Figures show that the specific forms of f 1(G) and f 2(G) are consistent with WEC and SEC.

Fig. 1
figure 1

The plots show the weak energy condition for f 1(G). (a) Corresponds to ρ eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗<G ∗1, G ∗=3×107, α≤−1.276

Full size image
Fig. 2
figure 2

The plots show the weak energy condition for f 1(G). (a) Corresponds to ρ eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗>G ∗2, G ∗=1.5×109, α≥0.115

Full size image
Fig. 3
figure 3

The plots show the weak energy condition for f 2(G). (a) Corresponds to ρ eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗1<G ∗<G ∗2, G ∗=4×108, α≤0.110

Full size image
Fig. 4
figure 4

The plots show the weak energy condition for f 2(G). (a) Corresponds to ρ eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗>G ∗2, G ∗=3×109, α≥0.06

Full size image
Fig. 5
figure 5

The plots show the strong energy condition for f 1(G). (a) Corresponds to ρ eff+3p eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗=4×107, α≥−2.68.

Full size image
Fig. 6
figure 6

The plots show the strong energy condition for f 1(G). (a) Corresponds to ρ eff+3p eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗=2×109, α≤0.08

Full size image
Fig. 7
figure 7

The plots show the strong energy condition for f 2(G). (a) Corresponds to ρ eff+3p eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗=9×108, α≥0.085

Full size image
Fig. 8
figure 8

The plots show the strong energy condition for f 2(G). (a) Corresponds to ρ eff+3p eff≥0 and (b) corresponds to ρ eff+p eff≥0. These figures have been plotted for G ∗=2×109, α≤0.135

Full size image

4 Conclusion

Late-time cosmic acceleration of the universe can be explained either by dark energy or modified gravity. f(R) gravity and modified Gauss-Bonnet gravity, f(G), are two well-known kinds of modified gravity theories. Unlike f(R) gravity, the f(G) theory does not have an action in the Einstein frame with a standard kinetic term of a scalar field. Also, in modified Gauss-Bonnet gravity there exists a de-Sitter point that can be used for cosmic acceleration [13].

In the present work following the Ref. [37], we have examined the weak and strong energy conditions for viable models of f(G) gravity proposed in Ref. [13] and given by (24) and (25). These models can be responsible for cosmic acceleration and pass the solar system constraints as well. We have obtained the bounds on the parameters of the above mentioned models which are required to ensure the fulfilment of weak and strong energy conditions as presented in Table 2. in order to satisfy the stability condition together with weak and strong energy conditions fulfillment, one needs to be in the G ∗>G ∗2 region.

Finally, we mention the following important point: as emphasized in [33], although the energy conditions in modified gravity theories have well-founded physical motivation (the Raychaudhury equation together with the attractiveness property of gravity) the question as to whether they should be applied to any modified gravity theory is an open question which is ultimately related to the confrontation between theory and observations.