Introduction

Research in mathematics education focusing on the teachers’ knowledge has traditionally been conducted at the elementary and secondary levels (e.g. An, Kulm, & Wu, 2004; Rowland, 2012). As a result, there is an evident paucity of studies that analyze categories of knowledge in mathematics lecturers, as pointed out by Speer, King, and Howell (2014). However, in recent years, researchers have focused on studying mathematics lecturers’ knowledge, as has been reported by studies presented in the session of the International Conference on Education in Mathematics, Science & Technology and at the Congress of the European Society for Research in Mathematics Education (e.g. Khakbaz, 2014; Mesa & Cawley, 2015). Following this trend, the study of mathematics lecturers’ knowledge has emerged as a new line of research that seeks to understand this knowledge, its development, and how it is reflected in the university teaching practices (Biza, Giraldo, Hochmuth, Khakbaz, & Rasmussen, 2016).

Within this line, Breen, Meehan, O’Shea, and Rowland (2018) investigated the knowledge of a group of lecturers (mathematicians without pedagogical training) who teach analysis and calculus at the university level. The authors use the knowledge quartet model (Rowland, Huckstep, & Thwaites, 2005) with the purpose of inquiring whether or not this model could be applied to studying teaching at the university level. As such, this work is a first approximation of a mathematics lecturer’s knowledge from the knowledge quartet model.

On the other hand, Pinsky (2013) addresses the knowledge of a lecturer who teaches an introductory course of differential geometry, using the mathematical knowledge for teaching model (Ball, Thames, & Phelps, 2008). The author reports that some knowledge that is identified as the lecturer’s specialized content knowledge might be common knowledge to a professional mathematician. In this line, Speer et al. (2014) analyze these subdomains and find that common and specialized content knowledge are useful for understanding the knowledge of elementary teachers, for which their distinction is relatively clear; but in the context of mathematics lecturers, who are usually mathematicians, distinguishing these two subdomains of knowledge becomes more complex.

In the work of Vasco and Climent (2018), the authors perform a detailed analysis of the knowledge of two lecturers based in the mathematics teacher’s specialized knowledge (MTSK) model proposed by Carrillo, Climent, Contreras, and Muñoz-Catalán (2013) and highlight its utility for understanding a mathematics lecturer’s knowledge. Additionally, Delgado-Rebolledo and Zakaryan (2018) obtain empirical evidence for the components of a mathematics lecturer’s knowledge inquiring the subdomain of the MTSK model knowledge of practices in mathematics.

Considering the literature review, among the different conceptualizations of teacher knowledge that are intrinsically connected to teaching and learning mathematics, we used the MTSK model to understand the mathematics lecturer’s knowledge for two main reasons. First, we emphasize that the MTSK model emerges from a critical stance to tendencies to compare the knowledge of the mathematics teacher with the knowledge required by other professionals, such as mathematicians or teachers of subjects other than mathematics. In this respect, Carrillo, Montes, Contreras, and Climent (2017) proposed to consider specialized teacher knowledge as useful knowledge in mathematics teaching and learning contexts regardless whether this knowledge, or part of this, is shared by others. Also, specialized it is not the type of knowledge, whether quantitatively or qualitatively different, that set mathematics teachers apart from other professionals, but the “how” teachers knowing comes into being (Scheiner, Montes, Godino, Carrillo, & Pino-Fan, 2019). This way of understanding the notion of specialization supposes a shift in perspective, from an extrinsic point of view to an intrinsic view of teacher knowledge, underlining the epistemological thread inherent in mathematics teacher knowledge and the complex interactions of knowledge within a dynamic structure (Scheiner et al., 2019). Second, according to previous research, the MTSK model has demonstrated its possible applicability (Charalambous & Pitta-Pantazi, 2016) in the sense that it allows capturing the knowledge of the teacher in content domains and educational levels beyond those in which was developed.

The above-mentioned characteristics of the MTSK model allow us to approximate the aim of this research. At the same time, this work is an empirically validating study (Charalambous & Pitta-Pantazi, 2016) of this theoretical construct. In this sense, we contribute to MTSK development, which is a relatively new approach to understanding mathematics teachers’ knowledge.

The MTSK model describes two domains of knowledge, namely, mathematical knowledge (MK) and pedagogical content knowledge (PCK). MK is defined in terms of mathematics itself (topics, connections, and ways of doing mathematics), and, as such, this domain can be used to study teachers’ mathematical knowledge independent of the level that they are working (Carrillo et al., 2018). Among the components of MK, we focus on the knowledge of practices in mathematics (KPM) subdomain that describes the teacher’s knowledge of how to explore and generate new knowledge in mathematics, elements that are present in some models of knowledge for teaching (e.g. Ball & Bass, 2009) but are not considered as core components of the mathematics teacher’s knowledge as they are in the MTSK model to include the KPM. As a subdomain about how knowledge is created and validated in mathematics, KPM allows the teacher to promote the construction of students’ own mathematical knowledge and the acquisition of reasoning and proof abilities, which, according to Ball, Hoyles, Jahnke, and Movshovitz-Hadar (2002), are important for learning mathematics at all grade levels. Zaslavsky, Nickerson, Stylianides, Kidron, and Winicki-Landman (2012) added that proofs provide a wide understanding of mathematical concepts and have potential to contribute to development of strategies, methods, and tools for solving problems.

Despite the relevance of KPM, Zakaryan and Sosa (2019) observed that studies performed with teachers at different educational levels provide scarce evidence of KPM in their mathematics classes. However, at the university level, Delgado-Rebolledo and Zakaryan (2018) show descriptors of KPM in the case of a mathematics lecturer. These descriptors were tentatively categorized as ways to proceed and validate in mathematics, nevertheless, as the descriptors’ grouping into categories is under study (Carrillo et al., 2018). In this sense, because the development of different mathematical abilities linked to mathematical practice is emphasized in university courses, it is interesting to study the KPM of teachers at this educational level.

On the other hand, we argue with Scheiner et al. (2019, p. 167) “that an account of specialization lies not in the sum of the parts of mathematics teacher knowledge but in its organic whole, that is, various knowledge facets being constantly in dialog with each other, informing each other, and interacting dynamically to form emergent structures.” From this perspective, a new discussion of the nature of the mathematics teacher knowledge allows us to better integrate knowledge and action. Also, different studies have reported a relationship between the teacher’s mathematical knowledge and pedagogical content knowledge. For example, in the study by Ma (1999) at the elementary level, the knowledge of subtraction, fractions, areas, and perimeters is expressed in relation to pedagogical content knowledge regarding the use of manipulative materials, the selection of representations for teaching, and the management of students’ mistakes. Sherin (2002) performed a study at the secondary level. The author affirms that teachers have knowledge structures called content knowledge complexes, where there are strong connections between disciplinary and pedagogical knowledge. In this way, we consider relevant to understanding the types of relationship between subdomains of teacher knowledge and how they are reflected in university teaching practices.

In this line, from a holistic perspective that considers the complexity and the integrated character of teacher knowledge, the aim of this study is to answer the following question: How is a lecturer’s knowledge of practices in mathematics (KPM) related to pedagogical content knowledge (PCK)?

Theoretical Background

Mathematics Teacher’s Specialized Knowledge

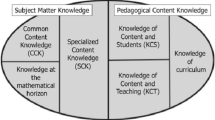
Mathematics teacher’s specialized knowledge (MTSK) is an analytical model for understanding mathematics teachers’ knowledge and a methodological tool that allows for analysis of teachers’ teaching practices (Carrillo et al., 2017). As shown in Fig. 1, in MTSK, two domains of teacher knowledge are distinguished, namely, mathematical knowledge (MK) and pedagogical content knowledge (PCK), which are permeated by a domain of beliefs about how mathematics is learned and how mathematics should be taught (Carrillo et al., 2018).

Fig. 1
figure 1

Mathematics teacher’s specialized knowledge model (Carrillo et al., 2018)

Full size image

MK in the MTSK model includes the mathematical topics and entities in the subdomain knowledge of topics (KoT), connections among mathematical entities in knowledge of the structure of mathematics (KSM), and ways of doing or creating mathematics in knowledge of practices in mathematics (KPM). On the other hand, PCK is a specific type of knowledge of pedagogy in which the mathematical content determines the teaching and learning that occurs. This domain considers the teacher’s knowledge of mathematical content as an object of teaching (knowledge of mathematics teaching, KMT) and as an object of learning (knowledge of features of learning mathematics, KFLM). Additionally, this knowledge is seen from the point of view of the learning standards that are expected to be achieved in a given course or educational level (knowledge of mathematics learning standards, KMLS).

Given the focus of this investigation on the KPM subdomain in relation to the PCK subdomains, these components are described in detail in the succeeding texts.

Knowledge of Practices in Mathematics

The idea of knowledge of the practice in mathematics (KPM) comes from the works of Schwab (1978), Ball (1990), and Ball and Bass (2009), who examined syntactic knowledge of mathematics and knowledge about mathematics. This perspective implies that the teacher should know how to reason mathematically and be able to determine in which mathematical contexts a specific type of reasoning is more appropriate than others. On this point, in KPM, the practice in mathematics is defined as any mathematical activity that is performed systematically, which represents a pillar of mathematical creation and conforms to a logical basis from which rules can be extracted (Carrillo et al., 2018).

The KPM includes the teacher’s knowledge of ways of proceeding, validating, exploring, and generating knowledge in mathematics, such as knowledge of ways to communicate mathematics. For example, ways of proceeding include the knowledge of heuristic strategies for solving problems, the role of abstraction and generalization in mathematics, the consideration of cases, knowledge about selecting or constructing elements, and the knowledge of how to define something in mathematics and the characteristics of a definition.

Likewise, ways of validating include the teacher’s knowledge of the role of counterexamples used in validation, what is the truth in mathematics, what constitutes a “proof,” the main methods to prove in mathematics (direct proof, proof by contradiction, proof by induction, proof by contraposition, among others), different roles of the proof (e.g. de Villiers, 1990; Oehrtman & Lawson, 2008), and different argumentative forms that are at stake in the mathematics class (e.g. Godino & Recio, 2001).

Furthermore, ways of communicating are essential for teaching mathematics, as they permit forming connections with a specific language of formal character and the proper symbols for thinking and communicating. According to Alcalá (2002), the mathematical language is formed by written and spoken symbols (terms and specific expressions), which are assigned a precise and peculiar meaning. Thus, mathematics is deepened and developed through communication, as mathematical ideas only become tangible when people find words and symbols to express them (Silver, Kilpatrick, & Schleisinger, 1990). For example, the teacher must possess adequate knowledge of the syntactic and semantic meaning of formal symbolisms and mathematical expressions and the role of symbols in different contexts.

Knowledge of Mathematics Teaching

The KMT includes three categories related to knowledge of the phenomena that arise when a teacher is teaching mathematical content. In the category theories of mathematics teaching, it is recognized that the teacher should know formal theories of teaching derived from research in mathematics education (e.g. anthropological theory of the didactic or ATD) or can build personal theories of teaching based on reflection on mathematical activities that take place in the classroom.

Knowledge of mathematical features, potentialities, benefits, or limitations that can have a material or a technological resource and that allow it to become an instrument for teaching is in the teaching resources category. For example, the teacher’s knowledge of the specific details of an analysis textbook that makes it more convenient than others for use in a course lies in this category.

Moreover, the category strategies, techniques, tasks and examples includes elements pertaining to teaching intentionality, which includes knowledge of analogies, metaphors, and examples that teachers consider useful in explaining a mathematical content. For example, knowledge of the white tiger analogy to illustrate the features of an existential quantifier (Dawkins & Roh, 2016) belongs in this category.

Knowledge of Features of Learning Mathematics

The KFLM includes four categories related to knowledge of the phenomena that occur when a student comprehends a mathematical topic. In the category theories of mathematics learning, this is recognized as the teacher’s knowledge of theories about student cognitive development that are constructed by personal experience or theories that are institutionalized through mathematics education (e.g. APOS theory).

The category strengths and weaknesses associated with learning refers to knowledge of potential capacities, errors, obstacles, and difficulties that students encounter when learning mathematical concepts, such as understanding a proposition with several quantifiers (Dubinsky & Yiparaki, 2000).

The category ways in which pupils interact with mathematical content refers to the teacher’s knowledge of habitual or unusual processes and strategies that students use to do mathematics, as well as the possible language or vocabulary they use to talk about specific content. For example, a teacher should be aware that students typically interpret the property of completeness of real numbers by relating it to the usual meaning of the complete word (Bergé, 2010).

Another element of KFLM concerns emotional aspects of learning mathematics, which involves knowledge about what motivates students, their interest, and their expectations of mathematics. For example, the teacher should be aware that students consider analysis more difficult than calculus.

Knowledge of Mathematics Learning Standards

The KMLS refers to the teacher’s awareness of the teaching and learning standards in mathematics that are proposed by the current curricula in each country, recognized institutions in mathematics education, local research groups, and teachers’ associations.

In the category expected learning outcomes, the focus is on the teacher’s knowledge of the mathematical content that is to be taught at the level in which the teaching is taking place. For example, the teacher should be aware that, in the real analysis course, the theoretical development of the mathematical content is expected.

The category expected level of conceptual or procedural development refers to the knowledge of the depth with which a mathematical topic must be approached in relation to a specific school level. An example is the teacher’s knowledge that, to grasp the content of analysis, the students must achieve a certain level of competence in mathematics.

Finally, in the category sequencing of topics, the focus is on the teacher’s knowledge from the learning standards that indicate how the course topics should be organized in relation to previous or subsequent courses. For example, the teacher should know that, in the analysis course, sequences are studied first and are followed by Cauchy sequences.

Table 1 provides a synthesis of PCK subdomains and their categories of knowledge.

Table 1 Pedagogical content knowledge subdomains and categories
Full size table

In order to answer how the KPM and the PCK subdomains are related, we present the context and method of the study in the following section.

Context and Method

In this research, based on an interpretive paradigm and following a qualitative methodology, an instrumental case study was conducted (Stake, 1995). Focusing on a one-semester real analysis course that was taught at a Chilean university in a mathematics teachers’ training program, a mathematics lecturer, Ph.D. in mathematics and researcher in Dynamic Systems, was analyzed. The lecturer, who will be called Diego is an experienced teacher; he has been teaching for more than 20 years at university level and has taught the real analysis course six times in recent years. Also, Diego possesses some primary characteristics of expert teachers (e.g. Rojas, Carrillo, & Flores, 2012), i.e., understanding mathematical contents, knowing about students’ learning, and using different strategies for solving problem. According to Li, Huang, and Yang (2011), a teacher with these characteristics will possess deeper knowledge of both mathematics and its teaching and learning. For this reason, Diego was selected as case study expecting to obtain rich evidence of relationships among his knowledge.

Data Collection and Analysis

The data for this study were obtained through video recordings of Diego’s classes, which were focused on the topic of real numbers and their properties. The recordings were transcribed and organized in class episodes according to Diego’s tacit or explicit goals; for example, from the moment Diego begins teaching until he finishes presenting a definition is considered a class episode. In each episode, Diego’s actions that show knowledge according to the KPM and PCK subdomains of the MTSK model are chosen as analysis units (lines of transcription were enumerated considering statements of students and teacher).

In interpreting the data, the differentiation between evidence and indication of knowledge was considered. In this context, evidence is an element that supports the presence of the teacher’s knowledge, whereas an indication is a suspicion of the existence of knowledge, but additional information is needed to confirm or refute this suspicion (Moriel-Junior & Carrillo, 2014). Evidence of relationships is considered as the units of analysis where a subdomain is identified, which supports or conditions the appearance of one or more subdomains. In this research, evidence of relationships between KPM and one or more PCK subdomains is established.

After the preliminary data analysis, the data were complemented with a semi-structured interview that was divided in two sessions for a total duration of three hours. A template of questions was constructed, and video clips of the classes were shown to stimulate Diego’s memories. In the first session of the interview, Diego’s KPM and elements of PCK were investigated. In the second session, the relationships established between KPM and PCK were investigated in further depth. Some questions focused on units of analysis that were identified as indicators of knowledge, searching for evidence of their manifestation. The results of this article consist of evidence of relationships confirmed and previously established.

Results and Discussion

This section describes the relationships that were established between Diego’s knowledge of practices in mathematics (KPM) and pedagogical content knowledge (PCK). The nature of the relationship is differentiated in the following way: relationships in which the KPM supports the appearance of one or more PCK subdomains are indicated with a slash (for example, KMT/KPM). In contrast, relationships in which the presence of KPM conditions the presence of one or more PCK subdomains are indicated with a hyphen (for example, KPM-KMT).

Diego begins his class by reviewing some properties and concepts from previous lessons. Although the session focuses on the properties of the density of Q and I in R, the lecturer refers to the characterization of the supreme, the property of the embedded intervals, and the Archimedean property, taking time to comment on these properties. When Diego is asked why his classes begin with the review of previous content, he says:

I do it for several reasons, but mainly because, in the analysis course, the focus is on the student knowing the theory …. Then, since theoretical development is the most important, connecting certain results that are concatenated with others is typical in mathematics. Thus, it is impossible for me to start a class without reviewing previously discussed elements.

[Lo hago por varias razones, pero esencialmente porque en el curso de análisis el foco está puesto en que el estudiante sepa la teoría … Entonces, dado que lo que importa es el desarrollo teórico, es propio de la matemática que uno va hilando ciertos resultados que van concatenados unos con otros. Entonces es imposible para mí, comenzar una clase sin recordar los elementos discutidos previamente.Footnote 1]

Diego affirms that “connecting certain results that are concatenated with others is typical in mathematics,” which is based on the knowledge of mathematics as a deductive science (Boyer, 1996). In this sense, he obtains new mathematical results based on a set of logical connections with other theorems, lemmas, or properties that have been presented previously; in this way, Diego shows his KPM regarding how to proceed in mathematics.

Diego discusses this in the interview as follows:

That is, when I start a class, what I do is reviewing the prior topic, at least what I have seen in the last class. For example, there are theorems that take a long time [to prove] because the proof has many steps, a lot of background information [lemmas, theorems, properties] … And there isn’t a way to do the proof [without remembering these elements]; otherwise you lose track. This happens in the more complex theoretical developments. They’re not immediate.

[O sea, cuando inicio una clase, lo que yo hago es recordar los elementos previos, por lo menos lo que he visto en la última clase. Por ejemplo, hay teoremas que toman mucho tiempo [demostrar] porque la demostración tiene muchos pasos, muchos previos [lemas, teoremas, propiedades] … y no hay forma de probar [sin recordar esos elementos], sino uno pierde el hilo. Eso pasa en los desarrollos teóricos más complejos, no son inmediatos.]

This consideration (using prior elements) for teaching mathematics in a similar manner as performing mathematics constructions accounts for one of Diego’s personal theory of teaching (KMT), which is reflected in his beginning each class by recalling these elements. The personal theory that Diego has constructed through his experience as a lecturer coincides with that described by Wu (1999), who asserted that “in any given point of a mathematical exposition, it is virtually impossible to understand what is taking place without first acquiring a thorough understanding of all that has gone on before that point” (p. 10). This cumulative characteristic of the discipline influences how class time is used and ultimately how mathematics is taught. The vision of mathematics university teaching in an expository and sequential mode is shared by mathematicians who work as lecturers as the research of Fuller, Weber, Mejía-Ramos, Rhoads, and Samkoff (2015) indicated. They pointed out that advanced mathematics courses are typically developed in the definition–theorem–proof format. In this sense, Diego’s personal theory of teaching allows him to present the curriculum content sequentially, starting with definitions, followed by theorems and proofs, and sometimes including examples or applications of the theorems. Diego’s personal theory of teaching is derived from his knowledge of how new mathematical results are obtained, establishing a relationship KPM-KMT.

In the next class episode, Diego is trying to prove that there is a rational number in the [a, b] interval assuming that a and b are positive irrational numbers. Thus, he introduces a number pr0 and proves that it is an irrational number greater than a. He, then, proposes to prove that pr0 < b:

194 Diego:

I have the smaller number r0 and the interval (p(r0 − 1), pr0). How long is it? Without calculations, how long is it?

195 Student:

p

196 Diego:

197

198

But p < ε = (b − a)/2. Then, how can the length of (p(r0 − 1), pr0) be greater than the length of [a, b]?

What I am saying is, if pro ≥ b is true, the tiny interval (p(r0 − 1), pr0) contains the [a, b] interval. Therefore, its length has to be greater.

So, how can (b − a)/2 be greater than b − a? This is a contradiction.

194 Diego:

Yo tengo el numerito r0 y el intervalo (p(r0 − 1), pr0), ¿cuál es su longitud? Sin hacer cálculos ¿cuál es su longitud?

195 Estudiante:

p

196 Diego:

197

198

Pero p < ε = (b − a)/2. Entonces, ¿cómo puede ser la longitud de (p(r0 − 1), pr0) mayor que la longitud de [a, b]?

Lo que estoy diciendo es, si pro ≥ b es cierto, el intervalito (p(r0 − 1), pr0) contiene al intervalo [a, b]. Por tanto, su longitud tiene que ser mayor.

Entonces, ¿cómo (b − a)/2 va a ser mayor que b − a? Esto es una contradicción.]

Diego uses the features of the rational number p [196] to generate an absurdity regarding the length of the intervals (p(r0 − 1), pr0) and [a, b] [197–198]. This shows his knowledge of proof by the contradiction method as a means of validation in mathematics (KPM). In this episode, and in others, when the method of proof by contradiction or reduction to absurdity is presented, we observe that Diego expresses how a contradiction is constructed [194–196], what should be assumed [197], and how it should be concluded [198]; Diego demonstrates a way to carry out a proof by contradiction with the aim that students know the method and could apply it by using some steps. He emphasizes the arguments that allow him to obtain the absurdity as a teaching technique (Monereo, Castelló, Clariana, Palma, & Pérez, 1999) of this method of proof. In this sense, Diego’s knowledge of the method of proof by contradiction (KPM) conditions his knowledge of a technique for teaching it (KMT) in a KPM-KMT relationship.

In line with the above-mentioned discussion, Diego refers to students’ difficulties with proofs. In the interview, Diego expresses the following:

The contrapositive method and the proof by reduction to absurdity are always difficult for them [the students], mainly because there is a negation …. There are difficulties related to constructive methods and methods that establish existence and the equivalences also present some difficulties that have to do with logic.

[El método contrapositivo y las demostraciones por reducción al absurdo siempre son una dificultad para ellos [los estudiantes], sobre todo porque hay una negación …, hay dificultades que tienen que ver con métodos constructivos y métodos que establecen la existencia y en las equivalencias también hay dificultades que tienen que ver con la lógica.]

Diego explains students’ difficulties to understand different methods of proof as a function of their lack of comprehension of logical, for instance, the negation of propositions and the equivalence p → q ↔ ~q → ~p. This affirmation is according to results of Stylianides, Stylianides, and Philippou (2004), who examined the performance of students in tasks related to the contraposition equivalence rule and pointed out the importance of students’ understanding of logical principles. In addition, Diego’s knowledge of students’ difficulties with proofs by contradiction is aligned with the assertion that the method of proof by contradiction “is the special transcendently in what mathematicians do and present an epistemological, cognitive and didactic problematic of great interest in the mathematics education” (Sáenz-Castro, 2002, p. 48).

As observed before, Diego does not only know the different methods of proofs (KPM) that he has mentioned but also knows students’ weaknesses (KFLM) for understanding and developing proofs with these methods. This shows a relationship KFLM/KPM, for which Diego’s KFLM is supported by KPM.

Regarding teaching strategies for the proof, Diego shared the following:

In class, you simply prove and, through those proofs, give the students ideas of how the techniques work … You show them a technique, and they repeat it. There is another important aspect to the proof because, as a teacher, you must show the creative process of the mathematician, where the problem was and explain how the mathematician solved it.

[En clase, uno simplemente demuestra y a través de esas demostraciones le va dando ideas a los estudiantes de cómo son las técnicas … Tú le das una técnica y ellos la repiten. También hay otra parte donde es importante que, uno como profesor, muestre en la demostración dónde estuvo el proceso creativo del matemático, dónde estuvo el problema y cómo el matemático solucionó el problema.]

Diego approaches the teaching of proofs by discussing arguments with the students and showing key elements of the proof, i.e., “the techniques and the creative process” the mathematician relies on to provide an argument. In this way, Diego’s knowledge of a teaching strategy for the proof (KMT) is identified.

Consistently, Diego says:

I remember, for example, in my first year of my bachelor’s degree, induction problems where a magical zero was added … at first, these things are surprising, but afterward they acquire a certain naturalness. Then, when you teach, you have to show the ideas, the things that you are thinking [the construction, the logical process] …, so, the students understand where things are coming from.

[Recuerdo, por ejemplo, en mi primer año de licenciatura, los problemas de inducción donde se sumaba un cero mágico … al principio, esas cosas son sorprendentes, pero después van adquiriendo cierta naturalidad. Entonces, cuando uno enseña, tiene que mostrar las ideas, lo que se te ocurre [la construcción, el proceso lógico] …, así, los estudiantes entienden de dónde es que aparecen las cosas.]

Based on his experience as a mathematician and as a lecturer, Diego has constructed a learning theory of proofs in which he considers that students learn in the same way he did, imitating the proofs developed by lecturers, or through presentation in books and papers. This personal theory of learning (KFLM) supports the knowledge of a teaching strategy; “show ideas, the thigs that you are thinking.” So, a relationship KMT/KFLM is established. From this relationship in his knowledge, the lecturer tries to illustrate a set of heuristics that a student could use to prove and he explains his work in a detailed way so that students can replicate it. Diego’s manner of teaching coincides with characteristics of the procedural teaching style described by Weber (2004) in his study about how a lecturer teaches a real analysis course. At the same time, the relationship KMT/KFLM is conditioned by Diego’s knowledge of how proofs are done as a way of validating in mathematics (KPM) for which the relationship KPM-(KMT/KFLM) is established.

Returning to the main goal of the class, Diego uses the Archimedean property to construct an argument in the density of Q in R proof. In the following class episode, regarding the existential quantifier present in the Archimedean property, Diego says:

137 Diego:

138

137 Diego:

138

When it is for all, I can always choose an element that works best for me, but when it is there exists, it is “whatever you are given,” nothing more.

Then, because there exists gives you “whatever you are given,” you have to do some work so that what you get is what you need.

[Cuando es para todo, yo siempre puedo escoger el elemento que me conviene, pero cuando es existe, es “lo que cayó,” no más.

Entonces, como el existe te da “lo que cayó,” tú tienes que hacer algún trabajo para que lo que caiga sea conveniente.]

Diego complements the aforementioned explanation in the interview as follows:

There exists says that you have at least one element, which could even be the only one. Then, you do not have any choice; you do not have the opportunity to choose in the universe; it is “whatever you’re given.” For example, the Archimedean property gives you a natural number that satisfies the assertion …, not all the natural numbers comply that.

[Existe te dice que hay uno que hasta podría ser el único, entonces no tienes posibilidad de elección, no tienes chance de escoger dentro del universo, es “lo que cayó”. Por ejemplo, la propiedad arquimediana te da un número natural que satisface la afirmación …, no son todos los naturales los que cumplen.]

In the class episode and in the interview fragment, Diego’s knowledge of the quantifier’s meaning in a proposition as a way of communicating in mathematics (KPM) is identified. Additionally, Diego uses the expression “whatever you’re given” [137–138]—literally, “just what fell into your lap”—as a manner of metaphor (Lakoff & Núñez, 2000) of the existential quantifier to highlight its features. Metaphors are recognized as powerful cognitive tools that help in comprehending or building new concepts (Soto-Andrade, 2014). For example, Dawkins and Roh (2016) show how analogies and metaphors, when used in teaching, can help students understand the meaning of the existential quantifier and interpret real analysis multiple quantified statements. The metaphor used by Diego as a teaching strategy (KMT) to refer to the meaning of the existential quantifier is constructed from KPM, and therefore, the relationship KPM-KMT is established.

Regarding multiple quantified statements, in the interview, the lecturer makes the following assertion:

Properties or statements that have many quantifiers, several for all and there exists, in general, are a problem for students, because we—even the mathematicians—have the bad habit of not using the fundamental rule when making propositions, that quantifiers should be presented first, but instead we put the for all at the end of propositions.

[Propiedades o proposiciones que tienen muchos cuantificadores, varios para todo y existe, son un problema en general para los estudiantes, porque además tenemos la mala costumbre—y esto hasta entre los matemáticos—de no usar una regla fundamental en la elaboración de las proposiciones, que primero van los cuantificadores, entonces ponemos el para todo al final de las proposiciones.]

In relation with the above-mentioned discussion, Selden and Selden (2013) pointed out that the following generally occurs in the proof text: proofs are logically concrete in the sense that quantifiers, especially universal quantifiers, are avoided where possible. The omission of quantifiers or the order in which they are presented modifies the intended meaning of a statement. These affirmations coincide with Diego’s comment about the use of quantifiers. Diego knows that a statement of the form “There exists … for all …” referred to as an ∃∀ statement does not have the same meaning of “For all … exists …”, an ∀∃ statement. Diego is also aware that this situation influences students’ difficulty in interpreting and proving mathematical statements involving quantification, as it has been documented by other researchers (e.g. Dubinsky & Yiparaki, 2000; Piatek-Jimenez, 2010). In line with this, the lecturer’s knowledge of how to work with quantifiers as way of communicating mathematical ideas (KPM) supports his knowledge of students’ weaknesses (KFLM) in working with these elements, for which the relationship KFLM/KPM is established.

Continuing with the density of Q in R proof, Diego required a proof of an inequality that allowed him to affirm that between two rational numbers there is always an irrational number. After introducing the inequality, Diego says the following to the students:

184 Diego:

185

184 Diego:

185

What do you think I should do? Who has not yet shown their qualities here? Someone here has to come to play.

If you have Alexis Sánchez sitting on the bench, you do not leave him there. Someone has to score. Who is going to score here?

[¿Qué se les ocurre que debería hacer?, ¿Quién no ha entrado todavía aquí a mostrar sus virtudes? Alguien allí tiene que entrar a jugar.

Si tienes a Alexis Sanchéz en la banca, no lo dejás ahí, alguien tiene que meter el gol ¿Quién es el que va a meter el gol aquí?]

In a recent soccer game that took place close to the class date, Alexis Sánchez, a famous Chilean soccer player, entered from the bench and scored the winning goal for his team at a decisive moment in the championship. Diego uses this situation to highlight the importance of the Archimedean property, which he will use to prove the inequality. Deepening the reasons behind this comment, the lecturer expresses in the interview:

Alexis Sánchez is the missing key element. It is an important element that makes everything work, he is the Archimedean property. I am talking about the theoretical element that allows us to make conclusions, because, the density is based on the fact that real numbers are different from rational numbers and the element that makes them different is the Archimedean property. The player, who makes the difference there is that property, and no other.

[Alexis Sánchez es el elemento clave que falta, es un elemento importante que hace que todo funcione, es la propiedad arquimediana. Me estoy refiriendo al elemento teórico que permite hacer conclusiones, porque lo que pasa es que la densidad se basa en que los reales son distintos de los racionales y el elemento que los hace distintos es la propiedad arquimediana. El jugador, que hace la diferencia ahí es esa propiedad, no es otra.]

Diego has shown knowledge of how to use the Archimedean property, as an exclusive property to real numbers, to build arguments in the proof of other statements, such as the density of Q in R; this knowledge is part of his KPM. Moreover, Diego compares the role of the soccer player with the role of the Archimedean property [185], showing students an analogy between elements that share similar functions. This functional analogy (Curtis & Reigeluth, 1984) has an explanatory character which emphasizes the Archimedean property as a fundamental element for understanding real numbers and exposes how daily activities, such as soccer, can be introduced seamlessly into the teaching of mathematics. The choice of this analogy as a teaching strategy (KMT) is a derivative of the lecturer’s KPM regarding how to construct arguments in a proof using the Archimedean property; in this way, a KPM-KMT relationship is established.

As shown, for Diego, the use of analogies and metaphors is a typical teaching strategy of mathematics. When asked for the reasons behind their use in the interview, he responds:

In the background, formulations in mathematical language are simply formulations of ideas, these ideas do not necessarily have to be presented from the beginning in a purely rigorous manner …, we have to accept a certain license of formality.

[En el fondo, las formulaciones en el lenguaje matemático son simplemente formulaciones de ideas que no tienen por qué ser necesariamente expresadas desde el inicio en un carácter puramente riguroso …, tenemos que aceptar cierta licencia de formalidad.]

Accordingly, Diego points towards the acceptance of a “certain license of formality”, referring to metaphors and analogies. Also, he knows the “rigorous manner” to present mathematical ideas, which identifies the lecturer’s knowledge of formal language as a way to communicate in mathematics (KPM).

In the following class episode, the lecturer writes the property of embedded intervals or the nested intervals theorem on the blackboard: Let an < bn and In = [an, bn ], if In is a set of closed and bounded intervals with In + 1 ⊂ In, then there exists x ∈ ℝ, such that an < x < bn, ∀n ≥ 1. The lecturer comments on the statement of the property saying:

11 Diego:

Then, the property says that, if I take embedded intervals that are becoming smaller that are closed and bounded intervals, there is something at their intersection, there is something in there.

11 Diego:

[Entonces, la propiedad dice que, si tomo intervalos encajados, que cada vez son más pequeños, que son intervalos cerrados y acotados, entonces, en la intersección de ellos hay algo, algo hay ahí.]

The lecturer uses the expression “that are becoming smaller” to point out the definition of the embedded intervals (In + 1 ⊂ In, ∀ n ≥ 1). He also says “there is something in there” as an explanation of the idea of a nonempty intersection. In this way, the lecturer uses these expressions as powerful explanations to communicate mathematical ideas in the class. These explanations are a teaching strategy (KMT) supported by his knowledge of formal language (KPM), establishing a relationship KMT/KPM.

On the other hand, in accordance with the characteristics of the real analysis course, proofs often are presented to demonstrate that mathematical objects have certain properties. In the following class episode, when the lecturer finishes the proof of the density of Q and I in R, he says:

204 Diego:

So, now you can say to your students with certainty that between any two rational numbers there is always an irrational number.

204 Diego:

[Entonces, ahora pueden decir a sus alumnos con propiedad que entre dos racionales siempre hay un irracional.]

The comment above [204] shows the lecturer’s knowledge of the importance of proofs for validation in mathematics. Diego knows that proofs are used to establish the truth of a statement and emphasizes this verification role of the proof (De Villiers, 1990) in his class for prospective mathematics teachers.

In reference to the previous remark, the lecturer shared the following in the interview:

Especially in this course, I am careful to show students many things that their teachers taught them and they learned like parrots: between two rationales there is an irrational, π is irrational, e is irrational, but, why? What is the proof that π is irrational? …. So, at any moment, they must see that behind a statement, there is an argument.

[Especialmente en este curso, tengo cuidado de mostrar a los estudiantes que hay un montón de cosas que sus profesores les enseñaron y ellos las aprendieron como loritos: entre dos racionales hay un irracional, π es irracional, e es irracional, pero ¿por qué?, ¿cuál es la demostración de que π es irracional? … Entonces en algún minuto hay que ver que detrás hay un argumento.]

The lecturer declared that the students have learned the properties of real numbers without understanding what they meant. Therefore, Diego’s knowledge of ways pupils interact with mathematical content is observed in his KFLM. From this knowledge, he aims to help students understand the properties of real numbers using a teaching strategy (KMT), from which a KMT/KFLM relationship is established. At the same time, Diego’s teaching strategy is the development of proofs to the properties of real numbers. In this sense, when the lecturer affirms “but, why? What is the proof that π is irrational?” He considers in his KPM that proofs provide insight into why a statement is true in a role of explanation (De Villiers, 1990). In this line, Weber (2012) affirms that the mathematicians studied in his work coincided with mathematics educators in the use of proofs in mathematics classes with an explanatory purpose. In this regard, knowledge of the explanation and verification roles of proofs (KPM) allows Diego to construct the teaching strategy present in the KMT/KFLM relationship, from which the relationship KPM-(KMT/KFLM) is established.

As a synthesis of the results presented in the preceding sections, Table 2 shows the relationships established between KPM and the KMT and KFLM subdomains of PCK. Relationships between KPM and the PCK subdomain KMLS were not supported by our findings.

Table 2 Relationship between knowledge of practices in mathematics and pedagogical content knowledge subdomains
Full size table

The relationships between KPM and KMT show how KPM conditions or supports the lecturer’s knowledge of personal teaching theories, techniques, and strategies. The relationships between KPM and KFLM account for how KPM supports the lecturer’s knowledge of students’ weaknesses. Finally, the relationships of KPM-(KMT/KFLM) show how KPM conditions relationships where KFLM supports KMT.

Conclusions

In this research, the knowledge of a mathematics lecturer was studied based on the mathematics teacher’s specialized knowledge (MTSK) model, deepening the understanding of the relationships between the KPM and PCK subdomains of the model. Additionally, we contribute to the development of this theoretical construct through empirical data that emerged from our study.

Relationships between KPM and KMT or KPM and KFLM were established, which offer empirical evidence for the theoretical relationships described by Flores-Medrano, Escudero-Avila, Montes, Aguilar, and Carrillo (2014). These authors point out that the PCK subdomains, particularly the KMT and the KFLM, require mathematical knowledge for their functioning. Our study also established the relationships between these subdomains, considering their nature of support or conditioning, ultimately contributing to the understanding the complexity and integral character of the knowledge of a mathematics lecturer.

Regarding relationships between KPM and KMT, Zakaryan and Ribeiro (2016) found this type of relationship in secondary mathematics teachers; however, in the case of the lecturer analyzed in this paper, the KPM conditions the KMT to such an extent that the lecturer’s teaching goal is that students, in addition to understanding mathematical contents, learn how to think mathematically to validate and construct arguments. In this sense, the lecturer promotes the development of KPM in his students, who are prospective secondary teachers. As such, the lecturer, who is a mathematician and researcher who does not identify as a teacher trainer, implicitly assumes this role. Leikin, Zazkis, and Meller (2018) indicate that it is relevant to understand the points of view of these lecturers in an effort to facilitate changes in the teaching of mathematics in teacher training.

Otherwise, although the research literature has already documented students’ difficulties in performing proofs and working with quantifiers due to a lack of comprehension of logical principles, we observed that relationships in which KFLM is supported by KPM, established by the lecturer, allow him to construct more detailed explanations of students’ weaknesses and understand them in depth. Epp (2009) affirms that understanding the complexity of some of the logical issues that arise even in simple mathematical proofs provides ways for teachers to respond more effectively to students’ difficulties. In this sense, the knowledge as result of the KFLM/KPM relationship is an opportunity for the lecturer to anticipate students’ weaknesses, as well as think about his teaching practice to strengthen the ways of addressing mathematical statements that include quantifiers or must be proven.

Moreover, relationships that involved three subdomains KPM, KFLM, and KMT, were established. In this case, KPM acts as a knowledge that conditions a relationship where KFLM supports KMT, or, KPM-(KMT/KFLM). These relationships have not been reported by other research that uses MTSK but allows us to explain how a subdomain of mathematical knowledge provides support to classroom actions that reflect the lecturer knowledge of teaching and learning mathematics. For example, in Zakaryan et al. (2018), different relationships between KMT and KFLM were reported without specifying how mathematical knowledge is involved in this relationship.

On the other hand, relationships between disciplinary knowledge and pedagogical content knowledge have been reported in studies of elementary teachers (Ma, 1999) and secondary teachers (Sherin, 2002), coinciding with the results obtained in this study with regard to the complex network these relationships create, giving structure and depth to a mathematics lecturer’s knowledge. In this way, this research contributes to the effort of recent studies that seek to understand the nature of mathematics lecturers’ knowledge and how this knowledge is reflected in university teaching practices (Biza et al., 2016). The evidence of relations among the different subdomains of lecturers’ specialized knowledge is a good starting point for investigating the development of his/her knowledge and “how” teachers knowing comes into being (e.g. Scheiner et al., 2019).