Since the pioneering demonstration of picosecond photoconducting Hertzian dipoles in 1984 [1], photoconductive antennas have been one of the most extensively used devices for generation and detection of terahertz waves [2]. Photoconductive antennas have been the major apparatus used for constructing the first terahertz imaging and spectroscopy systems [3–5], which helped revealing many unique applications for terahertz waves in chemical sensing, product quality control, medical imaging, biotechnology, pharmaceutical industry, and security screening [6–11].

A photoconductive terahertz antenna consists of an ultrafast photoconductor connected to a terahertz antenna. Pulsed or heterodyned laser illumination of the photoconductor active area generates photocurrent with terahertz frequency components which feed the antenna, producing terahertz radiation. Although the principle of operation in photoconductive antennas is very similar to conventional antennas, the differences between the nature of their input signal imposes different design rules compared with conventional antennas. While several small-signal and large-signal models have been presented for describing photoconductive antenna operation [12–15], little investigation has been focused on the impedance matching requirements of photoconductive antennas in various operational settings.

This paper describes the principles of impedance matching in photoconductive antennas in comparison with conventional antennas. It describes that due to the optical nature of the input signal, the optimum photoconductor impedance that maximizes the optical-to-terahertz conversion efficiency is not necessarily determined by the complex conjugate of the antenna impedance. The discussed principles are used to explain the higher optical-to-terahertz conversion efficiencies of asymmetrically pumped photoconductive antennas compared with photoconductive antennas with their semiconductor gap fully illuminated by the optical pump.

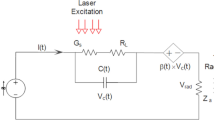
Figure 1a shows the equivalent circuit model of a conventional antenna in transmission mode, where R s and X s are the resistive and reactive components of the input source, and R A and X A are the antenna radiation resistance and reactive components, respectively. Radiated power from the conventional antenna is given by

$$ {P_{{rad}}}\left( \omega \right) = \frac{1}{2}{\left| {{V_{{in}}}\left( \omega \right)} \right|^2}\xi \frac{{{R_A}}}{{{{\left( {{R_A} + {R_s}} \right)}^2} + {{\left( {{X_A} + {X_s}} \right)}^2}}} $$
(1)

where V in is the input voltage to the antenna and ξ is the antenna efficiency. As the general impedance matching rule predicts, antenna impedance should be conjugate-matched to the source impedance (R A  = R s and X s  = -X a ) to maximize the radiated power [16].

Fig. 1
figure 1

The equivalent circuit model of a) a conventional antenna, b) a photoconductive antenna.

Full size image

The major difference of a photoconductive antenna with a conventional antenna is the optical nature of the input signal in the photoconductive antenna, which can be modeled as a current source. At low pump power densities, before the carrier screening effect, carrier recombination and semiconductor bleaching become dominant [17, 18], the amplitude of the photoconductor current, I(ω), at the angular frequency, ω is linearly proportional to the envelope of the optical pump power at that frequency, P opt (ω). Figure 1b shows the equivalent circuit model of a photoconductive antenna, where G p and C p are the conductance and capacitance of the ultrafast photoconductor connected to a terahertz antenna represented by a complex admittance \( {Y_A} = {G_A} + j{B_A} \) [12, 13], which includes the inductance of the photoconductor bias line. Radiated power from the photoconductive antenna is given by

$$ {P_{{rad}}}\left( \omega \right) = \frac{1}{2}{\left| {{S_p}\left( \omega \right){P_{{opt}}}\left( \omega \right)} \right|^2}\xi \frac{{{G_A}}}{{{{\left( {{G_A} + {G_p}} \right)}^2} + {{\left( {\omega {C_p} + {B_A}} \right)}^2}}} $$
(2)

where S p (ω) is the photoconductor current responsivity. As it can be seen from Eq. 2, conjugate-matching the photoconductor impedance to the antenna impedance does not necessarily maximize the radiated power from the photoconductive antenna. Independent of the photoconductive antenna structure, in order to maximize the radiated power from the photoconductive antenna, the reactive parasitic loading to the antenna should be minimized \( \left( {{G_A} + {G_p}} \right) \gg \left( {\omega {C_p} + {B_A}} \right) \). This can be achieved by maintaining low photoconductor capacitive loading and high bias line inductive loading to the antenna in broadband operational settings or by designing a bias line with a negative shunt susceptance that cancels the parasitic capacitance in narrowband operational settings [12, 13]. However, depending on the photoconductor conductance dependence on optical pump power, the optimum photoconductor conductance is not necessarily determined by the well-known conjugate-matching rule and should be calculated for each photoconductive antenna structure separately. In the following section, we analyze the impedance optimization criteria for two types of photoconductive antenna structures. The two categories are selected based on the photoconductor conductance dependence on the optical pump power.

The first category of photoconductive antennas that will be analyzed consists of ultrafast photoconductors with the semiconductor gap between their contact electrodes fully illuminated by the optical pump. Figure 2a shows a photoconductive antenna from this category. If the pump photons have a uniform intensity across the photoconductor active area and are uniformly absorbed within the absorption depth 1/α, the density of carriers generated within the photoconductor active region can be calculated from [19–21]

Fig. 2
figure 2

Schematic diagram of a photoconductive antenna with a) the semiconductor gap between photoconductor contact electrodes uniformly illuminated by the optical pump, b) asymmetric optical pump illumination near anode.

Full size image
$$ \frac{{dn}}{{dt}} = \frac{{{\eta_e}\alpha }}{{hv.{w_g}{w_e}}}{P_{{opt}}} - \frac{n}{\tau } $$
(3)

where η e is the photoconductor external quantum efficiency (number of generated electron-hole pairs per each incident photon), τ is the carrier lifetime in the semiconductor, hv is the photon energy, w g is the gap between photoconductor contact electrodes, and w e is the width of the photoconductor active region. Therefore, photogenerated carrier density is calculated as [14]

$$ n(t) = \frac{{{\eta_e}\alpha \tau }}{{hv.{w_g}{w_e}}}{P_{{opt}}}(0)\left[ {1 + \frac{{{P_{{opt}}}\left( {{\omega_1}} \right)\sin \left( {{\omega_1}t + \varphi \left( {{\omega_1}} \right)} \right)}}{{{P_{{opt}}}(0)\sqrt {{1 + \omega_1^2{\tau^2}}} }} + \frac{{{P_{{opt}}}\left( {{\omega_2}} \right)\sin \left( {{\omega_2}t + \varphi \left( {{\omega_2}} \right)} \right)}}{{{P_{{opt}}}(0)\sqrt {{1 + \omega_2^2{\tau^2}}} }} + \cdots } \right] $$
(4)

where φ(ω) = tan-1(1/ωτ), P opt (0) is the DC component of the envelope of the optical pump, and \( {P_{{opt}}}\left( {{\omega_i}} \right) = \gamma \left( {{\omega_i}} \right) \times {P_{{opt}}}(0) \) is the frequency components of the envelope of the optical pump at angular frequency ω i (i = 1, 2, …). It should be noted that angular frequencies ω i represent a single terahertz frequency for a heterodyned optical pump (for continuous-wave terahertz generation) and a continuous span of terahertz frequencies for a pulsed optical pump (for pulsed terahertz generation). Using the calculated photogenerated carrier density, the photoconductor conductance and photocurrent can be calculated as [13, 14]

$$ {G_p} = \frac{{{\eta_e}q\tau \left( {{\mu_e} + {\mu_h}} \right)}}{{hv.w_g^2}}{P_{{opt}}}(0)\left[ {1 + \frac{{\gamma \left( {{\omega_1}} \right)\sin \left( {{\omega_1}t + \varphi \left( {{\omega_1}} \right)} \right)}}{{\sqrt {{1 + \omega_1^2{\tau^2}}} }} + \frac{{\gamma \left( {{\omega_2}} \right)\sin \left( {{\omega_2}t + \varphi \left( {{\omega_2}} \right)} \right)}}{{\sqrt {{1 + \omega_2^2{\tau^2}}} }} + \cdots } \right] $$
(5)
$$ {I_p} = \frac{{{\eta_e}q\tau \left( {{V_e} + {V_h}} \right)}}{{hv.{w_g}}}{P_{{opt}}}(0)\left[ {1 + \frac{{\gamma \left( {{\omega_1}} \right)\sin \left( {{\omega_1}t + \varphi \left( {{\omega_1}} \right)} \right)}}{{\sqrt {{1 + \omega_1^2{\tau^2}}} }} + \frac{{\gamma \left( {{\omega_2}} \right)\sin \left( {{\omega_2}t + \varphi \left( {{\omega_2}} \right)} \right)}}{{\sqrt {{1 + \omega_2^2{\tau^2}}} }} + \cdots } \right] $$
(6)

where q is the electron charge, μ e and μ h are electron and hole mobilities, and V e and V h are electron and hole velocities, respectively. As it can be seen from Eqs. 5 and 6, when the semiconductor gap between photoconductor contact electrodes is uniformly illuminated by the optical pump, all frequency components of the induced photocurrent I p (ω), are linearly proportional to the average photoconductor conductance, \( \overline {{G_p}} \)

$$ {I_p}\left( \omega \right) = \frac{{\left( {{V_e} + {V_h}} \right)}}{{{\mu_e} + {\mu_h}}}\frac{{{w_g}\gamma \left( \omega \right)}}{{\sqrt {{1 + {\omega^2}{\tau^2}}} }}\overline {{G_p}} $$
(7)

Assuming a negligible reactive parasitic loading to the antenna \( \left( {{G_A} + \overline {{G_p}} } \right) \gg \left( {\omega {C_p} + {B_A}} \right) \), the radiated power from the photoconductive antenna is calculated as

$$ {P_{{rad}}}\left( \omega \right) = \frac{1}{2}w_g^2{\left[ {\frac{{{V_e} + {V_h}}}{{{\mu_e} + {\mu_h}}}} \right]^2}\frac{{\gamma {{\left( \omega \right)}^2}}}{{1 + {\omega^2}{\tau^2}}}\xi {G_A}{\left[ {\frac{{\overline {{G_p}} }}{{{G_A} + \overline {{G_p}} }}} \right]^2} \cong \frac{1}{2}{V_{{bias}}}^2\frac{{\gamma {{\left( \omega \right)}^2}}}{{1 + {\omega^2}{\tau^2}}}{G_A}{\left[ {\frac{{\overline {{G_p}} }}{{{G_A} + \overline {{G_p}} }}} \right]^2} $$
(8)

Equation 8 shows that the optimum photoconductor conductance that maximizes the radiated power from the photoconductive antenna is G P  = G A . Therefore, when the semiconductor gap between photoconductor contact electrodes is uniformly illuminated by the optical pump, conjugate-matching the photoconductor impedance to the antenna impedance maximizes the radiated power from the photoconductive antenna. Equation 8 also shows the direct dependence of the radiated power on the antenna radiation resistance at a given optical pump power level. Therefore, the use of high radiation resistance antennas [22–24] is as important as the impedance matching criteria in achieving high optical-to-terahertz conversion efficiencies. Without loss of generality, the discussed analysis is equally applicable for calculating the optimum design parameters in photoconductive antennas with interdigitated electrodes.

The second category of photoconductive antennas that will be analyzed consists of ultrafast photoconductors with the semiconductor gap between their contact electrodes partially illuminated by the optical pump. Figure 2b shows a photoconductive antenna from this category with an asymmetric pump illumination near the photoconductor anode contact. This design is attractive due to the bias field enhancement near the anode contact, enabling optical-to-terahertz conversion efficiency enhancement [25]. Similar analysis can be used to calculate the induced photocurrent. If the pump photons have a uniform intensity within a distance d i from anode contact and uniformly absorbed within the absorption depth 1/α, the frequency components of the induced photocurrent I p (ω) are calculated as

$$ {I_p}\left( \omega \right) = \frac{{{\eta_e}q\tau \left( {{V_e} + {V_h}} \right)}}{{hv.{d_i}}}{P_{{opt}}}(0)\frac{{\gamma \left( \omega \right)}}{{\sqrt {{1 + {\omega^2}{\tau^2}}} }} $$
(9)

Since the semiconductor gap between photoconductor contact electrodes are partially illuminated, photoconductor conductance is not linearly proportional to the optical pump power and is calculated as

$$ {G_p} = \frac{1}{{\frac{{hv.d_i^2}}{{{\eta_e}q\tau \left( {{\mu_e} + {\mu_h}} \right){P_{{opt}}}(0)}} + \frac{1}{{{G_{{p - dark}}}}}}} $$
(10)

where G p-dark is the conductance of the un-illuminated semiconductor area between photoconductor contact electrodes. Assuming negligible reactive parasitic loading to the antenna, the radiated power from discussed photoconductive antenna is calculated as

$$ {P_{{rad}}}\left( \omega \right) = \frac{1}{2}{\left[ {\frac{{{\eta_e}q\tau \left( {{V_e} + {V_h}} \right)}}{{hv.{d_i}}}} \right]^2}\frac{{\gamma {{\left( \omega \right)}^2}}}{{1 + {\omega^2}{\tau^2}}}P_{{opt}}^2(0)\xi \frac{{{G_A}}}{{{{\left( {{G_A} + {G_P}} \right)}^2}}} $$
(11)

In order to design a photoconductive antenna with optimum optical-to-terahertz conversion efficiency, the radiated power (Eq. 11) as a function of photoconductor conductance (Eq. 10) should be calculated and maximized by appropriate choice of photoconductor geometry and operational settings. For very small illumination spot sizes (d i << w g ) and short-carrier photo-absorbing substrates, the photoconductor conductance would be the same as the photoconductor dark conductance (independent of pump power level). Therefore, the optimum photoconductor conductance that maximizes the radiated power from the photoconductive antenna is G P << G A , different from the well-known impedance conjugate-matching criteria. Moreover, similar to the photoconductive antennas with the semiconductor gap between contact electrodes fully illuminated by the optical pump, the use of high radiation resistance antennas [22–24] is crucial for achieving high optical-to-terahertz conversion efficiencies.

Equation 11 shows that at the same optical pump power level, an asymmetrically pumped photoconductive antenna near anode contact electrode (Fig. 2b) can offer more than four times higher radiated power compared with an identical photoconductive antenna with the semiconductor gap between contact electrodes fully illuminated by the optical pump (Fig. 2a). This is possible because of the design flexibility of asymmetrically pumped photoconductive antennas that allows optimizing photoconductor conductance independent of the pump power level. Moreover, the use of low-conductance photoconductors, which is required for high optical-to-terahertz conversion efficiencies, offers an additional advantage of low DC power consumption by maintaining low DC currents even at high pump power levels.

Tight focusing of the optical pump can significantly enhance the radiated power of asymmetrically pumped photoconductive antennas at low pump power levels by reducing the carrier transport path to the anode electrode. However, the carrier screening effect and thermal breakdown severely limits the optical-to-terahertz conversion efficiency of asymmetrically pumped photoconductive antennas at high optical pump powers. Most of the presented solutions for mitigating the carrier screening effect and optical breakdown in large-aperture photoconductive antennas based on a variety of electrode configurations [26–33] are designed for devices with the semiconductor gap between photoconductor contact electrodes fully illuminated by the optical pump. In the meantime, utilizing nanoscale contact electrodes [34–39] in asymmetrically pumped photoconductive antennas enable suppressing the carrier screening effect and thermal breakdown, while benefiting from the design flexibility of asymmetrically pumped photoconductive antennas to achieve high optical-to-terahertz conversion efficiencies at high pump power levels.

It should be mentioned that the discussed photoconductor impedance optimization criteria is accurate when the ultrafast photoconductor is directly connected to the terahertz radiating antenna with a negligible connection length compared with the terahertz wavelength. When the connection length becomes comparable with the radiation wavelength [12], the corresponding transmission line should be included in the photoconductive antenna circuit model and accounted for while calculating the photoconductor impedance optimization criteria. Figure 3 shows the equivalent circuit model of a photoconductive antenna with a transmission line connecting the ultrafast photoconductor to the terahertz radiating antenna. Radiated power from the discussed photoconductive antenna is calculated as

$$ {P_{{rad}}}\left( \omega \right) = \frac{1}{2}{\left| {{S_p}\left( \omega \right){P_{{opt}}}\left( \omega \right)} \right|^2}{\left| {\frac{1}{{1 - {\Gamma_L}{\Gamma_S}{e^{{ - j2\beta L}}}}}} \right|^2}\xi \frac{{{G_A}}}{{{{\left( {Real\left[ {\frac{1}{{{Z_0}}}} \right] + {G_P}} \right)}^2} + {{\left( {\omega {C_P} + Imag\left[ {\frac{1}{{{Z_0}}}} \right]} \right)}^2}}} $$
(12)

where Z 0, β, and L are the characteristic impedance, wave propagation constant, and length of the transmission line, respectively, and Γ s and Γ L are the reflection coefficients at the photoconductor and antenna terminations of the transmission line, respectively. In case of perfect matching between the transmission line characteristic impedance and the antenna impedance, Eq. 12 would be the same as Eqs. 8 and 11 when the semiconductor gap between photoconductor contact electrodes are fully and partially illuminated by the optical pump, respectively. Therefore, the impedance optimization criteria would be the same as the situation where the ultrafast photoconductor is directly connected to the terahertz radiating antenna with a negligible connection length compared with the terahertz wavelength. In case of a mismatch between the transmission line characteristic impedance and the antenna impedance, the terahertz signal can bounce back and forth between the photoconductor and antenna until it attenuates along the connecting transmission line. Therefore, in order to optimize the photoconductive antenna design for high power efficiency, the radiated power (Eq. 12) as a function of photoconductor conductance should be calculated and maximized by the appropriate choice of photoconductor parameters and operational settings.

Fig. 3
figure 3

The equivalent circuit model of a photoconductive antenna with a transmission line connecting the ultrafast photoconductor to the terahertz radiating antenna.

Full size image

In conclusion, we have used the equivalent circuit model of photoconductive antennas to calculate the optimum photoconductor impedance that maximizes the optical-to-terahertz conversion efficiency. Our analysis shows that the optimum photoconductor impedance is not necessarily determined by the well-known conjugate-matching rule and should be calculated for each photoconductive antenna structure and operational settings. When the semiconductor gap between photoconductor contact electrodes is uniformly illuminated by the optical pump, conjugate-matching the photoconductor impedance to the antenna impedance maximizes the radiated power from the photoconductive antenna. In contrast, when the semiconductor gap between photoconductor contact electrodes is partially illuminated by the optical pump near the anode, using photoconductors with resistance values much larger than the antenna radiation resistance maximizes the radiated power from the photoconductive antenna. Independent of the photoconductive antenna structure, the maximum radiated power from a photoconductive antenna is achieved when maximizing the antenna radiation resistance, while maintaining low reactive parasitic loading to the antenna. Finally, it should be mentioned that photoconductive antennas are reciprocal devices and, thus, the described impedance optimization principles are applicable to both photoconductive terahertz sources and photoconductive terahertz detectors.