1 Introduction

Rate of change is a concept that many students find difficult to understand. We know this because for more than 25 years introductory calculus students’ difficulties with understanding of rate of change have been reported (see for example Orton 1983 and Ubuz 2007). Many texts written for students studying introductory calculus (Stewart 2007) use the context of the movement of some body or thing as their entry point to differentiation. These texts refer to speed as a prototypical example of rate of change with the underlying assumption that this concept is both experientially real for students and that they are able to analyse this experience and abstract the key components. It is assumed that students understand speed in a way that allows them to transfer this understanding to the solution of new problems by identifying similarities with speed and variations from speed in other rate of change examples. While all students have everyday physical experience of speed not all students demonstrate good understanding of rate of change in other contexts.

Wilhelm and Confrey (2003), who also recognised this issue, found little published research that explored the concept of rate of change outside the motion context. Their interviews with Algebra 1 students, following teaching in multiple contexts using multiple technologies, suggested that such experience enabled students to transfer understandings of rate of change from the context of motion to new contexts. In the project described below, also conducted with pre-calculus students, the teaching focussed only a motion context but the tests included non-motion context problems. The simulation of real world speed examples automatically linked to the corresponding graphic, numeric and symbolic representations, was explored for its efficacy to provide an appropriate model on which to build further understanding of rate of change that may be transferred to other contexts; in particular contexts which do not involve motion.

Facilitating students’ transfer of knowledge and understanding is the key to the issue of solving problems in multiple contexts, however, this is not trivial. It has been known for a long time (Thorndike 1913) that transfer between two apparently similar tasks can be negligible. Marton (2006), in his comprehensive review of research on transfer, pointed out that while there are different views of transfer what “they all have in common is that transfer is about people being able to do similar things in different situations because of similarities between those situations” (p. 507). He went on then to emphasise the perceptual aspects of learning and asserted that ‘transfer’ involves more than identifying similarities; it also involves perceiving differences or variations. The study of transfer, he said, requires the systematic manipulation of the differences between the context of the learning problems and application. In this regard, Wagner’s (2006) detailed case study of one student suggested that transfer is revealed through a refinement of knowledge that accounts for, rather than overlooks, contextual variation.

The concept of transfer is at the heart of the Gravemeijer’s ‘emergent models’ where a ‘model of’ becomes ‘model for’. Gravemeijer (1999) suggested that providing activities and problems set in a context that is experientially real for students facilitates the development of a ‘model of’ a concept in a particular context which may then be generalised into a ‘model for’ thinking about the same concept in a similar but different context. The student is thus able to transfer key understanding gained in a familiar situation to a range of new contexts. The ‘model for’ is an intermediate stage between the foundational ‘model of’ and what Gravemeijer calls an ‘emergent model’. The term ‘emergent model’ is used to refer to formal, abstract mathematical models that may be used without referring to their connection to any particular real-world context.

This project investigated two issues related to transfer between students’ mathematical understanding of rate of change from their everyday experience of speed (motion context) and their understanding of rate of change in contexts that do not involve motion (non-motion context). First, it investigated the usefulness of concepts ‘model of’ and ‘model for’ from Gravemeijer’s (1999) emergent model theory in interpreting the way students may transfer the concept of rate of change from problems involving speed to other contexts not involving motion. Second, it also examined the suitability of the use of the simulation software, JavaMathWorlds (JMW), which encourages the controlled exploration of multiple representations of rate of change in contexts that involve motion, for producing the desired transfer outcome to a ‘model for’ rate of change in a non-motion context. In the sections below, the conceptual framework is described; details of the classroom experiment, data collection and results are provided; and the manner in which the results can be described by the ‘emergent models’ theory is discussed.

2 Context

As stated above students’ (especially tertiary students’) difficulty with understanding of rate of change has been internationally recognised over the past 25 years (see for example, Orton 1983; Ferrini-Mundy and Graham 1993; Rasmussen and King 2000; Carlson et al. 2002; Ubuz 2007). Early work pointed to some of the problems exhibited by students. For example, Orton (1983) found confusion between a number of important ideas related to rate of change, such as, confusion between the rate of change for a straight line and the rate of change for a curve. More recently, Ubuz (2001) reported a lack of understanding of derivative and stresses the importance of the relationship between slope and derivative and Carlson et al. (2000) reported variation in students’ abilities to “apply co-variational reasoning when analysing dynamic events” (p. 372). Such studies suggest that rate of change persists in being a difficult concept for students to master and that it is important to explore more effective ways of teaching this concept in secondary schools. In addition, Roschelle et al. (2000) claimed that the traditional curriculum, where the mathematics of change and variation are packed away in calculus, excludes most children from such important concepts as rate of change and accumulation, which are needed to make informed decisions in today’s world.

Students often first meet the concept of rate of change in early secondary school grades, where constant rate of change is studied in conjunction with ratio, proportion and percentage (VCAA 2007). This teaching is usually focuses on procedures for arithmetic calculations. For real world contexts, such as speed and density, the various transpositions of the formulae are typically provided by the textbook or the teacher and these rates are calculated by the student after substitution of values into the appropriate formula. Rate-related reasoning in such contexts is seldom included and the ideas of the invariance of constant rate over the entire domain or the co-variation of dependant and independent variable, as advocated by Thompson (1994), are not considered. Later, with little or no connection to these earlier ideas, polynomial and exponential functions involving variable rate are studied in the middle secondary years (VCAA 2007). Teaching related to these functions usually focuses on such features as shape of graph, including informal discussion of gradient; location and interpretation of critical points. Rarely is the word rate mentioned nor is rate-related reasoning encouraged. Based on this background it is not surprising that students beginning calculus do not have a well established ‘model of’ rate of change to support the transfer of this concept to new problems. The manner in which Gravemeijer’s ‘emergent models’ theory can be used to describe the transfer of concepts developed in one context to a variety of different contexts is briefly outlined below.

3 Conceptual Framework

The ‘emergent models’ theory, described by Gravemeijer (1999) attempts to explain the manner in which concepts, learnt in one context, may be transferred to new problems and new contexts. Emergent modelling describes the extension of students’ knowledge and understanding by the connection of new concepts to experientially real contexts. An ‘emergent model’ is the final result of a process in which informal models, used by students to solve problems in a particular context, are transformed into more general models used to solve problems in other different, but similar contexts. Eventually “the model becomes an entity in its own right and serves more as a means of mathematical reasoning than as a way to symbolize mathematical activity grounded in particular settings” (Gravemeijer 1999, p. 164). The ‘emergent model’ has its beginnings in the ‘model of’ a familiar context moving onto a ‘model for’ problem solving in different contexts, finally coming to serve abstract reasoning about the concept. “Something is symbolized (model of) and the symbolization is used to reason with (model for)” (Gravemeijer and Stephan 2002, p. 159). Through this process students develop the ability to solve problems in a variety of contexts, which have both similarities to and variations from the original context. Over time students transfer their informal solution procedures, specific to a given context [model of], to more formal mathematical reasoning [model for].

The ‘model of’ to ‘model for’ shift is a dynamic process. Ideally, students progress through to the final abstract stage where they are “no longer dependent on the support of ‘models for’ to achieve mathematical activity” (Gravemeijer and Stephan 2002, p. 160). However, a student may also return to a familiar context in order to make sense of a new context by noting similarities and differences or clarify an understanding of an abstract mathematical construct. When a ‘model of’ becomes a ‘model for’ the student has abstracted key features of the prototypical example so that they can identify similarities and variation in different examples. In a sense their new knowledge and understanding is ‘ready’ for transfer. For example, when a student is trying to calculate and understand the meaning of the gradient of a linear function they may return to thinking about the speed of a lift (JMW elevator) in order to make sense of the required mathematical operation. “The shift from ‘model of’ to ‘model for’ concurs with a shift in the way a student thinks about the model, from models that derive their meaning from the modelled context situation, to thinking about mathematical relations” (Gravemeijer and Doorman 1999, p. 119).

Wilhelm and Confrey (2003) and Simpson et al. (2006) studied students who explored computer simulations of real-world rate-of-change contexts, where students learned to link their ‘model of’ the real-world context to graphs of linear functions. Doorman (2002), who studied older students, proposed that an ‘emergent model’ can be seen in calculus where “graphs of discrete functions come to the fore as models of situations in which velocity and distance vary, while these graphs later develop into models for formal mathematical reasoning about calculus” (p. 109). In his research, Doorman (2002) explored the extent that computer-supported modelling of motion can contribute to the teaching and learning of the principles of calculus and kinematics.

Gravemeijer and Stephan (2002) also suggested that teachers may facilitate the shift from a ‘model of’ to a ‘model for’ and onto an ‘emergent model’ by designing a hypothetical learning trajectory which allows students to re-invent formal mathematics on the premise that formal mathematics develops through students’ activity. Doorman (2002) further described ‘expressive modelling’ as an approach where the representations used by the students fit the learning history of the students. The representations support students as they express ideas about the meanings of the representations and their relationship to the contexts being modelled. He asserted that only an expressive model can serve as a ‘model of’ in students’ development of ‘emergent models’ because “models emerge from the activity of the students” (p. 109) so problem contexts must be experientially real for the students.

4 Computer Simulation

Along with considering the ‘emergent model’ as a theoretical basis for describing the process of learning, this paper also examines the proposal that an exploratory computer environment, such as JMW (MERG 2004), could be used to assist students’ development of a ‘model of’ speed to be transformed into a general ‘model for’ rate of change in contexts other than motion thus forming the foundation for an ‘emergent model’ of an abstract notion of rate of change which is not connected to any particular context.

Research studying the use of various software, to provide similar exploratory experience for students, has been reported. For example: Wilhelm and Confrey (2003) used motion detectors and Interactive Banking software to develop students’ understanding of rate in the contexts of motion and banking. They found that “using multiple rate of change contexts allowed the learners the opportunity to see the ‘like’ in the contextually unlike situation, enabling them to project these concepts into novel situations” (p. 887). Similarly, Simpson et al. (2006) studied a group of motivated, high ability students exploring velocity and acceleration and related graphs through building and observing relationships in a computer games programming environment. These students succeeded in deepening their understanding as they worked in an environment that was ‘real’ in their imagination but yet able to be controlled. While these reports are both positive we chose to use JMW as it provides a clearly structured environment and was designed specifically for educational purposes.

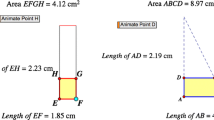
JMW is animated simulation software developed by the SimCalc project (MERG 2004), with mission of “research and development in technology and curriculum dedicated to democratizing access to the Mathematics of Change and Variation, including ideas underlying Calculus” (Kaput Center for Research and Innovation in Mathematics Education 2008). JMW software allows the user to manipulate a simulated environment.. Students may work with simulated elevators or walkers (see Fig. 1), which may be animated or dragged while the software provides automatic links to the corresponding numeric, graphic and symbolic representations of the mathematical functions that model this simulation. Likewise manipulations of the graph or the algebraic rule are reflected in the animation and the numeric table. When working with the simulation, students realise that the simulated elevators do not behave exactly as real world elevators however they none the less engage with the simulated, make believe world and make it meaningful. Like the younger students observed by Nemirovsky and Monk (2000), the students are able to use their imagination to make the ‘absent’ ‘present and ready at hand’. Computer software, such as JMW, may only be used to support progress on a hypothetical learning trajectory through guided exploration rather than the guided reinvention suggested by Doorman (2002).

Fig. 1
figure 1

Screen captures of JMW

Full size image

Roschelle et al. (2000) claimed that JMW software “provides a very rich set of tools in a flexible environment” in which students may explore the mathematics of chance and variation in the context of motion (p. 54). The power of this software is found in the interconnectivity of multiple representations associated with simulation. These connections encourage students to make mental associations between the graph, the table, the rule and the animation (Kaput 1998). It may be used to establish a ‘model of’ a context which is experientially real for students. The use of an experientially real context is important to facilitate a link to the students’ prior knowledge related to motion.

5 Methodology

This project is based on a classroom experiment consisting of pre-test; teaching intervention; post-test; and interviews. This section describes in detail each of these aspects of the classroom experiment, beginning with a description of the project pilot, which preceded the project reported in this paper.

5.1 Project Pilot

Ten, Grade 10 students from a different secondary school to that involved in the main project took part in the pilot to trial students’ worksheets; instructions to teachers; pre-test and post-test instruments. The group did not include any high ability mathematics students. The lessons, used in the pilot, were adapted from materials provided on the SimCalc website (MERG 2004). Students’ worksheets for the lessons and instructions to teachers on the delivery of the lessons were developed in consultation with teachers at the pilot school. Considerable attention was given to both the logical flow of the worksheets and the wording of statements and questions so that these would communicate clearly to the students. The researcher attended most of the lessons and then met again with the teachers. The constructive criticism of the teachers, together with the reflections of the researcher, guided the refinement of the materials with respect to wording; format; and design of activities.

The pilot tests consisted of three context questions: vertical motion; horizontal motion and non-motion. Each context question comprised of several items designed to determine a student’s location on a Hypothetical Learning Trajectory (HLT) (see Fig. 4). Although students were allowed up to 100 min of class time to complete the pre- and post-tests it became apparent that these tests were too long. Most students successfully answered test items based on the vertical motion context, on both tests, and so it was decided to omit this context from the main project tests. This shortened the test without the loss of interesting data.

The next section describes the main classroom experiment that is the focus of this paper.

5.2 Project Classroom Experiment

In Australian secondary schools, constant rate of change is typically included in a study of ratio and percent with an emphasis on arithmetic calculations (Bull et al. 2003) with no rate-related reasoning where the change in one variable is linked to a unit change in another variable. So the proposed teaching approach for this lesson sequence, focusing on rate of change, was quite different to that usually used at this school.

We were guided in the development of the classroom materials by the HLT and outlined in Fig. 2. This HLT is informed by the work of Stroup (2002), Confrey and Smith (1994), Thompson (1994) and Swedosh et al. (2007). Stroup (2002) considered young learners’ development of calculus-related ideas, including rate, well in advance of the stage when they would formally study this area of mathematics. His work emphasised the importance of students understanding of qualitative aspects of rate. Confrey and Smith (1994) and Thompson (1994) focussed on the importance of ratio-based quantification of rate while Swedosh et al. (2007), in their text book chapter on rate of change, appeared to follow a HLT for numerical aspects of rate similar to Confrey and Smith (1994) and Thompson (1994).

Fig. 2
figure 2

Hypothetical learning trajectory

Full size image

The teaching material used, in this project, consisted of four lessons that first introduced the software and then posed rate of change problems for students to solve. We decided to start with an experientially real context using the elevator simulation in JMW. Students initially used natural language to describe what they saw on the screen (DW) and the lessons encouraged them to elaborate on DW as they saw a number of similar but different examples. The lessons guided students to consider alternative, abstract representations of the motion through links between the simulation and its associated graph, table and, finally, the algebraic rule. We expected that working with these linked representations would strengthen their developing ‘model of’ speed and hence their ‘model for’ rate of change in other contexts and their emerging abstract ‘model’. The feature of JMW, where changes in one representation are automatically reflected in changes in the others, emphasises the connections between the representations assisting students’ development of NT, NG, NC, NS, GR, EN, and SR stages of the HLT described in Fig. 2. JMW allows the user to explore given scenarios until a workable solution is found thus encouraging the student to persevere until the problem is correctly solved. In this way, JMW supports students’ learning with positive reinforcement. Such repeated problem solving in closely related problems may establish a ‘model for’ similar thinking in different contexts.

The students’ worksheets consisted of rate of change problems set in the context of moving elevators. The first lesson introduced students to the JMW software, demonstrating the connection between the animation and the mathematical representations of the motion. Students were directed to explore various aspects of the problem context beginning with a hand-drawn graph connecting the movement of the elevator with the corresponding on-screen position graph. Next the values from the Numeric Display were recorded in a table in their workbooks as the animation is stepped through one time interval at a time. We chose to begin with a table, stressing the co-variation between the variables, as a table “involves the coordination of the variation in two or more columns as one moves down (or up) the table” thus building a correspondence between the variables (Confrey and Smith 1994, p. 137). The by-hand recording of the values from the Numeric Display was also intended to build a connection for students between what they saw on the screen and their previous work with pen and paper. The students also plotted the ordered pairs from this table as points on a Cartesian graph. Once this pen and paper link had been made to students previous work additional, more complex variations, of the animation of the elevator were provided to focus students’ attentions on both the similarities and differences evident in the extra animations. This emphasis on similarities and differences is consistent with Marton’s (2006) exposition on transfer. The extra animations provided variation in the motion of the elevator to assist in the development of a robust model for this context. The final question in this lesson introduced the connection between the Numeric Display and the Graph. The animations involved the elevator travelling at two different constant speeds, resulting in a graph consisting of two piece-wise linear sections. The JMW files were carefully prepared so that the ‘floors’ of the building serviced by the animated elevator coincided with the scale on the vertical axis of the graph.

The second lesson explored in more detail the connection between the graphic, symbolic and numeric representations of the movement of the elevator, posing such questions as:

In the Algebra Window, fill in the Initial Value, the Slope and the End Time. Repeat the editing as needed till the movement of the red (A) elevator and the blue (B) match exactly.

Write down a table of values by stepping through the animation and recording the values in the Numeric Display. Mark these values on the graph. Find the differences between successive floor values. How is the difference connected to the number of floors per seconds the elevator travels?

In this way, a connection was established between the coefficient of the x term, in the JMW Algebra Window, and the difference values in the JMW Table. Questions connecting this simulated environment to similar real world contexts were also included in this lesson. For example:

Anita and Becky are in glass elevators on the outside of a building. If Anita, went from the 12th floor and to the ground floor at 3 fl/sec, and Becky went up from the 2nd floor at 1 fl/sec stopping at the same time, would Anita and Becky be able to wave to each other as they go by, if so, where?

Solving this problem requires changing the coefficient of the x term, in the Algebra Window, in order to change the speed of the elevator.

Graphs with piece-wise linear segments were used, in the third lesson, to introduce the notion of average rate over sections of the elevator’s journey. In addition, the connection between position and velocity was made explicit by posing problems requiring consideration of both position and velocity, such as,

Add a green position segment so that the green (B) elevator reaches the 14th floor at the same time as the red (A) elevator. Write down the velocity of the red (A) elevator and the two velocities of the segments for the green (B) elevator. Prepare a position graph which causes the red (A) elevator to begin on the 4th floor, travels to the 10th floor, stopping at each floor for 2 seconds and returns to the ground floor at 2 floors per second.

In order to extend the students’ ‘models of’ the vertical motion of an elevator to another motion context the final lesson involved problem-solving in a different vertical motion context: a rocket ship. In addition, notions of variable and average rate were extended from piece-wise linear to a continuous quadratic.

The teachers in the project were provided with lesson plans with detailed instructions regarding the delivery of this series of lessons. These lesson plans specified where teacher-led whole-group explanations were expected, and suitable prompting questions to focus the students’ attention on similarities and differences in the different scenarios seen in the animations were provided. The lesson plans also identified when students should work, individually or in pairs, through sections of the worksheets with the teacher taking a roving role to assist where necessary. The researcher attended all classes and acted, both, as an observer and an advisor to the teachers. This helped to ensure that the lesson plans were implemented in the classroom as intended by the researchers.

5.3 Data Collection

Data was collected from 27 14–15 year old students from two classes, taught by different teachers, at a different school from the pilot school. The classes included mostly students of low to medium mathematics ability since the more mathematically able students were taught in a separate class. Since understanding rate of change has been reported (see above) as difficult for strong mathematics students it was expected that the students in this project would find it even more difficult. All 42 students from both classes were invited to participate, but only 27 returned positive consent forms. Data collected include: students’ pre- and post-test scripts, classroom observation by the researcher, and transcribed student interviews. Details are given below.

Pre- and post-tests were conducted under the time constraint of 150 min session each. The pre-test contained questions requiring rate-related reasoning, in, both, a motion context of students walking to school; and a non-motion context of the fee charged by a computer technician. Parallel questions were posed in the post-test but utilising the different contexts of a car trip and costing of a school magazine. Test items were designed to: probe the distinction between a qualitative and quantitative understanding of rate; and probe students’ understanding of rate of change in multiple representations. Figure 3 shows an item from the post-test where parts (i) and (ii) examine whether a student can describe in words a multi-segment position graph (DW). Part (iii) examines whether a student can use numbers to describe average rate of change for one variable per unit change in a second variable from a graph (NG).

Fig. 3
figure 3

Motion question from post-test

Full size image

Similarly, finding the value for the rate for each section of the graph shown in Fig. 7, determines whether a student can quantitatively interpret the non-motion graph (NG).

The dynamic nature of the shift from ‘model of’ through ‘model for’ to the ‘emergent model’ suggests that, for any group of students, at a given time, a variation will be seen in students’ progress. The items of the pre-test and post-test were chosen to assist the identification of individual students’ progress on this HLT and their developing ‘model of’ as a ‘model for’. For example, correct responses to items requiring a qualitative interpretation of speed and position graphs for horizontal motion would indicate the first steps on the journey showing that the use of the graphical ‘model of’ the vertical motion of a elevator could be used as a ‘model for’ the horizontal motion items. Similarly, a correct response to an item requiring a calculation of value for rate using information from a position graph indicates further progression along the journey, because such a correct response shows progress in a student’s understanding of rate from a general description of rate to working out a value for rate. In this project, it was hoped that students would learn to use of the ‘model of’ the elevator’s motion as a ‘model for’ solving problems in a non-motion context. Such a competence would be demonstrated by a correct response to items requiring a calculation of a value for rate (NG) from a graph of the non-motion context or drawing of a corresponding rate graph which matches a given total-cost graph.

A pair-wise analysis of scripts was performed with pre-test/post-test pairs examined for evidence of the development of a ‘model for’ rate of change. Tests were compared for evidence of improvement in rate-related reasoning demonstrated by progress on the HLT. Consideration was given to both correct responses and questions attempted as indicating signs of progress.

In addition to verifying the implementation of the lesson plans, observing the classes gave the researcher insights into the level of engagement and commitment of the students. It was noted that several students appeared completely disengaged and made little attempt to complete the activities; this was reflected in their tests.

Some students, considered by their teachers as representative of their classes, were interviewed after the post-test in order to discern whether students referred to their JMW experience when thinking about rate of change in a non-motion context. Some students were more helpful in verbalising their thinking than others; four are reported below. The interviews took the form of stimulated recall: each student was asked to think aloud as they considered their responses to the post-test non-motion question. They were also asked to comment on any connections they saw between the mathematical representations provided in the post-test non-motion question and the various mathematical representations of the motion of the JMW elevator.

6 Results and Discussion

6.1 Pre- and Post-tests

Based on the analysis of the students’ performance on the pre-test and the post-test, the paired data were used to track students’ progress on the HLT and their developing ‘emergent model’. For example, a comparison of one student’s (Sue’s—all names are pseudonyms) pre-test with her post-test is summarised in Fig. 4, where unshaded cells indicate no response; pale shading indicates an incorrect attempt; and dark shading indicates a correct response.

Fig. 4
figure 4

Summary of Sue’s pre/post-test performance

Full size image

Examination of the test scripts revealed that the greatest number of correct responses for both pre- and post-tests occurred in the questions requiring descriptive words for rate/speed graph (DW) and the calculation of a numeric rate/speed from a table (NT) and also the descriptive interpretation of distance graph (DW). The least number of correct responses for both pre- and post-tests was seen for items requiring the calculation of numeric rate from total cost or distance graph (NG) and also for drawing a non-motion rate graph (GR).

Eighteen out of the 27 students demonstrated progress on the HLT suggesting that their experience of speed in JMW assisted in building models for other problems and contexts. Fourteen students demonstrated progress on the HLT in the non-motion context. For these students, the ‘model of’ rate of change, developed through experiences of problem-solving in the motion context of the moving elevator, came to serve as a ‘model for’ rate of change in the non-motion context of costing the printing of a school magazine.

For example, Figs. 4 and 5 indicate Sue’s and Amy’s progress after their experience of working with JMW tasks (described above). Amy’s progress on the HLT for a motion context is indicated by the dark shading on six components and light shading on a seventh (Fig. 5).

Fig. 5
figure 5

Summary of Amy’s pre/post-test performance

Full size image

For non-motion on the post-test, light shading for four components and dark shading for two, indicate that her stronger ‘model of’ speed is reflected in her ‘model for’ rate in the non-motion context. Similarly, Sue’s progress, as mapped on Fig. 4 shows, both a strengthened ‘model of’ speed (changed shading in five components) and also strengthened ‘model for’ rate of change in the non-motion context (changed shading in three components).

Even four students, who only showed progress on the HLT for motion, demonstrated that their ‘model of’ speed developed in a vertical motion context could be used as a ‘model for’ speed in a context involving horizontal motion. For example, the comparison in Fig. 6 shows that Donavan demonstrated progress in developing a ‘model of’ motion, but had not progressed to a ‘model for’ the non-motion context.

Fig. 6
figure 6

Summary of Donavan’s pre/post-test performance

Full size image

It was expected that there would be a range in progress towards an ‘emergent model’ for rate of change. Some students may require more than four lessons to develop a suitable ‘model of’ speed as a rate whilst others may need to overcome existing incorrect or incomplete understandings of speed.

Analyses of test scripts provided information about students’ progress but a limited view of the students’ thinking. A more in-depth view can be seen in the following detailed analysis of the transcripts of the student interviews.

6.2 Interviews

Interviews focussed on the non-motion scenario in the post-test seen in Fig. 7. Students, who had not completed the questions relating to the non-motion scenario of costing the printing of a school magazine, were also asked to consider the scenario shown in Fig. 8.

Fig. 7
figure 7

Post-test question

Full size image
Fig. 8
figure 8

Scenario for post-test interview

Full size image

The interviews were intended to gauge the extent to which the JMW simulation of the moving elevator and its associated numeric, graphic and symbolic representations supported students thinking about rate of change in a non-motion context.

6.2.1 Case Study 1: Joe

Joe was a low ability student who did not answer correctly any questions on the pre-test (Fig. 9), but demonstrated improved understanding of speed on the post-test. For example, Joe was able to correctly answer the question, shown in Fig. 10, from the post-test. He did not answer any of the non-motion rate questions involving the table in either the pre-test or the post-test but he did demonstrate improvement on the questions relating to the horizontal motion context.

Fig. 9
figure 9

Summary of Joe’s pre/post-test performance

Full size image
Fig. 10
figure 10

Post test speed question

Full size image

This is indicated by the dark shading for DW, GR and EN. Joe’s responses in the post-test indicate that the symbolic and graphic representations had come to act as a ‘model of’ speed in the context of the moving elevator which he was able to use as a ‘model for’ this horizontal motion context. However, Joe’s post-test responses did not indicate that the ‘model for’ speed was not sufficiently robust to serve as a ‘model for’ a non-motion context.

During his interview Joe’s responses indicated that he had drawn a clear parallel between the graph for the non-motion scenario and the motion scenario of the simulated elevator he explored using JMW.

Researcher: If you saw that graph [Figure 7] in MathWorlds what would that tell us? Can you describe how the elevator is moving?

Joe: It would go fast then slower and then go really slow.

Later in the interview, he was able to correctly use descriptive words to interpret the position graph of this context.

6.2.2 Case Study 2: Stewart

The second interview extract is from a medium ability student, Stewart, whose post-test script, with all responses correct (Fig. 11), clearly shows a robust understanding of rate in both the horizontal motion context of a car trip and the non-motion scenario of the costing for a school magazine. He demonstrated the use of his ‘model of’ the vertical motion of the elevator as a ‘model for’ rate-related reasoning in the non-motion scenario of the post-test.

Fig. 11
figure 11

Summary of Stewart’s pre/post-test performance

Full size image

In his interview Stewart, showed his ability to interpret the symbolic and graphical representations of the non-motion scenario. It also indicates that Stewart is thinking differently about the graphic and symbolic representations. When sketching the graph, he started with the y-intercept and used rate-related reasoning to work out where the graph went from there. For the symbolic representation, he began with the rate and added the starting value onto the end of the expression.

Researcher: How did you work out the graph?

Stewart: Well I started there [pointing to 60 on the vertical axis], then $3 for each magazine.

Researcher: How did you work out the algebraic expression?

Stewart: Well since the magazines cost $3 each you times 3 by n [pause] which is how many magazines plus 60 because that’s how much you start with

He was also one of the few students to correctly calculate the numeric rate from total cost graph and draw the non-motion rate graph. The following extract demonstrates the depth of his understanding of the connection between the rate graph and the total-cost graph.

Researcher: Explain how the graphs in part (b)[rate graph] and part (c)[total cost graph] are related?

Stewart: This part is showing total cost [$6] and this is how much they cost per magazine [$2]

Researcher: So is there any relationship between 6 and this bit of the graph [pointing to the first segment of the total-cost graph]?

Stewart: That’s how much it costs for each magazine [pointing to the rate graph] and that’s the total [pointing to the total-cost graph] so they are related.

Stewart showed his understanding of the connection between the non-motion scenario of the post-test and JMW in the following extract. Not only could he interpret the graphical representations in terms of JMW in the same way as the other interviewees by the correct interpretation of the total-cost graph, he could also discern parallels when considering symbolic representations and between the rate graph and the velocity graph.

Researcher: If you saw this algebraic expression in the Algebra window of Mathworlds what would it mean?

Stewart: That the elevator goes up 3 floors per minute and starts at 60

6.2.3 Case Study 3: Lee

In the post-test, Lee demonstrated considerable improved performance on the motion questions, but had not answered the questions relating to the non-motion scenario of costing the printing of a school magazine (Fig. 12). It is possible that this scenario was unclear for this student, so it may have been this lack of understanding, which prevented his response to these questions, rather than his inability to answer the rate questions associated with it.

Fig. 12
figure 12

Summary of Lee’s pre/post-test performance

Full size image

In his interview, Lee gave the following the reason for not attempting the non-motion questions in the post-test:

Lee: You explained what the problem was because sometimes in the actual thing you don’t get half of the words …You just like put it in better words you said what the actual problem was and what I had to do so it was a lot easier to work out.

Since Lee had not attempted the post-test question the interview was based on the alternative non-motion scenario of the vacuum cleaner (Fig. 8) and he was shown the multi-segment total-cost graph. In the following exchange, Lee demonstrated the beginnings of ‘model for’ rate in the non-motion question. He incorrectly assumed that the first section would be the same as the initial cost given in part (a) of the question, and his reasoning follows on from that assumption.

Researcher: What does this graph show?

Lee: The price has decreased

Researcher: So how would you work out what the price per bag was for these 3 different prices?

Lee: Well it starts off at $3

Researcher: How did you work out the $3

Lee: Because that’s what it had there [pointing to part (a) of the question where the price per bag was $3]. There [pointing to the second section of the graph] I think it’s gone down

Researcher: Are you certain that the price has gone down a bit?

Lee: Probably like about 2½ or something like that its not too much less though. There [pointing to the third section of the graph] it’s about at 12, it’s gone up 5 I think so that’s like $1.20 or something.

Lee demonstrated the use of his ‘model of’ the vertical motion of the elevator as a ‘model for’ the horizontal motion scenario with correct descriptive words (DW) used to interpret the position and speed graphs and some facility in finding a numeric value for speed from the graph (GR).

In the interview, he was able to describe the connection between the total-cost graph of the non-motion context and the position graph seen in JMW.

Researcher: Now if you saw this graph in MathWorlds, how was the elevator moving?

Lee: It’s going up

Researcher: what can you tell me about the speed of the elevator?

Lee: It changes

Researcher: can you describe how it changes?

Lee: It slows down and stops

Researcher: In this first section, what can you tell me about the speed?

Lee: It’s a lot faster than the others the slower then slows down even more

It appears that the context of the non-motion scenario of the post-test was not well understood by Lee, resulting in the absence of responses to this question. However, his interview transcript suggests that he was able to use his ‘model of’ the vertical motion of the elevator as a ‘model for’ his thinking in the non-motion context, of the vacuum cleaner, presented in the interview. He demonstrated the use of descriptive words to interpret rates in the multi-segment graph, but experienced difficulties when attempting to quantify them.

6.2.4 Case Study 4: Jenny

Jenny demonstrated some improvement on the questions in the post-test relating to the horizontal motion context and similar improvement on the questions relating to the non-motion context (Fig. 13). This is indicated by the dark shading for NT, NG and SR for motion with dark shading NS and light shading for SR for non-motion.

Fig. 13
figure 13

Summary of Jenny’s pre/post-test performance

Full size image

The following extract from Jenny’s interview demonstrates her progress on the HLT in the non-motion context, but her lack of understanding of the other information in the question, that is, the value y-intercept and its meaning.

Researcher: I’ll get you to talk me through how you went about drawing this graph.

Jenny: We’ve got 60 for preparation fee and so you just add 60 and $3 for each magazine and 3 times 100 is 300, that’s 360.

Researcher: I see you plotted that last point [pointing to the graph] and the origin. Why did you do that?

Jenny: I don’t know

Later in the interview, whilst considering the graph shown in Fig. 7, Jenny needed considerable prompting to extract a numeric description of rate for the first section of the piece-wise linear graph (GR). She seemed to lack confidence in her correct responses.

Researcher: How would you work out how much it would cost for each magazine, for the first part of the graph?

Jenny: 120 divided by… I don’t know

Researcher: That sounds good to me keep going 120 divided by?

Jenny: 20

Researcher: 120 divided by 20?

Jenny: 6

Jenny was able to interpret the multi-segment total-cost graph in terms of the speed of the elevator in JMW, although, once again, she required much encouragement.

Researcher: if you saw this graph in MathWorlds, So first time period can you describe the motion? Is it fast, slow…?

Jenny: Fairly fast

Researcher: and what about in the second interval

Jenny: slower

Researcher: and…?

Jenny: slower

These students provide examples of students’ awareness of the similarities of the non-motion scenario with JMW. Students were able to draw parallels between the total-cost graph of the non-motion scenario and the position graph of the elevators. However, there was considerable variation in the interviewees’ progress on the HLT and development of a ‘model for’ problem solving involving rate in non-motion contexts from a ‘model of’ the vertical motion of the elevator.

7 Conclusions

This paper described a project where students studied rate of change in the context of speed within the exploratory environment of JMW. In this project, JMW was explored for its value in assisting the development a ‘model of’ speed where it is used to solve problems about speed, position and time related to a moving elevator. The teaching material, based on JMW, was designed to foster a deeper understanding of speed as a rate of change. The degree of robustness of students’ ‘model of’ speed varied from student to student, but most students showed some progress on the HLT for speed in a vertical context and a ‘model for’ speed in a horizontal context. This result supports the claims of earlier researchers for example, Kaput (1998) and Wilhelm and Confrey (2003) relating to the value of the use of computer simulations to allow students to investigate the mathematical aspects of speed in an environment that they can control.

In addition, the project aimed to examine whether Gravemeijer’s ‘emergent models’ framework could be used to interpret changes in student understanding as a result of a vertical motion focussed JMW instructional sequence. The results of this study showed that after this experience more than half of these low to medium ability students showed progress on the HLT in a non-motion context. Mapping their change on the HLT suggested that students’ ‘models of’ rate of change developing in a motion context had become ‘models for’ rate of change in a non-motion context. These summary maps showed that students did not need to complete the HLT in a motion context in order to transfer their understanding to a non-motion context. It seems that as a student’s ‘model of’ was strengthened through their experience of exploring the computer simulation of a familiar context it became a stronger ‘model for’.

The results of this study, added to others reported in the literature, support the use of computer simulations for teaching rate of change and point to the value of guiding students through a careful exploration of the mathematical aspects of speed rather than assuming that this understanding may be taken as given just because speed is part of our everyday experience.